1. No category

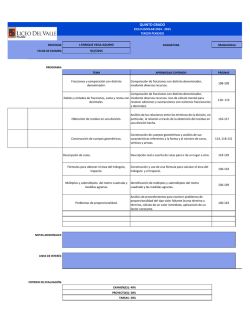
AMIGOS DE SANTIAGO VILA
APRENDEREMOS A CONOCER LAS
FRACCIONES Y A REALIZAR
OPERACIONES CON ELLAS
SITUACION DE APRENDIZAJE
CONCEPTO DE FRACCION
(términos y lectura)
EJERCICIOS DIAGNOSTICOS
UBICACIÓN EN LA RECTA
OPERACIONES CON FRACCIONES
SUMA Y RESTA DE FRACCIONES HOMOGENEAS
SUMA Y RESTA DE FRACCIONES HETEROGENEAS
MULTIPLICACION DE FRACCIONES
REPRESENTACION DE FRACCIONES
CLASES DE FRACCIONES
FRACCIONES HOMOGENEAS
FRACCIONES HETEROGENEAS
DIVISION DE FRACCIONES
PROBLEMAS CON OPERACIONES DE
FRACCIONES
COMPRUEBA LO QUE APRENDISTE
A diario estamos
relacionándonos con temas
que nos muestran
fracciones. VEAMOS (haz clic en el
dibujo) .
VOLVER
Los números fraccionarios hacen referencia a que hemos
dividido un trozo en partes iguales y después hemos cogido
varias de esas partes iguales. Tienen dos partes:
NUMERADOR. partes que tomo de la unidad.
DENOMINADOR: Partes en que divido la unidad.
VOLVER
REFUERZA
VOLVER
BIEN QUERIDO AMIGO, AHORA
VAMOS A ENTERARNOS DE TODO
LO QUE SABES DE FRACCIONES. NO
TE PREOCUPES SI NO PUEDES
CONTESTAR, SOLO RESPONDE LO
QUE SEPAS. Mas adelante
reforzaremos todos los temas.
Dale clic a la siguiente imagen:
VOLVER
¿COMO UBICAMOS FRACCIONES EN LA RECTA NUMÈRICA?
Sólo habrá que dividir cada unidad de la recta en las partes que indica el
denominador de la fracción; mientras, el numerador nos señala cuantas partes
hay que tomar.
Por ejemplo, si ubicamos 2/3 en la recta numérica, dividimos en 3 partes iguales
la unidad y tomas los dos primeros trozos desde el cero.
Complementa
VOLVER
MUY BIEN!!!!
Ahora veamos: LAS FRACCIONES también se pueden representar gráficamente
tomando una figura, dividiéndola en tantas partes como indica el numerador y
coloreando las que indique el numerador. Por ejemplo:
3
5
Otro ejemplo:
7
2
Como divido en 2 la
unidad y debo tomar
7. vemos que no
alcanza, entonces
debemos dibujar
cuantas unidades
sea necesario, hasta
que alcance a tomar
lo que dice el
numerador
VOLVER
CLASES DE FRACCIONES
Fracción Propia: Son
aquellas que tienen el
denominador mayor que el
numerador. Ej.:
5/8, 4/9,2/5.
Fracción Impropia: Son
Aquellas que tienen el
denominador menor que el
numerador. Ej.: 6/3,
7/5,8/6.
VOLVER
VOLVER
VOLVER
SUMA RESTA DE FRACCIONES HOMOGENEAS
Para sumar o restar fracciones homogéneas se deja
el mismo denominador y seguidamente se realiza
la operación indicada. Finalmente se simplifica la
fracción a la mínima expresión.
Da clic en la imagen.
VOLVER
Ejemplos:
1/4+ 5/4 +8/4 + 6/4 = (1+5+8+6)/4 = 20/4
1/5 + 17/5 + 9/5 + 4/5 = (1 + 17 + 9 +
4)/5 = 31/5 = 6+ 1/5 número mixto
15/8 - 5/8 = (15 – 5)
10/8 = 10/8 = 1 + 2/8
39/12 - 21/12 = 18/12
simplificando = 3/2 = 18/12
VOLVER
SUMA Y RESTA DE
FRACCIONES HETEROGENEAS
Para adicionar o restar
Fracciones con
Diferente denominador. se
buscan fracciones equivalentes
a las fracciones dadas , con
igual denominador, es decir se
convierten en fracciones
homogéneas y luego se suman
o se restan. Continúa.
VOLVER
Ejemplo:
Adición
2/4 + 4/10 = 2 x5/4 x5 + 4 x2 /10 x 2 =
10/20 + 8/20 = 18/20 = 9/10
Sustracción
21/5 - 8/3 = 21 x 3 /5 x3 - 8 x 5 /3 x 5 = 63/15 –
40/15 = 23/15
Otra manera de adicionar fracciones heterogéneas
es buscando el mínimo común múltiplo de sus
denominadores, para convertirlas en fracciones
equivalentes.
Da clic en la imagen.
VOLVER
MULTIPLICACION DE FRACCIONES
Para multiplicar dos o más fracciones,
se multiplican "en línea".
Esto es, el numerador por el numerador
y el denominador por el denominador.
Ejemplo:
3
---- x
2
7
---4
3x7
=
------2x4
21
=
--8
CLIC EN LA IMGEN
VOLVER
DIVISION DE FRACCIONES
Es muy sencillo. Para dividir dos o más
fracciones, se multiplican "en cruz". Esto es,
el numerador de la primera fracción por el
denominador de la segunda fracción (ya
tenemos el numerador) y el denominador
de la primera fracción por el numerador de
la segunda fracción (este es el
denominador).
Da clic en la imagen
VOLVER
PROBLEMAS CON FRACCIONES
1. En una competición se pueden
obtener un total 75 puntos. Juan
ha conseguido 3/5 del total.
¿Cuántos puntos le han faltado por
lograr para hacer una competición
perfecta?
RESPUESTA:
2. Andrés se comió 1/5 de los
bombones de una caja y Ana 1/2 de la
misma. ¿Qué fracción de bombones se
comieron entre las dos?. Si quedaron
12 bombones, ¿cuántos bombones
tenía la caja?
VOLVER
OK. AHORA VAMOS A COMRPOBAR
CUANTO APRENDIMOS,DESPUES DE
ESTE INTERESANTE RECORRIDO POR
LAS FRACCIONES!!!
DA CLIC EN LA FRASE
COMPRUEBA LO QUE APRENDISTE
VOLVER
BIEN AMIGOS ESPERO TENGAN MAS CLARO
TODO LO REFERENTE A LAS FRACCIONES.
DOCENTES
LUZ MARINA TAPIERO
YOVANA MARTINEZ MONROY
ESTUDIANTES: MAESTRIA EN INFORMATICA EDUCATIVA
INSTITUCION EDUCATIVA SANTIAGO VILA
GRADO SEXTO
IBAGUE
2015
VOLVER