1. No category

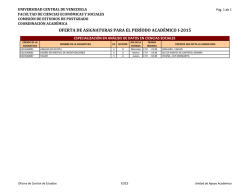
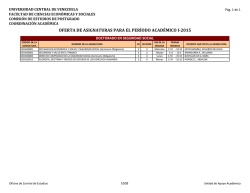
INSTITUTO POLITECNICO NACIONAL
SECRETARIA ACADÉMICA
DIRECCIÓN DE ESTUDIOS PROFESIONALES
ESCUELA: E . S . I . M . E . Culhuacan
CARRERA: INGENIERO DE COMPUTACIÓN
ESPECIALIDAD:
COORDINACIÓN:MATEMATICAS.
DEPARTAMENTO: Departamento de electrónica.
ASIGNATURA: CALCULO VECTORIAL.
CLAVE:
SEMESTRE: SEGUNDO.
CRÉDITOS:
VIGENTE: SEPT. 91
TIPO DE ASIGNATURA: BÁSICA..
Abierta
MODALIDAD: Escolarizado
X
FUNDAMENTACION DE LA ASIGNATURA
Considerando que la matemática valida los conocimientos de las ciencias mediante la cuantificacion en todo el proceso de investigación teórica y experimental y siendo el
calculo vectorial, una herramienta de la matemática precisa para hacerlo en base a ello, se hace la propuesta del programa del curso respectivo en el que aparecen los contenidos
temáticos ordenados de manera lógica y secuencial de tal forma que el alumno logre una comprensión clara de los conceptos y un dominio integral de los procedimientos básicos
del calculo, los que podrá aplicar sin ningún obstáculo, consecuentemente en las asignaturas de ecuaciones diferenciales, métodos numéricos y análisis de señales y
colateralmente en las asignaturas de álgebra lineal y física, todas ellas pertenecientes al plan de estudio de la carrera de Ingeniería en Computación.
En el perfil del programa se considera que el alumno tiene como antecedente conocimientos del calculo diferencial e integral y de álgebra superior, adquiridos en el primer grado
semestral de la citada carrera.
Para lograr el aprendizaje, el programa se ha organizado en cinco unidades: Vectores, Funciones vectoriales de un escalar, funciones reales de varias variables (Campos
escalares), funciones vectoriales de varias variables ( campos vectoriales) e integrales múltiples; conteniendo cada una de ellas los temas mas apropiados del curso.
OBJETIVO DE LA ASIGNATURA
Al finalizar el curso, el alumno:
-Aplicará los conceptos del calculo vectorial de manera eficiente en la resolución de problemas en los distintos campos de las ciencias, de la investigación y de la ingeniería,
describiendo cuantitativamente en términos de cantidades físicas los fenómenos físicos y geométricos.
TIEMPOS TOTALES ASIGNADOS
HAS/SEMESTRE: 90 HRS/SEMANA: 6
HRS/TEORÍA: 90 HRS/PRACTICA:
PROGRAMA ELABORADO O ACTUALIZADO POR:
REVISADO POR:DEPTO. DE INGENIERÍA MECÁNICA.
APROBADO POR: PDTE. DEL H.C.T.C.C. DIRECTOR DE LA ESCUELA
ESIME U.C.
AUTORIZADO POR:
ASIGNATURA: CALCULO VECTORIAL.
CLAVE ASIGNATURA:__ _________ HOJA:_ 2 _ DE ___ 11 _____
FUNDAMENTACIÓN
El calculo vectorial es presentado al alumno como una parte esencial de la matemática, necesaria en los distintos campos de la ciencias, de la investigación y de la ingeniería, no
solo proporcionando métodos concisos y precisos para analizar matemáticamente los fenómenos físicos y geométricos, sino también ayudando al desarrollo de la comprensión
intuitiva de las ideas relacionadas al medio que le rodea, para entender muchos de los principios fundamentales de la geometría, mecánica clásica, electromagnetismo y mecánica
de fluidos.
En vista de que se tiene prevista una evaluación continua de programa se harán las correcciones necesarias para los cambios significativos a que haya lugar en el proceso
enseñanza-aprendizaje, al termino del curso.
El curso de calculo vectorial es teórico que se desarrollara mediante exposición oral y escrita por parte del profesor, siendo el un conductor en todo el proceso, induciendo en el
alumno conocimientos de contenido temático, y habilidades para resolver problemas propios de la asignatura y de su futuro campo profesional. El curso será inductivodeductivo, aplicándose en el proceso el método científico.
La evaluación será sumaria, considerándose tres exámenes departamentales y aquellos procedimientos que el profesor considere apropiados durante el curso, ajustándose a los
lineamientos institucionales para el caso.
ASIGNATURA: CALCULO VECTORIAL.
No. UNIDAD: 1.
CLAVE ASIGNATURA:____
_______ HOJA:____3 _____ DE __ 11____
NOMBRE: VECTORES.
OBJETIVOS PARTICULARES DE LA UNIDAD
Al termino de la unidad el alumno:
-Definirá el concepto de espacio vectorial real n-dimensional y manejara sus propiedades.
-Representara geométricamente los vectores en R, R2, y R3.
-Definirá las operaciones entre vectores (producto escalar y producto vectorial).
-Aplicará las operaciones entre vectores (producto escalar y producto vectorial).
-Establecerá las propiedades del producto escalar y vectorial.
-Deducirá las situaciones de la recta y del plano en el espacio.
No.
TEMA
1.1
1.2
1.3
1.4
1.5
1.5.1
1.5.2
1.5.3
HORAS
TEMAS
Concepto de espacio R1, R2, R3...,Rn.
Concepto de vector libre y vector de posición, y
sus caracteristicas Vectores unitarios.
Suma y resta de vectores. Ley del triángulo, del
paralelogramo y sus propiedades.
Multiplicación de un escalar por un vector.
Vectores paralelos.
Operaciones definidas para los vectores.
Producto escalar y sus propiedades.
Producto vectorial y sus propiedades.
Triple producto escalar y sus propiedades.
INSTRUMENTACIÓN DIDÁCTICA
-Exposición de temas por parte del profesor.
-Investigación de temas por parte del alumno.
-Discusión de temas investigados.
-Ejecución de ejercicios en clase.
-Exposición de temas mediante acetatos.
-Utilización de rotafolios.
-Realización de programas de trabajo en computadora.
-Utilización de técnicas grupales.
T.
16:00
P.
CLAVE
E.C.
BIBLIOGRÁFICA
8:00
1B, 2B,
3B, 4B,
9B.
ASIGNATURA: CALCULO VECTORIAL.
No. UNIDAD: 1.
CLAVE ASIGNATURA:_
___________ HOJA:__ 4 ______ DE ____ 11___
NOMBRE: VECTORES.
No.
TEMA
1.5.4
1.6
1.6.1
1.7
1.7.1
HORAS
TEMAS
Triple producto vectorial y sus propiedades.
Ecuación de la recta en su forma parametrica y
cartesiana.
Distancia de un punto a una recta.
Ecuaciones del plano y del hiperplano.
Distancia de un punto a un plano.
INSTRUMENTACIÓN DIDÁCTICA
T.
P.
CLAVE
E.C.
BIBLIOGRÁFICA
ASIGNATURA: CALCULO VECTORIAL.
No. UNIDAD: II
CLAVE ASIGNATURA:____
_______ HOJA:____5 _____ DE __ 11____
NOMBRE: FUNCIONES VECTORIALES DE UN ESCALAR.
OBJETIVOS PARTICULARES DE LA UNIDAD
Al termino de la unidad, el alumno:
-Introducirá el concepto de función vectorial de un escalar y establecerá sus operaciones.
-Determinará las ecuaciones parametricas para diferentes tipos de curvas.
-Definirá el concepto de limite, continuidad, y describirá sus propiedades.
-Definirá la deriva y sus propiedades.
-Manejará la deriva y sus propiedades.
-Dominara la integral indefinida, la integral definida y sus propiedades.
-Aplicará los conocimientos en la solución de problemas de física, ingeniería, etc.
No.
TEMA
2.1
2.2
2.3
2.4
2.5
2.6
2.7
HORAS
TEMAS
Concepto de función vectorial de un escalar.
Operaciones de funciones vectoriales de un
escalar.
Parametrizacion de una curva.
Limites y continuidad de funciones vectoriales de
un escalar.
Derivadas de funciones vectoriales de un escalar.
Integración de funciones vectoriales de un escalar.
Longitudes de arco.
INSTRUMENTACIÓN DIDÁCTICA
-Exposición de temas por parte del profesor.
-Investigación de temas por parte del alumno.
-Discusión de temas investigados.
-Ejecución de ejercicios en clase.
-Exposición de tema mediante acetatos.
-Utilización de rotafolios.
-Realización de programas de trabajo en computadora.
-Utilización de técnicas grupales.
T.
12:00
P.
CLAVE
E.C.
BIBLIOGRÁFICA
6:00
1B, 2B,
3B, 4B
9B.
ASIGNATURA: CALCULO VECTORIAL.
No. UNIDAD: III
CLAVE ASIGNATURA:_ __________ HOJA:__ 6
DE ___11_
NOMBRE:FUNCIONES REALES DE VARIAS VARIABLES. CAMPOS ESCALARES
OBJETIVOS PARTICULARES DE LA UNIDAD
Al termino de la unidad, el alumno:
-Introducirá el concepto de función real de varias variables, y establecerá las operaciones.
-Definirá los conceptos de limites y continuidad, y describirá sus propiedades.
-Definirá las derivadas direccionales y las derivadas parciales.
-Aplicará las derivadas direccionales y las derivadas parciales.
-Determinara la ecuación del plano tangente a una superficie.
-Definirá el concepto de gradiente.
-Dominará las derivadas parciales de orden superior.
-Calculara los extremos de una función real de varias variables (multiplicadores de Lagrange).
No.
TEMA
HORAS
TEMAS
Conceptos de función real de varias variables.
Operaciones con funciones reales de varias
variables.
Limites de funciones reales de varias variables.
Concepto de derivada direccional.
Derivada parcial.
Concepto de plano tangente.
Gradiente. Operador Nabla.
Máximos, mínimos y puntos de ensilladura.
Multiplicadores de Lagrange.
INSTRUMENTACIÓN DIDÁCTICA
-Exposición de temas por parte del profesor.
-Investigación de temas por parte del alumno.
-Discusión de temas investigados.
-Ejecución de ejercicios en clase.
-Exposición de temas mediante acetatos.
-Utilización de rotafolios.
-Realización de programas de trabajo en computadora.
utilización de técnicas grupales.
-
T.
18:00
P.
CLAVE
E.C.
9.00
BIBLIOGRÁFICA
1B, 2B,
3B, 4B,
9B.
ASIGNATURA: CALCULO VECTORIAL.
No. UNIDAD: IV
CLAVE ASIGNATURA:_ __________ HOJA:__7______ DE __11__1
NOMBRE:FUNCIONES VECTORIALES DE VARIAS VARIABLES (CAMPOS VECTORIALES).
OBJETIVOS PARTICULARES DE LA UNIDAD
Al finalizar la unidad, el alumno:
-Introducirá el concepto de función vectorial de varias variables y discutirá sus operaciones.
-Definirá los conceptos de limite y continuidad, estableciendo sus propiedades.
-Definirá la deriva (matriz Jacobiana) y obtendrá las derivadas de orden superior.
-Definirá los conceptos de divergencia, rotacional y función potencial de un vector.
-Manejara los conceptos de divergencia, rotacional y función potencial de un vector.
-Definirá la Integral de línea.
-Aplicará la Integral de línea.
-Aplicará los conocimientos en la solución de problemas de física, ingeniería, etc.
No.
HORAS
TEMA
TEMAS
4.1
Concepto de función vectorial de varias variables.
Operaciones de las funciones vectoriales de varias
variables.
Limites de funciones vectoriales de varias
variables.
Concepto de derivada (Matriz Jacobina).
Divergencia rotacional.
Coordenadas curvilíneas.
Concepto de potencial.
Integral de línea.
Aplicaciones.
4.2
4.3
4.4
4.5
4.6
4.7
4.8
4.9
INSTRUMENTACIÓN DIDÁCTICA
-Exposición de temas por parte del profesor.
-Investigación de temas por parte del alumno.
-Discusión de temas investigados.
-Ejecución de ejercicios en clase.
-Exposición de temas mediante acetatos.
-Utilización de rotafolios.
-Realización de programas de trabajo en computadora.
-Utilización de técnicas grupales.
T.
18:00
P.
CLAVE
E.C.
BIBLIOGRÁFICA
9:00
1B, 2B,
3B, 4B,
9B.
ASIGNATURA: CALCULO VECTORIAL.
No. UNIDAD: V
CLAVE ASIGNATURA:_
__________ HOJA:__ __8_____ DE ____11 ___
NOMBRE:INTEGRALES MÚLTIPLES.
OBJETIVOS PARTICULARES DE LA UNIDAD
Al término de la unidad el alumno:
-Definirá el concepto de integral múltiple.
-Calculara integrales iteradas.
-Aplicará las integrales dobles para calcular áreas, centro de masa y momentos de inercia.
-Aplicará las integrales triples para calcular volúmenes, centro de masa y momentos de inercia.
-Aplicará el teorema de cambio de variable y el teorema de Green para calcular integrales múltiples.
-Discutirá dos generalizaciones del teorema de Green: el teorema de Stokes y el teorema de la divergencia.
-Aplicará los conocimiento en la solución de problemas de física, ingeniería, etc.
No.
TEMA
5.1
5.2
5.3
5.4
5.5
5.6
5.7
HORAS
TEMAS
Concepto de integral múltiple.
Integrales dobles y sus aplicaciones.
Integrales triples y sus aplicaciones.
Teorema de cambio variable.
Teorema de Green.
Teorema de la divergencia.
Teorema de Stokes.
INSTRUMENTACIÓN DIDÁCTICA
-Exposición de temas por parte del profesor.
-Investigación de temas por parte del alumno.
-Discusión de temas investigados.
-Ejecución de ejercicios en clase.
-Exposición de temas mediante acetatos.
-Utilización de rotafolios.
-Realización de programas de trabajo en computadora.
-Utilización de técnicas grupales.
T.
26:00
P.
CLAVE
E.C.
13:00
BIBLIOGRÁFICA
1B, 2B,
3B, 4B,
9B.
ASIGNATURA: CALCULO VECTORIAL.
CLAVE ASIGNATURA:_
PERIODO
UNIDADES
TEMÁTICAS
1
1 y II
II
III y IV
III
V,VI y VII.
PROCEDIMIENTOS DE EVALUACIÓN
La evaluación se efectuara en la forma siguiente:
Diagnostica, formativa, seguimiento y sumativa.
Aspectos a evaluar:
-Participación en las actividades en clase.
-Tareas extraclase.
-Pruebas objetivas.
El que se llevara a cabo mediante la:
-Aplicación de tres exámenes parciales o departamentales durante el semestre. La calificación final será el
promedio de las evaluaciones anteriores, siempre y cuando el alumno cumpla con lo estipulado en la
reglamentación institucional.
CLAVE
B
C
1
X
Serge Lang.
Calculo II
Editorial sistemas técnicas de edición, S.A. de C.V.
2
X
Haaser, Lasalle, Sullivan.
Análisis matemático.
Curso de introducción, Volumen II.
Editorial trillas.
3
-X
Protter/Morrey
Análisis matemático (Modern Mathematical Análisis, Bilingüe).
Editorial sistemas técnicos de edición, S.A. de C.V.
ASIGNATURA: CALCULO VECTORIAL.
___________ HOJA:__ 9 ______ DE ____ 11___
BIBLIOGRAFÍA
CLAVE ASIGNATURA:
___________ HOJA:__ 10_____ DE ____ 13___
CLAVE
B
C
BIBLIOGRAFÍA
5
X
Kolman
Álgebra lineal
Editorial Sistemas Técnicos de Edición, S.A. de C.V.
6
X
Serge Lang
Introducción al álgebra lineal.
Editorial Sistemas Técnicos de Edición, S.A. de C.V.
7
X
Strang
Álgebra lineal y sus aplicaciones
Editorial Sistemas Técnicos de Edición, S.A. de C.V.
8
X
Stanley I. Grossman
Álgebra lineal
Grupo editorial Iberoamérica.
9
X
Marsden y Tromba
Calculo Vectorial.
Editorial Sistemas Técnicos de Edición, S.A. de C.V.
10
X
Fraleigh Beauregard
Álgebra lineal.
Editorial Sistemas Técnicos de Edición, S.A. de C.V.
11
X
Francis G. Florey
Fundamentos de álgebra lineal y aplicaciones.
Editorial Prentice Hall Hispanoamérica, S.A.
ASIGNATURA: CALCULO VECTORIAL.
CLAVE ASIGNATURA:_ ___________ HOJA:__ 11____ DE ____ 11__
CLAVE
B
C
BIBLIOGRAFÍA
12
X
Howard Anton
Introducción al álgebra lineal
Editorial Limusa.
13
X
Juan Ramón Torregrosa Sánchez
Cristina Jordán Lluch
Álgebra lineal y sus aplicaciones
Serie Schaums
Editorial Mc. Graw Hill.
La Bibliografia señalada es básica para el desarrollo del curso.