1. No category

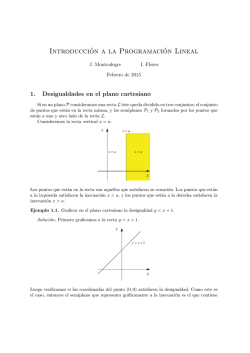
Matemática
Programación lineal (MÉTODO GRÁFICO)
Resolver los siguientes ejercicios utilizando el método gráfico. Para ello:
(a).
(b).
(c).
(d).
(e).
Modelar matemáticamente la situación planteada.
Graficar, en un mismo sistema de coordenadas, todas las restricciones del problema.
Identificar, claramente, la región factible.
Buscar todos los vértices de la región factible.
Hacer una tabla que muestre los vértices recién encontrados, junto al valor correspondiente de la
función objetivo.
(f). Por inspección de esta tabla, identicar la solución del problema
(g). No olvidar entregar la respuesta del ejercicio.
1) En una urbanización se van a construir casas de dos tipos: A y B. La empresa constructora dispone
para ello de un máximo de 1800 millones de pesos, siendo el costo de cada tipo de casa de 30 y
20 millones, respectivamente. la municipalidad exige que el número total de casas no sea superior
a 80. Sabiendo que el beneficio obtenido por la venta de una casa de tipo A es 4 millones y de 3
millones por una de tipo B, ¿cuántas casas deben construirse de cada tipo para obtener el máximo
beneficio?.
2) Una fábrica produce neveras utilitarias y de lujo. La fábrica esta dividida en dos secciones: montaje
y acabado. Los requerimientos de trabajo vienen dados por la siguiente tabla:
Montaje
Utilitaria 3 horas
Lujo
3 horas
Acabado
3 horas
6 horas
El máximo número de horas de trabajo disponibles diariamente es de 120 en montaje y 180 en
acabado, debido a las limitaciones de operarios. Si el beneficio es de 300 euros por cada nevera
utilitaria y de 400 euros por cada nevera de lujo. ¿Cuántas deben fabricarse diariamente de cada
una para obtener el máximo beneficio?
3) Una empresa fabrica dos tipos de colonia: A y B. La A contiene un 15 % de extracto de jazmı́n,
un 20 % de alcohol y el resto es agua, y la B lleva un 30 % de extracto de jazmı́n, un 15 % de
alcohol y el resto de agua. Diariamente se dispone de 60 litros de extracto de jazmı́n y 50 litros de
alcohol. Cada dı́a se pueden producir como máximo 150 litros de la colonia B. El precio de venta
por litro de la colonia A es 500 ptas. y el de la B 2,000 ptas. Hallar los litros de cada tipo que
deben producirse diariamente para que el beneficio sea máximo.
1
IMAFI
UTALCA
4) Una empresa de automóviles tiene dos plantas P y Q de montaje de vehı́culos en las que produce
tres modelos A, B y C. De la planta P salen semanalmente 10 unidades del modelo A, 30 del B
y 15 del C y de la Q, 20 unidades del modelo A, 20 del B y 70 del C., cada semana. La firma
necesita, al menos 800 unidades de A, 1600 de B y 1800 de C. Si el gasto de mantenimiento de
cada planta es de 6 millones de pesetas semanales, ¿Cuántas semanas ha de funcionar cada planta
para que el costo de producción sea mı́nimo?.
Matemática
Programación lineal (MÉTODO GRÁFICO)
5) Imaginemos que las necesidades semanales mı́nimas de una persona en proteı́nas, hidratos de
carbono y grasas son, respectivamente, 8, 12 y 9 unidades. Supongamos que debemos obtener un
preparado con esa composición mı́nima mezclando dos productos A y B, cuyos contenidos por kg
son los de la siguiente tabla:
A
B
Proteı́nas
2
1
Hidratos Grasa Costo (/ Kg.)
6
1
600
1
3
400
¿Cuántos Kg de cada producto deberá comprarse semanalmente para que el costo de preparar la
dieta sea mı́nimo?
6) Un Joyero fabrica dos tipos de joyas. La unidad de tipo A se hace con 1 g de oro y 1, 5 g de
plata y se vende a $25. La de tipo B se vende a $30 y lleva 1, 5 g de oro y 1 g de plata. Si solo
se dispone de 750 g de cada metal, ¿Cuántas joyas ha de fabricar de cada tipo para obtener el
máximo beneficio?
7) Se va a organizar una planta de un taller de automóviles donde van a trabajar electricistas y
mecánicos. Por necesidades de mercado, es necesario que haya mayor o igual nu?mero de mecánicos
que de electricistas y del número de mecánicos no supere al doble que el de electricistas. En total
hay disponibles 30 electricistas y 20 mecánicos. El beneficio de la empresa por jornada es de
$150 por electricista y $120 por mecánico. ¿Cuántos trabajadores de cada clase deben elegir para
obtener el máximo beneficio?
8) Una empresa fabrica dos tipos de tarjetas gráficas, de 16 Mb y 32 Mb de memoria, respectivamente.
Se utilizan dos máquinas que emplean 2min. en fabricar las de 16 Mb y 3 min. en fabricar las de
32 Mb. La cadena de montaje puede funcionar un máximo de 300 minutos diarios. Además cada
máquina tiene una capacidad máxima de fabricación diaria de 125 unidades, entre las cuales no
puede haber más de 90 tarjetas de 16 Mb ni más de 80 tarjetas de 32 Mb, siendo el beneficio neto
de las primeras de 45 pts y el de las segundas de 60 pts. ¿Cuántas tarjetas de 16 Mb y 32 Mb
debe fabricar diariamente cada máquina para que el beneficio sea máximo?.
10) La encargada de una floristerı́a ha de hacer el pedido semanal de plantas de interior y de exterior.
El precio que ha de pagar al proveedor por cada planta de interior es de $100 y de $200 por cada
una de exterior. Al dı́a de hoy, sabe que por lo menos ha de poder atender la demanda que un
cliente ya le ha hecho, de 20 unidades de interior y de 30 de exterior. Además, el transporte del
pedido semanal hasta la floristerı́a lo realiza una empresa especializada y le supone unos costos,
que son de $60 por cada planta de interior y de $80 por cada planta de exterior, y la floristerı́a
tiene por norma que estos costos de transporte no sobrepasen las $4,800 por pedido semanal.
Asimismo, la encargada obtiene una prima de $60 por cada planta de interior que venda y $50 por
cada una de exterior, y quiere que las primas que se puedan alcanzar vendiendo todo el pedido
sean de al menos $3,000.
2
IMAFI
UTALCA
9) Se quiere organizar un puente aéreo entre dos ciudades, con plazas suficientes de pasaje y carga,
para transportar a 1600 personas y 96 toneladas de equipaje. Los aviones disponibles son de dos
tipos: 11 del tipo A y 8 del tipo B. La contratación de un avión del tipo A, que puede transportar
a 200 personas y 6 toneladas de equipaje, cuesta 40000 euros; la contratación de uno del tipo
B, que puede transportar 100 personas y 15 toneladas de equipaje, cuesta 10000 euros. ¿Cuántos
aviones de cada tipo deben utilizarse para que el coste sea mı́nimo?
Matemática
Programación lineal (MÉTODO GRÁFICO)
Si la floristerı́a quiere además minimizar el precio que ha de pagar al proveedor por el pedido:
¿cuántas unidades de cada tipo ha de adquirir? ¿cuánto deberá pagar al proveedor?
Respuestas:
1) x = casas del tipo A e y = casas del tipo B
La función a maximizar, será:
Z = 4x + 3y
sujeta a las siguientes restricciones:
30x + 20y ≤ 1800;
x + y ≤ 80;
x, y ≥ 0;
Se deben construir 20 casas de tipo A y 60 de tipo B con un costo de 260 millones de pesetas.
2) x = nevera utilitaria e y = nevera de lujo.
La función a maximizar, será:
Z = 300x + 400y
sujeta a las siguientes restricciones:
3x + 3y ≤ 120;
3x + 6y ≤ 180;
x, y ≥ 0;
Se deben fabricar 20 neveras de cada uno de los dos tipos con un beneficio de 14000 euros.
3) x = colonia tipo A e y = colonia de tipo B.
La función a maximizar, será:
Z = 500x + 2000y
sujeta a las siguientes restricciones:
30
15
x+
y ≤ 60;
100
100
20
15
x+
y ≤ 50;
100
100
El Beneficio máximo se obtiene con 100 unidades tipo A y 200 unidades tipo B, siendo este de
350000 pts.
3
IMAFI
UTALCA
x, y ≥ 0;
Matemática
Programación lineal (MÉTODO GRÁFICO)
4) x = planta P e y = planta Q.
La función a minimizar, será:
Z = 6x + 6y
sujeta a las siguientes restricciones:
≥
≥
≥
≥
10x + 20y
30x + 20y
15x + 70y
x, y
800;
1600;
1800;
0;
El mı́nimo costo de producción se obtiene trabajando 40 semanas en la planta P y 20 dı́as en la
planta Q, siendo este costo de 360 millones.
5) x = producto A e y = producto B.
La función a minimizar, será:
Z = 600x + 400y
sujeta a las siguientes restricciones:
2x + y
6x + y
x + 3y
x, y
≥
≥
≥
≥
8;
12;
9;
0;
Se deben producir 3 de A y 2 de B para producir el mı́nimo costo de 2600
6) x = tipo A e y = tipo B.
La función a maximizar, será:
Z = 25x + 30y
sujeta a las siguientes restricciones:
x + 1,5y ≥ 750;
1,5x + y ≥ 750;
x, y ≥ 0;
Se deben fabricar 300 de cada tipo con un beneficio de $15500.
7) x = mecánico e y = eléctrico.
La función a maximizar, será:
Z = 120x + 150y
x
x
x
y
x, y
4
≥
≤
≤
≤
≥
y;
2y;
20;
30;
0;
IMAFI
UTALCA
sujeta a las siguientes restricciones:
Matemática
Programación lineal (MÉTODO GRÁFICO)
Se deben elegir 20 de cada tipo con un beneficio de $5400.
8) x = tarjeta de 16 Mb e y = tarjeta de 32 Mb.
La función a maximizar, será:
Z = 45x + 60y
sujeta a las siguientes restricciones:
2x + 3y
x+y
x
y
x, y
≤
≤
≤
≤
≥
300;
125;
90;
80;
0;
Se deben elegir 75 de 16 Mb y 50 de 32 Mb con un beneficio de $6375.
9) x = tipo A e y = tipo B.
La función a minimizar, será:
Z = 40000x + 10000y
sujeta a las siguientes restricciones:
200x + 100y
6x + 15y
x
y
x, y
≥
≥
≤
≤
≥
1600;
96;
11;
8;
0;
La solución óptima es de 240000 con 4 aviones del tipo A y 8 aviones del tipo B.
10) x = plantas de interior e y = plantas de exterior.
La función a minimizar, será:
Z = 100x + 200y
sujeta a las siguientes restricciones:
60x + 80y
60x + 50y
x
y
x, y
≤
≥
≥
≥
≥
4800;
3000;
20;
30;
0;
5
IMAFI
UTALCA
Por tanto, la floristerı́a deberı́a de pedir 25 plantas de Interior y 30 plantas de Exterior. Y su
mı́nimo valor es de 8500