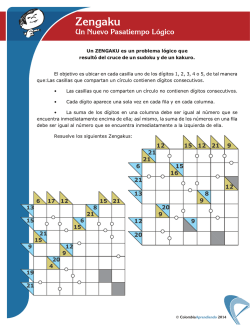
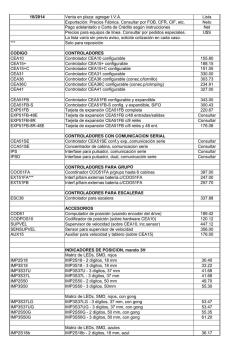
póster de fórmulas relacionadas con pi
π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π π Métodos para calcular π Series infinitas π π π Integrales π π π π π π Á REA DE UN DISCO : Z1 p π=2 1 − x2 dx π M ADHAVA ( C . 1400), L EIBNIZ (1674): π π π 1 1 1 = 1 − + − + ··· 4 3 5 7 π π π −1 π π Palabras clave: arco tangente. π π π π π Z∞ π π N EWTON (1665): π √ ∞ 2n 3 3 3X n π= +2− 4 4 n=0 (n + 1)(2n + 5)16n D ISTRIBUCIÓN DE C AUCHY: π π π= π π dx 2 −∞ x + 1 π π π π Palabras clave: áreas de sectores circulares. π π π π π Z∞ S ENO INTEGRAL : π sen x dx x −∞ π E ULER (1736): π= π ∞ ∞ ∞ X 1 π8 = ,... 9450 n=1 n8 π π π π X 1 π6 = , 945 n=1 n6 π π4 X 1 = , 90 n=1 n4 π ∞ π2 X 1 = , 2 6 n n=1 π π Palabras clave: función zeta de Riemann. π π D ISTRIBUCIÓN NORMAL : π √ π= Z∞ 2 π e−x dx π π −∞ π R AMANUJAN (1914): π π π π etc. π π π n=0 «Un matemático es alguien para quien esto es tan obvio como que dos veces dos son cuatro» — Lord Kelvin. π 1 = π √ ∞ 3 2n 42n + 5 2 2 X (4n)! 26390n + 1103 = , 212n+4 9801 n=0 n!4 3964n n ∞ X π π π Palabras clave: formas modulares. π Métodos empíricos π π π π π π D. Y G. C HUDNOVSKY (1988): π π ∞ π X (6n)! (−1)n (545140134n + 13591409) 1 12 =√ π 6403203n 6403203 n=0 (3n)! n!3 π π π L A AGUJA DE B UFFON : π π Una aguja de longitud L se lanza sobre una serie de líneas paralelas espaciadas por una distancia λ, con L < λ. La proporción p de veces que la aguja cruza una de las líneas satisface π π π Palabras clave: Ramanujan. π π π π π π π π B AILEY, B ORWEIN Y P LOUFFE (1997): π π π≈ π ∞ X 1 4 2 1 1 π= − − − n 8n + 1 16 8n + 4 8n + 5 8n + 6 n=0 π π 2L pλ π π π λ 2 π π Palabras clave: bloques independientes de dígitos. π Por ejemplo, si L = se obtiene π ≈ 1/p. π π π E L PÉNDULO SIMPLE : π π π π π π π etc. π π π T π≈ 2 r La aguja de Buffon g L π π π π Palabras clave: Ramanujan, método WZ, algoritmo PSLQ, relaciones conjeturadas. La relación entre el periodo de oscilación de un péndulo y su longitud es, para amplitudes pequeñas, π G UILLERA (2002,2003): 5 ∞ ∞ X 1 X (−1)n (6n)! 1 2n (−1)n (820n2 + 180n + 13) ? √ = = (5418n2 + 693n + 29), 2 20n+7 3n 6 π 2 n 128 5 n=0 2880 n! n=0 π π π π π (T = periodo, L = longitud, g = gravedad) π π π π π Productos infinitos π π π π π P UNTOS DE UN RETÍCULO DENTRO DE UN DISCO : π π π Sea DR el disco cerrado con centro el origen y radio R y N(R) el número de puntos con coordenadas enteras dentro de DR . Entonces N(R) π = lı́m R→∞ R2 π π V IÈTE (1593): π π π π π π π q p √ √ p √ 2+ 2+ 2 2 2 2+ 2 = · · ··· π 2 2 2 π π π π Por ejemplo, N(10) = 317 y N(100000) = 31415925457. π π π WALLIS (1655): π S UMAS DE DOS CUADRADOS : π 2 1·3 3·5 5·7 7·9 = · · · ··· π 2·2 4·4 6·6 8·8 π π π π Sea r(n) el número de representaciones de un natural n como suma de dos cuadrados enteros, contando signos y permutaciones como representaciones distintas. Por ejemplo, r(5) = 8 pues 5 = (±1)2 + (±2)2 = (±2)2 + (±1)2 . Entonces π π π π π π E ULER (1737): π π π π r(1) + · · · + r(n) =π n→∞ n lı́m π π p primo Puntos enteros en un disco π p primo π p primo π v v v u Y u u Y u1 u 1 Y 1 u1 1 1 1 4 6 =t 1− 2 =t 1− 4 =t 1 − 6 = ··· π 6 p 90 p 945 p π π π π π Es decir, un número tiene de media π representaciones como suma de dos cuadrados. Este resultado es la versión aritmética π π π π Fracciones continuas π del problema de contar puntos. π π π π π π π π π La distribución de los dígitos de π π B ROUNCKER (1665): π 12 π π 32 π π 2+ π 4 =1+ π π 52 π π 2+ π 72 π π 2+ π π 2+. Se espera que un número irracional e incluso trascendente como π sea normal, lo cual, para sus dígitos decimales, significa que cada uno de ellos, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, se halla estadísticamente en la misma proporción: 10 %. π π En general, dada una base b, entre los primeros k dígitos del desarrollo de π en esa base, cada una de las b cifras c = 0, 1, . . . , b − 1 aparece un número Nb (c, k) de veces. Se conjetura que para cualquier base debería ser π .. π π π π π π π L ANGE (1999): Nb (c, k) 1 = . k→∞ k b π π π π=3+ π 12 π π 6+ π 32 lı́m π π 6+ π 72 π π 6+ De hecho, cualquier sucesión finita σ de dígitos, con longitud fija `, debería aparecer con frecuencia 1/b` , correspondiente a la equidistribución de dichas sucesiones. π 52 π π π .. π π π π π π π P ICKETT Y C OLEMAN (2008): π π 1 π π 1 La normalidad de π a menudo se intenta divulgar de manera filosófica o poética: cualquier mensaje escrito, pasado o futuro, la letra de cualquier canción, internet al completo, la demostración de la conjetura de Riemann —o su refutación— etc., codificados como sucesiones binarias, por ejemplo, se hallarán (de ser cierta la normalidad) en algún lugar entre los dígitos binarios de π, incluso infinitas veces. Debe tenerse en cuenta, sin embargo, que esto incluye, como en la Biblioteca de Babel de Jorge Luis Borges, sucesiones sin sentido, libros que constan sólo de la letra «a», todo enunciado y su contrario, la paradoja del mentiroso, etc. Tampoco puede predecirse dónde entre los dígitos hay que buscar una sucesión dada y, aunque hallásemos alguna información, nada nos libraría de tener que decidir acerca de su valor, con lo cual es un pobre método de hallar verdades. π π 1 1 + 2 1 1 + 3 1 + 4 ... π 1+ π π =1+ 2 Borel demostró que casi todo número real, en el sentido de la medida de Lebesgue, cumple la propiedad de equidistribución de sucesiones finitas respecto a toda base, pero, a día de√hoy, ninguno de los enunciados anteriores ha sido demostrado para una constante concreta «natural» como π, e, ó 2 (para esta última hubo una supuesta demostración en 2005, pero no avalada por expertos), aunque sí existen ejemplos un tanto «artificiales» de tales números, como la constante de Champernowne 0,123456789101112 . . . . π 6+. π π π π π π π π π π π π π π π π π π π π π π π Para más información π π Más prosaicamente, podemos afirmar que la sucesión 999999 ocurre por primera vez en la posición 762 (aparece en el mural en la vuelta número 9, abajo a la izquierda), pero hay que esperar a la posición 193034 para verla otra vez. Añadiendo otro 9, la sucesión 9999999 aparece por primera vez en la posición 1722776. Existen diversas páginas web dedicadas a hallar sucesiones finitas dadas entre los dígitos de π calculados hasta hoy en día.
© Copyright 2026