1. No category

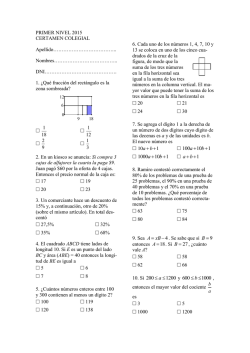
GOBIERNO DEL ESTADO DE MÈXICO
SECRETARÍA DE EDUCACIÓN
C.C.T. 15EES1133O
C.F. 1597599
DEPARTAMENTO REGIONAL No. 09 “NEZAHUALCOYOTL”
C.E. O708BSESUM0765
ZONA ESCOLAR S095
ESCUELA SECUNDARIA OFICIAL No. 0765
“JOSÉ VASCONCELOS”
Guía para examen extraordinario correspondiente a la asignatura de Matemáticas 1
Instrucciones: Lee, observa, analiza y resuelve las siguientes situaciones:
El Sr. Jorge se dedica a reparar y construir diferentes estructuras metálicas. Para realizar algunos trabajos
envío a su ayudante Juan a comprar los siguientes materiales.
1. Barras de solera de las siguientes medidas: 1 1/8 in, 1 ¼ in y 1/2 in. Al llegar a la ferretería, le muestran un
manual donde aparecen las medidas que están disponibles.
a) 0.933 in
b) 0.4375
in
c) 0.5 in
d) 1.375 in
e) 1.125 in
f) 1.933 in
g) 1.250 in
h) 1.012
¿Cuáles medidas del manual debe pedir Juan? ________________________
2. Ángulos de lados iguales con las siguientes medidas: 0.75 x 0.125 in, 0.1875 x 0.375 in, en el catálogo
disponible en la ferretería aparecen las siguientes medidas disponibles.
a) ¾ x 5/16 in
b) 3/16 x 3/8 in
c) 3/16 x 2/8 in
d) ¾ x 1/8 in
¿Cuáles medidas del catálogo debe pedir Juan? __________________________
Calcular el perímetro de la siguiente figura.
3.
3 2/15
m
3 1/8m
1.30 m
4.72
m
Calcular el mínimo común múltiplo (m.c.m.) de los números:
4.
5.
6.
7.
m.c.m. (10, 6) =
m.c.m. (100, 50) =
m.c.m. (12, 24, 40) =
m.c.m. (26, 19, 4) =
Resolver los siguientes problemas:
8. El suelo de una habitación, que se quiere revestir, tiene 5 m de largo y 3 m de ancho.
Calcula el lado del mosaico y el número mosaicos, tal que el número de mosaicos que se coloque sea
mínimo y que no sea necesario cortar ninguno de ellos.
9. Un faro se enciende cada 12 segundos, otro cada 18 segundos y un tercero cada minuto. A las 6.30 de la
tarde los tres coinciden.
Averigua las veces que volverán a coincidir en los cinco minutos siguientes.
1. Utilizar los puntos dados en la siguiente recta numérica para ubicar las fracciones
1
1
y 2 .
4
2
1
2. Ubicar en las siguientes rectas numéricas la fracción
5
considerando los puntos dados en cada recta.
3
Recta A
1
Recta B
1
3. Representar en la siguiente recta numérica las fracciones
12 6
y
4
2
4. Representar una fracción que pueda ubicarse entre las dos fracciones que ya están representadas.
1. Utilizar los puntos dados en la siguiente recta numérica para ubicar los números decimales 0.6 y 1.30
1
1.5
2. Ubicar en las siguientes rectas numéricas los números decimales 1.25 y 2.43 considerando los puntos dados
en cada recta.
Recta A
1
3
Recta B
2.50
1.100
5
3. En la siguiente recta numérica representar los números 3/5, 1.3, 0.6 y 1.35
1
5
4. En la siguiente recta numérica el segmento (0, 5) está dividido en tres partes iguales. Anotar el número que
corresponde al punto señalado con la flecha.
0
5
1. Para cumplir con los pedidos del día, una confitería calcula que necesita usar 4 kg de harina. En el estante
guardan 2 paquetes de ¾ kg, 2 paquetes de ½ kg y 2 de ¼ kg. Averigüen si la harina que tienen es
suficiente. Si falta o sobra harina, digan cuál es la diferencia. ____________________________________
2. De una pizza entera Ana comió 1/3 y María ¼. ¿Qué porción de la pizza queda? ____________________
3. De una bolsa de caramelos, Oscar sacó 1/4 y María 1/2. ¿Qué parte de los caramelos quedó en la bolsa?
___________________________________________________________
4. Natalia comió 2/3 de un chocolate y Juana comió 1/6. ¿Cuánto chocolate quedó? _____________________
Resolver las siguientes operaciones con fracciones:
1. 1/20 + 3/5 + 2/10 =
2. ½ + 1/3 + 1/8 =
3. 4/5 – ¼ - 1/6 =
4. 3/8 – ¼ + 12/16 =
Resolver los siguientes problemas:
1. En relación con su deporte favorito, a un grupo de estudiantes se le aplicó una encuesta, se obtuvieron los
siguientes resultados:

1/4 de los entrevistados prefiere jugar fútbol.

1/6 de los entrevistados contestó básquetbol.

1/3 de los entrevistados se decidió por el beisbol.

El resto de los entrevistados no tiene deporte favorito.
¿Qué parte del total de los entrevistados no tiene un deporte favorito? _______________
1. A Diego le proponen que elija la bolsa de golosinas más pesada. La primera pesa
20/6 kg. ¿Cuál es la que pesa más? ¿Cuánto pierde si elige la de menor peso?

a)
3 3/8 kg y la segunda
Escribe una regla general que permita determinar el número de cuadrados de cualquier figura de cada
una de las siguientes sucesiones:
Regla: __________________________________________________
b)
Regla: __________________________________________________

Genera una sucesión de números, cuya diferencia entre dos términos consecutivos sea siempre 5. Luego
escribe con palabras la regla que permita calcular cualquier término de la sucesión.

Para cada caso, escribir la regla general que permita determinar cualquier término de la sucesión.
a) 6, 10, 14, 18, 22, 26, …
Regla: _____________________________________________________
b) 3, 5, 7, 9, 11, 13, …
Regla: _____________________________________________________
c) 1/12, 4/12, 7/12, 10/12,…
Regla: _____________________________________________________
1. Encontrar el octavo término de cada una de las siguientes sucesiones.
a) 3, 9, 27, 81, 243,…
b) 3, 6, 12, 24, 48,...
c) 1, 0.1, 0.01, 0.001,...
d) 1,1/4,1/16,1/64,...
e) 2, 6, 18, 54, 162,...
f)
5, 5/3, 5/9, 5/27, …
g) 54, 36, 24, 16, …
1. Dado el siguiente marco cuadrado.
15 cm
15 cm
a) ¿Cómo se puede saber el perímetro del marco?________________________________________
b) ¿Y si el marco fuera de 20 cm de lado?_______________________________________________
c) ¿Y si fuera de 35 cm?_____________________________________________________________
d) Escribe con tus propias palabras, ¿cómo se determina el perímetro de cualquier cuadrado?
______________________________________________________________________________
e) Expresa en forma general, para cualquier medida del lado de un cuadrado: ______________________
2. Luisa quiere poner una tira bordada alrededor de un mantel rectangular que mide 2 m de largo y 1.60 m de
ancho:
a) ¿De qué forma calcularía Luisa, la medida de la tira bordada?_________________________________
b) ¿Y si el mantel midiera 80 por 60 cm?___________________________________________________
c) ¿Cómo obtendrías este dato (perímetro) para manteles de cualquier tamaño?
______________________________________________________________________________
d) Expresar de forma general el perímetro de cualquier rectángulo______________
1. Anoten los datos que hacen falta en la siguiente tabla.
Figura
Fórmulas
Datos
Perímetro
Área
l = 3 cm
a
P=6l
a = 2 cm
A = Pa/2
l = 8 cm
a = 5 cm
1. Ttrazar en su cuaderno las siguientes figuras con las medidas que se indican. En aquellos casos donde falte
información para obtener figuras congruentes, ustedes agréguenla.
a) Cuadrado
Lado: 6.5 cm
b) Rectángulo
Largo: 7 cm
Ancho: 5 cm
c) Trapecio isósceles
Base mayor: 7.5 cm
Base menor: 5 cm
d) Triángulo equilátero
Lado: 6 cm
e) Triángulo escaleno
Lado a: 5 cm
Lado b: 6.5 cm
1. Analizar los puntos donde se cortan las medianas, mediatrices, bisectrices y alturas en un triángulo
cualquiera y anotar una
Características Siempre
se
encuentra
en el
interior
del
triángulo
donde se cumplan las características señaladas y una X donde no se cumplan.
Se
puede
localizar
en un
vértice
del
triángulo
Puede
localizarse
fuera del
triángulo
Es el
centro de
un círculo
que toca
los tres
vértices
de
triángulo
Es el
centro
de un
círculo
que toca
los tres
lados
del
triángulo
Es el
punto de
equilibrio
de un
triángulo
Está a la
misma
distancia
de los
vértices
del
triángulo
Se
encuentra
alineado
con otros
puntos
notables
del
triángulo
Incentro (punto
donde se cortan
las bisectrices)
Baricentro
(punto donde
se cortan las
medianas)
Ortocentro
(punto donde
se cortan las
alturas o su
prolongación)
Circuncentro
(punto donde
se cortan las
mediatrices)
1. En una ciudad pequeña se quiere construir un quiosco que quede a la misma distancia del Palacio
Nacional, de la Secretaría de Educación y del Edificio del Congreso, ¿dónde deberán construirlo?
Palacio Nacional
Secretaría de Educación
Edificio del Congreso
2. Se tiene un terreno de forma triangular y se va a construir en él una fuente circular de tal manera que toque
los tres lados del terreno y la parte restante se cubrirá de pasto. Dibuja cómo quedaría la fuente en dicho
terreno.
3. Se quiere construir la estación del tren de tal forma que esté sobre la vía y a la misma distancia del pueblo
Arania y del pueblo Mosconia. ¿Dónde debe construirse la estación?
Arania
Mosconia
4. ¿Dónde se encuentra el centro de gravedad de estos tres cuerpos celestes de igual masa?
5. Carlos y Raúl participaron en una rifa de $1200.00 y se la ganaron. ¿Cómo deben repartirse el dinero si
para la compra del boleto Carlos cooperó con $8.00 y Raúl con $16.00?
6. Si el premio fuera de $1000.00 y para la compra del boleto Carlos puso $10.00 y Raúl $15.00, ¿cómo
deben repartirse proporcionalmente el dinero según sus aportaciones?
7. Tres amigos obtienen un premio de $1000.00 en la lotería, si uno de ellos aportó $14.00, el otro $9.00 y el
tercero $17.00, ¿cuánto le corresponde a cada uno, si la repartición del premio debe hacerse
proporcionalmente a sus aportaciones?
8. Una empresa va a repartir $35 900.00 entre cuatro empleados, en proporción directa a su antigüedad en el
trabajo. Roberto tiene dos años, Jesús 3.75 años, Macario cuatro años y Teresa 1.5 años, ¿cuánto le
corresponde a cada no?
9. Cuatro amigos ganaron un premio de $15000.00 en un sorteo y se lo repartieron proporcionalmente a lo
que cada uno aportó para la compra del boleto que costó $100.00. Al primero le tocó $2100.00, al segundo
$5700.00, al tercero $3300.00 y al cuarto el resto de los $15000.00 ¿Cuánto aportó cada amigo para la
compra del boleto?
Hallar el máximo común divisor de los siguientes pares de números.
a. 40 y 60
b. 35 y 48
c.
70 y 62
e. m.c.d. (225, 300) =
d. m.c.d. (100, 150) =
f.
m.c.d. (415, 520) =

Encontrar el MCM de los siguientes números:
225, 300
MCM = ______________
25, 75, 125
MCM = ______________
380, 420
18,
MCM = ____________
60, 75, 90
MCM = ____________
24, 36
MCM = ___________
140, 325,
490
MCM = ___________
Resolver los siguientes problemas:
1. Se quiere cortar dos tablones de madera, uno de 48 cm y el otro de 60 cm, en tablas de la mayor longitud
posible y que midan lo mismo, sin que sobre madera de ninguno de los tablones.
a) ¿Cuánto medirá cada una de las partes?
b) ¿Cuántas tablas se pueden sacar?
2. Se desea cubrir con azulejos cuadrados una pared de una cocina que mide 210 cm de ancho por 300 cm
de alto. Si se quiere que los azulejos sean lo más grande posible y que no haya que romper ninguno, ¿cuál
debe ser la medida por lado de los azulejos?
3. Se requiere embaldosar un patio de 1 620 cm de largo por 980 cm de ancho con baldosas cuadradas lo
más grandes posibles y enteras. ¿Cuál será la longitud del lado de cada baldosa?
4. Una fracción de cartulina mide 1 m por 45 cm y se quiere dibujar en ella una cuadrícula del mayor tamaño
posible cada cuadrado. ¿Cuál debe ser la medida de cada cuadrado de la cuadrícula?
1. Estimar el resultado de las siguientes operaciones:
a)
8
1
 2.95 

15
40
b)
6
1
 1.95   0.23  0.1 
8
9
2. Encontrar el resultado estimado o exacto, según crean más conveniente, de los siguientes problemas.
a) María está interesada en controlar su peso. Para ello, se pesó una vez por semana y registró los resultados
en la siguiente tabla:
Semana
1
2
3
4
5
6
7
Inicial
Subí
Subí
Bajé
Bajé
Subí
Bajé
Peso (kg)
57 ½ kg
1.12 kg
¼ kg
0.98 kg
1 ¾ kg
0.14 kg
0.28 kg
Después de las siete semanas, ¿subió o bajo de peso? ____________ ¿cuánto? __________
Resolver los siguientes problemas:
7
2
1. Un rectángulo tiene de área
y sabemos que uno de sus lados mide . ¿Cuánto medirá el otro lado?
3
5
2. Un rectángulo tiene de área
15
5
y sabemos que uno de sus lados mide . ¿Cuánto medirá el otro lado?
40
8
3. Un granjero colocó una cerca alrededor de su parcela para que no entraran los animales a comerse sus
verduras. La parcela es de forma cuadrada, cada lado mide 10 m, si puso los postes cada
3
de metro,
4
¿cuántos postes colocó?
4. Dados los siguientes segmentos, trazar una recta perpendicular a cada uno, de tal manera que los divida en
dos partes iguales. Señala con la letra que quieras el punto donde se cortan los dos segmentos.
J
B
P
A
C
D
Q
K
a) La recta que trazaste en cada caso se conoce como “mediatriz” del segmento dado. Escribe una
definición de mediatriz.
5. Trazar la mediatriz de cada segmento y marca un punto cualquiera sobre la mediatriz que trazaste.
Después, une los extremos del segmento dado con el punto marcado sobre la mediatriz.
a) ¿Qué tipo de triángulo se formó en cada caso?
b) ¿Todos los triángulos que formaste tienen la misma altura?__________ ¿Por qué?
c) Si las distancias de cada extremo del segmento dado al punto marcado sobre la mediatriz fueran
iguales, ¿qué tipo de triángulo se formaría?
6. Trazar con algún color la bisectriz de los ángulos interiores de cada figura, con otro color las diagonales y
con un color diferente la mediatriz de cada lado.
a) ¿En qué casos coinciden las diagonales del polígono con las bisectrices de sus ángulos?
b) ¿En qué casos coinciden las mediatrices y las bisectrices?
c) Tracen un círculo que quede inscrito en cada uno de los polígonos anteriores.
Tomar las medidas necesarias para calcular el perímetro y el área de cada una de las siguientes figuras:
.
Triángulo equilátero
Cuadrado
Perímetro: ___________
Perímetro: ___________
Área: ______________
Área: ________________
Pentágono regular
Perímetro: ______________
Área: __________________
1. Los lados de un cuadrilátero miden 5, 9, 2 y 11 cm, tal como se muestra en la figura; si se realiza una
reproducción a escala y el lado correspondiente a 5 cm, ahora mide 15 cm, ¿cuánto deben medir los demás
lados? Utilicen la tabla para escribir las respuestas.
9 cm
5 cm
2 cm
11 cm
Medidas de los lados
de la figura original
5 cm
2 cm
9 cm
11cm
Medidas de los lados de la
reproducción
15 cm
2. Consideren la situación del ejercicio 1, con la diferencia de que el lado correspondiente a 9 cm, en la
reproducción mide 3 cm, ¿cuánto deben medir los demás lados?
Medidas de los lados
de la figura original
9 cm
2 cm
5 cm
11cm
Medidas de los lados de la
reproducción
3 cm
3. Consideren la situación del ejercicio 1, con la diferencia de que el lado correspondiente a 2 cm, en la
reproducción mide 5 cm, ¿cuánto deben medir los demás lados?
Medidas de los lados
de la figura original
2 cm
5 cm
9 cm
11cm
Medidas de los lados de la
reproducción
5 cm
1. Una caja de refrescos cuesta $ 104.40. Si ésta contiene 24 refrescos, ¿cuál es el costo de cada refresco?
2. El ancho de un rectángulo mide 1.25 m y su área es de 10 m 2. Calcula la longitud de su largo.
10 m2
1.25 m
¿?
Encontrar el valor de x de los siguientes problemas:
b)
a)
c)
x
x
3
4
x
x
x
x
Perímetro = 80 cm
x = ________
2x
x
Área = 152 m2
x = ________
Área = 36 m2
x = ________
1. Se reparten 76 balones en 3 grupos, el segundo recibe 3 veces el número de balones que el primero y el
tercero recibe 4 balones menos que el primero. ¿Cuantos balones recibe cada grupo?
2. Se tienen 88 objetos que se reparten entre dos personas, la segunda persona recibe 26 menos que la
primera. ¿Cuántos recibe cada una?
Resolver las siguientes ecuaciones de primer grado.
3. X + 2 = 51
4. 72 + m = 10
5. 110a = 26
6. 11b - 5 = 458
7. 3y + 45 = - 70
Completar las siguientes tablas sobre las calificaciones obtenidas por los alumnos de dos grupos de primer
grado. Posteriormente contestar las preguntas que se hacen.
Calificación
10
9
8
7
6
5
Total
GRUPO 1º “Á”
Frecuencia
Frecuencia
absoluta
relativa %
3
15
5
6
15
2
5
25
20
100
Calificación
10
9
8
7
6
5
Total
GRUPO 1º “B”
Frecuencia
absoluta
3
4
2
6
24
Frecuencia
relativa %
12.5
21
16.67
8.33
100
1. ¿Cuál es el grupo con mejor índice de aprobación? y ¿Por qué?
2. ¿Cuántos alumnos reprobaron en cada grupo? ¿Cuál es el índice de reprobación en cada grupo?
3. ¿Por qué a frecuencias absolutas iguales en ambas tablas, les corresponde frecuencias relativas
diferentes?
El profesor de Educación Física recopiló las estaturas (en metros) de los alumnos de un grupo de nuestra
escuela. Analizar y organizar los datos para presentar la información en la tabla de la derecha.
Estatura
1.57, 1.53, 1.55, 1.56, 1.52, 1.54,
1.55, 1.58, 1.57, 1.56, 1.55, 1.53,
1.57, 1.54, 1.52, 1.55, 1.58, 1.56,
1.55, 1.55, 1.54, 1.58, 1.53, 1.56,
1.54, 1.56, 1.55, 1.54, 1.55, 1.53,
F. absoluta
F. relativa
Analizar la siguiente gráfica de barras que muestra los resultados de una encuesta a un grupo de alumnos,
respecto a su deporte favorito. Posteriormente contestar las preguntas.
No. Alumnos
20
15
10
5
0
Voleibol
a)
b)
c)
d)
e)
f)
Fútbol
Básquetbol
Béisbol
Tenis
¿Cuál es el deporte de mayor preferencia?
¿Cuál es el de menor preferencia?
¿Cuántos alumnos prefieren el básquetbol?
¿Cuál es el número total de alumnos encuestados?
¿Cuántos alumnos no eligieron el básquetbol?
¿Qué % de alumnos prefieren el fútbol?
Analizar la gráfica que muestra las tallas de los alumnos de un grupo, representadas en porcentajes (%) y
contesten las preguntas:
60
50
40
30
20
10
0
Grande
Mediana
Chica
Tallas
a) Si son 40 los alumnos del grupo, ¿cuántos son de cada talla?
Talla Grande______
Talla Mediana______ Talla Chica______
b) Suponiendo que en la escuela se quieren hacer chamarras para 160 alumnos, ¿cuántas chamarras de
cada talla se deberán confeccionar atendiendo la misma proporción?
Talla Grande______
Talla Mediana______ Talla Chica______
Investigar las edades de sus compañeros del grupo, completar la tabla con los datos que obtengan y construir la
gráfica de barras correspondiente.
EDAD
11 años o menos
12 años
13 años o más
Total
NO. ALUMNOS
(%)
Con las edades de sus compañeros del grupo, ahora construyan la tabla y gráfica empleando frecuencias
relativas (%).
11 ó
meno
12
13 ó
más
EDADES (años)
Analizar la siguiente gráfica que muestra las edades de los alumnos de un grupo de secundaria. Posteriormente
contesten las preguntas que se indican.
11 años
Si el grupo tiene 40 alumnos:
1. ¿Cuántos alumnos tienen 13 años? _________
2. ¿Cuántos alumnos tienen 11 años? _________
3. ¿Cuántos alumnos tienen 12 años? _________
13 años
12 años