1. No category

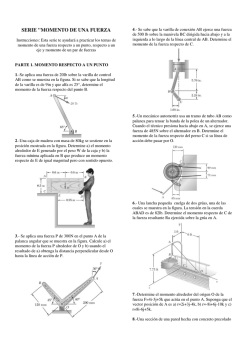
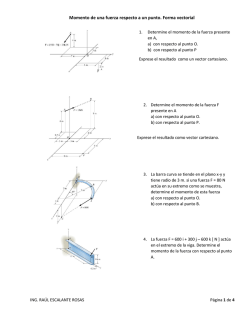
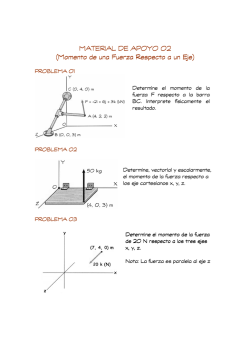
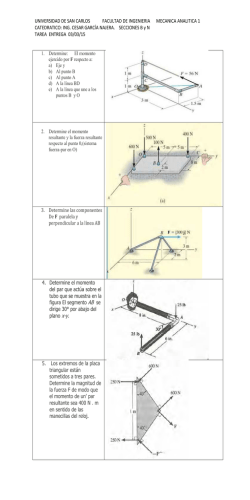
Mechanics of materials 2015 (Tarea 2) asignada el 11 de febrero, entregar, via email, el 18 de febrero.
Problema 1. Sea una barra AB de sección uniforme, de área 𝐴 = 2.2×10!! m2, tiene una masa
específica 𝜌 = 8000 kg/m3. Su extremo A está fijo al apoyo mediante un tornillo, en tanto que su
extremo B se apoya sobre una superficie lisa, como se muestra en la figura. Calcule el diámetro
requerido del tornillo sabiendo que puede resistir un esfuerzo de cortante de 85 MPa.
P1
Problem 2. Let the rigid bar BKD be fixed to support K by a pin and held by two bars BC and
DF, as shown in the figure. When the rigid bar BKD is in the horizontal position, there is a
backlash e between the mass and the platform. (a) For a large value of e, determine the
maximum distance b as a function of load P (due to mass m) such that the limits of stresses 𝜎!" ,
for i = 1, 2, in the bars remain below or at the most equal to the limits. (b) For 𝑒 = 1 mm and P =
4.9 kN, determine the stresses in the bars when the mass just touch the platform.
P2
1
Problem 3. In the system shown in figure below, the cable is driven by a motor for lifting a
mass 𝑚 = 5000 kg. Members BC and BD are made of the same material, being its Young's
modulus, E = 200 GPa. Assume that member BD has been designed optimally (of minimum
area). (The pulley is frictionless and negligible weight.)
i) Compute the normal stress in member BD
ii) Determine the minimum cross-sectional area of member BC
iii) What is the displacement of B?
P3
Problema 4. Sea una barra rígida OD sostenida por un cable BC, como se muestra en la figura.
La barra permanece horizontal antes de la aplicación de la carga P. Suponiendo que los pivotes O
y F sean perfectamente lisos, determine el desplazamiento del extremo D, así como los esfuerzos
en el cable.
P4
2
Problema 5. El eje circular sólido se somete a un par de torsión interno 𝑇 = 5 kN.m. Determine
el esfuerzo cortante desarrollado en los puntos A y B.
P5
Problema 6. El eje hueco circular se somete a un par de torsión interno 𝑇 = 10 kN.m.
Determine el esfuerzo cortante desarrollado en los puntos A y B.
P6
Problema 7. El eje mostrado en la siguiente figura es hueco desde A hasta B y sólido de B a C.
Determine el esfuerzo máximo desarrollado en el eje. El diámetro exterior del eje es de 80 mm y
el espesor de la pared en el segmento hueco es de 10 mm.
P7
3
Problema 8. Determine el esfuerzo cortante máximo desarrollado en el eje que tiene un diámetro
de 40 mm.
P8
Problema 9. Determine el esfuerzo cortante máximo desarrollado en la sección a-a del eje.
P9
Problema 10. Determine el esfuerzo cortante máximo desarrollado en el punto A sobre la
superficie del eje que tiene un radio de 40 mm.
P10
4
Problema 11. El eje de acero tiene un diámetro de 60 mm y está sometido a los pares de torsión
mostrados en la figura. Determine el ángulo de giro del extremo A con respecto a C.
P11
Problema 12. Determine el ángulo de giro de la rueda B con respecto a la rueda A. El eje tiene
un diámetro de 40 mm y está hecho de acero A-36.
P12
Problema 13. El eje hueco fabricado de aluminio 6061-T6 tiene radios exterior e interior
𝑐! = 40 mm y 𝑐! = 30 mm, respectivamente. Determine el ángulo de giro del extremo A. El
soporte flexible en B tiene una rigidez de torsión 𝑘 = 90 kN ∙ m/rad.
P13
5
Problema 14. Una serie de engranes se montan sobre el eje de acero A-36 con un diámetro de 40
mm. Determine el ángulo de giro del engrane B con respecto al engrane A.
P14
Problema 15. El eje con un diámetro de 80 mm está fabricado de acero A-36. Si se encuentra
sometido al par de torsión uniformemente distribuido que se muestra en la figura, determine el
ángulo de giro del extremo A con respecto a B.
P15
Problema 16. El eje con un diámetro de 80 mm está fabricado de acero A-36. Si se encuentra
sometido a la carga distribuida triangular que se muestra en la figura, determine el ángulo de giro
del extremo A con respecto a C.
P16
6