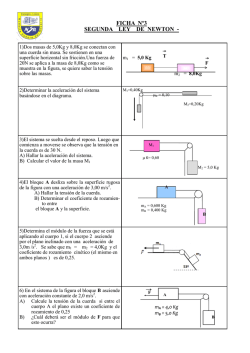
Ejercicios de rozamiento
PAQUETE N.º 11 ROZAMIENTO ROZAMIENTO ROZAMIENTO ESTÁTICO Y CINÉTICO 1. Un escritorio pesa 400N y descansa sobre el 5. peso empleando un plano inclinado que forma 37º con el horizonte. El coeficiente de piso de la oficina con el cual el coeficiente de rozamiento cinético entre la caja y el plano es rozamiento estático es 0,4. 0,2. Halle la fuerza de tracción del hombre de ¿Qué fuerza horizontal es necesaria para modo que la caja suba a velocidad constante. mover el escritorio? a) 160N d) 180 2. Se remolca una caja de madera de 800N de θ = 37º b) 120 e) 100 c) 140 Un bloque de 5kg es jalado por una a) 688N b) 658 fuerza c) 628 “F” a través de una pista rugosa. Hallar “F” si d) 668 el bloque se mueve a velocidad constante. 37º e) 608 2 (g = 10 m/s ) 6. Si el bloque está a punto de resbalar. ¿Cuál es el 0,4 0,5 valor del coeficiente de rozamiento estático μS? F θ = 37º a) 0,75 b) 0,25 3. a) 30N b) 20 d) 80 e) 10 c) 0,5 c) 40 d) 0,6 Suponga que el peso de un trineo es de 200N y del esquimal que viaja en él 700N. 7. esquimal viaja en el trineo a velocidad 4. El bloque está a punto de deslizar. Hallar: μS. Si: W = 96N θ = 53 º ¿Con qué fuerza jalan los perros cuando el constante sobre un lago congelado? a) 3/10 μK = 0,3 b) 3/8 a) 300N d) 320 e) 0,8 b) 280 e) 180 c) 5/13 c) 270 60N 18N W d) 9/113 e) 3/17 Una fuerza de 100N es capaz de iniciar el movimiento de un trineo de 300N de peso 8. Hallar el coeficiente de rozamiento cinético si sobre la nieve compacta. Calcule μS el cuerpo de masa 12kg se mueve a velocidad θ = 37º constante. (g = 10 m/s ) θ = 37º a) 0,13 100 N b) 0,23 c) 0,43 d) 0,33 e) 0,53 2 s 37º F = 40 N a) 0,9 b) 0,6 c) 0,5 d) 0,7 e) 0,13 16N PAQUETE N.º 11 ROZAMIENTO ROZAMIENTO CON ACELERACIÓN 14. De la figura, se pide calcular la mínima 9. El bloque mostrado es llevado con aceleración, aceleración de m2 para que la masa m1 no jalado por F = 60N. Hallar la fuerza de rozamiento. resbale sobre m2 con coeficiente de fricción 2 a) 35 N a = 10 m/s estático 0,2 ( considere g = 9,8 m/s ) 2 b) 70 a) 35 m/s c) 40 4 kg F d) 20 b) 12 c) 45 e) 45 10. m1 m2 d) 49 e) 18 El bloque mostrado es llevado con F = 30N y con aceleración “a”. Calcule “a” a) 1 m/s 15. Encontrar el valor de la aceleración del bloque si μK = 1/4 2 a k = 1/10 b) 7 c) 4 a) 5 m/s F 5 kg y θ = 37º. 2 b) 6 d) 2 c) 8 e) 5 11. 2 d) 6 e) 4 En la figura el bloque pesa 20N y los coeficientes de rozamiento valen 0,4 y 0,6, Halle la aceleración del bloque. Aquí tienes 2 problemas de desafío… 2 (g = 10 m/s ) θ = 37º a) 9 m/s F = 25 N 2 b) 8 c) 5 UNMSM d) 12 e) 7 12. 1. Calcular la aceleración en el sistema mostrado. a) 9 m/s b) 3 c) 4 2 6kg 3kg d) 8 1kg e) 14 13. coeficiente de rozamiento es 0,5. a) 68N ; mB = 8kg c) 80 El bloque de la figura tiene una masa de 5 kg; la constante del resorte es de 200 N/m. El máximo estiramiento que se puede dar al resorte sin que el bloque se mueva es de 20cm. El coeficiente de fricción estático entre el 2 bloque y el piso es entonces: (g = 10 m/s ) A b) 60 c) 40 d) 66 e) 30 b) 70 e) 95 UNI 2003 2. Determinar la tensión de la cuerda, si el mA = 4kg a) 100 N d) 90 μ K = 0,5 80 N Un borrador de pizarra es presionado perpendicularmente a una pizarra vertical. Si el coeficiente estático de fricción es 0,3 y el peso del borrador es de 30N. La fuerza de presión necesaria para mantener el borrador en reposo es: B a) 0,5 b) 0,8 c) 0,7 d) 0,3 e) 0,9 PAQUETE N.º 11 ROZAMIENTO 0,1. Halle la fuerza de tracción del hombre de modo que la caja suba a velocidad constante. θ = 37º TAREA DOMICILIARIA ROZAMIENTO ESTÁTICO Y CINÉTICO a) 698N 1. Un estante pesa 300N y descansa b) 649 sobre el piso de la oficina con el cual el coeficiente de c) 209 rozamiento estático es 0,4. d) 350 ¿Qué fuerza horizontal es necesaria para e) 270 37º mover el escritorio? 2. a) 120N b) 150 d) 170 e) 160 6. c) 144 Si el bloque está a punto de resbalar. ¿Cuál es el valor del coeficiente de rozamiento estático μS? θ = 30º Un bloque de 20kg es jalado por una fuerza a) 1/√3 “F” a través de una pista rugosa. Hallar “F” si b) 1/2 el bloque se mueve a velocidad constante. c) 1/√2 2 (g = 10 m/s ) d) 1/4 e) 1/6 0,2 0,5 F 7. El bloque está a punto de deslizar. Hallar μS si W = 48N. θ = 53º a) 3/5 b) 3/8 3. a) 35N b) 40 d) 60 e) 18 c) 5/12 c) 80 4. d) 350 e) 280 8. 2 c) 300 a) 1/8 200 N b) 1/5 d) 1/3 37º e) 1/9 5. F = 80 N a) 0,9 b) 0,6 sobre la nieve compacta. Calcule μS θ = 37º s Hallar el coeficiente de rozamiento cinético si el cuerpo de masa 24kg se mueve a velocidad constante. (g = 10 m/s ) θ = 37º c) 1/2 Una fuerza de 200N es capaz de iniciar el movimiento de un trineo de 600N de peso c) 1/4 W d) 9/11 un lago congelado? μK =0,3 b) 270 9N e) 4/17 Suponga que el peso de un trineo es de 250N y del esquimal que viaja en él 750N. ¿Con qué fuerza jalan los perros cuando el esquimal viaja en el trineo a velocidad constante sobre a) 320N 30N Se remolca una caja de madera de 400N de peso empleando un plano inclinado que forma 37º con el horizonte. El coeficiente de rozamiento cinético entre la caja y el plano es d) 01/5 32N e) 01/7 ROZAMIENTO CON ACELERACIÓN 9. El bloque mostrado es llevado con aceleración, jalado por F = 120N. Hallar la fuerza de rozamiento. a) 30 N b) 38 c) 68 d) 80 e) 54 a = 5 m/s 8 kg 2 F PAQUETE N.º 11 10. ROZAMIENTO El bloque mostrado es llevado con F = 60N y con aceleración “a”. Calcule “a” a) 2 m/s 14. aceleración de m2 para que la masa m1 no resbale sobre m2 con coeficiente de fricción 2 2 estático 0,4 ( considere g = 10 m/s ) a k = 1/5 b) 9 c) 6 F 10 kg a) 36 m/s d) 3 c) 48 En la figura el bloque pesa 20N y los coeficientes de rozamiento valen 0,4 y 0,6, Halle la aceleración del bloque. 2 (g = 10 m/s ) θ = 37º a) 8 m/s F = 25 N 2 d) 40 e) 24 15. Encontrar el valor de la aceleración del bloque si μK = 1/2 y θ = 37º. b) 4 c) 3 c) 9 d) 2 d) 7 e) 5 e) 2 Calcular la mostrado. a) 4 m/s b) 3 c) 7 aceleración en el sistema 2 μ K = 0,5 160 N 2kg 6kg d) 12 2kg e) 15 13. Determinar la tensión de la cuerda, si el coeficiente de rozamiento es 0,5 mA = 2kg a) 60N ; mB = 4kg A b) 50 c) 20 d) 56 e) 39 m1 m2 a) 6 m/s2 b) 7 12. 2 b) 38 e) 4 11. De la figura, se pide calcular la mínima B
© Copyright 2026