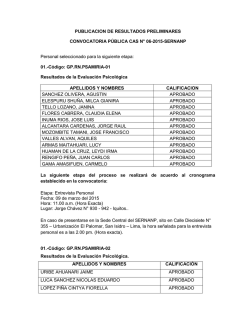
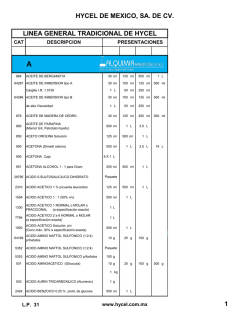
1. No category

Ingeniería Biomédica
Facultad de Ciencias Exactas y Tecnología
Universidad Nacional de Tucumán
Métodos Numéricos
TP N°6: Solución Numérica de Ecuaciones Diferenciales Ordinarias
1) Resolver los siguientes problemas de valor inicial utilizando el método de Euler como
se indica en cada caso:
 y ' = 1 + (t - y) 2
a) 
¨
 y ( 2) = 1
2≤t≤3
i)
Aproximar el valor de y(3) utilizando un paso h=0.25. Realizar las operaciones
utilizando aritmética de tres dígitos.
ii) Calcular el error local y global en cada paso sabiendo que la solución exacta es,
y (t ) = t +
1
1- t
iii) Completar el siguiente cuadro:
t
y real
Y aproximado
Elocal
Eglobal
iv) Grafique la solución exacta y la solución aproximada en un mismo sistema de
coordenadas.
v) Grafique el error global
vi) Que conclusiones puede sacar de los resultados obtenidos con este método?
2) Implementar el método de Euler en Matlab y rehacer nuevamente los cálculos del
apartado b) pero con un valor de h1=10-1 y h2=10-2.
3) Dado el siguiente problema de valor inicial
 y ' = t e 3t − 2 y

 y (0) = 0
0 ≤ t ≤1
a) Resolver utilizando el método de Euler Implícito como se indica en cada caso:
b) Sabiendo que la solución exacta es y (t ) =
1 3t 1 3t 1 − 2t
te − e + e
complete el
5
25
25
cuadro,
t
y real
Y aproximado
Elocal
Eglobal
c) Graficar las soluciones (exacta y aproximada) y graficar además los errores
4) Resuelva la siguiente EDO con un paso h constante con el método de Adams Bashford
(de orden 2)
Ingeniería Biomédica
Facultad de Ciencias Exactas y Tecnología
Universidad Nacional de Tucumán
Métodos Numéricos
 y ' = 2 x (1 + x 2 ) −1

 y (0) = 0
a) Estimar el error en el punto x = 1, la solución exacta es y ( x) = tg ( x ) , para
h=0.25.
b) Programar el método y rehacer los cálculos para valores pequeños de h
c) Grafique la solución verdadera, los valores calculados y los errores en cada caso.
2
5) Resulva le siguiente PVI utilizando el metodo de Huen
y 2 t

 y' = 2 + t e
t

 y (1) = 0
a) Pruebe manualmente con dos iteraciones del corrector y un valor de h = 0.25
b) Escriba un programa que implemente el método. Estimar el valor de y(2) aplicando
el método de Huen, con un paso h = 0.1 y con Epsilon=0.01.
6) Resuelva las siguientes ecuaciones usando alguno de los métodos vistos
 y ' ' = 3 y '−2 y + x

a)  y (0) = 1.75
 y ' (0) = 1.5

Su solución exacta es: y(x) = exp(x) + 0.5x + 0.75
u ' ' = −500u + 6880v
v' = 36u − 500v

b) 
u (0) = 83
v(0) = 6
Su solución exacta es: u(x) =83 exp(-2x), v(x) =6 exp(-2x)
Ejercicio adicional
Realice un cuadro comparativo entre los métodos para resolver EDOs que muestre:
características, orden, ventajas y desventajas.