1. No category

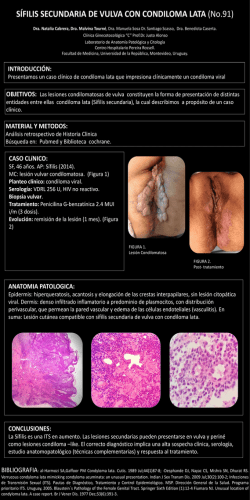
Problema:
¿De entre todas las latas cilíndricas de hojalata con capacidad de 100 cm cúbicos, cual requiere
menos metal?
Solución:
Arranquemos con el bosquejo de una lata cilíndrica: los datos que vamos a usar son el radio r
(dibujado en la figura con el color negro) y la altura h (color verde)
Recordar la fórmula para el volumen del cilindro:
De ahi, que según la condición que nos dá el problema: latas cilindricas de 100 cm cúbicos,
tendremos que tener en cuenta la siguiente restricción:
( )
Ahora hablemos de la superficie de la lata cilíndrica, dividámosla en tres partes diferenciables:
a) la tapa superior, cuya área se corresponde con el área del círculo:
b) la tapa inferior, área igual a la tapa superior:
c) el cuerpo de la lata cilíndrica: su área está dada por la fórmula de geometria: área de la
superficie del cilindro:
.
Sumando las tres areas anteriores obtenemos la superficie de nuestras latas cilíndricas, y la vamos
a expresar como la función área (A) respecto al radio r:
( )
( )
Esta es la función que debemos minimizar (es decir, hallar cual es el valor que debe tener r para
que A tenga su valor mas bajo), este propósito lo alcanzamos utilizando el cálculo diferencial,
recordar que se halla la derivada de la función que se desea maximizar/minimizar, esta derivada se
iguala a cero, se despeja la variable independiente (en este caso r) y luego se verifica si el valor
hallado (o valores) corresponden a máximos o mínimos de la función. (NOTA: Tener en cuenta que
en la función A depende de r, pero a su vez h es una función de r, por lo tanto la derivación que
hay que hacer es implícita como se muestra a continuación)
Comencemos:
Derivamos implícitamente la función del área de la lata cilíndrica respecto a r:
( )
(
(
))
( )
como vemos, al derivar implícitamente, nos ha resultado la expresión
, entonces procederemos
a derivar respecto a r el volumen, según la restricción que nos dió el problema, para poder hallar
el valor de
que luego reemplazaremos en (3):
(
)
(
(
Este valor de
)
)
que acabamos de obtener, lo reemplazamos en (3), igualamos la derivada
resultante a cero y por último procedemos a despejar a r:
(
(
))
(
(
(
)
)
)
( )
Notar que, según (2), la función superficie es una parábola que abre hacia arriba, por lo tanto el
número hallado en (4) es un MINIMO.
Sabiendo que
es un mínimo, y para cumplir con la restricción que hemos planteado desde
(1), vamos a despejar la h en (5):
y este resultado lo reemplazamos en (1):
(
)
√
Si tienes alguna duda, o esta respuesta te sirvió muy bien, no olvides usar la opción “Escribir al
autor”, en mi página www.gustavol.com