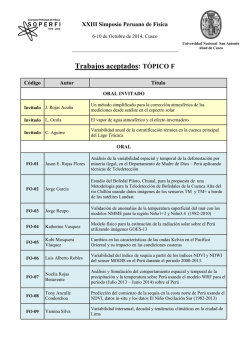
0500 MEDIDAS D VARIABILIDAD
Medidas de Variabilidad
Trabajo a realizar de este tema:
En Excel 2003 hoja 1, prepara un(os) cuadro(s) sinópticos o mapas
conceptuales o mapas mentales que sinteticen éste capítulo.
En la hoja 2 y en la hoja 3 del mismo libro de Excel resuelve los problemas 8 y
15 que están al final de este tema. Los ejercicios 5 y 9 los realizarás a mano y
los entregarás en sobre conforme al protocolo indicado. Anota las fórmulas
empleadas en ambos trabajos.
El nombre del archivo deberá ser:
05 MEDIDAS D VARIABILIDAD APELLIDO NOMBRE
Se calificará de la siguiente manera:
+ Ortografía (2 puntos)
Protocolo de envío:
+ Asunto: mal anotado el 100% del trabajo
+ Nombre (1 punto)
+ Comentario (2 punto)
+ Nombre del archivo (1 punto)
+ Versión diferente a 2003 (7 puntos)
En el trabajo solución, tanto en Excel como el trabajo escrito:
Comentario o conclusión del trabajo
(2 punto)
Ortografía: (1 punto)
Nombre
Universidad
Carrera
Materia
Tema
Fecha
(La ausencia total o de alguna parte
restará 1 punto)
A continuación, y sin dejar hoja en blanco, el desarrollo del trabajo (1 punto
menos de no cumplirlo). Se calificará la realización de las síntesis.
MEDIDAS DE VARIABILIDAD
0500 MEDIDAS D VARIABILIDAD.doc
1
Medidas de Variabilidad
¿Qué son las medidas de variabilidad?
Rango
Desviación media
La varianza y la desviación estándar
Coeficiente de variación
Rango intercuartilar
Problemas
¿Qué son las medidas de variabilidad?
La puntuación media en una distribución es importante en muchos contextos de
investigación. Pero también lo es otro conjunto de estadísticos que cuantifican que
tan variables, o que tan dispersas, tienden a ser las puntuaciones. ¿Las
puntuaciones varían mucho, o tienden a tener valores muy similares. A veces, la
variabilidad en las puntuaciones es la cuestión central en una investigación. La
variabilidad es un concepto cuantitativo, de modo que nada de esto se aplica a las
distribuciones de datos cualitativos.
Hay varias razones para analizar la variabilidad en una serie de datos. Primero, al
aplicar una medida de variabilidad podemos evaluar la medida de tendencia
central utilizada. Una medida de variabilidad pequeña indica que los datos están
agrupados muy cerca, digamos, de la media. La media, por lo tanto es
considerada bastante representativa de la serie de datos. Inversamente, una gran
medida de variabilidad indica que la media no es muy representativa de los datos.
Una segunda razón para estudiar la variabilidad de una serie de datos es para
comparar como están esparcidos los datos en dos o más distribuciones. Por
ejemplo, la calificación promedio de dos estudiantes, A = {90, 80, 75, 75 } y B =
{90, 55, 85, 90 }, es de 80. Basados en esto podríamos pensar que sus
calificaciones son idénticas. Pero si revisamos el detalle de sus calificaciones
vemos que esta conclusión no es correcta.
Hay muchas medidas de variabilidad intuitivamente atractivas, pero poco
utilizadas, como el rango, la desviación media y la desviación cuartilar. De
lejos, las medidas de variabilidad más ampliamente utilizadas son las que tienen
que ver con cómo extender los resultados a partir de la media. Estas son la
desviación estándar (s), y la varianza (s² o "var").
MEDIDAS DE VARIABILIDAD
0500 MEDIDAS D VARIABILIDAD.doc
2
Rango
La forma más sencilla de medir la variabilidad es el rango. Es la diferencia entre
los más altos y más bajos valores en un conjunto de datos no agrupados. En la
forma de una ecuación:
Rango = valor más alto - valor más bajo
El rango tiene la ventaja de ser fácil de calcular y entender.
Ejemplo:
Las calificaciones de cinco estudiantes de estadística son: 8, 8, 10, 6, y 8. ¿Cuál
es el rango de las calificaciones?
Rango = valor más alto - valor más bajo = 10 - 6 = 4
Rango para datos agrupados
Para estimar el rango de una distribución de frecuencia se resta el límite inferior
del intervalo de clase más chico del límite superior del intervalo de clase más
grande
Ejemplo:
Una muestra de las edades del público de un concierto se encuentra distribuida de
la siguiente manera:
Edades Número de personas
15 - 19
2
20 - 24
1
25 - 29
4
30 - 34
15
35 - 39
10
40 - 44
5
45 - 49
3
Rango = mayor limite superior - menor límite inferior = 49 - 15 = 34
(Valor absoluto de un número a = | a | es el número a sin su signo.)
MEDIDAS DE VARIABILIDAD
0500 MEDIDAS D VARIABILIDAD.doc
3
Desviación media (Dm)
La desviación media mide la cantidad promedio que varían los datos respecto a
su media. La definición es:
Desviación media es la media aritmética de los valores absolutos de las
desviaciones de los datos respecto a su media.
La fórmula de la desviación media para datos no agrupados (Dm) es:
Dm =
Σ| X -
|
n
Ejemplo:
Las calificaciones de cinco estudiantes de estadística son: 8, 8, 10, 6, y 8. ¿Cuál
es la desviación media de las calificaciones?
X
X-
|X -
8
0
0
8
0
0
10
+2
2
6
-2
2
8
0
0
Σ=4
X=8
Dm =
Σ| X n
MEDIDAS DE VARIABILIDAD
|
|
=
4
= 0.8
5
0500 MEDIDAS D VARIABILIDAD.doc
4
Desviación media para datos agrupados
En el caso de que los datos se encuentren agrupados en una distribución de
frecuencia la fórmula es :
Dm =
Σf | X -
|
n
Ejemplo:
Se tienen los siguientes datos agrupados:
LI LS X
F
FX
|X–X| F|X–X|
15 19 17
2
34
17.12
34.24
20 24 22
1
22
12.12
12.12
25 29 27
4
108
7.12
28.48
30 34 32
15
480
2.12
31.80
35 39 37
10
370
2.88
28.80
40 44 42
5
210
7.88
39.40
45 49 47
3
141
12.88
38.64
n =40 ΣfX = 1365
=
Σfx
n
Dm =
=
1365
Σ 213.48
= 34.12
40
213.48
5.337
40
Ventajas y Desventajas de la desviación media
La desviación media tiene dos ventajas. Utiliza para su cómputo todos los
elementos de la serie de datos y es facil de entender.
MEDIDAS DE VARIABILIDAD
0500 MEDIDAS D VARIABILIDAD.doc
5
La varianza (σ2 ó S2) y la desviación estándar (σ ó S)
Concepto de varianza y desviación estándar
La varianza y la desviación estándar sirven para cuantificar la variabilidad de una
muestra midiendo su dispersión alrededor de la media. La definición es la
siguiente:
2
Varianza. (σ ó S2) (σ = sigma) Es la media aritmética de las desviaciones
cuadradas de los datos respecto a la media.
Desviación estándar. (σ ó S) Es la raíz cuadrada de la varianza.
Varianza y Desviación Estándar para datos no agrupados
Las fórmulas de la varianza de una población y de una muestra son ligeramente
diferentes. Las fórmulas son:
σ 2=
(Σx)2
Σx2 -
(Σx)²
Σx2 -
N
n
S2=
N
n-1
varianza de una población
varianza de una muestra
Las desviaciones estándar de la población y muestra se calculan simplemente
sacando la raíz cuadrada a la respectiva varianza.
desviación estándar de una población
σ = σ2
desviación estándar de una muestra
MEDIDAS DE VARIABILIDAD
0500 MEDIDAS D VARIABILIDAD.doc
S= S2
6
Ejemplo
El contenido de cinco botellas de perfume seleccionadas de forma aleatoria de la
línea de producción son (en ml): 85.4, 85.3, 84.9, 85.4, y 84.0. ¿Cuál es la
varianza y la desviación estándar de las observaciones muestreadas?
X
85.4
85.3
84.9
85.4
84.0
Σx= 425.0
Σx 2
(Σx)2
n
S2=
=
36126.42 -
S=
S2 =
(425)2
5
n-1
X2
7293.16
7276.09
7208.01
7293.16
7056.00
2
Σx = 36126.42
= 0.355
5-1
0.355 = 0.5958
Varianza y Desviación Estándar para datos agrupados
Si los datos están agrupados en una distribución de frecuencia, la varianza y la
desviación estándar de la muestra se pueden aproximar sustituyendo Σfx² en Sx²
y Σfx en Sx. Las fórmulas quedarían de la siguiente manera:
σ 2=
(Σfx)2
Σfx2 -
Σfx2 -
N
S2=
N
varianza de una población
desviación estándar de una población
n
n-1
varianza de una muestra
σ = σ2
desviación estándar de una muestra
MEDIDAS DE VARIABILIDAD
(Σfx)2
0500 MEDIDAS D VARIABILIDAD.doc
S= S2
7
Ejemplo:
2
Calcular la varianza (σ ó S2) y la desviación estándar (σ ó S) de la siguiente
distribución de frecuencia del número de meses de duración de una muestra de 40
baterías para coche.
duración de las baterías (meses) Número de baterías
15 - 19
2
20 - 24
1
25 - 29
4
30 - 34
15
35 - 39
10
40 - 44
5
45 - 49
3
Primeramente, calculamos la marca de clase, para después calcular los productos
fX y fx2 para proceder finalmente a calcular las sumatorias ΣfX y Σfx2 y aplicar las
fórmulas.
LI LS X
F
FX
FX2
15
19
17
2
34
588
20
24
22
1
22
484
25
29
27
4
108
2916
30
34
32
15
480
15360
35
39
37
10
370
13690
40
44
42
5
210
8820
45
49
47
3
141
6627
n =40 ΣfX = 1365 Σfx2 = 48475
Σfx 2
(Σfx)2
n
S2=
48475 =
n-1
40
= 48.573
40 - 1
S=
MEDIDAS DE VARIABILIDAD
(1365)2
S2 = 48.573 = 6.969
0500 MEDIDAS D VARIABILIDAD.doc
8
Coeficiente de variación
El coeficiente de variación se define como la razón de la desviación estándar entre
la media aritmética.
C.V. =
σ
x
( 100 )
Ventajas
El coeficiente de variación es útil cuando pretende comparar la variabilidad de dos
o más conjuntos de datos expresados en diferentes unidades de medición, pues el
resultado será señalado en porcentajes.
Desventajas
Cuando el valor de la media es cercano a cero, el coeficiente de variación es muy
sensible a pequeños cambios en la media, limitando su utilidad
A diferencia de la desviación estándar este no puede ser utilizado para elaborar
intervalos de confianza para la media.
1
Interpolación es la construcción de nuevos puntos partiendo del conocimiento de un conjunto discreto de
puntos.
MEDIDAS DE VARIABILIDAD
0500 MEDIDAS D VARIABILIDAD.doc
9
Problemas
Para cada uno de los siguientes problemas calcule :
(a) el rango
(b) la desviación media r
(c) la varianza
(d) la desviación estánda
(e) el coeficiente de variación
1. Los resultados siguientes representan las calificaciones del examen final de un
curso de estadística elemental.
23
60
79
32
57
74
52
70
82
36
80
77
81
95
41
65
92
85
55
76
52
10
64
75
78
25
80
98
81
67
41
71
83
54
64
72
88
62
74
43
60
78
89
76
84
48
84
90
15
79
34
67
17
82
69
74
63
80
85
61
2. El gerente de una firma especializada en renta de condominios para
vacacionistas, quiere saber como están distribuidas los montos de las rentas
mensuales de los departamentos de la firma. Seleccionó una muestra de
departamentos cuyas muestras son mostradas abajo.
Rentas mensuales de los condominios
1170
1207
1581
1277
1305
1472
1077
1319
1537
1849
1332
1418
1949
1403
1744
1532
1219
896
1500
1671
1471
1399
1041
1379
821
1558
1118
1533
1510
1760
1826
1309
1426
1288
1394
1545
1032
1289
695
803
1440
1421
1329
1407
718
1457
1449
1455
2051
1677
1119
1020
1400
1442
1593
1962
1263
1788
1501
1668
1352
1340
1459
1823
1451
1138
1592
982
1981
1091
MEDIDAS DE VARIABILIDAD
0500 MEDIDAS D VARIABILIDAD.doc
10
3. Los siguientes datos representan la duración de la vida en meses de 30 bombas
de combustible similares.
24
36
4
40
16
15
18
6
30
60
3
72
66
78
3
28
67
72
15
3
18
48
71
22
57
9
54
4
12
72
4. Los siguientes datos representan la duración de la vida, en segundos, de 50
moscas sometidas a un nuevo atomizador en un experimento de laboratorio
controlado.
17
20
10
9
23
13
12
19
18
24
12
14
6
9
13
6
7
10
13
7
16
18
8
13
3
32
9
7
10
11
13
7
18
7
10
4
27
19
16
8
7
10
5
14
15
10
9
6
7
15
5. Se aplicó una encuesta donde se les pide indicar el número de amigos o
parientes que visitan cuando menos una vez al mes. Los resultados son los
siguientes:
3
5
2
3
3
4
1
8
4
2
4
2
5
3
3
3
0
3
5
6
4
3
2
2
6
3
5
4
14
3
5
6
3
4
2
4
9
4
1
4
2
4
3
5
0
4
3
5
7
3
5
6
2
2
MEDIDAS DE VARIABILIDAD
0500 MEDIDAS D VARIABILIDAD.doc
11
6. Una compañía de cambio de aceite tiene varias sucursales en la zona
metropolitana. El número de cambios de aceite en la sucursal de la calle Roble en
los pasados 20 días son:
66
98
55
62
79
59
51
90
72
56
70
62
66
80
94
79
63
73
71
85
7. El gerente local un negocio de comida rápida esta interesado en el número de
veces que un cliente compra en su tienda durante un periodo de dos semanas.
Las respuestas de los 51 clientes fueron:
5
3
3
1
4
4
5
6
4
2
6
6
6
7
1
1
14
1
2
4
4
4
5
6
3
5
3
4
5
6
8
4
7
6
5
9
11
3
12
4
7
6
5
15
1
1
10
8
9
2
12
8. El presidente de una agencia de viajes, quiere información sobre las edades de
la gente que toma cruceros por el Caribe. Una muestra de 40 clientes que tomaron
un crucero el año pasado reveló estas edades:
77
18
63
84
38
54
50
59
54
56
36
26
50
34
44
41
58
58
53
51
62
43
52
53
63
62
62
65
61
52
60
45
66
83
71
63
58
61
71
60
9. Una cadena de tiendas de artículos deportivos al servicio de esquiadores
principiantes, planea hacer un estudio de cuanto gasta un esquiador principiante
en su primera compra de equipo. Una muestra de recibos de sus cajas
registradoras reveló esas compras iniciales.
140
82
265
168
90
114
172
230
142
86
125
235
212
171
149
156
162
118
139
149
132
105
162
126
216
195
127
161
135
172
220
229
129
87
128
126
175
127
149
126
121
118
172
126
MEDIDAS DE VARIABILIDAD
0500 MEDIDAS D VARIABILIDAD.doc
12
10.- Se conduce un estudio de los efectos de fumar sobre los patrones de sueño.
La medición que se observa es el tiempo, en minutos, que toma quedar dormido.
Se obtienen estos datos:
69
56
22
28
41
28
47
53
48
30
34
13
52
34
60
25
21
37
43
23
13
31
29
38
26
36
30
11. Un banco seleccionó una muestra de 40 cuentas de cheques de estudiantes.
Abajo aparecen sus saldos de fin de mes.
404
74
234
149
279
215
123
55
43
321
87
234
68
489
57
185
141
758
72
863
703
125
350
440
37
252
27
521
302
127
968
712
503
498
327
608
358
425
303
203
12.- Una compañía de luz seleccionó una muestra de 20 clientes residenciales.
Los siguientes datos son las cuentas que se les facturó el mes pasado:
54
48
58
50
25
47
75
46
60
70
67
68
39
35
56
66
33
62
65
67
13.- Una muestra de suscriptores de una compañía telefónica reveló los siguientes
números de llamadas recibidas en la última semana.
52
43
30
38
30
42
34
46
32
18
41
5
MEDIDAS DE VARIABILIDAD
12
0500 MEDIDAS D VARIABILIDAD.doc
46
39
37
13
14. A los solicitantes del puesto de ensamblador de una empresa mueblera se les
aplica una prueba. La prueba consiste en tomar el tiempo que tardan en
ensamblar cierto mueble.
La siguiente es una distribución de frecuencia los tiempos registrados por una
muestra de 42 solicitantes.
Tiempo (minutos) Número de solicitantes
1-3
4
4-6
8
7-9
14
10 - 12
9
13 - 15
5
16 - 18
2
15. La siguiente es una distribución de frecuencia de una muestra de los pagos
realizados en un estacionamiento del centro de la ciudad el sábado pasado
Cantidad pagada ($) Número de clientes
MEDIDAS DE VARIABILIDAD
5-9
2
10 - 14
7
15 - 19
15
20 - 24
28
25 - 29
14
30 - 34
9
35 - 39
3
40 - 44
2
0500 MEDIDAS D VARIABILIDAD.doc
14
© Copyright 2026