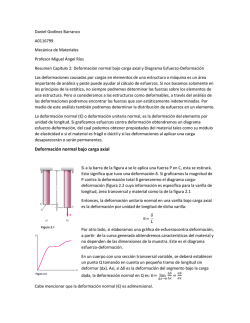
El ensayo de tracción 1.1 Curva esfuerzo
Comportamiento Mecánico de Sólidos Capítulo I. El ensayo de tracción El ensayo de tracción 1.1 Curva esfuerzo - deformación ingenieril El Ensayo de tracción se realiza bajo la norma ASTM E-8, o bien la norma chilena NCH 200, entre otras. Su importancia radica en que es válido y aceptado para especificación de materiales en ingeniería. La información básica que se puede extraer de un ensayo de tracción se resume en la figura siguiente: i P A0 Offset yield strength: Límite elástico convencional Resistencia tensil o UTS Esfuerzo de fractura Deformación uniforme Deformación a fractura Figura 1. Diagrama esfuerzo – deformación. i = esfuerzo ingenieril = P/A0 i = deformación ingenieril = l l0 i l l0 en que P es la carga aplicada a A0 es el área inicial siendo l = l – l0 el alargamiento de la probeta, l su longitud instantánea y l0 su longitud inicial El UTS (Ultimate Tensile Strength), se refiere al esfuerzo tensil en el punto de carga máxima. Durante la deformación elástica el volumen no se mantiene constante. Para esfuerzos comprendidos entre el esfuerzo de fluencia y el UTS se cumple que Al A0 l 0 Deformación elástica y plástica. Por sobre el límite elástico, coexisten la deformación elástica y plástica. En la figura 2 se muestra un diagrama esfuerzo-deformación, en el cual pueden verse las zonas elástica y plástica, para dos niveles de deformación. Departamento de Ingeniería Metalúrgica – USACH. 1-1 Comportamiento Mecánico de Sólidos Capítulo I. El ensayo de tracción Carga P2 P1 A' a b Deformación B' c d Figura 2. Diagrama esfuerzo – deformación mostrando las deformaciones elástica y plástica. En la figura, el segmento b viene dado por: b y el segmento d: d P1 A0 E P2 A0 E Además d > b dado que P2 P1 y por lo tanto, la deformación elástica es mayor en P2 que en P1. 1.2 Ductilidad La ductilidad se mide por la deformación ingenieril de fractura f y por la reducción de área. La deformación ingenieril a fractura se define como: f l f l0 l0 a su vez la reducción de área se define como: q A0 A f A0 A l 1 0 l0 A 1 q l0 y l son las longitudes inicial e instantánea; A0 y A son las áreas inicial e instantánea. Af y lf son el área y la longitud finales. 1-2 Departamento de Ingeniería Metalúrgica – USACH. Comportamiento Mecánico de Sólidos Capítulo I. El ensayo de tracción 1.3 Módulo de elasticidad (módulo de Young) El módulo de elasticidad corresponde a la pendiente de la parte lineal de la curva . Mide la rigidez del material y está relacionado con las fuerzas de enlace atómicas. En general, se encuentra que el módulo de elasticidad es poco afectado por los elementos de aleación, por tratamientos térmicos o por trabajo en frío. Al subir la temperatura, disminuye el módulo de elasticidad, tal como se desprende de la tabla 1. Tabla 1. Valores típicos del módulo de elasticidad a diversas temperaturas en GPa. Material Acero al Carbono Acero inoxidable austenítico Aleaciones de titanio Aleaciones de aluminio Tamb 477 K 207 186 193 176 114 97 72 66 700 K 155 159 74 54 810 K 134 155 70 922 K 124 145 1.4 Resiliencia Es la capacidad de un material para absorber energía cuando se deforma elásticamente. 1.5 Módulo de Resiliencia Corresponde a la energía de deformación por unidad de volumen requerida para deformar el material hasta el límite elástico 0 . 2 J 1 1 U R 0 0 0 · 0 0 3 2 2 E 2E m De esta relación se deduce que el material ideal para construir un resorte debe poseer un alto 0 y un bajo módulo de elasticidad. En la figura 3, se muestra una comparación entre dos aceros, uno de los cuales resulta apropiado para la construcción de resortes. En la tabla 2 se muestran valores del módulo de resiliencia para varios materiales. Tabla 2. Módulos de resiliencia de varios materiales. Material E(GPa) 0 (MPa) UR(kPa) Acero medio C Acero alto C para resortes Duraluminio Cobre Goma Acrílico 207 207 72 110 0.0010 3.4 Departamento de Ingeniería Metalúrgica – USACH. 310 965 124 28 2.1 14 232 2250 107 3.5 2140 28 1-3 Comportamiento Mecánico de Sólidos Capítulo I. El ensayo de tracción Acero alto C (Resortes) Acero estructural Resiliencia Figura 3. Curva esfuerzo – deformación para dos tipos de aceros. 1.6 Tenacidad Es la capacidad para absorber energía en el rango plástico. Corresponde al área bajo la curva . Esfuerzo y deformación verdaderos. El esfuerzo y la deformación verdaderos se definen como v P A d v l dl v ln f l l0 en que P es la carga aplicada, A el área instantánea y l la longitud instantánea Se cumplen las siguientes relaciones v ln 1 i v i 1 i En la figura 4 se muestran una comparación entre las curvas verdaderas e ingenieril. Estas ecuaciones son válidas hasta la deformación uniforme. Más allá de este punto se cumple que v ln A0 D 2 ln 0 A D En que D0 y D son el diámetro inicial e instantáneo respectivamente. Esfuerzo ingenieril a carga máxima. Se define como: 1-4 Departamento de Ingeniería Metalúrgica – USACH. Comportamiento Mecánico de Sólidos Capítulo I. El ensayo de tracción iu Pmáx A0 El superíndice, a veces subíndice u, se utiliza para especificar el punto de carga máxima. v-v ii Figura 4. Comparación entre curvas verdaderas e ingenieriles. El esfuerzo verdadero en la carga máxima uv se define como: vu Pmáx Au A su vez, la deformación verdadera en la carga máxima corresponde a vu ln A0 Au en que Au es el área en la carga máxima Eliminando Pmáx se obtiene vu iu A0 Au vu iu exp vu 1.7 Esfuerzo de fractura verdadero. Se define como: v PFract AFract PFract la carga de fractura y AFract es el área en la fractura. Departamento de Ingeniería Metalúrgica – USACH. 1-5 Comportamiento Mecánico de Sólidos Capítulo I. El ensayo de tracción 1.8 Deformación verdadera a fractura Corresponde a vf ln vf ln A0 Af 1 1 q q corresponde a la reducción de área y Af es el área de la probeta fracturada, medida en el cuello. 1.9 Deformación uniforme verdadera. Corresponde a la deformación verdadera en la carga máxima y se calcula a partir de las áreas, a partir de. vu ln A0 Au en que Au es el área a carga máxima. 1.10 Deformación verdadera local en el cuello Es la deformación necesaria para deformar la muestra desde la carga máxima hasta la fractura. Se calcula a partir de vn ln Au Af 1.11 Ajuste de Hollomon Para la zona de deformación plástica uniforme se puede relacionar el esfuerzo verdadero con la deformación verdadera por: v K v n en que K es una constante y n corresponde a la pendiente de ln 0 vs ln v .n recibe el nombre de índice de endurecimiento por deformación. K es una constante. n es el índice de endurecimiento por deformación. Si n=0 el material es perfectamente plástico. n=1 corresponde a un sólido elástico. Normalmente para la mayoría de los materiales, 0.10 < n <0.50 En la tabla 3 se muestran valores típicos de n y K para diversos materiales. 1-6 Departamento de Ingeniería Metalúrgica – USACH. Comportamiento Mecánico de Sólidos Capítulo I. El ensayo de tracción Tabla 3. Valores para n y K para metales a temperatura ambiente. Metal Condición n K (MPa) Acero 0.05%C Recocido 0.26 530 SAE 4340 Recocido 0.15 640 0.10 1570 0.19 1230 0.54 320 Templado y Revenido a 540ºC Templado y Revenido a 705ºC Acero 0.6%C Acero 0.6%C Cobre Recocido Latón 70/30 Recocido 0.49 900 d La expresión corresponde a la velocidad de endurecimiento por deformación. d n se calcula graficando ln v vs ln v hasta la deformación plástica uniforme. La pendiente de la recta resultante corresponde a n. n d ln d d ln d d n d 1.12 Otros ajustes Otros ajustes, son los que se muestran a continuación: 0 K n Ecuación de Ludwik en que 0 es el Esfuerzo de fluencia c(1 me n ) Ecuación de Voce En que c, m y n parámetros propios del material c( m ) n Potencia generalizada c, m y n son parámetros del material 1 E 0 Ecuación de Ramberg-Osgood 3 7 m m 1 1 n o, E y m dependen del material Departamento de Ingeniería Metalúrgica – USACH. 1-7 Comportamiento Mecánico de Sólidos Capítulo I. El ensayo de tracción E y y tgh Ecuación Prager 1.13 Inestabilidad en tensión. A continuación se estudia con algún detalle, el fenómeno de formación de cuello. El primer aspecto a tener en cuenta es que la formación de cuello ocurre en la carga máxima En este punto, el incremento de esfuerzo debido a la disminución en la sección transversal supera al incremento en la resistencia debida al endurecimiento por deformación. Matemáticamente esto corresponde a dP 0 Dado que: P vA v dA Ad v 0 d v dA v A Pero dV=0, por lo tanto con lo que o bien: d v v d v d v v dl dA d v l A d v ecuación que caracteriza al punto de inestabilidad. El punto de inestabilidad en la curva v v puede ser encontrado: a) b) Por el punto sobre la curva con subtangente unidad. Por el punto de la curva donde la velocidad de endurecimiento por deformación iguala al esfuerzo. d v d v En la figura 5(a) al trazar una tangente a la curva v - v de tal forma que la distancia horizontal entre la proyección del punto de tangencia al eje horizontal (u) y el punto de corte con el mismo eje de la tangente, sea uno, se cumple que la pendiente de la tangente es v/1. Además la pendiente de dicha tangente es igual a la de la curva, por lo tanto dv/dv = v. 1-8 Departamento de Ingeniería Metalúrgica – USACH. Comportamiento Mecánico de Sólidos Capítulo I. El ensayo de tracción v v d v v d v u 1 v u Figura 5. Determinación de la deformación uniforme. (a) Subtangente unidad (b) d/d = 0 En la figura 5(b) se muestra la relación se muestra la relación d v v superpuesta a la v d v v. En el punto de corte de ambas curvas se encontrará el UTS, dado que d v v para ese d v punto. 1.13.1 Criterio de Considere El criterio de Considere para la determinación del UTS, se basa en que en una gráfica v i , se cumple que d v v (*). d i 1 i La demostración de esta ecuación puede verse a continuación: dl d v d v d i d v l 0 d v l d v (1 i ) v d v d i d v d i dl d i l 0 d i l A partir de d v v , se traza v i d i 1 i Se marca el punto i 1 y se traza desde este punto la tangente a la curva v i . Así se determina vu cumpliéndose la ecuación (*). Departamento de Ingeniería Metalúrgica – USACH. 1-9 Comportamiento Mecánico de Sólidos Capítulo I. El ensayo de tracción v vu i u 1 Figura 6. Esquema del criterio de Considere. 1.13.2 Relación entre la deformación verdadera uniforme y el índice de endurecimiento por deformación. Dado que d v v y v K vn d v Kn vn 1 K vn vu n Es decir, la deformación uniforme es igual al índice de endurecimiento por deformación. 1 - 10 Departamento de Ingeniería Metalúrgica – USACH. Comportamiento Mecánico de Sólidos Capítulo I. El ensayo de tracción 1.13.3 Distribución de esfuerzos en el cuello Durante la formación de cuello aparece un estado triaxial de esfuerzos. x x 2a r R t x Figura 7. Triaxialidad de esfuerzos durante la formación de cuello. En la zona del cuello se producen esfuerzos radiales y transversales que elevan el valor del esfuerzo para generar deformación plástica. Bridgman (Premio Nobel de Física en 1946), demostró que: x AVG x AVG a 2R 1 ln 1 a 2 R es el esfuerzo promedio en la dirección axial = carga/área transversal mínima es esfuerzo uniaxial correspondiente a aquel que habría si el cuello no introdujera esfuerzos triaxiales. R es el radio de curvatura del cuello y a es el radio de la probeta en el cuello. Departamento de Ingeniería Metalúrgica – USACH. 1 - 11 Comportamiento Mecánico de Sólidos Capítulo I. El ensayo de tracción 1.13.4 Variación de la ductilidad local con la posición La elongación a rotura depende de la distancia que se use como referencia para medir deformación. En este sentido, la deformación no constituye una propiedad del material. En la figura 8, se muestra la dependencia de la deformación con el tamaño de la zona elegida para medir la deformación. Elongación Local Distancia Figura 8. Deformación en función de la distancia. 1.14 Efecto de la velocidad de deformación sobre las propiedades Uno de los parámetros importantes en la determinación de las propiedades mecánicas, lo constituye la velocidad de deformación , definida por: d dt s 1 En general se observa que al aumentar , se produce un aumento en el límite elástico del material, tal como puede apreciarse en la figura 9. Dicho aumento es más significativo a alta temperatura. El UTS no es tan influenciado por como lo es el esfuerzo de fluencia. En la tabla 4 se resumen los rangos de velocidad de deformación para varios tipos de ensayos. 1 - 12 Departamento de Ingeniería Metalúrgica – USACH. Comportamiento Mecánico de Sólidos Capítulo I. El ensayo de tracción 0 (Límite elástico) (MPa) 102 298 K 10 620 1 K K 720 K 820 K 870 100 10-5 10-4 10-3 10-2 s 1 Figura 9. Esfuerzo de fluencia a 0.2% de deformación frente a velocidad de deformación para aluminio 6063-0. Tabla 4. Velocidades de deformación. Rango (s-1) 10-8 – 10 –5 10-5 – 10-1 10-1 – 102 102 – 104 104 – 108 Tipo de Test Fluencia (creep) a = cte. Ensayo de tracción estático Ensayos de tracción o compresión dinámicos Ensayos a alta velocidad usando barras de impacto Ensayos a muy alta velocidad usando explosivos o propulsores de gas 1.15 Velocidad de la Cruceta. La velocidad a la que se desplaza la cruceta es usualmente una forma de controlar el ensayo de tracción. Algunas máquinas de ensayos, poseen una cruceta móvil en la parte superior, otras poseen la cruceta móvil en la parte superior. En cualquier caso, dicha velocidad es: v dL L dt La velocidad de deformación i es L Lo d L d i i o dt dt Departamento de Ingeniería Metalúrgica – USACH. 1 dL v L Lo dt Lo Lo 1 - 13 Comportamiento Mecánico de Sólidos Capítulo I. El ensayo de tracción cruceta probeta cruceta Figura 10. Esquema de la cruceta durante el ensayo de tracción. por lo que la velocidad de deformación ingenieril es proporcional a la velocidad de desplazamiento de la cruceta. La velocidad de deformación verdadera v es: d ln L L d 1 dL v L o v v dt dt L dt L L Se pueden relacionar i con v a través de: v v Lo d i 1 d i i L L dt 1 i dt 1 i v i 1 i v , si la velocidad de la cruceta es constante, la velocidad de deformación L verdadera disminuirá a medida que se alarga la muestra. dado que v 1.16 Relación entre el esfuerzo de fluencia y la velocidad de deformación A temperatura y deformación constantes, la relación entre el esfuerzo de fluencia y la velocidad de deformación en que C es una constante. C m m = sensibilidad a la velocidad de deformación y se obtiene de la pendiente de ln vs ln . Otra forma de evaluar m es a través de un ensayo a variable tal como se muestra en la figura 11, de acuerdo a: 1 - 14 Departamento de Ingeniería Metalúrgica – USACH. Comportamiento Mecánico de Sólidos Capítulo I. El ensayo de tracción ln ln 2 / 1 ln m ln 2 1 ln ,T ,T ln 2 2 1 2 1 1 1 Figura 11. Dependencia del esfuerzo de fluencia con la velocidad de deformación. En general, par metales a temperatura ambiente, m 0.1. Además, m crece con la temperatura. Para aceros, se puede escribir: k1 k2 ln o k1, k2 y o constantes: Ejemplo: Para aluminio puro, deformado un 25%, los valores de C y m se muestran en la Tabla 5. Tabla 5. Coeficientes C y m para aluminio puro con = 0,25. 294 K 713 K C 70.3 MPa 14.5 MPa m 0.066 0.211 Determinar el cambio en el esfuerzo de fluencia al cambiar en dos órdenes de magnitud. Respuestas 294 K 713 K 2/1=1.35 2/1=2.64 1.17 Enfoque microscópico El valor de m se relaciona con la movilidad de las dislocaciones. Departamento de Ingeniería Metalúrgica – USACH. 1 - 15 Comportamiento Mecánico de Sólidos Capítulo I. El ensayo de tracción La velocidad de movimiento de las dislocaciones depende del esfuerzo aplicado a través de: v A m´ en que A es una constante. A su vez la velocidad de deformación se relaciona con la movilidad de las dislocaciones por bv en que es la densidad de dislocaciones y b el vector de Burger asociado. ln m ln ,T 1 ln ln ln v m ln ln ln ln v m, ln pero m, 1 ln m ln si no hay cambios en la densidad de las dislocaciones al cambiar el esfuerzo, ln 0 , por n lo tanto: m, parámetro microscópico 1 m parámetro macroscópico Los valores de m para algunos materiales son: Aleaciones Superplásticas m Vidrio caliente m=1 Sólido Newtoniano = alto En un metal normal el ablandamiento geométrico que constituye la formación de cuello se d la muestra no forma cuello. opone al endurecimiento por deformación y siempre que d Para un material superplástico, la velocidad de endurecimiento por deformación es baja y d d 1 - 16 no forma cuello. Departamento de Ingeniería Metalúrgica – USACH. Comportamiento Mecánico de Sólidos Capítulo I. El ensayo de tracción 1.18 Influencia del índice m en la formación de cuello Para evaluar la influencia del índice m en la formación de cuello, se considerará una barra de un material superplástico de área A que se carga con una fuerza P. P m C A P C pero: m 1 A 1 m 1 dL 1 dA L dt A dt dA 1 1 P A A m dt C 1 1 m dA P dt C 1 m 1 1m / m A En la figura 11 puede observarse la dependencia de dA/dt con el área. Si m<1 cualquier disminución en el área produce una gran disminución en la sección transversal. Esto significa que el cuello debería agudizarse, en el sentido de acentuarse el estrechamiento. Si m = 1 la deformación es viscoso Newtoniana y dA/dt es independiente de A; cualquier cuello incipiente es preservado durante la elongación y no se propaga. Si m 1 disminuye la velocidad del crecimiento del cuello. Departamento de Ingeniería Metalúrgica – USACH. 1 - 17 Comportamiento Mecánico de Sólidos Capítulo I. El ensayo de tracción dA dt m=1 m = 3/4 m = 1/2 m = 1/4 A Figura 12. Dependencia de la velocidad de disminución de área con el área transversal para diferentes valores de m. Como consecuencia de este análisis, al crecer m, el valor de la elongación a rotura crece, tal % Elongación 103 102 .. . . . . . .. . .. 0.1 0.2 0.3 0.4 0.5 0.6 0.7 m Figura 13. Dependencia de la elongación con el índice m. como se muestra en la figura 13, que resume resultados de las aleaciones: Zircalloy 4, Ti – 5 Al – 2.5 Sn y Ti – 6Al – 4V. 1 - 18 Departamento de Ingeniería Metalúrgica – USACH. Comportamiento Mecánico de Sólidos Capítulo I. El ensayo de tracción 1.19 Efecto de la temperatura sobre las propiedades de flujo La curva esfuerzo deformación depende fuertemente de la temperatura. Al aumentar la temperatura disminuye la resistencia y aumenta la ductilidad, tal como se aprecia en la figura 14, para acero dulce. i -196ºC Figura 14. Efecto de la temperatura sobre la curva esfuerzo deformación para acero dulce. 25ºC 400ºC i En la figura 15 se muestra la dependencia entre el límite elástico y la temperatura para metales BCC. El límite elástico de los metales FCC no es afectado por la temperatura. Límite Elástico (MPa) Metales BCC 800 600 Ta W Ni (FCC) no es afectado por la temperatura 400 200 Fe Mo Ni -200 0 200 400 600 800 1000 T (ºC) Figura 15. Efecto de la temperatura sobre el límite elástico para metales BCC. En la figura 16 se muestra la influencia de la temperatura sobre el porcentaje de reducción de área. Tal como se aprecia, no se produce un efecto importante en el porcentaje de reducción de área en metales FCC, al subir la temperatura. Departamento de Ingeniería Metalúrgica – USACH. 1 - 19 Comportamiento Mecánico de Sólidos Capítulo I. El ensayo de tracción % de reducción de área 100 Ni Ta 80 W Mo F e 60 El W es frágil a 100 ºC El Ni no cambia drásticamente su ductilidad 40 20 -200 0 200 400 600 800 1000 T (ºC) Figura 16. Efecto de la temperatura sobre el porcentaje de reducción de área. La relación entre el esfuerzo y la temperatura a y constante es: Q RT , C2 exp en que C2 es una constante Q es la energía de activación para deformación plástica (J/mol). R = 8,314 (J/molK). T es la temperatura en K. Un aspecto importante a tener en cuenta es que durante los procesos de deformación cerca del 90% de la energía de deformación se transforma en calor. Sin embargo, a altas velocidades de deformación, no hay tiempo para la disipación de calor. Entonces, se puede considerar que el proceso se realiza adiabáticamente. A bajas temperaturas el proceso de deformación genera caídas en la curva / , tal como se puede apreciar en la figura 17. 1 - 20 Departamento de Ingeniería Metalúrgica – USACH. Comportamiento Mecánico de Sólidos Capítulo I. El ensayo de tracción Figura 17. Efecto de bajas temperaturas sobre la curva esfuerzo – deformación. De acuerdo al análisis propuesto por Backofen (1964) P A dP dA Ad Dado que d dA A dP 1 d d A d Como f ( , , T ) d d T d d T dT d dP Ad T d d Para calentamiento adiabático Si T es baja dT d c dT 0 0 T d Por lo tanto si se producirá inestabilidad. T c Departamento de Ingeniería Metalúrgica – USACH. 1 - 21 Comportamiento Mecánico de Sólidos Capítulo I. El ensayo de tracción 1.20 Fenómeno del punto de fluencia El fenómeno de punto de fluencia se da en algunos materiales que contienen solutos especialmente intersticiales como el acero de bajo contenido en carbono y consiste en la aparición de una oscilación de la curva esfuerzo – deformación cerca del inicio de la deformación plástica, tal como se muestra en la figura 18. Figura 18. Oscilación en la curva esfuerzo – deformación en un acero de bajo contenido en carbono, utilizado en barras de construcción denominado A 44. Este fenómeno se debe a la interacción entre átomos de soluto (C y N en el caso de los aceros) y las dislocaciones. En efecto, los átomos de soluto difunden hacia la zona de tracción de la dislocación, generando una configuración de baja energía, conocida como atmósfera de Cottrell. Esto hace que el límite elástico se incremente hasta uys (upper yield stress). A medida que se incrementa el esfuerzo aplicado, se produce el destrabamiento de las dislocaciones por los átomos de soluto, lo que se manifiesta en una caída del esfuerzo, ver figura 18, hasta lys (low yield stress). Nuevamente se generan dislocaciones que se entraban por los solutos, de tal manera que se requiere incrementar el esfuerzo para lograr deformación plástica. Este fenómeno también ha sido reportado en aleaciones Cu – Zn, Cu – 10% In y aleaciones de Al. La meseta (plateau) que caracteriza a este fenómeno está asociado en el acero a un avance de la deformación a través de la probetas a carga constante, lo que se realiza mediante la formación de bandas de Luders. 1 - 22 Departamento de Ingeniería Metalúrgica – USACH. Comportamiento Mecánico de Sólidos Capítulo I. El ensayo de tracción A medida que la temperatura aumenta, el uys se elimina gradualmente y en su lugar, la curva esfuerzo deformación muestra pequeñas oscilaciones que no se observan a bajas temperaturas, lo que se conoce como efecto Portevin – Le Chatelier. En este caso, al elevar la temperatura, los átomos de soluto son suficientemente móviles como para difundir hacia las dislocaciones, entrabándolas, después de lo cual ocurre el destrabamiento de las mismas, tal como se muestra en la figura 19. Figura 19. Efecto Portevin-Le Chatelier. Departamento de Ingeniería Metalúrgica – USACH. 1 - 23 Comportamiento Mecánico de Sólidos Capítulo I. El ensayo de tracción Estudio de la rotura a tracción por microscopía electrónica de barrido En las siguientes figuras se muestra cómo un material experimenta rotura en tracción. El ensayo ha sido hecho sobre una probeta de acero, en la cámara de vacío de un microscopio electrónico de barrido. Nótese cómo la grieta se origina en el centro del material y progresa hacia la periferia. 1 - 24 Departamento de Ingeniería Metalúrgica – USACH. Comportamiento Mecánico de Sólidos Capítulo I. El ensayo de tracción Departamento de Ingeniería Metalúrgica – USACH. 1 - 25 Comportamiento Mecánico de Sólidos Capítulo I. El ensayo de tracción Figura 20. La secuencia de imágenes muestra cómo se rompe un material por crecimiento de una grieta desde el interior del mismo. 1 - 26 Departamento de Ingeniería Metalúrgica – USACH. Comportamiento Mecánico de Sólidos Capítulo I. El ensayo de tracción Ejercicios propuestos 1.- Demostrar que para un material que tiene la siguiente ley constitutiva K n el valor de la deformación uniforme es u n Solución: Esfuerzo de fractura verdadero v Pfractura A fractura Deformación uniforme verdadera A v ln 0 Au Ajuste de Hollomon k n n: indica el endurecimiento por deformación. La formación del cuello ocurre en la cara máxima y en este punto, el incremento de esfuerzo debido a la variación en la sección transversal supera al incremento en la resistencia debido al endurecimiento por deformación. dP 0 P vA dP v dA Ad v d v dA (1) dA A como dV 0 dL dA d v (2) L A reemplazando (2) en (1) d v d v v d v v (3) d v Departamento de Ingeniería Metalúrgica – USACH. 1 - 27 Comportamiento Mecánico de Sólidos Capítulo I. El ensayo de tracción como v K vn (4) y si derivamos esta expresión d v K ·n· vn 1 d v (5) si reemplazamos (4) y (5) en (3) se obtiene: Kn vn 1 K vn n vn vu vn 1 la deformación verdadera uniforme es igual a n. el valor de la deformación uniforme es 2.- Demostrar que u n d v v d i 1 i 3.- Demostrar que durante la deformación elástica el volumen no se conserva. 4.- Sea un material sometido a tracción. Demostrar que: d ln A m 1 d ln A m en que ln m ln 1 Solución 1 - 28 Departamento de Ingeniería Metalúrgica – USACH. Comportamiento Mecánico de Sólidos Capítulo I. El ensayo de tracción P ·A f ( , ) dP 0 dL dA d A 0 dL dL Pero: d dL L L ln m ln 1 dA A 0 dL L L Además, AdL LdA 0 dA dL d A L d 1 dA A dt A dt A dA dA A A d dL dL 1 dA A dA dL A dL A 2 dL A2 dA A dL 1 dA m 1 dA A dA 0 A dL A dL A2 dL m A dA m dA A2 dL A dL A A Pero, A A 1 dA 1 m dA m dA m 1 A dL d LnA 1 dA d LnA dL m A dL A dL Departamento de Ingeniería Metalúrgica – USACH. 1 - 29 Comportamiento Mecánico de Sólidos Capítulo I. El ensayo de tracción 1 - 30 Departamento de Ingeniería Metalúrgica – USACH.
© Copyright 2026