1. No category

Teoría de Colas
Investigación de Operaciones II
Profesor: Leslie Pérez Cáceres
Departamento de Informática
UTFSM
Teoría
de Colas
Company
LOGO
Introducción
• Se estudian las filas de espera o colas.
• El objetivo del análisis de colas es diseñar un sistema
organización óptima de acuerdo a alguno criterios.
que permita la
• Criterios Posibles:
› Ganancia máxima
› Nivel de atención de deseado
• El análisis de los sistemas de colas requiere de una comprensión de la
medida del servicio apropiada.
• Posibles medidas del servicio
› Tiempo promedio de atención de clientes
› Largo promedio de la cola
› La probabilidad de que un cliente que llega deba esperar en la cola
para ser atendido
Teoría de Colas – Investigación de Operaciones II
2/46
Teoría
de Colas
Company
LOGO
Modelamiento
•Proceso de entrada
•Proceso de salida
•Ejemplos
› Banco:
− Clientes llegan → cajeros sirven a los clientes
› Entrega de pizzas:
− Requerimiento de una entrega → Salida de la pizza
Teoría de Colas – Investigación de Operaciones II
3/46
Teoría
de Colas
Company
LOGO
Modelamiento
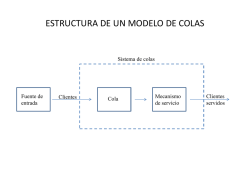
•Clientes requieren un servicio:
› Entrada de clientes
−¿cómo llegan?
› Espera en la cola
− ¿cuántas colas?
› Selección del cliente de la cola
− ¿cómo seleccionar?
› Se sirve al cliente
−¿cuánto tiempo?
› Salida del cliente
Teoría de Colas – Investigación de Operaciones II
4/46
Teoría
de Colas
Company
LOGO
Proceso de Entrada
• Fuente de entrada / población potencial
› Finito / Infinito
• Patrón de llegada
› Independiente de la cantidad de clientes
en el sistema
• No más de una llegada puede ocurrir en un
instante
Teoría de Colas – Investigación de Operaciones II
5/46
Teoría
de Colas
Company
LOGO
Cola
•
• Capacidad de la cola
› Finito / Infinito
• Disciplina de la cola
› FIFO (First In First Out – First Come First Served)
› LIFO (Last In First Out - Last Come First Served)
› RSS (Random selection of service – Service in Random Order
SIRO)
› Nivel de prioridad (Priority queuing discipline)
• Número de colas
› Cola única
› Una cola por servidor
› Intercambio permitido/prohibido
Teoría de Colas – Investigación de Operaciones II
6/46
Teoría
de Colas
Company
LOGO
Proceso de Servicio
•Número de servidores
›Servicio en paralelo
›Servicio en serie
•Tiempo de servicio
› Independiente de la cantidad de
clientes en el sistema
Teoría de Colas – Investigación de Operaciones II
7/46
Teoría
de Colas
Company
LOGO
Tipos de Sistemas
Teoría de Colas – Investigación de Operaciones II
8/46
Teoría
de Colas
Company
LOGO
Notación de Kendall
( [1] / [2] / [3] / [4] / [5] )
• [1] Proceso de llegada
› M: Proceso Markoviano
−Distribución de llegada con distribución Poisson
−Tiempos entre llegada con distribución Exponencial
› Ek: Distribución Erlang del tiempo entre llegadas, con parámetro k
› D: Tiempo entre llegadas determinista
› G: Distribución general
• [2] Proceso de servicio (M, K, D, G)
• [3] Número de servidores (S: cualquier número)
• [4] Tamaño de Población (I (∞): Infinito, F: Finito)
• [5] Largo de la cola (I: Infinito, F: Finito)
Teoría de Colas – Investigación de Operaciones II
9/46
Teoría
de Colas
Company
LOGO
Casos más comunes
(Llegada/Servicio/Servidores/Población/Cola)
(M/M/1/∞/∞)
(M/M/S/∞/∞)
(M/M/1/∞/F)
(M/M/S/F/∞)
Teoría de Colas – Investigación de Operaciones II
10/46
Teoría
de Colas
Company
LOGO
Proceso de Entrada
• Si se desea modelar con distribución de Poisson
• Las tres condiciones necesarias:
› Continuidad: Al menos un cliente debe llegar a la cola
durante un intervalo de tiempo.
› Estacionario: Para un intervalo de tiempo dado, la
probabilidad de que llegue un cliente es la misma que para
todos los intervalos de tiempo de la misma longitud.
› Independencia: La llegada de un cliente no tiene influencia
sobre la llegada de otro.
Estas condiciones no restringen el problema y son satisfechas en
muchas situaciones.
Teoría de Colas – Investigación de Operaciones II
11/46
Teoría
de Colas
Company
LOGO
Proceso de Entrada
• Supuestos
› Nacimiento puro: Los clientes llegan y no abandonan
› Si las llegadas siguen un proceso de Poisson:
−La probabilidad
de una ocurrencia entre t y t + h sólo depende
del ancho del intervalo h (sin memoria)
−Con h muy pequeño a lo mas puede ocurrir una llegada en el
intervalo (t, t + h)
› Disciplina FIFO
›
• Número de Ocurrencias se distribuye Poisson parámetro λt, con
λ igual a la tasa de llegada por unidad de tiempo
• Tiempo entre llegadas se distribuye exponencial con parámetro
λ
• Tiempo hasta la n-ésima llegada se distribuye Γ con parámetros
(n,1/λ)
Teoría de Colas – Investigación de Operaciones II
12/46
Teoría
de Colas
Company
LOGO
Proceso de Entrada
• Llegadas: La teoría de colas se sustenta en el supuesto de que
las llegadas de clientes al sistema siguen una distribución
Poisson, esto significa que:
−Si Xt = numero de llegadas en un intervalo t
−Xt ~ Poisson(λt), luego se trata de una variable aleatoria discreta
con la siguiente probabilidad:
x
t  − t
P  X t =x=
e
x!
El numero promedio de
ocurrencias en el intervalo t
El numero promedio de
ocurrencias por unidad de tiempo
E [ X t ]= t
Teoría de Colas – Investigación de Operaciones II
E[ Xt]
=
t
13/46
Teoría
de Colas
Company
LOGO
Tiempo entre llegadas
• Llegadas → distribución de Poisson
• ¿Cuál es la distribución del tiempo entre llegadas?
• Sea T el instante de tiempo de la primera llegada, y sea t un
1
instante de tiempo menor. T1 se puede interpretar como el tiempo
necesario para que suceda una ocurrencia, luego
P T 1t =P Número de ocurrencias hasta t = 0
P T 1t =P  X t =0=e− t
• Luego
P T 1t =1−e− t
• La que corresponde a la función acumulada de una distribución
exponencial, luego T1 se distribuye exp(λ)
Teoría de Colas – Investigación de Operaciones II
14/46
Teoría
de Colas
Company
LOGO
Tiempo entre llegadas
• Analizando ahora el tiempo necesario hasta la segunda
ocurrencia.
› Sea Yt el número de ocurrencias en el intervalo
[T1, T2], con T un instante de tiempo dentro de ese
intervalo. Luego,
P T t  = Pno hay ocurrencias en intervalo entre T 1 y T 1t 
−T
P T t  = P X t =0=e
› Así T ~ exp(λ)
Teoría de Colas – Investigación de Operaciones II
15/46
Teoría
de Colas
Company
LOGO
Tiempo Acumulado
•Idea: Si el Tiempo hasta la n-ésima ocurrencia es
mayor que un tiempo t dado, implica que hasta t
han habido sólo n - 1 ocurrencias.
P T n t =P  X t  n−1
n−1
t i e t
P T n t = ∑
i!
i=0
•Aproximando la sumatoria por la integral se obtiene
que Tn ~ Γ(n, λ-1)
•Una distribución exponencial con parámetro λ es
equivalente a una distribución Γ(1, λ-1)
Teoría de Colas – Investigación de Operaciones II
16/46
Teoría
de Colas
Company
LOGO
Ejemplo 1
• Los clientes llegan según distribución de Poisson a un
almacén que abre a las 08:00. Los martes entre 08:00 y
09:00 de la mañana llegan en promedio 6 clientes.
Manuel se junto con sus amigos a ver un partido el día lunes
en la noche, por eso le gustaría dormir una media hora mas
el martes en la mañana. Sabe que si abre muy tarde puede
perder muchos clientes. Para tomar una buena decisión
quiere estimar el número de clientes que llegarán entre las
08:00 y las 08:30 el día martes.
• ¿Cuál es la probabilidad que k = 0,1,2... clientes lleguen
entre las 8:00 y las 8:30 de la mañana?
Teoría de Colas – Investigación de Operaciones II
17/46
Teoría
de Colas
Company
LOGO
Ejemplo 1
1
t= [hora]
2
=6[clientes /hora] ,
0
P  X=0 =
P  X=1 =
P  X=2 =
P  X=3 =
P  X=4 =
6∗1/2
∗e−6 /2
0!
1
6/2
∗e−3 =
1!
6/22 −3
∗e =
2!
6/23 −3
∗e =
3!
4
6 /2
−3
∗e =
4!
= 0,049
3 e−3 = 0,149
2
3 −3
e = 0,224
2
3
3 −3
e = 0,224
6
34 −3
e = 0,168
24
P  X4 = P  X=0P  X =1P  X =2P  X=3P X =4 
= 0,0490,1490,2240,2240,168 = 0,814
P  X4 = 1−P  X4 = 1−0,814 = 0,186
Teoría de Colas – Investigación de Operaciones II
18/46
Teoría
de Colas
Company
LOGO
Proceso de Salida
• Supuestos:
› Fallecimiento Puro: Los clientes no pueden reingresar al
sistema
› Tasa de salida = μ = Numero de clientes servidos por
unidad de tiempo
• Tiempo de servicio.
› Si Z es el tiempo de servicio, Z ~ exp(μ)
• Número de Unidades Servidas durante el tiempo t.
› Sea Yt el numero de unidades servidas durante t,
luego Yt ~ Poisson(t)
Teoría de Colas – Investigación de Operaciones II
19/46
Teoría
de Colas
Company
LOGO
Ejemplo 2
• Manuel estimó que se demora 4 minutos en servir a un
cliente y los tiempos de servicio siguen una distribución
exponencial.
• Manuel tiene una cita importante así que desea
encontrar la probabilidad de demorarse menos de 3
minutos en servir al siguiente cliente.
1
= [clientes /minuto], t=3[minutos]
4
−t
P T t = 1−P T t=1−e
−3 / 4
= 1−e
= 1−0,47 = 0,53
Teoría de Colas – Investigación de Operaciones II
20/46
Teoría
de Colas
Company
LOGO
Estado Estacionario
• Un período transitorio ocurre al inicio de la operación.
› Un comportamiento transitorio inicial no es indicado para un
largo período de ejecución.
• Un período estacionario sigue al período transitorio.
› En un período estacionario , la probabilidad de tener n clientes
en el sistema no cambia a medida que transcurre el tiempo.
• De acuerdo a lo anterior, la tasa de llegada debe ser menor que
suma de las tasas de atención efectiva.

1 2...n
k∗
Para un servidor
Para k servidores
Para k servidores
con tasa μ
Teoría de Colas – Investigación de Operaciones II
21/46
Teoría
de Colas
Company
LOGO
Estado Estacionario
•En estado estacionario las medidas de interés de
desempeño del sistema a calcular son:
› Utilización del servidor (carga)
› Probabilidad de cero clientes en el sistema
› Probabilidad de n clientes en el sistema
› Número de clientes promedio en el sistema
› Número de clientes promedio en la cola
› Tiempo promedio de espera en la cola
› Tiempo promedio en el sistema
Teoría de Colas – Investigación de Operaciones II
22/46
Teoría
de Colas
Company
LOGO
Estado Estacionario
(M,M,1) Sistemas con una sola Cola, 1 servidor, Población
Infinita:
Restricción: ρ ≤ 1

 =

Ø
P 0 = 1−
Ø
P n = n 1−
Ø
Utilización del servidor
Probabilidad de cero clientes en el sistema
Probabilidad de n clientes en el sistema
Teoría de Colas – Investigación de Operaciones II
23/46
Teoría
de Colas
Company
LOGO
Estado Estacionario
(M,M,1) Sistemas con una sola Cola, 1 servidor, Población
Infinita:
Restricción: ρ ≤ 1
2
Lq =
1−
Ls =
Wq

=Lq 
1−
Lq
=

Ws =
Ø
1
−
Numero promedio de clientes en la cola
Numero promedio de clientes en el sistema
Ø
Ø
Tiempo promedio de espera en la cola
Ø
Tiempo promedio en el sistema
Teoría de Colas – Investigación de Operaciones II
24/46
Teoría
de Colas
Company
LOGO
Ejemplo 3
•Los clientes que llegan a la zapatería Mary’s son en
promedio 1 cliente en 12 minutos, de acuerdo a la
distribución Poisson.
El tiempo de atención se distribuye
exponencialmente con un promedio de 8 minutos
por cliente.
La gerencia esta interesada en determinar las
medidas de performance para este servicio.
Teoría de Colas – Investigación de Operaciones II
25/46
Teoría
de Colas
Company
LOGO
Ejemplo 3
=1/ 12[clientes/minuto ], =1/8 [clientes /minuto]
Estado estacionario :

2
 =
= 1

3
Largo de la cola :
2
2/ 32

4
Lq =
=
=
= 1,25 clientes
1−
1−2/ 3
3
Largo del sistema :
4 2
L s = Lq  =  = 2 cliente
3 3
Probabilidad de 0 clientes:
2
1
P0  = 1− = 1− =
3
3
Tiempo promedio enla cola :
Lq
Wq =
= 16 minutos

Tiempo promedio en el sistema:
1
Ws =
= 24 minutos
−
Teoría de Colas – Investigación de Operaciones II
26/46
Teoría
de Colas
Company
LOGO
Estado Estacionario
(M,M,k): Múltiples Servidores, Población Infinita:
Restricción: μi = μ
 =
k: número de servidores

k
1
=
P 0
P n=
,para todo i
{
Utilización del servidor
Ø
k −1
n
 k 
∑ n!
n=0
k
 k 

k !1−
Probabilidad de cero clientes
en el sistema
Ø
n
 k 
P 0, si nk
n!
n
 k 
P 0, si nk
n−k
n!n
Probabilidad de n clientes
en el sistema
Ø
Teoría de Colas – Investigación de Operaciones II
27/46
Teoría
de Colas
Company
LOGO
Estado Estacionario
(M,M,k): Múltiples Servidores, Población Infinita:
Restricción: μi = μ
,para todo i
k1 k k −1
Lq =
P 0
2
k −1!1−
k: número de servidores
Numero promedio de clientes en la cola
Ø
Ls =Lq  k
Ø
Lq
W q=

Ø
1 Ls
W s =W q  =
 
Numero promedio de clientes en el sistema
Tiempo promedio de espera en la cola
Tiempo promedio en el sistema
Ø
Teoría de Colas – Investigación de Operaciones II
28/46
Teoría
de Colas
Company
LOGO
Ejemplo 4
• La oficina postal Town posee 3 empleados y atiende público los
Sábados entre las 9:00 a.m. y la 1:00 p.m.
• Datos
› En promedio, 100 clientes por hora visitan la oficina postal
durante este período. La oficina tiene tres dependientes
› Cada atención dura 1.5 minutos en promedio
› La distribución Poisson y exponencial describen la llegada de
los clientes y el proceso de atención de estos respectivamente
• La gerencia desea conocer las medidas relevantes al servicio en
orden a:
› La evaluación del nivel de servicio prestado.
› El efecto de reducir el personal en un dependiente.
Teoría de Colas – Investigación de Operaciones II
29/46
Teoría
de Colas
Company
LOGO
Ejemplo 4
=100[clientes/hora ],
 =
1
[clientes/minuto] = 40 [clientes /hora],
1,5
k =3
Estado estacionario :
100

=
1
k
3∗40
¿ Es posible dismunuir k ? ⇒ No , 1
 =
Medidas de performance WinQSB
Teoría de Colas – Investigación de Operaciones II
30/46
Teoría
de Colas
Company
LOGO
Ejemplo 4
Teoría de Colas – Investigación de Operaciones II
31/46
Teoría
de Colas
Company
LOGO
Ejemplo 4
Teoría de Colas – Investigación de Operaciones II
32/46
Teoría
de Colas
Company
LOGO
Ejemplo 5
• Cuando se construyó un aeropuerto se pensó en una pista de
aterrizaje para atender 20 aviones por hora. Sin embargo
recientemente se anunció un aumento en el número de
aterrizajes.
Se ha predecido que en los próximos 3 años el tráfico aéreo
aumentará a 30 aterrizajes/hora.
• Ya que el aeropuerto se rediseñará, se desea determinar el
número de pistas de aterrizaje para asegurar que en promedio no
mas de un avión trendrá que esperar para aterrizar. Suponga que
la tasa de servicio se mantiene.
• Si el costo de operación de cada pista es C
= US$ 1000/hr.,
cuánto deberá ser el costo de espera de un avión para que no
convenga construir otra pista.
p
Teoría de Colas – Investigación de Operaciones II
33/46
Teoría
de Colas
Company
LOGO
Estado Estacionario
(M,G,1): Servicio general, 1 Servidor, Población Infinita:
 2 2
Lq =
21−
Fórmula de Pollaczek -Khintchine
Ø
Ls =Lq 
Ø
Lq
W q=

Ø
W s =W q 
Clientes en el sistema
Tiempo en la cola
1

Tiempo en la cola
Ø
Teoría de Colas – Investigación de Operaciones II
34/46
Teoría
de Colas
Company
LOGO
Ejemplo 6
• Ted repara televisores y videograbadores.
• Datos
›
›
›
›
El tiempo promedio para reparar uno de estos artefactos es de 2.25 horas.
La desviación estándar del tiempo de reparación es de 45 minutos.
Los clientes llegan a la tienda en promedio cada 2.5 horas, de acuerdo a
una distribución Poisson.
Ted trabaja 9 horas diarias y no tiene ayudantes.
• Si compra nuevos equipos:
›
›
En promedio, el tiempo de reparación esperado debería ser de 2 horas.
La desviación estándar esperada debería ser de 40 minutos.
• Ted desea conocer los efectos de usar nuevos equipos para:
›
Mejorar el tiempo promedio que debe esperar un cliente hasta que su
artefacto sea reparado.
Teoría de Colas – Investigación de Operaciones II
35/46
Teoría
de Colas
Company
LOGO
Ejercicio
• Wilson Foods tiene un línea 800 para responder las consultas de sus
clientes
• Datos
› En promedio se reciben 225 llamadas por hora.
› Una llamada toma aproximadamente 1.5 minutos.
› Un cliente debe esperar en línea a lo más 3 minutos.
› A un representante que atiende a un cliente se le paga $16 por hora.
› Wilson paga a la compañía telefónica $0.18 por minuto cuando el
cliente espera en línea o esta siendo atendido.
› El costo del grado de satisfacción de un cliente que espera en línea es
de $20 por minuto.
› El costo del grado de satisfacción de un cliente que es atendido es de
$0.05.
¿Qué cantidad de representantes para la atención de los clientes deben ser
usados para minimizar el costo de las horas de operación?
Teoría de Colas – Investigación de Operaciones II
36/46
Teoría
de Colas
Company
LOGO
K
6
7
8
9
10
Ejercicio
L
18,1249
7,6437
6,2777
5,8661
5,7166
Lq
12,5
2,0187
0,6527
0,2411
0,916
Wq
0,05556
0,00897
0,0029
0,00107
0,00041
Teoría de Colas – Investigación de Operaciones II
CT(K)
458,62
235,62
220,50
227,12
239,70
37/46
Teoría
de Colas
Company
LOGO
Colas con Restricciones
•Supuestos:
› El proceso de llegada es Poisson
› Tiempos de Servicios son Exponencial
› Disciplina FIFO
› Largo de la cola infinita
› Pocas llegadas, población finita
Teoría de Colas – Investigación de Operaciones II
38/46
Teoría
de Colas
Company
LOGO
Colas con Restricciones
• Pocas llegadas
› Ejemplo: Comportamiento de los pacientes en un
•
hospital
Sea:
› M: número de clientes en la población
› λ: tasa media de llegada de cada unidad individual
› k: número de colas
1
=
P 0
k−1
∑
n=0
 
M
n
M
M!
n
 
∑
k! n=k  M −n!k n−k
n
Teoría de Colas – Investigación de Operaciones II
39/46
Teoría
de Colas
Company
LOGO
•
Colas con Restricciones
Como P(0) es conocido:
P n=
{
 
M n P 0 , cuando 0nk
n
M !n P 0
, cuando knM
n−k
 M −n!k!k
• Las unidades L
S
M
Ls =
∑ n P n
n=1
que están en el sistema en ese momento no están en la
población.
• La tasa efectiva de llegada es:
e = M −L s 
• Además:
Ws
Ls
=
e
W q = W s−
1

Teoría de Colas – Investigación de Operaciones II
Lq = e W q
40/46
Teoría
de Colas
Company
LOGO
Problema
Teoría de Colas – Investigación de Operaciones II
41/46
Teoría
de Colas
Company
LOGO
Problema
• Los resultados:
› Existe un 21.98% de probabilidad que Pedro y su ayudante estén
›
›
›
›
sin trabajo que reparar.
En una hora típica 1,42 máquinas están en el taller de reparación.
Cada maquina permanece en promedio 0.4 [horas] ≈ 24 [min].
Cuando una máquina necesita un ajuste, ésta debe esperar (antes
de ser atendida) 0.06 [horas] = 3.6 [min].
La línea de espera tiene un promedio de 0.21 máquinas.
Teoría de Colas – Investigación de Operaciones II
42/46
Teoría
de Colas
Company
LOGO
Colas con Restricciones
• Sistema Poisson Exponencial con 1 sólo canal con
cola truncada
• Pueden existir 2 razones para limitar el largo de la cola:
› La cola se limita sola, llega un momento en que
ninguna persona desea ponerse en una cola con un
largo excesivo
› Los sistemas de servicios limitados físicamente, por
ejemplo, la sala de espera en un centro médico
Teoría de Colas – Investigación de Operaciones II
43/46
Teoría
de Colas
Company
LOGO
Colas con Restricciones
• Sistema Poisson Exponencial con 1 sólo canal con cola
truncada
• Propiedades del Estado Estacionario
• Sea:
› M el número máximo de unidades llegando al sistema, por lo tanto el
largo máximo de la cola será M-1
1−
1−m1
n
P n =  P0
M 1
 M 1 

Ls =
−
1−
1− M 1
L q = Ls  P 0−1
P 0 =
e = 1− P M 
Lq
Wq =
e
1
W s = W q

Teoría de Colas – Investigación de Operaciones II
44/46
Teoría
de Colas
Company
LOGO
Colas con Restricciones
• En el caso en que λ = μ
todos los estados son
igualmente probables, en este caso:
• Ahora si λ excede a μ se tendrá que el sistema llegará
a saturarse con LS ≈ M y P(M) ≈ 1
Teoría de Colas – Investigación de Operaciones II
45/46
Teoría
de Colas
Company
LOGO
Colas con Restricciones
• Ya que a lo mas pueden haber M unidades en el
sistema, P(M) es la probabilidad que el sistema esté
lleno, es decir, una unidad llegando en ese estado no
podrá ingresar al sistema.
• Por lo tanto, 1 - P(M) = probabilidad de que una unidad
pueda entrar al sistema.
• Y como los clientes varían entre 0 y M, entonces
M
∑ Pn=1
n=0
⇒ P 0 =
1−
M 1
1−
Teoría de Colas – Investigación de Operaciones II
46/46