1. No category

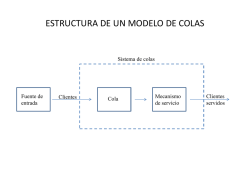
DIRECCIÓN DE OPERACIONES Y TOMA DE DECISIONES
INGENIERÍA INDUSTRIAL – CICLO DE PROFESIONALIZACIÓN
TEORIA DE COLAS: Líneas de Espera
Claro Ana Milena, Cardona Luz Dary, Ruiz Lina María, Gómez Juan Fernando, Estudiantes Ingeniería
Industrial – Universidad Católica de Oriente. Mayo 21 de 2011.
Resumen: La teoría de colas es el estudio matemático de las
líneas de espera o colas dentro de una red de comunicaciones.
Su objetivo principal es el análisis de varios procesos, tales
como la llegada de los datos al final de la cola, la espera en
la cola, entre otros.
La teoría de colas generalmente es considerada una rama de
investigación operativa porque sus resultados a menudo son
aplicables en una amplia variedad de situaciones como
negocios, comercio, industria, ingenierías, transporte y
telecomunicaciones.
En el contexto de la informática y de las nuevas tecnologías,
las situaciones de espera dentro de una red son más
frecuentes. Así, por ejemplo, los procesos enviados a un
servidor para su ejecución forman colas de espera mientras
no son atendidos; la información solicitada, a través de
Internet, a un servidor Web puede recibirse con demora
debido a la congestión en la red; también se puede recibir la
señal de línea de la que depende nuestro teléfono móvil
ocupada si la central está colapsada en ese momento, etc.
Otros campos de utilización son la logística de los procesos
industriales de producción, ingeniería de redes y servicios,
ingeniería de sistemas informáticos, y elaboración de
proyectos sustentables.
Palabras Claves: Teoría de Colas, Investigación de
Operaciones,
Optimización,
Estructura,
Modelos
Matemáticos.
I. INTRODUCCIÓN
Las "colas" son un aspecto de la vida moderna que nos
encontramos continuamente en nuestras actividades diarias. En
el contador de un supermercado, accediendo al Metro, en
los Bancos, etc., el fenómeno de las colas surge cuando
unos recursos compartidos necesitan ser accedidos para
dar servicio a un elevado número de trabajos o clientes.
El estudio de las colas es importante porque proporciona tanto
una base teórica del tipo de servicio que podemos esperar de
un determinado recurso, como la forma en la cual dicho
recurso puede ser diseñado para proporcionar un determinado
grado de servicio a sus clientes.
Debido a lo comentado anteriormente, se plantea como algo
muy útil el desarrollo de una herramienta que sea capaz de dar
una respuesta sobre las características que tiene un
determinado modelo de colas.
La teoría
de
colas es
el
estudio
matemático
del comportamiento de líneas de espera. Esta se presenta,
cuando los "clientes" llegan a un "lugar" demandando un
servicio a un "servidor", el cual tiene una cierta capacidad
de atención. Si el servidor no está disponible inmediatamente y
el cliente decide esperar, entonces se forma la línea de espera.
Una cola es una línea de espera y la teoría de colas es una
colección de modelos matemáticos que describen sistemas de
línea de espera particulares o sistemas de colas. Los modelos
sirven para encontrar un buen compromiso entre costes
del sistema y los tiempos promedio de la línea de espera para
un sistema dado.
Los sistemas de colas son modelos de sistemas que
proporcionan servicio. Como modelo, pueden representar
cualquier sistema en donde los trabajos o clientes llegan
buscando un servicio de algún tipo y salen después de que
dicho servicio haya sido atendido. Podemos modelar los
sistemas de este tipo tanto como colas sencillas o como un
sistema de colas interconectadas formando una red de colas.
En la siguiente figura podemos ver un ejemplo de modelo de
colas sencillo. Este modelo puede usarse para representar una
situación típica en la cual los clientes llegan, esperan si los
servidores están ocupados, son servidos por un servidor
disponible y se marchan cuando se obtiene el servicio
requerido.
El problema es determinar qué capacidad o tasa de servicio
proporciona el balance correcto. Esto no es sencillo, ya que un
cliente no llega a un horario fijo, es decir, no se sabe con
exactitud en que momento llegarán los clientes. También
el tiempo de servicio no tiene un horario fijo.
Los problemas de "colas" se presentan permanentemente en la
vida diaria: un estudio en EEUU concluyó que, por término
medio, un ciudadano medio pasa cinco años de su vida
esperando en distintas colas, y de ellos casi seis meses parado
en los semáforos.
II. DESARROLLO DE LA ACTIVIDAD
1. Definición de conceptos generales del fenómeno de
espera.
CONCEPTOS GENERALES
1.1. DISTRIBUCION DE LLEGADA
Los arribos pueden ser descritos como una distribución
determinística o probabilística. La distribución para el tráfico
promedio la describe usualmente la distribución de Poisson y
esta es generalmente usada en teoría de colas relacionada al
flujo de vehículos.
1.2. MÉTODO DE SERVICIO
Las colas también pueden clasificarse por el método que usan
para servir los arribos o elementos que llegan. Esto incluye la
DIRECCIÓN DE OPERACIONES Y TOMA DE DECISIONES
INGENIERÍA INDUSTRIAL – CICLO DE PROFESIONALIZACIÓN
conocida y generalizada ley de servicio: “el primero en llegar,
es el primero en recibir el servicio”, donde se sirve a las
unidades en el orden en que éstas arriban, o la ley de servicio
“último en llegar es el primero en ser servido”, que es en
reversa al orden de llegada. El método de servicio, también
puede basarse en prioridades, donde las llegadas son
direccionadas a colas específicas con apropiadas prioridades
de diferente nivel de servicio. Las colas son servidas en este
caso en diferentes órdenes de niveles de prioridad.
1.3. CARACTERÍSTICAS DE LA LONGITUD DE LA
COLA
La longitud máxima de la cola, esto es el máximo número de
unidades en la cola, se especifica en cada caso si la cola es
finita o trunca o si no hay restricción en la longitud de la cola.
Las colas finitas son algunas veces necesarias cuando el área
de espera es limitada.
1.4. DISTRIBUCIÓN DEL SERVICIO
Esta distribución es también considerada usualmente como
aleatoria, y las distribuciones de Poisson y Exponencial
Negativa son las más representativas y usuales para describir
el comportamiento del servicio.
1.5. NÚMERO DE CANALES
El número de carriles usualmente corresponde al número de
líneas de espera, lo que es utilizado también para clasificar las
colas. Así por ejemplo tenemos las colas de un canal único y
las colas de canales múltiples.
Disciplina de la cola
Establece el orden en que se va atendiendo a los clientes:
Por orden de llegada (FIFO)
Por orden inverso al de llegada (LIFO)
Selección aleatoria (RANDOM)
Según prioridades (PRIORITY, PR), Dos subtipos:
• Con interrupción, Si llega un cliente de más prioridad, el
trabajo que se estaba sirviendo se interrumpe para atenderlo.
• Sin interrupción, No se pueden interrumpir los trabajos
• Dentro de cada clase de prioridad se podrán aplicar
disciplinas LIFO, FIFO RANDOM,
Capacidad del sistema:
Es el número máximo de clientes que puede haber en el
sistema (finito o infinito), Si llega un cliente y el sistema está
lleno, se marcha,
Número de canales de servicio
Es el número de dependientes, Puede haber una cola para cada
dependiente o bien una sola cola global
Número de estados de servicio
Puede haber varias partes en las que se subdivide el trabajo
(estados), cada una con su cola y su dependiente, que deben
ser
3. Objetivos de la Teoría de Colas o Línea de espera.
1.6. COLAS SOBRESATURADAS Y NO SATURADAS
Las colas sobresaturadas son aquellas en las cuales la tasa de
arribo es mayor que la tasa de servicio y las colas no saturadas
son aquellas en las cuales la tasa de arribo es menor que la tasa
de servicio. La longitud de la cola no saturada podría variar
pero alcanzará un estado estable con el arribo de unidades. La
longitud de una cola sobresaturada, sin embargo nunca
alcanzará un estado estable, y continuará creciendo con el
arribo de las unidades.
Los objetivos de la teoría de colas consisten en:
2. Descripción acerca de la técnica utilizada para el
análisis de sistemas con características de colas o línea de
espera.
Identificar el nivel óptimo de capacidad del sistema que
minimiza el coste global del mismo.
Evaluar el impacto que las posibles alternativas de
modificación de la capacidad del sistema tendrían en el
coste total del mismo.
Establecer un balance equilibrado (“óptimo”) entre las
consideraciones cuantitativas de costes y las cualitativas de
servicio.
Prestar atención al tiempo de permanencia en el sistema o
en la cola de espera.
Un sistema de colas viene dado por varias características:
Estructura básica de una Cola o Línea de espera.
Modelo de llegada de clientes
El índice de llegadas será el número medio de llegadas por
unidad de tiempo. Alternativamente podemos usar el tiempo
entre llegadas, que es el tiempo medio entre llegadas
sucesivas.
Modelo Básico
Modelo de servicio
Puede venir dado por el tiempo deservicio o por el número de
clientes atendidos por unidad de tiempo. Tendremos una
variable aleatoria o bien un servicio determinista. Aquí
supondremos que el modelo deservicio es independiente del de
llegada
DIRECCIÓN DE OPERACIONES Y TOMA DE DECISIONES
INGENIERÍA INDUSTRIAL – CICLO DE PROFESIONALIZACIÓN
Una Línea, Un Servidor
El tiempo entre llegadas tiende a ser muy variable.
El número esperado de llegadas por unidad de tiempo se
llama tasa media de llegadas (λ)
El tiempo esperado entre llegadas es1/λ. Por ejemplo, si la
tasa media de llegada es λ = 20 clientes por hora, entonces el
tiempo de esperado entre llegadas es 1/λ = 1/20 = 0.05 horas
ó 3 minutos
Una Línea, Múltiples Servidores
Además es necesario estimar la distribución de probabilidad
de los tiempos entre llegadas. Generalmente se supone una
distribución exponencial. Esto depende del comportamiento
de las llegadas
Sistemas de colas: Las llegadas – Distribución exponencial
La forma algebraica de la distribuciónexponencial es:
Varias Líneas, Múltiples Servidores
Donde t representa una cantidad expresada en de tiempo
unidades de tiempo (horas, minutos, etc.)
La distribución exponencial supone una mayor probabilidad
para tiempos entre llegadas pequeños. En general, se
considera que las llegadas son aleatorias a la última llegada
no influye en la probabilidad de llegada de la siguiente.
Sistemas de colas: Las llegadas - Distribución de Poisson
Es una distribución discreta empleada con mucha frecuencia
para describir el patrón de las llegadas a un sistema de colas.
Una Línea, Servidores Secuenciales
Para tasas medias de llegadas pequeñas es asimétrica y se
hacemás simétrica y se aproxima a la binomial para tasas de
llegadas altas
Su forma algebraica es:
Dónde: P (k): probabilidad de k llegada por unidad de tiempo
λ = tasa media de llegadas
e = 2,7182818…
Sistemas de colas: La cola
4. Clasificación de los sistemas de colas o línea de espera.
Sistemas de colas: Las llegadas
El tiempo que transcurre entre dos llegadas sucesivas en el
sistema de colas se llama tiempo entre llegadas.
El número de clientes en la cola es el número de clientes
que esperan el servicio.
El número de clientes en el sistema es el número de clientes
que esperan en la cola más el número de clientes que
actualmente reciben el servicio.
DIRECCIÓN DE OPERACIONES Y TOMA DE DECISIONES
INGENIERÍA INDUSTRIAL – CICLO DE PROFESIONALIZACIÓN
La capacidad de la cola es el número máximo de clientes
que pueden estar en la cola.
Generalmente se supone que la cola es infinita, aunque
también la cola puede ser finita.
M: distribución exponencial
D: distribución degenerada
EK: distribución Erlang
C: Número de servidores
En principio el sistema está en un estado inicial.
La disciplina de la cola se refiere al orden en que se
seleccionan los miembros de la cola para comenzar el
servicio.
Se supone que el sistema de colas llega a una condición de
estado estable (nivel normal de operación)
La más común es PEPS: primero en llegar, primero en
servicio. Puede darse: selección aleatoria, prioridades,
UEPS, entre otras.
Existen otras condiciones anormales (horas pico, etc.)
Sistemas de colas:
El servicio
Formulación de Modelos para el análisis de la eficiencia del
sistema:
El servicio puede ser brindado por un servidor o por
servidores múltiples.
5. Modelos de una cola
El tiempo de servicio varía de cliente a cliente.
El tiempo esperado de servicio depende de la tasa media de
servicio (µ).
Lo que interesa es el estado estable.
M / M /1: Un servidor con llegadas de Poisson y tiempos de
servicio exponenciales
Fórmulas
El tiempo esperado de servicio equivale a 1/µ. Por ejemplo,
si la tasa media de servicio es de 25 clientes por hora.
Entonces el tiempo esperado de servicio es 1/µ = 1/25 = 0.04
horas, ó 2.4 minutos.
Es necesario seleccionar una distribución de probabilidad
para los tiempos de servicio.
Hay dos distribuciones que representarían puntos extremos:
La distribución exponencial (σ = media)
Tiempos de servicio constantes (σ =0)
Una distribución intermedia es la distribución Erlang.
Esta distribución posee un parámetro de forma k que
determina su desviación estándar:
Si k=1, entonces la distribución. Erlang es igual a la
exponencial
Si k=α entonces la distribución. Erlang es igual a la
distribución degenerada con tiempos constantes
La forma de la distribución Erlang varía de acuerdo con k
Sistemas de colas: Etiquetas para distintos modelos
Notación de Kendall: A/ B/ c
A: Distribución de tiempos entre llegadas
B: Distribución de tiempos de servicio
Ejemplo:
Un lava-carro puede atender un auto cada 5 minutos y la tasa
media de llegada es de 9 autos por hora. Obtenga las medidas
DIRECCIÓN DE OPERACIONES Y TOMA DE DECISIONES
INGENIERÍA INDUSTRIAL – CICLO DE PROFESIONALIZACIÓN
de desempeño de acuerdo con el modelo M/ M/ 1. Además la
probabilidad de tener 0clientes en el sistema, la probabilidad
detener una cola de más de 3 clientes y la probabilidad de
esperar más de 30 min., en la cola y en el sistema
λ = 9; µ = 12; ρ = 9/12 = 0.75
Ejemplo:
Un lava-carro puede atender un auto cada 5 min y la tasa
media de llegadas es de 9 autos/hora, σ = 2 min. Obtenga las
medidas de desempeño de acuerdo con el modelo M/G/1.
Además la probabilidad de tener 0clientes en el sistema y la
probabilidad de que un cliente tenga que esperar por el
servicio.
Modelos de servidores
M / M /s: s servidores con llegadas de Poisson y tiempos de
servicio exponenciales
Ejemplo:
Un lava-carro puede atender un auto cada 5 min y la tasa
media de llegadas es de 9 autos/hora, σ = 2 min. Obtenga las
medidas de desempeño de acuerdo con el modelo M/G/1.
Además la probabilidad de tener 0clientes en el sistema y la
probabilidad de que un cliente tenga que esperar por el
servicio.
M / G /1: Un servidor con tiempos entre llegadas
exponenciales y una distribución general de tiempos de
servicio
DIRECCIÓN DE OPERACIONES Y TOMA DE DECISIONES
INGENIERÍA INDUSTRIAL – CICLO DE PROFESIONALIZACIÓN
recursos, capacidad de producción, productividad y niveles
de inventario. A través del Modelamiento de los elementos
importantes de un sistema de producción tales como
utilización de recursos, capacidad del sistema y programas
de producción, se puede experimentar con diferentes
estrategias de operacionales y diseños para asegurar los
mejores resultados.
6.3. WIN QSB
6. Aplicativos (software) disponible para la solución de
modelos de Teoría de Colas
6.1 AQUAS
Es un sistema interactivo de ayuda a la toma de decisiones que
contiene herramientas muy útiles para resolver distintos tipos
de problemas en el campo de la investigación operativa. El
sistema está formado por distintos módulos, uno para cada tipo
de modelo o problema.
Es una aplicación realizada en MATLAB® que permite:
6.4. EXEL
Reducir el tiempo de resolución y eliminar la posibilidad de
cometer un error en la resolución de un problema de colas.
Resolver modelos de colas tanto de forma analítica (para
aquellos modelos en los que tanto la distribución del tiempo
de llegadas como la del tiempo de servicio sean de carácter
exponencial) como por simulación (la distribución del
tiempo de llegadas o de servicio puede ser de uno de los
siguientes tipos: exponencial, uniforme, determinista,
gamma, beta, normal, lognormal o de Weibull).
Hallar las características del modelo de colas (probabilidad
de que haya un determinado número de clientes, número
medio de clientes, tiempo medio de espera de un cliente en la
cola, intensidad de tráfico del modelo... ).
Poder analizar la influencia de la variación de algunos
parámetros de entrada del modelo en los parámetros de
salida y ayudar a la toma de decisiones (en caso de que se
trate de un modelo real)
Proporcionar una respuesta mediante simulación a aquellos
modelos que no tienen una solución analítica.
Fomentar la enseñanza y el aprendizaje de la teoría de colas
en un ámbito docente.
6.2. PROMODEL
Es una poderosa herramienta de simulación que trabaja bajo
ambiente Windows, para simular y analizar sistemas de todo
tipo y de diferentes complejidades y tamaños. ProModel
provee la perfecta combinación entre facilidad de uso y
completa flexibilidad para modelar cualquier situación. Las
capacidades de animación de ProModel permiten que la
simulación cobre vida.
ProModel provee a los Ingenieros y Gerentes la oportunidad
de probar nuevas ideas para el mejoramiento o diseño de
nuevos sistemas, antes de invertir tiempo y recursos
necesarios para construir o alterar el sistema actual.
ProModel se enfoca en objetivos tales como utilización de
Teoría de Colas (Excel interactivo)
Hay muchas situaciones de la vida diaria en las que hemos de
esperar haciendo cola. Las colas se producen en entornos tanto
industriales como de servicios, a veces de forma encubierta:
coches que esperan en semáforos, pensionistas que hacen cola
en la ventanilla de una caja de ahorros, máquinas estropeadas
que esperan su turno para ser reparadas, etc. Este Excel
explora situaciones en las que a pesar de que existe suficiente
capacidad para cubrir las demandas del proceso, se producen
colas debido a variaciones en el ritmo de llegada o en los
horarios de atención al cliente. Introduce algunas medidas de
eficacia en un sistema de colas: medidas "duras" u objetivas
(como el tiempo de espera del cliente) y "blandas" o subjetivas
(como la percepción que tienen los clientes de ser bien
atendidos). También presenta las distintas opciones de que
disponen los administradores para mejorar el rendimiento de
sus sistemas de colas, o al menos para mejorar la percepción
que de ellos tienen sus usuarios más importantes. El Excel
concluye con unas reflexiones sobre la "psicología de las
colas".
Modelos que resuelve AQUAS:
Analíticamente
Por Simulación
M/M/1
G/G/1
M/M/s
G/G/s
M/M/1/K
G/G/1/K
M/M/s/K
G/G/s/K
M/M/1/∞/H
G/G/1/∞/H
M/M/s/∞/H
G/G/s/∞/H
M/M/s/∞/H con Y repuestos
G/G/s/∞/H con Y repuestos
Para poder trabajar con AQUAS es necesario tener una
versión de MATLAB® posterior a la 5.0 y disponer además de
la librería estadística (statisticstoolbox).
Para descargar la versión de AQUAS para Windows Para
descargar la versión de AQUAS para Linux
DIRECCIÓN DE OPERACIONES Y TOMA DE DECISIONES
INGENIERÍA INDUSTRIAL – CICLO DE PROFESIONALIZACIÓN
Para ejecutar AQUAS hay que seguir los siguientes pasos:
1- Descargar el archivo aquas.zip
2- Descomprimir dicho archivo en una carpeta
3- Ejecutar MATLAB®
4- Añadir la carpeta al path de MATLAB® mediante la
opción"Set Path"
5- Teclear >>aquas en la línea de comandos de MATLAB®
la cual nos proporciona este valor teniendo como parámetros
los valores de S y de r.
Considerando los valores obtenidos podemos calcular el valor
de Po = 0.0130, la probabilidad de que el sistema este ocupado
será P (sistema ocupado) = 0.5547, utilizando este valor
obtenemos que:
6.5. Modelos de servidores
M / M /s: s servidores con llegadas dePoisson y tiempos de
servicio exponenciales
Unidades
L = 2.2188 + 4 = 6.2188 unidades
Ahora el tiempo promedio en del sistema quedará definido de
la siguiente forma:
III. CONCLUSIÓN
Ejemplo:
Para ejemplificar el modelo M / M / S, suponga que existen
cinco canales de servicio con tasas promedio de servicio m = 6
y una tasa de llegada de l = 24 unidades por hora, esto implica
que S = 5.
Datos
m=6
l = 24
S=5
Entonces tenemos que
Nota: Para encontrar los valores de Po con una mayor rapidez
nos podemos auxiliar de la tabla que se anexa a este sistema,
La teoría de las colas es el estudio matemático de las colas o
líneas de espera. La formación de colas es, por supuesto, un
fenómeno común que ocurre siempre que la demanda efectiva
de un servicio excede a la oferta efectiva.
Con frecuencia, las empresas deben tomar decisiones respecto
al caudal de servicios que debe estar preparada para ofrecer.
Sin embargo, muchas veces es imposible predecir con
exactitud cuándo llegarán los clientes que demandan el
servicio y/o cuanto tiempo será necesario para dar ese servicio;
es por eso que esas decisiones implican dilemas que hay que
resolver con información escasa. Estar preparados para ofrecer
todo servicio que se nos solicite en cualquier momento puede
implicar mantener recursos ociosos y costos excesivos. Pero,
por otro lado, carecer de la capacidad de servicio suficiente
causa colas excesivamente largas en ciertos momentos.
Cuando los clientes tienen que esperar en una cola para recibir
nuestros servicios, están pagando un coste, en tiempo, más alto
del que esperaban. Las líneas de espera largas también son
costosas por tanto para la empresa ya que producen pérdida de
prestigio y pérdida de clientes.
La teoría de las colas en si no resuelve directamente el
problema, pero contribuye con la información vital que se
requiere para tomar las decisiones concernientes prediciendo
algunas características sobre la línea de espera: probabilidad
de que se formen, el tiempo de espera promedio.
Pero si utilizamos el concepto de "clientes internos" en la
organización de la empresa, asociándolo a la teoría de las
colas,
nos
estaremos
aproximando
al
modelo
de organización empresarial "just in time" en el que se trata de
minimizar el costo asociado a la ociosidad de recursos en la
cadena productiva.
DIRECCIÓN DE OPERACIONES Y TOMA DE DECISIONES
INGENIERÍA INDUSTRIAL – CICLO DE PROFESIONALIZACIÓN
RECONOCIMIENTOS
A LA PROFESORA INGENIERA. DORA ALICIA ECHEVERRI
MORALES, LA CUAL ES GESTORA DE CONOCIMIENTO EN ESTE
CURSO
BIBLIOGRAFÍA
[1] http://www.simulart.cl/software_promodel_web.html
[2] http://es.wikipedia.org/wiki/Teor%C3%ADa_de_colas
[3] http://www.monografias.com/trabajos18/teoriacolas/teoria-colas.shtml