1. No category

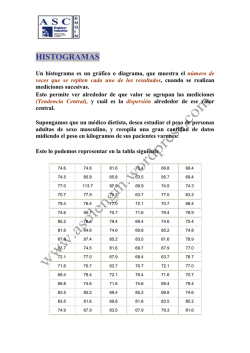
Manual del
Participante
Herramientas de la
Calidad Total
TECNICO NIVEL OPERATIVO
SEN@TI VIRTUAL
HERRAMIENTAS DE LA CALIDAD TOTAL
MANUAL DEL PARTICIPANTE
TERCERA EDICIÓN
JULIO 2015
Todos los derechos reservados. Esta publicación no puede ser reproducida total ni parcialmente, sin previa autorización del SENATI.
© Servicio Nacional de Adiestramiento en Trabajo Industrial - SENATI
Alfredo Mendiola 3520
Material auto instructivo, destinado a la capacitación del SENATI a nivel nacional.
Lima, Julio 2015
ESTRUCTURA DEL MÓDULO
Herramientas de la
Calidad Total
UNIDAD
1
Conceptos de Calidad y el Ciclo de
la Mejora Contínua
UNIDAD
2
Herramientas de la Calidad Total
Contenido
1.
OBJETIVOS DE LA UNIDAD 2........................................................................................................................ 6
2.CONTEXTUALIZACIÓN.................................................................................................................................. 6
3.
RECUPERACIÓN DE EXPERIENCIAS.............................................................................................................. 6
CASO DE ESTUDIO................................................................................................................................................. 6
Análisis de Caso de Estudio................................................................................................................................... 6
4.
GESTORES DEL CONCEPTO DE CALIDAD...................................................................................................... 7
5.
LAS 7 HERRAMIENTAS DE LA CALIDAD........................................................................................................ 7
6.HISTOGRAMA.............................................................................................................................................. 8
CONCEPTO BÁSICO RELACIONADO ..................................................................................................................... 8
CONSTRUCCIÓN DEL HISTOGRAMA..................................................................................................................... 10
7.
DIAGRAMA DE DISPERSIÓN......................................................................................................................... 15
PARA QUE SE UTILIZAN EL DIAGRAMA DE DISPERSIÓN...................................................................................... 15
PASOS A SEGUIR PARA CREAR UN DIAGRAMA DE DISPERSIÓN ........................................................................ 16
CASOS TÍPICOS DE DIAGRAMAS DE DISPERSIÓN................................................................................................ 16
EJEMPLO DE UN DIAGRAMA DE DISPERSIÓN...................................................................................................... 17
8.
CONTROL ESTADÍSTICO DE LA CALIDAD...................................................................................................... 19
Ejemplos con probabilidades................................................................................................................................ 21
9.
GRAFICO DE CONTROL ................................................................................................................................ 24
PARA QUE SE UTILIZA EL GRÁFICO DE CONTROL................................................................................................ 25
TIPOS DE GRÁFICOS DE CONTROL........................................................................................................................ 25
10.
PONIENDO EN PRÁCTICA LO APRENDIDO................................................................................................... 29
11.RESUMEN..................................................................................................................................................... 30
12.
AUTO EVALUACIÓN ..................................................................................................................................... 30
13.GLOSARIO.................................................................................................................................................... 30
14.
TEMA DEL FORO: DE LA CONCIENCIA DE LA CALIDAD................................................................................. 30
UNIDAD TEMÁTICA II
HERRAMIENTAS DE LA
CALIDAD TOTAL
HERRAMIENTAS DE LA CALIDAD TOTAL
1. OBJETIVOS DE LA UNIDAD 2
ÒÒ
Relacionar el concepto de la Gestión de la calidad enfocadas por los diferentes autores
ÒÒ
Conocer las herramientas de calidad que se aplican dentro de la Gestión de la Calidad.
ÒÒ
Conocer las herramientas para el control estadístico de la calidad
2. CONTEXTUALIZACIÓN
En esta segunda Unidad Temática exponemos conceptos sobre la Gestión de la Calidad,
los cuales son vistas desde la perspectiva de los diversos autores que han contribuido con
este concepto.
Se describen las 3 herramientas de la Gestión de la Calidad como son el Histograma, el
Diagrama de Dispersión o Correlación y el Grafico de Control donde se presentan casos
aplicados de cómo utilizar las principales herramientas de Gestión de la calidad, las que
permiten solucionar un problema o mejorar un proceso, para el personal operario, o tomar una decisión acertada en caso se tratare de personal directivo de la organización.
3. RECUPERACIÓN DE EXPERIENCIAS
CASO DE ESTUDIO
Análisis de Caso de Estudio
El análisis del caso de estudio debe resolverlo en la PLATAFORMA.
6
4. GESTORES DEL CONCEPTO DE CALIDAD
Podemos indicar algunos de ellos:
EDWARS DEMING: padre de la calidad; “La calidad es el grado predecible de uniformidad que proporciona fiabilidad a bajo costo en el mercado. Hacer las cosas bien desde la
primera”. Diseñó el ciclo PDCA y agrupo las herramientas estadísticas para el control del
proceso y producto. Definió 14 principios de la Calidad.
PHILIP CROSBY: su propuesta se basa en “La Calidad debe concentrarse en cumplir con los
requisitos del cliente”.
ARMAND V. FEIGENBAUM: “La calidad total es un eficaz sistema de integrar el desarrollo
de la calidad, su mantenimiento y los esfuerzos de los diferentes grupos en una organización para mejorarla, así permitir que la producción y los servicios se realicen al menor costo posible y que permitan la satisfacción del cliente”. Introdujo la frase control de calidad
total. Su idea de calidad es que es un modo de vida corporativa, un modo de administrar
una organización e involucra la puesta en marcha.
JOSEPH JURAN: “La calidad tiene que ver con la función que cumple el producto y su
adecuación al uso requerido”. Diseñó el diagrama de Pareto y la trilogía de Juran para la
calidad.
GENICHI TAGUCHI: “Los clientes desean comprar productos que atraigan su atención y
sean funcionales, así como las organizaciones deben de ofrecer productos que superen
los de la competencia en cuanto diseño y precio, que sean atractivos para el cliente y que
tenga un mínimo de variación con la competencia, además de ser resistentes al deterioro
y factores externos a su operación que aseguren su garantía de fabrica”.
DAVID GARVIN: Desarrolló lo que se conoce como las ocho dimensiones de la Gestión
de la calidad: Actuación, Características, Conformidad, Fiabilidad, Durabilidad, Utilidad,
Estética y Calidad percibida.
KAOURO ISHIKAWA: “La calidad no cuesta, es una función integral que toda organización
debe practicar”. Diseñó las 7 herramientas de la calidad.
5. LAS 7 HERRAMIENTAS DE LA CALIDAD
Hasta el momento hemos visto 4 de las 7 Herramientas de la Calidad, ahora detallaremos
las 3 restantes. Recordemos que las Herramientas de la calidad son técnicas gráficas que
se utilizan para dar solución a problemas enfocados a mejorar el análisis y solución de un
problema enfocado a la calidad y la mejora continua.
7
Nombres las 7 herramientas de la calidad, las cuales son:
1. Lista de Chequeo o Verificación (CheckList)
2. Diagrama de Flujo
3. Diagrama de Pareto
4. Diagrama de Causa – Efecto (Ishikawa)
5.Histograma
6. Diagrama de Dispersión o Correlación
7. Grafico de Control
6. HISTOGRAMA
El histograma es un gráfico o diagrama que muestra el
número de veces que se repiten cada uno de los resultados
cuando se realizan mediciones sucesivas.
Son barras verticales que permiten representar los datos
cuantitativos continuos.
CONCEPTO BÁSICO RELACIONADO
La construcción de histogramas se puede hacer con datos discretos (Variables discretas) y
con datos continuos (Variables continuas).
Las variables discretas, son aquellas que sólo admiten valores enteros, no aceptan valores fraccionarios ó intermedios, por ejemplo: Número de reclamos, pueden ser 1, 2, 3, etc.
pero no 3.4, 4.8, 9.7 generalmente son el resultado del conteo.
Las variables continuas, son aquellas que admiten valores fraccionarios, por ejemplo el
peso de un objeto puede ser 11Kg, 11.35 ó 11.398 Kg, dependiendo de la precisión del
instrumento de medida.
Para que se utilizan el Histograma
El Histograma, permite:
a) Muestra el resultado de un cambio en una actividad.
8
b) Identificar el comportamiento del conjunto de datos de la muestra.
c) Identificar la variabilidad de las observaciones respecto a la tendencia central (dispersión).
d) Identificar los valores extremos o atípicos.
Pasos a seguir para crear un Histograma
Los pasos a seguir para construir un histograma son:
1. Recopilar datos
2. Halla el valor mínimo y el valor máximo.
3. Determinar el ancho o recorrido del rango (R) cuya fórmula es:
R = Xmax - Xmin
Dónde:
Xmax = Valor máximo de los datos
Xmin = Valor mínimo de los datos
4. Determinar el número de intervalos ( M ) de secciones o barras, se puede obtener de
3 formas:
a)
M= √n
b)
M=1+3.3 (log n)
Donde: n=número de elementos o mediciones realizadas
c)
Otros autores recomiendan la siguiente tabla:
Nº de datos (n)
De 11 a 20
De 21 a 30
De 31 a 42
De 43 a 56
De 57 a 72
De 73 a 90
De 91 a 110
De 111 a 132
Nº de clase (M)
4
5
6
7
8
9
10
11
9
Nº de datos (n)
De 133 a 150
Nº de clase (M)
12
5. Determinar la amplitud de la clase o intervalo
A=R /m
Donde: R = ancho o recorrido
M=número de intervalos
6. Generar la tabla de intervalos y Frecuencias: Consiste en dividir el rango de valores de
la variable en intervalos, generalmente de la misma amplitud, de modo que cada observación se clasifique sin ambigüedad en un único intervalo. A continuación, hay que contar
cuantas observaciones de la muestra pertenecen a cada intervalo, es decir, calcular la
frecuencia de los intervalos.
7. Construir el gráfico en Excel considerando los intervalos y las frecuencias
8. Interpretar la gráfica del Histograma
Ejemplo de un histograma
Ejercicio N° 1: Prepare la tabla de frecuencia compuesto de cinco intervalos para el conjunto de los siguientes 20 datos, que representan al número de actividades que desarrollan los practicantes en distintos talleres de Lima Metropolitana:
5, 7, 8, 3, 7, 7, 1, 9, 6, 8
5, 6, 7, 8, 7, 9, 6, 8, 6, 6
CONSTRUCCIÓN DEL HISTOGRAMA
Paso 1: Recopilar los datos.
Solución:
5, 7, 8, 3, 7, 7, 1, 9, 6, 8
5, 6, 7, 8, 7, 9, 6, 8, 6, 6
10
Paso 2: Hallar el Valor mínimo y máximo
Solución: Valor máximo = 9, Valor Mínimo= 1
Paso 3: Determinar el ancho o recorrido R = Xmax - Xmin
Solución: R= 9 – 1 = 8
Paso 4: Determinar el número de intervalos (M) M= √n
Solución: M= raíz cuadrada(20) = 4.472 = 4
Paso 5: Determinar la amplitud de la clase o intervalo A=R /m
Solución: A=8/4 = 2
Paso 6: Generar la tabla de intervalos y frecuencias:
Solución: Antes de elaborar la tabla se recomienda ordenar los datos
13556666677777888899
Calcular el promedio: Promedio = Suma de todos datos / n
Solución: Promedio= 129 / 20 = 6.45
Paso 7: Construir el gráfico en Excel:
Solución: Señalar los intervalos y Frecuencias. Elegimos la siguiente secuencia de opciones INSERTAR/COLUMNA /COLUMNA 2-D. Vamos a obtener el grafico que mostramos a
continuación.
11
Nos ubicamos en uno de los rectángulos del histograma clic derecho y seleccionamos DAR
FORMATO A LA SERIE DE DATOS seleccione la alternativa OPCIÓN DE SERIE. Aquí elegimos
el ancho de intervalos para disminuir la distancia de las columnas. Obtendremos nuestro
histograma siguiente que le hemos dado 1% de separación.
Para colocar los valores dentro de cada barra seleccionamos dentro del menú de opciones
la alternativa PRESENTACIÓN dentro de esta alternativa la opción ETIQUETA DE DATOS /
EXTREMO EXTERNO.
12
Paso 8: Interpretación de la gráfica
Al concluir el presente HISTOGRAMA podemos apreciar que la mayor frecuencia de actividades se encuentra en el rango de 5 a 7, los cuales están dentro de la tolerancia promedio.
Se recomienda que para llegar al óptimo resultado se analice las actividades que desarrollan y realizar un estudio de tiempos con la finalidad de optimizar el trabajo y reducir los
errores en los procesos.
Ejercicio N° 2: Una empresa debe fabricar tornillos que tienen como valor especificado de
longitud 25±0,4 mm. Para evaluar el número de piezas con errores de tolerancia se toman
30 muestras, tal y como se muestra en la tabla.
Paso 1: Recopilar los datos.
Solución: Ordenamos los datos
Paso 2: Hallar el Valor mínimo y máximo
Solución: Valor máximo = 25.7 , Valor Mínimo= 24.3
Paso 3: Determinar el ancho o recorrido R = Xmax - Xmin
Solución: R= 25.7 – 24.3 = 1.4
Paso 4: Determinar el número de intervalos (M) M= √n
Solución: M= raíz cuadrada(30) = 5.48 = 5
Paso 5: Determinar la amplitud de la clase o intervalo A=R /m
Solución: A= 1.4 / 5 = 0.28
13
Paso 6: Generar la tabla de intervalos y frecuencias:
Paso 7: Construir el gráfico en Excel:
Paso 8: Interpretación de la gráfica
Es importante determinar en primer lugar de manera precisa el histograma, y luego proceder a su lectura ideal.
El caso es que una empresa debe fabricar tornillos que tienen un valor especificado, y que
al tomar una muestra de 30 tornillos ya existentes, con el propósito de evaluar el número
de piezas con errores de tolerancia, se llega a la siguiente conclusión:
• En el rango 24.3 – 24.58 con errores de tolerancia, se han encontrado 3 piezas
• En el rango 24.58 - 24.86 con errores de tolerancia, se han encontrado 5 piezas
• En el rango 24.86 – 25.14 con errores de tolerancia, se han encontrado 14 piezas
14
• En el rango 25.14 - 25.42 con errores de tolerancia, se han encontrado 6 piezas
• En el rango 25.42 - 25.7 con errores de tolerancia, se han encontrado 2 piezas
Lo que se ha hecho es tomar como referencia el eje vertical del grafico para determinar el
número de piezas de la muestra y su relación en un determinado límite de rango del eje
horizontal.
Es así como podemos ver que en la muestra de 30 tornillos se presentan el mayor número
de errores de tolerancia en catorce (14) tornillos, en un rango de 24.3 – 24.58. Con la finalidad de reducir errores es recomendable capacitar al personal nuevo asi como charlas
a todos los trabajadores sobre nuevos métodos que permitan evitar los errores en fabricación.
7. DIAGRAMA DE DISPERSIÓN
El diagrama de dispersión es una gráfica de tipo XY que se
utiliza para estudiar la posible relación entre 2 variables
numéricas. Este tipo de diagrama se utiliza para probar posibles relaciones entre causa y efecto.
PARA QUE SE UTILIZAN EL DIAGRAMA DE DISPERSIÓN
Se utiliza para:
a) Para estudiar una relación de causa y efecto entre variables cuantitativas.
b) Para mostrar relaciones entre dos efectos para ver si podrían derivarse de una causa
común o servir de sustituto uno del otro.
c) En la fase de diagnóstico, permite ensayar teorías de las posibles causas con la finalidad de identificar la causa raíz.
d) En la fase de corrección, permite diseñar posibles soluciones.
e) En el diseño de un sistema de control mantiene los resultados de una acción de mejora
de la calidad.
15
PASOS A SEGUIR PARA CREAR UN DIAGRAMA DE DISPERSIÓN
Los pasos a seguir para construir un diagrama de dispersión son:
1. Reunir la información en pares de datos de tal forma que permitan estar relacionados
ambos pares
2. Trazar los ejes del diagrama. Los valores deberán aumentar a medida que se mueva a
nivel del eje “Y” y hacia la derecha en el eje “X”. La variable que está siendo investigada
como posible causa se sitúa en el eje “X” y la variable para el efecto en el eje “Y”.
3. Determinar el tipo de diagrama e interpretar la gráfica generada.
CASOS TÍPICOS DE DIAGRAMAS DE DISPERSIÓN
Correlación Positiva
Un incremento en el eje “Y”
depende de un incremento
en el eje “X”. Si “X” es controlada “Y” también es controlada
Si “X” aumenta, “Y” incrementará un poco, aunque
Posible correlación positiva
“Y” parece tener otras causas diferentes a “X”
No correlación
16
No hay correlación entre
“X” e “Y”
Un aumento en “X”, causará
Posible correlación negativa una tendencia a disminuir
“Y”
Correlación Negativa
Un aumento en “X” causará
una diminución en “Y”, por
tanto como en la correlación positiva “X” puede ser
controlada en lugar de “Y”
EJEMPLO DE UN DIAGRAMA DE DISPERSIÓN
Ejercicio N° 1: La siguiente tabla muestra las notas obtenidas en el curso de matemáticas
de los alumnos de una clase.
Notas
5
8
9
10
11
12
13
14
15
16
17
18
Nº de Alumnos
1
3
2
4
4
4
6
4
6
7
9
10
17
Paso 1: Reunir en Pares de datos: La Finalidad es determinar la causa (X) y el efecto (y).
Notas (X)
5
8
9
10
11
12
13
14
15
16
17
18
Nº de Alumnos (Y)
1
3
2
4
4
4
6
4
6
7
9
10
Paso 2: Trace los ejes del diagrama. En este caso se considera como eje “X” a las Notas
y al Eje “Y” los alumnos. Para ello seleccione la tabla anterior. Ingrese a la ficha de Excel
INSERTAR elegir el botón DISPERSION y luego DISPERSION SOLO CON MARCADORES. A
Continuación se presentará la siguiente gráfica:
Para visualizar la fuerza o intensidad de esta correlación
debe hacer un clic en la gráfica aparece una ficha Diseño
y dentro de las alternativas ubicarse en la sección DISEÑOS DE GRAFICOS y elegir el botón Diseño 3.
18
Paso 3: Interpretación de la gráfica: “Existe una correlación entre las variables, su tendencia es hacia arriba esto nos indica que su CORRELACION CON DIRECCIÓN POSITIVA. La
correlación lineal entre ambas variables es fuerte. En conclusión existe correlación entre
ambas variables, su dirección es positiva y la fuerza o intensidad de esta es fuerte”.
Existen pruebas estadísticas disponibles para probar el grado exacto de relación,
pero están más allá del alcance de este manual.
8. CONTROL ESTADÍSTICO DE LA CALIDAD
La estadística es vital en el control y monitoreo de
procesos, y en la mejora en innovación de la calidad, ya que está conformada de un conjunto de
técnicas y conceptos orientados a la recolección y el
análisis de datos tomando en cuenta la variación de
los mismos.
19
a. CONCEPTO BASICO DE LA PROBABILIDAD
El término probabilidad tiene varios sinónimos, como posibilidad, azar y tendencia.
A partir de los siguientes ejemplos verás que el término es sencillo de entender:
Ejemplo 1) Al tirar una moneda al aire y luego caer, pueden ocurrir dos resultados: que salga “cara” y “cruz” (número total de
resultados), sin embargo solo una vez se obtendrá “cruz” (resultado exitoso).
De esta manera, la probabilidad de que salga cruz será ½ (50%).
Ejemplo 2) Al tirar un dado sobre la mesa, pueden resultar 6 resultados: 1 punto, 2 puntos, 3 puntos, 4 puntos, 5 puntos, 6 puntos (número total de resultados), sin embargo, solo una vez resultará que
ocurra el punto 2 (resultado exitoso). Es así que la probabilidad de
que ocurra el punto 2 será 1/6 (16.7%).
Como podrás observar, La probabilidad de un evento se asocia al número total de resultados posibles. así como a la cantidad de resultados
exitosos que pudiesen ocurrir.
b. CÁLCULO DE PROBABILIDADES
La probabilidad puede tomar valores entre 0 y 1.
La probabilidad igual a cero corresponde al suceso imposible: Por ejemplo si lanzamos un
dado al aire y la probabilidad de que salga el número 7 es cero, ya que el dado sólo está
numerado del 1 al 6.
La probabilidad igual a uno corresponde al suceso seguro: Por ejemplo si lanzamos un
dado al aire, la probabilidad de que salga cualquier número del 1 al 6 es igual a uno, es
decir siempre va a salir un uno, un dos, un tres, un cuatro, un cinco o un seis.
El resto de sucesos tendrá probabilidades entre cero y uno: que será tanto mayor cuanto
más probable sea que dicho suceso tenga lugar.
20
Para el desarrollo del cálculo de probabilidades se puede aplicar la siguiente fórmula:
Ejemplos con probabilidades
Ejemplo1: Probabilidad de que al lanzar un dado salga el número 2:
Caso favorable:
Casos posibles:
21
Luego,
Ejemplo 2: Probabilidad de que al lanzar un dado salga un número par:
Casos favorables:
Casos posibles:
Luego,
Ejemplo 3: Probabilidad de que al lanzar un dado salga un número menor que 5:
Casos favorables:
22
Casos posibles:
Luego:
Ejemplo 4: Probabilidad de que nos saquemos el premio mayor de la lotería
Supongamos que hay 100,000 tickets que se venden.
Como hay solamente un ticket ganador, entonces la probabilidad de sacarnos la lotería es:
P(sacar el premio mayor) = 1 / 100,000 = 0,00001
Ejemplo 5: Supongamos que se han fabricado 100 tornillos y se conoce que existen 2
tornillos defectuosos. ¿Cuál es la probabilidad de extraer al azar un tornillo defectuoso?
Casos favorables (obtener un tornillo defectuoso):
23
Casos posibles:
Luego,
9. GRAFICO DE CONTROL
Llamado también CARTAS DE CONTROL es herramienta más poderosa para analizar la variación en la
mayoría de los procesos.
Los gráficos de control enfocan la atención hacia las
causas especiales de variación cuando estas aparecen y reflejan la magnitud de la variación debida a
las causas comunes.
Las causas comunes o aleatorias se deben a la variación natural del proceso. Las causas
especiales o atribuibles son por ejemplo: un mal ajuste de máquina, errores del operador,
defectos en materias primas.
El gráfico cuenta con una línea central y con dos límites de control, uno superior (LCS) y
otro inferior (LCI), que se establecen a ± 3 desviaciones típicas (sigma) de la media (la
línea central). El espacio entre ambos límites define la variación aleatoria del proceso. Los
puntos que exceden estos límites indicarían la posible presencia de causas específicas de
variación.
24
PARA QUE SE UTILIZA EL GRÁFICO DE CONTROL
Se utiliza para:
a)
Evaluar la estabilidad de un proceso
b)
Dar información confiable de la operación en el momento en que se deben de tomar
ciertas acciones.
c)
Contar con niveles consistentes de calidad con el control estadístico y con costos estables para lograr ese nivel de calidad.
d) Distinguir las causas especiales y las causas comunes de variación, dan una buena indicación de cuándo un problema debe ser corregido localmente y cuando se requiere de
una acción en la que deben de participar varios departamentos o niveles de la organización.
TIPOS DE GRÁFICOS DE CONTROL
Existen dos tipos de Gráficos de Control, dependiendo del tipo de la característica de calidad a controlar:
ÒÒ
Gráficos de Control por Atributo
ÒÒ
Gráficos de Control por Variable
a. GRÁFICOS DE CONTROL POR ATRIBUTOS
Cualquier característica de calidad que pueda ser clasificada de forma binaria: “cumple o
no cumple”, “funciona o no funciona”, “pasa o no pasa”, etc., a los efectos de control del
proceso, será considerado como un atributo y para su control se utilizará un Gráfico de
Control por Atributos que son los siguientes:
Carta
P
NP
C
Descripción
Proporción de defectuosos
Número de defectuosos
Defectos por unidad
Campo de Aplicación
Control de la fracción global de defectuosos de un proceso.
Control del número de piezas defectuosas.
Control de número global de defectos por unidad
25
Carta
K
Descripción
Campo de Aplicación
Promedio de defectos por uni- Control del promedio de defectos
dad
por unidad.
Ejemplos: Evaluar la coloración de un tipo de aceite, verificar el estado de un equipo, piezas defectuosas, etc.
26
27
b. GRÁFICOS DE CONTROL POR VARIABLES
Se utiliza para cualquier característica de calidad “medible” y que por lo tanto son cuantificables, tal como longitud, peso, profundidad, tiempo de ciclo, temperatura, viscosidad,
etc., se utilizará un Gráfico de Control por Variables.
Ejemplo: si vamos a controlar el contenido de grasa en un derivado petróleo, nuestra alternativa será una carta de control por variables.
28
10. PONIENDO EN PRÁCTICA LO APRENDIDO
La Tarea debe desarrollarse en la Plataforma
29
11. RESUMEN
12. AUTO EVALUACIÓN
La auto-evaluación debe ser resuelta en la plataforma
13. GLOSARIO
GLOSARIO DE TÉRMINOS Y DEFINICIONES MÁS USUALES.
14. TEMA DEL FORO: DE LA CONCIENCIA DE LA CALIDAD
El foro debe ser resuelto en la plataforma
30