1. No category

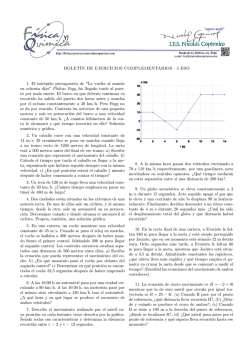
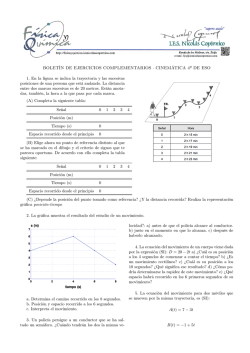
1
Función lineal
Para cada uno de los siguientes ejercicios, encuentra la función polinomial de primer
grado que modela la situación y grafícala. Indica para cada una su dominio, contradominio y su ordenada al origen. Explica la interpretación de la pendiente de cada
función de los ejercicios de acuerdo al contexto del problema.
Ejercicios
1) Un árbol crece a razón de 3.5 cm por mes. Si y representa la altura del arbol y x representa la
edad del árbol medida en meses, encuentra y = f ( x ).
y = 3.5 x
2) Una bomba de agua potable envía agua a razón de 100 litros por segundo. Si y es el volumen
de agua bombeado en x segundos, calcula y = f ( x ).
y = 100 x
3) Un disco de acetato gira a 35.2 revoluciones por minuto. Si y es el número de revoluciones y t
35.2
t
es el tiempo medido en segundos, calcula y = f (t).
y=
60
4) Una onda eléctrica oscila 60 veces por segundo en una línea de voltaje. Si y es el número de
oscilaciones y t es el número de segundos, calcula y = f (t).
y = 60 t
5) Una atleta puede correr 100 metros en 9.75 segundos. Suponiendo que en ese recorrido su
velocidad fuera constante, escribe una función que nos indica la distancia y recorrida en función
de las x milésimas de segundo que han transcurrido desde el instante en que arrancó.
y=
0.975 t
6) Una lámpara fluorescente (ahorradora) consume 35 watts (un watt es igual a una unidad de
energía por segundo). Calcula cuántas unidades de energía y consume la lámpara como una
función del tiempo t medido en segundos.
y = 35 t
7) En un accidente automovilístico se dañó una tubería de agua potable, por lo que ocasionó una
fuga que derramaba 25.5 litros de agua por segundo. Escribe la función y = f (t) que describe
el volumen de agua (medida en litros) que se derrama en t minutos.
y = 1 530 t
8) Una tienda de ropa ofrece un descuento del 25% en todos los precios debido a que desean
adquirir prendas con una nueva tendencia en moda. Si p es el precio con descuento y q era
el precio original (sin descuento) de cada prenda, ¿qué función les permite calcular los nuevos
precios?
p = 0.75 q
9) Una máquina para hacer tortillas produce 90 tortillas por minuto. Escribe la función que
expresa el número de tortillas n producidas por esa máquina en función del número t de
segundos que ha estado trabajando.
n = 1.5 t
10) Una avioneta viaja a 250 kilómetros por hora. Escribe la función que describe la relación entre
la distancia D recorrida medida en metros con el tiempo t medido en segundos.
D=
625
t ≈ 69.444 t
9
Para cada una de las siguientes funciones lineales, calcula su dominio, contradominio, ordenada al origen, pendiente y grafícala para −10 ≤ x ≤ 10. Explica en
cada caso qué transformación en la gráfica ocasiona un cambio en la expresión
(coeficiente o signo) respecto a las función anterior cuando las dos sean muy parecidas.
Efraín Soto A.
www.aprendematematicas.org.mx
Instruc.
2
11) f ( x ) = x − 3
29) f ( x ) = −
12) f ( x ) = 2 x + 1
13) f ( x ) = −2 x + 1
14) f ( x ) = −3 x + 5
30) f ( x ) =
x−1
+3
2
31) f ( x ) =
x+1
+3
2
32) f ( x ) =
x−1
−3
2
33) f ( x ) =
x+1
−3
2
34) f ( x ) =
3x
2
35) f ( x ) =
3x
+2
2
36) f ( x ) =
3x−1
2
37) f ( x ) =
3x+1
2
38) f ( x ) =
3x−1
+2
2
39) f ( x ) =
3x−1
−2
2
40) f ( x ) =
3x+1
+2
2
15) f ( x ) = 3 x + 5
16) f ( x ) = −3 x − 5
17) f ( x ) = 3 x − 5
18) f ( x ) = 2 ( x − 1) + 5
19) f ( x ) = 2 ( x − 1) − 5
20) f ( x ) = 2 ( x + 1) + 5
21) f ( x ) = 2 ( x + 1) − 5
22) f ( x ) = −2 ( x − 1) + 5
23) f ( x ) = −2 ( x − 1) − 5
24) f ( x ) = −2 ( x + 1) + 5
25) f ( x ) = −2 ( x + 1) − 5
x
26) f ( x ) = + 3
2
x
27) f ( x ) = − + 3
2
x
28) f ( x ) = − 3
2
Efraín Soto A.
x
−3
2
www.aprendematematicas.org.mx