1. No category

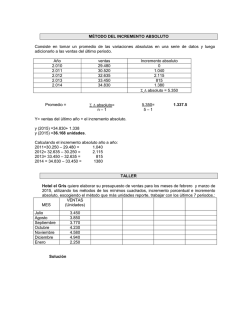
DEMOSTRACIÓN DE QUE EL TIEMPO ABSOLUTO NO EXISTE.
Aplicación práctica de la demostración mediante la ecuación de onda electromagnética
a través de cambio de sistemas coordenados usando la transformación de Galileo.
DEMONSTRATION THAT TIME THERE IS NOT ABSOLUTE.
Practical application of the demonstration by electromagnetic wave equation by
changing coordinate systems using the Galilean transformation.
Autor: José Manuel Gómez Vega
(ingeniero industrial en mecánica de máquinas)
junio de 2015.
1. Introducción. Movimiento relativo de Galileo y
tiempoabsoluto.
Desde los avances físicos de Newton el tiempo había sido considerado absoluto,
es decir, en cualquier punto del universo un reloj marcaría la misma hora que en otro
punto del espacio independientemente del sistema de referencia tomado. Galileo había
considerado previamente dos sistemas de referencia moviéndose uno respecto a otro.
Eso en física es conocido como relatividad de Galileo o transformación galileana. El
primer sistema de referencia está quieto en un punto y el segundo moviéndose a
velocidad constante respecto al primer sistema de referencia respecto a un eje. A los
sistemas de referencia que están quietos o a velocidad constante respecto a otros se les
conoce como inerciales. Son aquellos en los que no aparecen fuerzas ficticias. En una
palabra, un sistema es inercial si no existe aceleración. Es fácil de verlo con solo definir
que los sistemas se mueven a velocidad constante.
Si esto es así, es inmediato ver:
⟹
0
Con mayor rigor, en un sistema físico se pueden aplicar las leyes de la dinámica
clásica si no alcanzan velocidades cercanas a la de la luz pues ahí ya no se cumplen las
condiciones de sistemas inerciales. De hecho es ahí donde fallan las ecuaciones clásicas
de la física.
-1-
Durante mucho tiempo se aplicó a las leyes de la física la transformación de
Galileo, principalmente las de la mecánica, pues fue la primera de las disciplinas
desarrolladas ampliamente, y se observó siempre invariancia de las leyes ante dicha
transformación.
Fig. 1. El sistema de referencia S’ se mueve a velocidad v constante sobre el eje X.
Es decir, realizando un cambio de coordenadas entre los sistemas, una ecuación
física permanecía invariante frente a cualquier observador situado en cualquier sistema
de coordenadas de los descritos en la fig. 1. Eso hizo pensar a los físicos que el tiempo
era realmente absoluto en todo el universo. Además esta concepción arrancó con las
ideas de Newton basadas en comprobaciones respecto a dicha invariancia ante
transformaciones de Galileo. Y duró hasta finales del siglo XIX y principios del siglo
XX, donde ya se empezaban a encontrar incoherencias con las ecuaciones del
electromagnetismo donde no existía invariancia frente a cambios en dichos sistemas de
coordenadas aplicando la transformación de Galileo.
Obsérvese que se pudiera haber considerado el sistema S’ moviéndose en las 3
direcciones del espacio con 3 diferentes velocidades v a su vez constantes y tendríamos
igualmente sistemas inerciales, S quieto y S’ moviéndose respecto a S. También se
podrían haber considerado dos sistemas que se mueven el uno respecto al otro a
velocidades diferentes y también tendríamos sistemas inerciales. En definitiva, los
sistemas así definidos son inerciales pues cumplen la 1ª ley de Newton o de la inercia
que es que todo cuerpo al cual se somete a un impulso y se le deja en el espacio en un
sistema sin aplicación de fuerzas resultantes sobre él (de carácter disipativo
(rozamientos,…) u opositivas al propio movimiento) se desplazará indefinidamente con
movimiento rectilíneo y constante indefinidamente o estará en reposo si no se le somete
a ningún impulso.
Demostración práctica de que el tiempo absoluto no existe.
(José Manuel Gómez Vega, IngeMek – Ingenieros. Junio 2015)
-2-
El impulso no es más que una fuerza aplicada en un tiempo infinitesimal y que
no dura en el tiempo. Un impulso es, por ejemplo, tirar una piedra o empujar un objeto
un instante y soltarlo. Matemáticamente es:
d
,
Por simplicidad para llevar a cabo este estudio se considerará exclusivamente el
caso mostrado en la figura 1.
2. Cómodemostrarqueeltiemponoesabsoluto.
Para demostrar que el tiempo absoluto es irreal se puede hacer una
demostración con algún tipo de ecuación en la que, ante una transformación de Galileo,
la expresión en los dos sistemas de referencia no sea la misma. Si eso es cierto quiere
decir que, al no tener la fórmula la misma forma ante dos sistemas de referencia
distintos, el tiempo no es igual en todo el universo, es decir, no es absoluto, pues no
existen formas privilegiadas de observación para que la ecuación tenga una forma u
otra.
Cuando empezó a desarrollarse el electromagnetismo con Maxwell todavía no se
había tenido en cuenta problemas de simetrías a la hora de realizar cambios de
coordenadas ante transformaciones de Galileo como la planteada. Al principio, los
problemas de simetría indicaban a los físicos que ciertas nuevas ecuaciones de este
campo de la física tenían algunos sistemas de referencia preferentes, donde sus fórmulas
eran más sencillas y otros sistemas no tanto, dado que las ecuaciones se transformaban
en otras tras el cambio de coordenadas. Aunque el matemático Poincaré y el físico
Lorentz hicieron unos trabajos formidables en el campo del desarrollo previo de la
relatividad, no fue hasta Einstein donde se plantearon estos problemas de simetrías
ante cambios de coordenadas por transformación de Galileo. Entonces fue cuando
Einstein demostró que el tiempo no es absoluto en su artículo de 1.905 sobre la “teoría
de la relatividad especial” (o restringida) donde solo trataba un caso especial,
precisamente el de los sistemas inerciales en ausencia de efectos gravitatorios para
solucionar las inconsistencias detectadas en las ecuaciones del electromagnetismo. Luego
en 1.915 formuló la teoría general, reformulando la teoría de la gravedad newtoniana a
velocidades cercanas a la de la luz.
3. Obtención de la ecuación de onda para el campo
eléctrico y el campo magnético partiendo de dos
ecuacionesdiferencialesdeMaxwell.
para
Emplearemos la ecuación de onda electromagnética que tanto para
, tienen la misma expresión.
, como
Vamos a deducir dichas ecuaciones de onda partiendo de 2 de las 4 ecuaciones
de Maxwell.
Demostración práctica de que el tiempo absoluto no existe.
(José Manuel Gómez Vega, IngeMek – Ingenieros. Junio 2015)
-3-
⇔
.1 ⇔
.2
Vamos a definir lo que significan estas ecuaciones.
El operador
espaciales:
se conoce como nabla y se define así para las 3 coordenadas
donde la expresión
,
,
ec. 3
simboliza derivada parcial de algo respecto a la variable
, ,
y los vectores unitarios de cada componente
son respectivamente
, ,
es el del campo eléctrico y el vector
es el campo magnético (o
El vector
inducción magnética). Ambas expresiones están relacionadas mediante la fuerza de
Lorentz en su forma clásica para una partícula, donde
es la carga puntual y
la
velocidad:
El vector
.4
es la densidad de corriente eléctrica que en su forma integral es:
∬
.5
donde la intensidad de corriente eléctrica se consigue al tomar toda la densidad
de corriente en una superficie.
El escalar
es la permeabilidad magnética en el vacío, que tiene de valor:
donde
10 .6
son Newtons y , amperios.
El escalar
es la permitividad del vacío (o constante dieléctrica) cuyo valor es:
donde
4
es faradio y
8,8541878176 …
10
/
.7
metro.
Existe una relación trascendental entre la permitividad en el vacío y la
permeabilidad magnética en el vacío con respecto a la velocidad de la luz y es la
siguiente:
Demostración práctica de que el tiempo absoluto no existe.
(José Manuel Gómez Vega, IngeMek – Ingenieros. Junio 2015)
-4-
1
.8
Hemos detallado de donde proceden los términos en las 2 ecuaciones de Maxwell
descritas.
.
Nos falta definir el campo rotacional. Usaremos para definirlo sobre el vector
,
,
.9
Apliquemos el rotacional nuevamente a las dos ecuaciones de Maxwell.
Empecemos con la expresión que relaciona el campo eléctrico:
.1
Tenemos entonces:
Desarrollamos el doble rotacional y sustituimos el rotacional de
miembro, que era:
. 10
en el segundo
.2
resultando para el primer miembro de la ec. 10:
. 11
. 12
y para el segundo miembro de la ec. 10:
por lo que la ecuación queda, una vez transformados sus dos miembros:
. 13
Demostremos las expresiones anteriores. Empecemos por:
Demostración práctica de que el tiempo absoluto no existe.
(José Manuel Gómez Vega, IngeMek – Ingenieros. Junio 2015)
-5-
. 11
y desarrollaremos el primer miembro para llegar al segundo.
. 14
. 15
La mejor forma de desarrollar un rotacional siempre es mediante la expresión del
determinante:
. 16
Ahora se desarrollará el segundo miembro de la ec. 11 (el operador ∆ se llama
laplaciano),
∆
Demostración práctica de que el tiempo absoluto no existe.
(José Manuel Gómez Vega, IngeMek – Ingenieros. Junio 2015)
. 17
. 18
-6-
. 19
. 20
Entonces, Vemos que existen términos que se anulan (se suman y se restan) en la ec. 20.
Por lo tanto:
. 21
Y vemos como la ec. 16 y la 21 son iguales. Luego queda demostrado que:
. 11,
En la ec. 13 podemos simplificar:
El vector densidad de corriente
en el vacío es nulo. (
. 13
0
Por otra parte demostraremos que,
0
. 22
Para ello recurriremos al desarrollo del teorema de la divergencia o de Gauss
para el campo eléctrico:
∭
∬
∬
(ec. 23)
Hemos llegado a obtener el flujo del campo eléctrico a través de una superficie S
encerrada en un volumen V, que es:
Demostración práctica de que el tiempo absoluto no existe.
(José Manuel Gómez Vega, IngeMek – Ingenieros. Junio 2015)
-7-
∬
∭
(ec. 24)
donde es el flujo del campo eléctrico, es la densidad volumétrica de carga en
un punto de V (volumen) y es la carga total encerrada en el área .
Como por el Th. de Gauss, teníamos según la ec. 23,
1
ec. 25
Podemos tomar la expresión diferencial de la ec. 25 sencillamente,
ec. 26
Y considerando que la densidad volumétrica de carga
es constante, tenemos:
0 ec. 27
La conservación de la carga eléctrica está asociada a una simetría
del lagrangiano, llamada en física cuántica invariancia gauge. Además se puede
demostrar fácilmente mediante la ecuación de continuidad siguiente:
donde es la intensidad de corriente eléctrica producida a través de la superficie
S en el volumen encerrado V. Obsérvese que la ley de conservación de la carga es
análoga a la ley de conservación de la masa y otras variables análogas. Por tanto,
podemos afirmar categóricamente que es conservativa a menos que se aumente por
trabajos externos que afecten al área encerrada . donde está , hecho que no se aborda
ni se considera en condiciones de continuidad donde no existan efectos transitorios de
variación de carga, en este caso.
Por tanto, la ec. 13 quedaría,
. 28
que podemos expresar,
. 28
Y como por la ec. 8 teníamos:
Demostración práctica de que el tiempo absoluto no existe.
(José Manuel Gómez Vega, IngeMek – Ingenieros. Junio 2015)
-8-
1
.8
La ec. 28 queda, igualada a cero,
1
que es la ecuación de onda para
0
. 29
.
Para calcular la ecuación de onda para el campo magnético
, partimos de la
ec. 2,
.2
Realizando el rotacional en cada miembro de la ec. anterior:
. 30
Aplicando las mismas identidades en el primer miembro que las calculadas
anteriormente, tomando
0
í igual que antes y considerando la propiedad
saliendo fuera la derivada parcial,
del rotacional de introducirse dentro del campo
tenemos:
. 31
Según la ec. 1,
.1
.8
y aplicando la ec. 8,
1
la ec. 31 queda,
1
0
que es la expresión para la onda de un campo magnético
. 32
.
Obsérvese que las expresiones de las ecs. 29 y 32 son análogas tan solo
cambiando el vector correspondiente de campo, en un caso eléctrico y en otro
magnético.
Demostración práctica de que el tiempo absoluto no existe.
(José Manuel Gómez Vega, IngeMek – Ingenieros. Junio 2015)
-9-
4. Desarrollo de la ecuación de onda en las
coordenadasdelsistemaS’.
Denominemos la ecuación de onda de la siguiente forma:
1
0
. 33
que se puede transformar en la siguiente expresión:
1
0
. 34
dado que, como se ha comentado, tiene la misma forma para la onda eléctrica
como para la onda magnética.
Esta ecuación está definida para el sistema de referencia S, que es el que está
quieto en un punto del espacio. Recordamos que el sistema de referencia S’ se mueve a
velocidad constante v sobre el eje x (ver fig. 1). Por tanto, recordamos las ecuaciones
de transformación de Galileo:
⟹
. 35
Comenzamos a desarrollar los términos de la ec. 34:
Aplicamos la regla de derivación en derivadas parciales para todas las variables
∈ intervinientes , , , ∈ , , ,
1
0
0
1
Por lo tanto,
Y vemos que no es buen sistema para calcular las derivadas parciales pues
tenemos mezclas de ambos sistemas de coordenadas en el primer término del segundo
miembro. Por lo tanto, es mejor desarrollar la expresión
en derivadas parciales
desde el principio como se hizo con la derivada de primer orden.
Demostración práctica de que el tiempo absoluto no existe.
(José Manuel Gómez Vega, IngeMek – Ingenieros. Junio 2015)
-10-
2
2
2
2
2
2
El motivo de que aparezca un 2 multiplicando a algunos términos es por el
Th. de Schwartz de derivadas cruzadas que hace que cuente dos veces, dado que:
2
2
2
2
2
2
1 1
0 0
0 0
2
1 0
2
1 0
2
2
1 0
2
0 0
2
é
0 0
0 0
0 0
Por analogía para las otras componentes sobre ,
.
quedaría:
é
.
é
.
No siendo necesario el desarrollo formal pues se determina por observación y
similitud con respecto a la variable hallada.
Demostración práctica de que el tiempo absoluto no existe.
(José Manuel Gómez Vega, IngeMek – Ingenieros. Junio 2015)
-11-
Ahora falta resolver el término:
1
Dejaremos aparte la constante y desarrollaremos solo la parte entre paréntesis:
2
2
2
2
2
2
2
2
2
2
2
2
0 0
2
0
2
2
1
2
0 0
0
0 1
2
2
1 1
0 0
0 1
2
Ya podemos expresar la ec. 34 en los términos del sistema de referencia S’.
Teníamos para el sistema S:
1
0
. 34
Y vemos tras introducir los términos hallados anteriormente que nos conducen a
la siguiente expresión:
Demostración práctica de que el tiempo absoluto no existe.
(José Manuel Gómez Vega, IngeMek – Ingenieros. Junio 2015)
-12-
1
2
0⟹
0
. 36
Los términos en azul no aparecían en la ecuación original referida a un sistema
de coordenadas S fijo y hemos comprobado que ante un cambio de coordenadas,
mediante una transformación del movimiento relativo de Galileo, la ecuación no
permanece invariante. Esto es suficiente para demostrar que la ec. de onda tanto para
como para
no es válida para cualquier observador, es decir, no es invariante ante
varios observadores. Por lo tanto, el tiempo no puede ser absoluto pues si la
observación depende del movimiento, ésta a su vez lo es del tiempo, y no existe un
punto de vista absoluto en el cual la ec. 34 sea igual a la 36 variando sistemas de
referencia. Si en la ec. 35 hubiéramos tomado para las variables y otras expresiones
similares a las de , la ecuación 36 hubiera sido diferente y con toda probabilidad más
compleja.
Definitivamente el tiempo no puede ser absoluto y los fenómenos que
acontecieron a finales del siglo XIX y principios del XX primero con las
transformaciones de Lorentz y finalizando con la teoría de la relatividad especial de
Einstein, revolucionaron el concepto del tiempo, entendiéndose como relativo, NO
EXISTIENDO MOVIMIENTO ABSOLUTO REAL RESPECTO A NADA, a pesar de
que en ocasiones puede ser un buen sistema de referencia cierto conjunto de “estrellas
fijas” (que realmente no lo están pero valen como aproximación de sistema fijo), Por lo
tanto hemos erradicado el concepto de tiempo absoluto. A pesar de esta revolución de
la física, las ecuaciones para velocidades muy inferiores a la de la luz son correctas.
En este trabajo se ha hallado que el tiempo no puede ser absoluto, rompiendo
las reglas de invarianza de una ecuación física ante transformaciones galileanas,
c.q.d.
Demostración práctica de que el tiempo absoluto no existe.
(José Manuel Gómez Vega, IngeMek – Ingenieros. Junio 2015)
-13-