1. No category

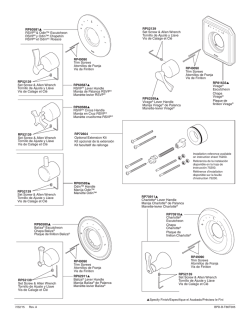
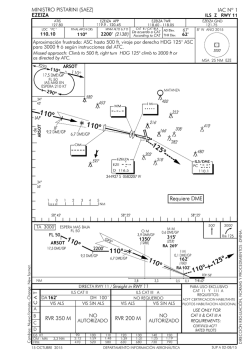
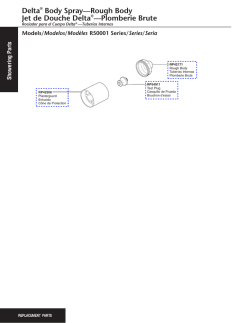
Ejemplo 1. Modelos con Variable Dependiente Binaria
9 Estamos interesados en analizar el efecto de algunos de los
determinantes de la decisión de acudir a una consulta médica en el
último mes (VIS). El objetivo es cuantificar la relación entre las
características individuales y la probabilidad de realiza alguna consulta
médica. En este caso:
⎧1 si el individuo i acude al médico durante el último mes
VISi = ⎨
⎩0 en caso contrario
9 Se considerarán como factores explicativos: el género (S2=1 si es
mujer y 0 si es hombre), la edad (EDAD), el estado de salud
autopercibido (ES=1 si es bueno y 0 si es malo) y la presencia de
enfermedades crónicas (CR=1 si están presentes y 0 en caso contrario).
9 A partir de la información referida a 1597 individuos se obtienen las
estimaciones de los siguientes modelos: Modelo de Probabilidad
Lineal (MPL), el LOGIT y el PROBIT.
Ejemplo 1. Estimación del MLP
Coeficientes(a)
Coeficientes no
estandarizados
Modelo
B
1
Coeficientes
estandarizados
t
Sig.
(Constante)
,373
Error típ.
,045
Beta
8,218
,000
s2
,089
,023
,092
3,915
,000
EDAD
,002
,001
,064
2,565
,010
ES
-,278
,027
-,268
-10,251
,000
cr
,110
,026
,108
4,200
,000
a Variable dependiente: VIS
Para este modelo, los coeficientes estimados de las variables cualitativas (S2, ES y CR)
se interpretan como cambios en la probabilidad de acudir al médico respecto a las
categorías de referencia. Para la EDAD, se interpreta como el cambio en la probabilidad
ante un cambio en una unidad en esta variable
1
Ejemplo 1. Estimación del Modelo Logit
Variables en la ecuación
B
E.T.
Wald
gl
Sig.
Exp(B)
I.C. 95,0% para EXP(B)
Inferior
Paso
1(a)
s2
Superior
,435
,113
14,840
1
,000
1,545
1,238
1,929
,008
,003
6,269
1
,012
1,008
1,002
1,015
-1,175
,126
86,515
1
,000
,309
,241
,395
,573
,135
18,078
1
,000
1,773
1,362
2,308
Constante
-,725
,221
10,737
1
,001
a Variable(s) introducida(s) en el paso 1: s2, EDAD, ESC, cr.
,484
EDAD
ES
cr
Los valores estimados de los coeficientes no pueden interpretarse directamente
como cambios en la probabilidad de acudir al médico. Su signo sí indica la
dirección del cambio. Para las variables cualitativas (S2, ES y CR) Exp(B)
representa los Odds Ratios. Para la EDAD, es el OR para una variación unitaria de
esta variable.
Ejemplo 1. Estimación del Modelo Probit
Estimaciones de los parámetros
Parámetro
PROBIT(a)
Estimación
Error
típico
Z
Sig.
Intervalo de
confianza al 95%
Límite
inferior
,132
Límite
superior
,398
s2
,265
,068
3,904
,000
EDAD
,005
,002
2,466
,014
,001
,009
ES
-,728
,077
-9,395
,000
-,880
-,576
cr
,343
,080
4,302
,000
,187
,499
-,425
,133
-3,192
a Modelo PROBIT: PROBIT(p) = Intersección + BX
,001
-,558
-,292
Intersección
Como en el modelo Logit, los valores estimados de los coeficientes no pueden
interpretarse directamente como cambios en la probabilidad de acudir al médico. Su
signo sí indica la dirección del cambio. Obsérvese que los coeficientes estimados
para cada variable explicativa es aproximadamente 1,6 veces menor para este
modelo que para el logit, en cambio su significación es prácticamente igual.
2
Ejemplo 1. Efectos Marginales
Para las variables no cualitativas puede llevarse a cabo una interpretación en
términos de los efectos marginales, como es el caso de la EDAD en este ejemplo.
Para individuos con S2=0, ES=0, CR=0 y para el valor medio de la edad (42 años) y
en los valores medios de todas las variables.
∂P(VIS i = 1)
e −0.725+ 0.008*42
=
0.008 = 0.001926
∂EDADi
(1 + e −0.725+0.008*42 ) 2
Modelo Logit:
∂P(VIS i = 1)
e −0.725+ +0.435*0.51+ 0.008*42−1.175*0.675+0.573*0.657
=
0.008 = 0.001838
∂EDADi
(1 + e −0.725+ +0.435*0.51+0.008*42−1.175*0.675+0.573*0.657 ) 2
∂P (VIS i = 1)
=
∂EDADi
Modelo Probit:
∂P(VIS i = 1)
=
∂EDADi
1
2π
e
−
( −0.725 + 0.008*42 ) 2
2
0.008 = 0.00295
1 − ( −0.725+ +0.435*0.51+ 0.008*422 −1.175*0.675+ 0.573*0.657 )
e
0.008 = 0.00269
2π
2
Ejemplo 1. Contrastes y Medidas de Bondad de Ajuste (Modelo Logit)
A continuación se presentan el test de razón de verosimilitudes, algunos pseudo-R2
y la tabla de contingencia entre valores predichos y observados
Resumen de los modelos
Pruebas omnibus sobre los coeficientes del modelo
Paso 1
Chi-cuadrado
233,597
Paso
gl
4
Sig.
,000
Bloque
233,597
4
,000
Modelo
233,597
4
,000
R cuadrado
-2 log de la
R cuadrado de
de
verosimilitud
Cox y Snell
Nagelkerke
1882,602(a)
,136
,185
a La estimación ha finalizado en el número de iteración 4
porque las estimaciones de los parámetros han cambiado en
menos de ,001.
Paso
1
Tabla de clasificación(a)
Pronosticado
VIS
Paso 1
Observado
VIS
Porcentaje global
0
Porcentaje
correcto
1
0
817
178
82,1
1
301
301
50,0
70,0
a El valor de corte es ,500
3
Ejemplo 1. Contrastes y Medidas de Bondad de Ajuste (Modelo Logit)
El test de Hosmer-Lemeshow compara entre valores estimados y valores
observados por grupos. Un valor elevado del contraste indica grandes diferencias
entre los valores predichos y reales.
Prueba de Hosmer y Lemeshow
Paso
1
Chi-cuadrado
10,162
gl
Sig.
,254
8
Tabla de contingencias para la prueba de Hosmer y Lemeshow
VIS = 0
Observado
Paso 1
VIS = 1
Esperado
Observado
Esperado
Total
1
138
136,022
23
24,978
161
2
136
130,704
25
30,296
161
3
118
123,441
42
36,559
160
4
125
119,202
35
40,798
160
5
115
114,939
49
49,061
164
6
99
104,464
61
55,536
160
7
91
93,939
69
66,061
160
8
59
68,642
101
91,358
160
9
58
57,850
102
102,150
160
10
56
45,798
95
105,202
151
Ejemplo 1. Predicción
A partir de las estimaciones de los coeficientes de los distintos modelos es posible
llevar a cabo la predicción de la probabilidad de acudir a consulta médica. En cada
caso, consiste en evaluar la función de distribución correspondiente para la
situación que desea predecirse. Por ejemplo, (1) evaluar la probabilidad para una
mujer de 35 años, con buen estado de salud y sin enfermedades crónicas; y (2) la de
un hombre de 40 años, con mala salud y enfermedades crónicas.
Modelo Logit:
(1) P (VIS i = 1) =
e −0.725+ 0.435+ 0.008*35−1.175
= 0.23
1 + e −0.725+ 0.435+ 0.008*35−1.175
(2) P (VIS i = 1) =
e −0.725+ 0.008*40 + 0.573
= 0.54
1 + e −0.725+ 0.008*40 + 0.573
Modelo Probit:
(1) P (VIS i = 1) = Φ ( −0.725 + 0.435 + 0.008 * 35 − 1.175 ) = 0.118
(2) P (VIS i = 1) = Φ(−0.725 + 0.008 * 40 + 0.573) = 0.56
4