1. Healthcare

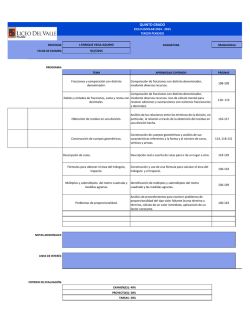
135
Lección 5.
Números Racionales
Los números racionales están formados por números tales como
1 5
y , que pueden ser
2 3
escritos como una razón o cociente de dos números enteros. El denominador o sea el
número de abajo ≠ 0. (El signo ≠ se lee “no es igual a.”) Todo número entero es
también un número racional ya que; por ejemplo, 2 lo podemos escribir como
2
.
1
Todos los números racionales los podemos convertir a números decimales:
Decimales exactos o sea que terminan, tales como
1
6
= 0.5 y
= 1.5.
2
4
Decimales que se repiten indeterminadamente. Aquellos que se componen de un grupo
de dígitos que se repiten infinitamente.
Ejemplo:
5
5
2
= 0.4545... , = 0.8333...
= 0.2222... ,
11
6
9
Fracciones
Comprendiendo las fracciones
Una fracción se obtiene cuando dividimos la unidad principal en partes iguales.
Los términos de
una fracción son
numerador y
denominador.
One hundred thirty-five
Ciento treinta y cinco
136
Lección 5
Se representa por dos números separados por una barra horizontal
numerador
denominador
.
Al número de arriba se le llama numerador, porque es el que cuenta, numera las
partes que se han tomado de la unidad, las partes que se han sombreado.
Al número de abajo se le llama denominador, porque denomina el nombre de la
fracción o sea le da el nombre a la unidad fraccionaria, y representa en cuantas
partes iguales se ha dividido la unidad. El denominador no puede ser 0, ya que nada se
puede dividir por cero. Se dice que es indeterminado.
Como leer las fracciones
1
2
1
4
3
4
1
3
2
3
1
8
3
8
5
8
7
8
un medio o uno sobre dos
one half or one over two
un cuarto o uno sobre cuatro
one fourth or one over four
tres cuartos o tres sobre cuatro
three fourths or three over four
un tercio o uno sobre tres
one third or one over three
dos tercios o dos sobre tres
two thirds or two over three
un octavo o uno sobre ocho
one eighth or one over eight
tres octavos o tres sobre ocho
three eighths or three over eight
cinco octavos o cinco sobre ocho
five eighths or five over eight
siete octavos o siete sobre ocho
seven eighths or seven over eight
Si el denominador es mayor de 10 se le agrega la terminación ~avos.
One hundred thirty-six
Ciento treinta y seis
137
Lección 5
1
16
un dieciseisavos o uno sobre dieciséis
3
16
tres dieciseisavos o tres sobre dieciséis
one sixteenth or one over sixteen
three sixteenths or three over
sixteen
5
17
cinco diecisieteavos o cinco sobre diecisiete
17
11
diecisiete onceavos o diecisiete sobre once
19
13
diecinueve treceavos o diecinueve sobre trece
11
14
once catorceavos u once sobre catorce
13
15
trece quinceavos o trece sobre quince
15
18
quince dieciochoavos o quince sobre dieciocho
One hundred thirty-seven
Ciento treinta y siete
138
Lección 5
¿Cómo leer y representar las unidades fraccionarias?
1
2
→
Un medio o uno sobre dos
Una fracción
representa una parte de
un todo o una parte de
un grupo. Siempre se
representa como una
parte sobre un total.
1
2
𝟏𝟏
En la fracción 𝟑𝟑 el 1
representa una parte de
1
3
un total de 3 partes
→
Un tercio o uno sobre tres
iguales.
Anteriormente hemos
dicho que una división
se puede representar
como una fracción. La
𝟏𝟏
fracción 𝟑𝟑 significa 1
dividido entre 3. (one
divided by three).
1
3
1
4
→
Un cuarto o uno sobre cuatro
1
4
One hundred thirty-eight
Ciento treinta y ocho
139
Lección 5
1
5
→
Un quinto o uno sobre cinco
1
5
1
6
→
Un sexto o uno sobre seis
1
6
1
7
→
Un séptimo o uno sobre siete
1
7
0ne hundred thirty-nine
Ciento treinta y nueve
140
Lección 5
1
8
→
Un octavo o uno sobre ocho
→
Un noveno o uno sobre nueve
→
Un décimo o uno sobre diez y así sucesivamente….
1
8
1
9
1
9
1
10
1
10
One hundred forty
Ciento cuarenta
141
Lección 5
Observe las diferencias de tamaño de las siguientes fracciones
0ne hundred forty-one
Ciento cuarenta y uno
142
Lección 5
Fracciones Equivalentes
Según la Real Academia Española, el término equivaler significa “dicho de
una cosa: ser igual a otra en la estimación, valor, potencia o eficacia.” La
definición de fracción equivalente dice que: “dos fracciones son equivalentes
cuando representan el mismo valor, pero con términos fraccionarios
diferentes.”
Ejemplo:
Dividamos este trozo en tres partes iguales.
La unidad fraccionaria es
1
3
. Si tomamos o sombreamos 2
partes la representamos como
2
3
.
Si dividimos cada una de las tres partes en dos partes iguales tendremos seis
partes, que son dos veces más pequeñas que las anteriores. Ahora tenemos
sombreada la fracción
casos,
2
3
y
4
6
4
6
, que es equivalente o sea igual a
2
3
, ya que en ambos
, tenemos igual porción del trozo original. Entonces
2
3
y
4
6
son
fracciones equivalentes.
Simplificación y Ampliación de Fracciones
Simplificar una fracción o reducirla a sus términos mínimos es hallar otra fracción
equivalente, cuyos términos son más pequeños. El proceso de simplificar una
fracción consiste en cancelar los factores comunes que comparten el numerador y el
denominador. (La tabla de factorización le ayudara a resolver estos ejercicios.)
Para cancelar los factores comunes se dividen el numerador y el denominador por UN
MISMO NÚMERO
que los divida exactamente.
One hundred forty-two
Ciento cuarenta y dos
143
Lección 5
Práctica 1.
a.
4
6
b.
18
24
b.
18 ÷ 6
3
18
=
=
24 ÷ 6
4
24
Respuestas
a.
4÷2
2
4
=
=
6÷2
3
6
Las respuestas de los ejercicios a y b son fracciones irreducibles ya que
no se pueden seguir simplificando por no existir ningún número que
divida exactamente al numerador y al denominador.
Algunos ejemplos de fracciones irreducibles:
8 5 4 12
, , ,
.
25 4 9 17
Ejercicios
Simplifique:
32
32 ÷ 2 16 16 ÷ 2 8
=
= =
=
Es la respuesta, ya que no se puede seguir
100 100 ÷ 2 50 50 ÷ 2 25
simplificando porque no existe ningún número que divida exactamente al
numerador y al denominador.
Otra manera abreviada de simplificar es de la siguiente forma:
0ne hundred forty-three
Ciento cuarenta y tres
144
Lección 5
Simplificar fracciones
Paso 1. Si el numerador y el denominador son divisibles por 2 divídalos entre 2. Si
ambos continúan siendo divisibles por 2 entonces continúe dividiéndolos.
Paso 2. Si ya no se pueden dividir entre 2 trate de dividirlo entre 3, luego entre 5
o entre 7… Continúe estos pasos hasta que este seguro que ya no existe
otro número que pueda dividir exactamente al numerador y al denominador
(únicamente entre 1.).
NOTA:
Recuerde que ambos, numerador y denominador, tienen que ser divididos
por el mismo número. Es decir si usted divide el numerador entre 2, el
denominador tiene que ser dividido entre 2. Si usted divide el numerador
entre 3 entonces el denominador tiene que ser dividido entre 3.
Ampliación de Fracciones
Amplificar una fracción es hallar otra fracción equivalente cuyos términos sean
mayores. Para amplificar tengo que multiplicar el numerador y el denominador por
un mismo número. Podríamos decir que es lo contrario a simplificar.
Práctica 2.
Amplíe las siguientes fracciones o encuentre una fracción equivalente con términos
(numerador y denominador) mayores.
a.
2
3
b.
8
25
Respuestas
2
a.=
3
2×3 6
=
3× 3 9
O sea que
2
6
es equivalente a .
3
9
One hundred forty-four
8
8× 2
16
b.= =
25 25 × 2 50
O sea que
8
16
= es equivalente a
.
25
50
Ciento cuarenta y cuatro
145
Lección 5
Reducción de fracciones a un mismo común denominador
Cuando trabajamos con fracciones que no tienen común denominador necesitamos
convertir esas fracciones en otras equivalentes que tengan todos los mismos
denominadores. Existen varias maneras de encontrar el común denominador de dos
o más fracciones.
Ejemplo, encuentre el común denominador de:
a.
2
3
y
3
4
a. Multiplicación cruzada:
Primero: multipliquemos ambos términos (numerador y denominador) de la primera
fracción
2 4
8
2
por el denominador (4) de la otra fracción, × =
.
3 4 12
3
Entonces
2
8
=
.
3
12
Segundo: multipliquemos ambos términos (numerador y denominador) de la otra
fracción
3
3 3 9
por el denominador (3) de la primera fracción, × = .
4
4 3 12
Entonces,
9
3
=
.
4
12
Resumiendo: Ambas fracciones ahora tienen un mismo común denominador.
a.
2
3
y
3
4
2
=
3
2 4
8
× =
3 4 12
3
=
4
3 3 9
× =
4 3 12
0ne hundred forty-five
Ciento cuarenta y cinco
146
Lección 5
b. Otra manera de encontrar el mínimo común denominador es hallando el mínimo
común múltiplo de los denominadores de las fracciones dadas.
Ejemplo, encuentre el mínimo común denominador de:
b.
2
3
y
3
4
El mínimo común múltiplo de 4 y 3 es 12. Ese número nos
va a servir como mínimo común
denominador. (El múltiplo de un número
es la tabla de multiplicar de ese
número.)
2
2 ? ?
= × =
3
3 ? 12
Encontremos un número que
multiplicado por 3 nos de doce.
Ese es 4. También, multiplique
4 por el numerador.
2
2 4
8
= × =
3
3 4 12
3
3 ? ?
= × =
4
4 ? 12
Encontremos un número que
multiplicado por 4 nos de doce.
Ese es 3. También, multiplique
3 por el numerador.
3
3 3 9
= × =
4
4 3 12
Ahora ambas fracciones tienen igual denominador:
8
9
y
12 12
Comparación de Fracciones
a. Si las fracciones tienen igual denominador (fracciones homogéneas) o sea que
todas las partes son iguales, es obvio que la que tenga el numerador más grande
es mayor.
Ejemplo
8 3 11
,
,
.
12 12 12
One hundred forty-six
11
es mayor.
12
Ciento cuarenta y seis
147
Lección 5
b. Si las fracciones tienen igual numerador pero distintos denominadores (fracciones
heterogéneas), será mayor la que tenga el menor denominador. Porque significa
que la unidad está dividida en partes más grandes.
Ejemplo:
5 5 5
, , .
8 6 9
5
es mayor.
6
c. Si las fracciones tienen numeradores y denominadores desiguales (fracciones
heterogéneas), entonces tenemos varias opciones para resolverlas y todas son
correctas.
Ejemplo, compare las siguientes fracciones:
4
6
y
12 8
c.1. Simplifiquemos a sus términos mínimos:
2
4÷2
2÷2
1
4
=
=
=
=
6
12 ÷ 2
6÷2
3
12
6
=
8
6÷2
3
=
8÷ 2
4
Recuerde que esta simplificación
la puede hacer en forma vertical.
Los denominadores obtenidos son desiguales,
3
1
y , entonces buscaremos el común
4
3
denominador y veremos cuál es el mayor.
Reduzcamos
3
1 4 4
1
y al mismo denominador: × =
4
3
3 4 12
3 3 9
× =
4 3 12
Ahora, ambas fracciones tienen
un común denominador.
Entonces
4
9
es menor que
.
12
12
Lo representamos así:
0ne hundred forty-seven
9
4
<
.
12 12
Ciento cuarenta y siete
148
Lección 5
c.2. Encontremos el mínimo común múltiplo de los denominadores:
4
6
y .
12 8
Es preferible simplificar primero para trabajar con números más pequeños.
En el paso c.1., ya simplificamos
1
3
y
3
4
6
4
y , y obtuvimos:
12 8
El mínimo común múltiplo de 4 y 3 es 12. Ese número
nos va a servir como mínimo común
denominador. (El múltiplo de un
número es la tabla de multiplicar de
ese número.)
Encontremos un número que
1 ? ?
1
× =
=
3 ? 12
3
multiplicado por 3 nos de doce.
Ese es 4. También, multiplique
1
=
3
1 4 4
× =
3 4 12
3
=
4
3 3 9
× =
4 3 12
4 por el numerador.
Encontremos un número que
3 ? ?
3
× =
=
4 ? 12
4
multiplicado por 4 nos de doce.
Ese es 3. También, multiplique
3 por el numerador.
Ahora ambas fracciones tienen igual denominador:
9
4
y
, y encontramos que:
12 12
4
9
<
.
12 12
One hundred forty-eight
Ciento cuarenta y ocho
149
Lección 5
c.3. Una manera rápida de comparar fracciones es “multiplicar cruzado”, el
denominador de la primera fracción por el numerador de la segunda
fracción. Luego el denominador de la segunda fracción por el
numerador de la primera fracción. No es necesario multiplicar los
denominadores.
Ejemplo, compare las siguientes fracciones:
4
6
y
12 8
12 x 6 = 72
Observamos que el producto mayor está al
8 x 4 = 32
lado de la fracción
6
y el producto menor
8
está al lado de la fracción
podemos decir que
4
, entonces
12
6
4
< .
8
12
Comparación de las Fracciones con Respecto a la Unidad
a. Toda fracción donde el numerador es igual al denominador,
6
, decimos que esa
6
fracción es igual a la unidad o sea igual a 1.
Las seis partes de la unidad están sombreadas.
Equivale a
0ne hundred forty-nine
6
= 1.
6
Ciento cuarenta y nueve
150
Lección 5
b. Toda fracción donde el numerador es menor que el denominador,
5
, decimos
6
que esa fracción es menor que la unidad o sea menor que 1, y recibe el nombre de
FRACCIÓN PROPIA.
5
es una FRACCIÓN PROPIA.
6
c. Toda fracción donde el numerador es mayor que el denominador,
7
, decimos
6
que esa fracción es mayor que la unidad o sea mayor que 1, y recibe el nombre de
FRACCIÓN IMPROPIA.
1
+
1
6
7
6
1
Es una FRACCIÓN IMPROPIA. Es igual a + .
6
6
6
1
1 +
6
Cuando las fracciones impropias se escriben como un
número entero y una fracción, se le denomina NÚMERO
MIXTO. 1
One hundred fifty
1
Es un número mixto.
6
Ciento cincuenta
151
Lección 5
Convertir una Fracción Impropia a Número Mixto
Ejemplo:
7
es una fracción impropia porque el numerador es mayor que el
4
denominador. Conviértala a número mixto.
Primero:
Divida el numerador 7 entre el denominador 4
7÷4=
1
4 7
−4
3
Segundo:
El cociente representa al número entero. En este ejemplo el 1 es el
entero.
Tercero:
El residuo pasa hacer el numerador. 3 es el residuo y pasa hacer el
numerador.
Cuarto:
El divisor pasa hacer el denominador. 4 es el divisor y pasa hacer el
denominador.
Quinto:
Si la fracción se puede *simplificar entonces simplifíquela.
0ne hundred fifty-one
Ciento cincuenta y uno
152
Lección 5
Utilizando la calculadora científica.
Convertir fracción impropia a número mixto. Ejemplo:
.
luego presione el 7, luego presione la flecha de abajo
Presione
para que el cursor se mueva hacia el denominador; presione el 4. Luego presione la
flecha de la derecha
. Obtiene:
y por último presione
One hundred fifty-two
. Ahora, presione
. La respuesta es
y luego
.
Ciento cincuenta y dos
153
Lección 5
Ejercicios
¿Cuál fracción es Mayor, Menor o Igual? (>, <, =). Escriba el signo
correspondiente.
1.
2
3
_____
3
4
2.
5
4
_____
7
10
3.
2
2
_____
3
5
4.
7
6
_____
8
9
5.
3
3
_____
9
10
6.
2
4
_____
3
5
7.
1
1
_____
4
3
8.
6
6
_____
8
10
9.
2
2
_____
4
5
10.
4
4
_____
6
5
11.
2
1
_____
4
2
12.
7
9
_____
8
10
0ne hundred fifty-three
Ciento cincuenta y tres
154
Lección 5
Ejercicios
Identifique cada una de las siguientes fracciones. Escriba a la par si es Fracción
Propia o Fracción Impropia.
1.
100
= _________
30
2.
147
________
30
3.
54
________
60
4.
87
= _________
24
5.
2
________
14
6.
20
________
28
7.
22
= _________
14
8.
74
________
16
9.
110
________
70
10.
10
= _________
70
11.
16
________
12
12.
7
________
14
13.
3
= _________
24
14.
52
________
24
15.
30
________
9
16.
120
= _________
42
17.
186
________
48
18.
12
________
18
19.
5
= _________
10
20.
54
________
30
One hundred fifty-four
Ciento cincuenta y cuatro
155
Lección 5
Convertir un Número Mixto a Fracción Impropia
Siga los siguientes pasos:
1. Multiplique el denominador por el número entero
2. Luego súmele el numerador
3. Escriba ese resultado como el numerador y escriba como denominador el
denominador original.
Ejemplo, convierta 3
1
a fracción impropia:
4
Paso 1:
3 ×+
1
4
Multiplique el denominador por el número entero 4 × 3 = 12
Paso 2:
Luego súmele el numerador 12 + 1 = 13
Escriba ese resultado como el numerador.
Paso 3:
3 ×+
1 13
=
?
4
Entonces el número mixto 3
0ne hundred fifty-five
Escriba como denominador el denominador
original
13
.
4
13
1
convertido a fracción impropia es igual a
.
4
4
Ciento cincuenta y cinco
156
Lección 5
Utilizando la calculadora científica.
Convertir número mixto a fracción impropia. Ejemplo:
Presione
luego presione
la pantalla muestra
Presione el 3, presione la flecha de la derecha
para que el cursor se
mueva hacia el numerador, presione el 1, luego presione la flecha de abajo
para que el cursor se mueva hacia el denominador; presione el 4. Luego presione la
flecha de la derecha. Obtiene:
y por último presione
One hundred fifty-six
Ahora, presione
. La respuesta es
y luego
.
Ciento cincuenta y seis
157
Lección 5
Convertir un Entero a Fracción Impropia
Únicamente escriba como denominador el número 1.
Ejemplo, convierta 3, 4, y 9 a fracción impropia.
3=
3
1
4=
4
1
9=
9
1
Ejercicios
Convierta las Fracciones Impropias a Número Mixto y los Números Mixtos a Fracciones
Impropias. Simplifique si es necesario.
a.
18
= _________
7
b.
72
________
7
c.
28
________
3
d.
37
= _________
6
e.
13
________
5
f.
50
________
9
3
= _________
5
h.
7
1
________
2
i.
2
1
________
2
k.
5
1
________
4
l.
5
1
________
3
g.
j.
1
5
4
= _________
5
0ne hundred fifty-seven
Ciento cincuenta y siete