1. No category

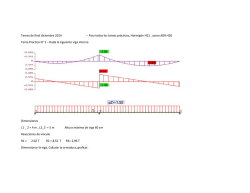
X Congreso Español sobre Metaheurísticas, Algoritmos Evolutivos y Bioinspirados (MAEB 2015)
Aplicación de metaheurísticas en la
optimización de pasos superiores de carreteras
José V. Martí1, Víctor Yepes2, Tatiana García-Segura3
Resumen--El artículo se ocupa de la optimización económica
de los tableros de los pasos superiores de carreteras formados
por una losa de hormigón ejecutada in situ y dos vigas artesa
prefabricadas de hormigón pretensado autocompactable. Se
comprueba la eficacia de las distintas metaheurísticas
aplicadas en la optimización: “descent local search” (DLS),
“simulated annealing” (SA), “threshold accepting” (TA),
“genetic algoritms” (GA) y “memetic algorithms” (MA). Los
cálculos de las tensiones y de sus envolventes, son
programados en lenguaje fortran directamente por los
autores. Los algoritmos de optimización heurística se aplican
a un tablero de 35 m de luz y 12 m de ancho. Los parámetros
que definen la forma de la sección de la viga se adaptan a los
moldes de una instalación de prefabricados. El ejemplo que se
analiza consta de 59 variables discretas. El módulo de la
evaluación incluye los estados límite último y de servicio que
se aplican comúnmente para estas estructuras: flexión,
cortante, torsor, fisuración, flechas, etc. Los algoritmos SA y
TA se han calibrado previamente a partir del DLS, y el MA a
partir del GA y del SA. Cada heurística se procesa nueve
veces, obteniéndose información estadística sobre el valor
mínimo, el medio y las desviaciones. Se realiza un análisis del
rendimiento de las distintas heurísticas, basado en un estudio
de las soluciones Pareto-óptimas entre tiempo de ejecución y
rendimiento. Los mejores resultados se obtienen para el SA y
el TA, siendo el coste mínimo de 108008 €, correspondiente al
SA. Finalmente, entre las principales conclusiones de este
estudio, destaca que las soluciones y los tiempos de proceso
computacional son tales, que estos métodos se pueden aplicar
de un modo práctico a casos reales, y que el conocimiento
derivado del uso de estos algoritmos permiten recomendar
rangos de valores para emplearlos en el diseño optimizado de
estas estructuras y en su aplicación para los
predimensionados de las variables.
Palabras clave—Optimización, metaheurística, puentes, pasos
superiores, diseño de estructuras.
I.
INTRODUCCIÓN
La inteligencia artificial, desde sus comienzos
hacia mediados de 1950, se ha ido utilizando
progresivamente como herramienta resolutiva en
distintos ámbitos técnicos. Una de sus aplicaciones
se ha dirigido hacia la optimización del diseño de
estructuras bajo diferentes objetivos, tales como la
reducción del coste económico en la fase de
construcción, la disminución de la emisión de gases
de efecto invernadero durante su ejecución o vida
útil, el aumento de la seguridad, etc. Para diseñar
una estructura se selecciona un grupo de variables
conforme a unos condicionantes estructurales de
contorno. Las variables del diseño incluyen entre
1
ICITECH. Universitat Politècnica de València, Camino de Vera
s/n 46022 Valencia. E-mail: [email protected]
2
ICITECH. Universitat Politècnica de València, Camino de Vera
s/n 46022 Valencia. E-mail: [email protected]
3
ICITECH. Universitat Politècnica de València, Camino de Vera
s/n 46022 Valencia. E-mail: [email protected]
241
otros, la tipología de los distintos materiales, las
dimensiones de las secciones transversales y los
refuerzos de acero. A pesar del alto potencial y los
buenos resultados obtenidos con la aplicación de la
inteligencia artificial en la optimización económica,
en el presente, el diseño de estructuras de hormigón
está muy condicionado por la experiencia de los
ingenieros calculistas. El diseño tradicional de
estructuras de hormigón se fundamenta en el
conocimiento y experiencia sobre la materia de los
proyectistas, que tienen como objetivo la obtención
de estructuras seguras y que a la vez cumplan los
condicionantes de durabilidad a lo largo de su vida
útil [1]. Hay que añadir que el ingeniero proyectista,
que inicialmente diseña y predimensiona las
distintas partes y secciones de la estructura, a
continuación, mediante la utilización de programas
informáticos prueba la bonanza del diseño inicial, y
lo ajusta en los lugares críticos que puedan
presentar. Si los valores geométricos o la resistencia
de los materiales son insuficientes, la estructura se
redefine sobre la base del ensayo de prueba y error.
Tal procedimiento conduce a diseños seguros, pero
en cambio, la economía de las estructuras de
hormigón queda muy condicionada a la experiencia
del diseñador calculista.
Los métodos metaheurísticos de optimización
pretenden minimizar una función objetivo, como
pueda ser en nuestro caso, el coste de un paso
superior de carreteras. Su aplicación a las
estructuras de hormigón ha sido muy reducida
comparada con las desarrolladas para las estructuras
de acero [2]. Nuestro grupo de investigación ha
presentado últimamente trabajos de optimización de
estructuras de hormigón armado y pretensado con
distintas técnicas heurísticas [3-10]. De un modo
general, los métodos de optimización estructural se
pueden clasificar en dos amplios grupos: métodos
exactos y métodos heurísticos. Los métodos exactos
se corresponden con el sistema tradicional. Se basan
en el cálculo de soluciones óptimas siguiendo las
técnicas iterativas de la programación lineal [11,12].
El segundo grupo principal es el de los métodos
metaheurísticos, cuyo reciente desarrollo va ligado a
la evolución de los procedimientos de la inteligencia
artificial. Este grupo incluye un amplio número de
algoritmos de búsqueda [13-16], tales como
búsqueda por gradiente (DLS), algoritmos genéticos
(GA), meméticos (MA), recocido simulado (SA),
búsqueda tabú (TS), aceptación por umbrales (TA),
Metaheurísticas en Empresas y Producción
colonias de hormigaas (ACO), etcc. Dichos méttodos
se han aplicado con éxito en áreaas diferentes de la
ingenierría estructuraal [17]. Se baasan en algoriitmos
sencilloos, pero quee necesitan un
u gran esfuuerzo
computtacional al coontener un nú
úmero elevaddo de
iteracioones en las cuales se valora
v
la funnción
objetivoo y se comprueban las restricciiones
estructuurales.
II.
preseenta los resulttados obteniddos, recogiénd
dose las
princcipales conclusiones.
Fig. 1.
Perfil longitudinall del paso superio
or.
DESSCRIPCIÓN DE LA
L ESTRUCTUR
RA
El pproblema plannteado preten
nde optimizarr una
estructuura utilizadaa como paaso superiorr de
carreterras. En la actuualidad, la prááctica totalidaad de
los tablleros de estos pasos superio
ores se constrruyen
ya sea con losa conttinua de horm
migón ejecutaddo in
situ o ccon vigas preefabricadas dee hormigón y losa
superiorr ejecutada en
e obra. La prefabricacióón de
tableross con vigas haa experimentaado una evoluución
importaante desde suss inicios, ofreeciendo soluciiones
de grann calidad esttética y un mayor
m
númerro de
tipologíías. En cuantoo a la sección transversal, ddesde
las proppuestas inicialles constituidaas por un conjjunto
de vigaas prefabricaddas doble T se
s ha pasado a la
utilización de vigas artesa con forma
f
de U, más
pesadass, con gran seeparación entrre ejes, que vaan de
5 o 6 m a 12 m,
m utilizando placas superriores
prefabriicadas, que constituyen
n un encoffrado
colaborrante de la lossa superior qu
ue se completaa con
un horm
migonado in situ. Estas so
oluciones perm
miten
eliminaar completameente los cabezzales sobre piila de
los tabbleros de vigga doble T que tanto eefecto
antiestéético producenn. El problem
ma de optimizaación
está baasado en la tesis
t
doctoral del primer aautor
[18]. Laa luz del vanoo es la habitu
ual de 35 m. E
Estos
puentess consisten en dos vig
gas de horm
migón
pretensaado con armaadura pretesaa HP en form
ma de
“U” y una losa supperior colaborrante parcialm
mente
prefabriicada o constrruida in situ (v
ver Fig.1 y Figg. 2).
Esta tippología cuentaa a su favor, entre
e
otras, coon las
ventajass derivadas dee la prefabricaación como s on la
los
mooldes
construcción
inddustrializada,
p
de ejecución en obra
reutilizaables, los plazos
reduciddos y la bajaa interferencia con el trráfico
inferiorr. Las dos vigas son
n de horm
migón
autocom
mpactante, quue integran en
n la parte supperior
una losaa de hormigónn armado HA
A para el tráficco de
vehículos de 12 m de anchu
ura (Fig. 2).. La
optimizzación del disseño se basa en el cálculoo del
coste dde cada una de
d las solucio
ones evaluadaas, en
funciónn de las variabbles geométriccas, los materriales
y los refuerzos activoo y pasivo. A continuación se ha
implem
mentado un módulo
m
que evalúa todoss los
estados límites relevvantes, y posteriormente see han
desarrollado, específficamente para este trabajoo, los
mos metaheuurísticos capaaces de encoontrar
algoritm
solucionnes optimizaddas en coste. El artículo,, tras
realizarr el planteeamiento deel problema de
optimizzación, definee los algorittmos aplicadoos y
Fig. 2.
III.
Sección transveersal del tablero.
DEFINICIÓN DE
EL PROBLEMA A RESOLVER
El
E problema matemáticoo consiste en la
optim
mización econ
nómica de la estructura. Para ello
se deeben encontraar los valoress de las variaables de
diseñ
ño (x1, x2,…, xn) capaces dde minimizar el coste
repreesentado por la expresiónn {1}, satisffaciendo
adem
más las condicciones formulladas en la ex
xpresión
{2}, que indican las
l restriccionnes geométriccas y de
consttructibilidad, así como los estados límitee que se
deben
n verificar. Los
L valores x 1, x2,…, xn son las
variaables de diseño
o del problem
ma, que pueden
n tomar
uno de los valo
ores discretoos indicados en la
expreesión {3}. Las solucioness que satisfaacen las
restriicciones en la expresión {2} se den
nominan
factib
bles, y las quee no, solucionees no factibless
r
{1}
C f x1 , x2 ,..., xn ¦ pi ˜ mi x1 , x2 ,..., xn i 1
g j ( x1 , x2 ,.....xn ) d 0
{2}
xi  di1 , di 2 ,..., diq
{3}
i
TABLA I
Precios unittarios de los mateeriales en euros
242
Descripcción
Precio
Precio
P
Kg. acero pasivo (B-500-S)
(
Kg. acero activo (Y
Y-1860-S7)
m de
d molde en vig
ga
m2 de encofrado en
n losa
m3 de hormigón HA-25
H
m3 de hormigón HA-30
H
m3 de hormigón HA-35
H
m3 de hormigón HA-40
H
m3 de hormigón HP-35
H
m3 de hormigón HP-40
H
m3 de hormigón HP-45
H
m3 de hormigón HP-50
H
en viga
2.63
3.38
75.11
NA
NA
NA
NA
NA
122.25
133.40
142.15
152.89
en
n losa
1.40
NA
N
NA
N
30
0.00
64
4.99
69
9.95
74
4.03
79
9.12
NA
N
NA
N
NA
N
NA
N
X Congreso Español sobre Metaheurísticas, Algoritmos Evolutivos y Bioinspirados (MAEB 2015)
El coste del tabllero depende tanto del vollumen
de los materiales em
mpleados com
mo de la manno de
obra, dde la maquinaria y de los medios auxiiliares
necesaarios para su ejecución.
ej
La función
f
de cooste se
obtienee como la suuma de los prrecios unitariios de
cada unnidad de obraa por su medición, incluyenddo los
costes indirectos (Taabla 1). Se traata de un probblema
de opptimización combinatoria,
c
, puesto quue se
formulla con valoress discretos dee las variabless para
garantiizar su construuctibilidad.
El análisis incluuye 59 variab
bles del diseñño. La
Figura 3 muestraa las variaables geoméétricas
princippales consideeradas en este
e
análisis. Las
variablles geométriccas incluyen siete variablees: el
canto dde la viga (h1), el espesor de la losa (ee4), el
ancho del ala inferiior de la vigaa (b1) y su esspesor
(e1), ell ancho y espesor de las allas superiores de la
viga (bb3 y e3) y el espesor de laas almas (e2) . Con
respectto a la resistencia del maaterial, son doos las
variablles que defineen el tipo de hormigón, el de la
losa y el de la vigga. El pretenssado con arm
madura
activa se encuentra definido por cuatro
c
variablles: el
númeroo de torones en
e las alas sup
periores, el núúmero
de toroones dispuestoo entre las priimeras, segunndas y
terceraas capas dell ala inferio
or, el númerro de
seccionnes con fundaas dispuestas en
e la segundaa capa
y el núúmero de seccciones con fu
undas en la teercera
capa. F
Finalmente, soon 46 variables las que definnen la
armaduura pasiva estándar dispuessta para la vigga y la
losa suuperior. Todaas las variablees en este annálisis
son disscretas, pudieendo tomar caada una de elllas un
determ
minado rango de valores que formaan un
6
espacioo aproximadoo de 1.60x1065
soluciones.. Este
desorbitado espacio de solucioness es el que jusstifica
la adoppción de algorritmos heurístticos para encoontrar
solucioones económ
micas en tiempos de cáálculo
razonab
ables.
Fig. 3.
Varriables geométricaas del tablero.
En cuanto a los parám
metros, éstas son
magnittudes que se toman como datos fijos y que,
por taanto, no afecctan a la op
ptimización dde la
estructu
tura. Los prrincipales paarámetros see han
divididdo en geoméétricos, de caarga, de costte, de
armadoo y de exposición. Entre ellos destaccan el
ancho del tablero, laa inclinación de
d las almas, la luz
de las vigas, la essbeltez mínim
ma de la vigaa, las
243
gas muertas, la distanciaa de transporte, la
carg
dificcultad de montaje de las vigas y los tipos de
acerro. Los paráámetros de las vigas han sido
esco
ogidos para facilitar la adapptación de su diseño a
los moldes
m
de fab
bricación existtentes en las empresas
e
de prefabricados
p
. Las condicciones de durrabilidad
son las relativas a la instruccióón de hormig
gón EHE
[19].
h considerad
do las restriccciones estructu
urales de
Se han
la IA
AP-98 [20], eso
e incluye coomprobacionees en los
estad
dos límite últimos y de sservicio para flexión,
cortaante y torsor,, así como faatiga, fisuració
ón y las
defo
ormaciones para
p
la envoolvente de teensiones
debiida al peso propio y a las ccargas del tráffico. Las
tensiones y las reacciones se obtienen
n como
resu
ultado de un programa
p
de ddesarrollo pro
opio que
conssidera los disstintos estadoos tensionaless que se
prod
ducen en la fabricación de lla viga y en su puesta
en obra,
o
mediantee dos modeloss de elemento
os finitos
de emparrillado
e
plano aplicanddo el conocido
o método
de laa rigidez. El primer
p
modello está compu
uesto por
20 barras
b
y 21 no
odos, y el seguundo por 103 barras y
84 nudos. Tanto el módulo
lo de comprrobación
uctural como los algoritmoos aplicados han
h sido
estru
prog
gramados en lenguaje FFortran 95 con un
com
mpilador Com
mpaq Visual Fortran Proffessional
6.6.0
0. en un orden
nador con un pprocesador In
ntel Core
TM2
2 Quad CPU Q6600
Q
2.40 G
GHz.
IV.
ALGORITMOS EMPLEADOS
A. Descent
D
locall search (DLS)
S)
Esta
E heurísticaa se aplica parra ayudar a caalibrar el
SA y TA, que a priori tienen mayor poten
ncia para
optim
mizar las fu
unciones objeetivo. El pro
oceso se
iniciia con la solución
s
obteenida de un
n modo
aleatorio. A conttinuación se modifica la solución
variaando el valo
or de algunaas de sus variables
v
(movimiento). Si el coste del nnuevo tablero
o mejora
al anterior,
a
entonces se com
mprueba y sii resulta
factiible se aceptaa, reemplazanndo al anterio
or como
solu
ución de trabaajo. Se repite el proceso hasta que
no se
s encuentre ninguna
n
nuevva solución co
on coste
inferrior a la de trabajo desp
spués de un número
deteerminado de itteraciones. Paara tener en cuenta
c
la
com
mponente aleaatoria del m
método se reepite el
procceso un númerro determinaddo de veces (9 veces).
El movimiento
m
que
q se ha em
mpleado mod
difica un
núm
mero fijo (tipo justo) de variiables elegidaas al azar
increementando o disminuyendoo un paso o unidad
u
el
valo
or de cada variiable también de forma aleaatoria.
Los
L movimien
ntos aplicadoss al problemaa se han
defin
nido modificaando el 5%, 1 0%, 15%, 20%
%, 25%,
y 30
0% de las variiables, equivaalente a 3, 6, 9,
9 12, 15
y 18
8 variables. Paara cada tipo el algoritmo se repite
9 veeces, y cada un
no se procesaa hasta que se produce
un máximo de 25000 iteraaciones seguiidas sin
mejo
ora de la solu
ución. En la FFigura 4 se mu
uestra la
evollución del co
oste y tiemppo para los distintos
Metaheurísticas en Empresas y Producción
movimiientos de las variables
v
y co
on 100, 500, 11000,
5000, 110000, 15000,, 20000 y 250
000 iteracionees sin
mejora.. Los óptimoos de pareto más equilibrrados
entre cooste/tiempo se
s correspond
den con V9 ((5000
iteracioones), y V12 (para 10000
1
y 1 5000
iteracioones). Se puedde apreciar que
q el movim
miento
V9 preesenta el meejor resultado
o, pues para este
movimiiento con 50000 iteracionees sin mejorra su
coste ess de 134529 € y su tiempo
o de proceso ees de
790 seggundos. A parttir de este pun
nto, una mejorra del
1.6% see consigue coon un incremeento del 72.2%
% en
tiemposs de compputación parra V12 (1 0000
iteracioones), y para el siguiente óptimo de paareto,
una m
mejora del 2.8%
2
en co
ostes implicaa un
incremeento de más del
d doble en tiempos.
t
La m
mejor
soluciónn encontrada se ha produccido en una dde las
ejecucioones variandoo el 15% de las variables (V
V9), y
su costee es de 1154599 €.
Fig. 4..
Evoluciónn del algoritmo DL
LS en el tiempo ppara
distintas iteraciones y variables
B. Sim
mulated annealing (SA) y Th
hreshold acceppting
(TA)
El pprimero de loss dos métodos, el SA, se ffunda
en el ffenómeno físiico de la cristalización dee los
metaless fundidos, originalmentee propuesto por
Kirkpattrick et al. [221]. Es una técnica simillar al
DLS, ppero admite soluciones
s
dee trabajo de peor
calidad (coste mayoor) siempre que cumplann un
cierto criterio de acepptación y a la vez sean factiibles,
permitieendo así escappar de óptimo
os locales. Hooy en
día es uuna técnica muy
m conocida y desarrolladda. El
criterio de aceptaciónn empleado ess probabilísticco. Al
principiio permite aceeptar solucion
nes de trabajoo más
costosas con muchha probabilid
dad, reduciénndose
dicha pprobabilidad conforme av
vanza el pro ceso,
siendo aal final de éstte la probabiliidad prácticam
mente
nula paara aceptar unna solución peeor, asemejánndose
en ese m
momento a unn DLS.
El segundo méétodo, el TA, originalm
mente
propuessto por Dueckk y Scheuer [22].
[
Se difereencia
básicam
mente del SA en que el criterio de aceptaación
es deterrminista, acepptando solucio
ones de trabajjo de
mayor ccoste siempree que la diferencia entre am
mbos
costees sea menor a un umbral que va decreciendo
duran
nte el proceso.
ambas
El
E
movimieento
empleeado
en
metaaheurísticas ess el mejor obbtenido con el DLS
(nuev
ve variables).. Los rangos de aceptació
ón para
fijar la temperatura inicial (umbbral inicial en TA) se
ha to
omado entre el
e 20% y el 400% (baja acep
ptación).
Se emplean
e
longitudes de la cadena de Markov
M
(CM), número de iteracionees (NI) a umbral
consttante en TA
A, iguales a 500, 1000 y 5000
iteracciones sin mejora.
m
La tem
mperatura deesciende
lineaalmente durantte el proceso, siendo el coeeficiente
reducctor (RT), (R
RU) en TA, ppara cada CM
M 0.80
(bajo
o), 0.90 (med
dio) y 0.95 (alto). En to
otal, 16
algorritmos distinttos. Cada uno
no se procesaa nueve
vecess. Se ha tomaado como tem
mperatura iniciial T0 el
0.5%
% del coste dee la primera ssolución obtenida de
modo
o aleatorio, que
q permite a lo sumo en tres
caden
nas de Markov fijar la T 0. Como critterio de
parad
da se estableece el cumpllimiento simu
ultáneo:
temp
peratura menor del 2% de lla temperaturaa inicial
T0 y agotamiento de la cadena de Markov siin haber
encon
ntrado ningun
na solución m
mejor que laa mejor
solucción enconttrada durannte dos cadenas
c
conseecutivas. El menor
m
coste obbtenido con el
e SA es
de 108008 € paraa CM=5000 y RT=0.85, mientras
m
que para el TA es
e de 1085800 € para NI=
=5000 y
=0.95.
RU=
En
E la Figura 5 se representaan los valores medios
de lo
os resultados obtenidos al aplicar las distintas
d
comb
binaciones, 16
1 para cadda una, de ambas
metaaheurísticas en
n función dell tiempo. Se señalan
cinco
o óptimos de pareto con fleechas indicatiivas. Se
han agrupado
a
los valores
v
por enncima de 1260
000 € en
“A”, y los valoress inferiores a 111000 € en
n “B” y
nde que:
“C”. De los valorees de la Figuraa 5 se despren
ptimos de pareeto, cuatro de ellos se
a) Dee los cinco óp
correesponden al SA
A. Ello equivaale al 80%. b)) Con el
SA, hay
h 3 proceso
os de los 16, qque están porr debajo
de 111000 €. Ello
o equivale al 119% de los casos. c)
Con el TA, hay un
n proceso por debajo de 111000 €,
que equivale
e
al 6%
% de los caso s. d) Con el TA,
T hay
2 pro
ocesos que están por encim
ma de 126000
0 €, que
equiv
vale al 13% de
d los casos. ee) Con el SA, no hay
ningú
ún proceso dee los 18 que están por enccima de
1260
000 €.
Fig. 5.
244
Costos medios SA vs TA pa
para las 16 combin
naciones
de cada
a una en función ddel tiempo
X Congreso Español sobre Metaheurísticas, Algoritmos Evolutivos y Bioinspirados (MAEB 2015)
Se puede resumiir al compararr las dos heuríísticas
(SA vs TA), lo sigguiente: a) El
E coste más bajo,
aunquee sea por unna magnitud insignificantte, le
correspponde al SA. b) Los costees medios sonn algo
menorees en el SA
A. c) Los tieempos medioos de
procesoo son similarres en amboss casos. d) P
Por lo
tanto, se puede connsiderar que ambas heuríísticas
proporrcionan resulttados similarres, aunque si se
toman valores medios, podría decanntarse
mente por el SA.
ligeram
C. Alggoritmos genééticos (GA)
Estta técnica meetaheurística fue propuesta
ta por
Hollannd [23], inspirrándose en el proceso obseervado
en la eevolución natuural de los serres vivos. Meddiante
el cruuzamiento genético
g
y la
l mutación,, los
individduos de una población ev
volucionan creeando
individduos mejor addaptados. De las
l solucioness de la
población anterior y las solucionees creadas meddiante
combinnación y muutación se seeleccionan lass que
formarrán parte de laa siguiente po
oblación. La nnueva
población puede seeleccionarse de
d manera ellitista,
aseguraando la suupervivencia de las meejores
solucioones de la pooblación actuaal. La combinnación
entre ddos solucioness se produce según un graado de
cruzam
miento de una de las variables al azar. Enn esta
técnicaa se aplican peenalizaciones para las solucciones
no facttibles afectanddo de ese mod
do a su aptitudd.
Prim
meramente se han realizado nnueve
ejecuciiones con la combinación de los valorres de
cruzam
miento 0.25, 0.50
0
y 0.75, y con tamañños de
población de 100, 250
2 y 500 in
ndividuos, tom
mando
5 75, 100, 125, 150, 175 y 200
resultaados para 25, 50,
generaaciones. A esttos procesos se les ha apllicado
mo y no elitism
mo. En este prrimer análisis no se
elitism
ha apliicado mutacióón. Los resulltados muestraan un
compoortamiento sim
milar al aplicaar o no elitism
mo. El
coste m
medio mejora y el tiempo de
d proceso aum
menta
mejor
con el aumento del tamaño de población. El m
coste medio se obbtiene para un tamaño dde la
población de 5000 individuos y un valoor de
cruzam
miento de 0.500, siendo dich
ho valor de 1338863
€, con una mejora deel 3.1% respeccto a sin elitissmo.
Costes/generaciones
s
Individuos=
=500, Elit.=Si, Cruz.=0.5
50 Mutación=4
Coste €
Apliccación de la m
mutación en ell GA
TABLA
T
II
D. Algoritmos meméticos
m
(MA
A)
Los
L
algoritm
mos meméticcos, Moscató [24],
com
mbinan la búsqueda gglobal de carácter
pobllacional y unaa metaheurístiica de búsqued
da local.
Tal como se ha comprobadoo en GA, cu
uando se
apliccaba mutació
ón –equivalennte a una búsqueda
b
locaal de carácteer reducido-, algunas soluciones
mejo
oraban significativamente.
Para
P
la mejo
ora de las ssoluciones ap
plicando
búsq
queda local see ha utilizado la metaheurísstica que
mejo
ores resultado
os ha ofrecidoo anteriormentte, como
es el
e SA, pero con
c el objetoo de no llegaar a una
conv
vergencia preematura, se hhan considerrado los
sigu
uientes parámeetros: CM iguual a 50, T0 igual al
5% del coste, y criterio de parada 10, 25
2 y 50
cadeenas. Para caada uno de los tres criteerios de
paraada, se han reaalizado 9 ejeccuciones con la mejor
heurrística obtenid
da del GA, cuuyos valores son:
s
500
indiv
viduos, 200 generaciones,
g
elitismo, cruzzamiento
iguaal a 0.50, mutación
m
= 44. Los resulttados se
mueestran en la siguiente Tablla III, donde el coste
med
dio se refiere a la media dee los valores mínimos
m
de laas 9 ejecucion
nes. Es de desttacar el increm
mento en
tiem
mpo computaccional que see produce respecto al
GA,, variando desde el 194% haasta el 575%.
TABL
LA III
Resultad
dos aplicando MA
En la
l Figura 7 se representa laa evolución reespecto a
las generacionees, de loss valores medios
pobllacionales y lo
os mínimos ppara los parám
metros de
la Tabla III.
275000
255000
Costes/generaciones
s
Individuo
os=500, Elit.=Si, Cruz.=0.5
50 Mutación=4
C. Markov = 50
Coste
e€
1950
000
235000
Coste Medio
Coste Mínimo
1850
000
215000
Coste Medio 10
Coste Mínimo 10
Coste Medio 25
Coste Mínimo 25
Coste Medio 50
Coste Mínimo 50
1750
000
195000
1650
000
175000
1550
000
155000
1450
000
135000
1350
000
1250
000
115000
0
25
50
75
100
125
150
175
200
1150
000
0
Nº Generaciones
s
Fig. 6.
25
5
50
75
100
125
150
1
175
200
Nº Generacio
ones
Fig. 7.
Evolución dee los costes medio
os y mínimos de uun GA
con mutación
245
Evolución
n de los costes meedios y mínimos en
e un MA
Metaheurísticas en Empresas y Producción
El ppunto de parttida viene determinado ppor la
aproxim
mación a un óptimo locall de baja caalidad
mediantte un SA. Se
S observa un
n comportam
miento
similar para las trees metaheurísticas, dondee los
nte al
valores medios vann reduciéndosse rápidament
principiio, para despuués ir haciénd
dolo más lentoo, y a
continuuación permannecer prácticaamente consttante.
Hay quue resaltar que
q
al princip
pio aumentann los
costes m
medios respeccto a los obtenidos por ell SA,
pero míínimamente, y a continuacción continúann con
un com
mportamiento típico
t
de un GA.
G Si se com
mpara
la mejoor heurística del
d MA con la
l mejor estuddiada
hasta ell momento, el
e SA, se tien
ne con respeccto al
coste, qque el menor valor medio,, 119703 €, ees un
8.4% suuperior al del SA, 110477 €,
€ y que el tieempo
empleaddo ha sido máás de 7 veces al
a empleado ppor el
SA. Enn cuanto al coste mínimo, en el MA ees de
116933 € (Figura 7),, mientras quee en el SA haa sido
de 1080008 €, es decirr un 8.3% superior.
nes de las aalas y el núm
mero de
con las dimension
toron
nes en todos lo
os niveles.
Las
L dimension
nes de las alaas inferiores son del
orden
n de magnitud
d del canto dde la viga, ello
o puede
estar asociado a los parámeetros del prroblema
(anch
hura del tab
blero y núm
mero de vigaas). La
optim
mización estru
uctural del hoormigón va dirrigida a
dimeensionar alas superiores
s
corrtas, puesto qu
ue éstas
no ay
yudan a mejo
orar la resisteencia a solicittaciones
norm
males. El meenor canto dee la viga del TA es
comp
pensado con un
u hormigón de mayor resistencia
(HP-45). Hay quee señalar, quee la aplicació
ón en el
GA de
d elitismo o no,
n no afecta a la geometría de las
mejo
ores solucionees, puesto quue los valoress de las
variaables son los mismos. Su diferencia en
e coste
vienee determinadaa por la armaddura pasiva, taal como
se pu
uede ver en la Tabla VI.
TABLA VI Re
esultados:
Arm
madura pasivaa
V. RES
SUMEN DE LO
OS COSTES Y COMPARACIÓN
N DE
LAS SOL
LUCIONES
En la Tabla IV se
s presenta un cuadro resuumen
con los valores de loos mejores parrámetros obtennidos
de las hheurísticas aplicadas.
TABLA IV
R
Resumen
de lo
os costes
Se iincluyen los costes medios y tiempos meedios,
el costee mínimo y ell incremento en
e % de los ccostes
medios de cada una de ellas respeecto a la mejoor, el
SA. Laas heurísticas que han obtenido mej
ejores
resultaddos son el SA
A y el TA, laas cuales desttacan
sobre laas demás. Dee lo descrito en
e el apartadoo 4.B
de este artículo, y enn especial porr la representaación
de los óptimos de pareto dentro
o de la Figurra 5,
podríam
mos decantarnnos por el SA
A, aunque deebería
señalarsse que cualquuiera de las do
os podría utilizzarse
indistinntamente.
En la Tabla V se resumeen los resulttados
geométrricos, hormigones y armad
dura activa parra las
mejoress soluciones.
TA
ABLA V
Geom
metría, hormigo
ones y activa
Tannto el SA como
c
el TA
A tienen vaalores
geométrricos muy sim
milares, con caantos de viga altos
y espessores de la lossa pequeños; además coincciden
Las
L menores cantidades
c
dee acero en la viga se
correesponden con el DLS y a continuación
n con el
SA y el TA. Los mayores
m
espessores de la losa en el
DLS le permiten disponer de menos cantiidad de
acero
o en ella que el SA y el T
TA. En conjun
nto, son
bastaante similares en el SA, DL
LS, TA y MA
A, todos
ellos tienen en común que hann dispuesto, all menos
en allgún momento
o de su proceeso, una búsqu
ueda de
aprox
ximación a un
n óptimo locall.
De
D los resultad
dos de las tablaas se desprend
de que:
a)) Las tres heu
urísticas de bú
búsqueda local (DLS,
TA y SA), tienden
n a cantos mááximos con esspesores
mínim
mos. De heccho, coinciden
en todos los valores
geom
métricos para los
l mejores de
del TA y del SA,
S sólo
camb
bia el canto dee la viga.
b) Se tiende a economizzar el volum
men de
horm
migón. Hay un
na búsqueda de una secciión que
propo
orcione mayo
or inercia y ssea a la vez lo más
ligeraa posible. Ello
o se refleja enn cantos de viga altos
y esp
pesores pequeeños, y repercuute en una neecesidad
meno
or de pretensaado, por lo quue no hay torones en
el terrcer nivel.
c)) En el intento de aligeerar la estrucctura se
cond
diciona a utilizar
u
horm
migones de mayor
resisttencia, entre 40
4 y 50 MPa,, en viga. En la losa,
cuanto mayor es el canto, m
menor resisten
ncia del
horm
migón se necessita, entre 30 y 40 MPa.
d)
d La medición
n de acero enn la armaduraa pasiva
se asemeja en el DLS,
D
SA, TA y MA.
e)) Los mejorres resultadoos se obtienen con
armaadura activa mínima en el ala superior, la
suficciente para im
mpedir que fisuure dicha ala durante
el tessado.
f)) Los espesorees menores dee losa en el TA
A y SA,
respeecto al DLS, se
s compensa con mayor arrmadura
pasiv
va.
246
X Congreso Español sobre Metaheurísticas, Algoritmos Evolutivos y Bioinspirados (MAEB 2015)
g) La optimización tiende a dimensiones cortas
de las alas superiores de la viga.
VI.
CONCLUSIONES
Las conclusiones resumidas son las siguientes:
a) Se han aplicado cinco metaheurísticas con sus
variantes –DLS, SA, TA, GA y MA-, para el diseño
automatizado y optimizado de tableros de pasos
superiores de carreteras con vigas artesa
pretensadas, siendo las más eficaces el SA y el TA.
Los tiempos de proceso para estas dos últimas son
suficientemente aceptables como para poder
utilizarse de un modo práctico en casos reales.
b) La heurística que mejores resultados ha
obtenido se corresponde con el algoritmo SA, con
cadenas de Markov de 2500 iteraciones y
coeficiente de enfriamiento de 0.95. Su tiempo de
proceso es de unas cinco horas con el procesador
utilizado en este trabajo.
c) El conocimiento derivado del uso de las
metaheurísticas permiten recomendar rangos de
valores para emplearlos en el diseño optimizado de
estas estructuras y en su aplicación para los
predimensionados de las variables.
AGRADECIMIENTOS
Los autores agradecen la financiación del
Ministerio de Ciencia e Innovación (Proyecto de
Investigación BIA2011-23602) y de la Universitat
Politècnica de València (Proyecto de Investigación
SP20120341).
REFERENCIAS
[1] British Standards, BS 8110-1: 1997 Structural use of
concrete. Part 1: Code of practice for design and
construction, British Standards, London, 1997.
[2] Cohn, M.Z. and Dinovitzer A.S., Application of structural
optimization. ASCE Journal of Structural Engineering,
120(2), pp 617-649, 1994.
[3] Martinez, F. J., González-Vidosa, F., Hospitaler, H. and
Yepes, V. Heuristic optimization of RC bridge piers with
rectangular hollow sections, Computers & Structures 88 375386, 2010.
[4] Martí, J.V. and González-Vidosa, F. Design of prestressed
concrete precast pedestrian bridges by heuristic optimization,
Advances in Engineering Software 41 916-922, 2010.
[5] Carbonell, A., González-Vidosa, F. and Yepes, V. Design of
reinforced concrete road vaults by heuristic optimization,
Advances in Engineering Software 42 151-159, 2011.
[6] Martínez, F.J., González-Vidosa, F., Hospitaler, A. and
Yepes, V. A parametric study of optimum tall piers for
railway bridge viaducts, Structural Engineering and
Mechanics 45 723-740, 2013.
[7] Yepes, V., González-Vidosa, F., Alcalá, J. and Villalba, P.
CO2-Optimization design of reinforced concrete retaining
walls based on a VNS-threshold acceptance strategy. ASCE
Journal of Computing in Civil Engineering, 26 (3):378-386,
2012.
[8] Martí, J.V., González-Vidosa, F., Yepes, V. and Alcalá, J.
Design of prestressed concrete precast road bridges with
hybrid simulated annealing, Engineering Structures 48 342352 2013
247
[9] García-Segura, T.; Yepes, V.; Martí, J.V. and Alcalá, J.
Optimization of concrete I-beams using a new hybrid
glowworm swarm algorithm. Latin American Journal of
Solids and Structures, 11(7):1190-1205, 2014.
[10]Martí, J.V.; Yepes, V. and González-Vidosa, F. A memetic
algorithm approach to designing of precast-prestressed
concrete road bridges with steel fiber-reinforcement. ASCE
Journal of Structural Engineering, 04014114, 2015.
[11] Hernández S. and Fontan A., Practical Applications of
Design Optimization, WIT Press: Southampton, 2002.
[12] Fletcher, R., Practical Methods of Optimization, Wiley:
Chichester, 2001.
[13] Jones,
M.T.,
Artificial
Intelligence
Application
Programming,
Charles
River
Media:
Hingham
(Massachussets), 2003.
[14] Holland, J.H., Adaptation in natural and artificial systems,
University of Michigan Press: Ann Arbor, 1975.
[15] Goldberg, D.E., Genetic algorithms in search, optimization
and machine learning, Addison-Wesley, 1989.
[16] Glover, F. and Laguna M., Tabu Search, Kluwer Academic
Publishers: Boston, 1997.
[17] Yepes, V. and Medina J.R. Economic heuristic optimization
for the heterogeneous fleet VRPHESTW. ASCE Journal of
Transportation Engineering, 132(4), pp 303-311, 2006.
[18] Martí, J.V., Optimización de tableros isostáticos de vigas
artesa. Lap Lambert Academic Publishing GmbH & Co. KG.
ISSN 9783844339451. 2011.
[19] M. Fomento, EHE. Instrucción de Hormigón Estructural (in
Spanish), M.Fomento, Madrid, 2008.
[20] M. Fomento, IAP-98. Instrucción sobre las acciones a
considerar en el proyecto de puentes de carretera,
M.Fomento: Madrid, 1998.
[21] Kirkpatrick, S., Gelatt, C.D. and Vecchi, M.P., Optimization
by simulated annealing, Science, 220(4598), pp. 671-680,
1983.
[22] Dueck, G. and Scheuer, T. Threshold accepting: A general
purpose optimization algorithm superior to simulated
annealing. Journal of Computation Physics 1990, 90: 161175.
[23] Holland, J. “Adaptation In Natural and Artificial Systems.”,
The University of Michigan Press, Ann Arbour, 1975.
[24] Moscato, P., “On evolution, search, optimization, genetic
algorithms and Martial Arts: Towards Memetic Algorithms“,
Caltech Concurrent Computation Program, C3P Report 826,
1989.