1. Educación

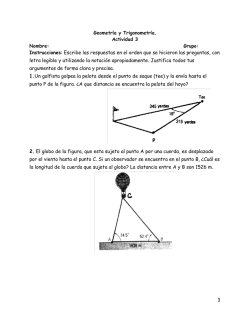
Universidad Nacional Aut´onoma de Honduras
Facultad de Ciencias
Escuela de F´ısica
F´ısica General I FS-100
Repaso De La Unidad I
2-47. Mary y Sally participan en una carrera (figura 1). Cuando Mary est´a a 22 m de la l´ınea
de meta, tiene una rapidez de 4.0 m/s y est´a 5.0 m detr´as de Sally, quien tiene una rapidez de
5.0 m/s. Sally cree que ganar´a f´acilmente y desacelera durante el tramo restante de la carrera
a una raz´on constante de 0.50 m/s2 hasta la l´ınea de meta. ¿Qu´e aceleraci´on constante necesita
ahora Mary durante el tramo restante de la carrera, si quiere cruzar la l´ınea de meta empatada
con Sally?
Figura 1: Problema 2.47
Datos:
Marry
ViM = 4.0m/s
xiM = 0m
aM =?
xfM = 22m
Sally
ViS = 5.0m/s
xiS = 5m
aS = −0.5m/s2
xfS = 2mm
Soluci´on:
- Ya que se quiere determinar que aceleraci´on debe tener Marry para alcanzar a Sally y cruzar la
meta al mismo tiempo, y se conoce la aceleraci´on de Sally, es preciso determinar que tiempo le
tomar´a a Sally llegar a la meta, una vez encontrado est´e se puede saber que aceleraci´on deber´ıa
tener Marry para realizar el recorrido en el mismo tiempo que Sally y por ende llegar a la meta
en el mismo momento.
- Para determinar el tiempo que le tomar´a a Sally recorrer la meta debemos aplicar ecuaciones
de movimiento (cinem´atica) que expresen la posici´on como funci´on de la velocidad y el tiempo,
en este caso:
1
xf = xi + vi t + at2
(1)
2
Elaborado por Belkiss H. Galindo C.
1
- Si ahora sustituimos en (1) los datos de Sally y aplicamos la f´omula cuadr´atica para determinar
el tiempo obtenemos:
1
22 = 5 + 5t + (−0,5)t2
2
t2 − 20t + 68 = 0
t ≈ 4.34s
o´
t ≈ 15.66s
Lo anterior nos devuelve dos posibles respuestas, pero ¿C´omo seleccionar el tiempo correcto?,
si se analiza gr´aficamente el comportamiento de la aceleraci´on de Sally se observa una par´abola
con conc´aba hacia abajo (desacelera a raz´on constante) lo que nos indica que Sally podr´ıa estar
en dos tiempos distintos en la misma posici´on, pero como nuestro punto de inter´es est´a antes
o justo antes de que Sally se detenga y comience nuevamente su recorrido de reversa (seg´
un su
comportamiento gr´afico) se selecciona el tiempo m´as corto, es este caso 4.34 s (15.66 s ser´ıa el
tiempo que le tom´o a Sally llegar a la meta nuevamente pero, de reversa).
- Ahora que ya conocemos el tiempo que le toma a Sally llegar a la meta, podemos sustituir en
(1) los datos de Mary y dicho tiempo para determinar la aceleraci´on que deber´ıa tener Maty
para llegar a la meta en el mismo momento que Sally:
1
22 = 4t + aM t2
2
22 = 4(4.34) + aM (4.34)2
aM =
2[22 − 4(4.34)]
(4.34)2
Finalmente...
aM = 0.4927m/s2
Elaborado por Belkiss H. Galindo C.
2
(2)
2.61. A una piedra que cae le toma 0.33 s pasar frente a una ventana de 2.2 m de altura (figura
2). ¿Desde qu´e altura por arriba de la parte superior de la ventana se dej´o caer la piedra?
Figura 2: Problema 2.61
Datos:
Altura de la ventana: 2.2 m
Tiempo recorrido frente a la ventana: 0.33 s
vi =?
Soluci´on:
- Tomando por conveniencia el sistema de referencia positivo hacia abajo. - Analizando primero
el movimiento de la piedra cuando pasa frente a la ventana se puede determinar la velocidad con
la que llega al comienzo de la ventana, luego asumiendo ´esta como la velocidad final (recordar
que el objeto parte del reposo) para el tramo sobre la ventana se logra encontrar la altura desde
la que fue lanzada la piedra.
- Para el tramo frente a la ventana se plantea una ecuaci´on de movimiento que describa la
posici´on en funci´on de la velocidad y el tiempo (asumiendo como origen de referencia la esquina
interna superior derecha) y luego se despeja para la velocidad:
1
yf = yi + Vi t + ay t2
2
0
1 2
yf = y ✒
i + Vi t + gt
2
yf − 12 gt2
t
- Sustituyendo ahora lo datos que conocemos y encontramos que:
⇒ Vi =
Vi ≈ 5.05m/s
Elaborado por Belkiss H. Galindo C.
3
(3)
(4)
- Ahora analizando el tramo que la piedra recorre sobre la ventana, como no se conoce el tiempo
que la piedra recorre en ese momento, entonces se necesita una ecuaci´on de movimiento que
exprese la velocidad en funci´on de la posici´on y el tiempo:
Vf2 = Vi2 + 2ay (yf − yi )
(5)
- Asumiendo el origen de referencia para este tramo en el punto desde el cual se “deja caer”(Vi =
0) la piedra y como velocidad final para este recorrido la velocidad encontrada en (4), si se despeja
para la posici´on final (h) se encuentra la altura sobre la ventana desde la que se dej´o caer la
piedra:
Vi2 0
h 0
2
2
✒
✒
❃
+ 2g(✚
y✚
y Vf = Vi ✒
f − i)
Vi2 = 2gh
Vi2
⇒h=
2g
Finalmente...
h ≈ 1.301m
Elaborado por Belkiss H. Galindo C.
4
(6)
3.43. El piloto de un avi´on que viaja horizontalmente a 170 km/h quiere lanzar suministros a las
v´ıctimas de una inundaci´on, que est´an aisladas en una porci´on de terreno situada a 150 m abajo.
¿Cu´antos segundos antes de que el avi´on est´e directamente sobre las v´ıctimas deben dejarse caer
los suministros?
Datos:
Vi = 170 km/h
Altura a la cual se encuentra el avi´on del suelo: H=150 m
Soluci´on:
- Cuando el avi´on deja caer lo suministros, ´estos tiene la misma velocidad que lleva el avi´on (170
km/h) y como ´este se desplaza horizontalmente el ´angulo inicial para los suministro es ’0’; si
descomponemos vectorial mente dicha velocidad encontramos que:
Vix = 170
V iy = 0
km
h
km
h
- Si ahora planteamos la ecuaci´on de movimiento (en y) que describe el comportamiento de los
suministros mientras van cayendo (asumiendo como origen de referencia el punto desde el cual
caen los suministros y positivo hacia arriba y hacia la derecha) podemos conocer el tiempo que
le toma a los suministros caer y este tiempo representa el tiempo de antelaci´on con el que el
piloto debe lazar los suministros para que lleguen justo donde se encuentran las v´ıctimas:
0 1
0 ✚
Vy❃
t + ay t2
yf = y ✒
i +✚
2
1
yf = ay t2
2
1
−H = − gt2
2
⇒t=
2H
g
Finalmente...
t ≈ 5.53 s
Elaborado por Belkiss H. Galindo C.
5
(7)
3.49. Resuelva de nuevo el ejemplo 3-9 suponiendo ahora que el ni˜
no con la resortera est´a justo
debajo del ni˜
no en el a´rbol (figura 3), por lo que apunta hacia arriba, directamente hacia el ni˜
no
en el a´rbol. Demuestre que el ni˜
no en el a´rbol hace nuevamente un movimiento equivocado al
dejarse caer en el momento en que se dispara el globo de agua.
Ejemplo 3.9: Un ni˜
no situado en una peque˜
na colina apunta horizontalmente su lanzadera (resortera) de globos de agua, directamente a un segundo ni˜
no que cuelga de la rama de un a´rbol
a una distancia horizontal d. En el momento en que se dispara el globo de agua, el segundo
ni˜
no se suelta del ´arbol, esperando que el globo no lo toque. Demuestre que esto es una medida
´ a´
equivocada. (El
un no hab´ıa estudiado f´ısica). Desprecie la resistencia del aire.
Figura 3: Problema 3.49
Datos:
Distancia horizontal del ni˜
no en la colina al ni˜
no en el a´rbol = d
Altura a la que se encuentra el ni˜
no en el ´arbol del suelo = H
Altura a la que se encuentra el ni˜
no en el ´arbol desde el origen de referencia = h
Velocidad inicial del globo = v0
´
Angulo
de lanzamiento para el globo (respecto a la horizontal)= θ0
Soluci´on:
- Se define como origen de referencia el punto desde donde el ni˜
no en la colina lanza lo globos
con agua y luego se plantean ecuaciones que describen el movimiento para el globo con agua que
lanza el ni˜
no en la colina y del ni˜
no en el ´arbol respectivamente:
- Para el globo: 1) En x:
1
xf = xi + Vix t + ax t2
2
xf = V i x t
como el globo inicialmente est´
a en el origen xi = 0 y como la velocidad en x es constante, entonces ax = 0
⇒ xf = v0 cos θ0 t
Elaborado por Belkiss H. Galindo C.
6
• Despejando para t encontramos el tiempo (tiempo de vuelo) que le tomar´a al globo llegar
hasta d (posici´o final del globo):
d
(8)
t=
v0 cos θ0
2) En y:
1
yf = yi + Viy t + ay t2
2
1
yf = Viy t − gt2
2
como el globo inicialmente est´
a en el origen yi = 0
1
⇒ yf = v0 sin θ0 t − gt2
2
Sustituyendo (8) en la expresi´on anterior:
1
d2
yf = d tan θ0 − g
2 v0 cos θ0
(9)
- Para el ni˜
no en el ´arbol:
yf = yi + vi t + ay t2
1
yf = h − gt2
2
como el ni˜
no se deja caer vi = 0
Observando la figura 3 se puede apreciar que h se puede obtener aplicando la definici´on de
tangente de un a´gulo en un tri´angulo rect´angulo, entonces:
h = d tan θ0
Si sustituimos el resultado anterior en la ecuaci´on que describe el movimiento del ni˜
no que cae
del ´arbol encontramos:
1
(10)
yf = d tan θ0 − gt2
2
- Como nos interesa saber donde se encontrar´a el ni˜
no que cae del ´arbol cuando el globo llegue
a d, entonces evaluamos (10) con el tiempo que le toma llegar al globo llegar a ese punto [(8)],
entonces:
1
d2
yf = d tan θ0 − g
(11)
2 v0 cos θ0
Como (9) y (11) son iguales el ni˜
no que cae del a´rbol estar´a en d en el mismo momento en que
llega el globo por tanto; el ni˜
no se equivoca nuevamente al dejarse caer al mismo tiempo que es
lanzado el globo con agua.
Elaborado por Belkiss H. Galindo C.
7