Download Report

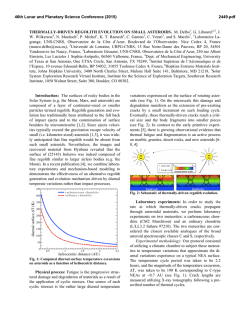
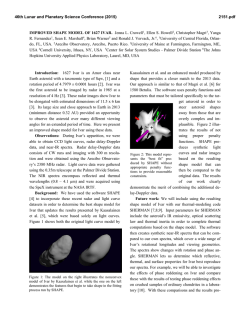
46th Lunar and Planetary Science Conference (2015)
2996.pdf
REJUVENATING ASTEROIDS DURING PLANETARY FLYBYS: APPLICATIONS TO (99942)
APOPHIS AND OTHER NEAR-EARTH ASTEROIDS. J. T. Keane1 and I. Matsuyama1. 1Lunar and Planetary
Laboratory, Department of Planetary Science, University of Arizona, Tucson, AZ, 85721, USA
([email protected]).
Introduction: Laboratory measurements of meteorite reflectance spectra rarely match telescopic observations of asteroid reflectance spectra due to the process (es) of space weathering, which rapidly darken
and redden asteroid surface on million-year timescales
[e.g. 1-2]. While most main belt asteroids appear
weathered, a fraction of near-Earth asteroids (the Qtypes) appear unweathered – possibly the result of a
previously unrecognized resurfacing mechanism associated with planetary encounters [3-7]. If the number
of “fresh,” unweathered asteroids is assumed to be in
steady state, this resurfacing mechanism must operate
large planetary flyby distances, between 5~20 planetary radii. These large flyby distances are well beyond
typical tidal disruption distance of 2~5 planetary radii
[8-10].
In this paper, we propose that the weaker tidal perturbations during these distant flybys are still large
enough to trigger avalanching on the surface of these
asteroids. While not as dramatic as tidal disruption,
this process may still be able to resurface the uppermost layers of the asteroid, uncovering unweathered
regolith material, and changing the asteroid’s spectral
properties. Constraining the efficiency of this process
will provide insight into the widely debated space
weathering timescale.
Asteroid Resurfacing Model: Hill slope stability
can be analyzed using classic Mohr-Coulomb failure
criterion [e.g. 11]. A block of regolith, characterized
by some angle of internal friction (ϕ) and cohesion (c)
will remain stable if the shear stress at the failure plane
remains below the critical shear stress (σS):
σS = c + σN tan(ϕ)
where σN is the normal stress. In terrestrial applications, the shear and normal stresses can be easily calculated by projecting the weight of the block due to
gravity into the down-slope (shear) and normal directions. This threshold shear stress can be related to a
maximum hill slope angle, or angle of repose. (It is
important to note: for the case of an asteroid, the angle
of repose is dependent on both the cohesion and absolute size and gravity of the asteroid.) For an asteroid
during a planetary flyby, the total force acting on the
regolith test block is non-trivial: it is the sum of gravitational force, centrifugal force, and tidal force (Fig 1).
The gravitational force across an asteroid’s surface
can vary dramatically [e.g. 12-14], due to the irregular
shapes of most asteroids. For simplicity (and to enable
Figure 1: Snapshots of the gravitational force (A), centrifugal force
(B), and tidal force (C) during a close (2 earth radii) flyby of an
Apophis-like asteroid. Snapshots are taken at closest approach. (D)
and (E) show the probability for hill slope failure and gravitational
unbinding at each surface element at that time.
a large parameter space-survey), we limited our asteroid shape models to triaxial ellipsoids of uniform density (although more general models are possible). From
the asteroid’s triaxial shape, we are able to analytically
calculate the surface gravity across the surface of the
asteroid, as well as the asteroid’s moments of inertia
and spherical harmonic gravity coefficients.
The centrifugal and tidal forces acting on surface
elements of the asteroid are more complicated – as
they depend on both the asteroid’s bulk properties
(shape and spin-state), and the flyby geometry. Tidal
torques during planetary flybys can alter the spin-states
of asteroids – both changing the absolute spin period
and inducing non-principal axis rotation [e.g. 15]. In
order to accurately model these time-varying forces,
we numerically integrate the coupled orbital-rotational
evolution of the asteroid during the flyby.
With all of the relevant forces evaluated as a function of position on the asteroid, and time during the
flyby, we then proceed to evaluate the stability of asteroid regolith during the flyby. In order to account for
the variety of observed asteroid hill slopes and slope
orientations [e.g. 16], we take a statistical approach in
order to determine hill slope stability across the surface
of the asteroid. At each surface location, we consider
an array of all possible, initially stable hill slopes and
slope orientations, with respect to the total force before
the planetary flyby (Fig 2A.). We then track the timeevolution of that stability field during the planetary
flyby (Fig 2B and 2C). For each surface element, we
46th Lunar and Planetary Science Conference (2015)
calculate the expected probability (and variance) of hill
Figure 3: Schematic of stability fields for asteroid hill slopes. (A)
Initial stability field (blue). As the total force acting on each surface
element changes with time, portions of this initially stable region
become unstable to hill slope failure (red) and can even become
unbound (pink).
slope failure at that location during the flyby. From
this, we can determine the expected total amount of
surface area that becomes unstable during a flyby. It is
important to note that we only track the surface area
that becomes unstable to hill slope failure. The surface
area that becomes resurfaced is necessarily larger.
Parameter Space Results: We have completed a
preliminary parameter space survey investigating the
efficiency of tidal resurfacing as a function of flyby
distance, asteroid spin period, and flyby geometry (Fig
3). For these models, we the flyby of a (99942)
Apophis-like asteroid.
As expected, the single most significant factor controlling the tidal resurfacing efficiency is the flyby
distance; closer flybys are more damaging than distant
flybys. While catastrophic, global resurfacing only
occurs for the closest flybys (flybys within ~3 planetary radii) significant fractions of the asteroid’s surface
remain susceptible to avalanching out to flyby distances of ~5 planetary radii.
Rapidly rotating asteroids are also more likely to
have debris flows than slowly rotating asteroids, as the
increased centrifugal force mitigates the asteroid’s
surface gravity and decreases the threshold failure
stress.
The orientation of the asteroid in 3D space during
the close approach also has a significant impact on the
efficacy of tidal resurfacing. Protrude flybys (where
the spin vector of the asteroid and the asteroid’s hyperbolic orbit normal are aligned) tend to be more damaging than retrograde flybys. This result was previously
observed in numerical studies of tidal disruption [10].
Implications for Apophis. In 2029, Asteroid
(99942) Apophis will undergo a close planetary flyby
of the Earth, within 5.6 Earth radii. This flyby distance,
coupled with Apophis’ slow rotation, indicates that
only a small amount of the asteroid’s surface will become unstable: <0.1% of the total surface area. This is
consistent with results from numerical modeling results [17]. Nonetheless, observations of (99942) Apo
2996.pdf
phis, or other asteroids during flybys, may be able to
directly test this hypothesis. If avalanching is observed,
it will help constrain the efficacy of this mechanism, as
well as the bulk properties of the asteroidal regolith
(such as cohesion).
References: [1] Hapke (2001) JGR, 107. [2] Chapman
(2004) Annu. Rev. Earth. Planet. Sci., 32. [3] Marchi et al.
(2006) MNRAS, 368. [4] Binzel et al. (2010) Nature, 463. [5]
Nesvorny et al. (2010) Icarus, 209. [6] DeMeo, Binzel, &
Lockhart (2014) Icarus, 227. [7] Endicott et al. (2014) DPS
46, 304.02. [8] Chandrasekhar (1969) Ellipsoidal Figures of
Equilibrium. [9] Sridhar & Tremaine (1992) Icarus, 95. [10]
Richardson, Bottke, & Love (1998) Icarus, 134. [11] Melosh
(2011) Planetary Surface Processes. [12] Yeomans et al.
(2000) Science, 289. [13] Zuber et al. (2000) Science, 289.
[14] Fujiwara et al. (2006) Science, 312. [15] Scheeres et al.
(2000) Icarus, 147. [16] Richardson & Bowling (2014) Icarus, 234. [17] Yu et al. (2014) Icarus, 242.
Figure 2: Preliminary parameter space results for the efficiceny of
tidal resurfacing during the flyby of a (99942) Apophis-like asteroid.
Figure 4: Effect of the asteroid obliquity on the efficiency of
tidal resurfacing.