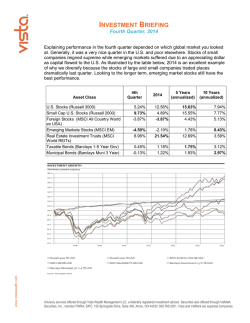
On Binomial Models of the Term Structure of Interest
ON BINOMIAL
ON BINOMIAL
MODELS
OF THE TERM
STRUCTURE
MODELS
OF THE TERM
INTEREST
RATES
OF ...
STRUCTURE
833
OF
WERNERHURLIMANN
WINTERTHUR-LEBEN
ALLCEMEINE MATHEMATIK
.PAULSTRASSE
9
CH-8401 WINTERTHLJR
- SWITZERLAND
TELEPHONE: 41-52-261 58 61
AND
SCH~NI~OLZWEG
24
CH-8409 WINTERTIXJR- SWITZERLAND
ABSTRACT
A general analysis of arbitrage-free binomial models of the term structure
of interest rates is given. Several of the previous modelsencounteredin the financial
economicsliterature are included in the discussion.The proposedapproach allows
the construction of models which satisfy the following property. At each discrete
time the current market forecast of the one-period bond price implied by the initial
term structure is equal to the expected value of the one-period bond prices with
respect to the risk-neutral probabilities. As a special case one obtains a simple
(degenerate)diatomic binomial model with only two different bond price values at
each time and for each maturity of the bond. Several properties of this new classof
binomial models are discussed. It is possible to get a term structure with no
negative and no arbitrarily large interest rates. This class of models is useful in
modelling the bond price uncertainty in the immediate future and near bond
maturity. Furthermore the relation between conditional yields of the bonds and
conditional variances of the bond prices is analyzed and lower and upper boundsfor
these quantities are derived.
Keywords
: term structure of interest rates, bond price modelling, arbitrage-free
pricing, binomial model, discrete time model
834
5TH AFIR INTERNATIONAL
SUR
LES
MODELES
TERME
BINOMES
DES TAUX
COLLOQUIUM
DE LA STRUCTURE
D’INTERET
A
WIZRKER HURLIMANN
WI~Tl:l~~~ll~:l~-~~l~I:r
ALLGEMEISI;
MA’~‘IIE~A’I’IK
PAULSTRhSSE 9
CH-8401 WIN’I‘ERTIKX - SWITZERLAND
T~?LEPIIONE
: 41-52-261 58 61
ASI)
S~FK~~~L%WI~ 24
CH-8409
WINTERTII~JR - SWITZERLAND
RESUME
Uric analysegemkaledesmodclesbinome et librc d’arbitragc dc la structure
a terme des taux d’interet est presentee. Plusieurs des modclcs precedents de la
literature Cconomiquefinanciere sont inclus dansla discussion.L’approcheproposdc
permet la construction de modeles qui satisfont la proprick? suivante. A chaque
instant l’estimation actuelle de marche du prix des obligations z&o-coupon
impliquee par la structure a terme initiale est Cgalea l’esptrancemathematiquedcs
prix zero-coupon prise par rapport aux probabilites d’arbitragc. Comme cas
particulier on obtient un modele binome diatomique (degendre) simple ayant
seulement deux valeurs distinctes de prix zero-coupon h chaque instant et pour
chaque echeance.Plusieursproprietes de la nouvelle classede modelcsbinbme sent
discuttes. I1 est possibled’obtenir une structure a terme dont les taux d’inttrets sont
ni negatifs ni arbitrairement larges. Cette classe de modelcs est utile pour la
modelisation de l’incertitude des prix zero-coupon dans le futur immediat et a
l’tchtance. DC plus la relation entre rcndcments conditionnels et variances
conditionnelles des prix zero-coupon est analysde, et dcs bornes inferieures et
suptrieures dc ces quantites sont d&i&es.
ON BINOMIAL
MODELS OF THE TERM STRUCTURE
OF .. .
835
The most widely used common language in tam slruclun: modclling
is that of continuous-lime
stochastic Calculus. Arbilrngc-ftcc
consistent
models i\rc usually constmctcd starting frr)m Markov dif’fusions, that
It2pltZSClll
thC current tarn slructule in il linitc-<iimcnsional
SliilC
SpXC
(SCC
Duflic imti Kan(l994)). The most gcncntl m cth~d~l~gy, ol‘whi~h alI cxisling
ilrbitr:tgc pricing models arc special GISCS, has been
dcvclopcd by Heath,
JiIrrow imd Morton( 1992).
Practitioners, which arc ol’tcn not ;~warc ol’ the higher mathematics
underlying this ilbstmct structutc, need simple models whose conslmclion
is
b;tscd on lirst principles. Some classes of discrctc-time models share this
tcquilcmcnt, cspccially binomial models.
Among the single-factor models, the lirst arbitrage-flee binomial
model of the tcnn structutc,
which makes lull USC of’ iill inlbnnalion
aviGlitblc ~~UITI the CUITCIU
tc~m
st~uctun:
obscrvcd in the market, W~IS
dcvclopcd by 110 and Lcc( 1986). Howcvcr this model sull‘crcd lir)m scvcral
shortcomings as IlCgiiliVC
inlcmst ralcs, arbitrarily large inlclcst WCS iIIld
constant volatility of intclcst wtcs. In the subscqucnl analysis Pcdci?;cn and
ill .(1989) ;~7d Morgan iuld Ncilvc(l991/93)
have COIISLI~CLC~
models wilhoul
WSC dritwbaCks. Howcvcr the gcncral CliiSs of alI arbitrrtgc-l’lcc binomial
models hits not yet been dclcnnincd. The scicnlilic intacst in a description
of the full class lies in a bctler understanding oI’ the fcasiblc movcmcnts of
intcrcst WCS in im arbitrage-Ircc economic cnvimnmcnt.
This knowlcdgc
WOUI~ cniiblc 10 1~~1 the range of ‘~7 cxhaustivc CILSS of models :md LhC
empirical validity agi~inst iIltcmiltivc
arbitragefree models.
As mcntioncd by Pcdcrscn and al.(l989), p.28, their class of models
cannot satisfy the prr~pcrty, dcnotcd (P) in the following, that the Current
market L‘orccast or‘ the one-period bond price implied by the initial tam
sttuclun: is cqual to the cxpcctcd value ol’ the one-period bond prices wilh
rcspcct to the risk-neutral pn)babilitics.
The main purpose of’ the prcscnl
paper consists to dcvclop a method, which overcomes this pmblcm, and to
show that Insulting L‘casiblc models may Ibllow intcrcst rate bchaviour
obscrvcd in the modcm economic world. A molt dctailcd outline of the
study Ibllows.
In Section 1 the fntmcwork pn)poscd by Pcdcrscn iuld :I.(1 989) is
dcvclopcd in its full generality. A product rcpresentalion of the fcasiblc bond
prices is display& in Pmposition
1.I, and a simpler stalcmcnt for lhc oncperiod bond prices is found under l’ormula (I .lO). The models obtitincd
5TH AFIR INTERNATIONAL COLLOQUIUM
836
previously by Ho and Lec(1986), Pedcrsen and al.(l989), and Morgan and
Neave(1991/93) are recovered as special cases. In Section 2 a sufficient
condition, which implies the validity of property (P), is derived. It is
obtained by induction from the particular case of a three-period bond. The
main result is the product representation Thcotem 2.1. The existence of
arbitrage-free binomial models with the property (P) is settled in Proposition
3.1. The proposed special class of models do possessstate independent nskneutral pmbabilities, and contains even a very simple (degcncrate) diatomic
model with only two distinct bond price values at each time and for each
maturity of the bond. It is also shown how a subclass,whose interest rates
fluctuate within a reasonable range, can be obtained by imposing quite
simple parameter constraints. The final Section 4 is devoted to elementary
properties of the new alternative binomial model. In particular the problem
of “hetetoskedasticity” (proper English spelling in McCulloch(l985)!), that
is the variability of the interest rate volatility, can be solved as illustrated in
Example 4.1.
1. -acre-free
binmels
of
the
te
I
of merest
rti
.
In the arbitrage-free theory of pricing interest rate contingent claims
one postulates according to the path-breaking paper by Ho and Lee(1986)
that the term structure of interest rates at the initial time is exogeneously
given, that is the present values Pt(O,O) of default-free discount bonds
maturing for the value of one unit at time t are those currently observed in
the market. It follows that for each stream of fixed and certain cash flows,
the price obtained from a model coincides with the market price.
A considerable amount of additional tefetences on the subsequent
development of the subject is found in Sercu(l991), Heath, Jarrow and
Morton( 1992), Duffie( 1992) and Vetzal( 1994).
In this paper we follow the approach proposed by Pcdersen, Shiu
and Thorlacius(l989) to construct arbitrage-free binomial models of the term
structure of interest rates. In a discrete-time and discrete-space setting the
basic model assumptions are the perfect capital market assumptions :
(Al) The market is frictionless. This means that there are no taxes, no
transaction costs, and all securities are perfectly divisible. Information is
available to all investors simultaneously and each investor acts rationally.
(A2) The market clears at discrete points in time, which are separated in
ON BINOMIAL
MODELS
OF THE TERM
STRUCTURE
831
OF ...
regular intervals. For simplicity one uses each period as unit of time.
(A3) The bond market is complete. Then= exist default-fee discount bonds
for all maturities t=1,2,... .
(A4) At each time n, there are finitely many states of nature. The
equilibrium price of the discount bond of maturity t at time n and in state i
is denoted by P,(n,i). One requites that for all non-negative integers t,n,i:
0 I P,(n,i) I 1, P,(n,i)=l,
lim P,(n,i)=O.
t-+@
To describe the evolution of the tetm structure of interest rates, one
considers the following binomial lattice. At the initial time 0 one has, by
convention, the state 0 and the bond price Pt(O,O)for a discount bond of
maturity t. At time 1 there are only two states of natute, denoted by 0 and
1, and the bond prices are P,(l ,O), P,(l ,l). Proceeding by induction one
assumes that at time n-l there are n states, denoted 0, 1, .... n-l, and the
bond prices are P,(n - 1, i), i = 0, 1, .... n-l. Passing from time n-l to time
n, each state i gives rise either to an upward movement to state i+l or to a
horizontal
movement to state i. Thus at time n there am n+l states
i=O,1,...,n, and the bond prices are P,(n,i), i=O,l,...,n. This construction
defines a binomial lattice labelled by vertices (nj).
Following Pedersen et al.(1989), to define a binomial lattice model,
one needs to prescribe at each vertex (m,k) of the binomial lattice :
POnk) : a risk-neutral probability
Pm+,CmJO : a one-period bond price (at time m in state k)
Arbitrages are eliminated
(1.1)
if and only if (cf. (3.2) in Pedersen et aL(1989))
P&k)= 1, k=O,...,t,
P,(m,k)=P,+,(m,k) -(p(m,k) -P,(m+lb+l)+[l-p(mk)l
0 I m 5 t-l, k=O,...,m.
-P,(m+lk)),
We use the following notation
(1.2)
c(mC) = P,+l(m ,k+l)P,+,(mk),
k=O,...,m-1.
Earlier authors make one of the following simplifying assumptions :
(A5)
p(m,k)=p, c(m,k)=c, for all m,k (Ho and Lee(1986))
83X
(A6)
5TH AFIR INTERNATIONAL
COLLOQUIUM
p(m k)=p(m), c(m,k)=c(m), for all m, k (Pcdcrscn et af.(1989))
In the gcncral cast it follows that
k-i-l
P,+l(m ,k) = P,+,(m ,i) n c(m ,i+j), k=i,i+l,..., m.
(1.3)
j=O
As suggested by Pedersen et al.(1989), section IV, the idea is to dcrivc a
formula for P,(n,i), n < t, in terms of the one-period bond prims P,+,(i,i),
j=n, n+l, .... t-l.
1J. For all n=O,l ,...,t-l , k=i,i+l,..., II, one has
t-1
k-i-l
P,(nk)
=
G(n,t-lC)
n
]Pj+~(i,i)
n c(jj+01,
(1.4)
j=n
Q=O
whcm the function G is defined recursively as follows :
on
(1.5)
(1.6)
G(s,s,k) = 1, k=O,...,s
G(i,s,k) =[I-p&k)]
-G(j+l,sk) + p(i,k) -[ A c(0)]
t=j+ 1
j < s, k=O,l,...,j.
-G(j+l,s,k+l),
Proof. This is shown by backward induction. For n=t-1 this is (1.3) above.
By induction assumption assume (1.4) tme for n=m+l ,m+2,...,t-1 and show
it for n=m. Consider (1.1) for k=i,i+l ,...,m. From (1.3) and (1.4) one has the
relations
k-i-l
P,+l(m kk) = P,+l(m ,i> II c(m ,i+j)
j=O
t-l
k-i
P,(m+l,k+l) = G(m+l,t-l,k+l) n Ip,+,(‘j,i) n c(j,i+B)]
j=m+l
P=O
k-i-l
t-1
P,(m+lk) = G(m+l,t-lk) II [P,+,(j,i) II c(j,i+I)]
j=m+l
&O
Inserting these exptcssions in (1.1) one obtains
ON BINOMIAL
MODELS
OF THE TERM
STRUCTURE
k-i-l
P,(mk) = { l-l [Pj+l(j,i) l7 cCj,i+4)]} -([l-p(mk)]
j=m
Q=O
OF ...
839
t-1
-G(m+l,t-1Jc) +
t-l
n c&k)),
j=m+ 1
which is (1.4) for n=m by taking (1.6) into account.
+ p(m,k) ii(m+l,t-lk+l)
The special case of the structure (1.4) in Pedersen et aL(1989) is
recovered as follows. Assume that the recursively defined function
r” c(Pk), j < s, g(s,s)=l,
L!=j+l
is independent of k, then one has the nested product representation
(1.7)
g&s) = 1 - p(W) + p&Q
GCj,sk) = r; g(b).
kj
(1.8)
It follows that
t-l
(1.9)
P,(n,i) = ll l$(jJ-l)Pj+,(ji)l,
j=n
which is relation (4.5) in Pedersen et aL(1989).
To express the one-period bond prices in terms of market forecasts
of one-period bond prices, let us apply (1.4) twice to get
P,+,(O,O)/P,(O,O) = [G(O,WG(O,t-1
,O)l -P,+l(LO).
On the other side rewrite (1.3) as
i-l
P,+l(n,i) = P,+l(n,O) II c&i>.
j=O
By comparison one obtains the formula
i-l
(1.lO)
r,,P,+,W
= IGKh-l,O)/G(Osl,O)l
n chj),
j=O
where r,=P,(O,O)/P,+,(O,O) is the market forecast of the one-period
accumulated rate of interest at time n. In other words the r,‘s are the one-
840
5TH AFIR
INTERNATIONAL
COLLOQUIUM
period forward interest rate factors, which describe the initial term sttuctun:
of interest rates (each factor equals one plus the forward rate of interest).
Ezar.ttt.
In the case considetcd by Pedcrsen et al.( 1989) one has
c(n,i)=c(n), hence (1.7) and (1.8) hold. One gets the formula
(see (4.7) in Pcdcrsen ct al(1989)) :
n-2
n-l
(1.11)
rnPn+l(n,i)= c(n)’ I7 g&n-l)/ II g&n)
j=O
j=O
phi>=p(n>,
&uuQU.J.
The model of Ho and Lcc(1986) is obtained sclting p(n)=p,
c(n)=c. One shows that gCj,s)=l - p + p -I? and (1.1 1) mads
(1.12)
r,P,+,(n,i) = ?/(I - p + p -c”).
To determine now the risk-neutral probabilities p(n,i) consistent with
the bond prices
n+ 1
Pn+2(0rO)= [ II r, .I-‘, n=O,1,2,...,
k=O
data which is known at time 0, consider again the formula (1.4) :
n+l
(1.13)
P”+z(O,O)
= G(On+ltO) lI cj+1Q,O>.
j=O
By comparison ‘and using that r,P,(O,O)=l one gets immediately
conditions
n+l
(1.14)
G(O,n+l,O) n r,P,+,(j,O)= 1, n=O,1,2,...
j=l
the
Exam&AA.
In the case p(n,i)=p(n), c(n,i)=c(n), one obtains using the
multiplicative representation (1.8) the relation
n+l
(1.15)
I n” g(k,n+l)l -[ n rkPk+,O(,O)]
= 1, n=0,1,2 ,..., where
k=O
k=l
n+l
(1.16)
.uw+l)
= 1 - p(k) + P(k) -[ l-l ml.
j=k+ 1
It is possible to solve for p(n), n=0,1,2,..., using a backward
induction
ON BINOMIAL
MODELS
OF THE TERM
STRUCTURE
procedure. One gets the recursive formula
n-l
n+l
(1.17)
OF .. .
841
n+l
n-l
p(~)=(l-~g(ksl+l)~~,P,+,o<,O))/(c(n+1)-1)~go<sl+~)~~,~,+,~c,O)
k=O
k=l
k=O
k=l
This formula determines the risk-neutral probabilities p(n) provided c(k) and
rkP,+,(k,O)are known, k=1,2 ,...
mole
1.4. Morgan and Neave(1991) proposes to model the TSIR by
considering a discrete time multiplicative binomial model of the futute
forward interest rate factor, which moves stochastically around the initial
TSIR described by r,, n=0,1,2 ,... If R,,(i) is the random value the future
forward factors may take at time n in state i, then they assume that
(1.18)
R,,(i) = ud(“‘) -r,, i=O,.,.,n, with d(n,i) = (2 -i/n - 1) -S(n),
where S(n) may formally be any sequence. One has P,+,(n,i)=R,(i)-’ and
(1 .19)
c(k) = u~(‘“~(~), k=l,2 ,..., rkPk+l(k,O)= uSCk),k=0,1,2 ,...,
One obtains
(1.20)
p(0) = u”“‘/(l + US(‘)), p(1) = us(‘)+s@)/(l+ us(‘)+s(2)),
(1.21)
n-l
p(n)={ l-u ~~~~+...+~~n+~~~g(kJ+~)}/{(U-2S~”+l~/~”+l~~~)US~1~+...+S~n+l~
k=O
whem
(1.22)
g(ks7+1)=l
- p(k)
+ P(k)
_U-2(S(k+lX(k+l)+...+S(n+l)/(n+l)),
n-l
n
g(ka+l)j
k=O
k=O ,.“, n-l.
To imply reversion to the mean of both the future forward factor and the
underlying term structure, Morgan and Neave(1991) assume that the series
C S(k) is a convergent one, for example S(k)=2‘k. In Morgan and
Neave(1993) the divergent case S(k)=k is considered. In this quite simple
situation one gets c(~)=c=u-~,p(k)=~~~+‘/(l+u~~+‘),k=0,1,2,...
842
5TH AFIR INTERNATIONAL
2. Svfficient
. .
concl&ons
for
a new
c&
of bin&
*,
COLLOQUlUM
mod&.
In their general analysis of binomial models, Pcdcrscn ct a1.(1989),
p. 28, have considered the condition that the cuncnt market forecast
r”-‘=P,+,(O,O)/P,(O,O)of the one-period bond price at time n is equal to the
expected value of the bond prices P,+,(n,i), O<iln, with respect to the riskneutral pmbabilitics p(n,i). This condition is exptcsscd by the equation
n
P,+,(O,O)/P,(O,O)= C P,+,(n,i)Pr(n,i), n=1,2 ,...,
(2.1)
i=O
when: Pr(n,i) is the probability to bc in state (n,i). As shown by Pedcrscn ct
al.(1989), provided that p(n,i)=p(n) and c(n,i)=c(n) are independent of i, the
condition (2.1) cannot be fulfilled if n=2, except for the trivial dcgencrate
case c(n,i)=l . However if the restriction on c(n,i) is relaxed, it is possible to
fulfill the desirable property (2.1). In particular we construct in Section 3 a
binomial model for which p(n,i)=p(n) and (2.1) holds.
Using (1.10) the condition (2.1) is equivalent to the formula
n
i-l
G(O,n,O) = G(O,n-l,O) C lJ’r(n,i) n c(nj)], n=1,2 ,...
(2.2)
i=O
j=O
To motivate the sufficient conditions given below in (2.4) under which the
condition (2.2) is always fulfilled, let us first analyze the non-trivial case
n=2 of a three-period bond, and then pass to the general case n22. Observe
that for a two-period bond n=l the condition (2.2) reads
G(O,l ,O)=l -p(O)+p(O)c(l ,O) and is always satisfied by definition of G.
2.1 Particular
case n=2.
By the dclinition of G in Proposition 1.1 the Icft-hand side of (2.2)
equals G(0,2,0) = (1-p(O))G(1,2,0) + p(O)c(l ,O)c(2,O)G(1,2,1).For the righthand side one gets
G(O,l,O)
-IO-p@M-pU,W+
t~l-p~O~~p~~,~~+(~-p~~,l~~p~~~~~~~,~~
+ PKuP(l ~~w,ok(2,1)1
kOJ,O)
W-p(O)){
l+p(l,O)(c(2,0)-1))
+ ~~~~~~P~~~I~+P~~,~~~c~~~~~-~~ll
&J,O)
-[Cl-p(O))G(1,2,0)
+ c(2,0)p(O)GU,2,1)1.
ON BINOMIAL
MODELS
OF THE TERM
STRUCTURE
OF .. .
843
It follows that (2.2) is equivalent with the condition
(l-p(O))G(1,2,0)(G(O,l,O)-1)
+ c(2,0)p(O)G(1,2,1){G(O,1,0)-c(l,O)]=O.
But one has G(O,l ,O)-l=p(O)(c(l,O)-l), G(0,l ,O)-c(1,O)=-(l-p(O))(c(l,O)-I).
Therefore (2.2) is equivalent with the condition
p@)U -p(ON{c(l,O)-1)
{GU ,2,0) - c(2,O)G(1,2,1)) = 0.
In the following let us assume that p(O)(l-p(O))(c(l,O)-1) f 0. Then (2.2) is
equivalent with the condition G(1,2,0) = c(2,O)G(1,2,1), which is the
inductive step n=2 of the sufficient conditions (2.4) given in the general
analysis of Subsection 2.2. Using that
G(lA0) = 1 + p(l,O)(c(2,0)-l), G(1,2,1) = 1 + p(l,l)(c(2,1)-l),
this condition is further equivalent to the relation
(1-p(1m(cw)-1)
= - p(1,1M2,0)(c(2,1)-1).
Let us illustrate its resolution for two special cases.
Case 1 : c(2,O)=c(2,1)=c(2) f 1
The derived condition implies that 1-p( 1,O)=-p( 1,l)c(2)<0, which is
impossible. In the special case p(l,O)=p(l,l)=p(l) this fact has already been
shown by Pedersen et al.(1989), p.28.
Case 2 : c(2,O) f c(2,l)
If one assumesthat p(l,O)=p(l,l)=p(l), then this risk-neutral probability is
given by l/p(l) = 1 - c(2,O) +(2,1)-l]/[c(2,0)-11. If p(l,O)#p(l,l), then one
has the relation l-p(1,O) = -p(l,l)c(2,0) <c(2,1)-l]/[c(2,0)-11.
In both subcasesone has necessarily [c(2,1)-l]/[c(2,0)-13 < 0.
Note that the present relatively simple analysis is the basic inductive step for
the construction of our new class of binomial models in Section 3 (see the
relations (3.2) and (3.3)).
844
5TH AFIR
2.2. Qgeral
INTERNATIONAL
COLLOQUIUM
w.
Under appropriate
assumptions
(2.2) simplilics
considerably.
For each n=l,2 ,..., one has the identity
n
i-l
n-l
i-l
C [Pr(n,i) I-I c(nj)l = C lPr(n-1 ,i) -G(n-1 ,n,i) n c(nj)]
i=O
j=O
i=O
j=O
Lemma.
(2.3)
Proof. Start with the right-hand side and reorder it using that
G(n-l,n,i)
= 1 - p(n-l,i) + p(n-1,i) -c(n,i). One has
n-l
i-l
n-l
C Pr(n-1 ,i)[l -p(n-1 ,i)] l-l c(n,j) + C Pr(n-1 ,i)p(n-1 ,i) ;I c(n,j)
i=O
i=O
j=O
j=O
i-l
n-l
= Pr(n-l,O)]l-p(n-l,O)]
+ C Pr(n-l,i)[l-p(n-l,i)]
IJ c(nj)
i=l
j=O
n-2
i
n-l
+ 1 Pr(n-1 ,i)p(n-1 ,i) n c(nj) + Pr(n-1 n-l)p(n-ln-1)
TI c(nj)
i=O
j=O
j=O
Change the index of summation in the second sum to get
i-l
n-l
Pr(n,O) + 1 [Pr(n-l,i)[l-p(n-l,i)]
+ Pr(n-l,i-l)p(n-l,i-I)]
l-l c(nj)
i=l
j=O
n-l
+ Wwn) I7 chj>
j=O
Observing that the state probabilities satisfy the recursive relations
Pr(n-l,i)[l-p(n-l,i)]
+ Pr(n-l,i-l)p(n-l,i-1)
= Pr(n,i),
i=l,...,n-1,
the result follows immediately.
In the subsequent discussion assume the following
(2.4)
G(n-l,n,i-1)
= c(n,i-1)
-G(n-l,n,i),
i=l,...,n-1,
relations hold :
or equivalently
ON BINOMIAL
MODELS
OF THE TERM
STRUCTURE
OF . ..
(2.5)
i-l
G(n-1 ,n,O) = G(n-1 ,n,i) n c(nj>, i=l,...,n-1.
j=O
845
Inserted in (2.2) using (2.3) the equation to solve is
G(O,n,O)= G(O,n-1,O) -G(n-1 sl,O>.
(2.6)
WC show below that under the assumption (2.4) the equation (2.6) is always
fuhilled. For this one needs the following intermediate result.
Lemma.
(2.7)
For each n=2,3,... assume that
G(k,k+l,i-I)
= c(k+l,i-1) -G(k,k+l,i),
i=l,,.., k, k=O,l,...,n.
Then one has
(2.8)
n+l
G(i,n+l,k-1) = G(ip+l,k) n c(j,k-1), i=l,..., n-l, k=l,..,, i.
j=i+l
Proof. This is shown using induction on the indices n and i. As induction
step let n=2. In this case (2.8) reads
(2.9)
G(1,3,0) = c(2,O) ~(370) -G(l,3,1).
Using the recursive definition (1.6) of G the formula (2.9) is equivalent to
(2.10)
(l-p(l,O))
-G(2,3,0) + P(l,O)c(2~O)c(3~0) -G(2*3,l)
:(2,O)c(3,0) -{(l-P(M))
*(2,311)
+ p(l,l)c(2,1)c(3,1) *(2,3,2)1.
From the assumption (2.7) one has
(2.11)
(2.12)
~(2,3,0) = ~(30 +(2,3,1),
~(2,3,1) = ~(3~1) %(2,312).
Inserting in (2.10) using again (1.6) one gets
5TH AFIR
846
(2.13)
G(1,2,0)
-G(2,3,0)
Using (2.11) this is cquivalcnl
(2.14)
INTERNATIONAL
= c(2,O) -G(1,2,1)
COLLOQUIUM
-c(3,0)
-G(2,3,1).
to
G(1,2,0) = c(2,O) -G(l,2,1),
which is satisfied by the assumption (2.7). Hcncc (2.8) is shown for n=2. By
induction assumption assume now the lcsult is tme for the indices 2,3,...,n-1,
and show it for the index n. This is shown by backward induction OI I the
index i.
Ster, 1 : i=n-1. Using (1.6) the formula (2.8) for i=n-1 is cquivalcnt to
(I-p(n-l,k-1))
(2.15)
-G(n,n+l,k-1)
+ p(n-l,k-l)c(n,k-l)c(n+l,k-I)
=
c(n,k-l)c(n+l,k-1)
-((l-p(n-1,k))
-G(n,n+l,k)
+ p(nl,k)c(n,k)c(n+l,k)
-G(n,n+l,k+l)]
Using assumption
(2.16)
(2.7) and (1.6) this is equivalent
G(n-l,n,k-1)
-G(n,n+l k-l)
=
c(n,k-1) -G(n-l,n,k)
-c(n+l,k-1)
Using again (2.7) this is equivalent
(2.17)
G(n-1 ,n,k) = c(n,k-1)
-G(n,n+ lJ<)
to
-G(nn+l,k).
to
-G(n-lp,k).
But this relation is fulfilled by assumption (2.7).
Step 2. Assume the relation (2.8) is valid for the indices i=r+l,...,n-1,
k=l,...,i, and show it for the index i=r. This is similar to step 1. One has
n+l
G(r,n+l,k-1)
= G(r,n+l,k)
n c(j,k-1)
j=r+ 1
n+l
<=>
(l-p(r,k-I))
-G(r+l,n+l,k-1)
+ p(r,k-I)
-G(r+l,n+l,k)
n c(j,k-1)
j=r+ 1
n+l
n+l
=[ n c(j,k-l)]
-{[l-p(r,k)]
-G(r+l,n+l,k)
+ p(r,k) -G(r+l,n+l,k)
n c(j,k))
j=r+ 1
j=r+ 1
ON BINOMIAL
MODELS
<=>
G(r,r+l,k-1)
-G(r+ln+I,k-1)
= c(r+lk-1)
-G(r,r+lJ<) -G(r+ln+lk)
<=>
OF THE TERM
STRUCTURE
OF .. .
847
n+l
II c&k-l)
j=r+2
G(r,r+l,k-1) = c(r+l,k-1) -G(r,r+lk).
Since the last relation is fulfilled by assumption (2.7) the result follows.
Let us show that under the validity of (2.4) for all n=2,3,..., the
relation (2.6) is always satisfied. This follows immediately from the special
case k=i=O of the following main result.
2.1. (product representation of the function G) For all n=2,3,...
assume that the tclations (2.4) are satisfied. Then one has
n-l
G(k,n,i) = n G(i,j+l,i), k=O,...,n-2, i=O,...,k.
(2.18)
j=k
Proaf. For n=2, k=i=O, one has
Theorem
G(0,2,0) = (l-p(O,O)) -G(1,2,0) + p(O,O)c(l ,O)c(ZO) +(1,2,1).
Since c(2,O)G(1,2,1)=G(1,2,0) by (2.4) one gets
G(0,2,0) = [l - p(O,O)+ p(O,O)c(l,O)l -G(1,2,0) = G(O,l,O)G(l,2,0).
Let now n 2 3. By assumption the formulas (2.7) are fulfilled. From Lemma
2.2 one has
(2.19) G(s,n,i) = G(ssl,i+l) i c&i), s=l,...,n-2, i=l,..., s-l.
We show by induction on I?~~
r-l
(2.20) G(k,n,i) = G(r,n,i) fl G(jj+l,i),
j=k
First of all one has
G(k,n,i) = [l-p&i)]
Using (2.19) one gets
t=k+l,..., n.
-G(k+l,n,i) + p&i)
n
-G(k+l,n,i+l) n c&i>.
j=k+l
5TH AFIR INTERNATIONAL COLLOQUIUM
848
Gg<,n,i)=[l-p(k,i)+p(k,i)c(k+l,i)]
-G(k+l,n,i)=G(kk+l,i)
-Go<+ln3i)7
which is (2.20) for t=k+l. By induction assumption assumenow that (2.20)
is true for r and show it for r+l. One has
n
G(r,n,i) = [I-p(r,i)] -G(r+l,n,i) + p(r,i) -G(r+l,n,i+l) l-I c(i,i).
j=r+ 1
Using (2.19) it follows that
G(r,n,i) = [I -p(r,i) + p(r,i)c(r+l,i)]
S(r+l n,i) = G(r,r+l ,i) -G(r+l ,n,i).
From the induction assumption one obtains now
r
G(k,n,i) = G(r+l,n,i) n G(j,j+l,i).
j=k
Hence (2.20) is shown and (2.18) follows setting t=n.
We have shown that binomial models satisfying the property (2.1)
are obtained if one solves the relations (2.4). Let us construct such models
for which additionally the risk-neutral probabilities p(n,i)=p(n) are
indepcndcnt of the state i. Written out the relations (2.4) are equal to the
system of equations
(3.1)
1 + p(n-1) -@(n,i-1)-l> = c(n,i-1) -{l + p(n-l)(c(n,i)-I)},
n=2,3 ,..., i=l,..., n-l.
Let us starch for nondegenerate binomial models, that is assume that
c(n,i)#l, i=O,...,n-l. Then one has
(3.2)
l/P(n-1)=1 - c&i-l)
-[c(n,i) - l]/[c(n,i-1) - l], i=l,...,n-1.
To obtain a value 0 < p(n-1) < 1, let us choose
(3.3)
u(n,O) = -[c(n,l) - l]/[c(n,O) - 11 > 0.
Defining further
(3.4)
u(nk) = -[c(nk+l) - l]/[c(n,k) - 11, k=l,...,n-2,
ON BINOMIAL
MODELS
OF THE TERM
STRUCTURE
OF .. .
849
one seesthat (3.2) is fulfilled if
(3.5)
c(n,k)u(n,k) = c(n,k-l)u(n,k-1),
k=l,...,n-2.
Combining (3.4) and (3.5) one sees that c(n,k), k=2,...,n-1, can be evaluated
by mcursion. The obtained result is summarized as follows.
on 3.1. Given is a nondegcnerate binomial model such that
p(n,i)=p(n), i=O,...,n. Then for all n=2,3 ,... there exists c(n,O)#l and u(n,O>>O
such that
(3.6)
(3.7)
(3.8)
p(n-1) = l/U + c(n,O)u(n,O)),
c(n,i> = 1 - (c(n,i-1) - 1) -u(n,i-l), i=l,..., n-l,
u(nd) = u(n,i-1) -c(n,i-l)/c(n,i), i=l,..., n-l.
Having shown the existence of binomial models satisfying (2.1), let
us derive some consequences following from such a model. Given is a
nondegenerate binomial model as in the pmceding result. From the product
representation (2.18), (2.5) and (1.10) one has the formula
i-l
r,,P,+,(n,i) = l/G(n-l,n,i) = [ n c(nj)YG(n-ln,O),
(3.9)
j=O
n=l,2 ,..., i=O,...,n.
In particular for i=O one has
(3.10)
r,P,+,(n,O) = l/(1 - p(n-1) + p(n-1) -c(n,O)), n=1,2 ,...
Using (3.6) this implies that
(3.11) r,P,+,(n,O)= (1 + c(n,O)u(n,O))/c(n,O) -(l + u(n,O)), n=2,3 ,...
From (1.4) and (3.8) one gets the bond price formula :
t-1
t-l
P,(n,i) = G(n,t-1,i) n Pj+l(i,i) = P,+,(n,i)[ n G(i-l,j,i)P,+,(j,i)l.
j=n+ 1
Using (3.9) one obtains he-!!“with
850
5TH AFIR
INTERNATIONAL
COLLOQUIUM
t-1
(3.12)
P,(G) = P,+,(n,i)[ I-l rile’.
j=n+ 1.
Applying (3.9) and (3.11) this expression transforms to
i-l
t-l
(3.13) P,(n,i) =[ l-l r,]-l -l-I c(nj> -[ 1 + c(n,O>u(n,O)]/[c(n,O)ll + u(n,O>l),
j=O
j=n
n=2,3,...
This formula means that the bond prices of arbitrary maturity date at time n
dcpcnd only on the one-period bond prices at time IL that is on c(n,O),
u(n,O), and on the market forecast of future intemst rates.
Using the relations (3.7) and (3.8) it is possible to cxpmss P,(n,i)
cxplicitcly as a function of the pammeters c,,:=c(n,O)and u,,:=u(n,O).Setting
futther x,:=u,c, one observes that
(3.14) c(n,m)c(nm-1) = (1 - x,)c(nm-1) + x,,, n=2,3 ,..., m=l,..., n.
This follows fmm the following calculation :
c(nm)c(nm-1) = (1 - u(nm-l)[c(nsn-1)
= 11 - u(n,O)c(n,O) + u(nm-l))c(nm-1)
= { 1 - x,}c(nJn-1) + x,,.
- l])c(nm-1)
Lemma 3.1. For all n=2,3 ,..., m=l,..., n, one has
(3.15)
G c(nj) = (c, + x”y; (-1 ,‘x,J + (-1)“~~
j=O
j=O
= (c, + X”) -(l + (-1)“.‘x,,“‘)/(l + x,,) + (-l)mC,,X,“.
This is shown by induction on m. If m=l one has from (3.14)
c(n,l)c(n,O)=(c,+x,,)-c,x,, which is (3.15) for m=l. Assume the result true for
m=l2, ,...,r, r 2 1, and show it for m=r+l. From (3.14) one has c(n,r+l)c(n,r)
= (1 - x,)c(n,r) + x,. Multiplying this relation with
r- 1
II ch.j>
j=O
and using twice the induction assumption the result follows by
straightfonvard algebra. The details of the verification are left to the madcr.
Proof.
With the formula (3.15) the bond prices at time n=2,3,... mad
ON BINOMIAL
MODELS
OF THE TERM
STRUCTURE
OF ...
851
t-1
P,(n,O) = [ TI ‘jl-l -0 + X,)/(C, + X,>,
j=n
t-1
(3.16)
P,(n,l) = [ ll rjl-l -C,(l + XJKC, + %I,
j=n
t-1
P,(n,i) = [ n rj]-l -{ 1+(-1)‘~2x,i~‘+(-1)i~1c~x~i~1(1
+x,)/(C,+x,)}.
j=n
Simplifying further one sees that
t-1
(3.17)
P,(n,i) = [ l-I rj]-l 31 + (-l)?Xnxni],
j=n
n=2,3,..., i=O,...,n, with a, = (1 - c,)/(c, + x,).
The class of alternative binomial models contains a degenerate diatomic
model of the term structure of interest rates obtained by setting x,=1, or
p(n-l)=%, for n=2,3,... From (3.15) one derives immediately that
(3.18)
c(n,2k)=c,, c(n,2k+l)=l/c,, k=0,1,2 ,...
(degenerate binomial lattice)
Furthermom for n=2,3,... one has
t-1
P,(n,i) = [ lJ 41-l -241 + c,), if i is even,
j=n
(3.19)
t-1
P&i) = [ n rj]-’ -2c,/(l + c,), if i is odd.
j=n
If one puts further p(O)=%, then (3.19) is also valid for n=l. In this special
case the bond prices of a given maturity date t take only two different values
at time n.
It is natural to put further restrictions on the bond prices. One
usually tequites at least the following fundamental properties :
(3.20) no negative interest rates, and no arbitrarily large interest rates.
As pointed out by Pedersen et al.( 1989), the first binomial model by Ho and
Lee(1986) does not fulfill this condition. On the other side the multiplicative
852
5TH AFIR INTERNATIONAL
COLLOQUIUM
binomial model by Morgan and Neavc(l991) satisfies this property.
However in the litcratute on binomial models it is not clarified if there exist
models satisfying additionally the condition (2.1).
To satisfy (3.20) with formula (3.17), one has to choose the model
numbers (y.,and x, such that
(3.21)
r,,/rmax
I rJ,+,(n,i)=l
+ (-l)‘o,,x,’ I r,, i=O,...,n.
With the upper bound one avoids negative interest rates and with the lower
bound one avoids accumulated interest rates higher than r,,. Assume that
&,=r,/rm,<l. It is easy to check that (3.21) is fullilled if one assumesthat
(3.22)
0 < cx,I i,=r, - 1, 0 < x, I min{(l-E,,)/i,,,l].
If one assumesfurther that rmax1 (l+i,)/(l -i,) for all n, then (3.22) simplifies
to the quite simple parameter constraints O<cr,,li,,,O<x,ll, tctaincd in the
next Section.
4. Some elementarv
oroDerw
of the new altermlve
.
.
bin&
.
modfl.
Consider the constructed alternative binomial bond price model
(4.1)
r,P,+,(n,i) = 1 + (-l)jclnxni, n=l,2 ,..., i=O,...,n,
with 0 I cr, I i,, 0 5 x,, 5 1.
First of all note that the mean and the variance of the random variable
P,+l(n, -), rcptcsenting the one-year bond prices at time n, can be obtained
in an elementary way. One needs the following identity.
Lemma.
Assume a binomial lattice such that p(n-l)=p(n-1 ,i), n=1,2,...,
i=O,...,n-l, is independent of i. Then one has
n
C (-l)‘[(l-p(n-l))/p(n-l)]‘Pr(n,i)
= 0, n=1,2,...
(4.2)
i=O
Proof. This is shown immediately using the recursive relations for the
transition probabilities Pr(n,i), namely
(4.3)
Pr(O,O)=1,
Pr(n,O)=Pr(n-1 ,O)(l -p(n-I)), Pr(nn)=Pr(n-1 n-l)p(n-1),
Pr(n,i)=Pr(n-l,i)(l-p(n-1))
+ Pr(n-l,i-l)p(n-l), i=l,...,n-1.
ON BINOMIAL
MODELS
OF THE TERM
STRUCTURE
OF .. .
853
on 4.1. For the binomial bond price model (4.1) one has
(4.4)
(4.5)
EkP,+,(n, -)I = 1,
VarkR+,h
->I = ~~[(l -p(n-l)Yp(n-1 )I
n-2
- l3 11 - p&<>+ po<)[(l-p(n-l))/p(n-1)12j,
n=l,Z... .
k=O
Let p(k)=p for k=O,...,n-1, then one has the simpler formula
(4.6)
Var[r,P,+,(n, ->I = a,2[(1 -p>/p12.
Observing that x,=(1-p(n-l))/p(n-1) by (3.6), the property (4.4) which
is nothing else than the condition (2.1), follows directly fmm the identity
(4.2). Using the same result one obtains the formula
Proof.
Var[r,P,+,(n, -)] = q2 i [(1-p(n-l))/p(n-l)]”
-Pr(n,i>.
i=O
Let us denote by S, the sum on the right-hand side of (4.7). One has
(4.7)
(4.8)
s, = Pr(l,O) + [(l-p(O>>/p(O>l2Pr(l,l) = (I-P(ON/P(O).
Assume nil and let us compute Sn+lusing the recursion (4.3). One has
n+l
%+, = C [(I -p(nN/p(n>12’Pr(n+l ,i>
i=O
n
= PrhOXl-p(n)) + C [(l-p(n>)/p(n>l”(1-p(n))Pr(n,i)
i=l
n-l
+ C [(I -p(n>>/p(n)l*‘+‘(1-p(n>>Pr(n,i) + [(l -p(n))/p(n)l*“+‘(l -p(n)>Pr(nd
i=O
= PrhOW -p(nNV + (I -p(n>>/p(n>l
+ i Pr(n,iN(l -p(n>>/p(n>l*‘(1-p(n))U + (1-p(n))/p(n)l
i=l
= (I-p(nN/p(n) ITZ[(I -p(n>>/p(n>l*‘Pr(n,i>.
i=O
Pmcceding similarly using (4.3) and induction one gets
854
5TH AFIR INTERNATIONAL
COLLOQUIUM
%+l = [U-p(n)Yp(n)l
n-l
-I 1 - p(n-1) + p(n-1X(1-p(n))/p(n)12) C Kl-p(n))/p(n)12’Pr(n-1 ,i).
i=O
n-2
= [Wp(n>>/p(n>l
II t 1 - PO<) + p(k)[(l-p(n))/p(n)12},
k=O
which shows (4.5). The formula (4.6) follows immediately finm (4.5).
mle
4.1. This result is useful in modelling the bond price uncertainty.
A first desirable property of bond pricing can already been fulfilled for the
simple case (4.6). As pointed out by Ho and Lee(l986), p. 1016, the bond
price uncertainty should be small at the two extmme points, namely for the
time horizon in the immediate future and near bond maturity. If the implied
term structure of interest rates is such that r, first increases and then
decreases this desirable property (with the variance as measure of
uncertainty) can be fulfilled setting a,,=i,, in (4.6).
.
As next step we analyze how conditional variances and yields of the
bonds are tclatcd and in which bounds they can actually move. Relatively
simple bounds are obtained in the conditional case.The one-year yield of the
bond
. at time n is described by the random variable R, :
(4.9)
R,,(i) = l/P,+,(n,i) = t-,/(1 + (-l)%x,,xni), i=O,...,n.
Consider the conditional means and variances of the accumulated yield at
time n+l
(4.10)
(4.11)
P,,+,~= E[R,+,/R,=R,(i)l, i=O,....n,
(<T~,+,J~= Var@,+,/R,=R,(i)], i=O,...,n,
and the conditional variances of the bond prices
(4.12)
(opll+li)2 = VarP,,(n+l,
-)/P,,+,(n,i)], i=O,...,n+l.
In the following let us use the abbreviations
(4.13)
Since p(n)=l/(l +x) one gets from (4.9) that
ON BINOMIAL
MODELS
OF THE TERM
STRUCTURE
OF ...
855
(4.14) P”+l,/m+l= (x/[l + (-l)‘crx’] + l/[l + (-l>i+laxi+ll)/( 1 + x)
= (1 + (-l)‘crx’(l-x))/([l
+ (-l)‘ax’][l + (-l>i+‘cxxi+‘]}
A further calculation shows that
(4.15)
1 + (- 1)‘ax’( 1-x)1.
@n+lj - rn+Jh+,j = cr;?xzi+l/[
On the other side one gets similarly
(4.16) c2,+lj = [[l+(-l)‘ax’]2x
+ [l+(-l)i+‘oxi+~]2}/{ 1+x) - 1 = &x2’+’
In this simple conditional situation let us now apply the mean/variance
criterion of portfolio theory. For a given fixed conditional variance c2,,+,
j=c2
try to maximiTe the conditional accumulated yield un+lj of the bond.
Equivalently one can maximize the relative conditional excessyield given by
(4.15). Making the change of variable /3=crx’ one has to solve the
optimization problem
(4.17)
(P”+,~- rn+,)/)ln+lj= C*/U + (-1)‘@-C2/P>l= mad
under the constraints xp2=c2, 0 < p I in+l, 0 < x 5 1.
For this it suffices to minimiz the function f(p) = 1 + (-l)@ - c2/p). Since
the derivative f(p) = 1 + (-l)‘[l + (c/p)]2 is either positive or negative, two
casesmust be considered.
Case : i even
Since f(p)=2+(~/p)~>O the function f(p) is monotone increasing. From the
constraint x=(~/p)~<l one deduces that c21p2. It follows that f@)=min! if
p=c, whem O<cli,+,. Hence x=1, thus p(n)=%, which leads to the degenerate
diatomic binomial model.
Case : i odd
Since ~(P)=-(c/P)~<Othe function f(p) is monotone decreasing. Hence f(p)
takes its minimum when p is the maximum possible value. Since x=(c/~)~
one gets c~=p/x~=p~~+~/c~~.
From c&in+l one sees that p is maximum if
p2i+l=c2iin+l.It follows that x=(c/in+1)2’@i+1),
where O<cG,+,.
To summariz the discussion we have shown the following result.
. .
s.
At time n+l the conditional accumulated yields of the
bonds and the conditional variances of the bond prices satisfy the relations:
5TH AFIR
856
INTERNATIONAL
COLLOQUIUM
Case 1 : i even
One has the inequalities
(4.18)
(4.19)
1 + in+l 5 pn+lj 5 Ml - in+J,
QL+,~- rn+lYh+lj 5 k+l~pn+lj)2 5 i2,+,.
Furtherm om one has equalities in (4.19) only in the dcgcncmtc case p(n)=%,
x=1, CI=((~,,+~~-r,+,)/p.+,j}“,and then one has
(4.20)
(ORrl+lj)2= L+~~(P,,+~,
- r,+J
Case : i odd
Define the function of two variables
(4.21)
F(a,x) = c~~x~‘+‘/[l+ (-l)‘ax’(l-x)].
Let OSc,+,li,+, and set eY1l+l=F(in+l
,(c/i,,+,)2’(2’+‘)).Assume that Olali,,, ,
05x51, arc such that F(a,x)Q19,+, and ~2x2i+11c2.Then one has the
inequalities
(4.22)
(4.23)
0 2
Pn+li
=
r,,+,/[l
-F(a,x>l
5
r,+,/[l
-tin+,1
5
141
-in+Jr
0 5 (t-,+,0’,+,J2 = a2x2i+15 c2 I iz,+,.
Furthermore one has equalities of the middle terms only if
a = in+l, x = (c/in+l)2’(2i+‘),
(4.24)
Equalities of the three upper terms hold only in the degenerate case p(n)=%,
x= 1, cx=c=in+l,and then one has
(4.25)
(OR,+1
j12 = Ml -i+J12.
Up to the computation of the conditional variance (o~,+~~)~,this
follows fmm the discussion preceding Proposition 4.2. The fotm ula (4.20) is
verified as follows :
Proaf.
(OR
.+1j)2
=
Wrn+l)2W(l+a>2
=
(rn+1)2(1+a2)/(1
=
(Iln+~j)*(l+~*)
+
-a2>2
-
1/(l-a)2l
-
(P,+I~>~
-
(pn+l
(pn+lj)2
j>2
=
CaPn+l
j>* = Pn+lj(lJn+lj-rn+l).
ON BINOMIAL
MODELS
OF THE TERM
STRUCTURE
OF 1..
857
The formula (4.25) follows from (4.20) setting un+lj=l/(l-i,+,).
Further steps towards the determination of the complete class of all
exogenously given arbitrage-free binomial models of the term structure of
interest rates have been undertaken. A new parametric binomial model with
the following properties has been constructed :
property (P) (condition (2.1), or (2.2), or (4.4))
no negative interest rates and no arbitrarily high interest rates
flexible volatility structure of interest rates : long term volatility smaller
than short term one, high volatility by high interest rates, etc.
flexible yield curve by given initial tetm stmctute : variety of realistic
shapesincluding flat, upward and downward sloped and humped shaped
simple parametrization (end of Section 3)
simple understanding from first principles (follows from (4.4))
A remaining drawback is the fact that short and long term interest
rates are perfectly correlated while in the real world they are not, but often
mover together. Since this property is shared by all single-factor models,
only the mom general framework of multi-factor models can resolve this
inconvenience (consult e.g. Duffie and Kan(1994)).
Finally let us mention another more methodological problem, but
quite important from the point of view of the interaction between academics
and practitioners, which concerns the proper passage from discrete-time to
continuous-time models and vice-versa. Early in Theoretical Physics one has
shown that a discrete random walk converges to Brownian motion and that
an Ehrenfest urn model converges to the Omstein-Uhlenbeck process, as
sketched among others by Kac(l947). To which continuous-m ode1 does the
new parametric binomial model converge ? Does the most important limit
theorem in the theory of stochastic processes by Donsker(l951) and
Prohorov(l956) (see also Glynn(1990)) help solve this question ?
l
l
l
l
l
l
858
5TH AFIR INTERNATIONAL
COLLOQUIUM
Donskcr, M.D. (1951). An invariance principle for certain probability limit
theorems. Memoirs of the American Mathematical Society 6.
DufIie, D. (1992). Dynamic Asset Pricing Theory. Princeton Univ. Press.
DufIie, D., Kan, R. (1994). Multi-factor tctm structure models. Phil.
Transactions Royal Society of London, Series A, 577-86.
Glynn, P.W. (1990). Diffusion appmximations. In Heyman, D.P., Sobel,
M.J. (cds.) Stochastic Models, Handbooks in Operations Research
and Management Science, vol. 2, chap. 4, 145-98.
Heath, D., Jarrow, R., Morton, A. (1992). Bond pricing and the tctm
structure of interest rates : a new methodology for contingent claims
valuation. Econometrica 60, 77-105.
Ho, T.S.Y., Lee, S. (1986). Term structure movements ‘and pricing intetcst
rate contingent claims. Journal of Finance 41, 1011-1029.
Kac, M. (1947). Random walk and the theory of Btownian motion.
American Mathematical Monthly 54, 369-9 1.
McCulloch, J.H. (1985). On hetetoscedasticity. Economctrica 53, 483.
Morgan, LG., Neave, E. (1991). A mean reverting process for pricing
treasury bills and futures contracts. Proceedings of the 2nd AFIR
Colloquium, Brighton, vol. 1, 237-266.
Morgan, LG., Neave, E. (1993). A discrete time model for pricing treasury
bills, forward, and futures contracts. ASTIN Bulletin 23, 3-22.
Pedersen, H.W., Shiu, E.W.S., Thorlacius, A.E. (1989). Arbitrage-free
pricing of interest-rate contingent claims. Transactions of the Society
of Actuaries 41, 231-65. Discussion, 267-79.
Ptohorov, Y. (1956). Convergence of random pmcesscsand limit theorems
in probability theory. Theory of Prob. and Applications 1, 157-214.
Semu, P. (1991). Bond options and bond portfolio insurance. Insurance :
Mathematics and Economics 10, 203-30.
Vetzal, K.R. (1994). A survey of stochastic continuous time models of the
term structure of interest rates. Insurance : Mathematics and
Economics 14, 139-61.
© Copyright 2026