1. No category

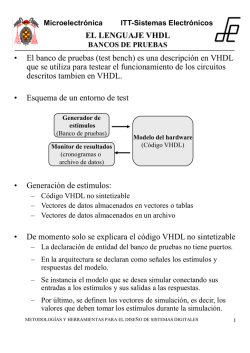
 1 Curso de LATEX
TP/TD 4
Fórmulas Matemáticas Complejas en LATEX
Este tercer trabajo práctico (TP) corresponde a la edición de formulas matemáticas complejas en
documentos en latex.
1. Crear una nueva sección llamada Formulas Complejas
2. Crear la siguiente fórmula con el uso de una raíz cuadrada
En la formula \ref{eqc-1} presenta el uso de una raíz cuadrada.
Crear la siguiente fórmula
\begin{equation}
\label{eqc-1}
\frac{\sqrt{b-a^2}}{c}
\end{equation}
3. Integrales
En la formula \ref{eqc-2} presenta la edición de una integral.
Crear la siguiente fórmula
\begin{equation}
\label{eqc-2}
D\Psi(u)[v]=p\int_{\Omega}|u|^{p-2}uv\,dx.
\end{equation}
4. Crear la siguiente fórmula esta creada con el entorno “Align”
En el entorno align :
&= establece una igualdad en una misma columnas mientras que & establece un cambio de
columna.
&= establece una igualdad en una misma columnas mientras que & establece un cambio de
columna.
2014 – Mauricio Iturralde, PhD
2 Crear la siguiente expresión
\begin{align*}
\intertext{Agrupamos,}
\frac{a+ay+ax+y}{x+y} &= \frac{ax+ay+x+y}{x+y} &\mbox{Agrupar}\\
\intertext{sacamos el factor común,}
&= \frac{a(x+y)+x+y}{x+y} &\mbox{Factor común}\\
&= \frac{(x+y)(a+1)}{x+y} &\mbox{Simplificar}\\
&= a+1
\end{align*}
5. En la formula 1.4 presenta el desarrollo de una fórmula con la clausula {eqnarray}
\begin{eqnarray}
\label{eqc-3}
y=\sqrt[n]{x} &\Longrightarrow & y^n=x \\
&\Longrightarrow & n\log \,y=\log \,x,\;\mbox{si}\;x,y>0\\
& \Longrightarrow & \log \sqrt[n]{x}={1 \over n}\log \,x
\end{eqnarray}
6. Si se necesita realizar una numeración selectiva se debe usar la clausula "nonumber"
Crear la siguiente fórmula
2014 – Mauricio Iturralde, PhD
3 Resultado del ejercicio 6
\begin{eqnarray}
y=\sqrt[n]{x} &\Longrightarrow &y^n = x \nonumber\\[0.5cm]
&\Longrightarrow &n\log \,y=\log\,x,
\;\mbox{si}\; x,y>0 \\[0.5cm]
&\Longrightarrow &\log \sqrt[n]{x}={1 \over n}\log \,x
\end{eqnarray}
7. Crear la siguiente expresión
Resultado del ejercicio 7
\begin{equation}
\forall x \in X, \quad \exists y \leq \epsilon
\end{equation}
8. Crear la siguiente fórmula
Resultado del ejercicio 8
\begin{equation}
\cos (2\theta) = \cos^2 \theta - \sin^2 \theta
\end{equation}
9. Crear la siguiente fórmula
Resultado del ejercicio 9
\begin{equation}
\lim_{x \to \infty} \exp(-x) = 0
\end{equation}
10. Crear la siguiente fórmula
Resultado del ejercicio 10
\begin{equation}
k_{n+1} = n^2 + k_n^2 - k_{n-1}
\end{equation}
2014 – Mauricio Iturralde, PhD
4 11. Crear la siguiente fórmula
Resultado del ejercicio 11
\begin{equation}
\frac{n!}{k!(n-k)!} = \binom{n}{k}
\end{equation}
12. Crear la siguiente fórmula
Resultado del ejercicio 12
\begin{equation}
\frac{1}{k}\log_2 c(f)\;\tfrac{1}{k}\log_2 c(f)\;
\end{equation}
13.
Crear la siguiente fórmula
Resultado del ejercicio 13
\begin{equation}
\Re{z} =\frac{n\pi \dfrac{\theta +\psi}{2}}{
\left(\dfrac{\theta +\psi}{2}\right)^2 + \left( \dfrac{1}{2}
\log \left\lvert\dfrac{B}{A}\right\rvert\right)^2}.
\end{equation}
14.
Crear la siguiente fórmula
Resultado del ejercicio 14
\begin{equation}
\frac{\sum_{n > 0} z^n}
{\prod_{1\leq k\leq n} (1-q^k)}
\end{equation} 2014 – Mauricio Iturralde, PhD
5 15. Crear la siguiente fórmula
Resultado del ejercicio 15
\begin{equation}
\frac{\sum_{n > 0} z^n}
{\prod_{1\leq k\leq n} (1-q^k)}
\end{equation}
2014 – Mauricio Iturralde, PhD