1. No category

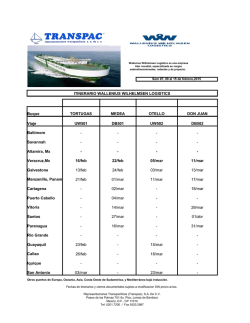
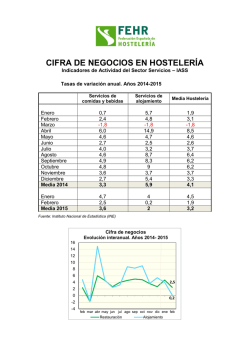
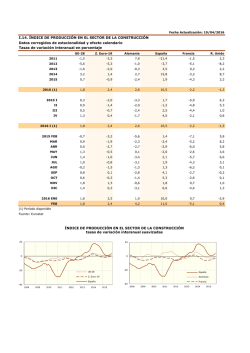
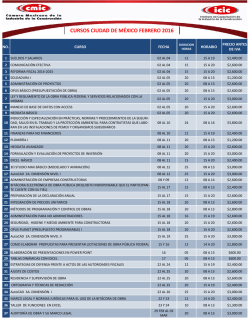
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
“Endurecimiento Superficial por Difusión de Boro
en un Acero AISI D2: Caracterización Mecánica y
Cinética de Crecimiento de Compuestos FeB Y Fe2B”
TESIS
Que para obtener el grado de:
MAESTRO EN CIENCIAS EN INGENIERIA MECANICA
Presenta:
Ing. Eduardo Chávez Gutiérrez
Directores de tesis:
Dr. Iván Enrique Campos Silva
Dr. German Anibal Rodríguez Castro
México, D.F. Marzo del 2012
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN

La culminación de este trabajo la dedico a mis padres Demetrio y Gloria,
quienes me han brindado su amor, apoyo y esfuerzo incondicional en cada
etapa de mi formación académica, por ser ejemplo de vida y grandeza.
A mis hermanos Omar y Abraham, por su apoyo a lo largo de mi desarrollo
profesional.
A Gaby, por su compañía, atención, comprensión y amor durante todo el
tiempo que hemos estado juntos, por impulsarme a seguir adelante.
A mi tía Rosa por sus atenciones, cuidados y amor que me ha brindado desde
mi infancia.
ChávezGutiérrezEduardo
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN

A la vida, por tener junto a mí a mis amados padres Demetrio y Gloria, quienes
me han entregado su ser para hacer de mi una persona de bien.
A mis hermanos Omar y Abraham, mi cuñada Maritza, mis sobrinos Santiago,
Sebastián y Diego, por ser parte importante de vida.
A Gaby, por complementar mis alegrías y éxitos, por compartir
momentos felices.
tantos
A mi tía Rosa, mi abuelito Fernando, mis primos Rodolfo y Wendy, por su
cariño y atención.
A mi tío Ing. Florencio Chávez y mi tía Patricia, por confiar en mi y apoyar mi
desarrollo profesional.
A mi tía Irma y mi abuelita Petra, quienes me han brindado su apoyo en todo
momento.
A la familia Pimentel Acosta por su amistad y apoyo.
A los buenos amigos Omar D. Quintero Reyes y César Torres Meléndez, por su
sincera amistad y enseñanzas, por ser parte fundamental en la culminación de
este trabajo.
Al Dr. Iván E. Campos Silva por sus enseñanzas, paciencia y disposición a lo
largo de este ciclo, por ser una gran persona, especialmente por creer en mí y
alentarme a siempre seguir adelante.
Al Dr. German A. Rodríguez Castro, por su compromiso, disposición y
enseñanzas, por sus comentarios y dedicación en este trabajo.
ChávezGutiérrezEduardo
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
Al Instituto Politécnico Nacional.
A la Escuela Superior de Ingeniería Mecánica y Eléctrica, Unidad Zacatenco.
Al CONACyT por su valioso apoyo.
Al Grupo “Ingeniería de Superficies”.
A los integrantes del jurado. Dr. Orlando Susarrey, Dr. Iván E. Campos Silva,
Dr. German A. Rodríguez Castro, Dr. Ulises Figueroa, Dr. José Martínez.
A mis compañeros Rafael Carrera, Abraham López, y Jesús González, por su
apoyo y disposición en la realización de este trabajo.
Al Dr. Enrique Hernández, por su apoyo y enseñanzas.
ChávezGutiérrezEduardo
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
Índice
Contenido
Página
Lista de figuras.
Lista de tablas.
I
VIII
Resumen.
X
Abstract.
XII
Introducción.
XIV
Antecedentes.
XVI
Justificación.
XXI
Objetivo general.
XXII
Metodología experimental.
XXIII
Capítulo I
Modelo cinético que describe la evolución de capas boruradas.
1
1.1
Introducción.
2
1.2
Modelo de difusión.
4
1.3
Procedimiento experimental.
10
1.4
Resultados y discusiones.
14
Conclusiones.
27
ChávezGutiérrezEduardo
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
Capítulo II
Ensayos de micro y nanodureza sobre capas tipo FeB y Fe2B.
28
2.1
Introducción.
29
2.2
Ensayo de microdureza Vickers.
31
2.3
Ensayo de nanodureza Berkovich.
33
2.3.1 Modelo de contacto elástico.
33
2.4
Procedimiento experimental.
39
2.5
Resultados y discusiones.
41
2.5.1 Microdureza Vickers.
42
2.5.2 Nanodureza Berkovich.
43
2.5.3 Módulo elástico.
45
2.5.4 Razón H/E.
47
2.5.5 Trabajo (W).
49
Conclusiones.
54
Capítulo III
Efecto de tamaño de huella en la dureza de capas boruradas.
55
3.1
Introducción.
56
3.2
Modelos de ISE.
57
3.2.1 Modelo de Meyer.
57
3.2.2 Modelo de recuperación elástica (REM).
58
3.2.3 Modelo de resistencia proporcional del espécimen (PSR).
59
3.3
Procedimiento experimental.
60
3.4
Resultados y discusiones.
61
ChávezGutiérrezEduardo
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
3.4.1 Modelo de Meyer.
66
3.4.2 Modelo de recuperación elástica (REM).
70
3.4.3 Modelo de resistencia proporcional del espécimen (PSR).
74
Conclusiones.
79
Capítulo IV
Estimación de la tenacidad a la fractura y esfuerzos residuales en
capas duras tipo FeB y Fe2B.
80
4.1
Introducción.
81
4.2
Modelo de Tenaciadad a la fractura.
84
4.3
Procedimiento experimental.
85
4.4
Resultados y discusiones.
86
Conclusiones.
92
Perspectivas de trabajo.
93
Referencias bibliográficas.
94
Publicaciones y distinciones.
98
ChávezGutiérrezEduardo
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
Lista de Figuras
Figura
FeB
Figura 1.1 Esquema representativo de los valores de a) (C upFeB ) y (Clow
) y
Fe 2 B
b) ( C upFe B ) y (C low
) obtenidos del diagrama de fase Fe-B.
2
Figura 1.2 Perfil de concentración de boro en las capas FeB/Fe2B.
Página
4
5
10
Figura 1.3 Geometría de probetas para el tratamiento de borurización en
caja.
11
Figura 1.4 Esquema representativo de la geometría del contenedor y
colocación de probetas.
Figura 1.5 Dispositivo de sujeción utilizado durante el proceso metalográfico
de las probetas de acero AISI D2 borurizado.
12
13
Figura 1.6 Medición de los espesores de capa FeB y capa total formadas en
la superficie de un acero AISI D2 endurecido por difusión de boro.
15
Figura 1.7 Microfotografía de la sección transversal de un acero AISI D2
borurizado a la temperatura de 1223 K con tiempos de exposición de:
a) 1 h , b) 3 h , c) 5 h y d) 7 h .
Figura 1.8 Microfotografía de la sección transversal de un acero AISI D2
borurizado a la temperatura de 1253 K con tiempos de exposición de:
16
a) 1 h , b) 3 h , c) 5 h y d) 7 h .
EduardoChávezGutiérrez
I
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
Figura 1.9 Microfotografía de la sección transversal de un acero AISI D2
borurizado a la temperatura de 1273 K con tiempos de exposición de:
17
a) 1 h , b) 3 h , c) 5 h y d) 7 h .
Figura 1.10 Microfotografía de la sección transversal de un acero AISI D2
borurizado a la temperatura de 1223 K con tiempos de exposición de:
18
a) 1 h , b) 3 h , c) 5 h y d) 7 h .
Figura 1.11 Patrón de difracción de rayos X (XRD) obtenido en la superficie
de un acero AISI D2 borurizado a la temperatura de 1273 K con 7 h de
19
exposición.
Figura 1.12 Crecimiento de las capas superficiales en función del tiempo de
exposición: a) FeB, b) (FeB + Fe2B)
20
Figura 1.13 Dependencia entre los coeficientes de difusión del boro en el
sistema FeB/Fe2B y la temperatura de tratamiento: a) capa FeB,
22
b) capa Fe2B.
Figura 1.14 Parámetro a) η(T) y b) ε(T) en función de la temperatura de
tratamiento.
24
Figura 2.1Esquema representativo de la geometría de un indentador tipo
31
Vickers.
Figura 2.2 Representación esquemática de la curva  P  -  hc  en un ensayo
de nanoindentación.
34
Figura 2.3 Representación esquemática de la sección transversal de una
indentación.
EduardoChávezGutiérrez
34
II
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
Figura 2.4 Esquema representativo de la geometría de un indentador tipo
36
Berkovich.
Figura 2.5 Esquema representativo del trabajo W  en función de la curva
 P  -  hc  , donde WT
Figura
a)
2.6
 W plast  Welast
Equipo
Microdurómetro
utilizado
marca
37
.
durante
Wolpert
los
ensayos
Group
modelo
de
dureza:
401MVD,
40
b) Nanoindentador TTX-NHT, CSM Instruments.
Figura 2.7 Ensayo de microdureza realizado a través del espesor de las
capas FeB-Fe2B formadas en la superficie de un acero AISI D2 borurizado
41
a la temperatura de: a) 1273 K -5 h , b) 1323 K -7 h .
Figura 2.8 Ensayo de nanodureza realizado a través del espesor de las
capas FeB-Fe2B formadas en la superficie de un acero AISI D2 borurizado
a la temperatura de: a) 1253 K -5 h , b) 1323 K -7 h .
41
Figura 2.9 Perfiles de microdureza obtenidos a una carga de 490 mN en un
acero AISI D2 borurizado a la temperatura de: a) 1223 K , b) 1253 K ,
42
c) 1273 K , d) 1323 K .
Figura 2.10 Perfiles de nanodureza obtenidos a una carga de 250 mN en un
acero AISI D2 borurizado a la temperatura de: a) 1223 K , b) 1253 K ,
43
c) 1273 K , d) 1323 K .
Figura 2.11 Comportamiento del módulo de elasticidad obtenido a una
carga de 250 mN a lo largo de las capas FeB-Fe2B en un acero AISI D2
borurizado a la temperatura de: a) 1223 K , b) 1253 K , c) 1273 K , d) 1323 K .
45
EduardoChávezGutiérrez
III
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
Figura 2.12 Ensayo de AFM realizado en el acero AISI D2 borurizado a la
temperatura de 1273 K -7 h : a) micrografía del ensayo de nanoindentación
realizado, b) presencia del efecto “sink in” en el ensayo de nanoindentación.
46
Figura 2.13 Comportamiento del índice de plasticidad  H E  obtenido a una
carga de 250 mN a lo largo de las capas FeB-Fe2B en un acero AISI D2
borurizado a la temperatura de: a) 1223 K , b) 1253 K , c) 1273 K , d) 1323 K .
47
Figura 2.14 Comportamiento de Welast  obtenido a una carga de 250 mN a
lo largo de las capas FeB-Fe2B en un acero AISI D2 borurizado a la
temperatura de: a) 1223 K , b) 1253 K , c) 1273 K , d) 1323 K .
49
Figura 2.15 Comportamiento de Wplast  obtenido a una carga de 250 mN a
lo largo de las capas FeB-Fe2B en un acero AISI D2 borurizado a la
temperatura de: a) 1223 K , b) 1253 K , c) 1273 K , d) 1323 K .
50
Figura 2.16 Coeficiente de deformación elástica obtenido a una carga de
250 mN a lo largo de las capas FeB-Fe2B en un acero AISI D2 borurizado a
la temperatura de: a) 1223 K , b) 1253 K , c) 1273 K , d) 1323 K .
51
Figura 2.17 Parámetro de disipación obtenido a una carga de 250 mN a lo
largo de las capas FeB-Fe2B en un acero AISI D2 borurizado a la
temperatura de: a) 1223 K , b) 1253 K , c) 1273 K , d) 1323 K .
52
Figura 3.1 Ensayos de nanoindentación realizados en el acero AISI D2
borurizado a la temperatura de 1253 K -7 h : a) capa FeB con cargas de 50,
100,150 y 200 mN ; b) capa Fe2B con cargas de 10, 50, 100 y150 mN ;
61
c) capa FeB con cargas de 50, 100,150 mN , capa Fe2B con cargas de 200
y 250 mN .
EduardoChávezGutiérrez
IV
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
Figura 3.2 Curvas
 P  -  hc 
obtenidas en la capa FeB formada en la
superficie de un acero AISI D2 borurizado a la temperatura de:
62
a) 1273 K -7 h , b) 1323 K -7 h .
Figura 3.3 Curvas
 P  -  hc  obtenidas
en la capa Fe2B formada en la
superficie de un acero AISI D2 borurizado a la temperatura de:
a) 1273 K -7 h , b) 1323 K -7 h .
63
Figura 3.4 Comportamiento de la dureza en función de la profundidad de
contacto en la capa FeB formada en la superficie de un acero AISI D2
borurizado a la temperatura de: a) 1223 K , b) 1253 K , c) 1273 K , d) 1323 K .
64
Figura 3.5 Comportamiento de la dureza en función de la profundidad de
contacto en la capa Fe2B formada en la superficie de un acero AISI D2
65
borurizado a la temperatura de: a) 1223 K , b) 1253 K , c) 1273 K , d) 1323 K .
Figura 3.6 Carga de indentación respecto a la profundidad de contacto en la
capa FeB formada en la superficie de un acero AISI D2 borurizado a la
66
temperatura de: a) 1223 K , b) 1253 K , c) 1273 K , d) 1323 K .
Figura 3.7 Carga de indentación respecto a la profundidad de contacto en la
capa Fe2B formada en la superficie de un acero AISI D2 borurizado a la
temperatura de: a) 1223 K , b) 1253 K , c) 1273 K , d) 1323 K .
67
Figura 3.8 Relación de los parámetros A y n del modelo de Meyer en el
acero AISI D2 borurizado en función de las condiciones de tratamiento
establecidas.
69
Figura 3.9 Modelo de recuperación elástica evaluado en la capa FeB
formada en la superficie de un acero AISI D2 borurizado a la temperatura
70
de: a) 1223 K , b) 1253 K , c) 1273 K , d) 1323 K .
EduardoChávezGutiérrez
V
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
Figura 3.10 Modelo de recuperación elástica evaluado en la capa Fe2B
formada en la superficie de un acero AISI D2 borurizado a la temperatura
de: a) 1223 K , b) 1253 K , c) 1273 K , d) 1323 K .
71
Figura 3.11 Gráficas Pmax hc vs hc conforme al modelo PSR evaluado en la
capa FeB formada en la superficie de un acero AISI D2 borurizado a la
74
temperatura de: a) 1223 K , b) 1253 K , c) 1273 K , d) 1323 K .
Figura 3.12 Gráficas Pmax hc vs hc conforme al modelo PSR evaluado en la
capa Fe2B formada en la superficie de un acero AISI D2 borurizado a la
temperatura de: a) 1223 K , b) 1253 K , c) 1273 K , d) 1323 K .
75
Figura 4.1Morfología de grietas generadas por indentación: a) radial-media,
b) Palmqvist, donde a es la mitad de la diagonal de indentación, l es la
longitud de la grieta y c=l  a .
82
Figura 4.2 Morfología de grieta generada por indentación Berkovich, donde
a es la mitad de la diagonal de indentación y l es la longitud de la grieta
83
( c=l  a ).
Figura 4.3 Esquema representativo de la medición de grietas y diagonal de
indentación de las huellas generadas por nanoindentación Berkovich en el
85
acero AISI D2 borurizado.
Figura 4.4 Agrietamiento generado mediante el ensayo de nanoindentación
Berkovich en la capa FeB formada en la superficie de un acero AISI D2
borurizado a la temperatura de1223 K , a) 3 h y b) 5 h .
86
Figura 4.5 Agrietamiento generado mediante el ensayo de nanoindentación
Berkovich en la capa Fe2B formada en la superficie de un acero AISI D2
86
borurizado a la temperatura de1223 K , a) 3 h y b) 5 h .
EduardoChávezGutiérrez
VI
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
Figura 4.6 Relación entre PX r c3 2 y 2  c  
12
para las capas FeB y Fe2B
formadas en la superficie de un acero AISI D2 borurizado a la temperatura
87
de: a) 1223 K -7 h , b) 1253 K -7 h , c) 1273 K -7 h , d) 1323 K -7 h .
Figura 4.7 Relación entre
 KC 
y  R  para las capas: a) FeB, b) Fe2B
formadas en la superficie de un acero AISI D2 borurizado a las condiciones
de tratamiento establecidas.
EduardoChávezGutiérrez
90
VII
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
Lista de tablas
Tabla
Página
Tabla 1.1 Valores experimentales de la constante de crecimiento y tiempo
de incubación capa FeB y capa total, en función de la temperatura de
21
tratamiento.
Tabla 1.2 Valores del coeficiente de difusión en FeB y Fe2B obtenidos
23
respecto a las temperaturas de tratamiento.
Tabla 1.3 Valores de los espesores de capa FeB y capa total para las
condiciones experimentales de tratamiento en un acero AISI D2 borurizado.
26
Tabla 2.1 Valores de la relación
48
H E
obtenidos para diferentes
recubrimientos aplicados en diversos aceros.
Tabla 2.2 Valores de los parámetros
 Ke 
y
 Kd 
obtenidos para
53
recubrimientos aplicados en diversos aceros.
Tabla 3.1 Mejor ajuste para los valores de A y n para las capas FeB y
Fe2B en función de las condiciones de tratamiento del acero AISI D2
68
borurizado.
Tabla 3.2 Parámetros del modelo de recuperación elástica obtenidos para
la capa FeB en función de las condiciones de tratamiento del acero AISI D2
borurizado.
72
Tabla 3.3 Parámetros del modelo de recuperación elástica obtenidos para
la capa Fe2B en función de las condiciones de tratamiento del acero
AISI D2 borurizado.
EduardoChávezGutiérrez
73
VIII
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
Tabla 3.4 Parámetros del modelo PSR obtenidos para la capa FeB en
función de las condiciones de tratamiento del acero AISI D2 borurizado.
76
Tabla 3.5 Parámetros del modelo PSR obtenidos para la capa Fe2B en
77
función de las condiciones de tratamiento del acero AISI D2 borurizado.
Tabla 3.6 Valores de hCC y PC para los modelos REM y PSR en las capas
78
FeB y Fe2B en función de las condiciones de tratamiento del acero AISI D2
borurizado.
Tabla 4.1 Valores del coeficiente de expansión térmica para las capas FeB,
81
Fe2B y el acero AISI D2.
Tabla 4.2 Mejor ajuste para los valores de  R  ,  K C  y  B  para la capa
FeB en función de las condiciones de tratamiento del acero AISI D2
borurizado.
88
Tabla 4.3 Mejor ajuste para los valores de  R  ,  K C  y  B  para la capa
Fe2B en función de las condiciones de tratamiento del acero AISI D2
89
borurizado.
EduardoChávezGutiérrez
IX
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
Resumen
En el presente trabajo de investigación se estudia la cinética de crecimiento de
compuestos sólidos intersticiales formados en la superficie de un acero AISI D2
expuesto al tratamiento termoquímico de borurización bajo condiciones variables de
tiempo y temperatura. Asimismo, se realizó la caracterización mecánica mediante
ensayos de microindentación y nanoindentación instrumentada en las capas formadas.
La cinética de crecimiento de las capas FeB y Fe2B se evalúa mediante un modelo
matemático de balance de masa en las interfaces de crecimiento que considera los
perfiles de concentración de boro en cada capa, las mediciones experimentales de los
espesores de las capas, los tiempos de incubación de los boruros para estimar
numéricamente el coeficiente de difusión del boro ( DFeB, DFe2 B ) en cada una de las
capas.
Como resultado del trabajo realizado, se obtuvo que la energía de activación (Q)
estimada para la capa FeB es 194 kJ / mol , mientras que para la capa total es
181 kJ / mol ; los mayores espesores de capa son de 49.95 μm y 119.03 μm para la
capa FeB y capa total, respectivamente.
La caracterización mecánica se llevó a cabo mediante ensayos de micro y nano dureza
realizados con indentadores tipo Vickers y Berkovich respectivamente, con la finalidad
de determinar gradientes de dureza a lo largo del sistema capa/substrato. Para
microdureza se efectuaron ensayos con cargas de 490 mN , mientras que para
nanodureza las cargas aplicadas fueron de 250 mN . Al aplicar el tratamiento de
borurización se incrementó la dureza superficial del acero hasta 2500 H V .
EduardoChávezGutiérrez.
X
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
Con la técnica de nanoindentación instrumentada se estudia el efecto del tamaño de
indentación (ISE por sus siglas en inglés) en condiciones de cargas variables en el
sistema bicapa FeB-Fe2B, evaluado mediante modelos descriptivos existentes en
literatura.
Se concluye la caracterización mecánica con la evaluación de la tenacidad a la fractura
 K IC 
y la estimación de esfuerzos residuales  R  bajo el principio de fractura por
indentación para cada una de las condiciones de tratamiento. Se estimaron valores de
tenacidad a la fractura  K IC  en un rango de 1.27 a 3.02 MPa m para la capa FeB
y de 1.98 a 4.65 MPa m para la capa Fe2B con un campo de esfuerzos residuales
 R 
tipo compresivo.
EduardoChávezGutiérrez.
XI
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
Abstract
In this study, the growth kinetics of the FeB and Fe2B layers formed at the surface of
AISI D2 borided steel was established under different temperatures and exposure times
by development of the powder-pack boriding process. The kinetics of boride layers was
estimated by a diffusion model that considers the mass balance equation at the growth
interfaces (FeB/Fe2B and Fe2B/substrate). Moreover, the model was extended to
evaluate the boride layer thicknesses in the set of experimental parameters of the
boriding process.
In addition, the mechanical characterization of the FeB and Fe2B layers was carried out
by indentation at micro and nano scales for the set of experimental conditions of the
boriding process. First, Vickers microindentation tests were established at a constant
load of 490 mN along the depth of boride layers in order to evaluate the hardness
gradient from the surface of the borided steels to the steel core. In similar form,
Berkovich nanoindentation tests were performed at a constant load of 250 mN to
establish mechanical properties such as Young’s modulus and nanohardness along of
the boride layers. Furthermore, applied loads in the range of 10 to 300 mN were carried
out in the “pure” zone of the FeB layer at 10 microns from the surface, and in the “pure”
zone of the Fe2B layer (40 microns), respectively.
The results from the nanoindentation tests showed, for a constant load of 250 mN , that
the hardness of both FeB and Fe2B layers are a function of the temperature and
exposure time of the process, where the hardness decreases due to the presence of
grain coarsening in the surface layers at a temperature of 1323 K with more than 5 h of
exposure. Moreover, the presence of the indentation size effect (ISE) in the FeB and
Fe2B layers was verified in the range of applied loads (10-300 mN ), in which the
apparent or real hardness was estimated by traditional models according to the boriding
experimental parameters.
EduardoChávezGutiérrez.
XII
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
Finally, the fracture resistance and residual stresses of the boride layers was evaluated
in the range of nanoidentation loads as a function of boriding temperatures and
exposure times; the estimated values are in the range of 1.27 to 3.02 MPa m and
1.98 a 4.65 MPa m , with the presence of compressive stresses for the FeB and Fe2B
layers, respectively.
EduardoChávezGutiérrez.
XIII
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
Introducción
En la industria nacional existe gran diversidad de maquinaria y componentes mecánicos
que están expuestos a fenómenos propios del trabajo realizado, tales como corrosión,
desgaste, fátiga, entre otros. Por lo que, es de sumo interés mejorar las condiciones de
trabajo y propiedades mecánicas de dichos elementos para hacer más eficiente su
desempeño y prolongar su tiempo de servicio.
Es posible modificar las propiedades de materiales ferrosos mediante diversos
tratamientos térmicos. La borurización es un tratamiento termoquímico que permite
mejorar drásticamente las propiedades mecánicas en la superficie de un material
mediante la difusión de átomos de boro en los intersticios del substrato, y la
consecuente formación de capas duras tipo FeB y Fe2B en la superficie del acero. En
función del potencial de boro y de la composición química del material base, se puede
formar la capa FeB o el sistema bicapa FeB-Fe2B.
En el presente trabajo se realiza dicho tratamiento en aceros AISI D2, acero grado
herramienta para trabajo en frío, tipo alto carbono-alto cromo.
En el Capítulo I se determina la cinética de crecimiento de capas duras tipo FeB y Fe2B
en función de las condiciones de
tiempo y temperatura variables mediante la
evaluación de un modelo matemático de balance de masa (Campos-Silva et al., 2010)
que determina el coeficiente de difusión del boro ( DFeB, DFe2 B ) en ambas capas, y permite
estimar los espesores de capa considerando los parámetros de tiempo de incubación
(t0 ) , energía de activación (Q) y perfiles de concentración de boro.
En los Capítulos II, III y IV se realiza la caracterización mecánica del material sobre la
capa de boruros de hierro para evaluar propiedades mecánicas presentes en el acero
endurecido AISI D2.
EduardoChávezGutiérrez.
XIV
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
En el Capítulo II se determinan los gradientes de dureza a través del espesor de las
capas mediante ensayos de micro y nanodureza respecto al tiempo y temperatura de
tratamiento. Para microdureza se utiliza un indentador tipo Vickers, mientras que para
nanodureza un indentador tipo Berkovich.
En el capítulo III se estudia la influencia del efecto de tamaño de indentación
(ISE, por sus siglas en inglés) en la dureza de los boruros de hierro formados en la
superficie del acero, mediante la aplicación de cargas variables para cada condición de
tratamiento establecida. Se evalúan diferentes modelos que establecen las causas que
originan el efecto ISE (Peng et al., 2004). Entre los más representativos se tienen:
modelo de Meyer, modelo de recuperación elástica, y el modelo de resistencia
proporcional del espécimen (PSR, por sus siglas en inglés). Algunos modelos implican
determinar un valor de dureza independiente de la carga de prueba, conduciendo así, a
efectuar un análisis de la aplicabilidad de dichos modelos.
En el Capítulo IV, mediante la técnica de fractura por nanoindentación Berkovich, se
determina el estado de esfuerzos residuales y la tenacidad a la fractura, utilizando
expresiones existentes en literatura para el régimen de agrietamiento tipo radial-media.
Se consideraron cargas variables de indentación a una distancia constante desde la
superficie del acero borurado en el conjunto experimental del tratamiento de
borurización. El modelo para evaluar el estado de esfuerzos residuales
tenacidad a la fractura
 K IC 
 R 
y la
en las capas FeB y Fe2B considera los parámetros de
carga de prueba ( P) , módulo de elasticidad ( E) , dureza ( H ) , y longitud de grieta desde
el centro de la indentación (c) (Marshall y Lawn, 1997).
EduardoChávezGutiérrez.
XV
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
Antecedentes
El tratamiento termoquímico de borurización ha sido objeto de estudio con el creciente
interés de optimizar dicho proceso en aplicaciones industriales, con la finalidad de
sustituir algunos aceros por otros de menor costo y/o que presenten mejores
propiedades físicas, mecánicas y químicas superficialmente.
De los materiales endurecidos mediante este proceso, se encuentran aceros de alto
contenido de carbono (estructurales y grado herramienta). Los estudios realizados se
basan principalmente en la cinética de crecimiento y caracterización mecánica de los
compuestos formados.
Campos et al., (2003) estimó el coeficiente de difusión del boro ( DFe2 B ) en la capa Fe2B
formado en la superficie de un hierro puro. El modelo cinético fue establecido con la
idea propuesta por Brakman et al., (1989), que asume una difusión unidireccional del
boro en la capa borurada, y dicho crecimiento obedece la ley de crecimiento parabólico
v 2  kt siendo v el espesor de capa, k la constante de crecimiento y t el tiempo de
exposición. La ecuación de balance de masa se expresa como:
C Fe2 B  DFe 2 B  C b - Cc   k  Cc - bC0 
(I )
donde CFe2 B es el perfil de concentración del boro en la capa Fe2B, Cb la concentración
del boro en la superficie del material, Cc la concentración del boro en la interface
Fe2B/substrato, C0 es la concentración de boro en el substrato ( C 0  0 ), b es el volumen
específico entre el substrato y la capa Fe2B , DFe2 B es el coeficiente de difusión del boro
en la capa Fe2B.
EduardoChávezGutiérrez.
XVI
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
El valor obtenido del coeficiente de difusión ( DFe2 B ) del boro en la capa Fe2B es
representado por la siguiente expresión:
 151x103 kJ  2 -1
D( Fe2 B)  1.311x106 exp  
  m s  para1223K<T<1323K ( II )
RT


donde la energía de activación es 151 kJ / mol .
Para el acero borurado AISI D2, existe la contribución realizada por Oliveira et al.,
(2010), en la cual las capas FeB y Fe2B fueron formadas a través del tratamiento de
borurización en sales considerando temperaturas de 1123 y 1273 K con un tiempo de
exposición constante de 4 h .
El crecimiento de las capas boruradas se calculó mediante la expresión:
d  kt 0.5 ( III )
donde d es el espesor de capa, k es la constante de crecimiento parabólico y t es el
tiempo de tratamiento.
La caracterización fue realizada por microscopia óptica, microdureza Vickers, difracción
de rayos X (XRD, por sus siglas en inglés) y espectroscopia óptica por descarga
(GDOS, por sus siglas en inglés). Los resultados obtenidos son capas con morfología
de dientes de sierra en la interface del substrato, espesores de capa de 60 a 120 μm y
durezas en el rango de 1596-1744 H V .
Sista et al., (2011) desarrollo el tratamiento de borurización electroquímico sobre la
superficie de aceros AISI D2 sometidos a temperaturas de 1123, 1173, 1223 y 1273 K
con tiempos de exposición de 15 a 60 minutos por cada temperatura.
EduardoChávezGutiérrez.
XVII
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
El crecimiento de las capas formadas obedece la ecuación ( III ) , donde la constante de
crecimiento k está en función de la difusión del boro y la temperatura de tratamiento, de
acuerdo a la siguiente expresión:
 Q 
k  k0 exp  
 ( IV )
 RT 
siendo k0 una constante pre-exponencial, Q la energía de activación, T la temperatura
kJ 

de tratamiento y R la constante universal de los gases  8.314
 . Las capas
mol K 

boruradas se caracterizaron mediante microscopía electrónica de barrido (SEM por sus
siglas en inglés), difracción de rayos X (XRD por sus siglas en inglés), ensayos de
microdureza y adhesión. Los resultados obtenidos son la formación de la capa Fe2B de
30 μm de espesor en un tiempo de 15 min, mientras que para un tiempo de 60 min, se
forman las capas FeB y Fe2B con un espesor total de 60 μm , las durezas obtenidas
están en el rango de 14 a 22 GPa . La energía de activación requerida para producir la
difusión de boro en las capas duras fue de 137 kJ / mol .
La caracterización mecánica de boruros de hierro ha tenido un interés particular en
años recientes para determinar propiedades superficiales presentes en aceros
sometidos al proceso de borurización. Técnicas de micro y nanoindentación
instrumentada han sido aplicadas exitosamente en la caracterización de capas duras
formadas en la superficie de diversos aceros, para evaluar algunas propiedades
mecánicas tales como: módulo de elasticidad
E,
tenacidad a la fractura
 K IC  ,
esfuerzos residuales  R  , dureza  H  , etc.
EduardoChávezGutiérrez.
XVIII
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
Ozbek y Bindal, (2002), caracterizaron un acero AISI W4 borurado, donde la presencia
de los boruros de hierro fue confirmada mediante difracción de rayos X (XRD),
microscopía electrónica de barrido (SEM por sus siglas en inglés) y microscopía óptica.
La distribución de los elementos de aleación fue estimada vía la técnica de
espectroscopia de energía dispersiva de rayos X (EDS por sus siglas en inglés).
Asimismo, se evaluó la microdureza y la tenacidad a la fractura de las capas boruradas
con cargas de 0.5 N y 10 N respectivamente. La expresión empleada para la
estimación de la tenacidad a la fractura fue:
 P 
K C  A  1.5  (V )
c 
E
donde P es la carga, c longitud de la grieta. La constante A es 0.028  
H
0.5
(E y H)
son el módulo de Young y la dureza de la capa, respectivamente). Como resultado de la
caracterización mecánica, se obtienen durezas en un rango de 1407 a 2093 H V y
valores de tenacidad a la fractura en un rango de 1.39 a 6.40 MPa m en las capas FeB
y Fe2B, respectivamente. Se establece de igual manera, un campo de esfuerzos
residuales  R  tensil y compresivo respectivamente.
En general, es poca la información que se reporta en literatura para el estudio del efecto
ISE en capas boruradas.
Campos-Silva et al., (2011) evaluó mediante la técnica de nanoindentación Berkovich,
el efecto de tamaño de indentación (ISE por sus siglas en inglés), la tenacidad a la
fractura  K IC  y el estado de esfuerzos residuales  R  en la interfase Fe2B/substrato de
un acero borurado AISI 1018.
EduardoChávezGutiérrez.
XIX
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
Para determinar la presencia del efecto ISE se emplearon cargas en el rango de 10 a
500 mN , aplicando el modelo de Meyer:
Pmax  Ahcn
(VI )
A y n son constantes, donde n < 2 establece la presencia del efecto ISE y hc es el
valor de la profundidad de contacto del indentador. Así mismo, el efecto ISE fue
evaluado utilizando el modelo de recuperación elástica:
0.5
Pmax
 X 0.5 hc  X 0.5 h0
(VII ) .
donde h0 es la corrección propuesta para hc y X  H 0 / k ; constante relacionada a la
dureza real.
Para determinar la tenacidad a la fractura
 K IC 
y el estado de esfuerzos residuales
 R  , en la interfase Fe2B/substrato del acero borurado AISI 1018 se utilizó un modelo
propuesto por Marshall y Lawn (1997), que ha sido empleado satisfactoriamente en el
estudio de capas duras por autores como Malzbender (1999):
 P 
c
X r  1.5   K IC  2  
c 
 
0.5
(VIII )
siendo
E
X r  0.016  
H
0.5
( IX ) .
Los resultados obtenidos para la dureza aparente se estimaron en el rango de 13.2 a
14.7 GPa . Asimismo, la naturaleza de los esfuerzos residuales  R  en la interfase
Fe2B/substrato es de tipo compresivo, con valores en el rango de 351 a 471 MPa , y con
valores de la tenacidad a la fractura  K IC  de 2.41 a 2.72 MPa m .
EduardoChávezGutiérrez.
XX
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
Justificación
En la industria metal-mecánica existen diferentes tratamientos superficiales que brindan
mejoras en las propiedades mecánicas de materiales de ingeniería. El tratamiento
termoquímico de borurización ha ganado terreno en este campo, ya que es un proceso
relativamente sencillo y económico, con el cual se mejoran drásticamente las
propiedades superficiales tales como resistencia a la abrasión, corrosión, desgaste, etc.
La aplicación del tratamiento termoquímico de borurización abre la posibilidad de
diseñar materiales priorizando ciertas propiedades mecánicas para aplicaciones
específicas. Mientras el substrato puede ser diseñado para resistencia y tenacidad, las
capas boruradas pueden ser sometidas a desgaste, fricción o corrosión. Por lo cual, es
de gran importancia el estudio de los parámetros que infieren la cinética de crecimiento
de capas duras tipo FeB-Fe2B para controlar espesores de capa respecto a tiempos y
temperaturas de tratamiento en función de las aplicaciones industriales. Por ejemplo,
para desgaste adhesivo un espesor de capa entre 10 y 20 μm es deseable, mientras
que para desgaste por erosión se emplean espesores mayores a 75 μm .
Asimismo, es vital determinar las propiedades mecánicas de las capas FeB y Fe2B ya
que pueden repercutir de manera positiva o negativa, en la fiabilidad y tiempo de vida
de los boruros formados. Propiedades como la dureza aparente del material, el estado
de esfuerzos residuales  R  y la tenacidad a la fractura  K IC  inciden directamente en
el rendimiento mecánico, por ejemplo: la resistencia al desgaste está relacionada con la
tenacidad a la fractura de la capa  K IC  ; al generarse fractura y propagación de grietas
que origina desprendimiento de material; en componentes estructurales un estado de
esfuerzo residual tipo compresivo mejora la resistencia a la propagación de grieta,
mientras que los esfuerzos residuales tipo tensil la disminuyen.
EduardoChávezGutiérrez.
XXI
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
Objetivo General
Aplicar el tratamiento termoquímico de borurización en polvo en un acero AISI D2 bajo
condiciones de tiempo y temperatura variables para la formación de capas duras tipo
FeB-Fe2B en la superficie del acero.
Objetivos particulares
 Determinar el crecimiento de los boruros de hierro formados en la superficie de
un acero AISI D2 bajo condiciones de tratamiento variables para estimar el
coeficiente de difusión del boro ( DFeB, DFe2 B ) , y los espesores de capas FeB y
Fe2B en un proceso de difusión controlado por medio de un modelo matemático
de balance de masa.
 Determinar la dureza característica de las capas FeB y Fe2B mediante ensayos
de micro y nanoindentación a lo largo de los espesores de capa, con cargas de
490 mN y 250 mN respectivamente para determinar el gradiente de dureza
desde la superficie del acero hasta el núcleo del acero.
 Evaluar el efecto de tamaño de indentación (ISE) presente en las capas FeB y
Fe2B a 10 y 40 μm de distancia respectivamente desde la superficie del acero
endurecido considerando cargas variables mediante ensayos de indentación
instrumentada para estimar valores de dureza real en ambas capas en un rango
de 10 a 300 mN .
 Estimar el valor de la tenacidad a la fractura  K IC  y esfuerzos residuales  R  en
las capas FeB y Fe2B a 10 y 40 μm de distancia respectivamente, mediante la
técnica de nanoindentación instrumentada, empleando cargas variables de 300 a
500 mN
respecto a cada condición de tratamiento para determinar el
comportamiento mecánico del sistema bicapa FeB-Fe2B.
EduardoChávezGutiérrez.
XXII
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
Metodología experimental.
Para el presente trabajo de investigación se planteó la siguiente metodología:
i. Realizar el tratamiento termoquímico de borurización en polvo sobre un acero AISI
D2, con probetas de dimensiones 10 x 10x 5 mm3; en condiciones variables de
temperatura a 1223 K, 1253 K, 1273 K y 1323 K con tiempos de exposición de 1h, 3h,
5h y 7h por cada temperatura.
ii. Medición de los espesores de capa formados para cada condición de tratamiento
utilizando un microscopio óptico marca Olympus GX51 y software analizador de
imágenes Image Pro Plus V 6.0.
iii. Estimación del coeficiente de difusión del boro en las capas FeB y Fe2B mediante un
modelo matemático que considera la ecuación de balance de masa en la interfase
FeB/Fe2B y Fe2B/substrato.
iv. Estimación teórica de los espesores de capa FeB y Fe2B en la superficie de un acero
AISI D2 endurecido por difusión de boro mediante una expresión originada a partir de la
ecuación de balance de masa. Los resultados teóricos de los espesores de capa FeB y
Fe2B fueron confrontados con el conjunto de datos experimentales del proceso de
borurización
v. Determinación del gradiente de micro y nanodureza a lo largo del espesor de las
capas FeB y Fe2B para el conjunto de datos experimentales del proceso de
borurización. Para el ensayo de microdureza, se emplea un durómetro marca Wolpert
Group modelo 401MVD con un indentador tipo Vickers a una carga constante de
490 mN . Para el ensayo de nanodureza Berkovich, se estableció una carga constante
de 250 mN a lo largo de las capas FeB y Fe2B empleando un equipo TTX-NHT, CSM
Instruments.
EduardoChávezGutiérrez.
XXIII
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
vi. Se estudia el efecto ISE en las capas FeB y Fe2B para el conjunto de datos
experimentales del proceso de borurización, mediante el ensayo de nanoindentación
Berkovich con cargas en el rango de 10 a 300 mN , considerando una distancia de10 y
40 μm desde la superficie del acero para la capa FeB y Fe2B respectivamente. El efecto
ISE se estimó mediante los modelos de Meyer, recuperación elástica, y resistencia
proporcional del especímen.
vii. Evaluación de la tenacidad a la fractura  K IC  y esfuerzos residuales  R  utilizando
la técnica de fractura por indentación en las capas boruradas FeB y Fe2B mediante
ensayos de nanoindentación Berkovich para el conjunto de datos experimentales del
proceso de borurización. El modelo que establece la tenacidad a la fractura y los
esfuerzos residuales considera un agrietamiento tipo radial media. Los parámetros
experimentales que se consideraron durante el ensayo de nanoindentación Berkovich
fueron cargas variables de indentación (300 a 500 mN ) y distancias constantes de
indentación en cada una de las capas (10 μm para FeB y 40 μm en Fe2B).
EduardoChávezGutiérrez.
XXIV
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloI
Capítulo I
Modelo cinético que describe la evolución de capas boruradas.
El presente Capítulo describe la evolución del crecimiento de la capa borurada con la
presencia de las fases FeB y Fe2B formadas en la superficie de un acero AISI D2. El
crecimiento de la capa borurada es descrito por un modelo de difusión que interpreta las
ecuaciones de balance de masa en las interfaces de crecimiento. Los coeficientes de
difusión del boro en cada una de las fases ( DFeB y DFe2B ) son establecidos en función de
las temperaturas de tratamiento para estimar la energía de activación necesaria para la
formación de la capa borurada. Finalmente, el modelo es extendido para determinar los
espesores de capa conforme a los parámetros experimentales del proceso de
borurización en caja.
EduardoChávezGutiérrez.
‐ 1 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloI
1.1 Introducción
El tratamiento termoquímico de endurecimiento superficial por difusión de boro es un
proceso que se lleva a cabo a temperaturas en el rango de 1123 a 1273 K con tiempos
de exposición entre 1 y 10 h (Campos-Silva et al., 2011). En materiales ferrosos, la
capa de boruro de hierro se compone de una capa FeB o el sistema bicapa FeB-Fe2B.
La capa FeB (estructura ortorrómbica) tiene un contenido de 16.23 wt% B y es más
frágil que la capa Fe2B (estructura tetragonal) con contenido de 8.8 wt% B. También se
puede dar la formación de boruros en combinación con otros elementos como Cr, V,
Mo.
El estudio de la cinética de crecimiento de capas boruradas en aleaciones ferrosas se
ha incrementado en años recientes, ya que es de gran importancia establecer los
parámetros que afectan la cinética de crecimiento de las capas en el tratamiento
termoquímico de borurización a fin de establecer las condiciones óptimas del proceso.
Modelos típicos de difusión sugieren que la formación de las capas FeB y Fe2B
obedece la ley de crecimiento parabólico. Para estimar la energía de activación (Q ) , se
determina la constante de crecimiento en función de la temperatura de tratamiento. Un
valor preciso de la energía de activación (Q ) es fundamental para estimar la formación
de capas duras tipo FeB-Fe2B en la superficie de un acero. Otros modelos han sido
desarrollados para determinar la cinética de crecimiento de los boruros de hierro, como
el modelo de Brakman et al., (1989) que considera la diferencia del volumen específico
entre las capas FeB y Fe2B, así como perfiles de concentración lineal de boro en las
interfaces FeB/Fe2B y Fe2B/substrato; el modelo de Campos et al., (2003) que
considera una expresión de balance de masa; o el modelo de Keddam y Chentouf
(2005) aplicado al proceso de borurización en pasta.
EduardoChávezGutiérrez.
‐ 2 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloI
En el presente trabajo, se evalúa un modelo matemático de balance de masa para
estimar el coeficiente de difusión del boro en las capas FeB y Fe2B ( DFeB
y
D Fe 2 B ) .
Los valores del coeficiente de difusión se representan por medio de la expresión de
Arrhenius; por lo cual, la energía de activación del sistema debe ser conocida (CamposSilva et al., 2010).
El modelo de difusión utilizado, considera la ley de crecimiento parabólico como una
solución a las ecuaciones de balance de masa; además, considera los perfiles de
concentración del boro en cada capa y los tiempos de incubación del boruro de hierro
FeB y capa total (t0FeB ) .y (t0 ) , respectivamente.
El modelo se extiende para estimar el valor de los espesores de capa FeB y Fe2B; los
cuales, son confrontados con los resultados experimentales obtenidos.
EduardoChávezGutiérrez.
‐ 3 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloI
1.2 Modelo de difusión.
Para el estudio de la cinética de crecimiento de los boruros de hierro formados sobre la
superficie del acero AISI D2 se considera un perfil de concentración lineal de boro para
cada capa. Las concentraciones máximas y mínimas de boro en las capas FeB y Fe2B
x
están representadas por ( C upx ) y (C low
) (x = FeB o Fe2B), como muestra la fig. 1.1 en el
diagrama de fases Fe-B.
Fe B
FeB
Fe 2 B
FeB
Fig. 1.1 Esquema representativo de los valores de a) ( C up
) y (C low ) y b) ( C up
) y ( C low2 )
obtenidos del diagrama de fase Fe-B (Campos-Silva et al., 2010).
Las capas boruradas tienen un rango estrecho de concentración de boro con contenido
aproximado del 1 wt. %B. La solubilidad del boro en las capas FeB y Fe2B puede
expresarse como ( a1 ) y (a3 ) ; mientras que los parámetros ( a2 ) y ( a4 ) , definen la
miscibilidad del boro en las interfases FeB/Fe2B y Fe2B/substrato respectivamente.
Finalmente, (c0 ) es la concentración de boro en la fase γ-Fe (0.003 wt. % B).
EduardoChávezGutiérrez.
‐ 4 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloI
Las condiciones iniciales y de frontera del proceso de difusión, se representan a través
de las siguientes ecuaciones, como se expresa en la fig. 1.2:
Fig. 1.2 Perfil de concentración de boro en las capas FeB/Fe2B (Campos-Silva et al., 2010).
EduardoChávezGutiérrez.
‐ 5 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloI
CFeB  x  t  0   C0 CFe2B  x  t  0   C0  




B
CFeB x t  t0FeB T    0  CupFeB paraCads
 16.23wt.%B,
FeB
B
CFeB x t  t0FeB T    0  Clow
paraCads
 16.23wt.%B y con la capa FeB


B
CFe2B x t  t0Fe2B T    0  CupFe2B parawt Cads
 16.23wt.%B y
(1.2)
sin la capa FeB,


Fe2 B
B
CFe2B x t  t0Fe2B T    0  Clow
paraCads
 .83wt.%B y sin la capa FeB,
FeB
CFeB  x  t  t   u   Clow
(1.3) ,
CFe2B  x  t  t   u   CupFe2B (1.4) ,
Fe2B
CFe2B  x  t  t   v  Clow
(1.5) ,
CFe2B  x  t  t   v  C0 (1.6) ,
B
representa la concentración de boro efectivamente adsorbida durante el proceso
C ads
de borurización (Yu et al., 2005). Las ecuaciones de balance de masa de las interfases
FeB/Fe2B y Fe2B/substrato pueden describirse de la siguiente manera:
1
FeB  a2 du  a1du  J1dt  J 2 dt (1.7)
2
1
Fe2B  a4  du  dl   a3du  a3dl  J 2 dt  J 3dt (1.8)
2
EduardoChávezGutiérrez.
‐ 6 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloI


donde J1 , J 2 y J 3 se obtienen de la primera ley de Fick, J   D dC  x  t   / dx  t  . Las
ecuaciones representativas de las concentraciones de boro en las capas FeB y Fe2B se
expresan como:
C FeB  x  t    C upFeB 
C Fe2 B  x  t    C upFe2 B 
FeB
Clow
 C upFeB
u
Fe 2 B
Clow
 C upFe2 B
l
x  t  (1.9)
 x  t   u 
(1.10)
Si el substrato se satura de boro en un corto periodo de tiempo y la solubilidad del boro
es extremadamente baja en γ-Fe (0.003 wt. %B), entonces J 3  0 . Por lo que, los flujos
J1 y J 2 se pueden expresar de la siguiente manera:
J1  DFeB a1 / u (1.11)
J 2  DFe 2 B a3 / l
(1.12)
DFeB es el coeficiente de difusión del boro en la capa FeB, DFe B es el coeficiente de
2
difusión del boro en la capa Fe2B, u y l representan el espesor de capa FeB y Fe2B,
respectivamente.
Sustituyendo las ecuaciones. (1.11) y (1.12) en las ecuaciones (1.7) y (1.8) , se
obtiene:
 a2  a1 / 2
 a4  a3 
EduardoChávezGutiérrez.
a
du
a
 DFeB 1  DFe2B 3
dt
u
l
a
du
dl
  a4  a3 / 2  DFe2B 3
dt
dt
l
(1.13)
(1.14)
‐ 7 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloI
Además, las ecuaciones de continuidad (1.13) y (1.14) pueden rescribirse como se
muestra a continuación:
du
l
l
 DFeB P1  DFe2B P2
(1.15)
dt
u
l
dl
l
l
 DFe2B P3  DFeB P4
(1.16)
dt
l
u
P1 
Con
P4 
a1
,
a2  a1 / 2
P2 
a3
,
a2  a1 / 2
P3  a3

a3  a4  1
1


,
a4  a3 / 2  a3  a4 a2  a1 / 2 
y

a3  a4 
a1


a4  a3 / 2  a2  a1 / 2 
La solución a las ecuaciones (1.15) y (1.16) pueden obtenerse considerando las
ecuaciones de crecimiento parabólico de las capas superficiales (Campos-Silva et al.,
2010):
u  kFeB  t  t0FeB T  
12
(1.17)
k FeB es la constante de crecimiento de la capa FeB, t 0FeB T  es el tiempo de incubación

FeB
del boruro FeB en función de la temperatura, y t  t0 T 

12
es el tiempo efectivo de
crecimiento de la capa FeB. De manera similar, la ecuación de crecimiento de la capa
Fe2B se define como:
l  v  u  k  t  t0 T    kFeB  t  t0FeB T  
12
12
(1.18)
donde v es el espesor de capa total, t es el tiempo de tratamiento, t 0 T  es el tiempo
de incubación de la capa total de boruro FeB-Fe2B  t0FeB T   t0 T   , y k es la constante
de crecimiento parabólico de la capa total.
EduardoChávezGutiérrez.
‐ 8 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloI
Basados en las hipótesis mencionadas, los coeficientes de difusión de boro en las


capas FeB y Fe2B DFeB y DFe2 B se pueden expresar utilizando las ecuaciones (1.15) y
(1.16) :
DFe2B 
DFeB 
l 
 du dl 
 du 
a

a
/
2


a
/
2




3
4
3


 
a3 
 dt dt 
 dt 
m s 
u
du dl
du 
 a4  a3 / 2      a3 / 2  a2  a1 / 2  

a1 
 dt dt 
 dt 
EduardoChávezGutiérrez.
2 -1
(1.19)
m s 
2 -1
(1.20)
‐ 9 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloI
1.3 Procedimiento experimental.
Para el desarrollo de este trabajo se utilizó un acero AISI D2, acero grado herramienta
para trabajo en frío; con composición nominal (% en peso) 1.6 % C, 13.0 % Cr, 1.2 %
Mo, 0.6 % Mn, 1.0 % Co, 0.6 % Si, 0.03 % P y 0.03 % S. Se emplearon probetas
cúbicas con dimensiones 10 x 10 x 5mm, como se muestra en la fig. 1.3.
Fig. 1.3 Geometría de probetas para el tratamiento de borurización en caja.
Las probetas fueron empaquetadas con una mezcla de carburo de boro (B4C), carburo
de silicio y tetrafluoruro de potasio, dentro de contenedores cilíndricos fabricados de
acero al carbono (fig. 1.4), previamente saturados con la mezcla borurante a una
temperatura de 1023 K durante 8h tiempo de exposición. Las capas FeB y Fe2B fueron
formadas en la superficie del acero a las temperaturas de 1223, 1253, 1273 y 1323 K ,
con tiempos de exposición de 1, 3 ,5 y 7 h por cada temperatura.
El tratamiento de borurización fue realizado introduciendo el contenedor en un horno
marca “Felisa”, iniciando el tiempo de tratamiento una vez que el horno alcanza la
temperatura establecida.
EduardoChávezGutiérrez.
‐ 10 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloI
Al finalizar el tratamiento, el contenedor es extraído del horno y es enfriado lentamente
a temperatura ambiente.
Fig. 1.4 Esquema representativo de la geometría del contenedor y colocación de probetas.
Posteriormente, las probetas endurecidas se cortan transversalmente (espesor 3 mm)
para realizar el proceso metalográfico sobre la sección transversal y caracterizar las
capas formadas. Para el proceso metalográfico, se diseñó y fabricó un dispositivo de
sujeción que simplifica la metalografía (fig. 1.5); se realiza el desbaste con lijas de
tamaño de grano desde 80 hasta 1500; posteriormente se pulen las muestras con
alúmina de 0.3 micras mezclada con agua sobre un paño microcloth hasta dejar un
acabado espejo.
EduardoChávezGutiérrez.
‐ 11 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloI
Fig. 1.5 Dispositivo de sujeción utilizado durante el proceso metalográfico de las probetas de
acero AISI D2 borurizado.
Para revelar las capas formadas FeB y Fe2B se empleó un ataque químico denominado
Vilella (1 g ácido pícrico, 5 mL HCl, 100 mL ethanol). Las capas formadas se
digitalizaron con la ayuda de un microscopio óptico marca Olympus GX-51. Se
realizaron 100 mediciones desde una referencia perfectamente plana en 3 diferentes
secciones de las capas boruradas con la ayuda del software Image Pro Plus para
determinar el espesor de la capa FeB y la capa total (fig. 1.6).
Adicionalmente, la caracterización físico-química fue establecida por difracción de rayos
X (XRD) en una muestra de acero AISI D2 borurizado, con condiciones de tratamiento
de 1273 K – 7 h ; para caracterizar la naturaleza de los boruros formados en las capas
superficiales.
EduardoChávezGutiérrez.
‐ 12 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloI
La caracterización por XRD se llevó a cabo con la ayuda de un difractómetro GBC MMA
(CoKα radiación en λ=1.54 A)
Fig. 1.6 Medición de los espesores de capa FeB y capa total formadas en la superficie de un
acero AISI D2 endurecido por difusión de boro.
EduardoChávezGutiérrez.
‐ 13 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloI
1.4 Resultados y discusiones.
El tratamiento termoquímico de borurización en acero AISI D2, revela la formación de
las capas FeB/Fe2B en un proceso de difusión controlado sobre la superficie del acero.
Las figs. 1.7, 1.8, 1.9, 1.10 muestran el crecimiento de las capas FeB y Fe2B para las
condiciones experimentales establecidas, donde se observa que la morfología de las
capas formadas en la superficie de un acero AISI D2 borurizado es semi-aserrada,
debido
a
la
concentración
de
elementos
de
aleación
en
el
substrato.
Característicamente, existe difusión de Cr desde el substrato hacia los boruros
formados, sustituyendo al hierro con tendencia a formar compuestos tipo CrB y Cr2B.
Los elementos de aleación presentes en el acero reducen el crecimiento de las capas
boruradas debido a la formación de una barrera de difusión, disminuyendo el flujo activo
de boro en estas zonas inhibiendo el crecimiento de las capas.
Según la teoría de crecimiento de boruros en materiales ferrosos (Martini et al., 2004),
la formación de la capa FeB es consecuencia de la transformación de los cristales Fe2B
en el exterior de la muestra debido al alto potencial de boro en la superficie. Al
incrementar la temperatura y tiempo de tratamiento, la capa FeB crece a partir de
cristales compactos tipo Fe2B haciéndose más profunda.
El crecimiento de la capa FeB induce el incremento de esfuerzos mecánicos en la
interfase FeB/Fe2B debido a las distorsiones de red en esta zona (Taktak, 2006).
EduardoChávezGutiérrez.
‐ 14 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloI
a)
b)
c)
d)
Fig. 1.7 Microfotografía de la sección transversal de un acero AISI D2 borurizado a la
temperatura de 1223 K con tiempos de exposición de: a) 1 h , b) 3 h , c) 5 h y d) 7 h .
EduardoChávezGutiérrez.
‐ 15 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloI
a)
b)
c)
d)
Fig. 1.8 Microfotografía de la sección transversal de un acero AISI D2 borurizado a la
temperatura de 1253 K con tiempos de exposición de: a) 1 h , b) 3 h , c) 5 h y d) 7 h .
EduardoChávezGutiérrez.
‐ 16 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloI
a)
b)
c)
d)
Fig. 1.9 Microfotografía de la sección transversal de un acero AISI D2 borurizado a la
temperatura de 1273 K con tiempos de exposición de: a) 1 h , b) 3 h , c) 5 h y d) 7 h .
EduardoChávezGutiérrez.
‐ 17 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloI
a)
b)
c)
d)
Fig. 1.10 Microfotografía de la sección transversal de un acero AISI D2 borurizado a la
temperatura de 1223 K con tiempos de exposición de: a) 1 h , b) 3 h , c) 5 h y d) 7 h .
EduardoChávezGutiérrez.
‐ 18 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloI
Los resultados del ensayo de XRD (fig.1.11) confirman que los boruros de hierro FeB y
Fe2B, además de los boruros de cromo CrB y Cr2B se forman en la superficie del acero
AISI D2 sometido al tratamiento termoquímico de borurización en polvo.
La composición química de Cr en un acero AISI D2 es del 13 wt % Cr, el Cr reacciona
con los átomos de boro durante el tratamiento de borurización, formando boruros de
cromo con características cristalográficas similares a los boruros de hierro FeB y Fe2B.
Estudios previos sugieren que el cromo se acumula en la parte más externa la capa
FeB/Fe2B (Badini et al. 1989).
Fig. 1.11 Patrón de difracción de rayos X (XRD) obtenido en la superficie de un acero AISI D2
borurizado a la temperatura de 1273 K con 7 h de exposición.
EduardoChávezGutiérrez.
‐ 19 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloI
El crecimiento de las capas FeB-Fe2B en función del tiempo de tratamiento se
representa en la fig. 1.12. La tendencia de crecimiento parabólico se mantiene en el
intervalo de tiempo establecido para el acero AISI D2 borurizado.
Espesor de la capa FeB (µm) 2
a)
2500
1223 K
1253 K
1273 K
1323 K
2000
1500
1000
500
0
0
b)
10
15
20
Tiempo de exposición (x103)(s)
25
30
10
15
20
Tiempo de exposición (x103)(s)
25
30
16000
1223 K
14000
Espesor de la capa total (µm) 2
5
1253 K
1273 K
12000
1323 K
10000
8000
6000
4000
2000
0
0
5
Fig. 1.12 Crecimiento de las capas superficiales en función del tiempo de exposición:
a) FeB, b) (FeB + Fe2B)
EduardoChávezGutiérrez.
‐ 20 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloI
Se estimaron los valores de las constantes de crecimiento de las capas FeB y capa total
( k FeB , k1 respectivamente) a partir de la pendiente de la rectas mostrada en la fig. 1.12, en
función de la temperatura de tratamiento (tabla 1.1).
Brackman et al., (1989), estableció la contribución del tiempo de incubación (t0 ) , el cual,
es menor que el tiempo más corto de tratamiento utilizado. Los resultados
experimentales del presente trabajo muestran este comportamiento para la capa FeB y
Fe2B; a mayor tiempo de tratamiento, menor es el tiempo de incubación del boro en
ambas capas (tabla 1.1). Además, el tiempo de incubación denota la formación en
primera instancia de la capa Fe2B.
Tabla 1.1 Valores experimentales de la constante de crecimiento y tiempo de incubación capa
FeB y capa total, en función de la temperatura de tratamiento.
Temperatura
(K )
( K FeB )
(t0FeB )
 m / s
2
(s)
( K1 )
(t0 )
2
(s)
 m / s
14
1534.88
1.51 10
14
1481.74
2.18 10
14
1418.87
3.51 10
14
1016.22
5.80 10
1223
2.54 10
1253
3.61 10
1273
7.31 10
1323
9.79 10
13
993.81
13
593.29
13
495.57
13
419.30
El coeficiente de difusión de las capas FeB y Fe2B ( DFeB y DFe B ) para cada
2
temperatura de tratamiento, se evaluó mediante las ecuaciones (1.19) y (1.20) . Los
coeficientes de difusión del boro ( DFeB y DFe B ) se manifiestan mediante la expresión de
2
Arrhenius como se muestra en la fig. 1.13 y se resumen en la tabla 1.2.
EduardoChávezGutiérrez.
‐ 21 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloI
‐25
a)
Ln DFeB= ‐23354T‐1 ‐ 7.6647
R² = 0.9587
Ln DFeB (m2/s)
‐25.5
‐26
‐26.5
‐27
7.4
7.6
7.8
8
8.2
8.4
Inverso de la Temperatura (x10‐4)(K‐1)
b)
‐25
Ln DFe2B = ‐21861T‐1 ‐ 8.9986
R² = 0.9707
Ln DFe2B (m2/s)
‐25.5
‐26
‐26.5
‐27
7.4
7.6
7.8
8
8.2
8.4
Inverso de la Temperatura (x10‐4)(K‐1)
Fig. 1.13 Dependencia entre los coeficientes de difusión del boro en el sistema FeB/Fe2B y la
temperatura de tratamiento: a) capa FeB, b) capa Fe2B.
EduardoChávezGutiérrez.
‐ 22 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloI
 194kJ mol1  2 -1
DFeB  4.7 104 exp  
  m s  (1.21)
RT


Por lo que:
DFe2B
 182kJ mol1  2 -1
 1.2 10 exp  
  m s  (1.22)
RT


4
Tabla 1.2 Valores del coeficiente de difusión en FeB y Fe2B obtenidos respecto a las
temperaturas de tratamiento.
Temperatura
(K )
DFeB  m 2 s 1 
DFe2B  m2 s 1 
1223
1253
1273
1323
2.39 10 12
3.77 10 12
5.06 10 12
10.1 10 12
2.13 10 12
3.27 10 12
4.30 10 12
8.24 10 12
La energía de activación de ambas capas en el rango de temperaturas, sugiere una
difusión homogénea, los factores pre-exponenciales son altamente dependientes de la
composición del acero endurecido por borurización (Matiasovsky et al., 1988).
El valor relativamente alto de la energía de activación propuesto en las ecuaciones
(1.21) y (1.22) , se puede atribuir a la formación de las fases CrB y/o Cr2B además de las
capas FeB y Fe2B, y a la concentración de elementos de aleación en el substrato.
Utilizando las ecuaciones (1.19) y (1.20) , se estimó el valor de los espesores de capa
FeB y Fe2B para establecer la validez del modelo de difusión:

12
l  2t1 2 a3 DFe2B /  a4  a3 / 2  k / 1  t0Fe2B T  / t    a2 / 2  kFeB / 1  t0FeB T  / t 

12
  m
(1.23)
u  2t1 2 a1DFeB /  a4  a3 / 2  k / 1  t0Fe2B T  / t    a3 / 2  a2  a1 / 2  kFeB / 1  t0FeB T  / t 
  m
EduardoChávezGutiérrez.
‐ 23 -
12
12
(1.24)
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloI
FeB
Los parámetros kFeB / 1  t0 T  / t 
12
12
Fe B
y k / 1  t0 2 T  / t  son dependientes de la
temperatura de tratamiento, por lo que se expresan de la forma siguiente (ver fig. 1.14):
12
 T   k / 1  t0Fe B T  / t 
2
 2x10 T8.1821  m s 1 2  (1.25)
 T   k FeB / 1  t0FeB T  / t   8x10 T8.218  m s1 2  (1.26)
12
El Parámetro ƞ (T) (x10‐6)
a)
0.90
0.75
ƞ(T) = k/[1‐t0Fe2B(T) /t]1/2 = 2x10‐26 T8.1821
R² = 0.9757
0.60
0.45
0.30
0.15
0.00
1200
El Parámetro ε (T) (x10‐6)
b)
0.45
1240
1280
Temperatura (K)
1320
1360
1320
1360
ε(T) = kFeB/[1‐t0FeB(T) /t]1/2 = 8x10‐27 T8.218
R² = 0.8751
0.30
0.15
0.00
1200
1240
1280
Temperatura (K)
Fig. 1.14 Parámetro a) η (T) y b) ε (T) en función de la temperatura de tratamiento.
EduardoChávezGutiérrez.
‐ 24 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloI
Por consiguiente, las ecuaciones (1.25) y (1.26) pueden rescribirse como sigue (fig.
1.13):
l  2 t 1 2 a 3 D Fe 2 B /  a 4  a 3 / 2  T    a 2 / 2   T   m 
u  2t 1 2 a1 DFeB /
 a
 a3 / 2  T    a3 / 2  a2  a1 / 2   T 
12
4
(1.27)
m 
(1.28)
Estas expresiones, pueden utilizarse como una herramienta para estimar los espesores
de capa FeB/Fe2B, en función de posibles aplicaciones. En aceros borurizados con alto
contenido de elementos de aleación, son deseables espesores de capa de 15-20 μm,
para aplicaciones en herramientas empleadas en la fabricación de piezas sin arranque
de viruta (Fichtl, 1981).
Los valores estimados del espesor de capa FeB/Fe2B obtenidos a través de las
ecuaciones (1.27) y (1.28) muestran buena concordancia respecto a los resultados
experimentales, como ejemplifica la tabla 1.3.
EduardoChávezGutiérrez.
‐ 25 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloI
Tabla 1.3 Valores de los espesores de capa FeB y capa total para las condiciones
experimentales de tratamiento en un acero AISI D2 borurizado.
Capa FeB
Capa FeB
Capa total
Capa total
experimental
estimado
experimental
estimado
1
10.68±2.77
9.54
24.11±2.69
21.08
3
17.92±4.44
16.52
38.26±5.25
36.52
5
24.01±3.20
21.33
46.09±5.97
47.15
7
27.96±5.19
25.24
54.47±5.65
55.79
1
14.19±3.95
12.92
29.80±3.92
28.19
3
23.76±5.69
22.38
46.69±6.04
48.83
5
28.98±7.22
28.89
60.45±7.97
63.05
7
32.76±6.14
34.18
69.99±7.24
74.60
1
18.54±3.68
13.31
40.19±5.91
29.26
3
25.92±5.20
23.06
53.23±6.35
50.68
5
29.02±7.64
29.77
77.57±8.62
65.43
7
35.11±6.70
35.22
84.13±11.29
77.42
1
26.04±6.01
21.66
55.58±7.47
45.55
3
31.64±8.33
37.52
79.39±9.79
78.90
5
35.24±8.85
48.44
93.46±11.89
101.86
7
39.97±9.98
57.32
105.88±13.15
120.52
Tiempo de
Temperatura
exposición
(K)
(h)
(μm)
(μm)
(μm)
(μm)
1223
1253
1273
1323
EduardoChávezGutiérrez.
‐ 26 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloI
Conclusiones
La cinética de crecimiento de las capas FeB/Fe2B formadas en la superficie de un acero
AISI D2 borurizado se estimó a temperaturas de 1223, 1253, 1273 y 1323 K y tiempos
de exposición de 1, 3 ,5 y 7 h . Los resultados obtenidos muestran un proceso de
difusión controlado respecto a la evolución de las capas superficiales formadas. La
presencia de los elementos de aleación en el substrato reduce el crecimiento de la capa
FeB y capa total. El modelo de difusión propuesto se utilizó para estimar los coeficientes
de difusión de las capas FeB/Fe2B y se extendió a evaluar los espesores de las capas
borurizadas para el conjunto de datos experimentales; los cuales, muestran buena
concordancia respecto a los resultados experimentales obtenidos.
EduardoChávezGutiérrez.
‐ 27 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloII
Capítulo II
Ensayos de micro y nanodureza sobre capas tipo FeB y Fe2B.
El presente Capítulo describe los gradientes de dureza a través del espesor de las
capas FeB-Fe2B formadas en la superficie de un acero AISI D2 hasta el sustrato. La
dureza característica se describe mediante ensayos de microdureza Vickers y
nanodureza Berkovich. Se evalúa el comportamiento del módulo de elasticidad
mediante la técnica de nanoindentación instrumentada. Adicionalmente, se establece el
índice de plasticidad de las capas boruradas mediante la relación  H E  , así como el
coeficiente de deformación elástica  K e  y el parámetro de disipación de energía  K d  .
EduardoChávezGutiérrez
‐ 28 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloII
2.1 Introducción
El proceso de borurización en materiales ferrosos y diversos tipos de aleaciones, tiene
la finalidad de incrementar drásticamente propiedades mecánicas superficiales, tales
como la dureza, la resistencia al desgaste y corrosión de componentes ingenieriles.
Ensayos de micro y nanodureza han sido ampliamente utilizados para caracterizar el
comportamiento mecánico de componentes microestructurales. Estos ensayos son
útiles para estimar la variabilidad de propiedades mecánicas en diversas zonas de una
muestra. Los ensayos consisten en aplicar una carga de prueba mediante un indentador
sobre la superficie a evaluar. La geometría del indentador para estos ensayos
comúnmente es tipo piramidal.
La estimación de la nanodureza se realiza mediante la técnica de nanoindentación
instrumentada, donde el análisis se efectúa a través de las curvas carga  P  profundidad de indentación  hc  formadas durante la prueba.
Un tema esencial de investigación en el análisis de curvas  P  -  hc  es la evaluación de
propiedades mecánicas como el módulo de elasticidad  E  y la dureza  H  (Casals y
Alcalá, 2005). Estas propiedades se establecen en función de la respuesta del material
a la aplicación de una carga durante la indentación, la recuperación durante la descarga
y el valor del área residual.
Antunes et al., (2007) sugiere que la evaluación de propiedades mecánicas en capas
y/o recubrimientos requiere el uso de cargas bajas de indentación, para obtener la
contribución específica de la capa o recubrimiento.
EduardoChávezGutiérrez
‐ 29 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloII
En el presente Capítulo, se determina la dureza característica de boruros de hierro tipo
FeB-Fe2B formados en la superficie de un acero AISI D2 endurecido por difusión de
boro. Se describen los gradientes de dureza a escala micro y nano con un indentador
tipo Vickers y Berkovich respectivamente, utilizando una carga constante de indentación
a través del espesor de las capas para establecer la influencia del indentador en los
valores de dureza de las capas.
También, se evalúa el comportamiento del módulo de elasticidad  E  a lo largo de las
capas FeB-Fe2B mediante la técnica de nanoindentación instrumentada, empleando un
indentador tipo Berkovich bajo una carga constante de indentación.
EduardoChávezGutiérrez
‐ 30 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloII
2.2 Ensayo de microdureza Vickers.
El ensayo de dureza Vickers es una prueba no destructiva que permite evaluar la
resistencia a la deformación plástica de diversos materiales basado en la técnica de
indentación. El método consiste en aplicar una carga sobre una superficie durante un
tiempo de 10 a 15 s, posteriormente el indentador es removido dejando una huella de
indentación sobre la superficie.
Para ensayos de microdureza Vickers se emplean cargas en el rango de 0.098 a
9.81 N . La metodología de ensayo está definida por la noma ASTM E384. El indentador
característico para este ensayo es tipo piramidal de base cuadrada, cuyo ángulo entre
sus caras opuestas es 136° (fig. 2.1).
Fig. 2.1 Esquema representativo de la geometría de un indentador tipo Vickers.
La relación carga-área residual de indentación, establece el valor de dureza estimado.
Por consideraciones geométricas, el área residual de indentación se expresa en función
de la diagonal de indentación  d  , y se determina por microscopía óptica al medir la
distancia entre los vértices opuestos de la huella de indentación.
EduardoChávezGutiérrez
‐ 31 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloII
El valor de dureza Vickers, se define mediante la siguiente expresión:
HV 
P
d

 2
2

 sin  68 

 P
 1.8544  2   MPa  (2.1)
d 
La expresión (2.1) considera la mitad del valor del ángulo entre las caras opuestas del
indentador, donde H V se expresa en MPa , si la carga de prueba  P  está dada en N , y
la diagonal de indentación  d  en mm .
EduardoChávezGutiérrez
‐ 32 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloII
2.3 Ensayo de nanodureza Berkovich.
La técnica de nanoindentación instrumentada constituye un método potente para
determinar propiedades mecánicas a escala nanométrica. En años recientes, esta
técnica ha sido utilizada para estimar las propiedades mecánicas en las capas de
boruros de hierro formadas en la superficie de aceros endurecidos por borurización
(Culha et al., 2008).
A través del análisis de curvas carga  P  - profundidad de indentación  hc  , se estiman
las propiedades de módulo de elasticidad  E  y dureza  H  . La evaluación de estos
parámetros mecánicos se realiza mediante el modelo de contacto elástico, que se
describe a continuación.
2.3.1 Modelo de contacto elástico.
En el análisis de curvas  P  -  hc  (fig. 2.2) se asume que la deformación en la zona de
descarga es puramente elástica. El contacto entre el indentador y la superficie puede
estudiarse mediante un modelo analítico para indentación en medios elásticos.
El efecto del indentador en la curva  P  -  hc  puede describirse definiendo un módulo
elástico reducido  Er  :
1 1  v 2 1  vi2


Er
E
Ei
(2.2)
donde  E  y  v  son el módulo de elasticidad y la razón de Poisson de la muestra;  Ei 
y  vi  son los mismos parámetros para el indentador.
La sección transversal de una indentación se muestra en la fig.2.3.
EduardoChávezGutiérrez
‐ 33 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloII
Fig. 2.2 Representación esquemática de la curva  P  -  hc  en un ensayo de nanoindentación.
Fig. 2.3 Representación esquemática de la sección transversal de una indentación.
EduardoChávezGutiérrez
‐ 34 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloII
Durante la carga, la profundidad total de indentación  h  se expresa como:
h  hc  hs
(2.3)
donde h es la distancia vertical a lo largo de la cual se presenta la profundidad de
contacto, hs es el desplazamiento vertical desde la superficie al perímetro de contacto y
hc es la profundidad de penetración del indentador bajo la carga. Una vez removido el
indentador, la profundidad resultante de la indentación por la acción de la carga es h f .
El módulo de elasticidad se evalúa basándose en la ecuación de contacto de Hertz, por
lo que:
Er 
S 
2 A
(2.4)
donde A es el área de contacto y S es la rigidez en la curva de descarga:
S  dP dh
(2.5)
Según Oliver y Pharr, (1992), la medición de la rigidez sobre la curva de descarga
puede expresarse como sigue:
P  B h  hf
Siendo P la carga,  h  h f


m
(2.6)
es el desplazamiento elástico, B y m son constantes del
material. Los valores de B , m y h f son estimados por el método de mínimos cuadrados
para la curva de descarga.
Para este análisis se asume que la geometría del indentador se establece en función de
su área:
A  A  h  (2.7)
Está expresión relaciona el área de sección transversal del indentador y la distancia a
la punta del mismo. El área de contacto a carga máxima está definida por:
A  A  hc  (2.8)
EduardoChávezGutiérrez
‐ 35 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloII
La profundidad de contacto  hc  a carga máxima se expresa como sigue:
hc  hmax    hmax  hi  (2.9)
donde hmax es la profundidad de contacto máxima y hi es la profundidad en la cual hace
tangencia la curva de descarga a carga máxima. El parámetro  es una constante en
función de la forma de la punta del indentador y se considera igual a 0.75 para un
indentador tipo Berkovich; los valores de hmax y hi son obtenidos de los datos
experimentales de la curva  P  -  hc  .
El área representativa  A  en función de  hc  , depende de la geometría del indentador.
Para el caso de un indentador tipo Berkovich cuya geometría es piramidal con un
ángulo de 65.3° entre el eje de simetría y sus caras (ver fig. 2.4), se expresa como
sigue:
A  hc   5.196 hc2 tan 2  65.3   24.5hc2
(2.10)
Entonces, la dureza queda definida de la siguiente forma:
H 
Pmax
Ac
(2.11)
donde Pmax es la carga de indentación y Ac es el área de contacto a carga máxima.
Fig. 2.4 Esquema representativo de la geometría de un indentador tipo Berkovich.
Esta definición de dureza difiere del concepto tradicional que considera el área como el
área residual medida después de remover el indentador, mientras que en ensayos de
nanoindentación el área utilizada es el área de contacto bajo carga máxima.
EduardoChávezGutiérrez
‐ 36 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloII
Adicionalmente, mediante el análisis de curvas
 P  -  hc 
se estima el trabajo W 
realizado durante la indentación, en función de la deformación elástica y plástica del
espécimen (fig. 2.5).
El trabajo total WT  debido a la deformación elástica y plástica se estima por medio de
la integral de una función F de la curva de carga, teniendo los valores de 0 como límite
inferior de integración y la profundidad máxima de contacto  hmax  como límite superior
de integración:
WT  
hmax
0
F  h  dh (2.12)
El trabajo debido a la deformación elástica Welast  se determina mediante la integral de
la curva de descarga; mientras que el trabajo debido a la deformación plástica Wplast 
se obtiene mediante la siguiente expresión:
W plast  WT  Welast
(2.13)
Fig. 2.5 Esquema representativo del trabajo W  en función de la curva  P  -  hc  , donde
WT  W plast  Welast
.
EduardoChávezGutiérrez
‐ 37 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloII
En base a los resultados obtenidos, se obtiene el coeficiente de deformación elástica
 Ke  ,
que se define como la razón entre el trabajo elástico y el trabajo total de
deformación durante la indentación (Fox-Rabinovich et al., 2004):
K e  Welast WT
(2.14)
Finalmente, la energía perdida que se presenta durante la deformación plástica
conocida como el parámetro de disipación  K d  , se estima mediante la siguiente
expresión:
Kd  1  Ke
EduardoChávezGutiérrez
(2.15)
‐ 38 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloII
2.4 Procedimiento experimental.
Ensayos de micro y nanodureza se realizaron a lo largo de la sección transversal de las
capas FeB-Fe2B hasta llegar al sustrato, en las muestras del acero AISI D2 borurizado
a las temperaturas de 1223, 1253, 1273 y 1323 K con tiempos de exposición de 1, 3, 5
y 7 h por cada temperatura. Se establecieron perfiles de dureza a una profundidad de
capa de 10, 25, 40, 55, 70, 85, 100, 115, y 130 μm . Las distancias a partir de la
superficie fueron establecidas de acuerdo al espesor de capa total, el tamaño de la
huella de indentación y la carga de prueba.
El conjunto de probetas para realizar la experimentación, se sometió al proceso de
metalografía hasta dejar la superficie completamente plana con acabo espejo, para
garantizar el contacto totalmente perpendicular entre el indentador y la superficie.
Se realizaron ensayos de microdureza mediante el uso de un durómetro marca Wolpert
Group modelo 401MVD (ver fig. 2.6) con una carga constante de indentación de 490
mN Para obtener un perfil estadísticamente confiable, se realizaron 5 mediciones por
cada distancia de indentación.
Para ensayos de nanodureza, se utilizó un equipo de nanoindentación instrumentada
TTX-NHT,CSM Instruments (ver fig. 2.6). Se estableció una carga constante de
indentación de 250 mN y se consideraron 2 curvas
 P  -  hc 
por cada distancia de
indentación, las cuales fueron analizadas mediante el modelo de contacto elástico para
estimar la evolución de la dureza  H  y el módulo de elasticidad  E  .
EduardoChávezGutiérrez
‐ 39 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloII
a)
b)
Fig. 2.6 Equipo utilizado durante los ensayos de dureza: a) Microdurómetro marca Wolpert
Group modelo 401MVD, b) Nanoindentador TTX-NHT, CSM Instruments.
EduardoChávezGutiérrez
‐ 40 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloII
2.5 Resultados y discusiones.
Se realizaron indentaciones a escala micro y nano a lo largo de las capas FeB-Fe2B en
las muestras del acero AISI D2 borurado a las temperaturas de 1223, 1253, 1273 y
1323 K con tiempos de exposición de 1, 3, 5 y 7 h por cada temperatura (ver fig. 2.7 y
2.8).
a)
b)
Fig. 2.7 Ensayo de microdureza realizado a través del espesor de las capas FeB-Fe2B formadas
en la superficie de un acero AISI D2 borurizado a la temperatura de: a) 1273 K -5 h ,
b) 1323 K -7 h .
a)
b)
Fig. 2.8 Ensayo de nanodureza realizado a través del espesor de las capas FeB-Fe2B formadas
en la superficie de un acero AISI D2 borurizado a la temperatura de: a) 1253 K -5 h ,
b) 1323 K -7 h .
EduardoChávezGutiérrez
‐ 41 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloII
2.5.1 Microdureza Vickers.
La distribución de los valores de dureza de las capas formadas en el acero AISI D2
borurizado se muestran en las figs. 2.9 y 2.10 para micro y nanodureza
respectivamente.
30
30
t = 1 h
t = 3 h
t = 5 h
t = 7 h
20
t = 1 h
t = 3 h
t = 5 h
t = 7 h
25
Microdureza (GPa)
Microdureza (GPa)
25
15
10
20
15
10
5
5
0
0
0
50
100
Distancia desde la superficie (µm)
150
0
a)
150
b)
30
30
t = 1 h
t = 3 h
t = 5 h
T = 7 h
20
15
t = 1 h
t = 3 h
t = 5 h
t = 7 h
25
Microdureza (GPa)
25
Microdureza (GPa)
50
100
Distancia desde la superficie (µm)
10
5
20
15
10
5
0
0
0
50
100
150
Distancia desde la superficie (µm)
c)
200
0
50
100
150
200
Distancia desde la superficie (µm)
d)
Fig. 2.9 Perfiles de microdureza obtenidos a una carga de 490 mN en un acero AISI D2
borurizado a la temperatura de: a) 1223 K , b) 1253 K , c) 1273 K , d) 1323 K .
EduardoChávezGutiérrez
‐ 42 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloII
2.5.2 Nanodureza Berkovich.
25
t = 1 h
t = 3 h
t = 5 h
t = 7 h
20
15
Nanodureza (GPa)
Nanodureza (GPa)
25
10
5
t = 1 h
t = 3 h
t = 5 h
t = 7 h
20
15
10
5
0
0
0
20
40
60
0
80
Distancia desde la superficie (µm)
100
150
Distancia desde la superficie (µm)
a)
b)
25
t = 1 h
t = 3 h
t = 5 h
t = 7 h
20
15
10
5
Nanodureza (GPa)
25
Nanodureza (GPa)
50
t = 1 h
t = 3 h
t = 5 h
t = 7 h
20
15
10
5
0
0
0
50
100
150
Distancia desde la superficie (µm)
c)
0
50
100
Distancia desde la superficie (µm)
150
d)
Fig. 2.10 Perfiles de nanodureza obtenidos a una carga de 250 mN en un acero AISI D2
borurizado a la temperatura de: a) 1223 K , b) 1253 K , c) 1273 K , d) 1323 K .
EduardoChávezGutiérrez
‐ 43 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloII
Se establece que el valor de dureza de la capa de boruro formada en la superficie del
acero AISI D2 es considerablemente mayor que la dureza del sustrato, lo que se
establece como consecuencia de la presencia de las fases FeB, Fe2B, CrB y Cr2B, que
fueron confirmadas por difracción de rayos X (XRD), ver fig. 1.10.
Los perfiles de dureza están conformados por tres regiones, las cuales son: i) capa de
boruro de hierro formada en la superficie del sustrato, ii) zona de difusión constituida por
carburos primarios, iii) sustrato.
Los valores obtenidos para micro y nanodureza son dependientes de la carga de
indentación, cuyos valores oscilan en el rango de 10-30% (Qian et al., 2005). Para el
presente trabajo los valores obtenidos por micro y nanodureza difieren en el rango de
10-15%, siendo mayores los obtenidos por microdureza. Los valores de dureza
obtenidos a escala micro y nano dependen directamente del área de indentación: para
microdureza, se establece el área residual obtenida después de remover el indentador,
medida por microscopía óptica tradicional; mientras que para nanodureza, se considera
el área de contacto entre el indentador y la superficie bajo carga máxima, lo que puede
inducir diferencias en los valores de dureza obtenidos.
Los valores más estables de dureza se establecen a la temperatura de 1273 K donde
se muestra mínima variación dentro del rango de 10 a 55 μm (22 ±2.34 GPa). Para las
temperaturas 1223 y 1253 K , la dureza se mantiene casi constante hasta 25 μm , ya que
el espesor de capa es notablemente menor.
Al incrementar la temperatura a 1323 K para tiempos de exposición de 5 y 7 h , la dureza
y el módulo de elasticidad de la capa borurizada disminuyen para ambos ensayos. Este
|resultado de amplios tiempos de exposición a altas temperaturas de tratamiento
(Genel et al., 2003).
EduardoChávezGutiérrez
‐ 44 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloII
2.5.3 Módulo elástico.
La fig. 2.11 muestra el comportamiento del módulo de elasticidad para las condiciones
de tratamiento del acero AISI D2 endurecido.
400
t = 1 h
t = 3 h
t = 5 h
t = 7 h
350
300
Módulo Elástico (GPa)
Módulo Elástico (GPa)
400
250
200
t = 1 h
t = 3 h
t = 5 h
t = 7 h
350
300
250
200
150
150
0
20
40
60
Distancia desdee la superficie (µm)
0
80
a)
150
b)
450
450
t = 1 h
t = 3 h
t = 5 h
t = 7 h
400
350
Módulo Elástico (GPa)
Módulo Elástico (GPa)
50
100
Distancia desde la superficie(µm)
300
250
200
t = 1 h
t = 3 h
t = 5 h
t = 7 h
400
350
300
250
200
150
150
0
50
100
Distancia desde la superficie (µm)
c)
150
0
50
100
Distancia desde la superficie (mµ)
150
d)
Fig. 2.11 Comportamiento del módulo de elasticidad obtenido a una carga de 250 mN a lo largo
de las capas FeB-Fe2B en un acero AISI D2 borurizado a la temperatura de: a) 1223 K ,
b) 1253 K , c) 1273 K , d) 1323 K .
EduardoChávezGutiérrez
‐ 45 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloII
El comportamiento del módulo de elasticidad describe la anisotropía de los boruros de
hierro, que varía en función de la distancia de indentación. El valor de  E  para la capa
FeB es notablemente mayor que en Fe2B, como consecuencia de la dureza
característica de ambas capas; es decir, la capa FeB presenta mayor resistencia a la
deformación plástica que la capa Fe2B.
Los valores de  H  y  E  evaluados por nanoindentación, dependen directamente del
efecto “pile-up” o “sink-in” presente al realizar la indentación. Bolshakov y Pharr (1998,
citados en Habbab et al., 2006) sugieren que al presentarse el efecto “pile-up”, el valor
del área obtenida por el análisis de Oliver y Pharr (1992), puede subestimar el valor del
área real de contacto hasta en un 60%, lo que origina errores considerables en los
valores estimados.
El método analítico utilizado durante la experimentación en el acero AISI D2 borurizado,
sugiere que al realizar la indentación se presenta el efecto “sink in”, lo cual se confirmó
mediante el ensayo de microscopía de fuerza atómica (AFM por sus siglas en inglés),
fig. 2.12. Por lo tanto los valores de  H  y  E  obtenidos a través de la formulación de
Oliver y Pharr son confiables.
100
(nm)
‐100
‐300
‐500
‐700
0
a)
1
2
3
4
5
(µm)
6
7
8
b)
Fig. 2.12 Ensayo de AFM realizado en el acero AISI D2 borurizado a la temperatura de
1273 K -7 h : a) micrografía del ensayo de nanoindentación realizado, b) presencia del efecto
“sink in” en el ensayo de nanoindentación.
EduardoChávezGutiérrez
‐ 46 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloII
2.5.4 Razón H E .
La fig. 2.13 muestra la relación entre las propiedades anteriormente evaluadas ( H y E ),
que define el índice de plasticidad a lo largo de las capas FeB y Fe2B para el conjunto
0.07
0.07
0.06
0.06
0.05
0.05
Razón H/E
Razón H/E
de datos experimentales.
0.04
0.03
1h
3h
5h
7h
0.02
0.01
0.04
0.03
1h
3h
5h
7h
0.02
0.01
0
0
0
0
20
40
60
80
Distancia desde la superficie (µm)
20
40
60
80
100
Distancia desde la superficie (µm)
b)
0.08
0.07
0.07
0.06
0.06
0.05
Razón H/E
Razón H/E
a)
0.05
0.04
1h
3h
5h
7h
0.03
0.02
0.01
120
0.04
0.03
1h
3h
5h
7h
0.02
0.01
0
0
0
20
40
60
80 100
Distancia desde la superficie (µm)
c)
120
0
20
40
60
80 100
Distancia desde la superficie (µm)
120
d)
Fig. 2.13 Comportamiento del índice de plasticidad  H E  obtenido a una carga de 250 mN a lo
largo de las capas FeB-Fe2B en un acero AISI D2 borurizado a la temperatura de: a) 1223 K ,
b) 1253 K , c) 1273 K , d) 1323 K .
EduardoChávezGutiérrez
‐ 47 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloII
Para las capas FeB y Fe2B formadas en el acero AISI D2 borurizado, el valor de H E
se establece en el rango de 0.068-0.022, su valor es máximo a 10 μm de distancia
desde la superficie (en la capa FeB), decrementa su valor a lo largo del espesor de
capa a 115 μm de distancia desde la superficie (en la capa Fe2B). Este comportamiento
establece que la capa FeB es considerablemente más frágil que la capa Fe2B, lo cual
puede ser no deseable en términos de aplicaciones industriales.
En
este
contexto,
Krella
(2011)
establece
el
valor
de
la
relación
H E
para recubrimientos tipo TiN y Cr-N, depositados sobre un acero inoxidable tipo
X6CrNiTi18-10; los cuales, se resumen en la tabla 2.1.
Tabla 2.1 Valores de la relación H E obtenidos para diferentes recubrimientos aplicados en
diversos aceros.
Acero
X6CrNiTi18-10
Recubrimiento TiN200
H E
0.078
TiN500
0.049
X6CrNiTi18-10
CrN200 CrN500
0.080
0.067
AISI D2
FeB
0.066-0.048
Fe2B
0.047-0.022
Fox-Rabinovich et al., (2004), establece que la relación H E puede ser utilizada para
caracterizar el desgaste de un material, por ejemplo: para una aleación AlTiN con
recubrimiento PVD, una mayor relación de H E es equivalente a menor tiempo de
servicio durante operaciones de taladrado para desgaste adhesivo. Por lo que se
sugiere que para este tipo de aplicación, la capa FeB presenta menor tiempo de servicio
respecto a la capa Fe2B.
EduardoChávezGutiérrez
‐ 48 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloII
2.5.5 Trabajo (W).
El trabajo elástico y plástico presente durante los ensayos de nanoindentación a lo largo
de las capas FeB y Fe2B formadas en la superficie del acero AISI D2, se muestra en las
40
40
35
35
30
30
Welast x103(pJ)
Welast x103(pJ)
figs. 2.14 y 2.15
25
20
t= 1h
t= 3h
t= 5h
t= 7h
15
10
5
25
20
15
t= 1h
t= 3h
t= 5h
t= 7h
10
5
0
0
0
20
40
60
Distancia desde la superficie (m)
0
80
40
40
35
35
30
30
25
20
t= 1h
t= 3h
t= 5h
t= 7h
15
10
5
100
b)
Welast x103(pJ)
Welast x103(pJ)
a)
20
40
60
80
Distancia desde la superficie (m)
25
20
t= 1h
t= 3h
t= 5h
t= 7h
15
10
5
0
0
0
20
40
60
80
100
Distancia desde la superficie (m)
c)
120
0
20
40
60
80
100
Distancia desde la superficie (m)
120
d)
Fig. 2.14 Comportamiento de Welast  obtenido a una carga de 250 mN a lo largo de las capas
FeB-Fe2B en un acero AISI D2 borurizado a la temperatura de: a) 1223 K , b) 1253 K ,
c) 1273 K , d) 1323 K .
EduardoChávezGutiérrez
‐ 49 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
140
120
120
100
100
80
60
t= 1h
t= 3h
t= 5h
t= 7h
40
20
Wplast x103(pJ)
Wplast x103(pJ)
CapítuloII
20
40
60
Distancia desde la superficie (m)
60
t= 1h
t= 3h
t= 5h
t= 7h
40
20
0
0
0
80
0
80
a)
80
b)
120
100
100
80
Wplast x103(pJ)
Wplast x103(pJ)
20
40
60
Distancia desde la superficie (m)
80
60
t= 1h
t= 3h
t= 5h
t= 7h
40
20
0
60
40
t= 1h
t= 3h
t= 5h
t= 7h
20
0
0
20
40
60
80
100
Distancia desde la superficie (m)
c)
120
0
20
40
60
80
100
Distancia desde la superficie (m)
120
d)

Fig. 2.15 Comportamiento de Wplast
 obtenido a una carga de 250 mN
a lo largo de las capas
FeB-Fe2B en un acero AISI D2 borurizado a la temperatura de: a) 1223 K , b) 1253 K ,
c) 1273 K , d) 1323 K .
El trabajo elástico es mayor en la capa FeB y disminuye a lo largo del espesor de capa
hasta la capa Fe2B (fig. 2.14); en contraste, el trabajo plástico incrementa su valor a
partir de la capa FeB hasta la capa Fe2B (fig. 2.15). Este comportamiento se debe a la
dureza característica de ambas capas, al presentar mayor dureza la capa FeB respecto
a la capa Fe2B, existe mayor deformación plástica en la capa Fe2B.
EduardoChávezGutiérrez
‐ 50 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloII
En función de los datos obtenidos para Welast  y Wplast  , se estimaron los valores de
 Ke 
y  K d  como muestran las figs. 2.16 y 2.17.
0.5
0.4
0.4
0.3
0.3
Ke
Ke
0.5
0.2
0.2
t= 1h
t= 3h
t= 5h
t= 7h
0.1
t= 1h
t= 3h
t= 5h
t= 7h
0.1
0
0
0
20
40
60
Distancia desde la superficie (m)
0
80
20
60
80
100
Distancia desde la superficie (m)
a)
b)
0.6
0.5
0.5
0.4
0.4
0.3
Ke
Ke
40
0.3
0.2
t= 1h
t= 3h
t= 5h
t= 7h
0.2
0.1
t= 1h
t= 3h
t= 5h
t= 7h
0.1
0
0
0
20
40
60
80
100
Distancia desde la superficie (m)
c)
120
0
20
40
60
80
100
Distancia desde la superficie (m)
120
d)
Fig. 2.16 Coeficiente de deformación elástica obtenido a una carga de 250 mN a lo largo de las
capas FeB-Fe2B en un acero AISI D2 borurizado a la temperatura de: a) 1223 K , b) 1253 K ,
c) 1273 K , d) 1323 K .
EduardoChávezGutiérrez
‐ 51 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloII
0.9
0.8
0.8
0.7
0.7
Kd
Kd
0.9
0.6
0.6
t= 1h
t= 3h
t= 5h
t= 7h
0.5
0.4
0
20
40
60
t= 1h
t= 3h
t= 5h
t= 7h
0.5
0.4
0
80
20
40
60
80
100
Distancia desde la superficie (m)
Distancia desde la superficie (m)
a)
b)
0.9
0.8
0.8
0.7
0.7
Kd
Kd
0.9
0.6
t= 1h
t= 3h
t= 5h
t= 7h
0.5
0.4
0.6
t= 1h
t= 3h
t= 5h
t= 7h
0.5
0.4
0
20
40
60
80
100
Distancia desde la superficie (m)
c)
120
0
20
40
60
80
100
120
Distancia desde la superficie (m)
d)
Fig. 2.17 Parámetro de disipación obtenido a una carga de 250 mN a lo largo de las capas FeBFe2B en un acero AISI D2 borurizado a la temperatura de: a) 1223 K , b) 1253 K , c) 1273 K ,
d) 1323 K .
EduardoChávezGutiérrez
‐ 52 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloII
La fig. 2.16 describe el coeficiente de deformación elástica a lo largo de las capas FeBFe2B en el acero AISI D2 borurizado, su valor a partir de la capa FeB es de 0.50 y
disminuye a lo largo del espesor de capa hasta la capa Fe2B, donde su valor es 0.17.
En contraste, el parámetro de disipación de energía durante la deformación plástica
(fig. 2.17), incrementa su valor a partir de la capa FeB hasta la capa Fe2B, en un rango
de 0.49 a 0.82. Estos parámetros definen la capacidad de los boruros de hierro para
disipar la energía mecánica de deformación y adquieren relevancia en términos de
aplicaciones industriales.
La tabla 2.2 resume valores de  K e  y  K d  para recubrimientos aplicados en diferentes
aceros.
Tabla 2.2 Valores de los parámetros  K e  y  K d  obtenidos para recubrimientos aplicados en
diversos aceros.
Acero
AISI 1040
AISI D2
Recubrimiento
 Ke 
PVD TiN
FeB
Fe2B
0.44-0.34
0.50-0.27
0.26-0.17
 Kd 
0.66-0.56
0.73-0.50
0.83-0.74
Fox-Rabinovich et al., (2004), sugiere que en condiciones de desgaste adhesivo, la
capacidad de la superficie de un material para disipar energía de deformación se
traduce en un beneficio: valores altos de
 Kd  ,
corresponden a mayor resistencia al
desgaste y parámetros de fricción bajos.
En base a los resultados obtenidos del parámetro  K d  , se establece que la capa Fe2B
es más deseable respecto a la capa FeB en términos de aplicaciones de desgaste.
EduardoChávezGutiérrez
‐ 53 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloII
Conclusiones.
La dureza característica de las capas FeB-Fe2B se estableció mediante la descripción
de perfiles de dureza a escala micro y nano, desde la superficie de la capa borurizada
hasta el sustrato.
La dureza característica de los boruros de hierro formados en la superficie del acero
AISI D2 es considerablemente mayor que la dureza del sustrato, debido a la presencia
de las capas FeB y Fe2B, donde la capa FeB presenta mayor dureza respecto a la capa
Fe2B.
Los valores más altos y estables de dureza se establecen a la temperatura de 1273 K .
Para la temperatura de 1323 K se decremento el valor de  H  y  E  para tiempos de 5
y 7 h debido al incremento del tamaño de grano por la influencia de la alta temperatura.
La estimación de  H  y  E  depende directamente del área de indentación considerada
(área residual o área de contacto), así como del efecto “pile-up” o”sink-in” presente al
realizar la indentación. El efecto presente para los ensayos de nanoindentación en las
capas FeB y Fe2B es “sink-in”.
El valor de la relación  H E  tiende a disminuir a partir de la capa FeB hasta Fe2B, lo
que índica mayor fragilidad de la capa FeB.
El trabajo W  realizado durante los ensayos de nanoindentación, establece mayor
deformación plástica en la capa Fe2B respecto a FeB debido a la dureza de ambas
capas. Considerando
 Ke 
y
 Kd 
se establece que la capa Fe2B es más deseable
respecto a la capa FeB para aplicaciones de desgaste.
EduardoChávezGutiérrez
‐ 54 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloIII
Capítulo III
Efecto de tamaño de huella en la dureza de capas boruradas.
En el presente Capítulo se estudia la influencia del efecto de tamaño de indentación
(ISE, por sus siglas en inglés) en la dureza de las capas FeB-Fe2B formadas en la
superficie de un acero AISI D2 borurizado.
Mediante la evaluación de 3 modelos empíricos, se analizan los parámetros que
sugieren las causas del efecto ISE, a través de ensayos de nanoindentación
instrumentada que consideran la profundidad de contacto y la carga de prueba.
Asimismo, se establece un valor de dureza real independiente de la carga de
indentación.
EduardoChávezGutiérrez
‐ 55 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloIII
3.1 Introducción.
En ingeniería, la dureza de un material es un criterio de diseño de gran importancia. La
dureza aparente de un material depende directamente de la carga aplicada durante el
ensayo de dureza, especialmente en cerámicos. El valor de dureza disminuye al
incrementar la carga de prueba, conforme aumenta el tamaño de la indentación. A este
fenómeno se le conoce como “efecto de tamaño de indentación” (ISE por sus siglas en
inglés). Por esta razón, es claramente insuficiente considerar el valor de dureza
aparente como criterio de diseño. Es conveniente establecer un valor de dureza real,
independiente de la carga empleada durante el ensayo de dureza.
Asimismo, es importante establecer las causas que originan el efecto ISE. Existen en
literatura diversos autores que han dedicado sus estudios a determinar el origen de este
efecto y contribuyen con modelos empíricos para estimar un valor de dureza
independiente de la carga de prueba.
Para describir la variación del tamaño de indentación respecto a la carga de prueba,
han sido propuestos diversos modelos empíricos como son: el modelo de Meyer, el
modelo de recuperación elástica (REM por sus siglas en inglés), el modelo de
resistencia proporcional del espécimen (PSR por sus siglas en inglés), el modelo de
resistencia proporcional del espécimen modificado (MPSR por sus siglas en inglés), que
involucran determinar un valor de dureza real. Entre otros enfoques, el propuesto por
Hays-Kendall, el que considera la influencia del coeficiente de fricción, también han sido
utilizados para analizar los datos obtenidos de un ensayo de nanoindentación.
EduardoChávezGutiérrez
‐ 56 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloIII
3.2 Modelos de ISE.
Los modelos representativos del efecto ISE son evaluados a través de los datos
experimentales obtenidos del análisis de curvas
 P  -  hc  ,
mediante la técnica de
nanoindentación instrumentada descrita en el Capítulo anterior.
3.2.1 Modelo de Meyer.
El modelo propuesto por Meyer es el más utilizado para describir el efecto ISE. Este
modelo relaciona la carga de prueba y el tamaño de la indentación resultante; se
expresa de la siguiente forma:
Pmax  Ahcn
(3.1)
donde A y n son constantes. Específicamente, el exponente n , es referido como el
coeficiente de endurecimiento por deformación y/o índice de Meyer, el cual se considera
como la medida del efecto ISE. Este efecto se da especialmente en cerámicos frágiles
bajo cargas pequeñas de indentación. El modelo establece que cuando n<2, la dureza
disminuye al aumentar la carga aplicada; si n =2, la dureza es independiente de la carga
aplicada.
Los valores de A y n son obtenidos mediante las gráficas de Pmax  hc , por medio de un
análisis de regresión potencial.
EduardoChávezGutiérrez
‐ 57 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloIII
3.2.2 Modelo de recuperación elástica (REM).
Al indentar una superficie, el material experimenta una recuperación elástica al remover
el indentador, la cual se presenta en la zona que rodea la indentación remanente. Por lo
que el tamaño de la huella se reduce un cierto valor. Considerando este efecto,
Tarkanian et al., (1973, citado en Peng et al., 2004) sugiere que el valor del tamaño de
la indentación debe ser ajustado para obtener el valor de dureza real.
Por lo que:
H0  k
P
 d  d0 
2
(3.2)
donde d 0 es el valor ajustado del tamaño de huella d como consecuencia de la
recuperación elástica y k es una constante dependiente de la geometría del indentador.
El valor de hc obtenido de los ensayos de nanoindentación, se considera como el valor
del tamaño de indentación después de presentarse la recuperación elástica. Para
analizar los datos obtenidos por nanoindentación, la expresión  3.2  puede rescribirse
como sigue:
12
Pmax
 X 1 2 h c  X 1 2 h 0 (3.3)
donde h0 es la corrección para hc y X  H 0 k es una constante relacionada con la
12
dureza real. Los valores de X y h0 son obtenidos de los gráficos de Pmax
contra hc .
El valor de dureza real se estima a partir de X  H 0 k utilizando k  1 24.5 para
ensayos de nanoindentación Berkovich.
EduardoChávezGutiérrez
‐ 58 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloIII
3.2.3 Modelo de resistencia proporcional del espécimen (PSR).
Este modelo fue propuesto por Li y Bradt (1993), el cual considera que la resistencia del
espécimen a la deformación permanente no es constante, se incrementa linealmente
respecto al tamaño de indentación.
W  a1hc (3.4)
donde W es una pequeña parte del valor de la carga de indentación donde no se
presenta deformación permanente, solo deformación elástica; y a1 es una constante
independiente de la carga para un material específico.
Por lo que, la carga efectiva de indentación y el tamaño de la huella de indentación
pueden describirse como sigue:
Peff  Pmax  W  Pmax  a1h c  a2 hc2 (3.5)
donde a1 y a2 son constantes para un material específico. Li y Bradt (1993), sugieren
que estos parámetros definen las propiedades elásticas y plásticas del material de
prueba. Específicamente a2 se relaciona con el valor de dureza real H0 . Para ensayos
de nanoindentación Berkovich H0 pude ser estimada a partir de a2 :
H0 
Peff
P a h
a
(3.6)
 max 12 c  2
2
24.5hc
24.5hc
24.5
expresado de otra forma:
Pmax
 a1  a2 hc
hc
(3.7)
Los valores de a1 y a2 se obtienen a partir de la gráfica de
EduardoChávezGutiérrez
Pmax
respecto a hc .
hc
‐ 59 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloIII
3.3 Procedimiento experimental.
Se realizaron ensayos de nanoindentación Berkovich mediante el uso de un equipo de
nanoindentación instrumentada (TTX-NHT, CSM Instruments).
Los especímenes de prueba fueron colocados en el dispositivo de sujeción diseñado
para este trabajo y se sometieron al proceso metalográfico para obtener una superficie
completamente plana con acabado espejo. Cabe resaltar que dicho dispositivo, se
adapta perfectamente a las condiciones del equipo de nanoindentación,
Los ensayos se realizaron en la zona pura de las capas FeB y Fe2B a una distancia
aproximada desde la superficie de 10 μm (capa FeB) y 40 μm (capa Fe2B), para las
condiciones de tiempo y temperatura de tratamiento del conjunto de datos
experimentales del acero AISI D2 borurizado . Las cargas de indentación utilizadas
fueron de 10, 50, 100, 150, 200, 250 y 300 mN . La relación de Poisson de las capas
FeB y Fe2B se estableció en 0.3.
La distancia establecida entre una indentación y otra, fue de al menos 4 veces el valor
de la diagonal de indentación, para descartar la influencia de una indentación respecto
a otra.
Los datos obtenidos del equipo de nanoindentación instrumentada fueron analizados de
acuerdo al método de contacto elástico, para evaluar el comportamiento de la dureza
 H  , al incrementar la carga de indentación y la profundidad de contacto del indentador.
EduardoChávezGutiérrez
‐ 60 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloIII
3.4 Resultados y discusiones.
Se realizaron ensayos de nanoindentación instrumentada en la zona pura de las capas
FeB y Fe2B formadas en la superficie del acero AISI D2 borurizado, para las
condiciones de tiempo y temperatura del proceso (fig. 3.1).
a)
b)
c)
Fig. 3.1 Ensayos de nanoindentación realizados en el acero AISI D2 borurizado a la
temperatura de 1253 K -7 h : a) capa FeB con cargas de 50, 100,150 y 200 mN ; b) capa Fe2B
con cargas de 10, 50, 100 y150 mN ; c) capa FeB con cargas de 50, 100,150 mN , capa Fe2B
con cargas de 200 y 250 mN .
EduardoChávezGutiérrez
‐ 61 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloIII
El comportamiento de las curvas
 P  -  hc 
obtenidas durante los ensayos de
nanoindentación en el acero AISI D2 borurizado para las diferentes condiciones de
tiempo y temperatura de tratamiento, se muestran en la fig. 3.2 y 3.3.
350
10mN
50mN
100mN
150mN
200mN
250mN
300mN
300
P (mN) 250
200
150
100
50
0
0
150
300
450 600
hC (nm) 750
900 1050
a)
350
10mN
50mN
100mN
150mN
200mN
250mN
300mN
300
P (mN) 250
200
150
100
50
0
0
150
300
450
600
750
900 1050
hC (nm) b)
Fig. 3.2 Figura 3.2 Curvas  P  -  hc  obtenidas en la capa FeB formada en la superficie de un
acero AISI D2 borurizado a la temperatura de: a) 1273 K -7 h , b) 1323 K -7 h .
EduardoChávezGutiérrez
‐ 62 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloIII
350
10mN
50mN
100mN
150mN
200mN
250mN
300mN
300
P (mN) 250
200
150
100
50
0
0
150 300 450 600 750 900 1050
h (nm)
a)
350
10mN
50mN
100mN
150mN
200mN
250mN
300mN
300
P (mN) 250
200
150
100
50
0
0
150 300 450 600 750 900 1050
h (nm) b)
Fig. 3.3 Curvas
 P  -  hc  obtenidas
en la capa Fe2B formada en la superficie de un acero
AISI D2 borurizado a la temperatura de: a) 1273 K -7 h , b) 1323 K -7 h .
Las figuras 3.2 y 3.3 muestran el comportamiento elasto-plástico de las curvas de carga
y descarga para las capas FeB y Fe2B; la diferencia entre las curvas define la
deformación plástica del material.
EduardoChávezGutiérrez
‐ 63 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloIII
La dureza obtenida en las capas FeB y Fe2B para el rango de cargas utilizadas,
muestran un decremento en su valor al incrementar la profundidad de contacto. Por lo
que, la profundidad de contacto depende directamente de la carga de indentación
(fig. 3.4 y 3.5).
25
30
Dureza (GPa)
Dureza (GPa)
25
20
1h
3h
5h
7h
15
10
0
150
20
15
1h
3h
5h
7h
10
300
450 600
hc (nm)
750
0
900
150
30
30
25
25
20
1h
3h
5h
7h
15
10
0
150
450 600
hc (nm)
750
900
750
900
b)
Dureza (GPa)
Dureza (GPa)
a)
300
20
1h
3h
5h
7h
15
10
300
450 600
hc (nm)
c)
750
900
0
150
300
450 600
hc (nm)
d)
Fig. 3.4 Comportamiento de la dureza en función de la profundidad de contacto en la capa FeB
formada en la superficie de un acero AISI D2 borurizado a la temperatura de: a) 1223 K ,
b) 1253 K , c) 1273 K , d) 1323 K .
EduardoChávezGutiérrez
‐ 64 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloIII
1h
3h
5h
7h
20
15
25
Dureza (GPa)
Dureza (GPa)
25
1h
3h
5h
7h
20
15
10
10
0
150
300
450
600
750
0
900 1050
150 300 450 600 750 900 1050
hc (nm)
hc (nm)
a)
b)
1h
3h
5h
7h
Dureza (GPa)
25
20
25
Dureza (GPa)
30
1h
3h
5h
7h
20
15
15
10
10
0
150
300
450 600
hc (nm)
750
c)
900 1050
0
150
300
450 600
hc (nm)
750
900 1050
d)
Fig. 3.5 Comportamiento de la dureza en función de la profundidad de contacto en la capa Fe2B
formada en la superficie de un acero AISI D2 borurizado a la temperatura de: a) 1223 K ,
b) 1253 K , c) 1273 K , d) 1323 K .
EduardoChávezGutiérrez
‐ 65 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloIII
3.4.1 Modelo de Meyer.
Se utilizó el modelo de Meyer para graficar el comportamiento de la carga aplicada con
respecto a la profundidad de contacto en función de las capas FeB y Fe2B, como
350
350
300
300
250
250
200
Pmax (mN)
Pmax (mN)
muestran las figs. 3.6 y 3.7.
200
150
1h
3h
5h
7h
100
50
150
1h
3h
5h
7h
100
50
0
0
0
150
300
450 600
hc (nm)
750
900
0
150
350
350
300
300
250
250
200
150
1h
3h
5h
7h
100
50
0
0
150
300
450 600
hc (nm)
c)
450 600
hc (nm)
750
900
b)
750
900
Pmax (mN)
Pmax (mN)
a)
300
200
150
1h
3h
5h
7h
100
50
0
0
150
300
450 600
hc (nm)
750
900
d)
Fig. 3.6 Carga de indentación respecto a la profundidad de contacto en la capa FeB formada en
la superficie de un acero AISI D2 borurizado a la temperatura de: a) 1223 K , b) 1253 K ,
c) 1273 K , d) 1323 K .
EduardoChávezGutiérrez
‐ 66 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloIII
300
300
250
250
200
150
1h
3h
5h
7h
100
50
Pmax (mN)
350
Pmax (mN)
350
200
150
1h
3h
5h
7h
100
50
0
0
0
150
300
450 600
hc (nm)
750
900 1050
0
b)
350
350
300
300
250
250
200
150
1h
3h
5h
7h
100
50
0
Pmax (mN)
Pmax (mN)
a)
150 300 450 600 750 900 1050
hc (nm)
200
150
1h
3h
5h
7h
100
50
0
0
150 300 450 600 750 900 1050
hc (nm)
c)
0
150 300 450 600 750 900 1050
hc (nm)
d)
Fig. 3.7 Carga de indentación respecto a la profundidad de contacto en la capa Fe2B formada
en la superficie de un acero AISI D2 borurizado a la temperatura de: a) 1223 K , b) 1253 K ,
c) 1273 K , d) 1323 K .
Los parámetros del modelo de Meyer A y n se obtuvieron por medio de las gráficas de
las figuras 3.6 y 3.7. Los resultados obtenidos del análisis de regresión potencial,
confirman la presencia del efecto ISE en las capas FeB y Fe2B para el conjunto de
cargas aplicadas, siendo n <2.
EduardoChávezGutiérrez
‐ 67 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloIII
El valor de los parámetros A y n , se resumen en la tabla 3.1. El valor de R 2 muestra
una correlación muy alta, lo que garantiza la confiabilidad de las mediciones realizadas
en los boruros de hierro formados en la superficie del acero AISI D2.
Tabla 3.1 Mejor ajuste para los valores de A y n para las capas FeB y Fe2B en función de las
condiciones de tratamiento del acero AISI D2 borurizado.
Temperatura
(K)
1223
1253
1273
1323
AFe2B
AFeB
Tiempo de
exposición
(h)
nFeB
(mN nmn )
R2
nFe2B
(mN nmn )
R2
1
1.77±0.04
0.0019
0.9987
1.78±0.03
0.0016
0.9992
3
1.73±0.07
0.0027
0.9977
1.75±0.08
0.0021
0.9967
5
1.69±0.02
0.0038
0.9997
1.63±0.03
0.0047
0.9996
7
1.80±0.02
0.0016
0.9997
1.79±0.03
0.0016
0.9992
1
1.78±0.10
0.0016
0.9959
1.75±0.04
0.0018
0.9993
3
1.75±0.05
0.0022
0.9992
1.57±0.08
0.0066
0.9979
5
1.76±0.03
0.0023
0.9993
1.72±0.05
0.0023
0.9988
7
1.74±0.02
0.0028
0.9996
1.71±0.04
0.0027
0.9985
1
1.75±0.03
0.0022
0.9994
1.79±0.05
0.0015
0.9983
3
1.77±0.02
0.0021
0.9997
1.73±0.01
0.0025
0.9998
5
1.84±0.02
0.0014
0.9998
1.67±0.03
0.0037
0.9992
7
1.70±0.01
0.0035
0.9999
1.73±0.03
0.0028
0.9992
1
1.73±0.03
0.0028
0.9994
1.58±0.06
0.0062
0.9964
3
1.83±0.01
0.0016
0.9999
1.59±0.09
0.0063
0.9927
5
1.67±0.05
0.0038
0.9988
1.57±0.02
0.0068
0.9996
7
1.65±0.04
0.0046
0.9986
1.65±0.04
0.0033
0.9986
Diversos estudios han sido conducidos a establecer una relación entre los parámetros
A y n descritos en el modelo de Meyer. Sargent y Page (1978), sugieren que valores
bajos de n se asocian a valores altos de ln A . Sin embargo, la relación entre estos
parámetros no define las causas que originan el efecto ISE.
EduardoChávezGutiérrez
‐ 68 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloIII
La fig. 3.8 establece la relación entre los parámetros n y A obtenidos en las capas FeB
y Fe2B, la cual describe claramente que valores bajos de A se asocian a valores altos
de n .
Indice de Meyer (n)
1.9
1.85
FeB
1.8
F́e2B
1.75
1.7
1.65
1.6
1.55
1.5
0
0.001
0.002
0.003
0.004
0.005
0.006
0.007
0.008
A (mN / nm2)
Fig. 3.8 Relación de los parámetros A y n del modelo de Meyer en el acero AISI D2 borurizado
en función de las condiciones de tratamiento establecidas.
EduardoChávezGutiérrez
‐ 69 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloIII
3.4.2 Modelo de recuperación elástica (REM).
El modelo de recuperación elástica establece que la recuperación elástica presente
después de remover el indentador, reduce el tamaño de la huella de indentación y el
valor de la profundidad de contacto. Los parámetros establecidos en este modelo, se
20
18
16
14
12
10
8
6
4
2
0
P1/2 (mN1/2)
P1/2 (mN1/2)
12
obtuvieron de la gráfica Pmax
vs hc , como se muestra en las figs.3.9 y 3.10.
1h
3h
5h
7h
0
150
300
450 600
hc (nm)
750
20
18
16
14
12
10
8
6
4
2
0
900
1h
3h
5h
7h
0
150
20
18
16
14
12
10
8
6
4
2
0
1h
3h
5h
7h
0
150
300
450 600
hc (nm)
c)
450 600
hc (nm)
750
900
b)
P1/2 (mN1/2)
P1/2 (mN1/2)
a)
300
750
900
20
18
16
14
12
10
8
6
4
2
0
1h
3h
5h
7h
0
150
300
450 600
hc (nm)
750
900
d)
Fig. 3. 9 Modelo de recuperación elástica evaluado en la capa FeB formada en la superficie de
un acero AISI D2 borurizado a la temperatura de: a) 1223 K , b) 1253 K , c) 1273 K , d) 1323 K .
EduardoChávezGutiérrez
‐ 70 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
20
18
16
14
12
10
8
6
4
2
0
1h
3h
5h
7h
0
P1/2 (mN1/2)
P1/2 (mN1/2)
CapítuloIII
20
18
16
14
12
10
8
6
4
2
0
150 300 450 600 750 900 1050
hc (nm)
1h
3h
5h
7h
0
150 300 450 600 750 900 1050
hc (nm)
20
18
16
14
12
10
8
6
4
2
0
b)
1h
3h
5h
7h
0
150 300 450 600 750 900 1050
hc (nm)
c)
20
18
16
14
12
10
8
6
4
2
0
P1/2 (mN1/2)
P1/2 (mN1/2)
a)
1h
3h
5h
7h
0
150
300
450 600
hc (nm)
750
900 1050
d)
Fig. 3.10 Modelo de recuperación elástica evaluado en la capa Fe2B formada en la superficie de
un acero AISI D2 borurizado a la temperatura de: a) 1223 K , b) 1253 K , c) 1273 K , d) 1323 K .
EduardoChávezGutiérrez
‐ 71 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloIII
Asimismo, el mejor ajuste de los valores de la recuperación elástica en función del
tamaño de huella de indentación, y el parámetro X del modelo de recuperación elástica,
se muestran en las tablas 3.2 y 3.3
Tabla 3.2 Parámetros del modelo de recuperación elástica obtenidos para la capa FeB en
función de las condiciones de tratamiento del acero AISI D2 borurizado.
Tiempo de
Temperatura
exposición
(K)
(h)
1223
1253
1273
1323
EduardoChávezGutiérrez
X
( x104 )
2
(mN nm )
h0
H0
(nm)
(GPa)
R2
1
3.7636
57.04
15.36
0.9989
3
5
4.3264
4.41
55.83
50.84
17.65
18
0.9969
0.9975
7
3.9601
51.79
16.16
0.9997
1
3.3489
65.01
13.66
0.9976
3
5
3.9204
4.3264
45.51
44.20
16.01
17.65
0.9992
0.9986
7
4.6656
41.42
19.04
0.9985
1
3.7636
63.42
15.36
0.9992
3
5
4.3264
4.6225
42.48
39.46
17.65
18.86
0.9991
0.9999
7
4.2436
58.99
17.32
0.9983
1
4.1616
54.75
16.98
0.9988
3
5
4.6656
3.5721
38.63
76.56
19.04
14.58
0.9998
0.9971
7
4.1616
64.75
16.98
0.997
‐ 72 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloIII
Tabla 3.3 Parámetros del modelo de recuperación elástica obtenidos para la capa Fe2B en
función de las condiciones de tratamiento del acero AISI D2 borurizado.
Tiempo de
Temperatura
exposición
(K)
(h)
1223
1253
1273
1323
X
( x104 )
(mN nm2 )
h0
H0
(nm)
(GPa)
R2
1
3.4225
59.37
13.96
0.9993
3
5
3.3856
3.5344
65.23
79.55
13.81
14.42
0.9963
0.9964
7
3.7249
54.94
15.20
0.9993
1
2.9584
78.83
12.07
0.9993
3
5
3.3489
3.1684
54.89
73.74
13.66
12.93
0.995
0.9981
7
3.6481
63.15
14.89
0.9997
1
3.3124
61.91
13.52
0.9991
3
5
3.6864
3.8025
60.71
61.31
15.04
15.52
0.9989
0.9974
7
4.0000
62.94
16.32
0.9989
1
2.9929
121.49
12.21
0.9935
3
5
3.6864
3.2041
72.43
87.58
15.04
13.07
0.9933
0.9935
7
3.7636
61.62
15.36
0.9975
El factor de corrección del tamaño de huella de indentación, tiene un valor positivo
como consecuencia de la reducción del tamaño de huella por la recuperación elástica.
Los parámetros X y h0 sugieren posible dependencia a las condiciones de tratamiento:
los valores de X aumentan al incrementar el tiempo de exposición, mientras que los
valores de h0 disminuyen. La capa Fe2B presenta mayor recuperación elástica debido a
que la capa FeB tiene mayor resistencia a la deformación plástica. El valor de dureza
real independiente de la carga de prueba en la capa FeB se establece en el rango de
13.66 a 19.04 (GPa) , mientras que en la capa Fe2B es de 12.07 a 16.32 (GPa) .
EduardoChávezGutiérrez
‐ 73 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloIII
3.4.3 Modelo de resistencia proporcional del espécimen (PSR).
El enfoque del modelo PSR sugiere que las propiedades elásticas y plásticas del
espécimen, son parámetros a considerar en el estudio del efecto ISE, los cuales se
determinaron por medio de gráficas Pmax hc vs hc , como se muestra en las figs.3.11
0.45
0.45
0.4
0.35
0.3
0.25
0.2
0.15
0.1
0.05
0
0.4
1h
3h
5h
7h
Pmax/hc(mN/nm)
Pmax/hc(mN/nm)
y 3.12.
0.35
0.3
0.25
0.2
0.15
1h
3h
5h
7h
0.1
0.05
0
0
150
300
450 600
hc (nm)
750
900
0
150
0.45
0.4
0.35
0.3
0.25
0.2
0.15
0.1
0.05
0
1h
3h
5h
7h
0
150
300
450 600
hc (nm)
c)
450 600
hc (nm)
750
900
b)
750
900
Pmax/hc(mN/nm)
Pmax/hc(mN/nm)
a)
300
0.45
0.4
0.35
0.3
0.25
0.2
0.15
0.1
0.05
0
1h
3h
5h
7h
0
150
300
450 600
hc (nm)
750
900
d)
Fig. 3.11 Gráficas Pmax hc vs h c conforme al modelo PSR evaluado en la capa FeB formada en
la superficie de un acero AISI D2 borurizado a la temperatura de: a) 1223 K , b) 1253 K ,
c) 1273 K , d) 1323 K .
EduardoChávezGutiérrez
‐ 74 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloIII
0.35
0.35
0.3
0.3
0.25
0.2
0.15
1h
3h
5h
7h
0.1
0.05
Pmax/hc(mN/nm)
0.4
Pmax/hc(mN/nm)
0.4
0.25
0.2
0.15
1h
3h
5h
7h
0.1
0.05
0
0
0
0
150 300 450 600 750 900 1050
hc (nm)
b)
0.4
0.4
0.35
0.35
0.3
0.3
0.25
0.2
1h
3h
5h
7h
0.15
0.1
0.05
0
Pmax/hc(mN/nm)
Pmax/hc(mN/nm)
a)
150 300 450 600 750 900 1050
hc (nm)
0.25
0.2
1h
3h
5h
7h
0.15
0.1
0.05
0
0
150 300 450 600 750 900 1050
hc (nm)
c)
0
150 300 450 600 750 900 1050
hc (nm)
d)
Fig. 3.12 Gráficas Pmax hc vs h c conforme al modelo PSR evaluado en la capa Fe2B formada
en la superficie de un acero AISI D2 borurizado a la temperatura de: a) 1223 K , b) 1253 K ,
c) 1273 K , d) 1323 K .
EduardoChávezGutiérrez
‐ 75 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloIII
A través de las gráficas anteriores se obtiene el valor de los parámetros descritos en la
ecuación (3.7) , siendo a 2 la pendiente de la recta y a1 la ordenada al origen. Los
valores de a1 , a 2 y H 0 se resumen en las tablas 3.4 y 3.5.
Tabla 3.4 Parámetros del modelo PSR obtenidos para la capa FeB en función de las
condiciones de tratamiento del acero AISI D2 borurizado.
Temperatura
(K)
a1
a2
( x103 )
( x106 )
Tiempo de
exposición
(h)
(mN nm)
1
1223
1253
1273
1323
EduardoChávezGutiérrez
(mN nm )
H0
(GPa)
R2
50.62
369.3
15.07
0.9952
3
5
57.5
51.68
422.9
432.1
17.26
17.63
0.9849
0.9892
7
48.14
386
15.75
0.9992
1
53.39
323.6
13.20
0.9886
3
5
42.15
43.04
384.2
427.6
15.68
17.45
0.9967
0.9942
7
43.69
459.7
18.76
0.9937
1
57.76
365.8
14.93
0.9973
3
5
41.96
42.17
424.2
456.6
17.39
18.63
0.9963
0.9994
7
59.04
415.3
16.95
0.9925
1
53.67
405.1
16.53
0.9953
3
5
41.43
67.81
458.5
343.4
18.71
14.01
0.9993
0.9854
7
65.59
404.9
16.52
0.9863
2
‐ 76 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloIII
Tabla 3.5 Parámetros del modelo PSR obtenidos para la capa Fe2B en función de las
condiciones de tratamiento del acero AISI D2 borurizado.
Temperatura
(K)
a1
Tiempo de
exposición
(h)
(mN nm)
1
48.26
3
1223
1253
1273
1323
3
a2
H0
(GPa)
R2
335.2
13.68
0.9969
53.43
328.5
13.40
0.9812
5
68.66
340.1
13.88
0.9827
7
47.99
363.9
14.58
0.9972
1
58.65
284.1
11.59
0.9972
3
5
41.27
57.2
329.9
305.9
13.46
12.48
0.978
0.9915
7
54.51
356.3
14.54
0.9893
1
49.18
322
13.24
0.9963
3
5
52.78
54.39
359.2
370.8
14.66
15.13
0.9956
0.9889
7
61.03
389
15.87
0.9957
1
88.21
287.3
11.72
0.9644
3
5
64.33
68.2
357.2
309
14.57
12.61
0.97
0.9688
7
55.07
368.8
15.05
0.989
( x10 )
( x106 )
2
(mN nm )
La contribución de las propiedades elásticas y plásticas ( a1 y a 2 respectivamente), así
como los valores de dureza real estimados en función de a 2 , muestran un factor de
correlación muy alto, lo que sugiere la aplicabilidad del modelo PSR para describir el
efecto ISE.
Para el conjunto de cargas aplicadas, el valor de dureza real independiente de la carga
de indentación para la capa FeB se establece en el rango de 13.20 a 18.76 (GPa) ,
mientras que para la capa Fe2B es de 11.59 a 15.87 (GPa) .
EduardoChávezGutiérrez
‐ 77 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloIII
Los resultados mostrados en las tablas 3.2, 3.3, 3.4, y 3.5 establecen que la dureza de
las capas FeB y Fe2B depende claramente de la carga de indentación aplicada; sin
embargo, existe un valor de carga crítica
 PC 
en el cual el valor de H 0 se vuelve
independiente de la carga utilizada. Los valores de  PC  en función de la profundidad
crítica de indentación  hCC  para los modelos REM y PSR, se resumen en la tabla 3.6.
Tabla 3.6 Valores de hCC y PC para los modelos REM y PSR en las capas FeB y Fe2B en
función de las condiciones de tratamiento del acero AISI D2 borurizado.
Temperatura
(K)
Tiempo de
exposición
1223
1253
1273
1323
EduardoChávezGutiérrez
hCC (nm)
Modelo REM
PC (mN)
Modelo PSR
PC (mN)
(h)
FeB
Fe2B
FeB
Fe2B
FeB
Fe2B
1
835.6
879.4
314.5
301
308.6
294.8
3
780.6
879.4
337.7
297.7
330.1
288.9
5
789.0
852.8
347.9
301.4
340.9
290.1
7
824.6
843.7
326.5
314.2
318.3
301.4
1
875.7
934.1
293.2
276.3
283.3
265.3
3
843.5
926.3
330.6
310.2
324.1
305.6
5
805.4
908.3
348.4
287.8
344.4
277.8
7
776.8
851.8
362.4
310.7
357.1
303.5
1
832.1
888.1
313.1
294.1
304.3
288.1
3
794.1
851.8
343.5
314.1
338.4
305.9
5
768.3
851.3
355.1
323.7
350.8
315.6
7
791.9
805.9
336.1
322.3
328.9
313.5
1
806.5
894.1
335.6
267.5
326.7
256.8
3
770.1
866.5
359.3
319.4
353.1
309.5
5
830.2
911.8
296.5
292.1
285.1
281.7
7
800.8
844.3
333.3
317.7
324.2
311.3
‐ 78 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloIII
El valor de  hCC  es mayor en la capa Fe2B, debido a que la capa FeB ofrece mayor
resistencia a la deformación plástica. Asimismo, los valores de carga crítica son
mayores para la capa FeB respecto a la capa Fe2B.
Conclusiones.
El análisis de los datos obtenidos por nanoindentación realizado mediante los modelos
de Meyer, recuperación elástica y PSR, describe satisfactoriamente la relación existente
entre la carga de indentación y el tamaño de huella de indentación.
En el modelo de Meyer, el parámetro n cuantifica la presencia del efecto para los
ensayos de nanodureza realizados en las capas FeB y Fe2B en el acero AISI D2
borurizado. Sin embargo, la relación entre los parámetros A y n parece no ser
trascendente para entender las causas que originan el efecto ISE.
El efecto ISE presente en los ensayos de nanodureza es un fenómeno muy complejo,
las probables causas de su origen en capas borurizadas son muy diversas: la
recuperación elástica del material, la fricción entre el indentador y la superficie,
porosidad en las capas, propiedades elásticas y plásticas del material, entre otras.
Los valores de dureza real expresados en las tablas 3.2, 3.3, 3.4 y 3.5 parecen no ser
dependientes de las condiciones experimentales del tratamiento de borurización.
EduardoChávezGutiérrez
‐ 79 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloIV
Capítulo IV
Estimación de la tenacidad a la fractura y esfuerzos residuales en
capas duras tipo FeB y Fe2B.
En el presente Capítulo se analiza el estado de esfuerzos residuales  R  y la tenacidad
a la fractura  K C  de las capas FeB y Fe2B formadas en la superficie del acero AISI D2
borurizado. El análisis de basa en el agrietamiento generado en los vértices de las
indentaciones realizadas en un equipo de nanoindentación con punta Berkovich,
utilizando cargas variables de indentación (300 a 500 mN ). Asimismo, en función de
estas propiedades, se estima la fragilidad  B  de las capas FeB y Fe2B.
EduardoChávezGutiérrez
‐ 80 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloIV
4.1 Introducción.
Una de las principales razones por las que se aplican recubrimientos en materiales de
ingeniería, es mejorar el comportamiento mecánico de los mismos. La formación de
capas duras tipo FeB-Fe2B en la superficie de diversos aceros incrementa propiedades
como la dureza, el módulo de elasticidad, resistencia al desgaste, entre otras. Sin
embargo, al formarse un sistema capa/sustrato se inducen esfuerzos residuales debido
al tratamiento termoquímico, a partir de la diferencia de valores entre el coeficiente de
expansión térmica de la capa y del sustrato durante el proceso de enfriamiento
(tabla 4.1). Esto afecta significativamente el rendimiento mecánico, la fiabilidad y el
tiempo de servicio de componentes mecánicos.
Tabla 4.1 Valores del coeficiente de expansión térmica para las capas FeB, Fe2B y el acero
AISI D2.
Sistema capa/sustrato
FeB
Fe2B
AISI D2
Coeficiente de expansión
8.4x10-8
(473 a 873 K -1 .)
2.9x10-8
(473 a 873 K -1 .)
4.4x10-8
térmica  K
1

La tenacidad a la fractura  K C  es una propiedad que se relaciona directamente con el
estado de esfuerzos residuales  R  . Esta propiedad define la resistencia del material
al crecimiento de una grieta que puede generar fractura; bajo un estado de esfuerzos
tipo tensil, se reduce la resistencia a la propagación de la grieta, mientras que en un
estado de esfuerzos tipo compresivo, se incrementa su resistencia (Jang, 2009).
En términos de capas delgadas y/o capas duras, la estimación de  K C  y  R  no se
rige en la actualidad por algún procedimiento estándar o metodología común a seguir
(Zhang et al., 2005). Sin embargo, diversos estudios han dedicado sus esfuerzos para
hacer frente a este tema y han propuesto algunos métodos de ensayo basados en
técnicas de indentación instrumentada (Jang, 2009), (Malzbender, 2000).
EduardoChávezGutiérrez
‐ 81 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloIV
La técnica de nanoindentación instrumentada, ha sido recientemente utilizada para
caracterizar propiedades mecánicas de capas y recubrimientos. Con el estudio de
grietas superficiales resultantes de una indentación, es posible evaluar el estado de
esfuerzos residuales y la tenacidad a la fractura de capas duras y recubrimientos.
Esta técnica se ha extendido en años recientes, ya que es una técnica viable para el
estudio de volúmenes a escala micrométrica y la preparación de las muestras es
relativamente sencilla, pues solo demanda una superficie completamente plana y
pulida.
Modelos existentes en literatura basados en la técnica de agrietamiento por indentación,
se clasifican en dos grupos; el primero que asume un agrietamiento tipo radial-media, y
el segundo que asume agrietamiento tipo Palmqvist (fig. 4.1). La morfología de grietas
obtenida dependerá de la carga de indentación, la geometría del indentador y la
tenacidad del material.
a)
b)
Fig. 4.1 Morfología de grietas generadas por indentación: a) radial-media, b) Palmqvist, donde
a es la mitad de la diagonal de indentación, l es la longitud de la grieta y c=l  a .
EduardoChávezGutiérrez
‐ 82 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloIV
Diversos modelos han sido aplicados para la estimación de  K C  , como el modelo de
Anstis et al., (1981) y el modelo de Laugier (1987), para agrietamiento tipo radial-media
y tipo Palmqvist, respectivamente.
La morfología de agrietamiento tipo radial-media ha sido comúnmente aplicada para los
indentadores de geometría simétrica como la Vickers, y también ha sido extendida para
un indentador tipo Berkovich a pesar de que su geometría no es simétrica (fig. 4.2).
Estudios realizados por Malzbender et al., (2000) y Campos-Silva et al., (2011)
consideran este tipo de agrietamiento, obteniendo resultados satisfactorios.
Fig. 4.2 Morfología de grieta generada por indentación Berkovich, donde a es la mitad de la
diagonal de indentación y l es la longitud de la grieta ( c=l  a ).
EduardoChávezGutiérrez
‐ 83 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloIV
4.2 Modelo de Tenacidad a la fractura.
Marshall y Lawn (1977), sugieren un modelo matemático basado en la técnica de
fractura por indentación, en el cual la longitud de grieta alrededor de una indentación
proporciona una medida de la resistencia a la propagación de la grieta. Para un patrón
de agrietamiento tipo radial media, el factor de intensidad de esfuerzos puede definirse
como la suma de 2 términos matemáticos:
PX r
12
 K C  2  c  
32
c
(4.1)
donde P es la carga de indentación, c es la longitud radial de la grieta,  R la medida
del estado de esfuerzos residuales, K C el valor de la tenacidad a la fractura, y X r es
una constante relacionada con la geometría del indentador, cuyo valor para un
indentador tipo Berkovich se representa mediante la siguiente expresión:
12
E
X r  0.016  
H
(4.2)
Los parámetros P , c , E y H son obtenidos experimentalmente a través de los
ensayos de naoindentación. Los valores de K C y  R se obtienen mediante la gráfica
PX r
12
vs 2  c   , en la cual  R está representado por la pendiente de la recta y K C es
32
c
el punto donde el eje de las abscisas intersecta la recta.
Se estima la fragilidad  B  de las capas FeB y Fe2B mediante un modelo propuesto por
Quinn y Quinn (1997). Estos autores, sugieren que la fragilidad
 B  de
un material
define en términos de la tenacidad a la fractura, el módulo de elasticidad y la dureza del
material:
B
EduardoChávezGutiérrez
HE
K C2
(4.3)
‐ 84 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloIV
4.3 Procedimiento experimental.
Para la estimación de  K C  y  R  mediante el modelo de Marshall y Lawn (1977), se
realizaron ensayos de nanoindentación Berkovich en la zona pura de las capas FeB y
Fe2B a una distancia aproximada desde la superficie de 10 y 40 μm , respectivamente;
en las muestras de acero AISI D2 borurizado a las temperaturas de 1223, 1253, 1273 y
1323 K con tiempos de exposición de 3, 5 y 7 h por cada temperatura.
Las cargas de indentación utilizadas para la generación de agrietamiento se establecen
en el rango de 300 a 500 mN para ambas capas. Cabe resaltar que para la condición
de 1323 K   h en la capa Fe2B, no se generó agrietamiento en las indentaciones,
motivo por el cuál se descartó esta condición para la aplicación del modelo.
La distancia establecida entre una indentación y otra, fue de al menos 4 veces el valor
de la diagonal de indentación, para descartar la influencia de una indentación respecto
a otra. La medición de las grietas generadas en los vértices de las indentaciones, se
llevó a cabo con la ayuda del software Image Pro Plus, (fig. 4.3).
Fig. 4.3 Esquema representativo de la medición de grietas y diagonal de indentación de las
huellas generadas por nanoindentación Berkovich en la capa Fe2B, acero AISI D2 borurizado.
EduardoChávezGutiérrez
‐ 85 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloIV
4.4 Resultados y discusiones.
Se realizaron ensayos de nanoindentación Berkovich en las capas FeB y Fe2B
formadas en el acero AISI D2 borurizado, el agrietamiento generado para la estimación
de  K C  y  R  se muestra en las figs. 4.4 y 4.5.
a)
b)
Fig. 4.4 Agrietamiento generado mediante el ensayo de nanoindentación Berkovich en la capa
FeB formada en la superficie de un acero AISI D2 borurizado a la temperatura de1223 K ,
a) 3 h y b) 5 h .
a)
b)
Fig. 4.5 Agrietamiento generado mediante el ensayo de nanoindentación Berkovich en la capa
Fe2B formada en la superficie de un acero AISI D2 borurizado a la temperatura de1223 K ,
a) 3 h y b) 5 h .
EduardoChávezGutiérrez
‐ 86 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloIV
A través del análisis de los datos experimentales se estimaron los esfuerzos residuales
 R 
y la tenacidad a la fractura  K C  mediante gráficas
PX r
12
vs 2  c   como se
32
c
muestra a continuación:
1
0.6
FeB
PXr/c3/2 (mN/µm3/2)
PXr/c3/2 (mN/µm3/2)
FeB
0.5
F́e2B
0.4
0.3
0.2
0.8
F́e2B
0.6
0.4
0.2
0
0.1
2
2.5
3
2
3.5
2.25
2.5
2(c/)1/2
2(c/)1/2 (µm1/2)
a)
2.75
3
b)
1
1
FeB
PXr/c3/2 (mN/µm3/2)
FeB
PXr/c3/2 (mN/µm3/2)
3.25
(µm1/2)
0.8
F́e2B
0.6
0.4
0.2
0.8
0.6
0.4
0.2
0
0
2
2.5
3
1/2
1/2
2(c/) (µm )
3.5
2
2.2
2.4
2.6
2.8
3
2(c/)1/2 (µm1/2)
c)
d)
Fig. 4.6 Relación entre PX r c 3 2 y 2  c  
12
para las capas FeB y Fe2B formadas en la
superficie de un acero AISI D2 borurizado a la temperatura de: a) 1223 K -7 h , b) 1253 K -7 h ,
c) 1273 K -7 h , d) 1323 K -7 h .
EduardoChávezGutiérrez
‐ 87 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloIV
Los valores de los esfuerzos residuales  R  , la tenacidad a la fractura
 KC 
y la
fragilidad  B  de las capas FeB y Fe2B formadas en el acero AISI D2 borurizado, se
resumen en las tablas 4.2 y 4.3.
Tabla 4.2 Mejor ajuste para los valores de  R  ,  K C  y  B  para la capa FeB en función de
las condiciones de tratamiento del acero AISI D2 borurizado.
Tiempo de
Temperatura
exposición
(K)
(h)
1223
1253
1273
1323
EduardoChávezGutiérrez
R
(MPa)
3
KC
 B
(MPa m)
 μm-1 
R2
-749.6
2.33
1029.50
0.9386
5
7
-909.4
-475.4
2.82
1.60
762.42
1898.69
0.9707
0.9794
3
-357.4
1.27
3418.74
0.9428
5
-381.6
1.36
3504.09
0.9465
7
3
-359.6
-428.2
1.3
1.48
4232.23
2908.61
0.9449
0.9866
5
-449.8
1.57
2579.53
0.9496
7
-446.0
1.50
2684.66
0.9579
3
5
-522.9
-965.8
1.72
3.02
2301.23
521.06
0.9856
0.9625
7
-892.0
2.76
810.38
0.9829
‐ 88 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloIV
Tabla 4.3 Mejor ajuste para los valores de  R  ,  K C  y  B  para la capa Fe2B en función de
las condiciones de tratamiento del acero AISI D2 borurizado.
Tiempo de
Temperatura
exposición
(K)
(h)
1223
1253
1273
1323
 B
R
(MPa)
(MPa m)
 μm 
R2
3
-908.2
2.76
625.69
0.9551
5
7
-996.6
-610.0
3.09
2.01
546.39
1113.10
0.969
0.9239
3
-777.1
2.57
676.23
0.9751
5
-989.0
3.17
423.39
0.9557
7
3
-558.3
-1604.9
1.98
4.65
1273.50
237.86
0.9763
0.984
5
-849.1
2.72
710.68
0.9209
7
-935.7
2.93
724.59
0.9763
3
5
-1159.0
-1270.7
3.47
3.80
427.23
300.11
0.933
0.9561
7
-
-
KC
-1
-
La tenacidad a la fractura y el estado de esfuerzos residuales son propiedades de
importancia crítica para el uso de materiales en aplicaciones mecánicas, las cuales
dependen del contenido de elementos de aleación presentes en el sustrato. Estas
propiedades, están en función del tipo de boruros de hierro que se forman en la
superficie del acero y del tiempo de tratamiento (Ozbek y Bindal, 2002).
Los datos obtenidos de  R  para las capas FeB y Fe2B formadas en la superficie del
acero AISI D2 borurizado mediante la técnica de nanoindentación instrumentada,
establecen su naturaleza de tipo compresivo para ambas capas. Su valor, se define en
el rango de 205 a 909.4 (MPa) para la capa FeB, mientras que para la capa Fe2B en el
rango de 532.8 a 1602.9 (MPa) .
EduardoChávezGutiérrez
‐ 89 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloIV
El comportamiento de los esfuerzos residuales a lo largo de la capa borurada, establece
que en la zona más cercana a la superficie la naturaleza de los mismos tiende a
volverse de tipo tensil; mientras que al alejarse de la superficie, los esfuerzos residuales
de tipo compresivo tienden a ser de mayor magnitud.
En términos de  K C  , se estimaron valores en el rango de 1.27 a 3.02 (MPa m) para la
capa FeB; de manera similar, para la capa Fe2B su valor oscila en el rango de 1.98 a
4.65 (MPa m) . Estudios realizados por Ozbek y Bindal (2002), establecen valores de
 KC 
para la capas FeB y Fe2B formadas en un acero AISI W4 borurizado en el rango
de 1.39 a 1.50 (MPa m) y de 5.24 a 6.40 (MPa m) , respectivamente.
La relación existente entre  R  y  K C  , se ilustra en la fig. 4.7.
1200
800
600
1223 K
1253 K
1273 K
1323 K
400
200
0
0
0.5
1
1.5
2
KC (MPa • √m)
a)
2.5
3
3.5
‐σR (MPa)
‐σR (MPa)
1000
1800
1600
1400
1200
1000
800
600
400
200
0
1223 K
1253 K
1273 K
1323 K
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
KC (MPa • √m)
b)
Fig. 4.7 Relación entre  K C  y  R  para las capas: a) FeB, b) Fe2B formadas en la superficie
de un acero AISI D2 borurizado a las condiciones de tratamiento establecidas.
Las gráficas de la figura 4.7 muestran una estrecha relación entre la tenacidad a la
fractura y el estado de esfuerzos residuales de los boruros de hierro formados en el
acero AISI D2 determinados mediante la técnica de indentación instrumentada.
EduardoChávezGutiérrez
‐ 90 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloIV
Se establece que los esfuerzos residuales tipo compresivo en la capa Fe2B son de
mayor magnitud respecto a la capa FeB, lo que sugiere mayor resistencia a la
propagación de grietas en la capa Fe2B. Se observa también, que la tenacidad a la
fractura incrementa su resistencia en presencia de un estado de esfuerzos residuales
tipo compresivo.
En términos de la fragilidad, se establece que un material con valor bajo de  B  es más
propenso a la deformación elástica o plástica que ha generar fractura, e inversamente.
La fragilidad de un material se incrementa al aumentar la dureza, y reduce su valor
considerablemente al incrementar la tenacidad a la fractura.
Para el conjunto de datos experimentales, se estableció el valor de  B  en el rango de
521.06 a 4232.23  μm 1  y de 237.86 a 1273.50  mμ 1  para las capas FeB y Fe2B,
respectivamente.
Es previsible mayor fragilidad para la capa FeB respecto a la capa Fe2B, pues en
términos de la dureza característica de cada capa, se establece mayor resistencia a la
deformación que a la distribución de una carga y concentración de esfuerzos en FeB,
por lo que se incrementa la capacidad de generar agrietamiento. De manera similar, el
módulo elástico define la rigidez de las capas y su incapacidad de distribuir una carga,
lo cual induce comportamiento frágil y se acentúa en la capa FeB que presenta un
módulo elástico mayor respecto a la capa Fe2B. En contraparte, la tenacidad a la
fractura en la capa Fe2B define mayor resistencia a la propagación de grietas respecto a
FeB, en consecuencia, la fragilidad de la capa Fe2B es menor que en la capa FeB.
EduardoChávezGutiérrez
‐ 91 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
CapítuloIV
Conclusiones.
La técnica de nanoindentación instrumentada es un método eficaz, práctico y sencillo
para el estudio de propiedades mecánicas como la tenacidad a la fractura y el estado
de esfuerzos residuales en capas duras tipo FeB y Fe2B.
La tenacidad a la fractura de las capas de boruro de hierro se ve beneficiada por un
estado de esfuerzos residuales de tipo compresivo. La capa Fe2B es más tenaz
respecto a la capa FeB, siendo mayor el valor de los esfuerzos residuales en Fe2B.
Los resultados obtenidos para
 KC 
y  R  mediante la técnica de nanoindentación
Berkovich, muestran buena concordancia con los valores propuestos en literatura para
las capas de boruro de hierro formadas en la superficie de diversos aceros. Por lo que
se establece que el modelo de Marshall y Lawn (1977), estima valores de  K C  y  R 
aceptables para un indentador tipo Berkovich.
Asimismo, se establece que la capa FeB presenta mayor fragilidad que la capa Fe2B en
el acero AISI D2 borurizado.
EduardoChávezGutiérrez
‐ 92 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
Perspectivas de trabajo.
Como perspectivas de trabajo, se plantean los siguientes puntos:
I.
Establecer la influencia de altas temperaturas de tratamiento ( T  1323K ) y
tiempos largos de exposición ( t  h ) en la evolución de las capas FeB y Fe2B en
diversos aceros sometidos al proceso de borurización.
II.
Analizar la recuperación elástica presente en la superficie de diversos aceros
borurizados al realizar ensayos de nanoindentación y establecer su relación en
términos de los parámetros establecidos por el modelo de recuperación elástica.
III.
Disminuir la fragilidad del sistema bicapa FeB-Fe2B mediante la mejora de
propiedades mecánicas como la tenacidad a la fractura, a través de tratamientos
termoquímicos posteriores a la borurización.
IV.
Estimar el valor de  R  mediante la técnica de difracción de rayos X, para
corroborar los datos obtenidos mediante la técnica de agrietamiento por
nanoindentación Berkovich.
EduardoChávezGutiérrez
‐ 93 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
Referenciasbibliográficas
Referencias bibliográficas.
Anstis G R, Chantikul P, Lawn B R and Marshall D B (1981), “A critical evaluation of
indentation techniques for measuring fracture toughness I. Direct crack measurements”,
J Am Ceram Soc, 64, 533-538.
Antunes J M, Fernandes J V, Sakharova N A, Oliveira M C, Meneses L F (2007), “On
the determination of the Young´s modulus of thin films using indentation tests”,
Inter. J. Solid Struct., 44, 8313-8334.
Badini C, Gianoglio C, and Pradelli G (1989), “The effect of carbon, chromium and nickel
on the hardness of borided layers”, Surf. Coat. Tech., 30, 157-170.
Brakman C M, Gommers A W J and Mittemeijer E J (1989), “Proceedings of Heat
Treatment”, The Institute of Metals, 211-230.
Campos I, Oseguera J, Figueroa U, García J. A, Bautista O, Kelemenis G (2003),
“Kinetic study of boron diffusion on the paste-boriding process”, Mater. Sci. Eng.,
A352, 261-265.
Campos I, Ramírez G, Figueroa U, Martínez J, Morales O (2007), “Evaluation of boron
mobility on the phases FeB, Fe2B and diffusion zone in AISI 1045 and M2 steels”,
Appl. Surf. Sci., 253, 3469-3475.
Campos-Silva I, Ortiz-Dominguez M, Tapia-Quintero C, Rodriguez-Castro G, JimenezReyes Y, Chávez Gutiérrez E (2010), “Kinetics and Boron Diffusion in the FeB/Fe2B
Layers Formed at the Surface of Borided High-Alloy Steel”, J. Mater. Eng. Perform.
doi:10.1007/s11665-011-0088-9.
EduardoChávezGutiérrez
‐ 94 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
Referenciasbibliográficas
Campos-Silva I, Hernández-Sánchez E, Rodríguez-Castro G, Rodríguez-Pulido A,
López-García C, Ortíz-Dominguez M (2011), “Indentation size effect on the
Fe2B/substrate interface”, Surf. Coat. Tech., 206, 1809-1815.
Casals O and Alcalá J (2005), “The duality in mechanical property extractions from
Vickers and Berkovich instrumented indentation experiments”, Acta Mater., 53,
3545-3561.
Culha O, Toparli M, Sahin S, Aksoy T (2008), “Characterization and determination of
FexB layers mechanical properties”, J. Mater. Proc. Tech., 206, 231-240.
Fox-Rabinovich G S, Veldhuis S C, Scvortsov V N, Shuster L Sh, Dosbaeba G K,
Migranov M S (2004), “Elastic and plastic work of indentation as a characteristic of wear
behavior for cutting tools with nitride PVD coatings”, Thin Solid Films, 469-470, 505-512.
Genel K, Ozbek I, Bindal C (2003), “Kinetics of boriding of AISI W1 steel”, Mater. Sci.
Eng., A347, 311-314.
Gong J, Wu J and Guam Z (1998), “Description of the indentation size effect in hotpressed silicon-nitride based ceramics”, J Mater. Sci. Letters 17, 473-475.
Habbab H. Mellor B G, Syngellakis S (2006), “Post-yield characterization of metals with
significant pile-up through spherical indentation”, Acta Mater., 54, 1965-1973.
Jang J (2009), “Estimation of residual stress by instrumented indentation: A review”,
J Ceram. Proc. Research, 10, 391-400.
Keddam M and Chentouf S M. (2005), “A diffusion model for describing the bilayer
growth (FeB/Fe2B) during the iron powder-pack boriding”, Appl. Surf. Sci., 252, 393-399.
Kim H and Kim F (2002), “Measurement of hardness on traditional ceramics”,
J. Eur. Ceram. Soc. 22, 1437-1445.
EduardoChávezGutiérrez
‐ 95 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
Referenciasbibliográficas
Krella A (2011), “An experimental parameter of cavitation erosion resistance for TiN
coatings”, Wear, 270, 252-257.
Laugier M T (1987), “Palmqvist indentation toughness in WC-Co composites”,
J MaterSci, Lett 6, 897-900.
Li H and Bradt R C (1993), “The microhardness indentation load/size effect in rutile and
cassiterite single cristals”, J Mater. Sci., 28, 917-926.
Malzbender J, de With G and den Toonder J M J (2000), “Elastic modulus, indentation
pressure and fracture toughness of hybrid coating on glass”, Thin Solid Films, 366,
139-149.
Marshall D.B and Lawn B.R (1977), “An indentation technique for measuring stresses in
tempered glass surfaces”, Amer. Ceram. Soc., 60, 86-87.
Martini C, Palombarini G, Carbucicchio M (2004), “Mechanism of thermochemical
growth of iron borides on iron”, J. Mater. Sci., 39, 933-937.
Matiasovsky K, Chrenkova-Paucirova M, Fellner P, Makyta M (1988), “Electrochemical
and Thermochemical boriding in molten salts”, Surf. Coat. Tech., 35, 133-194.
Oliveira C K N, Casteletti L C, Lombardi Neto A, Totten G E, Heck S C (2010),
“Production and characterization of borided layers on AISI D2 tool steel”, Vacuum, 84,
792-796.
Oliver W C, Pharr G M (1992), “An improved technique for determining hardness and
elastic modulus using load and displacement sensing indentation experiments”,
J. Mater. Res., 7, 1564-1583.
Ozbek I and Bindal C (2002). “Mechanical properties of boronized AISI W4 steel”,
Surf. Coat. Tech., 154, 14-20.
EduardoChávezGutiérrez
‐ 96 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
Referenciasbibliográficas
Peng Z, Gong J, Miao H (2004), “On the description of indentation size effect in
hardness testing for ceramics: Analysis of the nanoindentation data”, J. Eur. Ceram.
Soc., 24, 2193-2201.
Quian L, Li M, Zhou Z, Yang H, Shi X (2005), “Comparison of nano-indentation hardness
to microhardness”, Surf. Coat. Tech., 195, 264-271.
Quinn J B and Quinn G D (1997), “Indentation brittleness of ceramics; a frech
approach”, J Mater. Sci., 32, 4331-4346.
Sangwal K, Surowska B. and Blaziak P (2002), “Analysis of the indentation size effect in
the microhardness measurement of some cobalt-based alloys”. Mater. Chem. Phys., 77,
511–520.
Sargent P M. and Page T F (1978), “The influence on the microhardness of ceramic
materials”, Proc. Brit. Ceram. Soc., 26, 209–224.
Sidjanin L, Rajnovic D, Ranogajec J, Molnar E (2007), “Measurement of Vickers
Hardness on ceramic floor tiles”, J. European Ceram. Soc., 27, 1767-1773.
Sista V, Kahvecioglu O, Eryilmaz O.L, Erdemir A, Timur S (2011), “Electrochemical
boriding and characterization of AISI D2 steel”, Thin Solid Films, 520, 1582-1588.
Taktak S (2006), “Tribological behaviour of borided steels at elevated temperatures”,
Surf. Coat. Tech., 201, 2230-2239.
Yu L G, Chen X J, Khor K A, Sundararajan G (2005), “FeB/Fe2B phase transformation
during SPS pack-boriding: Boride layers growth kinetics”, Acta Mater., 53, 2361-2368.
EduardoChávezGutiérrez
‐ 97 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
Publicaciones
y
distinciones.
EduardoChávezGutiérrez
‐ 98 -
INSTITUTO POLITÉCNICO NACIONAL
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA
SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN
Artículos publicados.
Rodríguez-Castro G, Campos-Silva I, Chávez-Gutiérrez E, Martínez-Trinidad J,
Hernández-Sánchez E, Torres-Hernández A (2012), “Mechanical properties of FeB and
Fe2B layers estimated by nanoindentation on tool borided steel”, Enviado a: Surf. Coat.
Technol.
Campos-Silva I, Ortiz-Domínguez M, Tapia-Quintero C, Rodríguez-Castro G, JímenezReyes M. Y and Chávez-Gutiérrez E (2011), “Kinetics and Boron Diffusion in the
FeB/Fe2B Layers Formed at the surface of Borided High-Alloy Steel”. DOI:
10.1007/s11665-011-0088-9
Distinciones.
Segundo lugar en el concurso “Premio de Ingeniería de la Ciudad de México” con el
trabajo “Análisis Numérico Experimental de Propiedeades Mecánicas en la Zona
Crítica de Interfase Fe2B/substrato en Superficies Metálicas Endurecidas por
Difusión de Boro”
En la categoría de Trabajo de tesis o proyecto terminal cuya contribución a la ingeniería
sea en beneficio de la población de la ciudad de México o del país en general de nivel
posgrado, en el área de ingeniería industrial, en la modalidad de equipo.
EduardoChávezGutiérrez
‐ 99 -
Elsevier Editorial System(tm) for International Conference on Metallurgical Coatings
and Thin Films
Manuscript Draft
Manuscript Number:
Title: Mechanical properties of FeB and Fe2B layers estimated by Berkovich nanoindentation on tool
borided steel
Article Type: Full Length Article
Section/Category: Symposia E, TS1, and TS3
Keywords: boriding; boride layer; nanoindentation; mechanical properties; ISE; residual stresses.
Corresponding Author: Dr. Ivan Campos,
Corresponding Author's Institution: Instituto Politecnico Nacional
First Author: German Anibal Rodriguez-Castro
Order of Authors: German Anibal Rodriguez-Castro; Ivan Campos; Eduardo Chavez-Gutierrez; Jose
Martinez-Trinidad; Enrique Hernandez-Sanchez; Alfredo Torres-Hernandez
Abstract: In this study the mechanical behavior of FeB and Fe2B layers formed at the surface of AISI D2
steels was estimated by the Berkovich nanoindentation technique. The boriding of AISI D2 steels was
developed by the powder-pack method at temperatures of 1223, 1273 and 1323 K with exposure times
of 3 - 7 h for each temperature. The mechanical characterization was performed to determine the effect
of the set of experimental parameters of the boriding process with two experimental procedures: first,
nanoindentation was performed along the depth of the surface layers at a constant load of 250 mN to
determine the hardness gradient and the state of the thermal residual stresses in the boride layers;
then, loads in the range of 10 to 300 mN were applied to the "pure" zone of the FeB layer at a distance
of 10 microns from the surface, and in the "pure" zone of the Fe2B layer (40 microns), respectively.
For a constant load of 250 mN, the results showed that the state of thermal residual stresses and the
hardness of both the FeB and Fe2B layers were a function of the temperature and exposure time of the
process, in which the hardness at the surface layers decreased at a temperature of 1323 K with more
than 5 h of exposure. Moreover, the presence of the indentation size effect (ISE) in the FeB and Fe2B
layers was verified in the range of applied loads (10-300 mN), in which the apparent or real hardness
was estimated by the elastic recovery (ER) model according to the boriding experimental parameters.
Finally, the fracture resistance and brittleness of the boride layers was evaluated in the range from 300
to 500 mN as a function of the boriding temperatures and exposure times; the estimated values fell
within the range of 1.48-3.02 and 2.01-4.65 , with the presence of compressive stresses in the range
of 428 to 1604 MPa for the FeB and Fe2B layers, respectively.
Suggested Reviewers: Didier Chicot
Laboratoire de Mecanique de Lille, Lille University
[email protected]
Expert in the field of mechanical characterization
Ramon Escobar Galindo
ICMM, Materials Science Institute of Madrid
[email protected]
Expert in the field of surface engineering
Cover Letter
In this study the mechanical behavior of FeB and Fe2B layers formed at the surface of AISI
D2 steels was estimated by Berkovich nanoindentation technique. The nanoindentations
were performed along the depth of surface layers with a constant load of 250 mN to
determine the hardness gradient and the state of thermal residual stresses in the boride
layers. In addition, applied loads in the range of 10 to 300 mN were carried out in the
“pure” zone of the FeB layer at 10 microns from the surface, and in the “pure” zone of the
Fe2B layer (40 microns), respectively. The existence of the ISE was verified by Berkovich
nanoindentations in both layers considering the set of applied loads of 10-300 mN. In
addition, the fracture resistance, compressive residual stresses and brittleness of the boride
layers were estimated with the cracks developed by the Berkovich nanoindentation marks at
10 and 40 microns from the surface of borided steel
Research Highlights
Mechanical properties of the FeB and Fe2B layers formed on the AISI D2 borided steel
were evaluated by Berkovich nanoindentation. The state of thermal residual stresses along
the boride layers was compressive. The presence of the indentation size effect was verified
in the boride layers. Both boride layers revealed low fracture toughness values with high
brittleness.
Mechanical properties of FeB and Fe2B layers estimated by Berkovich nanoindentation on
tool borided steel
G. Rodríguez-Castro , I. Campos-Silva , E. Chávez-Gutiérrez , J. Martínez-Trinidad ,
E. Hernández-Sánchez , A. Torres-Hernández
Instituto Politécnico Nacional, Grupo Ingeniería de Superficies, SEPI-ESIME, U.P. Adolfo López
Mateos, Zacatenco, México D.F., 07738, México.
Abstract. In this study the mechanical behavior of FeB and Fe2B layers formed at the surface of
AISI D2 steels was estimated by the Berkovich nanoindentation technique. The boriding of AISI
D2 steels was developed by the powder-pack method at temperatures of 1223, 1273 and 1323 K
with exposure times of 3 - 7 h for each temperature. The mechanical characterization was
performed to determine the effect of the set of experimental parameters of the boriding process
with two experimental procedures: first, nanoindentation was performed along the depth of the
surface layers at a constant load of 250 mN to determine the hardness gradient and the state of the
thermal residual stresses in the boride layers; then, loads in the range of 10 to 300 mN were applied
to the “pure” zone of the FeB layer at a distance of 10 microns from the surface, and in the “pure”
zone of the Fe2B layer (40 microns), respectively.
For a constant load of 250 mN, the results showed that the state of thermal residual stresses and the
hardness of both the FeB and Fe2B layers were a function of the temperature and exposure time of
the process, in which the hardness at the surface layers decreased at a temperature of 1323 K with
more than 5 h of exposure. Moreover, the presence of the indentation size effect (ISE) in the FeB
and Fe2B layers was verified in the range of applied loads (10-300 mN), in which the apparent or
real hardness was estimated by the elastic recovery (ER) model according to the boriding
experimental parameters. Finally, the fracture resistance and brittleness of the boride layers was
evaluated in the range from 300 to 500 mN as a function of the boriding temperatures and exposure
times; the estimated values fell within the range of 1.48-3.02 MPa m and 2.01-4.65 MPa m ,
with the presence of compressive stresses in the range of 428 to 1604 MPa for the FeB and Fe2B
layers, respectively.
Keywords: boriding; boride layer; nanoindentation; mechanical properties; ISE; residual stresses.
4
Kinetics and Boron Diffusion in the FeB/
Fe2B Layers Formed at the Surface of
Borided High-Alloy Steel
I. Campos-Silva, M. Ortiz-Domínguez,
C. Tapia-Quintero, G. Rodríguez-Castro,
M. Y. Jiménez-Reyes & E. ChávezGutiérrez
Journal of Materials Engineering and
Performance
ISSN 1059-9495
J. of Materi Eng and Perform
DOI 10.1007/s11665-011-0088-9
1 23
Your article is protected by copyright and
all rights are held exclusively by ASM
International. This e-offprint is for personal
use only and shall not be self-archived in
electronic repositories. If you wish to selfarchive your work, please use the accepted
author’s version for posting to your own
website or your institution’s repository. You
may further deposit the accepted author’s
version on a funder’s repository at a funder’s
request, provided it is not made publicly
available until 12 months after publication.
1 23
Author's personal copy
ASM International
1059-9495/$19.00
JMEPEG
DOI: 10.1007/s11665-011-0088-9
Kinetics and Boron Diffusion in the FeB/Fe2B Layers
Formed at the Surface of Borided High-Alloy Steel
I. Campos-Silva, M. Ortiz-Domı́nguez, C. Tapia-Quintero, G. Rodrı́guez-Castro, M.Y. Jiménez-Reyes, and E. Chávez-Gutiérrez
(Submitted October 29, 2010; in revised form June 19, 2011)
In the present study, boron diffusion in the surface layers of AISI M2 borided steels and the growth kinetics
of the FeB/Fe2B layers were estimated. The boriding of AISI M2 steel was performed according to the
powder-pack method and was conducted at 1173-1323 K and at various exposure times. As a result of the
boriding process, the diffusion-controlled growth of the FeB/Fe2B layers was obtained at the surface of the
high-alloy steel, and the kinetics of the growth process changed parabolically over time. The boron diffusion
coefficients were estimated by solving two simultaneous equations based on the limits of the boron
concentration in each layer, the boride incubation time, and the parabolic growth constant. With the
proposed diffusion model, an expression, which describes the evolution of the FeB/Fe2B layers, was
obtained. Moreover, the proposed model and diverse empirical models presented in the literature provided
a good fit to the experimental data obtained for 10 h of exposure and different boriding temperatures.
Keywords
boride layers, boriding, boron diffusion coefficients,
diffusion model, growth kinetics
1. Introduction
Boriding is a thermochemical surface treatment, whereby
boron is diffused into, and combines with, the substrate
material forming a single- or double-phase metal boride layer at
the surface. Unlike many other surface treatments, hard boride
layers can be developed on most alloys and metals by boron
diffusion. The boriding of ferrous materials results in the
formation of either a single layer (Fe2B) or double-layer (FeB/
Fe2B) with definite composition. The thickness of the layer
formed (known as the case depth), which affects the mechanical
and chemical behavior of borided steels, depends on the
boriding temperature, the treatment time, and the boron
potential that surrounds the surface sample (Ref 1). The
optimum boride layer thickness for low-carbon steels and lowalloy steels ranges from 50 to 250 lm, while the optimum
boride layer thickness for high-alloy steels ranges from 25 to
76 lm (Ref 2). In addition, the thickness of the boride layer has
an effect on the dimensions and superficial roughness of the
materials exposed to the treatment. It has been demonstrated
that the dimensions of the borided samples increased by onefifth to one-third of the total depth of boride coating (Ref 3).
Therefore, the estimation of the kinetic parameters for the
evolution of the FeB and Fe2B surface layers during the
boriding process is of great importance.
Interest in the study of the growth kinetics of boride layers in
ferrous alloys has increased over the last 20 years (Ref 1, 4-14).
Traditional diffusion models (Ref 4-6, 8) suggest that the FeB and
Fe2B layers obey the parabolic growth law x2 ¼ Kt, where x is the
mean thickness of the boride layer, K is the growth constant, and t
is the exposure time of the substrate to the boriding process. To
estimate the activation energy (Q), the behavior of the growth
constant as a function of the boriding temperature must be
determined. Moreover, an accurate estimation of the activation
energy is necessary to stimulate the formation of the boride layer
at the steel surface. Other diffusion models based on the mass
balance equations of the FeB/Fe2B and the Fe2B/substrate
interface as well as the boron concentration profile of the surface
layers have been developed (Ref 1, 5, 7, 9, 11-14). One solution to
the mass balance equations of the surface layers is based on the
parabolic growth law and can be used to estimate the boron
diffusion coefficients of the FeB and Fe2B layers (DFeB and
DFe2 B , respectively). The boron diffusion values obtained for
each surface layer are represented by the Arrhenius equation;
thus, the activation energy of the system must be known.
Likewise, in many diffusion models, the boride incubation time
(t0 ) is considered to be an additional variable in the parabolic
growth equation for the solution of the mass balance equation.
The results of previous studies (Ref 14-16) have shown that the
boride incubation time is dependent on the boriding temperature
and decreases with an increase in temperature. Based on the
experimental data of the boriding process, which includes
exposure time, boride incubation time, temperature, and boron
potential of the medium, several kinetic parameters have been
estimated, including the weight gain due to the formation of
boride layers at the surface of steel, the instantaneous velocity of
the Fe2B/substrate interface, and the boron diffusion coefficient
is dependent on the parabolic growth
of the Fe2B layer,
which
constant and the
I. Campos-Silva, M. Ortiz-Domı́nguez, C. Tapia-Quintero,
G. Rodrı́guez-Castro, M.Y. Jiménez-Reyes and E. ChávezGutiérrez, Instituto Politécnico Nacional, Grupo Ingenierı́a de Superficies, SEPI-ESIME, U.P. Adolfo López Mateos, Zacatenco,
07738 Mexico, D.F., Mexico. Contact e-mail: [email protected].
Journal of Materials Engineering and Performance
t
t0
ratio.
In the present study, a diffusion model was proposed to
determine the boron diffusion coefficients of the FeB and Fe2B
layers at the surface of AISI M2 steel produced by powder-pack
boriding. The diffusion model was based on the boron concen-
Author's personal copy
tration profiles of the surface layers, the parabolic growth law
which considers the boride incubation time, and the mass balance
equations of the FeB/Fe2B and Fe2B/substrate interfaces. The
model was extended to evaluate variations in the thicknesses of
the FeB/Fe2B layers, and the results were compared to those of
empirical models proposed in the literature.
FeB
FeB
Clow
Cup
xðtÞ
u
Fe2 B
CFe2 B ½xðtÞ ¼ Cup
þ
Fe2 B
Fe2 B
Clow
Cup
l
A linear boron concentration profile was assumed for each
i
i
and Clow
of the boride layers formed at the steel surface. Cup
represent the maximum and minimum boron concentration in
the FeB and Fe2B layers (i = FeB or Fe2B), as shown in the
Fe-B phase diagram (see Fig. 1a, b). The boride layers
possessed a narrow range of boron concentrations of about
1 wt.% (Ref 17, 18). Likewise, the homogeneity of the
distribution of boron in the FeB and Fe2B layers can be
described by a1 and a3, and the parameters a2 and a4 express
the miscibility gap between the FeB/Fe2B and Fe2B/substrate
layers, respectively. Finally, C0 is the boron concentration in
the c-Fe phase (0.003 wt.% B).
The initial and boundary conditions of the diffusion problem
were represented by the following equations, as shown in
Fig. 1(c):
½xðtÞ u
ðEq 10Þ
CFe2 B ½xðt ¼ 0Þ ¼ C0 ;
ðEq 1Þ
J1 ¼ DFeB a1 =u
ðEq 11Þ
J2 ¼ DFe2 B a3 =l
ðEq 12Þ
where DFeB is the boron diffusion coefficient of the FeB layer,
DFe2 B is the boron diffusion coefficient of the Fe2B layer, and
u and l represent the depths of the FeB and Fe2B layers,
respectively.
By substituting Eq 11 and 12 into Eq 7 and 8, the mass
balance equations of the interfaces can be expressed as
ða2 þ a1 =2Þ
ða4 þ a3 Þ
du
a1
a3
¼ DFeB DFe2 B
dt
u
l
ðEq 2Þ
ðEq 3Þ
Fe2 B
CFe2 B ½xðt ¼ tÞ ¼ u ¼ Cup
;
ðEq 4Þ
Fe2 B
CFe2 B ½xðt ¼ tÞ ¼ v ¼ Clow
;
ðEq 5Þ
dl
1
1
¼ DFe2 B P3 DFeB P4
dt
l
u
CFe2 B ½xðt ¼ tÞ ¼ v ¼ C0 ;
ðEq 6Þ
with
1
DFeB ¼ a2 du þ a1 du ¼ J1 dt J2 dt
2
1
¼ a4 ðdu þ dl Þ þ a3 du þ a3 dl ¼ J2 dt J3 dt
2
ðEq 7Þ
ðEq 8Þ
where J1 , J2 and J3 were obtained from FickÕs First Law,
J ¼ DfdC ½xðtÞ=dxðtÞg. The equations that represent the
boron concentration in the FeB and Fe2B layers can be
described as follows (see Fig. 1c):
ðEq 14Þ
Furthermore, the continuity Eq 13 and 14 can be rewritten
as follows:
FeB
;
CFeB ½xðt ¼ tÞ ¼ u ¼ Clow
B
represents the effective adsorbed boron concentration
Cads
during the boriding process (Ref 9).
The mass balance equations of the FeB/Fe2B and Fe2B/
substrate interfaces can be described as follows:
ðEq 13Þ
du
dl
a3
þ ða4 þ a3 =2Þ ¼ DFe2 B
dt
dt
l
9
FeB
B
CFeB x t ¼ t0FeB ðT Þ ¼ 0 ¼ Cup
for Cads
> 16:23 wt:% B;
>
>
>
>
FeB
B
>
>
for Cads
< 16:23 wt:% B and with FeB layer;
CFeB x t ¼ t0FeB ðT Þ ¼ 0 ¼ Clow
=
Fe2 B
Fe2 B
B
for 8:83 wt:% B < Cads < 16:23 wt:% B and >
CFe2 B x t ¼ t0 ðT Þ ¼ 0 ¼ Cup
>
>
>
without FeB layer;
>
>
;
Fe2 B
Fe2 B
B
CFe2 B x t ¼ t0 ðT Þ ¼ 0 ¼ Clow
for Cads < 8:83 wt:% B and without FeB layer;
DFe2 B
ðEq 9Þ
If the substrate becomes saturated within a short period of
time and the solubility of boron is extremely low in c-Fe
(0.003 wt.% B), then J3 ¼ 0. Thus, the fluxes J1 and J2 can be
expressed by the following equations:
2. Diffusion Model
CFeB ½xðt ¼ 0Þ ¼ C0 ;
FeB
þ
CFeB ½xðtÞ ¼ Cup
du
1
1
¼ DFeB P1 DFe2 B P2
dt
u
l
a1
P1 ¼ a2 þa
,
1 =2
1
a2 þa1 =2Þ,
a3
P2¼ a2 þa
=2,
1
3 þa4
and P4 ¼ aa4 þa
3 =2
ðEq 15Þ
ðEq 16Þ
1
3 þa4
P3 ¼ a3 aa4 þa
a3 þa4 þ
3 =2
a1
a2 þa1 =2
The solutions to Eq 15 and 16 can be obtained by
considering the parabolic growth equations of the surface
layers (Ref 1, 19, 20):
1=2
ðEq 17Þ
u ¼ kFeB t t0FeB ðT Þ
where kFeB is the growth constant of the FeB layer, t0FeB ðT Þ is
the boride
incubation
1=2 time as a function of the temperature,
is the effective growth time of the FeB
and t t0FeB ðT Þ
layer. In a similar manner, the growth equation of the Fe2B
layer can be defined as
1=2
l ¼ v u ¼ k ðt t0 ðT ÞÞ1=2 kFeB t t0FeB ðT Þ
ðEq 18Þ
Journal of Materials Engineering and Performance
Author's personal copy
FeB
FeB
Fig. 1 (a) Schematic representation of the Cup
and Clow
values obtained from the Fe-B phase diagram for a range of temperatures, (b) scheFe2 B
Fe2 B
and Clow
values obtained from the Fe-B phase diagram for a range of temperatures, and (c) boron concentramatic representation of the Cup
tion profile in the FeB/Fe2B layers
where v is the thickness of the total boride layer, t is the
treatment time, t0 ðT Þ is the boride incubation time of the total
boride layer (t0FeB ðT Þ > t0 ðT Þ), and k is the parabolic growth
constant of the total boride layer.
Journal of Materials Engineering and Performance
Based on the aforementioned assumptions, the boron
diffusion coefficients in the FeB and Fe2B layers (DFe2 B
and DFeB ) can be derived by applying Eq 15 and 16 as
follows:
Author's personal copy
DFe2 B ¼
l
du dl
du
ða4 þ a3 =2Þ
þ
þ ða3 =2Þ
;
a3
dt dt
dt
m2 s1
ðEq 19Þ
"
u
du dl
þ
ða4 þ a3 =2Þ
a1
dt dt
#
du
þða3 =2 þ a2 þ a1 =2Þ
;
dt
DFeB ¼
ðEq 20Þ
composition of the layers were determined by the activity of
boron on the steel surface, the temperature of the boriding
process, and the composition of the substrate. Once compact
boride layers have formed on the surface, their growth can be
described by the following reactions (Ref 21):
Bdif þ Fe2 B ¼ 2FeB
ðEq 21Þ
Fedif þ FeB ¼ Fe2 B
ðEq 22Þ
2 1
m s
3. Experimental Procedure
AISI M2 steels with a nominal composition of 0.85 wt.% C,
0.3 wt.% Mn, 0.3 wt.% Si, 4.5 wt.% Cr, 5 wt.% Mo,
1.95 wt.% V, and 6.40 wt.% W were sectioned into cubic
samples with dimensions of 13 9 13 9 13 mm. The samples
were embedded in a closed, cylindrical case (AISI 304L)
containing a B4C Durborid fresh powder mixture with a powder
size of 50 lm. Both FeB and Fe2B layers on the surface of the
steel were grown at 1173, 1223, 1273, and 1323 K for 4, 6, and
8 h. Boriding was accomplished by placing the container in a
furnace in the absence of inert gases, and the boriding time
began when the temperature of the furnace reached the boriding
temperature. When the treatment was complete, the container
was removed from the furnace and was slowly cooled to room
temperature.
Cross sections of the samples were prepared for microscopic examinations by standard metallographic techniques
using GX51 Olympus equipment. Eighty measurements were
performed from a fixed reference on different sections of
borided samples to determine the FeB and the total layer
thickness. In addition, x-ray diffraction (XRD) and energy
dispersive x-ray spectroscopy (EDS) were conducted on
material borided at 1223 K for 8 h to characterize the nature
of the borided products and the distribution of heavy elements
in the surface layers. For these purposes, a Siemens D5000
(Cu Ka radiation at k = 1.54 A) diffractometer and a Leica
Cambridge Stereoscan 440 spectrometer were employed.
Finally, Vickers microindentation was conducted to evaluate
the hardness-depth profile of the boride layers on the borided
steel surface, and a constant indentation load of 50 g was
applied to the samples by means of a Wolpert 402MVD
apparatus.
The presence of alloying elements in the steel reduces the
growth rate of the boride layers because of the formation of a
diffusion barrier, which slows the growth of the FeB/Fe2B layer
(Ref 22). In addition, the results of x-ray diffraction analysis,
which are depicted in Fig. 3, revealed the presence of the iron
borides at the steel surface. In addition, chromium and
vanadium tend to dissolve in FeB/Fe2B layers and form
independent borides with a lattice constant similar to that of
iron borides. Moreover, the results of previous studies suggest
that chromium accumulates in the outermost region of the FeB/
Fe2B layer (see (Ref 23) and references therein). Alternatively,
molybdenum displays a much lower tendency to dissolve in the
boride layer and tends to concentrate beneath the surface layers
(Ref 24). As shown in Fig. 4, the results of EDS analyses
4. Results and Discussions
The characteristics of borided AISI M2 steel indicated that
the formation of FeB/Fe2B layers was controlled by the
diffusion of boron at the steel surface. Figure 2 shows the
smooth morphology of the microstructure of the FeB/Fe2B
layers. The diffusion of boron was dependent on the crystallographic direction of anisotropic crystals in the boride layers.
Nuclei of iron borides were oriented with respect to the surface
in such a way that the crystallographic directions and lattice
imperfections were oriented perpendicularly to the diffusion
front, which caused the FeB/Fe2B layers to grow in the
direction of the substrate. Moreover, the growth rate and phase
Fig. 2 Cross-sectional views of FeB and Fe2B layers formed at the
surface of AISI M2 steel with boriding conditions of (a) 1173 K
with exposure time of 8 h, and (b) 1323 K with exposure time of
6h
Journal of Materials Engineering and Performance
Author's personal copy
revealed that the chemical composition of the steel propitiates
the dissolution of tungsten in the surface layer, which results in
the formation of WC interstitial compounds.
Vickers microhardness indentations were applied along the
FeB/Fe2B layers of the samples produced at different boriding
Fig. 3 XRD pattern of AISI M2 steel boriding at the temperature
of 1273 K with 8 h of exposure
temperatures and exposure times, as shown in Fig. 5. At a
distance of approximately 10 lm from the AISI M2 borided
steel, the hardness values of the specimens approximately
ranged from 1900 to 2700 HV. Moreover, at an exposure time
of 8 h, the hardness of the boride layer decreased as the
temperature increased to 1273 K, as shown in Fig. 6. As
stated by Genel et al. (Ref 25), a reduction in the hardness of
the layer can be attributed to grain coarsening. In contrast,
according to Galibois et al. (Ref 26), thermal residual stresses
produced by the growth of the surface layers and the
difference between the specific volume of the substrate and
the coating can have a significant effect on the hardness-depth
profile.
As shown in Fig. 7, the dependence of the thicknesses of the
FeB layer (u) and the entire boride layer (FeB + Fe2B) (v) on
the exposure time was parabolic, which is indicative of
diffusion-controlled growth. Moreover, for both layers, the
boride incubation time decreased with an increase in boriding
temperature. The values of k and kFeB were obtained from the
slope of the straight line shown in Fig. 7, and the boron
diffusion coefficients of the Fe2B and FeB layers, (DFe2 B and
DFeB , respectively) were obtained from Eq 19 and 20. The
diffusion coefficients of each exposure time and boriding
temperature were strongly related to the thickness of the boride
Fig. 4 (a) SEM image of cross-sectional view of AISI M2 steel boriding at 1273 K with 8 h of exposure and (b) EDS spectrum of the borided
sample
Journal of Materials Engineering and Performance
Author's personal copy
1600
T = 1173 K
T = 1223 K
1200
T = 1273 K
u2(µm2)
T = 1323 K
800
400
0
0
5
10
15
(a)
20
25
30
35
25
30
35
Time (x103) (s)
12000
T = 1173 K
10000
T = 1223 K
T = 1273 K
v 2(µm2)
8000
T = 1323 K
6000
4000
2000
0
0
5
10
(b)
Fig. 5 Vickers microhardness testing performed across the FeB/
Fe2B layers formed in AISI M2 steel boriding at (a) 1273 K with
8 h of exposure and (b) 1323 K with 6 h of exposure
207 kJ=mol
; m2 s1
DFe2 B ¼ 1:06 10 exp RT
223 kJ=mol
; m2 s1
DFeB ¼ 3:4 103 exp RT
2500
Microhardness (Hv)
20
Fig. 7 (a) Evolution of the FeB layer as a function of exposure
time and (b) Evolution of the (FeB + Fe2B) layers as a function of
exposure time
3
2300
2100
1900
1700
1500
1150
15
Time (x103) (s)
1200
1250
1300
1350
Boriding temperature (K)
Fig. 6 Hardness behavior as a function of the boriding temperatures with 8 h of exposure at 10 lm from the surface of AISI M2
borided steel
layer. In the Arrhenius equation, the mean values of the
diffusion coefficients were expressed as a function of the
temperature, as shown in Fig. 8. The behaviors of the boron
diffusion coefficients in the studied range of the boriding
temperatures can be described by the following equations:
ðEq 23Þ
ðEq 24Þ
The activation energies of both layers over the entire
temperature range were indicative of homogeneous diffusion,
and the pre-exponential factors were strongly dependent on the
composition of the borided steel (Ref 22). The relatively highactivation energies shown in Table 1 were attributed to the
formation of FeB, Fe2B, CrB, and/or Cr2B phases in the boride
layer, and the relatively high concentration of the alloying
element. In addition, the diffusion kinetics of the boride layer
had a significant effect on the boron potentials of surface layers
produced through different boriding methods. In powder-pack
boriding, boron diffusion is affected by the contact surface
between the boriding agent and the substrate. In other words,
fine particle sizes allow for better diffusion of boron atoms into
the material (Ref 27). In the paste-boriding process, the growth
kinetics of the boride layer are a function of the thickness of the
boron paste on the surface of the material. For instance, as the
paste thickness increases, higher boron mobility in the boride
layer is observed (at a constant treatment temperature), along
with a reduction in the activation energy (Ref 28).
Journal of Materials Engineering and Performance
Author's personal copy
Nevertheless, the optimal boride layer is not necessarily the
thickest layer. Thus, the thickness of the boride layer should be
matched to the intended application (Ref 30). Using Eq 19 and
20, the diffusion model was extended to estimate the thickness
of the Fe2B and FeB layers formed at the surface of AISI M2
borided steel:
The behaviors of the parameters kFeB =½1 t0FeB ðT Þ=t1=2 and
k=½1 t0Fe2 B ðT Þ=t1=2 are dependent on the boriding temperature and can be expressed by the following equations, as shown
in Fig. 9:
gðT Þ ¼ k=½1 t0Fe2 B ðT Þ=t1=2 ¼ 1 1033 T 8:5852 ;
ðEq 27Þ
l ¼2t1=2 a3 DFe2 B =fða4 þ a3 =2Þk=½1 t0Fe2 B ðT Þ=t1=2
þ ða3 =2ÞkFeB =½1 t0FeB ðT Þ=t1=2 g;
m
u ¼2t a1 DFeB = ða4 þ a3 =2Þk=½1 t0Fe2 B ðT Þ=t1=2
þða3 =2 þ a2 þ a1 =2ÞkFeB =½1 t0FeB ðT Þ=t ; m
m s1=2
ðEq25Þ
eðT Þ ¼ kFeB =½1 t0FeB ðT Þ=t1=2 ¼ 2 1033 T 8:3633 ;
m s1=2
ðEq 28Þ
1=2
ðEq25Þ
Thus, Eq 25 and 26 can be modified in the following
manner:
l ¼ 2t1=2 a3 DFe2 B =½ða4 þ a3 =2ÞgðT Þ þ ða3 =2ÞeðT Þ;
m
ðEq 29Þ
Fig. 8 Dependence between the boron diffusion coefficients and
boriding temperature: (a) FeB layer and (b) Fe2B layer
Fig. 9 (a) Behavior of the gðT Þ parameter as a function of temperature and (b) eðT Þ parameter as a function of boriding temperature
Table 1 Activation energy values obtained for different borided steels
Material
AISI
AISI
AISI
AISI
M2
H13
316L
M2
Method of
boriding
Paste
Powder pack
Powder pack
Powder pack
Phases in
boride layer
FeB,
FeB,
FeB,
FeB,
Fe2B
Fe2B, CrB, Cr2B
Fe2B, CrB, Cr2B, Ni3B
Fe2B, CrB, Cr2B
Journal of Materials Engineering and Performance
Morphology
of the boride
layer
Activation
energy of FeB
layer, kJ mol21
Activation
energy of Fe2B
layer, kJ mol21
Reference
Smooth
Smooth
Smooth
Smooth
283
…
204
223
239.4
186.2
198
207
28
29
20
This study
Author's personal copy
u ¼ 2t 1=2 a1 DFeB =½ða4 þ a3 =2ÞgðT Þ
þ ða3 =2 þ a2 þ a1 =2ÞeðT Þ; m
ðEq 30Þ
Using Eq 29 and 30, the variations in the thicknesses of the
Fe2B and FeB layers as a function of the temperature and
exposure time for the powder-pack boriding of AISI M2 steel
are represented by contour plots (Fig. 10). In borided highalloy steels, the optimal thickness of the boride layer is 1520 lm, which allows the FeB/Fe2B layers to be applied to tools
used for the chipless formation of metals (Ref 30).
Sen et al. (Ref 8) proposed several empirical equations (i.e.,
Paraboloid, Gaussian, and Lorentzian equations) to determine
the thicknesses of the composite boride layers (FeB + Fe2B) of
different borided steels as a function of the exposure time and
boriding temperature. In this study, the constant values of the
Paraboloid, Gaussian, and Lorentzian equations presented in
Tables 2 and 3 were adjusted to the experimental data of boride
layers (FeB and Fe2B) obtained at temperatures of 11731323 K and exposure times of 4, 6, and 8 h for the powderpack boriding of AISI M2 steel.
In addition, the Paraboloid, Gaussian, and Lorentzian
equations were used to estimate the thicknesses of the Fe2B
and FeB layers at an exposure time of 10 h and different
boriding temperatures (Fig. 11), and the results were compared
to those obtained from Eq 29 and 30 for AISI M2 borided
steels. The results obtained from Eq 29 and 30 were in good
agreement with the experimental data and the theoretical results
of the empirical equations shown in Tables 4 and 5. Hence,
Eq 29 and 30 can be used as a simple tool to predict the
thickness of the FeB and Fe2B layer on borided steels,
according to their practical applications.
5. Conclusions
The growth kinetics of FeB/Fe2B layers formed at the
surface of AISI M2 borided steel were estimated at temperatures of 1123-1323 K and different exposure times. The results
revealed that diffusion-controlled growth occurred in both
Fig. 10 Contour plots estimated by Eq 29 and 30 that describe the evolution of surface layers obtained by the powder-pack boriding of AISI
M2 steel: (a) Fe2B layer and (b) FeB layer
Table 2 Empirical equations used in the estimation of the Fe2B layer thickness formed at the surface of AISI M2 steel
boriding by the powder-pack method
Equations
Formulas
Paraboloid
lðt; T Þ ¼ 1053:817254 þ 1:202368 103 t 1:940696T 9:999302 109 t 2 8:834597 104 T 2
Gaussian
Lorentzian
(
1
lðt; T Þ ¼ 518:033219 exp 2
"
#)
t 42512:505551 2
T 1823:888569 2
þ
28413:326830
251:659694
78:832122
#"
#
t 37324:695805 2
T 1361:633125 2
1þ
1þ
29750:474383
104:111833
lðt; T Þ ¼ "
ðR2 ¼ 0:960356Þ
ðR2 ¼ 0:998574Þ
ðR2 ¼ 0:996017Þ
t = exposure time, s; T = boriding temperature, K
Journal of Materials Engineering and Performance
Author's personal copy
Table 3 Empirical equations used in the estimation of the FeB layer thickness formed at the surface of AISI M2 steel
boriding by the powder-pack method
Equations
Formulas
Paraboloid
uðt; T Þ ¼ 215:154790 þ 1:343046 103 t 0:495677T 1:750426 108 t 2 þ 2:574646 104 T 2 ðR2 ¼ 0:942907Þ
(
"
#)
1 t 34159:854302 2
T 1535:069970 2
þ
uðt; T Þ ¼ 84:607731 exp ðR2 ¼ 0:963663Þ
2
18705:046854
174:201179
Gaussian
45:223055
#"
#
t 32346:112903 2
T 1356:470711 2
1þ
1þ
19368:700584
102:338823
t = exposure time, s; T = boriding temperature, K
Lorentzian
uðt; T Þ ¼ "
ðR2 ¼ 0:940648Þ
Table 4 Experimental and predicted values of the Fe2B
layer thicknesses at temperatures of 1173, 1223, 1273,
and 1323 K with 10 h of exposure
Temperature, K
Equations
1173
1223
1273
1323
Predicted Fe2B layer thicknesses, lm
Paraboloid
Gaussian
Lorentzian
From Eq 29
Experimental Fe2B layer thickness, lm
23.28
17.79
18.37
17.48
19.66
32.08
29.17
28.37
30.50
32.81
45.30
45.96
45.61
45.90
51.83
62.94
69.61
69.15
70.60
72.28
Table 5 Experimental and predicted values of the FeB
layer thicknesses at temperatures of 1173, 1223, 1273,
and 1323 K with 10 h of exposure
Temperature, K
Equations
1173
1223
1273
1323
Predicted FeB layer thicknesses, lm
Paraboloid
13.64 19.70 27.05 35.68
Gaussian
9.71 16.92 27.15 40.13
Lorentzian
10.36 16.17 26.22 39.44
From Eq 30
9.07 16.05 27.01 42.51
Experimental FeB layer thickness, lm 10.17 20.98 28.30 40.24
Acknowledgments
Fig. 11 Cross-sectional views of FeB/Fe2B layers formed as a consequence of the boriding of AISI M2 steel: (a) 1173 K with 10 h of
exposure and (b) 1323 K with 10 h of exposure
boride layers, and the presence of alloying elements in the
substrate diminished the kinetics of the layers. The proposed
diffusion model was used to estimate the boron diffusion
coefficients of the FeB/Fe2B layers and the thicknesses of the
boride layers under the applied set of experimental parameters.
In addition, the experimental data obtained at 10 h of exposure
and different boriding temperatures were in agreement with the
theoretical results of the proposed model and various empirical
models presented in the literature.
Journal of Materials Engineering and Performance
This study has been supported by the research grants 150556
from CONACyT and 20120594 from the Instituto Politecnico
Nacional in Mexico. The authors wish to thank M. en C. Omar
Novelo and Omar Damian Mejia for their valuable collaboration
for this study.
References
1. C.M. Brakman, A.W.J. Gommers, and E.J. Mittemeijer, Boriding of Fe
and Fe C, Fe-Cr, and Fe-Ni Alloys: Boride Layer Growth Kinetics,
J. Mater. Res., 1989, 4, p 1354–1370
2. J.R. Davis, Surface Hardening of Steels: Understanding the Basics,
ASM International, Materials Park, OH, 2002
3. S. Sahin, Effects of Boronizing Process on the Surface Roughness and
Dimensions of AISI, 1020, AISI, 1040 and AISI, 2714, J. Mater.
Process. Technol., 2009, 209, p 1736–1741
Author's personal copy
4. J. Pelleg and M. Judelewicz, Diffusion in the B-a-Fe System and
Compound Formation Between Electron Gun Deposited Boron Thin
Films and Steel Substrate, Thin Solid Films, 1992, 215, p 35–41
5. K. Raic, Z. Acimovic, N. Vidojevic, and N. Novovic-Simovic,
Modelling of Fe2B Boride Layer Growth, J. Serb. Chem. Soc., 1996,
61, p 181–188
6. E. Meléndez, I. Campos, E. Rocha, and M.A. Barrón, Structural and
Strength Characterization of Steels Subjected to Boriding Thermochemical process, Mater. Sci. Eng. A, 1997, 234–236, p 900–903
7. I. Campos, J. Oseguera, U. Figueroa, J.A. Garcı́a, O. Bautista, and G.
Kelemenis, Kinetic Study of Boron Diffusion in the Paste Boriding
Process, Mater. Sci. Eng. A, 2003, 352, p 261–265
8. S. Sen, U. Sen, and C. Bindal, An Approach of Kinetic Study of
Borided Steels, Surf. Coat. Technol., 2005, 191, p 274–285
9. L.G. Yu, X.J. Chen, K.A. Khor, and G. Sundararajan, FeB/Fe2B Phase
Transformation During SPS Pack-Boriding: Boride Layer Growth
Kinetics, Acta Mater., 2005, 53, p 2361–2368
10. I. Campos, R. Torres, G. Ramı́rez, R. Ganem, and J. Martı́nez, Growth
Kinetics of Iron Boride Layers: Dimensional Analysis, Appl. Surf. Sci.,
2006, 252, p 8662–8667
11. M. Keddam, Computer Simulation of Monolayer Growth Kinetics of
Fe2B Phase During the Paste-Boriding Process: Influence of the Paste
Thickness, Appl. Surf. Sci., 2006, 253, p 757–761
12. I. Campos, O. Bautista, G. Ramı́rez, M. Islas, J. De la Parra, and L.
Zúñiga, Effect of Boron Paste Thickness on the Growth Kinetics of
Fe2B Boride Layers During the Boriding Process, Appl. Surf. Sci.,
2005, 243, p 429–436
13. V.I. Dybkov, Growth of Boride Layers on the 13% Cr Steel Surface in
a Mixture of Amorphous Boron and KBF4, J. Mater. Sci., 2007, 42,
p 6614–6627
14. I. Campos-Silva, M. Ortiz-Domı́nguez, M. Keddam, N. LópezPerrusquia, A. Carmona-Vargas, and M. Elias-Espinosa, Kinetics of
the Formation of Fe2B Layers in Gray Cast Iron: Effects of Boron
Concentration and Boride Incubation Time, Appl. Surf. Sci., 2009, 255,
p 9290–9295
15. I. Campos-Silva, M. Ortiz-Domı́nguez, N. López-Perrusquia, A.
Meneses-Amador, R. Escobar-Galindo, and J. Martı́nez-Trinidad,
Characterization of AISI, 4140 Borided Steels, Appl. Surf. Sci., 2010,
256, p 2372–2379
16. I. Campos-Silva, M. Ortiz-Domı́nguez, H. Cimenoglu, R. EscobarGalindo, M. Keddam, M. Elias-Espinosa, and N. López-Perrusquia,
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
Diffusion Model for Growth of Fe2B Layer in Pure Iron, Surf. Eng.,
2011, 27, p 189–195
T.B. Massalski, Binary Alloys Phase Diagrams, ASM International,
Cleveland, OH, 1990
T. Van Rompaey, K.C. Hari Kumar, and P. Wollants, Thermodynamic
Optimization of the B-Fe System, J. Alloys Compd., 2002, 334, p 173–
181
U. Roy, Phase Boundary Motion and Polyphase Diffusion in Binary
Metal-Interstitial Systems, Acta Metall., 1968, 16, p 243–253
I. Campos-Silva, M. Ortiz-Domı́nguez, O. Bravo-Bárcenas, M.A.
Doñu-Ruiz, D. Bravo-Bárcenas, C. Tapia-Quintero, and M.Y. JiménezReyes, Formation and Kinetics of FeB/Fe2B Layers and Diffusion
Zone at the Surface of AISI, 316 Borided Steels, Surf. Coat. Technol.,
2010, 205, p 403–412
V.I. Dybkov, W. Lengauer, and P. Gas, Formation of Boride Layers at
the Fe-25% Cr Alloy-Boron Interface, J. Mater. Sci., 2006, 41, p 4948–
4960
K. Matiasovsky, M. Chrenkova-Paucirova, P. Fellner, and M. Makyta,
Electrochemical and Thermochemical Boriding in Molten Salts, Surf.
Coat. Technol., 1988, 35, p 133–149
C. Badini, C. Gianoglio, and G. Pradelli, The Effect of Carbon,
Chromium and Nickel on the Hardness of Borided Layers, Surf. Coat.
Technol., 1989, 30, p 157–170
I.S. Dukarevich, M.V. Mozharov, and A.S. Shigarev, Redistribution
of Elements in Boride Coatings, Metallovedenie i Termicheskaya
Obrabotka Metallov, 1973, 2, p 64–66
K. Genel, I. Ozbek, and C. Bindal, Kinetics of Boriding of AISI, W1
Steel, Mater. Sci. Eng. A, 2003, 347, p 311–314
A. Galibois, O. Boutenko, and B. Voyzelle, Mécanisme de formation
des couches borurées sur les aciers a haut carbone-1 Technique des
pates, Acta Metall., 1980, 28, p 1753–1763
A. Graf von Matuschka, Boronizing, Carl Hanser Verlag, Munich,
Germany, 1980
I. Campos, R. Torres, O. Bautista, G. Ramı́rez, and L. Zuñiga, Effect of
Boron Paste Thickness on the Growth Kinetics of Polyphase Boride
Coatings During the Boriding Process, Appl. Surf. Sci., 2006, 252,
p 2396–2403
K. Genel, Boriding Kinetics of H13 Steel, Vacuum, 2006, 80, p 451–
457
W. Fichtl, Boronizing and Its Practical Applications, Mater. Eng., 1981,
2, p 276–286
Journal of Materials Engineering and Performance