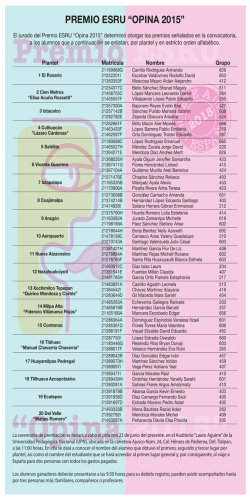
Laboratorio de Mecánica de los Fluidos II CIHAM-UC
Laboratorio de Hidráulica Elías Sánchez Díaz CIHAM-UC Pag. 1 Universidad de Carabobo Facultad de Ingeniería Escuela de Ingeniería Civil Departamento de Ingeniería Ambiental Centro de Investigaciones Hidrológicas y Ambientales. MANUAL DE PRACTICAS DE LABORATORIO MECANICA DE LOS FLUIDOS II. (Versión 2-2016) Actualizada por: Ing. Adriana Márquez Ing. Maryelvi Jiménez Publicado: 31/10/2016 Revisada por: Ing. Betty Farías Ing. Daniel Carrión Ing. Martha Campos Laboratorio de Hidráulica Elías Sánchez Díaz CIHAM-UC Pag. 2 Índice General 1. 2. 3. 4. 5. 6. Breve descripción del laboratorio. Plan de evaluación. Cronograma de Actividades. Reglamentos del Laboratorio de Mecánica de los Fluidos. Conocimientos Básicos para el proceso de enseñanza del laboratorio de mecánica de los fluidos II. Practicas a realizar: a. Medición de Caudales. b. Descarga sobre vertederos c. Resalto Hidráulico d. Flujos Laminar y Turbulento. e. Distribución de Velocidades. f. Pérdida de Energía en Válvulas. g. Flujo sobre cuerpos sumergidos. 7. Taller a realizar: a. Medición de Caudales con tecnología moderna. 8. Anexos. Breve Descripción del Laboratorio. Sabemos por experiencia que el proceso de enseñanza aprendizaje de la asignatura Mecánica de los Fluidos se hace compleja al alumnado, ya que el comportamiento de los fluidos no lo pueden ver con sus propios ojos y el aprendiz debe creer en todas las formulas que les suministran los profesores y confiar en el resultado que ellas dictan. A través del laboratorio se puede apreciar el comportamiento de los fluidos y a su vez entenderlos mucho mejor. Es nuestro interés como facilitadores del aprendizaje motivar el aprovechamiento máximo de cada práctica que se va desarrollar a lo largo del semestre. El Laboratorio de Mecánica de los Fluidos “Elías Sánchez Díaz”, cuyo nombre es en honor a un gran Investigador de la Hidráulica en Venezuela, fue diseñado en los años 70 por el Ingeniero Zindrich Brezzina, experto en ingeniería Hidráulica, recordado principalmente por haber diseñado el puerto de la Guaira. Se le coloca el nombre de Elías Sánchez Díaz motivado a que el ingeniero Sánchez, quien realizó estudios de Postgrado en Ingeniería Ambiental en la Universidad de Florida en el Campo de Gainsville, muere de cáncer a mediados de los 80 cuando Brezzina termina la construcción del laboratorio y le colocan el nombre en su honor. El primer técnico de máquina, quien junto a Brezzina construyó el laboratorio fue Severino Manfredinni y en ese entonces formaban parte del grupo docente profesores como Emilio Porta Lilly, Ron de la Rica, Francisco Camacho, Humberto Cartaya, Miguel Montilva y por supuesto Elías Sánchez. Este grupo de profesores crearon el Centro de Investigaciones Hidráulicas (CIH) y formaron parte de una época donde Venezuela era la cuna de las obras hidráulicas. El Ingeniero Arnoldo Gómez narra que solo el Ingeniero Humberto Cartaya diseñó 235 presas en su vida. En el año 2007 el profesor Edilberto Guevara reactiva el CIH y le cambia el nombre a Centro de Investigaciones Hidrológicas y Ambientales de la Universidad de Carabobo (CIHAM-UC) El laboratorio cuenta con equipos que fueron donados por el Príncipe de Gales, formados por bancos de turbinas hidráulicas. Estos bancos se encuentran en recuperación gracias a convenios realizados por la Ing. Adriana Márquez con CORPOELEC. El laboratorio ha sido adaptado y remodelado hasta esta época gracias al aporte de profesores que en conjunto con los estudiantes y con la ayuda institucional han logrado cambios importantes en las instalaciones. Actualmente se logró unificar las instalaciones con el Centro de Investigaciones Hidrológicas y Ambientales de la Universidad de Carabobo (CIHAM-UC), con el fin de incentivar a los Investigadores y tesistas en el desarrollo de la hidráulica y la hidrología; ramas de gran importancia para la protección y el estudio del medio ambiente. Adicionalmente podemos contar con los equipos del CIHAM-UC para instruir sobre tecnologías modernas a los estudiantes. En el año 2015 a través de proyectos de Laboratorio de Hidráulica Elías Sánchez Díaz CIHAM-UC Pag. 3 fortalecimiento de FONACYT desarrollados por la Prof. Adriana Márquez se desarrolla el mantenimiento del sistema de recirculación, equipos y espacios físicos del laboratorio. El laboratorio consta de siete equipos y un taller, donde el aprendiz podrá poner en práctica los conocimientos adquiridos en Mecánica de los Fluidos I y II. Estas prácticas son las siguientes: - Medición de Caudales. - Descarga sobre vertederos. - Resalto Hidráulico. - Flujos Laminar y Turbulento. - Distribución de Velocidades. - Pérdida de Energía en Válvulas. - Flujo sobre cuerpos sumergidos. El taller se realiza con unos equipos del CIHAM-UC de tecnología de punta y es el siguiente: - Medición de caudales con tecnología moderna. A excepción de las practicas “Distribución de Velocidades” y “Flujo Laminar y Turbulento” las otras cinco funcionan a través de un sistema de recirculación que permite mantener un flujo permanente en cada equipo. El equipo de la práctica “Flujo Laminar y Turbulento” funciona independientemente en un aparato modificado de Reynolds y “Distribución de Velocidades” es el único equipo del Laboratorio cuyo fluido que se analiza es aire (generado por una aspiradora), ya que en los otros se utiliza agua. El sistema de recirculación consta de dos tanques, uno elevado de nivel constante a una altura de 6mts, de capacidad de 45.000 lts y otro subterráneo de capacidad 150.000 lts, en los cuales, un sistema de seis (6) bombas centrifugas colocadas en paralelo impulsan el agua del tanque subterráneo al tanque elevado, este último tiene un sistema de rebose que permite mantener el nivel de carga hidráulica en cada equipo. Un tubo de 10”y un canal rectangular de concreto en el piso del laboratorio para el retorno al tanque subterráneo y tuberías de 10”, 6” y 4” que se conectan a los diferentes equipos: túnel de agua, el banco de tuberías de plástico de diferentes diámetros, el chorro en descarga libre y los dos canales de vidrio de 30 y 60cm de ancho respectivamente. Si todos los equipos están en funcionamiento para mantener condiciones estables hay que encender tres de las bombas. En la Figura 1 se puede observar el esquema del funcionamiento. FIGURA 1: Rebose del tanque superior para conservar el nivel. TANQUE ELEVADO Cap.:45.000lts Sistema de Tuberías que Distribuyen a cada equipo. B1 B2 B3 B4 B5 B6 Sistema de Bombeo en Paralelo TANQUE SUBTERRANEO Cap.:150.000 LTS Sistema de canales que recirculan el fluido al tanque inferior. Laboratorio de Hidráulica Elías Sánchez Díaz CIHAM-UC Pag. 4 A fin de conservar las instalaciones del Laboratorio, el sistema de bombeo, el encendido y apagado de cada equipo solo debe ser manipulado por el Técnico de Maquinas, el Docente a cargo de la Practica, los preparadores o a su defecto, bajo la supervisión de los mismos. Plan de Evaluación El laboratorio de Mecánica de los Fluidos II, tiene un valor del 20% de la nota de Teoría de la asignatura, y si un alumno no aprueba el laboratorio automáticamente reprueba la teoría. 1 PRESENTACION, FORMACION DE GRUPOS, NORMAS DEL LABORATORIO. INTRODUCCION TEORICA 1 3 4 INTRODUCCION TEORICA 2 REALIZACION DE LA PRACTICA #1 5 REALIZACION DE LA PRACTICA #2 6 REALIZACION DE LA PRACTICA #3 7 REALIZACION DE LA PRACTICA #4 8 REALIZACION DE LA PRACTICA #5 9 REALIZACION DE LA PRACTICA #6 10 REALIZACION DE LA PRACTICA #7 11 12 TALLER DE LABORATORIO SOBRE NUEVAS TECNOLOGICAS UTILIZADAS EN LA HIDRÁULICA ENTREGA DE PROYECTO AMBIENTAL Estrategia de Evaluación: La evaluación se desarrollará a través de las siguientes estrategias: - Informes y Taller ……………. 70% - Evaluación corta………....…. 10%. - Proyecto Ambiental Final…... 20% ___________________ Total: 100% FLUJO SOBRE CUERPOS SUMERGIDOS PERDIDA DE ENERGIAEN VALVULA DISTRIBUCION DE VELOCIDADES FLUJO LAMINAR Y TURBULENTO RESALTO HIDRAULICO SEMANA DESCARGA SOBRE VERTEDEROS ACTIVIDAD A DESARROLLAR MEDICION DE CAUALES Modo de Trabajo: Se formarán cinco (5) grupos de un máximo de tres (3) personas, cada grupo se le asignará una letra de la A a la E, esa será la identificación del grupo, en la tabla siguiente se muestra el cronograma de actividades donde podrán visualizar la práctica que le corresponde a cada grupo en el transcurso del semestre. INTRODUCCIÓN A LAS BASES TEORICAS DEL LABORATORIO - - - A,B,C D,E D,E A,B,C - - A, E D C B - A,B,C, D,E B A D, E C - - - C B, E A D - D C B A, E - A,B,C,D,E EVALUACIÓN SUMATIVA Laboratorio de Hidráulica Elías Sánchez Díaz CIHAM-UC Pag. 5 Informes: Tienen un valor de 70%, deben ser realizados a bolígrafo y el contenido del mismo se muestra en la tabla [1]. Tabla 1. Contenido del Informe de Laboratorio Contenido Portada Tabla de Recolección de Datos Objetivo de la Practica Introducción teórica Cálculos Preliminares Informe a presentar Conclusión Bibliografía Observación del Contenido Nombre de la Práctica, Nombres de los integrantes del grupo, Nombre del grupo y Fecha. Deberá estar firmada por el profesor y los integrantes del grupo que asistieron. Aparece en la guía Favor no utilizar la de la guía, la idea es que profundicen. Estos los realizan en el laboratorio el día de la práctica, seguir instrucciones de la guía. Colocar 1 ejemplo de cálculo y los repetitivos colocarlos en tablas. Seguir las instrucciones de la guía en la sección informe a presentar. Colocar 1 ejemplo de cálculo y los repetitivos ponerlos en tablas. En las gráficas los puntos experimentales no se les debe trazar la curva probable a menos que le guía lo indique. A los puntos teóricos siempre se deben trazar la curva. Concluir en base a la experiencia, haciendo referencia a los gráficos y los resultados obtenidos. Recuerde que cada practica tiene un objetivo y en la conclusión debo dar respuesta al mismo. Se agradece no usar mafias. Colocar todos los textos y páginas web utilizadas. Puntos Obligatorio Obligatorio 0.5 2 1 3 graficas 5 cálculos informe 8 0.5 Taller: El taller está incluido en el 70%, junto a los informes. Trata sobre las últimas tendencias tecnológicas en la medición de la hidráulica. El taller será desarrollado y guiado por el profesor utilizando los equipos pertenecientes al Centro de Investigaciones Hidrológicas y Ambientales de la Universidad de Carabobo (CIHAM-UC). Evaluación Corta: Las evaluaciones cortas tienen un valor del 10%. Al comenzar la práctica, el docente deberá realizar una prueba corta de la práctica que están desarrollando, la cual podrá ser oral o escrita. Las preguntas contemplarán los principios teóricos de la práctica y las aplicaciones de la misma en el ejercicio de la profesión. Proyecto Ambiental Final: Al final del semestre el docente realizará una evaluación denominada Proyecto Ambiental Final, el cual consiste en introducir a los estudiantes en el desarrollo de proyectos grupales para mejorar problemas de su entorno, tomando como lugar piloto, el laboratorio Elías Sánchez Díaz. Tiene un valor de 20%. Laboratorio de Hidráulica Elías Sánchez Díaz CIHAM-UC Pag. 6 Importancia de la Asistencia. La asistencia al laboratorio no tiene ponderación en la nota del alumno, sin embargo, solo podrán recuperar (1) una sola practica con su debido justificativo. La práctica perdida será recuperada al final del semestre según el cronograma de actividades. El técnico de maquina al pasar los 15 minutos del horario de inicio de la practica automáticamente cerrará la puerta del laboratorio y los alumnos que queden rezagados serán tomados como no asistentes. Normativa Interna del Laboratorio. 1. Está terminantemente prohibido comer y tomar bebidas en las instalaciones del Laboratorio. 2. Se prohíbe fumar. 3. Por normas de seguridad e higiene le sugerimos a los alumnos asistir a clases con pantalón largo y zapatos cerrados para evitar posibles accidentes. 4. Los informes serán entregados al comienzo de la práctica, si se entrega el informe posterior a la hora de entrada se descontará 1 punto y por cada día de retraso se descontarán 2 puntos. 5. Solo se permitirá la recuperación de 1 práctica con su debido justificativo, la cual se recuperará al final del semestre. 6. El alumno que llegué después de que el técnico de maquina haya cerrado la puerta (pasados 15 minutos), perderá automáticamente la práctica. 7. Mantener el orden y el respeto mutuo en el desarrollo de las prácticas de Laboratorio. 8. Cada grupo deberá traer la hoja de recolección de datos de la práctica que le corresponde desarrollar. “Afina tus oídos a la sabiduría y concéntrate en el entendimiento. Clama por inteligencia y pide entendimiento. Búscalos como si fueran plata, como si fueran tesoros escondidos.” Proverbios 2:2-4 Laboratorio de Hidráulica Elías Sánchez Díaz PRACTICA: CIHAM-UC Pag. 7 Medición de Caudales OBJETIVO: Calibración de un codo corto de 90°, mediante medición del caudal y de la diferencia piezométrica entre el exterior e interior de dicho codo. Introducción Para la determinación del caudal sobre un escurrimiento se dispone de métodos directos e indirectos, cuyo uso dependerá de las facilidades de implementación y de la precisión con que se quiera hacer el ensayo. El método directo consiste en determinar el volumen o el peso del fluido que pasa por una sección en un lapso de tiempo específico. Los métodos indirectos suelen requerir una carga piezométrica, una diferencia de presiones o de velocidad en varios puntos de una sección, con base a cualquiera de estos datos se calcula posteriormente el gasto, mediante una ecuación específica del medidor usado. Uno de los métodos más sencillos que pueden aplicarse a desagües de líquidos, se basa en la geometría característica de los chorros al estar sometidos a la acción gravitatoria. En el ensayo a realizar, se dispone de un chorro de agua en salida horizontal de modo que, midiendo su alcance y altura de caída, se puede determinar la velocidad del mismo. Las ecuaciones a usar son idénticas a las que se aplican para el cálculo de movimiento de proyectiles, dado que son fenómenos equivalentes, es decir, 𝑥 = (𝑉𝑜)𝑥 . 𝑡 (1ª) 1 𝑦 = (𝑉0 )𝑦 . 𝑡 − 𝑔𝑡 2 2 (1b) Donde las coordenada (𝑥, 𝑦) corresponden al alcance y la altura de caída del chorro; (𝑉0 )𝑥 Y (𝑉0 )𝑦 son las componentes de la velocidad en el origen de coordenadas ubicado a la salida del chorro,𝑔 es la aceleración de gravedad y 𝑡 es el tiempo de caída libre de la vena líquida. La aproximación que se logra con este método es satisfactoria, siempre y cuando la dispersión del chorro no sea muy grande. Medidores de Presión diferencial Se han inventado o adaptado numerosos dispositivos para la medición de volúmenes de flujo, con una amplia gama de complejidad, tamaño y exactitud. Los medidores de presión diferencial se utilizan ampliamente en aplicaciones y laboratorios industriales por su sencillez, confiabilidad, robustez y bajo costo. Los tipos más comunes son: el medidor de placa orificio, el medidor Venturi, la tobera de flujo y el medidor de codo. Medidor de Codo: Se puede fabricar un medidor relativamente sencillo colocando derivaciones de presión en las partes exterior e interior de un codo de tubería. Si aplicamos la ecuación de momentum lineal a un volumen de control que abarca el fluido que está en el codo (o la ecuación de Euler normal a las líneas de corriente), podemos deducir la ecuación siguiente: Laboratorio de Hidráulica Elías Sánchez Díaz CIHAM-UC 𝑄=𝐶 Pag. 8 𝜋𝐷 2 4 𝑅 √ 𝑔∆ℎ (2) 𝐷 Donde Q es el caudal, C el coeficiente de descarga del codo, R es el radio de curvatura del codo, 𝐷 el diámetro del tubo, g la gravedad, ∆ℎ la diferencia piezométrica tomada con un manómetro diferencial. La forma más exacta de determinar el coeficiente de flujo C es mediante una calibración in situ del medidor. Sin embargo, se ha informado (Bean, 1971) de una relación para C de codos de 90º con derivaciones de presión situadas en un plano radial a 45º de la entrada: 𝑝𝑜 − 𝑝𝑖 ∆ℎ = 𝛾 𝐶 =1− 6.5 √𝑅𝑒 (3) Donde Re es el número de Reynolds, esta ecuación es válida con 104 ≤ 𝑅𝑒 = 𝑉.𝐷 𝜈 CODO PRESION PVC ½” ≤ 106 . El medidor de codo cuesta mucho menos que cualquiera de los medidores de presión diferencial, y por lo regular no aumenta la perdida de carga global del sistema de tuberías porque casi siempre el sistema de por sí incluye codos. D=16,6mm, R=30mm EQUIPO DE LABORATORIO C D B A F E Descripción del Equipo de Laboratorio: Medición de Caudales A Plomo para establecer nivel de salida D Cinta Métrica pegada a la malla. del chorro. B Válvula de control de ½” E Codo Soldado de ½” a calibrar C Manómetro diferencial F Tubería de Presión PVC ½” Laboratorio de Hidráulica Elías Sánchez Díaz CIHAM-UC Pag. 9 Tabla de Recolección de Datos MEDICION DE CAUDALES Practica: Grupo: Practica No.: Medición 1 Xo(cm) X(cm) h(cm) 2 DATOS DE LA EXPERIENCIA: Diámetro interior de la tubería PVC: 16,6 mm 3 Radio de curvatura del codo R: 30mm 4 Altura del chorro a la malla: 𝑦 = −108,5𝑐𝑚 5 Diámetro de salida del chorro: 7mm 6 7 8 9 10 Nombre y Apellido C.I. Firma Nombre del Profesor Firma del Profesor Fecha: / / Laboratorio de Hidráulica Elías Sánchez Díaz CIHAM-UC Pag. 10 PROCEDIMIENTO: 1. Tenga a mano la hoja de recolección de datos de la práctica. 2. Asegurarse que esté en funcionamiento el sistema de recirculación de agua. 3. Tomar la medida inicial indicada en la cinta métrica (D) en el punto donde se encuentra la plomada (A). 4. Abrir la válvula (B) para establecer un caudal. Esperar aproximadamente cinco (5) minutos para asegurar la estabilidad y permanencia del flujo. 5. Tomar la lectura del alcance del chorro al caer sobre la malla en la cinta métrica (D). 6. Medir la diferencia piezométrica indicada en el manómetro diferencial (C). 7. Repita los pasos 2 al 5 hasta completar ocho (8) lecturas distintas. 8. Cierre la válvula de control de flujo (B). 9. Llene la tabla de recolección de datos y realice los cálculos preliminares de las primeras dos mediciones realizadas. 10. Verifique con el profesor o los preparadores que los cálculos preliminares sean correctos y para la firma de la hoja de recolección de datos, la cual deberán anexar al informe. CALCULOS PRELIMINARES: 1. Haciendo uso de las ecuaciones (1ª y 1b) calcule los caudales con las velocidades y el área de salida. Recuerde Q=V.A 2. Determine el coeficiente de descarga experimental del codo para cada condición de corriente, haciendo uso de la ecuación (2). 3. Calcule el número de Reynolds del flujo en la tubería, recuerde que la velocidad de salida es diferente a la velocidad de la tubería. INFORME A PRESENTAR: 1. Introducción teórica, incluyendo un análisis de medidores de flujo de diferentes tipos y las ecuaciones utilizadas en cada caso. 2. Elabore en papel milimetrado la curva de calibración del codo, el caudal en función de las alturas piezométricas (Q vs ∆ℎ) 3. Encuentre el coeficiente según Bean “C” del codo bidimensional en estudio con la ecuación (3). 4. Mediante la ecuación (2) y con el coeficiente calculado en el paso anterior obtenga la curva de calibración del codo basada en los estudios de Bean (Q vs ∆ℎ). Superponga esta gráfica a la realizada en el paso 2. 5. Asuma en la ecuación (2) C=0.657 coeficiente obtenido de análisis de redes de corriente y obtenga la curva de calibración del codo (Q vs ∆ℎ) . Superponga esta gráfica a las realizadas en los pasos 2 y 4. 6. Grafique en papel semilogaritmico (C vs Reynolds), los coeficientes experimentales C calculados en el paso 2 de cálculos preliminares y los C de paso 3 de informe a presentar. 7. Los análisis de redes de corriente indican que el C del codo es de 0.657, superponga este valor a la gráfica anterior. Recuerde que se representa con una recta constante. 8. Comente sus resultados, posibles fuentes de error, precisión del método de medición de caudales utilizado. Establezca conclusiones. 9. Referencias bibliográficas. Laboratorio de Hidráulica Elías Sánchez Díaz PRACTICA: CIHAM-UC Pag. 11 Descarga sobre Vertederos OBJETIVO: Determinación de los coeficientes de descarga de un vertedero vertical en un canal rectangular y de un vertedero triangular en V90°, en función de su altura y carga. Se define como vertedero a toda estructura construida en un canal abierto por encima de la fluye una corriente, con el propósito de aforarlo. Si se clasifican los vertederos en relación a la forma de la abertura por la que vierte el líquido, pueden ser rectangulares, parabólicos o cualquiera otra forma regular. El borde o la superficie superior en contacto con el líquido recibe el nombre de Cresta y de acuerdo con su forma, se consideran de cresta aguda, según sea el borde de contacto afilado, donde el líquido solo tiene una línea de contacto al desaguar con el vertedor; o bien ancha, que el borde sea una superficie donde el líquido al pasar entra en contacto con una parte significativa del dispositivo. Vertederos Rectangulares: La ecuación general de descarga de un vertedero rectangular, se obtiene a partir de la teoría general de orificios y ranuras. La integración de la ecuación diferencial de la lámina vertiente que vierte por una ranura da lugar a una expresión de la forma: 2 𝑄 = 3 𝐶𝑑 𝐵ℎ√2𝑔 ℎ (1) ℎ 𝑤 Donde B es el ancho del canal, g es la aceleración de gravedad, h la carga de agua sobre el vertedero, Cd el coeficiente de descarga y Q el caudal en el canal. Un vertedero bidimensional de pared delgada sin contracciones extremas pero con influencia de la gravedad, hace que 𝐶𝑑 tenga como ecuación la siguiente: ℎ 𝐶𝑑 = 𝐶𝑐 [( ℎ𝑣 + 1) 3⁄ 2 ℎ 3⁄ 2 − ( ℎ𝑣) ] (2) En la cual, ℎ𝑣 = 𝑣02 ⁄2𝑔 es la carga de velocidad en el canal y 𝐶𝑐 es el coeficiente de contracción de la lámina vertiente. En primera aproximación, este último se estima en forma similar a orificio bidimensional, con la relación 𝑏⁄𝐵 = Laboratorio de Hidráulica Elías Sánchez Díaz CIHAM-UC Pag. 12 ℎ⁄(ℎ + 𝑤) y el ángulo del vertedero con la dirección horizontal del flujo; el parámetro w es la altura del vertedero. La tabla 1 muestra los valores de coeficiente de contracción bidimensional referido para vertederos con pared vertical. 0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1 ℎ/(ℎ + 𝑤) 0,611 0,612 0,616 0,622 0,631 0,644 0,662 0,687 0,722 0,781 1,000 𝐶𝑐 90º Tabla1.: Coeficiente de contracción en Vertederos Rectangulares con pared de 90º (Vertical) Para determinar a 𝐶𝑑 se resuelve la ecuación (2) por tanteos sucesivos, asumiendo inicialmente nula la carga de velocidad. En los casos de paredes verticales sin contracción lateral, a veces se prefiere el uso de formulas explícitas de naturaleza empírica o experimental. Las de uso más común son las siguientes: ℎ 𝐶𝑑 = 0,611 + 0,075 𝑤 (3) Siempre que h mayor a 5 cm. Una fórmula más reciente es: ℎ 𝐶𝑑 = 0,605 + 0,08 𝑤 + 0,001 ℎ (4) Vertederos Triangulares: Los vertederos triangulares descargan una lámina vertiente tridimensional que los diferencia claramente del orificio bidimensional. Se les usa ampliamente para la medición precisa de pequeños caudales, siendo estos determinados mediante la ecuación general: 8 𝑄 = 15 𝐶𝑑 𝑡𝑎𝑛(𝛼⁄2)√2𝑔×𝐻 5⁄ 2 H (5) Donde 𝛼 es el ángulo del vertedero. En algunos textos, el coeficiente de descarga es un vertedero en V-90° con cargas que oscilen entre 5 y 25cm, le asignan un valor de 0,58. EQUIPO DE LABORATORIO F G 2 G 1 B D C B A E Laboratorio de Hidráulica Elías Sánchez Díaz CIHAM-UC Pag. 13 Descripción del Equipo de Laboratorio: Descarga sobre Vertederos A Canal rectangular con paredes de vidrio. E Codo de 90º calibrado y tubería de diámetro de 4”, destinado a la medición de los caudales. No se observa en foto. B Diques de malla plástica para evitar excesiva F Manómetro diferencial agua-aire conectado al turbulencia de la corriente en el canal. codo. C Vertedero Rectangular sin contracciones G1 Medidores de punta ubicados en los vertederos. laterales y de cresta aguda con lámina en caída G2 libre. D Vertedero Triangular de cresta delgada en VH Válvula de 4” (No se observa en la foto) 90º, con lamina vertiente en caída libre. Laboratorio de Hidráulica Elías Sánchez Díaz CIHAM-UC Pag. 14 Tabla de Recolección de Datos DESCARGA SOBRE VERTEDEROS Practica: Grupo: Practica No.: Medición lo(cm) Lo(cm) li(cm) h(cm) Li(cm) 1 2 3 4 5 6 Datos de la Experiencia: Ancho del Canal rectangular: B=60cm; ℎ Altura del Vertedero rectangular: w=23,4cm Altura al vértice del vertedero triangular: W=19,6cm 𝑤 Diámetro interno codo calibrado de 4”: d= 9,93cm Nombre y Apellido C.I. Firma Nombre del Profesor Firma del Profesor Fecha: / / Laboratorio de Hidráulica Elías Sánchez Díaz CIHAM-UC Pag. 15 PROCEDIMIENTO 1. Tenga a mano la hoja de recolección de datos de la práctica. 2. Tome las lecturas iniciales de los medidores de punta (G1 y G2) del vertedero bidimensional “𝑙𝑜” y del triangular “𝐿𝑜”, estos valores se encuentran en los laterales de cada vertedero. 3. Accione la válvula de 4” para fijar el caudal y espere 5 minutos para la estabilización de la corriente y la inamovilidad de las cargas sobre los vertederos. Esta válvula se encuentra ubicada el lado del sistema de bombeo como lo muestra la foto. 4. Con el medidor de punta (G1), tome el nivel de agua anterior a la cresta del vertedero Valvula. bidimensional “𝑙𝑖”. 4” 5. Con el medidor de punta (G2), tome el nivel de agua anterior a la cresta del vertedero triangular “𝐿𝑖”. 6. En el manómetro (F) mida la diferencia piezométrica ∆ℎ en el codo de 90º. 7. Repita los pasos 3,4, 5 y 6 hasta completar seis (6) caudales distintos. 8. Llene la tabla de recolección de datos y realice los cálculos preliminares de las primeras dos mediciones realizadas. 9. Verifique con el profesor o los preparadores que los cálculos preliminares sean correctos y para la firma de la hoja de recolección de datos, la cual deberán anexar al informe. CALCULOS PRELIMINARES: 1. Determine el caudal de cada uno de los regímenes de flujo establecidos, usando la siguiente ecuación: 𝑄 = 𝐶𝑑 𝜋𝑑 2 4 √2𝑔∆ℎ , donde d es el diámetro del tubo 4. 5. alimentador y ∆ℎ es la diferencia piezométrica tomada con el manómetro (F). Asuma Cd = 0.657 Para cada condición de flujo determine la cresta de los vertederos para el Bidimensional ℎ = 𝑙𝑖 − 𝑙𝑜 y para el Triangular 𝐻 = 𝐿𝑖 − 𝐿𝑜. Usando la ecuación de continuidad, calcule la velocidad media del canal rectangular y su carga de velocidad ℎ𝑣 = 𝑣02 ⁄2𝑔 para cada caudal, observe que el área es A=B.(h+w). Determine Cd, el coeficiente de descarga práctico del vertedero bidimensional, utilizando la ecuación (1). Calcule el Cd práctico del vertedero triangular mediante la ecuación (5). INFORME A PRESENTAR: 2. 3. 1. Introducción teórica, en donde se incluyan aspectos básicos y aplicados de los vertederos. 2. Cálculos preliminares colocando un ejemplo de cálculo y tabulación de la data experimental y de los resultados obtenidos. 3. Compare gráficamente las ecuaciones de Cd en vertederos bidimensionales, representadas por las ecuaciones (2), (3) y (4), en función del parámetro ℎ/(ℎ + 𝑤). Para la ecuación (2) solo use los valores de ℎ y ℎ𝑣 obtenidos experimentalmente. 4. Superponga a la grafica del paso anterior los puntos experimentales del coeficiente de descarga del vertedero bidimensional obtenidos en el paso 4 de cálculos preliminares. 5. Represente gráficamente el Cd del vertedero de V-90º en función de 𝐻/(𝐻 + 𝑊), siendo W la altura del vértice del vertedero. No trace curva. Compare esta grafica con el valor teórico constante Cd=0,58. 6. Comente sus resultados, posibles fuentes de error, precisión del método de medición de caudales utilizado. Establezca conclusiones. 7. Referencias bibliográficas. Laboratorio de Hidráulica Elías Sánchez Díaz PRACTICA: CIHAM-UC Pag. 16 Resalto Hidráulico OBJETIVO: Determinación de las características de un resalto hidráulico provocado en el flujo supercrítico posterior a una compuerta plana vertical. Introducción: Entre los fenómenos de oleaje, el resalto por la significativa y repentina elevación de la superficie del agua en la dirección de flujo y por la fuerte disipación de energía en su frente rompiente es de aplicación frecuente en el campo de la hidráulica, pues se le utiliza como disipador de energía del flujo de alta velocidad que se forma al pie de los aliviaderos o aguas debajo de una compuerta. Además, es un claro ejemplo del uso del principio de cantidad de movimiento en el análisis de problema de flujo. Se conoce como resalto hidráulico aquel cuya posición no varía, como consecuencia de que la velocidad de flujo 𝑉1 se iguala en magnitud a la celeridad del resalto, como se aprecia en la figura 1. Si se aplica el principio de cantidad de movimiento a este flujo permanente, se demuestra que la relación de profundidades antes (Sec.1) y después del resalto (Sec.2) es función única del número de Froude. Su expresión es: 𝑦2 𝑦1 = 12 (√(1 + 8𝐹1 2 ) − 1) Linea de Energía 𝑉2 ∆𝐻 h 𝑉1 b 𝑦2 𝑦1 RESALTO Figura1. (1) En el estudio de los canales es fundamental conocer el valor de un número adimensional llamado Froude. Cuando se le 𝐹 = 𝑉 ⁄𝑐 donde V es la velocidad media del canal y c es la celeridad de la onda elemental de gravedad, 𝑐 = √𝑔. 𝑦 , donde “y” es la profundidad de flujo, siendo antes del resalto y1 y y2 después del resalto. Si vemos la figura (1), es de hacer notar que antes del resalto (V1 y y1) el número de Froude es restringe a canales rectangulares. Se tiene que mayor a 1 (𝐹 > 1), a estos flujos se les denomina supercríticos. Mientras que en el flujo posterior al resalto (V2 y y2) el número de Froude es menor a uno (𝐹 < 1), los cuales se les llaman flujos subcríticos. La aplicación del principio de energía al fenómeno, permite demostrar que la disipación del resalto hidráulico tiene como expresión final: ∆𝐻 = (𝑦2 −𝑦1 )3 (2) 4.𝑦1 .𝑦2 Compuerta plana vertical: En el ensayo la condición de flujo supercrítico se logra, mediante el uso de una compuerta plana vertical; las características de este dispositivo de contención y aforo son las siguientes: Independientemente de su forma y proporción, la ecuación de desagüe por unidad de ancho de una compuerta es de la forma: 𝑞 = 𝐶𝑑 𝑏√2𝑔ℎ (3) Donde b es la abertura de la compuerta, h el nivel del agua y Cd el coeficiente de descarga (Ver figura 1). El caudal calculado a través de está formula está expresado en 𝑚2 /𝑠. El coeficiente de descarga 𝐶𝑑 es adimensional y su expresión en compuertas es de la forma: 𝐶𝑑 = 𝐶𝑐 𝑏 √1+𝐶𝑐 ℎ (4) Laboratorio de Hidráulica Elías Sánchez Díaz CIHAM-UC En la ecuación (4), 𝐶𝑐 se define como el coeficiente de contracción y es igual a la profundidad de la vena contracta de la lámina descargada dividida entre la profundidad de la abertura. Ensayos en compuertas planas verticales, para valores de ℎ⁄𝑏 ≥ 2, muestra una constancia muy acentuada del 𝐶𝑐 alrededor del valor 0,61, lo cual define a 𝐶𝑑 como función única de 𝑏⁄ℎ. El valor de la lamina contracta después de pasar la compuerta es: 𝑦1 = 𝐶𝑐. 𝑏 Pag. 17 (5) EQUIPO DE LABORATORIO F 1 D B E C A Descripción del Equipo de Laboratorio: Resalto Hidráulico. A Canal rectangular con paredes de vidrio. D B C Compuerta plana vertical para generar flujo supercrítico. Compuerta de mariposa de eje vertical al final del canal para control de la posición y profundidad del resalto. E F1 F2 F 2 1 1 Banco piezométrico conectado a orificios de 1 fondo del canal Vertedero Calibrado en V-90º de cresta delgada para el aforo del canal. Medidores de punta, uno ubicado en el canal de vidrio y otro en el vertedero en V-90o PROCEDIMIENTO: 1. Tenga a mano la hoja de recolección de datos de la práctica. 2. Tome las siguientes lecturas iniciales, estas lecturas corresponden a los niveles cuando no está circulando agua por el equipo y las mismas están escritas en lugares cercanos a los dispositivos a medir: a. Lectura inicial del medidor de punta (F2) ubicado en el vertedero en V-90º “𝐿𝑜”. b. Lectura del medidor de punta (F1) al fondo del canal rectangular de vidrio “𝑙𝑜”. c. Lectura inicial de las tomas conectadas al banco piezométrico (D) “ℎ𝑜”. 3. Accione la válvula mariposa para producir el resalto y por aproximaciones sucesivas ubicarlo inmediatamente después del medidor de punta (F) del canal de vidrio. Evite ahogar la compuerta plana vertical. 4. Una vez estabilizado el resalto y las lecturas del banco piezométrico, proceda a efectuar las siguientes mediciones: a. Lectura del medidor de punta (F2) en el vertedero V-90º “𝐿𝑖”. b. Lectura del medidor de punta (F1) al ras del agua en el canal de vidrio “ 𝑙𝑖”. c. Mediana de los niveles del banco piezométrico (D) correspondientes a las tomas ubicadas antes de la compuerta, que son los piezómetros 1, 2,3 y 4, el promedio de los cuatro será “ℎ𝑐”. d. Mediana de los niveles del banco piezométrico (D) correspondientes a las tomas ubicadas después del resalto, piezómetros 15, 16 y 17, el promedio lo llamaremos “ℎ𝑟”. 5. Fije un nuevo caudal cerrando la válvula de alimentación de 4” que le indique el instructor y repita los pasos hasta contemplar cinco (5) caudales distintos. 6. Llene la tabla de recolección de datos y realice los cálculos preliminares de las primeras dos mediciones realizadas. 7. Verifique con el profesor o los preparadores que los cálculos preliminares sean correctos y para la firma de la hoja de recolección de datos, la cual deberán anexar al informe. Laboratorio de Hidráulica Elías Sánchez Díaz CIHAM-UC Pag. 18 Tabla de Recolección de Datos RESALTO HIDRAULICO Practica: Grupo: Practica No.: Antes de la Compuerta Medición ho (cm) lo (cm) Lo (cm) li (cm) Li (cm) h1 (cm) h2 (cm) Después del resalto h3 (cm) h15 (cm) h16 (cm) h17 (cm) 1 2 3 4 5 6 DATOS DE LA EXPERIENCIA: Ancho del Canal: B=29,6cm Abertura de la compuerta: b=2,94cm Nombre y Apellido C.I. Firma Nombre del Profesor Firma del Profesor Fecha: / / Laboratorio de Hidráulica Elías Sánchez Díaz CIHAM-UC Pag. 19 CALCULOS PRELIMINARES 1. Calcule para cada condición de flujo la Carga H sobre la cresta del vertedero triangular 𝐻 = 𝐿𝑖 − 𝐿𝑜. 2. Determine los caudales Q del vertedero V-90º mediante la ecuación 𝑄 = 1,48𝐻5/2 ; la constante 1,48 no es adimensional. Por tanto, la carga del vertedero H sobre el vértice de la “V” debe expresarse en metros, para así obtener a Q en m3/s. 3. Determine los caudales por unidad de ancho q en el canal rectangular 𝑞 = 𝑄 𝐵 , donde B es el ancho del canal. 4. 5. 6. 7. Calcule la carga sobre la compuerta ℎ = ℎ𝑐 − ℎ𝑜. Determine la profundidad antes del resalto 𝑦1 = 𝑙𝑖 − 𝑙𝑜 Calcule la profundidad después del resalto 𝑦2 = ℎ𝑟 − ℎ𝑜 Para cada condición de flujo calcule: a) La relación 𝑦2/𝑦1, b) La velocidad de la corriente supercrítica antes del resalto 𝑉1 = 𝑞/𝑦1. c) La velocidad de la corriente subcritica después del resalto 𝑉2 = 𝑞/𝑦2. d) La celeridad de la onda elemental de gravedad, antes 𝐶1 y después del resalto 𝐶2 , 𝑐 = √𝑔. 𝑦. e) El número de Froude antes del resalto 𝐹1 = 𝑉1 ⁄𝐶1 y después del resalto 𝐹2 = 𝑉2 ⁄𝑐2 f) La disipación adimensional de energía ∆𝐻 por medio de la ecuación (2) INFORME A PRESENTAR. 1. Introducción teórica, en donde incluya características, aplicaciones del resalto hidráulico y la deducción de la ecuación (1). 2. Calcule el coeficiente de descarga de la compuerta plana vertical mediante la ecuación (3). 3. Determine los caudales q utilizando la carga h medida sobre la compuerta y el coeficiente de descarga de la ecuación (4). 4. Estime teóricamente: a. El valor de 𝑦1 teórico, mediante la ecuación (5). b. Con el caudal del paso 3 y el y1 calculado anteriormente determine la velocidad V1 y el F1. c. La relación de profundidades 𝑦2/𝑦1, mediante la ecuación (1). d. Con la relación anterior y el 𝑦1 teórico, determine 𝑦2. e. Con el y2 anterior y el caudal del paso 3, calcule la velocidad teórica después del resalto, V2. f. Número de Froude (F2) después del resalto. g. La disipación adimensional de energía ∆𝐻 teórica. 5. Compare gráficamente la relación de profundidades 𝑦2/𝑦1 obtenida en el paso anterior con la obtenida experimentalmente (cálculos preliminares), en función del número de Froude antes del resalto F1. (𝑦2/𝑦1 vs F1) 6. Compare gráficamente el coeficiente de descarga obtenido en el paso (2) con los de la ecuación (4), en función de b/h. 7. Comente sus resultados y establezca conclusiones sobre los aspectos relevantes de la práctica. 8. Referencias bibliográficas. Laboratorio de Hidráulica Elías Sánchez Díaz PRACTICA: CIHAM-UC Pag. 20 Flujos Laminar y Turbulento OBJETIVO: Comparación de la perdida de carga en los flujos laminar y turbulento. Introducción: Fig.1. TURBULENTO En el Siglo XIX, el científico inglés Osborne Reynolds demostró que las corrientes fluidas se manifiestas en dos formas claramente definitivamente: el régimen turbulento (fig.1) y el laminar (fig.2); como consecuencia de la interacción entre las dos propiedades mecánicas más importantes del movimiento como lo son la densidad y la viscosidad del fluido. Reynolds condujo una serie de experimentos en los cuales inyecto un Fig.2 LAMINAR colorante en agua que fluía en una tubería de vidrio. A bajos caudales, el colorante permaneció uniforme y regular a medida que fluía corriente abajo. A caudales más elevados, parecía que el colorante explotaba mezclándose rápidamente a través de toda la tubería. Una fotografía moderna de alta velocidad de la mezcla del colorante revelaría un patrón de flujo muy completo, no discernible en los experimentos de Reynolds. Los experimentos de Reynolds demostraron que la naturaleza del flujo en tuberías depende del número de Reynolds 𝑅 = 𝑉. 𝐷/𝜈 , donde V es la velocidad media del flujo, D el diámetro interno de la tubería y 𝜈 la viscosidad cinemática del fluido. Reynolds encontró que cuando R<2000 El flujo era laminar, R>4000 el flujo era turbulento y 2000<R<4000 el flujo era en transición. Cuando una corriente es laminar, las fuerzas tangenciales viscosas superan, envuelven y absorben a las inerciales, lo cual se manifiesta en un movimiento donde las capas de fluido fluyen paralelamente como en láminas que se deslizan unas sobre las adyacentes, sin observarse un proceso de mezclado entre ellas. En cambio, en el turbulento, las partículas fluidas no se retienen en capas sino que por el contrario, se desplazan masas vorticosas a uno y otro lado de la corriente. Resultado un movimiento temporalmente de la corriente en determinada dirección pero se superponen desplazamiento transversales y movimientos rotacionales de diferentes volúmenes de fluido, que traen como consecuencia un intercambio de flujo entre las distintas zonas de la corriente y un proceso de mezcla que no se observa en el régimen laminar. Obviamente este caso, las fuerzas viscosas no son capaces de detener o absorber el movimiento inercial. En un tubo circular, el flujo permanente de un líquido sufre una pérdida de energía mecánica o pérdida de ‘’carga’’ que disminuye linealmente con la distancia recorrida por la corriente en la dirección de movimiento. Experimental y analíticamente, se demuestra que en una sección transversal de tubería, el esfuerzo cortante en un punto dado es proporcional a la pendiente de pérdida de carga o gradiente piezométrico, y además, que disminuye linealmente con la distancia radial del punto al centro del tubo; es decir: 𝑑ℎ 𝑟 𝜏 = −𝛾 𝑑𝑥 4 (1) Siendo 𝛾 el peso específico del fluido; r, la longitud radial del punto al eje de la tubería y (− 𝑑ℎ⁄𝑑𝑥 ) el gradiente piezométrico. Luego, este último es un índice de la velocidad con que se disipa la energía en el flujo de un líquido. El gradiente piezométrico se relaciona con las características cinemáticas y dinámicas de la corriente en una ecuación fundamental que se conoce con el nombre de Darcy-Weisbach, en honor a los científicos que la concibieron. Establece que: − 𝑑ℎ 𝑑𝑥 = 𝑓 𝑉2 𝐷 2𝑔 (2) Laboratorio de Hidráulica Elías Sánchez Díaz CIHAM-UC Pag. 21 Donde d es el diámetro de un tubo circular, 𝑉 2 ⁄2𝑔 es la cota de velocidad y la f es el factor de fricción, quien, según puede demostrarse por el análisis dimensional de las variables en juego, es una función de la forma de la conducción (en este caso circular), de la relación denominada rugosidad relativa (𝑘⁄𝐷 ) y del número de Reynolds R. Factor de Fricción: Tanto analítica como experimental se demuestra que en el régimen laminar en tuberías circulares, el factor de fricción tiene como expresión: 𝑓 = 64⁄𝑹 (3) Y es válido para 𝑹 = 𝑉𝐷 ⁄𝝂 <= 2000 (Límite crítico), pudiendo alcanzar valores mayores en algunos casos. En cambio, régimen turbulento de una tubería con contorno liso, el factor de fricción se determina por la fórmula semiempírica de Blasius: 𝑓 = 0,316⁄𝑹0,25 (4) Al sustituir las ecuaciones (3) y (4) en la ecuación (2), resultan las expresiones: LAMINAR TURBULENTO − 𝑑ℎ 𝒅𝒙 − = 𝑑ℎ 𝑑𝑥 32𝜈 𝑔𝐷2 = 𝑽 (5) 0,158𝜈0,25 𝑔𝐷1.25 Log –dh/dx 𝑉1,75 (6) Turbulento: –dh/dx Transición Laminar : –dh/dx Log V Fig.3 Comparación de las Velocidades de disipación de energía en régimen laminar y turbulento. Laboratorio de Hidráulica Elías Sánchez Díaz CIHAM-UC Pag. 22 EQUIPO DE LABORATORIO F C B D A Descripción del Equipo de Laboratorio: Flujo Laminar y turbulento. A Aparato de Reynolds modificado, consistente de Válvula de ¼ ”para controlar el caudal del sistema una tubería de vidrio de diámetro pequeño, con D tomas piezométricas a cada 50cm. Tiene un sistema de recirculación de agua propio. B Banco Piezométrico conectado a la tomas para E Cilindro graduado en cc, para la determinación medir la carga piezométrica y visualizar su del caudal por el método volumétrico. (No variación a lo largo del tubo. aparece en foto) C Recipiente con sustancia colorante, válvula e F Tanque estabilizador del flujo. inyector, para visualizar cualitativamente el tipo de régimen de flujo., 1. 2. 3. 4. 5. 6. 7. 8. PROCEDIMIENTO. Tenga a mano la hoja de recolección de datos de la práctica. Verificar que el instructor haya puesto en funcionamiento el dispositivo. Abrir completamente la válvula (D) fijar el máximo caudal que puede dar el sistema. Esperar 3 minutos para la estabilización del flujo. Mida con el cilindro graduado (E) el volumen “Vol” almacenado en un tiempo específico “t”. Anote las lecturas del banco piezométrico (B), que corresponden a las alturas piezométricas “h” de los puntos 1, 2, 3, 4 y 5. Determine el número de Reynolds (Vea paso 1 de cálculos preliminares), este primer caudal el flujo deberá ser turbulento. Repita los pasos 3, 4, 5 y 6 hasta completar 6 caudales distintos donde los primeros 3 sean turbulentos y los últimos laminares. Para facilitar la obtención de lo anterior se recomienda después del primer caudal (con la llave totalmente abierta), cerrar muy poco la válvula (D) para obtener el 2do y otro poco para el 3ero. Para obtener los laminares se recomienda cerrar la válvula (D) y abrir el caudal mínimo (un hilito), después de este abrir muy poco para obtener los otros dos faltantes. Sí por alguna razón en el paso 6 el caudal en estudio le da como resultado un régimen en transición, deberá descartar esas mediciones y tomar una nueva. Laboratorio de Hidráulica Elías Sánchez Díaz CIHAM-UC Pag. 23 9. Al terminar las mediciones indique al instructor que le muestre el funcionamiento de la tinta en el aparato de Reynolds. 10. Llene la tabla de recolección de datos y realice los cálculos preliminares de las primeras dos mediciones realizadas. 11. Verifique con el profesor o los preparadores que los cálculos preliminares sean correctos y para la firma de la hoja de recolección de datos, la cual deberán anexar al informe. Laboratorio de Hidráulica Elías Sánchez Díaz CIHAM-UC Pag. 24 Tabla de Recolección de Datos FLUJO LAMINAR Y TURBULENTO Practica: Grupo: Practica No.: Medición Volumen Tiempo (ml) (seg) 1 h1 (cm) h2 (cm) h3 (cm) h4 (cm) h5 (cm) Reynolds Tipo de V.D/ν Flujo 2 3 4 5 6 Datos de la Experiencia: Diámetro de la tubería de vidrio: 5,85mm Distancia entre orificios piezométricos: 50cm Viscosidad cinemática del fluido a 32,2º : 0,765x10−6m2/s Nombre y Apellido C.I. Firma Nombre del Profesor Firma del Profesor Fecha: / / Laboratorio de Hidráulica Elías Sánchez Díaz CIHAM-UC Pag. 25 CALCULOS PRELIMINARES 1. Para cada condición de flujo, Determine: a. El caudal Q por el método volumétrico, Q=Vol/t b. Velocidad media V, por continuidad Q=V.A c. El número de Reynolds. Asuma la viscosidad del agua a 32,2º => 𝜈 = 0,765𝑥10−6 𝑚2 /𝑠 INFORME A PRESENTAR 1. Introducción teórica, incluyendo características de los flujos laminar y turbulento. 2. Para cada conjunto de medidas, realice un gráfico de altura piezométrica h en función de la distancia x. Trace la recta más probable. Cada toma piezométrica está ubicada a cada 50cms. 3. Determine la pendiente de las rectas obtenidas en el paso (2). Estas serán los gradientes piezométricos – 𝑑ℎ/𝑑𝑥 obtenidos experimentalmente. 4. Calcule el factor de fricción 𝑓 a través de la ecuación (2) y utilizando los gradientes piezométricos determinados en el paso 2. 5. Calcule el factor de fricción 𝑓 y el gradiente piezométrico que predicen las ecuaciones (3), (4), (5) y (6), para cada condición de flujo. 6. Encuentre el error porcentual medio entre los gradientes piezométricos y los factores de fricción determinados en los pasos 3 y 5. 𝐸% = 𝑉𝑎𝑙𝑜𝑟 𝑇𝑒𝑜𝑟𝑖𝑐𝑜 − 𝑉𝑎𝑙𝑜𝑟 𝐸𝑥𝑝𝑒𝑟𝑖𝑚𝑒𝑛𝑡𝑎𝑙 𝑥100 𝑉𝑎𝑙𝑜𝑟 𝑇𝑒𝑜𝑟𝑖𝑐𝑜 7. Determine la velocidad V, asumiendo los Reynolds: 1000, 2000, 4000, 6000, para cada caso determine el gradiente piezométrico – 𝑑ℎ/𝑑𝑥 usando las ecuaciones (5) y (6). 8. Represente gráficamente en papel logarítmico el gradiente piezométrico – 𝑑ℎ/𝑑𝑥 calculado en el paso anterior en función de V. Debe darle una gráfica similar a la de la figura 3. 9. Ubique en la gráfica del paso 8 los puntos experimentales del gradiente piezométrico – 𝑑ℎ/𝑑𝑥 en función de V. No trace curva experimental. 10. Represente gráficamente en papel logarítmico las ecuaciones (3) y (4) de 𝑓 en función de Reynolds. Superponga sobre ellas los puntos experimentales respectivos, sin trazar curva experimental. 11. Comente sus resultados y establezca conclusiones sobre los aspectos relevantes de la práctica. 12. Referencias bibliográficas. Laboratorio de Hidráulica Elías Sánchez Díaz PRACTICA: CIHAM-UC Pag. 26 Distribución de Velocidades OBJETIVO: Obtener una Curva de Distribución de Velocidades para una tubería circular de PVC y una de Hierro Galvanizado, utilizando como instrumento los Tubos de Pitot. Introducción: Al establecer un flujo permanente de un fluido gaseoso a lo largo de una tubería uniforme, se observa que la caída de presión varía linealmente con la distancia recorrida por la corriente. En razón de que no se extrae ni se suministra ningún tipo de energía al flujo, se deduce que las diferencias de presión detectadas, corresponderán a las pérdidas de energía mecánica por la fricción, constantes por unidad de longitud y generadas tanto por la acción de masas de fluidos que interactúan entre sí, como por el contacto del fluido con el contorno que lo confina. El gradiente de la caída de presiones referida ∆𝑝⁄𝐿 puede calcularse por la conocida ecuación de Darcy-Weisbach: ∆𝑝 - 𝐿 2 𝑓 = 𝜌 𝑉 ⁄2 𝐷 (1) Donde V es la velocidad media de la corriente, D el diámetro de la tubería, 𝜌 la densidad del fluido y 𝑓 es el factor de resistencia o fricción, coeficiente adimensional que depende, según pueda demostrarse por análisis dimensional, de la forma de conducción que confina al fluido, de la rugosidad relativa (𝜀 ⁄𝐷 ) y del número de Reynolds R, expresado como 𝑹 = V D⁄𝜈 , donde 𝜈 es la viscosidad cinemática, se conoce que el número de Reynolds es un índice de la intensidad y escala de la turbulencia pues representa la relación entre fuerzas inerciales (viscosidad de remolinos) y viscosas. Perfil Turbulento Medio de Velocidades: El principio de cantidad de movimiento aplicado en un tramo de tubería, relaciona al gradiente de presiones obtenido en la ecuación (1) con el esfuerzo de corte que ocurre tangencialmente sobre las paredes del conducto (𝜏𝑜 ). Se deduce de allí que: ∆𝑝 𝜏𝑜 = ( ) 𝐷⁄4 (2) 𝐿 A la relación √𝜏𝑜 ⁄𝜌 se conoce como velocidad de corte (v*) , debido a sus dimensiones [𝐿⁄𝑇], pero físicamente no tiene significación alguna. Al sustituir la ecuación (1) en (2), resulta que: v*= 𝑉√𝑓⁄8 (3) , donde V es la velocidad media en la tubería. El perfil de velocidades medias temporales del flujo turbulento confinado en tuberías está íntimamente relacionado con el material de la pared. En el caso de un contorno hidráulicamente liso existe una subcapa laminar (sin turbulencia) dentro de la cual la velocidad puntual varía linealmente con la distancia de la pared (y), de a cuerdo a la expresión: v/v*= v∗ 𝑦 𝜈 (4) Laboratorio de Hidráulica Elías Sánchez Díaz CIHAM-UC Pag. 27 Donde v es la velocidad puntual ubicada a la distancia “y” de la pared y "𝜈" la viscosidad cinemática. Se estima que la ecuación (4) es válida para 0 ≤ 𝑦 ≤ 𝛿; donde 𝛿 es el espesor de la subcapa laminar. Basado en sus evidencias experimentales, Nikuradse, un discípulo de Prandtl, padre de la Mecánica de Fluidos moderna, definió el espesor de subcapa laminar como: 𝛿= 11,6𝜈 v∗ (5) Cuando 𝑦 > 𝛿, la distribución de velocidades sigue una ley logarítmica, que de acuerdo a Kárman-Prandtl es de la forma: v⁄v ∗ = 5,75 𝑙𝑜𝑔(v ∗ . 𝑦/𝜈 ) + 5,5 (6) Si el contorno es rugoso, y siempre que las rugosidades no estén absorbidas parcial o totalmente por la subcapa laminar, se cumple: 𝑦 v⁄v ∗ = 5,75𝑙𝑜𝑔( ⁄𝜀 ) + 8,5 Donde 𝜀 (7) es la rugosidad de la tubería en m. Las ecuaciones (6) y (7) definen tipos distintos de flujo turbulento completamente desarrollado. La primera corresponde a un flujo turbulento en contorno liso que es posible siempre y cuando 𝜀 ⁄𝛿 sea ≤ 0,25 aproximadamente. La segunda corresponde a un flujo turbulento completamente rugoso y se estima su validez a partir de 𝜀 ⁄𝛿 ≥ 6. En el intervalo media la zona corresponde al comportamiento liso rugoso, donde debido a la complejidad del fenómeno no ha sido posible tipificar una distribución única de velocidades. Tabla 1. Posición respecto al contorno, relativa al radio (y/ro) de los tubos de estancamiento. El termino y representa la distancia a la que se encuentra la velocidad puntual vn medida desde el borde de la tubería, mientras que ri representa la distancia medida desde el centro de la tubería hasta la mitad contenida entre una velocidad puntual y otra, Δri será el espesor entre dos velocidades puntuales consecutivas, tal como se muestra en la figura 1. Laboratorio de Hidráulica Elías Sánchez Díaz CIHAM-UC Pag. 28 Figura 1. Representación gráfica sobre la posición de y respecto a las velocidades puntuales vn TUBERIA DE 2" PVC y/ro 1,20 Valores Experimentales 1,00 1,00 Valores Teoricos 0,80 0,60 0,50 0,40 0,15 0,20 0,02 Velocidad Puntual (m/s) 0,00 0,00 5,00 10,00 15,00 20,00 25,00 Figura 2. Representación gráfica de la Distribución de las Velocidades Puntuales Experimentales y Teóricas respecto a la relación (y/ro) Placa Orificio La placa orificio consiste en una placa perforada que se instala en la tubería, el orificio que posee es una abertura cilíndrica o prismática a través de la cual fluye el fluido. Dado que el caudal calculado de esta manera no es el caudal real, ya que no contempla las pérdidas de energía existentes en el dispositivo, es necesario corregirlo, para lo cual se define el coeficiente de descarga Cd como la relación entre el caudal real y el caudal teórico, este coeficiente depende de otro denominado Coeficiente de Contracción Cc, cuyos valores se encuentran en la Tabla 3. Tabla 3. Valores del Coeficiente de Contracción Cc. Laboratorio de Hidráulica Elías Sánchez Díaz CIHAM-UC Pag. 29 EQUIPO DE LABORATORIO F D1 1 A D2 C B E Descripción del Equipo de Laboratorio: Distribución de Velocidades Conjunto de tuberías de distinto material y D1 Dos manómetros diferenciales agua aire, A diámetro, por donde circula aire. Las tuberías que D2 acoplados mediante distribuidores de presión a las: utilizaremos en la práctica son la de PVC y Hierro (D2) tomas de la tubería y cámara de ensayos, y Galvanizado de 2”. (D1) tomas de la placa orificio de 2” y 4” B E Placas orificios de Bronce de 2” y 4” C Cámaras de ensayos, donde se ubican 4 tubos de estancamiento para cada tubería de 2” 1. 2. 3. F Manifold donde se encuentran un grupo de válvulas que permiten conectar el punto que se desea medir al manómetro diferencial. Aspiradora (es un tambor de metal con un motor arriba). PROCEDIMIENTO Tenga a mano la hoja de recolección de datos de la práctica. Verifique que el instructor haya encendido la aspiradora. Inicie abriendo la válvula de la tubería de PVC de 2”. Efectúe la medición en el manómetro (D2) de las cargas de presión a lo largo del tubo ∆ℎ(tubería) de los puntos P1 hasta el P8. Cada medición se hace por separado Laboratorio de Hidráulica Elías Sánchez Díaz 4. 5. 6. 7. 8. CIHAM-UC Pag. 30 abriendo la válvula en el Manifold (F) correspondiente a cada punto de la tubería, se recomienda que entre medición y medición se abra la válvula de purga (la verde) del Manifold (F), se espere a que el líquido manométrico esté en cero, se cierra la válvula de purga y se pase a la siguiente medición. Efectúe las mediciones de presión en el manómetro (D2) correspondientes a cada tubo de estancamiento 1,2,3,y 4, así como la presión de la cámara de ensayos “0”, ∆ℎ(camara). Al igual que el paso (2), estas mediciones se hacen por separado abriendo la llave respectiva en el Manifold (F). Tome la lectura de la diferencia de presión del manómetro (D1), las dos válvulas de la derecha son la de la placa orificio de 2” ∆ℎ(placa orificio), una vez anotado el valor, ciérrelas y abra las dos válvulas del lado izquierdo correspondiente a la placa oricio de 4”, anote el valor. Llene la tabla de recolección de datos y realice los cálculos preliminares. Indique al instructor que cierre completamente la llave de la tubería de PVC de 2” y abra la de Hierro Galvanizado de 2” completamente, repita los pasos del 3 al 6. Verifique con el profesor o los preparadores que los cálculos preliminares sean correctos y para que firmen la hoja de recolección de datos, la cual deberán anexar al informe. Laboratorio de Hidráulica Elías Sánchez Díaz CIHAM-UC Pag. 31 Tabla de Recolección de Datos DISTRIBUCIÓN DE VELOCIDADES Practica: Grupo: Practica No.: Punto No. Δh (cm) Tubería Tubería PVC H.G Tubo de Δh (cm) Δh (cm) Pitot PVC H.G No. P1 1 PVC P2 2 H.G P3 3 P4 4 P5 0 P6 P7 P8 Δh (cm) Placa Orificio 2" NOTA: El Tubo de Pitot No4 de Hierro Galvanizado (H.G) no funciona. Se calculará sumándole 0,3 cm a la medición del Tubo de Pitot No2 Datos de la Experiencia: Diámetro interno de la tubería PVC 2”: 4,965 cm Diámetro interno de la tubería HG 2”: 5,660 cm Distancia entre orificios piezométricos: 1,00 m Diámetro placa orificio de Bronce 2”: Interno d= 2,63cm, Externo D= 5,40cm Diámetro placa orificio de Bronce 4”: Interno d= 5,14cm, Externo D= 10,48 cm Nombre y Apellido C.I. 4" Firma Nombre del Profesor Firma del Profesor Fecha: / / Laboratorio de Hidráulica Elías Sánchez Díaz CIHAM-UC Pag. 32 CALCULOS PRELIMINARES 1. Convierta las lecturas manométricas de las tomas en el tubo y cámara de ensayos en presión relativa ∆𝑝 = ∆ℎ ∗ 𝛾, verifique el signo de las presiones (mayor o menor que la presión atmosférica). asumir γ del agua como 1000 Kg/m3 2. Calcular el Coeficiente de Descarga (Cd) para la placa de orificio 2” y la placa de orificio 4”, Nota: para encontrar el valor del Coeficiente de Contracción (Cc) se debe calcular la relación entre el diámetro interno (d) y el diámetro externo (D) es decir (d/D) en la placa orificio seleccionada, luego con esa relación y mediante la interpolación de la Tabla 3, se obtiene el valor de Cc, el ángulo de ambas placas oricio es 90°. 𝐶𝑐 C𝑑 = 4 √1−(𝐶𝑐 2 ∗(𝑑 ⁄ 4 )) 𝐷 3. Con los coeficientes de descarga (Cd) del paso anterior determine el caudal de aire en la placa orificio de 2” y 4”, para la tubería de PVC y H.G mediante la ecuación de desagüe de una placa orificio que se muestra a continuación. Recuerde que "d" es el diámetro interno de la placa orificio en estudio. Asuma la densidad del aire a 27 °C es decir 𝜌 = 0,12 Kg-s2/m4: 𝑄 = 𝐶𝑑 𝜋𝑑 2 4 √ 2.∆𝑝 𝜌 luego, determine el caudal total del sistema sumando los resultados de ambas placas. INFORME A PRESENTAR 1. Introducción teórica, incluyendo características de los perfiles de velocidad en flujos laminar y turbulento. 2. Trace los puntos de presión ∆𝑝 a lo largo de la tubería (P1 a P8) en función de la distancia recorrida (x) por la corriente, buscar la recta más probable y determinar la pendiente de la recta, este será el gradiente de presiones ∆𝑝/𝐿. 3. Determine: a. La velocidad media en el tubo V, aplicando la ecuación de continuidad. b. El factor de fricción experimental 𝑓, despejándolo de las ecuación 1. c. El número de Reynolds, la viscosidad del fluido (v) será asumido con un valor de 0.0000157 m2/seg 𝑅 = 𝑉∗𝐷 𝑣 d. La rugosidad relativa de la tubería ε/D, para ello utilice una rugosidad (Ɛ) de PVC igual a 0 metros y una rugosidad (Ɛ) para Hierro Galvanizado de 0,000061 metros. e. A través del diagrama de Moody determine el factor de fricción teórico f (página 4 tablas hidráulicas). f. La velocidad de corte v* (m/seg) con la ecuación (3) y el f en el paso (3.b) g. Encuentre el error porcentual entre el factor de fricción f teórico y el f experimental. 𝐸% = 𝑉𝑎𝑙𝑜𝑟 𝑇𝑒𝑜𝑟𝑖𝑐𝑜 − 𝑉𝑎𝑙𝑜𝑟 𝐸𝑥𝑝𝑒𝑟𝑖𝑚𝑒𝑛𝑡𝑎𝑙 𝑥100 𝑉𝑎𝑙𝑜𝑟 𝑇𝑒𝑜𝑟𝑖𝑐𝑜 4. Determinar las velocidades puntuales experimentales (Vn) en la sección transversal utilizando las presiones Δp de estancamiento y de la cámara (1,2,3,4) NOTA: asumir la densidad del aire a 27 °C es decir p = 0,12 Kg-s2/m4 Δpn es la diferencia de presión en el punto de estancamiento "n" y Δpo es la presión de cámara, es decir la diferencia de presión en el punto de estancamiento 0. 2 ∗ (∆𝑝𝑛 − ∆𝑝𝑜) 𝑉𝑛 = √ 𝜌 Laboratorio de Hidráulica Elías Sánchez Díaz CIHAM-UC Pag. 33 . 5. Determinar el Espesor de la subcapa laminar (δ) mediante la ecuación (5) (la viscosidad del fluido será asumido con un valor de 0.0000157 m2/seg). 6. Determine las Velocidades Puntuales Teóricas, siendo estas las velocidades en los puntos de estancamiento (1,2,3,4) de la sección transversal tomando en cuenta las ecuaciones (4,6 y 7). Para ello utilice una rugosidad relativa (Ɛ) de PVC igual a 0 metros y una rugosidad relativa (Ɛ) para Hierro Galvanizado de 0,000061 metros 7. Determinar el Caudal para el sistema utilizando el método de integración numérica. NOTA: Vn corresponde a las velocidades puntuales experimentales, mientras que los valores de ri y Δri se encuentran tabulados en la Tabla 1. 4 𝑄 = ∑ vn . 2. 𝜋. 𝑟𝑖 . ∆𝑟𝑖 𝑖=1 8. Grafique la Distribución de Velocidades Puntuales Experimentales en función de y/ro y compare con las Velocidades Puntuales Teóricas. (ver figura 2) 9. Comente sus resultados, compare el caudal por integración numérica con el caudal de salida del sistema calculado por las ecuaciones de la placa orificio, compare los gradientes piezométricos entre la tubería de PVC y H.G, compare las velocidades entre ambas tuberías y establezca conclusiones sobre los aspectos relevantes de la práctica. 10. Referencias bibliográficas. Laboratorio de Hidráulica Elías Sánchez Díaz PRACTICA: CIHAM-UC Pag. 34 Perdida de Energía en Válvulas OBJETIVO: Determinación experimental del coeficiente de pérdida de energía mecánica en una válvula de globo y una válvula de compuerta comercial. Introducción: Siempre que la corriente de un fluido se encuentre con dispositivos de control de gasto, acoplamientos, codos ó cambios de área que provoquen cambios repentinos de la velocidad de flujo, o induzcan separación de la superficie límite, se produce una disipación de energía cuya magnitud depende de la forma y material del dispositivo y del tipo de régimen de flujo y se le denomina perdida local o “menor” para diferenciarla de las perdidas por fricción ó “mayores”. Los vocablos mayor o menor adjudicados son relativos dado que en una tubería de gran longitud, las perdidas locales pueden ser de poca monta frente a la del conducto; pero, si la tubería corta, término “menor” puede ser engañoso. Las pérdidas menores se clasifican en: Pérdidas por entrada Pérdidas por salida Pérdidas por ampliación o reducción Pérdidas por cambios de dirección Pérdidas por válvulas Válvula de Globo En líneas generales, la perdida de energía se produce como consecuencia turbulencia provocada por el artefacto, la cual se supone sobre la turbulencia normal de la corriente confinada, Este flujo varicoso adicional se genera corriente debajo de la fuente y se mantiene por espacio de 20 a 50 diámetros; posteriormente, la propia corriente disipa los remolinos y vuelven a restablecerse las condiciones iniciales de turbulencia del flujo en el tubo. Las variables que intervienen en el fenómeno son: 𝜌 𝑦 𝜇 que identifican la densidad y viscosidad dinámica del fluido respectivamente. 𝐷 𝑦 𝜀 se refieren al diámetro del tubo y la rugosidad absoluta del material del dispositivo. 𝑉 la velocidad media de la corriente en el conducto. La pérdida de energía local. Tabla 1. Coeficientes de Perdida K de Válvulas Comerciales. Laboratorio de Hidráulica Elías Sánchez Díaz CIHAM-UC Pag. 35 Tuberia 1/2" M.C.A 2,50 2,2166 2,0166 2,00 1,5966 y = -0,1869x + 2,4856 1,50 1,2566 0,8566 1,00 antes de la valvula 0,50 0,4766 y = -0,2053x + 2,3738 despues de la valvula valvula Distancia (m) 0,00 0 1 2 3 4 5 6 7 8 9 10 Figura 1. Grafica de la energía h en función de la distancia X La pérdida de energía 𝐻𝐿 se determina experimentalmente mediante la extrapolación de las líneas de altura piezométrica, trazada en las zonas de flujo uniforme antes y después del artefacto, hasta el sitio donde esté ubicado. Como muestra la figura 2. Figura 2. Determinación de Hl por extrapolación Para un caudal determinado debe cumplirse en el caso de las válvulas que las líneas piezométricas deben tener la misma pendiente en las zonas uniformes agua arriba y debajo de la fuente, dado que no hay cambios en el diámetro del tubo. Sin embargo, es importante advertir que aunque en la zona anterior a la válvula la uniformidad de la línea piezométrica se mantiene a poca distancia del dispositivo, aguas abajo la distancia a la cual se restablece la turbulencia normal de la corriente es mayor, la distancia vertical entre las dos líneas paralelas en el sitio de la válvula, se toma entonces como la pérdida de carga correspondiente a la válvula 𝐻𝑙 , puesto que la pérdida por fricción ha sido substraída por el procedimiento descrito. Un término común utilizado para las perdidas por accesorios es la Longitud Equivalente Le (m), que representa la cantidad en metros de tubería cuya perdida de energía mecánica es igual a la perdida de carga del accesorio. Laboratorio de Hidráulica Elías Sánchez Díaz CIHAM-UC Pag. 36 Tabla 2. Longitud Equivalente Le (m) de Válvulas Comerciales. El término K es el coeficiente de perdida localizada dependiente principalmente de la forma geométrica de la pieza o accesorio y secundariamente del número de Reynolds, el cual deja de tener influencia cuando sus valores son muy altos. para aplicaciones prácticas, los flujos con Re <2000, se encuentran en régimen laminar, y Re>4000, están en régimen turbulento. Los 2000<Re<4000, están en la región de transición o región crítica. En la figura 3, se muestra como debe quedar la gráfica de K vs Re. Tuberia 1" K 10,00 7,80 8,24 7,80 K teorico K Diametro Interno mas Probable N° de Reynolds 1,00 36000 36500 37000 37500 38000 38500 39000 39500 40000 Figura 3. Gráfica del Coeficiente K vs el Numero de Reynolds 40500 Laboratorio de Hidráulica Elías Sánchez Díaz CIHAM-UC EQUIPO DE LABORATORIO C F E G D B Descripción del Equipo de Laboratorio: Perdida de Energía en A Banco de tuberías de plástico del sistema. E B Accesorio del sistema (Válvulas Comerciales) F C Manómetro diferencial agua-aire G D Pag. 37 A Válvulas Manifold del sistema para los puntos P2 a P7 Manómetros puntuales. Balanza con tanque metálico para medir volúmenes de agua. Manifold de los puntos iniciales del sistema (P1) 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. PROCEDIMIENTO Tenga a mano la hoja de recolección de datos de la práctica. Verifique que el equipo se encuentre encendido. Tome la lectura del manómetro (F) en unidad psi, esa será la presión del P1, la apreciación del instrumento en psi es de 1,25 cada rayita. Abra la válvula de la tubería de ½” del Manifold C Mida la diferencia de presiones en el manómetro (D) de los puntos de P1-P2, P1-P3, P1-P4, P1-P5, P1-P6 y P1-P7 abriendo las válvulas en el Manifold (E) correspondiente a cada punto. Determine en la Balanza (G) el peso del agua contenida en el tanque en determinado lapso de tiempo “t”, se recomienda un t de 60 seg. Indique al instructor que cierre la válvula de la tubería de ½” y abra la válvula de la tubería 1”. Repita los pasos 2 al 6. Llene la tabla de recolección de datos y realice los cálculos preliminares. Verifique con el profesor o los preparadores que los cálculos preliminares sean correctos y para la firma de la hoja de recolección de datos, la cual deberán anexar al informe. Laboratorio de Hidráulica Elías Sánchez Díaz CIHAM-UC Pag. 38 Tabla de Recolección de Datos Practica: PERDIDA DE ENERGÍA EN VALVULAS Grupo: Practica No.: Datos de la Experiencia: Diámetro de la tubería de PVC 1/2” = 1.65 cm. Diámetro de la tubería de PVC 1” = 2,848 cm P1-P2 Distancia del Punto 1 al punto en estudio. (m) 1,420 P1-P3 2,538 P1-P4 4,746 P1-Válvula 5,020 P1-P5 5,460 P1-P6 7,358 P1--P7 9,260 Punto (n) Medición 1 Tubería ½” Δh(P1-Pn) (cm) Medición 2 Tubería 1” Δh(P1-Pn) (cm) Válvula de Compuerta Válvula de Globo Peso (kg) Tiempo (seg) P1 (psi) Nombre y Apellido C.I. Firma Nombre del Profesor Firma del Profesor Fecha: / / Laboratorio de Hidráulica Elías Sánchez Díaz CIHAM-UC Pag. 39 CALCULOS PRELMINARES 1. Convertir los valores de las diferencias manométricas de P1-P2, P1-P3, P1-P4, P1-P5, P1-P6 y P1-P7 a metros columna de Agua (m.c.a), como Δh(P1-Pn) está en cms, se debe dividir la lectura manométrica entre 100. 2. Transforme la presión del P1 a metros de columna de agua (m.c.a), sabiendo que 1 psi equivale a 0,7031 m.c.a, el valor de esta transformación será ℎ𝑃1 3. Calcular el Volumen circulante en las tuberías, dividiendo el Peso del Agua entre su Densidad. (Asumir densidad del agua como 1000 Kg/m3). 4. Calcular el Caudal, dividiendo el Volumen de Agua entre el Tiempo. 5. Determine la energía para cada tubería en metros de columna de agua de los puntos P2, P3, P4, P5, P6 y P7. Esta se obtiene ℎ𝑛 = ℎ𝑃1 − ∆ℎ(𝑃1−𝑃𝑛) INFORME A PRESENTAR 1. Introducción teórica sobre el tema, incluyendo el K de los dispositivos de tuberías más comunes. 2. Haga un gráfico de la energía ℎ en función de la distancia X para cada uno de los caudales establecidos. Incluya la posición de la válvula en el eje x, (ver figura 1.) 3. Determinar la Perdida de Energía Hl. NOTA: para esto se deben extrapolar las rectas de las mediciones antes y después de la válvula e intersectarlas con la línea de salto de la válvula, la diferencia entre los dos puntos de intersección será el Hl. (ver figura 2) 4. Determinar los Gradientes Piezométricos -dh/dx. NOTA: el gradiente piezométrico debe tener la misma pendiente antes de la válvula y después de la válvula (debido a que el diámetro de la tubería se mantiene constante). En el cálculo estas presentan una pequeña variación, se tomará el promedio entre ambas pendientes. 5. Calcular el Numero de Reynolds e indicar si el flujo es de régimen laminar o turbulento, asumir el valor de la viscosidad cinemática (v) como 0,000000864 (m2/seg) esta es equivalente a una temperatura del agua a 26°C 4𝑄 𝑅= 𝜋𝐷𝜈 6. Calcular el coeficiente de Fricción f por medio de la Ecuación de Blasios, según el tipo de régimen. 𝑓= 0,316 𝑅 0,25 para régimen Turbulento 𝑓= 64 𝑅 para régimen laminar 7. Usando los gradientes piezométricos calculados anteriormente y las ecuaciones siguientes, determine el diámetro interno “D” más probable para cada tubería. 𝑑ℎ 𝑓.𝑄2 Gradiente Piezométrico – = 𝜋 2 𝑑𝑥 𝐷5 2𝑔( ) 4 4∗𝑄 8. Calcular la Velocidad Media para el Diámetro Interno más Probable 𝑉 = 𝜋 ∗ 𝐷² 9. Calcular el Coeficiente de Perdida K, y la Longitud Equivalente Le (m) con el Diámetro Interno más Probable 𝐻𝑙 ∗ 𝐷 ∗ 2𝑔 𝐻𝑙 𝐿𝑒 = 𝐾= 𝑓 ∗ 𝑉² 𝑉²⁄ 2𝑔 10. Realice para cada tubería, una gráfica en papel semilogaritmico de los coeficientes K, en función del número de Reynolds, en la misma grafica trace una línea recta horizontal para el valor del K teórico (ver figura 3) 11. Comente sus resultados y establezca comparaciones entre los coeficientes K de una válvula de compuerta y una de globo (ver tabla 1), de igual manera establezca comparaciones sobre las longitudes equivalentes teóricas con las calculadas (ver tabla 2). 12. Referencias bibliográficas. Laboratorio de Hidráulica Elías Sánchez Díaz PRACTICA: CIHAM-UC Pag. 40 Flujo sobre Cuerpos Sumergidos OBJETIVO: Determinación de la fuerza que ejerce la corriente contra un cilindro circular con su eje normal al flujo, siendo el fluido un líquido. Introducción: Cuando un sólido se sumerge en un fluido y existe un movimiento relativo entre ellos, se generan fuerzas contra el sólido que no dependen de sus velocidades absolutas sino de la velocidad relativa entre ambos. Usualmente se consideran dos tipos de fuerza: el empuje ascensional, perpendicular a la dirección de flujo, y el empuje de arrastre que se produce en la dirección de la corriente. El ultimo siempre estará presente en cualquier condición de corriente, mientras que el primero sólo tiene lugar cuando no existe simetría del cuerpo con respecto a la dirección de flujo (por ejemplo, el perfil de un ala de avión) o cuando se le imprime un movimiento rotatorio Fig.1 Cilindro Circular alrededor de su eje, como es el caso de un lanzador al tirar una curva con la pelota de beisbol. En la práctica a realizar se utiliza un túnel de agua, en cuya sección de ensayos se dispone de un cilindro circular sumergido en agua, con su eje normal a la dirección de la corriente, tal como lo muestra la figura 1. Con el paso de la corriente, el cilindro estará sometido solo a las fuerzas de arrastre, originadas parcialmente por los esfuerzos de corte viscoso entre el contorno y el líquido, que generan una fricción en la parte anterior del cilindro, en el punto A se encuentra el punto de estancamiento de la línea de flujo. Además, se produce una separación de la corriente en la parte posterior del cilindro (punto C) provocada por la interrelación entre la fricción con el contorno y la presencia de gradientes de presión que retardan el movimiento fluido. De esta manera, el sólido en la parte posterior no guía la corriente principal y toma su lugar una corriente secundaria altamente vorticosa llamada zona de separación, la cual se caracteriza por mantener bajas presiones más o menos constantes. En consecuencia, existe una distribución asimétrica de presiones respecto al diámetro vertical del cilindro, hecho que justifica una fuerza global de presión adicional a la de fricción, cuya magnitud depende de la forma del cuerpo. La experiencia indica que en un cilindro circular, estas fuerzas de presión son mucho más importantes que la debida al rozamiento, aunque no sea posible separarlas experimentalmente. 𝜌𝑉 2 La ecuación de la fuerza de empuje sobre un cuerpo es de la forma: 𝐹 = 𝐶𝐷 𝐴 (1) 2 En donde, V es la velocidad no perturbada de la corriente, 𝜌 es la densidad del fluido, A es el area del cuerpo proyectada sobre un plano perpendicular a la corriente y 𝐶𝐷 es el coeficiente adimensional de empuje. Mediante análisis dimensional, puede demostrarse que el coeficiente de empuje depende de la geometría del cuerpo y del número de Reynolds. Flujo Potencial alrededor de un cilindro: Bajo la suposición de flujo ideal, se deduce una forma analítica de la distribución de presiones alrededor de un cilindro, cuando está sometido a una corriente libre (no confinada como es el caso del cilindro del laboratorio). En efecto, si en la zona no perturbada de la corriente irrotacional se conocen la altura piezométrica ℎ𝑜 y la velocidad 𝑣𝑜 la forma adimensional de la ecuación de Bernoulli establece que, en cualquier otro punto de la corriente donde la altura piezométrica sea h y la velocidad v, el coeficiente piezométrico Cp en un punto i del cilindro es: Laboratorio de Hidráulica Elías Sánchez Díaz CIHAM-UC Pag. 41 (ℎ𝑖−ℎ𝑜 ) 𝑣𝑖 2 = 1 − (2) ( ) 2 𝑉𝑜 ⁄ 𝑣𝑜 2𝑔 𝑖 Según la teoría de flujo potencial, la superposición de 𝑜 un doblete bidimensional (dipolo formado por una fuente y un sumidero) con una corriente uniforme, da como resultado el campo de flujo irrotacional alrededor de un cilindro circular. De allí se deriva que en un fluido ideal, el patrón de velocidades a lo largo del contorno del cilindro, obedece a la siguiente relación: 𝑣𝑜 𝑣𝑖 𝐶𝑝𝑖 = 𝑣 = 2𝑣𝑜 . 𝑠𝑒𝑛(𝛽) (3) Siendo v la velocidad puntual tangente al contorno en un punto de mismo, y 𝛽 es él ángulo que forma la horizontal con la línea que une al punto con el centro de curvatura del cilindro. Si sustituimos en el miembro derecho de la ecuación (2) la ecuación (3), se encuentra que: 𝐶𝑝 = 1 − 4𝑠𝑒𝑛2 𝛽 (4) E indica que la distribución ideal de las alturas piezométricas en líquidos (o de presiones en gases) es simétrica tanto al eje vertical como horizontal. El valor máximo de 𝐶𝑝 se obtiene en los puntos del contorno donde el radio es paralelo a la corriente y el mínimo en los puntos donde el radio es normal a la corriente. La simetría del perfil piezométrico y la ausencia de esfuerzos viscosos del campo irrotacional a lo largo del contorno, indican que el empuje sobre el cilindro es cero (0), hecho que se conoce en la Historia de la Hidráulica como la “Paradoja de D’Alembert”. La fuerza de arrastre debida a la presión que ejerce un flujo de agua sobre un cilindro con el eje perpendicular a la dirección del flujo se puede determinar con la siguiente integración: 𝜋 𝐹 = 2𝛾𝑅𝐿 ∫0 ℎ. 𝑐𝑜𝑠𝛽. 𝑑𝛽 (5) Donde R y L son el radio y la longitud del cilindro, h energía piezométrica en el punto ubicado en ángulo 𝛽. Si sustituimos el término izquierdo de la ecuación (2) en la ecuación (5) se puede demostrar analíticamente que el empuje sobre un cilindro en flujo irrotacional es igual a cero (0). Comparando las ecuaciones (1) y (5) podemos determinar el coeficiente de arrastre para el cilindro: 𝜋 𝐶𝐷 = ∫0 𝑐𝑝 . 𝑐𝑜𝑠𝛽. 𝑑𝛽 (6) En la gráfica 1 se muestra el valor del coeficiente de arrastre teórico para un cilindro circular, note que 𝐶𝐷 = 1,2 para números de Reynolds 104 < 𝑅 < 1.5𝑥105 , Laboratorio de Hidráulica Elías Sánchez Díaz CIHAM-UC Pag. 42 Grafica. 1. Coeficiente de Arrastre para Cilindros Circulares y esferas en función del número de Reynolds. EQUIPO DE LABORATORIO D C A E B Descripción del Equipo de Laboratorio: Flujo sobre cuerpo sumergidos A Túnel de Agua con sección bidimensional de D Manómetro diferencial en “U”, conectado al ensayos que contiene un cilindro circular, manifold (B) y al punto “0”. alrededor del cilindro y en la línea media de la sección se disponen orificios piezométricos. B Manifold, al cual se conectan la totalidad de E Válvula de 4” orificios piezométricos. C Tanque estabilizador. Laboratorio de Hidráulica Elías Sánchez Díaz 1. 2. 3. 4. 5. 6. 7. 8. CIHAM-UC Pag. 43 PROCEDIMIENTO Tenga a mano la hoja de recolección de datos de la práctica. Verifique que esté en funcionamiento el equipo. Fijar un caudal mediante la válvula E. Para el primer caudal, abra la válvula #8 del manifold y aumente el flujo hasta observar que la lectura del manómetro sea de 25cm a 30 cm. Esta lectura no debe sobrepasar los 30cms. Efectúe la medición en el manómetro D de los puntos 8, 9, 10, 11, 12, 13 y 14. Cada lectura se hace por separado abriendo la válvula correspondiente en el Manifold y esperando al menos 5 minutos de estabilización. Fije un caudal menor al anterior cerrando 1 vuelta la válvula E. Repita el paso 4. Llene la tabla de recolección de datos y realice los cálculos preliminares. Verifique con el profesor o los preparadores que los cálculos preliminares sean correctos y para la firma de la hoja de recolección de datos, la cual deberán anexar al informe. 10 o 𝑣𝑜 9 𝑜 8 30o 11 00 12 13 00 14 00 Fig.2 Ubicación de los Orificios Piezométricos en la sección de ensayos del túnel. Laboratorio de Hidráulica Elías Sánchez Díaz CIHAM-UC Pag. 44 Tabla de Recolección de Datos Flujo sobre cuerpos sumergidos Practica: Grupo: Practica No.: Punto No. (i) Medición 1 Medición 2 Datos de la Experiencia: Δh(i-0) (cm) Δh(i-0) (cm) Diámetro del Cilindro: 5cm 8 Área de la sección: (5x20)cm2 9 10 11 12 13 14 Nombre y Apellido C.I. Firma Nombre del Profesor Firma del Profesor Fecha: / / Laboratorio de Hidráulica Elías Sánchez Díaz CIHAM-UC Pag. 45 CALCULOS PRELIMINARES 1. El punto ubicado en la proa del cilindro (8) es el punto de estancamiento y por tanto, su lectura piezométrica es igual a la carga de velocidad de la corriente no perturbada, ∆ℎ0−8 = 𝑣𝑜 2 2𝑔 , determine la velocidad, el gasto y el número de Reynolds que caracterizan a la corriente para cada uno de los caudales. 2. Ubique el ángulo de los puntos del cilindro en la fig.2 y determine el coeficiente piezométrico irrotacional de los puntos 8, 9, 10, 11, 12, 13 y 14 a través de la ecuación (4). 3. Determine los valores del coeficiente piezométrico experimental a través de la ecuación (2) de los puntos 8, 9, 10, 11, 12, 13 y 14. Recuerde que ∆ℎ𝑖−𝑜 = ℎ𝑖 − ℎ𝑜 . INFORME A PRESENTAR 1. Introducción teórica en donde incluye el concepto y tipos de capa límite y el mecanismo de la separación. 2. Represente gráficamente en un papel milimetrado o polar, el coeficiente piezométrico 𝐶𝑝 determinado en el paso 2 de cálculos preliminares en función de 𝛽 para cada caudal e identifíquelos con el número de Reynolds respectivo. Compare estos gráficos con los experimentales. 3. Represente gráficamente el parámetro 𝐶𝑝 . 𝐶𝑜𝑠(𝛽) en función de 𝛽 tanto experimentales como los teóricos y encuentre por integración numérica el coeficiente de empuje para cada número de Reynolds con la ecuación (6), (Utilice el método matemático de integración por partes ó método de los trapecios). 4. Busque en la gráfica 1 el coeficiente de arrastre para cilindros y compare con los calculados anteriormente. 5. Calcule la fuerza de arrastre que ejerce el flujo sobre el cilindro con la ecuación (1) y los coeficientes de arrastre obtenidos en el paso 3 y 4. 6. Diga a qué tipo de capa limite pertenecen las distribuciones piezométricas y justifique (El tipo de capa limite depende del número de Reynolds y del objeto en estudio, investigue en los libros los casos de cilindros sumergidos en fluidos). 7. Comente los resultados y establezca conclusiones sobre los aspectos relevantes de la práctica. 8. Referencias bibliográficas. Laboratorio de Hidráulica Elías Sánchez Díaz TALLER: CIHAM-UC Pag. 46 Medición de caudales con tecnología moderna. OBJETIVO: Determinar el gasto que circula en un canal rectangular mediante el uso de Minimolinete M-1 e instrumentos de tecnología moderna marca SEBA y comparar el resultado obtenido con el método del vertedero. Introducción: La hidrometría permite determinar el caudal del agua que fluye en un río, una tubería o canal, así como determinar la cantidad de agua que produce un pozo de agua subterránea, la que llega a una planta de tratamiento o sale de ella, la que se consume en una ciudad, industria o residencia, entro otros. Existen muchas maneras de determinar el caudal y a través de las practicas realizadas en el laboratorio de fluidos se experimentan algunos métodos de medición como: placa orificio, vertederos, dividiendo el volumen entre el tiempo, método del codo calibrado, dividiendo el peso entre el tiempo y hasta analizando la caída de un chorro por lanzamiento de proyectiles. Estos métodos antiguos todavía se siguen utilizando en las obras hidráulicas que la ingeniería enfrenta en su ejercicio profesional y muchos de ellos aunque sencillos son de suma importancia tener el conocimiento básico para aplicarlos. Figura.1 Con el pasar de los años la hidrometría ha tenido avances y han aparecido nuevos dispositivos digitales y controladores que facilitan al profesional la obtención de resultados de maneras rápidas y confiables. Otra manera de medir el caudal de los cursos de agua con flujo superficial es mediante el empleo del molinete, correntómetro o corrientímetro (figura 1), que es un aparato compuesto por una hélice que combina su movimiento giratorio con un indicador registrador. El número de rotaciones de la hélice en un determinado tiempo define la velocidad de la corriente de agua. Sobre la base de las tablas suministradas por el fabricante, es posible determinar la velocidad del curso de agua en un punto definido de la sección transversal del río o canal de estudio. En este caso, se acostumbra hacer mediciones de velocidad en diferentes puntos de la sección transversal del curso de agua, a diferentes anchos y profundidades, para obtener la velocidad promedio del curso de agua. La sección del río o canal elegida para la medida con el molinete debe estar situada en un tramo recto y una sección lo más homogénea posible a lo largo de dicho tramo (figura 2). El molinete posee un sistema electromecánico para contar las revoluciones que se producen en un determinado tiempo, llamado contador de impulsos, que recibe una señal eléctrica a través de un cable cada vez que la hélice realiza una vuelta. Las empresas dedicadas a la construcción de molinetes, entregan en el momento de la venta, las ecuaciones de calibración, las cuales tienen la forma de una ecuación por partes y son diferentes para cada molinete y cada tipo de hélice. El molinete que será usado en el desarrollo de este taller es un Mini molinete M1 de marca SEBA, con una hélice de 50mm de diámetro y una paso de 100. El fabricante indica que según la calibración de este equipo con la hélice de 50/100 las ecuaciones son las siguientes: 𝑆𝑖 0 < 𝑛 < 2,35 𝑒𝑛𝑡𝑜𝑛𝑐𝑒𝑠 𝑆𝑖 2,35 < 𝑛 < 8,32 𝑆𝑖 8,32 < 𝑛 < 25 𝑉 = 0,0093 + 0,1012. 𝑛 (Ec. 1) 𝑒𝑛𝑡𝑜𝑛𝑐𝑒𝑠 𝑒𝑛𝑡𝑜𝑛𝑐𝑒𝑠 𝑉 = 0,0180 + 0,0975. 𝑛 (Ec. 2) 𝑉 = 0,0338 + 0,0956. 𝑛 (Ec. 3) Dónde: n = número de impulsos por segundo (1/s) V= velocidad media en la sección (m/s) Figura 2. Ejemplo de sección en estudio. Laboratorio de Hidráulica Elías Sánchez Díaz CIHAM-UC Pag. 47 El molinete mide solamente la velocidad en un punto, es por esto que, para calcular el caudal total se deben realizar varias mediciones. Según sea el grado de precisión que se quiera obtener en la determinación del caudal, se tomará un mayor o menor de verticales. Cuando se pretenda obtener una alta precisión, se elegirá mayor número de verticales, las cuales deben estar separadas entre sí la misma distancia. En la figura 3 se muestra un esquema explicativo. Figura 3. Sección Transversal indicando las verticales En cada vertical, dependiendo del grado de precisión, se pueden tomar medidas según las siguientes recomendaciones (ver también figura 4): a) Si se hace una sola lectura, debe ser tomada al 60% de la altura, medida a partir de la superficie libre del agua. Esto en el caso de profundidades menores que 60cm. b) Si se hacen dos lecturas, deben ser tomadas al 20% y al 80% de la altura, medidas a partir de la superficie libre del agua. Esto es en el caso de profundidades comprendidas entre 60cm y 300cm. c) Si se hacen cuatro lecturas, deben ser tomadas al 20%, 40%, 60% y 80% de la altura, medida a partir de la superficie libre del agua. Esto es en el caso de profundidades mayores que 300cm. Figura 4. Diferentes puntos para medir velocidad según profundidad del agua Las recomendaciones para calcular la velocidad media en cada vertical se muestran en la tabla 1. Tabla 1. Recomendaciones para calcular la velocidad media. Número de Puntos de observación Velocidad media en la vertical mediciones 1 0,6H 𝑉 = 𝑉0,6 (Ec. 4) 2 0,20H y 0,8H 𝑉= 3 𝑉0,2 + 𝑉0,8 (Ec.5) 2 0,2H, 0,4H, 0,6H y 0,8H 𝑉= 3.𝑉0,2 + 𝑉0,4 + 𝑉0,6 +𝑉0,8 6 (Ec.6) Laboratorio de Hidráulica Elías Sánchez Díaz CIHAM-UC Pag. 48 Para cada sección entre dos verticales, el área se calcula como el promedio de la altura H por el ancho ∆B; y la velocidad media como el promedio de las velocidades medias en las verticales. El caudal parcial, entre dos verticales, resulta de multiplicar el área parcial por la velocidad media, mientras que el caudal total se calcula como la sumatoria de las caudales parciales entre las verticales, es decir: 𝑚 𝑄 = ∑ 𝐴𝑝𝑎𝑟𝑐𝑖𝑎𝑙 . 𝑉𝑚𝑒𝑑𝑖𝑎 𝑣𝑒𝑟𝑡𝑖𝑐𝑎𝑙 (𝐸𝑐. 7) 0 El Minimolinete M1 trabaja con el contador de alta tecnología Z6 (figura 5), en el cual con solo grabar en la memoria del equipo las ecuaciones de la hélice (1,2 y 3) de forma automática transmite digitalmente el valor de la velocidad en la sección en estudio. Adicionalmente existen controladores de mano multifuncionales para manejo en agua. Son resistentes contra golpes, de fácil manejo, ligeros y a prueba de agua. Además son asistentes perfectos para desenvolverse con innumerables tareas en campo. Uno de los equipos de esta tecnología es el TDS de SEBA (figura 6) que está equipado con cómodas herramientas de software que permite una cómoda colecta de datos de mediciones (mediciones con sondas de contacto) que puede sustituir o reemplazar los tradicionales contadores para mediciones de descarga. El software Q permite a ambos el proceso de propulsión por impulsos (por ejemplo el Molinete) y el análisis directo de mediciones de las descargas en el sitio de medición. Adicionalmente estos equipos se les puede instalar un GPS para facilitar la ubicación de los sitios de medición. Figura 5. Contador Z6 Figura 6. Controlador TDS EQUIPO DE LABORATORIO D C B A Laboratorio de Hidráulica Elías Sánchez Díaz CIHAM-UC Pag. 49 Descripción del Equipo de Laboratorio: Medición de caudales con tecnología moderna. A Canal rectangular con paredes de vidrio. D Medidor de punta vertedero triangular. B Diques de malla plástica para evitar excesiva E Minimolinete M1 SEBA con contador Z6 turbulencia de la corriente en el canal. C Vertedero Triangular de cresta delgada en VF Controlador TDS Recon SEBA con software Q y 90º, con lamina vertiente en caída libre. convertidor de pulsos. PROCEDIMIENTO 1. Tenga a mano la hoja de recolección de datos de la práctica. 2. Tome las lectura inicial del medidor de punta (D) del vertedero triangular “𝐿𝑜”, este valor se encuentra en el lateral del vertedero. 3. Con el medidor de punta (D), tome el nivel de agua anterior a la cresta del vertedero triangular “𝐿𝑖”. 4. Con una cinta métrica tome la medida de la altura Ha del nivel del agua en el canal, la cual será la medida desde el fondo hasta la superficie del agua. 5. Como el canal tiene una altura menor a 60cm, se recomienda realizar una sola medición a 0,6Ha según fig.4 y tabla 1, ajuste el minimolinete M1 a una altura de Hm1= Ha-0,6Ha 6. El canal se dividió en 10 secciones que aparecen indicadas en el equipo, tome las medidas de los impulsos o número de vueltas con el contador Z6 en el centro de cada sección. Determine la velocidad parcial que transmite el Z6 solo para la medición 1. 7. Repita los pasos anteriores hasta obtener los datos de 10 verticales. CALCULOS PARA EL TALLER: 1. Para la condición de flujo determine la cresta del vertedero Triangular 𝐻 = 𝐿𝑖 − 𝐿𝑜. 2. Usando la ecuación del vertedero triangular 8 𝑄 = 15 𝐶𝑑 𝑡𝑎𝑛(𝛼⁄2)√2𝑔×𝐻 5⁄ 2 y con un Cd=0,58 determine el caudal del sistema. 3. Determine el número de impulsos por segundo n= No.Vueltas/tiempo (el Z6 tiene predeterminado un tiempo de 30seg) y mediante las ecuaciones (1,2 o 3) determine las velocidades medias en cada sección. 4. Compare las velocidades V calculadas anteriormente con la velocidades dadas por el contador Z6. 5. Calcule el caudal utilizando la ecuación 7. 6. Compare los resultados de caudal obtenidos a través de los pasos 2 y 5. 7. Establezca sus conclusiones. Vm1 1 2 3 4 5 6 7 8 9 10 Laboratorio de Hidráulica Elías Sánchez Díaz CIHAM-UC Pag. 50 Tabla de Recolección de Datos MEDICIÓN DE CAUDALES CON TECNOLOGÍA MODERNA Practica: Grupo: Practica No.: Lo(cm) Li(cm) Ha (cm) Sección No.Vueltas V (m/s) Z6 1 2 3 4 5 6 7 8 9 10 Datos de la Experiencia: Ancho del Canal rectangular: B=60cm; Altura al vértice del vertedero triangular: W=19,6cm ∆B en secciones = 60/10 = 6cm Nombre y Apellido C.I. Firma Nombre del Profesor Firma del Profesor Fecha: / / Laboratorio de Hidráulica Elías Sánchez Díaz CIHAM-UC Pag. 51 Introducción a los Proyectos Ambientales OBJETIVO: Brindar la oportunidad a los estudiantes de hacer algo constructivo en su entorno y de desarrollar sus talentos en situaciones prácticas a través del modelo JCI para la planificación de proyectos. Introducción Un proyecto se puede definir como una planificación para alcanzar unos objetivos específicos, consiste en un conjunto de actividades que se encuentran interrelacionadas y coordinadas dentro en área definida y un lapso de tiempo previamente definido. En este proyecto, les explicaremos la estrategia utilizada por la JCI, cuyas siglas significan Cámara Junior Internacional, la cual, es una de las mayores organizaciones juveniles en todo el mundo; es decir, es una ONG. Se trata de una comunidad internacional de ciudadanos de entre 18 y 40 con el objetivo y el propósito de crear un cambio positivo en el mundo. La organización cree que estos cambios deben resultar de tomar una "acción colectiva para mejorar ellos mismos y el mundo que les rodea." ¿Cuáles son las características de un buen plan? Según la JCI, las principales características de un proyecto son: 1. ES ORGANIZADO. Un buen plan debe estar muy bien organizado y ser fácil de entender. Debe definir claramente las distintas etapas, establecer estrategias y pasos de acción e indicar quién es responsable de llevar a cabo cada actividad. 2. SATISFACE LAS NECESIDADES DE LOS MIEMBROS DEL GRUPO. El plan debe satisfacer las necesidades y expectativas de los miembros del grupo. Si desea que el plan tenga éxito, los miembros deben beneficiarse con él de alguna forma: pudiera ser la satisfacción que se siente ayudando a los demás o la adquisición de nuevos conocimientos o técnicas. 3. LE OFRECE A CADA MIEMBRO DEL GRUPO LA OPORTUNIDAD DE APORTAR SUS HABILIDADES. Cada miembro debe poder hallar en el plan alguna actividad en que pueda participar. El trabajo debe dividirse entre los miembros de acuerdo con sus capacidades, habilidades y deseos. Hay que evitar sobrecargar de trabajo a los miembros de más experiencia y dejar sin nada que hacer a los que están deseosos de ayudar. 4. ES FACTIBLE. Un buen plan debe ser práctico e indicar que es factible. Los integrantes del grupo deben tener fe en las posibilidades y el éxito del plan. Deben poder ver las metas y los resultados que ayudarán a alcanzar. 5. ES SENCILLO. La terminología que se utilice en el plan ha de estar al alcance de todos los miembros del grupo sin necesidad de consultar con un especialista. 6. ES CLARO, ESPECÍFICO Y PRECISO. El plan debe indicar cantidades, plazos, calidad, especificaciones, responsabilidades, costos, etc. 7. ES FLEXIBLE. Las cosas pueden cambiar después de formulado el plan. Es preciso, pues, que sea flexible para adaptarse a los cambios. Laboratorio de Hidráulica Elías Sánchez Díaz CIHAM-UC Pag. 52 8. TIENE UN PROGRAMA EQUILIBRADO. El plan debe tener un programa equilibrado de actividades, distribuidas entre todos los miembros y repartidas durante su período de ejecución. Esta precaución evita el exceso de trabajo en ciertos momentos y para ciertos miembros. 9. DEBE ESTAR BIEN FINANCIADO. El plan debe tener su presupuesto y cada actividad debe indicar su costo. Todos los miembros deben ver claramente de dónde salen los fondos y a dónde van a parar. Muchos buenos planes fracasan porque sus presupuestos no son realistas. Todos los patrocinios deben confirmarse antes de incluirse en el presupuesto. 10. DEBE SER COMPLETO. El plan debe incluir todos los detalles posibles. Nada debe dejarse al azar o a la improvisación. Hay que considerar todas las circunstancias de modo que no se produzcan imprevistos. Una vez que el plan esté formulado, alguien debe revisarlo con ojo crítico para detectar errores u omisiones. Muchas veces las personas no se atreven a realizar un proyecto ambiental porque piensan que para desarrollarlo deben crear prácticamente una tesis de grado, cuando en realidad con unos simples pasos se puede armar un proyecto básico capaz de solucionar algún problema. Existen muchos métodos para desarrollar un proyecto, uno de los más sencillos es el utilizado por la JCI, quienes han desarrollado una estrategia que consiste en cinco (5) pasos para el proceso de planificación de proyectos, los cuales se indican a continuación: Paso 1. Encuesta o Diagnostico: La mejor manera de describir una necesidad es realizar una encuesta. La misma debe contener preguntas acerca de los problemas y las necesidades de la comunidad. Existen varios tipos de encuestas, la encuesta publica, encuestas de líderes y la encuesta representativa. Paso 2. Análisis: Una vez concluido el diagnostico, los resultados deben organizarse lógicamente y estudiarse a fondo, de manera de poder identificar alguna problemática. Se debe elaborar un informe que presente los resultados de la encuesta al profesor. Paso 3: Planificación: La base del éxito de todo proyecto es un equipo bien organizado que lo lleve a cabo. La primera tarea es seleccionar un director de proyecto. Posteriormente el director junto a los colaboradores estudia a fondo el proyecto y con detenimiento. El plan de acción debe incluir los elementos siguientes: 1. El propósito del proyecto. Hay que establecer la razón por que el comité lleva a cabo el proyecto. El propósito debe precisar los fines del proyecto en una sola oración que todos los que trabajan en él puedan entender fácilmente. 2. Las responsabilidades principales de los aspectos fundamentales. Las actividades del proyecto deben dividirse en distintos aspectos fundamentales tales como finanzas, promoción, registros, administración, etc. 3. Los objetivos de cada aspecto. Se deben establecer los objetivos principales de cada aspecto fundamental. Los objetivos deben ser posibles y fáciles de entender. 4. Estrategias para alcanzar cada objetivo. Determínese con respecto de cada objetivo quién es responsable de la tarea y cuándo debe quedar ésta concluida. 5. Pasos de acción para cada estrategia. Cada estrategia debe dividirse en pequeños pasos de acción que indiquen claramente lo que debe hacerse y quién tiene la responsabilidad de hacerlo. Una vez concluido el plan de acción, es necesario recabar la información siguiente: un orden cronológico de acontecimientos o actos; un cronograma; un presupuesto; listas de los deberes de todos los miembros del comité; y una lista de organizaciones ajenas al capítulo, recursos y personas que toman parte en el proyecto. El plan de acción se le presenta a la Junta Directiva (Profesor de Laboratorio) que, con su aprobación, ratifica el compromiso de la Catedra para con el proyecto. Paso 4. Acción: En la fase de la acción, el proyecto se pone en marcha y todos los participantes llevan a cabo sus responsabilidades. La fase de acción exige que el director del proyecto aplique habilidades muy importantes como la delegación, la supervisión, las comunicaciones, el manejo de los recursos humanos, la oratoria y muchas otras más. Al Laboratorio de Hidráulica Elías Sánchez Díaz CIHAM-UC Pag. 53 asignar responsabilidades, téngase en cuenta la necesidad de hacer sacrificios. Los miembros sacrifican tiempo libre, pasatiempos e intereses hasta que el proyecto quede terminado. Paso 5. Evaluación: La evaluación es la culminación natural del proyecto. Es posible que el proyecto haya sido un éxito rotundo pero que no haya satisfecho las necesidades que se propuso atender. Y si el proyecto fracasó, es necesario saber las razones de su fracaso y las medidas correctivas que pueden aplicarse ahora o en un futuro, cuando se vuelva a intentar un proyecto semejante. Muchas veces se pasa por alto la evaluación porque los participantes estiman que con terminar el proyecto basta. RESUMEN Una vez concluido el proyecto, los miembros del comité podrán sentirse orgullosos de su labor y satisfechos de la experiencia que han adquirido, de su superación personal, de haber dado más realce a la imagen del Laboratorio de Hidráulica y de haber mejorado a la comunidad universitaria. En las páginas siguientes, se presentan los formularios 1, 2 y 3 que sirven de apoyo para la planificación avanzada del proyecto utilizado por la JCI, con algunas adaptaciones para ser aplicado en al Laboratorio Elías Sánchez Díaz. El formato [1], lo deben entregar al inicio de semestre después de realizado el diagnostico. Posteriormente deben llenar el formato [2] donde indican los objetivos planteados y los costos aproximados. Para culminar solo deben entregar el Formato [3] para poder dar cumplimiento a la actividad. Evaluación del Proyecto Ambiental: Material a entregar. 1) Seleccionar alguna problemática que exista en el Laboratorio Elías Sánchez Díaz, en función de su experiencia en las instalaciones y el diagnostico preliminar desarrollado. 2) Llenar el formato 1. 3) Entregar el formato 1 al profesor para su debida aprobación. 4) Planificar el Proyecto llenando el formato 2. 5) Realizar el proyecto y finalmente entregar el Formato 2 y 3 al profesor para su evaluación correspondiente. Laboratorio de Hidráulica Elías Sánchez Díaz CIHAM-UC Pag. 54 FORMATO 1. PROPUESTA DEL PROYECTO Proyecto Propuesto: Propósito del proyecto: Número estimado de miembros y sus funciones: Posibles beneficios para el Laboratorio: Comentarios Generales sobre el proyecto propuesto: Resultados de las investigaciones preliminares o del estudio de factibilidad: Aprobado por la Junta Directiva (Profesor de Laboratorio): Firma del Profesor de Laboratorio Fuente: . www.jci.cc Laboratorio de Hidráulica Elías Sánchez Díaz CIHAM-UC Pag. 55 FORMATO 2. OBJETIVOS PRINCIPALES Proyecto Propuesto: Fecha en que se estima se iniciará el proyecto: Fecha en que se estima se concluirá el proyecto: Objetivos principales Resultados esperados Publicidad y promoción: Materiales especiales necesarios: Presupuesto Ingresos Bs. Egresos Bs. Fuente: . www.jci.cc Laboratorio de Hidráulica Elías Sánchez Díaz CIHAM-UC Pag. 56 FORMATO 3. INFORME SOBRE EL PROYECTO CONCLUIDO Nombre del Proyecto: Breve descripción del proyecto: Sección: Horario: Prof.Lab.: Objetivo Descripción resumida Medidas Tomadas Resultados Recomendaciones: Fecha Inicio Fecha Conclusión Número de miembros del grupo Número de otros voluntarios Ingresos totales (proyección) Ingresos totales (reales) Egresos totales (proyección) Egresos totales (reales) Firma del Técnico de Laboratorio: Firma del Profesor: Fuente: . www.jci.cc Laboratorio de Hidráulica Elías Sánchez Díaz CIHAM-UC Pag. 57 Anexos INSTRUMENTOS DE MEDICIÓN DEL LABORATORIO a) MANIFOLD: Es un sistema que permite centralizar funciones y por el cual se recogen varios flujos agua o aire en diferentes puntos y son controlados a través de la abertura o cierre de las válvulas que integran el dispositivo. b) MANÓMETROS DIFERENCIALES: Un manómetro diferencial es un dispositivo que mide la diferencia de presión entre dos lugares. El manómetro diferencial más simple es un tubo en forma de U con ambos extremos a la misma altura. Un líquido, generalmente agua o mercurio, descansa en la parte inferior del tubo. En el laboratorio se tienen 3 tipos de manómetros los cuales se presentan a continuación: Manómetro Diferencial agua-aire Funcionamiento: A través de un dispositivo giratorio con una cinta métrica y una escala que funciona como un vernier se toma la diferencia piezométrica entre dos puntos de interés que se encuentran conectados en los tubos de vidrio. Apreciación: 1mm Manómetro Diferencial agua-mercurio Funcionamiento: En una escala de medición en papel milimetrado se coloca una tubería de vidrio en forma de “U” en la cual se introduce mercurio, a los dos extremos del tubo se conectan los puntos donde se desea medir la diferencia piezométrica. Apreciación: 1mm. Manómetro Dial de 2” de Diámetro FTB: Funcionamiento: Este manómetro da como resultado la presión relativa en el punto donde se ubique. Apreciación: 0,11kg/cm2 Laboratorio de Hidráulica Elías Sánchez Díaz CIHAM-UC c) BANCO PIEZOMÉTRICO: Banco con el fondo con escala en papel milimetrado, en donde se instalan paralelamente piezómetros que se encuentran conectados en diferentes puntos de una línea de flujo. Apreciación: 1mm d) BALANZA CON TANQUE METÁLICO: Consiste en un tanque de almacenamiento con control de entrada y salida, el cual está acoplado a una balanza donde se toma el peso del fluido almacenado en un tiempo especifico. Para su funcionamiento hay que cerrar la llave de salida y derivar el flujo al tanque, dejar fluir el líquido en el tanque por el tiempo establecido y colocar el flujo en su dirección original. Antes de comenzar a medir es importante verificar que el tanque se encuentre vacio. Apreciación: 1kg. e) MEDIDOR DE PUNTA (SONDA DE MEDICIÓN): Es un instrumento de medición que se usa con el fin de determinar alturas o profundidades de agua. Consta de: a. Barra deslizante móvil con una escala o regla principal con divisiones cada milímetro y en la parte inferior una punta o aguja. b. Base de apoyo donde se fija la barra deslizante al canal. c. Una segunda escala llamada nonio o vernier, que permite realizar mediciones con mayor apreciación que las divisiones de la escala principal. d. Perilla para la movilización de la escala principal o deslizante. Apreciación: 0,2mm Pag. 58 Laboratorio de Hidráulica Elías Sánchez Díaz CIHAM-UC Medidor de Punta o Sonda de Medición. Pag. 59 Laboratorio de Hidráulica Elías Sánchez Díaz CIHAM-UC Pag. 60 Referencias Bibliográficas. Bisquerra, R. (1988). Métodos de investigación educativa: Guía práctica. Barcelona: CEAC. Cazau, P. (2005). La Programación Neurolinguistica. Recuperado de: http://archivo.iered.org/.../2005-03-08_Programacion-Neurolinguistica.doc de la Torre S., Violant V. (2012), Estrategias Creativas en la Enseñanza Universitaria, Universidad de Barcelona, España. Escalona, L. (2009). Diseño de un sistema de enseñanza basado en instrumentación virtual para el laboratorio de instrumentación y control de la Facultad de Ingeniería. Trabajo de Ascenso. Facultad de Ingeniería, Universidad de Carabobo. Fernández, L. (2009). Guía de Laboratorio de Mecánica de los fluidos I. Facultad de Ingeniería, Universidad de los Andes. Camara Junior Internacional JCI (2013). Manual de Participante Planificación de Proyectos, Un curso de una hora de la JCI. www.jci.cc Jiménez, M. (2013). Propuesta para la enseñanza del Laboratorio de Mecánica de los Fluidos II. Trabajo para ascender a la categoría de profesor Asistente. Universidad de Carabobo, Facultad de Ingeniería, Escuela de Ingeniería Civil. Mora, C. (2012). La Universidad de Carabobo necesita de acciones que rescaten su excelencia académica. Articulo recuperado de: http://educaciondinamica.lacoctelera.net/post/2012/01/11/la-universidad-carabobo-necesita-acciones-rescaten-su Romo, M., Lopéz, D., López, I. (2006) ¿Eres visual, auditivo o kinestésico? Estilos de aprendizaje desde el modelo de la Programación Neurolingüística (PNL). Revista Iberoamericana de Educación, Número 38/2. Universidad Pedagógica Experimental Libertador [UPEL]. (2008). Manual de trabajos de grado y Especialización y Maestría y Tesis Doctorales. (4ta edición). Caracas, Venezuela. Editorial FEDUPEL. Urdaneta, R. (1998). 2da revisión de la Guía de Laboratorio de Mecánica de los Fluidos. Departamento de Ingeniería Ambiental, Facultad de Ingeniería de la Universidad de Carabobo.
© Copyright 2026