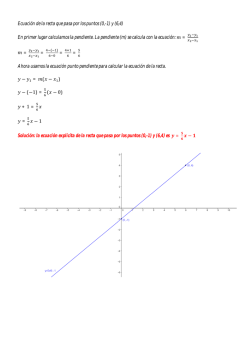
M - Instituto Educacional Aragua
República Bolivariana de Venezuela Ministerio del Poder Popular Para La Educación U.E.P. “Instituto Educacional Aragua” Maracay-Edo. Aragua Prof. Rafael Girón T Electrostática: Es la arte de la física que se encarga de estudiar los fenómenos eléctricos producidos por las cargas eléctricas en reposo. Existen dos tipos de cargas eléctricas las positivas (+) y las negativas (-), entre ellas existen interacciones eléctricas, las cuales pueden ser de atracción, si las cargas son de signos contrarios y repulsión, si las cargas son de signos iguales. Dos cuerpos de distintas naturaleza, pueden ser electrizados, por cualquiera, de los procesos, ya sea: frotamiento, contacto o inducción electrostática. Cuando se produce una electrización, lo que existe es una transferencia de electrones de un cuero a otro, quedando cargado negativamente aquel que gano electrones y positivamente el que cedió los electrones. El fenómeno de la electrostática esta regido por la ley de Coulomb: “Dos cargas eléctricas puntuales, se atraen o repelen con una fuerza directamente proporcional al producto de sus cargas e inversamente proporcional, al cuadrado de la distancia que las separa” 𝑞 𝑥 𝑞0 𝐹∝ 𝑟2 Donde: F es fuerza; q es carga eléctrica y r es distancia; cuando en física, aparece el símbolo de proporcionalidad es por que existe una constante de proporcionalidad, la cual en este caso se llama constante dieléctrica y se identifica con “K”. 1 𝑁 𝑥 𝑚2 𝐾= = 9𝑥109 𝐶 2 4𝜋 𝑥𝜀0 Quedando: 𝑞 𝑥 𝑞0 𝐹=𝐾𝑥 𝑟2 Ley que fue demostrada con un instrumento llamado “Balanza de Torsión”, la cual constaba de un soporte, un hilo inextensible y de masa despreciable, una barra conductora y en sus extremos dos cargas eléctricas separadas por una distancia “r”. +q0 +q r Contenido: Electrostática Ley de Coulomb Nivel Bajo. Instrucciones: a continuación se presentan una serie de ítems, con cuatro posibles respuestas. Marque con una equis (X), dentro del paréntesis la respuesta correcta. Solo una de ellas es la verdadera. 1.- Se tienen dos cargas eléctricas q1 = + 3 x 10-6 C y qB = +6 x 10-6 C, están en el vacío y en línea recta separadas por una distancia de 8 cm. Calcular la fuerza resultante sobre q2 por efecto de q1. ( ) F12 = 25,3 N; hacia la derecha ( ) F12 = 25,3 N; hacia la izquierda ( ) F12 = 25 N; hacia la izquierda ( ) F12 = 25 N; hacia la derecha Solución. Datos Para hallar F12 , aplicamos la ecuación de la Ley de Coulomb. 𝑞1 = + 3 x 10−6 C 𝑞2 = + 6 𝑥 10−6 𝐶 𝑟12 = 8 𝑐𝑚 𝐹12=𝐾 𝑞1 𝐹12 =? 𝐹12 = 9 𝑥 109 𝑥 𝑞2 𝑟2 𝑁 𝑥 𝑚2 3 𝑥 10−6 𝑥 6 𝑥 10−6 𝐶2 ( 8 𝑥 10−2 𝑚 )2 𝐹12 = 25, 3 𝑁; ℎ𝑎𝑐𝑖𝑎 𝑙𝑎 𝑑𝑒𝑟𝑒𝑐ℎ𝑎. q1 q2 F12 8 cm Como las cargas eléctricas son del mismo signo, la fuerza entre ellas es de repulsión; siendo la fuerza sobre q2, el vector fuerza tiene su origen en ella. Ya que es q1 quien actúa sobre q2. La distancia “r” siempre que este en centímetro (cm), debe ser transformado a metro (m) que es la unidad de medida de la distancia en el sistema M.K.S., o sistema internacional de medida. 2.- En la figura se muestran dos cargas eléctricas: q1 = - 5 x 10-6 C y q2 = +6 x 10-6 C; que están en el vacío y en línea recta separadas por una distancia de 3 m. Calcular la magnitud de la fuerza que actúa sobre q2 por efecto de q1. ( ( ( ( )- 0,015 N; hacia la derecha ) 0,015 N; hacia la derecha ) 0, 015 N; Hacia la izquierda ) -0,015 N; hacia la izquierda Datos: q1 = -5 x 10-6 C q2 = +3 x 10-6 C r12 = 3 m 𝐹12 =? 𝑒𝑛 𝑞2 q1 Diagrama FR q2 3m Ecuación Aplicamos la ecuación de la Ley de Coulomb, para hallar “F12 “ 𝐹 12=𝐾 Conversión de Unidades No es necesario. Solución 𝐹12 = 9 𝑥 109 𝑁 𝑥𝑚2 𝐶2 5 𝑥 10−6 𝐶 𝑥 3 𝑥 10−6 𝐶 (3 𝑚)2 𝐹12 = 0,015 𝑁 𝑞1 𝑥 𝑞2 𝑟2 Los signos de las cargas solo se utilizan para el análisis vectorial (fuerzas), en la ecuación no se toman en cuenta. 3.- Dos cargas eléctricas iguales están separadas por una distancia de 4 Cm y se repelen con una fuerza de 10 N. Calcular el valor de las cargas. ( ( ( ( ) 6,66 x 10-6 C ) 6 x 10-6 C ) 6,06 x 10-6 C ) 1,33 x 10-5 C Datos: 𝑟12 = 4 𝐶𝑚 = 4 𝑥 10−2 𝑚 𝐹12 = 10 𝑁 𝑞1 = 𝑞2 =? Diagrama: No hace falta realizarlo, ya que nos piden es el valor de las cargas Ecuación: Aplicamos la ecuación de la Ley de Coulomb y despejamos “q”. Como son iguales la elevamos al cuadrado. 𝐹12=𝐾 𝑞1 𝑥 𝑞2 𝑟2 ; como 𝑞1 = 𝑞2 = 𝑞2 ; entonces: 𝑞2 𝐹12 = 𝐾 𝑟 2 , Despejamos “q” 𝐹 2 𝑞2 = 12𝐾𝑥 𝑟 , para eliminar el cuadrado de la carga, introducimos dentro de una raíz cuadrada el resto de los términos. 𝑞= √ Conversión de Unidades: Solución: Transformamos la distancia de centímetros (Cm) a metros 10 𝑁 𝑥 (4 𝑥 10−4 )2 (m), multiplicando por 10−2 𝑞=√ 9 𝑥 109 𝑞 = 6,66 𝑥10−6 𝐶 𝐹12 𝑥 𝑟2 𝐾 Es decir, el valor de las cargas: 𝑞1 = 𝑞2 = 6,66 𝑥 10−6 𝐶, de igual signo y por esa razón es que hay una fuerza de repulsión 4.- Se tienen dos cargas eléctricas 𝑞1 = +5 µ𝐶 y 𝑞2 = +3𝜇𝐶; están en el vacio y en línea recta, separadas por una distancia de 5 Cm. Calcular la fuerza resultante sobre 𝑞1 por efecto de 𝑞2 . ( ( ( ( ) -54 N, hacia la derecha ) 54 N hacia la derecha ) 54 N, hacia la izquierda ) -54 N, hacia la izquierda Datos: 𝑞1 = +5𝜇𝐶 = +5 𝑥 10−6 𝐶 𝑞2 = +3µ𝐶 = +3 𝑥 10−6 𝐶 𝑟12 = 5𝐶𝑚 = 5 𝑥 10−2 𝑚 𝐹21 =? 𝑒𝑛 𝑞1 Diagrama: q1 𝐹21 q2 Ecuación: Aplicamos la ecuación de la Ley de Coulomb: 5 Cm Conversión de Unidades: Solución: Transformamos los microcoulomb (µC) a Coulomb 𝐹21 2 −6 −6 ( C ), multiplicando por 10−6 y = 9𝑥109 𝑁 𝑥 𝑚 3𝑥10 𝑥5𝑥10 2 −2 2 𝐶 (5𝑥10 𝑚) los centímetros ( Cm ) a metros ( m ), multiplicando por 10−2 𝐹21 = 54 𝑁 𝐹21=𝐾 𝑞2 𝑥 𝑞1 𝑟2 La fuerza resultante sobre 𝑞1 es de 54 N, hacia la izquierda. 5.- Dos cargas eléctricas 𝑞𝐴 = −5𝑥10−6 𝐶 y 𝑞𝐵 = −3𝑥10−6 𝐶 están en el vacio y en línea recta. ¿A qué distancia se encuentran separadas, cuando sobre ellas actúa una fuerza de 5,4 Newton? ( ( ( ( ) 0,158 m ) 158 m ) 0,15 cm ) 0,158 cm Datos: 𝑞𝐴 = −5𝑥10−6 𝐶 𝑞𝐵 = −3𝑥10−6 𝐶 𝑟12 =? 𝐹𝐴𝐵 = 5,4 𝑁 Diagrama: Ecuación: No es necesario, ya que piden Aplicamos la ecuación de la es el valor de la distancia “r” Ley de Coulomb y despejamos de ella, la distancia “r” 𝐹 𝐴𝐵=𝐾 𝑞1 𝑥 𝑞2 𝑟2 Despejamos “r” y eliminamos cuadrado introduciendo dentro de una raíz cuadrada el resto de los términos: 𝑟 = √𝐾𝑥 Conversión de unidades: Solución: No es necesario realizar ninguna transformación. 𝑟𝐴𝐵 = √9𝑥109 𝑥 5𝑥10−6 𝐶𝑥 3𝑥10−6 𝐶 5,4 𝑁 𝑟𝐴𝐵 = 0,158 𝑚 𝑞𝐴 𝑥 𝑞𝐵 𝐹𝐴𝐵 La distancia de separación entre las cargas es de 0,158 m, el signo de las cargas no se toma en cuenta cuando sustituimos; ya que estos son únicamente para el análisis de fuerzas (vectorial). 6.- Dos cargas eléctricas puntuales se atraen con una fuerza de 50 Newton, si sus cargas son iguales en magnitud 𝑞 = 2𝑥10−6 𝐶 y de signos contrarios. Calcular la distancia de separación entre ellas. ( ( ( ( ) 0,02 m ) 0,026 Cm ) 0,026 m ) 0,02 m Datos: +2𝑥10−6 𝑞1 = 𝐶 𝑞2 = −2𝑥10−6 𝐶 𝐹12 = 50 𝑁 𝑟12 =? Diagrama: Ecuación: No es necesario, debido a que Aplicamos la ecuación de la solo se pide la distancia de Ley de Coulomb: 𝐹 𝑞1 𝑥 𝑞2 separación entre las cargas. 12=𝐾 𝑟2 Despejamos “r” y eliminamos cuadrado, introduciendo dentro de una raíz cuadrada los términos restantes. 𝑟 = √𝐾𝑥 Conversión de Unidades: Solución: No es necesario hacer transformaciones. 𝑟12 𝑁𝑥𝑚 = √9𝑥109 𝐶 2 𝑞1 𝑥 𝑞2 𝐹12 La distancia de separación entre las cargas es de 0,026 m. 2 𝑥 2𝑥10−6 𝑥2𝑥10−6 50 𝑁 𝑟12 = 0,026 𝑚 7.- Dos cargas eléctricas 𝑞1 = +9𝑥10−6 𝐶 y 𝑞2 = −1,2𝑥10−6 𝐶, están en el vacio separadas por una distancia de 50 Cm. Calcular la fuerza resultante sobre q2 por efecto de q1 y sus características. ( ( ( ( ) 3,9 N; fuerza de atracción ) 3,9 N; fuerza de repulsión ) 3 N; fuerza de atracción ) -3,9 N; fuerza de atracción Datos: 𝑞1 = +9𝑥10−6 𝐶 𝑞2 = −1,2𝑥10−6 𝐶 𝑟12 = 50 𝐶𝑚 = 50𝑥10−2 𝑚 𝐹𝑅 =? 𝑒𝑛 𝑞2 Diagrama: Hacemos el análisis vectorial; es decir, de fuerzas según el signo de las cargas: q1 F12 q2 Ecuación: Aplicamos la ecuación de la Ley de Coulomb, para hallar la fuerza resultante sobre q2. 50 cm 𝐹 12=𝐾 Conversión de unidades: Solución: Transformamos los centímetros (cm) a 𝐹12 2 9𝑥10−6 𝐶𝑥 1,2𝑥10−6 𝐶 metros (m), 9𝑁 𝑥 𝑚 𝑥 = 9𝑥10 -2 multiplicando por 10 𝐶2 (50𝑥10−2 𝑚)2 𝐹12 ≅ 3,9 𝑁 𝑞1 𝑥 𝑞2 𝑟2 Como las cargas eléctricas son de signos contrarios, podemos decir que la fuerza entre ellas es de Atracción y su valor es de aproximadamente 3,9 N. 8.- La fuerza de repulsión entre dos cargas iguales es de 120 N, cuando se encuentran separadas por una distancia de 20 cm. ¿Cuál es el valor de dichas cargas? ( ( ( ( ) 2,3𝑥10−6 𝐶 ) 2,31𝑥10−6 𝐶 ) 2,31𝑥10−6 𝐶 ) 2,3𝑥10−5 𝐶 Datos: 𝑟12 𝐹12 = 120 𝑁 = 20 𝑐𝑚 = 20𝑥10−2 𝑚 𝑞1 = 𝑞2 = 𝑞 =? Diagrama: Ecuación: No es necesario hacer Aplicamos la ecuación de la diagrama; ya que, solo piden Ley de Coulomb: el valor de las cargas. 𝐹 12=𝐾 𝑞1 𝑥 𝑞2 𝑟2 Despejamos “q” y como ambas son iguales la elevamos al cuadrado, es decir: q x q = 𝑞2 𝐹 𝑥 𝑟2 𝑞2 = 12𝐾 Eliminamos cuadrado de “q”, introduciendo, los términos restantes en una raíz cuadrada. 𝐹12 𝑥 𝑟 2 𝑞= √ 𝐾 Conversión de unidades: Solución: Transformamos los centímetros (cm) a metros 120 𝑁 𝑥 (20𝑥10−2 )2 𝑞= √ (m), multiplicando por 10−2 2 9𝑥109 𝑁 𝑥𝐶 2𝑚 𝑞 ≅ 2,31𝑥10−5 𝐶 𝑞1 = 𝑞2 = 𝑞 Sabemos que las cargas son iguales; ya que, el enunciado del problema nos impone esa condición, las cargas tienen un valor de aproximadamente 2,31x10-5 C. 9.- Se tienen dos cargas eléctricas, cuyos módulos son: 𝑞1 = +6 𝑛 𝐶 y 𝑞2 = +3 𝑛𝐶, separadas por una distancia de 3 cm, en el vacio y en línea recta. Calcular la magnitud de la fuerza resultante y sus características, sobre q1 por efecto de q2. ( ( ( ( ) −1,8𝑥10−4 𝑁; 𝐻𝑎𝑐𝑖𝑎 𝑙𝑎 𝑖𝑧𝑞𝑢𝑖𝑒𝑟𝑑𝑎 ) 1,8𝑥10−4 𝑁; 𝐻𝑎𝑐𝑖𝑎 𝑙𝑎 𝑑𝑒𝑟𝑒𝑐ℎ𝑎 ) −1,8𝑥10−4 𝑁; 𝐻𝑎𝑐𝑖𝑎 𝑙𝑎 𝑑𝑒𝑟𝑒𝑐ℎ𝑎 ) 1,8𝑥10−4 𝑁; 𝐻𝑎𝑐𝑖𝑎 𝑙𝑎 𝑖𝑧𝑞𝑢𝑖𝑒𝑟𝑑𝑎 Datos: 𝑞1 = +6 𝑛𝐶 = +6𝑥10−9 𝐶 𝑞2 = +3 𝑛𝐶 = +3𝑥10−9 𝐶 𝑟12 = 3 𝑐𝑚 = 3𝑥10−2 𝑚 𝐹21 =? Diagrama: F21 q1 q2 3 cm La fuerza que ejerce q1 sobre q2 es de repulsión, por ser ambas cargas de signos contrarios y el vector F21 tiene su origen en q1; ya que, sobre esta actúa la otra carga. Conversión de unidades: Solución: Transformamos las cargas eléctricas que están 𝐹12 expresadas en nanocoulomb = 9𝑥109 𝑁 𝑥 𝑚2 𝑥 3𝑥10−9 𝐶 𝑥 6𝑥10−9 𝐶 𝐶2 (3𝑥10−2 𝐶)2 (nC) a Coulomb (C), -9 multiplicando por 10 y los 𝐹21 = 1,8𝑥10−4 𝑁 centímetros (cm) a metros (m), multiplicando por 10-2. Ecuación: Aplicamos la ecuación de la Ley de Coulomb, para hallar la fuerza. 𝐹 21=𝐾 𝑞2 𝑥 𝑞1 𝑟2 Los signos de las cargas no se utilizan al momento de sustituir en la ecuación; estos, solo se utilizan para el análisis vectorial. Es decir, para las características de la fuerza. 10.- ¿Cuál es la distancia de separación entre dos cargas, de módulos: 𝑞1 = −5𝑥10−6 𝐶 𝑦 𝑞2 = −8𝑥10−6 𝐶 . Si sobre ellas actúa una fuerza de repulsión de 60 N? ( ( ( ( ) -0,08 m ) 0,08 m ) 0,08 cm ) 0,08 Km Datos: 𝑞1 = −5𝑥10−6 𝐶 𝑞2 = −8𝑥10−6 𝐶 𝐹12 = 60 𝑁 𝑟12 =? Diagrama: Ecuación: No es necesario, ya que, se Aplicamos la ecuación de la calculara la distancia de separación Ley de Coulomb. entre las cargas. 𝐹 𝑞1 𝑥 𝑞2 12=𝐾 𝑟2 Despejamos “r” Y eliminamos el cuadrado de la distancia, introduciendo los términos restantes en una raíz cuadrada. 𝑟 = √𝐾𝑥 Conversión de Unidades: Solución: No es necesario, todas 𝑟12 están en el mismo sistema 𝑁 𝑥 𝑚2 5𝑥10−6 𝐶 𝑥8𝑥10−6 𝐶 = √9𝑥109 𝐶 2 𝑥 60 𝑁 de medida. M.K.S. 𝑟12 ≅ 0,08 𝑚 𝑞1 𝑥 𝑞2 𝐹12 Los signos de las cargas solo se utilizan para el análisis vectorial ( fuerzas) 11.- Dos cargas eléctricas q1 y q2 están en el vacio separadas por una distancia de 8 m. ¿Cuál es el valor de dichas cargas, si la fuerza que actúa sobre ellas es de 360 N? ( ( ( ( ) −1,6𝑥10−3 𝐶 ) 1,6𝑥10−3 𝐶 ) 1,6𝑥10−4 𝐶 ) 1,6𝑥10−6 𝐶 Datos: 𝑟12 = 8 𝑚 𝑞1 = 𝑞2 = 𝑞 =? 𝐹12 = 360 𝑁 Diagrama: No es necesario Ecuación: Aplicamos la ecuación de la Ley de Coulomb. 𝐹 𝑞1 𝑥 𝑞2 12=𝐾 𝑟2 Asumimos que las cargas eléctricas son iguales. 𝑞1 = 𝑞2 = 𝑞 Entonces, despejamos de la ecuación anterior “q” 𝐹12 𝑥 𝑟 2 𝑞= √ 𝐾 Conversión de unidades: No es necesario Solución: 360 𝑁 𝑥 (8 𝑚)2 q=√ 2 9𝑥109 𝑁 𝑥 2𝑚 𝐶 q= 1,6𝑥10−3 𝐶 Como hemos asumido que las cargas son iguales, entonces cada una tiene un valor de: 1,6 x 10-3 C. 12.- En un átomo de helio un electrón atrae a un protón, con una fuerza de 3𝑥10−9 𝑁. ¿Qué distancia los separa? El electrón y el protón tienen cargas iguales a 1,6𝑥10−19 𝐶, pero de signos contrarios. ( ) 2,77𝑥10−10 𝑚 ( ) 2,77𝑥10−10 𝑐𝑚 ( ) 2,77𝑥10−10 𝐾𝑚 ( ) −2,77𝑥10−10 𝑚 Datos: 𝑞𝑒− = 1.6𝑥10−19 𝐶 𝑞𝑝 = 1,6𝑥10−19 𝐶 𝐹 = 3𝑥10−9 𝑁 𝑟 =? Diagrama: No es necesario Ecuación: Aplicamos la ecuación de la Ley de Coulomb. 𝐹 𝑞1 𝑥 𝑞2 12=𝐾 𝑟 = √𝐾𝑥 Conversión de Unidades: No es necesario 𝑟2 Como piden la distancia a la cual se encuentran dichas partículas, despejamos “r”, al despejarla nos quedaría elevada al cuadrado, para eliminar el cuadrado de la distancia “r”, introducimos dentro de una raíz cuadrada, los términos restantes. Solución: 𝑟 2 1,6𝑥10−19 𝐶𝑥 1,6𝑥10−19 𝐶 𝑥 3𝑥10−9 𝑁 = √9𝑥109 𝑁𝑥𝑚 𝐶2 𝑟 = 2,77𝑥10−10 𝑚 𝑞1 𝑥 𝑞2 𝐹12 La distancia de separación entre las partículas elementales protón y electrón es de: 𝑟 = 2.77𝑥10−10 𝑚 13.- Un electrón atrae a un protón, con una fuerza de 2𝑥10−6 𝑁. ¿A qué distancia de separación se encuentran dichas particulas? El electrón y el protón tienen cargas iguales a 1,6𝑥10−19 𝐶, pero de signos contrarios. ( ( ( ( ) 1,07𝑥10−11 𝑚 )1,07𝑥10−11 𝑐𝑚 ) 1,07𝑥10−11 𝐾𝑚 ) −1,07𝑥10−11 𝑚 Datos: 𝑞𝑒− = 1,6𝑥10−19 𝐶 𝑞𝑝 = 1,6𝑥10−19 𝐶 𝐹 = 2𝑥10−6 𝑁 𝑟 =? Diagrama: No es necesario. Ecuación: Aplicamos la ecuación de la Ley de Coulomb. 𝐹 12=𝐾 𝑞1 𝑥 𝑞2 𝑟2 Despejamos “r”; pero, como nos queda elevada al cuadrado, eliminamos el cuadrado, introduciendo dentro de una raíz cuadrada el resto de los términos. 𝑟 = √𝐾𝑥 Conversión Unidades: No es necesario. de Solución: 𝑟 = √9𝑥109 𝑁𝑥𝑚2 1,6𝑥10−19 𝐶𝑥 1,6𝑥10−19 𝐶 𝑥 𝐶2 2𝑥10−6 𝑁 𝑟 = 1,07𝑥10−11 𝑚 𝑞1 𝑥 𝑞2 𝐹12 Ya sabemos que ambas partículas tienen la misma magnitud, pero de signo contrario y su distancia de separación es de: 𝑟 = 1,07𝑥10−11 𝑚 14.- Dos cargas eléctricas 𝑞1 = +10−6 𝐶 y 𝑞2 = −3𝑥10−6 𝐶; están en el vacío separadas por una distancia de 6 cm. Calcular la magnitud de la fuerza que actúa sobre ellas y cuál es su característica? ( ( ( ( ) 7,5 N; Fuerza de atracción ) -7,5 N; Fuerza de atracción ) 7,5 N; Fuerza de repulsión ) -7,5 N; Fuerza de repulsión Datos: 𝑞1 = +10−6 𝐶 𝑞2 = −3𝑥10−6 𝐶 𝑟12 = 6 𝑐𝑚 = 6𝑥10−2 𝑚 𝐹12 =? 𝐶𝑎𝑟𝑎𝑐𝑡𝑒𝑟í𝑠𝑡𝑖𝑐𝑎𝑠 Diagrama: q1 F12 q2 Ecuación: Aplicamos la ecuación de la Ley de Coulomb. 6 cm 𝐹 12=𝐾 Conversión de unidades: Solución: Transformamos los centímetros (cm) a metros 𝐹12 𝑁𝑥𝑚2 10−6 𝐶𝑥 3𝑥10−6 𝐶 (m), multiplicando por 10-2 = 9𝑥109 𝐶 2 𝑥 (6𝑥10−2 𝑚)2 𝐹12 = 7,5 𝑁 𝑞1 𝑥 𝑞2 𝑟2 Las cargas son de signos opuestos, esto nos indica que la característica de la fuerza es de atracción. 15.- Calcular la magnitud y característica de la fuerza resultante sobre q1 por efecto de q2, sabiendo que sus módulos son: +12𝑥10−6 𝐶 y −15𝑥10−6 𝐶, respectivamente. Si ellas están separadas a una distancia de 30 cm. ( ( ( ( ) 18 N; Fuerza de atracción ) -18 N; Fuerza de repulsión ) 18 N; Fuerza de repulsión ) -18 N; Fuerza de atracción Datos: 𝑞1 = +12𝑥10−6 𝐶 𝑞2 = −15𝑥10−6 𝐶 𝐹21 =? 𝑟21 = 30 𝑐𝑚 = 30𝑥10−2 𝑚 Diagrama: No es necesario, ya que sabemos que las cargas son de signos opuestos; entonces, su fuerza será de atracción. Ecuación: Aplicamos la ecuación de la Ley de Coulomb, para hallar la fuerza. 𝐹21=𝐾 𝑞2 𝑥 𝑞1 𝑟2 Conversión de Unidades: Solución: Transformamos los centímetros (cm) a metros 𝐹21 𝑁 𝑥 𝑚2 15𝑥10−6 𝐶 𝑥 12𝑥10−6 𝐶 (m), multiplicando por 10-2. = 9𝑥109 𝐶 2 𝑥 (30𝑥10−2 )2 𝐹21 = 18 𝑁 Por las características de las cargas la fuerza es de atracción. Y tiene una magnitud de 18 N 16.- Dos cargas eléctricas 𝑞1 = −8𝑥10−6 𝐶 y 𝑞2 = −6𝑥10−6 𝐶, están en el vacío y en línea recta separadas por una distancia de 9 cm. Calcular la magnitud y característica de la fuerza que actúa sobre q2 por efecto de q1. ( ( ( ( ) -53,3 N; Fuerza de atracción ) 53,3 N; fuerza de repulsión ) 53,3 N; Fuerza de atracción ) -53,3 N; Fuerza de repulsión Datos: 𝑞1 = −8𝑥10−6 𝐶 𝑞2 = −6𝑥10−6 𝐶 𝑟12 = 9 𝑐𝑚 = 9𝑥10−2 𝑚 𝐹12 =? Diagrama: Por las características de las cargas la fuerza que ejerce la carga 1 sobre la carga 2 es de repulsión, por ser del mismo signo. q1 q2 F12 Ecuación: Aplicamos la ecuación de la Ley de Coulomb, para hallar la fuerza. 𝐹 12=𝐾 𝑞1 𝑥 𝑞2 𝑟2 9 cm Conversión de Unidades: Solución: Transformamos los 9 cm a metros (m), multiplicando 𝐹12 𝑁 𝑥 𝑚2 8𝑥10−6 𝐶 𝑥 6𝑥10−6 𝐶 por 10-2. = 9𝑥109 𝐶 2 𝑥 (9𝑥10−2 )2 𝐹12 = 53,3 𝑁 Debemos recordar que los signos de las cargas solo se utilizan en el análisis vectorial; es decir característica de la fuerza. 17.- Dos cargas eléctricas: 𝑞1 = +4𝑥10−6 𝐶 y 𝑞2 = −5𝑥10−6 𝐶, están ene el vacío separado por una distancia de 5 cm. Calcular el módulo y característica de la fuerza con que se accionan. ( ( ( ( ) Se atraen con una fuerza de 72 N ) Se repelen con una fuerza de 72 N ) Se atraen con una fuerza de 7,2 N ) Se repelen con una fuerza de 7,2 N Datos: 𝑞1 = +4𝑥10−6 𝑁 𝑞2 = −5𝑥10−6 𝐶 𝑟12 = 5 𝑐𝑚 = 5𝑥10−2 𝑚 𝐹𝑅 =? Diagrama: q1 Ecuación: Aplicamos la ecuación de la Ley de Coulomb, para 5 cm hallar la fuerza con que se Como las cargas eléctricas son de accionan las cargas. signos opuestos, la fuerza con que se accionan es de atracción. 𝐹 𝑞1 𝑥 𝑞2 F12 q2 12=𝐾 Conversión de unidades: Solución: Al igual que en los anteriores, transformamos 𝐹12 2 4𝑥10−6 𝐶 𝑥5𝑥10−6 𝐶 los 5 cm a metros (m), 9𝑁 𝑥 𝑚 𝑥 = 9𝑥10 -2 multiplicando por 10 . 𝐶2 (5𝑥10−2 𝑚)2 𝐹12 = 72 𝑁 𝑟2 Recordemos que los signos de las cargas no se toman en cuenta, en la ecuación; solo, para el análisis vectorial. Por las características de las cargas, podemos afirmar que la fuerza es de atracción y tiene una magnitud de 72 N. 18.- Dos cargas eléctricas: 𝑞1 = −3𝑥10−6 𝐶 y 𝑞2 = +4𝑥10−6 𝐶, están en el vacío separadas por una distancia de 8 cm. Calcular el módulo y característica de la fuerza con que se accionan. ( ( ( ( ) 16,9 N; Fuerza de atracción ) 16,9 N; Fuerza de repulsión ) – 16,9 N; Fuerza de atracción ) – 16,9 N; fuerza de repulsión Datos: 𝑞1 = −3𝑥10−6 𝐶 𝑞2 = +4𝑥10−6 𝐶 𝑟12 = 8 𝑐𝑚 = 8𝑥10−2 𝑚 𝐹12 =? Características Diagrama: q1 F12 q2 8 cm Como las fuerzas son de signos diferentes, la fuerza entre ellas es de atracción. Conversión de unidades: Solución: Transformamos los cm a m, multiplicando por 10-2. 𝐹12 = 9𝑥109 𝑁 𝑥 𝑚2 𝑥 𝐶2 𝐹12 = 16,9 𝑁 3𝑥10−6 𝐶 𝑥 4𝑥10−6 𝐶 (8𝑥10−2 𝑚)2 Ecuación: Aplicamos la ecuación de la Ley de Coulomb, para hallar la fuerza con que se accionan las cargas. 𝐹 12=𝐾 𝑞1 𝑥 𝑞2 𝑟2 Recordemos que los signos de las cargas solo lo utilizamos en el análisis vectorial, no en la sustitución de la formula. Las características de las cargas, nos indica que la fuerza es de atracción. 19.- ¿Cuál es la magnitud de la fuerza con que se accionan dos cargas eléctricas: 𝑞1 = +9𝑥10−6 𝐶 y 𝑞2 = +3𝑥10−6 𝐶, están en el vacío separadas por una distancia de 81 cm? ( ( ( ( ) -0,37 N ) 0,37 N ) 3,7 N ) -3,7 N Datos: 𝑞1 = +9𝑥10−6 𝐶 𝑞2 = +3𝑥10−6 𝐶 𝑟12 = 81 𝑐𝑚 = 81𝑥10−2 𝑚 𝐹12 =? Diagrama: Ecuación: En este caso, no es necesaria la Aplicamos la ecuación de la realización del diagrama; ya que, solo Ley de Coulomb: nos piden magnitud o módulo de la 𝐹 𝑞1 𝑥 𝑞2 fuerza y no características. 12=𝐾 Conversión de Unidades: Solución: Transformamos los centímetros (cm) a metros 𝐹12 9𝑥10−6 𝐶𝑥3𝑥10−6 𝐶 (m), multiplicando por 10-2 𝑁 𝑥 𝑚2 = 9𝑥109 𝐶 2 𝑥 (81𝑥10−2 )2 𝐹12 = 0,37 𝑁 𝑟2 La magnitud de la fuerza con que se accionan las cargas es de 0,37 N 20.- La fuerza de atracción entre dos cargas es de 180 N, siendo sus módulos: +25𝑥10−6 𝐶 y −15𝑥10−6 𝐶. ¿Cuál es la distancia de separación entre las cargas? ( ( ( ( ) 0,14 m ) 14 m ) -0,14 m ) -14 m Datos: 𝑞1 = +25𝑥10−6 𝐶 𝑞2 = +15𝑥10−6 𝐶 𝐹12 = 180 𝑁 𝑟12 =? Diagrama: No es necesario, ya que solo piden la distancia de separación entre las cargas. Ecuación: Aplicamos la ecuación de la Ley de Coulomb: 𝐹 12=𝐾 𝑞1 𝑥 𝑞2 𝑟2 Como nos piden hallar la distancia “r”, despejamos de la ecuación y para eliminar el cuadrado de la distancia, introducimos los términos restantes dentro de una raíz cuadrada. 𝑟 = √𝐾𝑥 Conversión de Unidades: Solución: No es necesario; porque, todas las magnitudes 𝑟12 están en un mismo 25𝑥10−6 𝐶𝑥 15𝑥10−6 𝐶 𝑁𝑥𝑚2 sistema de medida. = √9𝑥109 𝐶 2 𝑥 180 𝑁 𝑟12 ≅ 0,14 𝑚 𝑞1 𝑥 𝑞2 𝐹12 La distancia de separación entre las cargas es de aproximadamente 0,14 m 21.- Dos cargas eléctricas: 𝑞1 = +20𝑥10−6 𝐶 y 𝑞2 = −5𝑥10−6 𝐶, están en el vacío separadas por una distancia de 9 cm. Calcular el módulo y la característica de la fuerza con que se accionan las cargas. ( ( ( ( ) Fuerza de atracción de módulo 111,11 N ) Fuerza de atracción de 11,11 N ) Fuerza de atracción de 11 N ) Fuerza de repulsión de 111,11 N Datos: 𝑞1 = +25𝑥10−6 𝐶 𝑞2 = −5𝑥10−6 𝐶 𝑟12 = 9 𝑐𝑚 = 9𝑥10−2 𝑚 𝐹12 =? Diagrama: q1 F12 q2 9 cm Como las cargas son de signos contrarios, la fuerza que se ejerce sobre ellas es de atracción. Conversión de unidades: Solución: Transformamos los centímetros (cm) a metros 𝐹12 2 20𝑥10−6 𝐶 𝑥 5𝑥10−6 𝐶 (m), multiplicando por 109 𝑁𝑥𝑚 𝑥 = 9𝑥10 2 . 𝐶2 (9𝑥10−2 𝑚)2 𝐹12 = 111,11 𝑁 Ecuación: Aplicamos la ecuación de la Ley de Coulomb: 𝐹 12=𝐾 𝑞1 𝑥 𝑞2 𝑟2 La magnitud de la fuerza es de 111,11 N y es de atracción. Ejercicios de Ley de Coulomb Nivel Medio: 22.- Se tienen tres cargas eléctricas: 𝑞1 = +3𝑥10−6 𝐶; 𝑞2 = −3𝑥10−6 𝐶 y 𝑞3 = +4𝑥10−6 𝐶; están en el vacío y en linea recta separadas por las distancias: 𝑟12 = 3 𝑐𝑚 y 𝑟23 = 5 𝑐𝑚. Calcular la fuerza resultante sobre 𝑞3 , por efecto de 𝑞1 y 𝑞2 . ( ) 0 N; En el origen ( ) 27 N; Hacia la izquierda ( ) 27 N; Hacia la derecha ( ) -27 N; Hacia la izquierda Datos: 𝑞1 = +3𝑥10−6 𝐶 𝑞2 = −3𝑥10−6 𝐶 𝑞3 = +4𝑥10−6 𝐶 𝑟12 = 3 𝑐𝑚 = 3𝑥10−2 𝑚 𝑟23 = 5 𝑐𝑚 = 5𝑥10−2 𝑚 𝐹𝑅 =? 𝑠𝑜𝑏𝑟𝑒 𝑞3 𝑟13 = 8 𝑐𝑚 = 8𝑥10−2 𝑚 Diagrama: q1 q2 q3 F23 5 cm F13 3 cm Ecuación: Como los vectores a sumar, tienen la misma dirección pero sentido contrario, decimos que: 𝐹𝑅 = 𝐹23 − 𝐹13 Para hallar las 𝐹13 y 𝐹23 aplicamos la ecuación de la Ley de Coulomb; para, cada una de las fuerzas: 𝐹=𝐾 𝑞 𝑥 𝑞0 𝑟2 Conversión de Unidades: Solución: 2 Transformamos las 3𝑥10−6 𝐶 𝑥 4𝑥10−6 𝐶 9 𝑁𝑥𝑚 𝐹 = 9𝑥10 𝑥 13 distancias de 𝐶2 (8𝑥10−2 𝑚)2 centímetros (cm) a metros (m), 𝐹13 ≅ 16,9 𝑁 multiplicando por 10-2m. Para hallar la distancia 2 3𝑥10−6 𝐶 𝑥 4𝑥10−6 𝐶 9 𝑁𝑥𝑚 𝐹23 = 9𝑥10 𝐶 2 𝑥 entre la carga 1 y la (5𝑥10−2 𝑚)2 carga 3, sumamos las distancias “r12” mas “r23” 𝐹23 = 43,2 𝑁 𝐹𝑅 = 43,2 𝑁 − 16,2 𝑁 𝐹𝑅 = 27 𝑁 La fuerza resultante es de 27 N; hacia la izquierda queda el vector resultante; ya que, la fuerza que ejerce 2 sobre 3 es mayor a la fuerza que ejerce 1 sobre 3. Esto se debe a que la fuerza es inversamente proporcional al cuadrado de la distancia que separa a las cargas; entonces la fuerza que ejerce 2 sobre 3 es mayor a la fuerza que ejerce 1 sobre 3. 23.- Tres cargas eléctricas: -2nC; -5nC y +3nC respectivamente, están en el vacío y en línea recta separadas por las distancias: r12= 2 m y r23 = 4 m. Calcular la fuerza resultante “FR”, sobre la carga de -5nC, por efecto de las otras dos cargas. ( ( ( ( ) 2,75x10-9 N; hacia la derecha ) 2,75x10-6 N; hacia la derecha ) -2,75x10-9 N; hacia la derecha ) 2,75x10-9 N; hacia la izquierda Datos: 𝑞1 = −2 𝑛𝐶 = −2𝑥10−9 𝐶 𝑞2 = −5 𝑛𝐶 = −5𝑥10−9 𝐶 𝑞3 = +3 𝑛𝐶 = +3𝑥10−9 𝐶 𝑟12 = 2 𝑚 𝑟23 = 4 𝑚 𝐹𝑅 =? 𝑠𝑜𝑏𝑟𝑒 𝑞2 Diagrama: q1 q2 2m F12 F32 q3 4m Ecuación: Como los vectores a sumar, tienen la misma dirección y sentido, nos queda que: 𝐹𝑅 = 𝐹12 + 𝐹32 Para hallar: F12 y F32, aplicamos la ecuación de la Ley de Coulomb, para cada fuerza, respetando el orden de posición de las cargas, siendo primero, la carga que actúa y segundo la carga sobre la cual están actuando. 𝐹=𝐾 𝑞 𝑥 𝑞0 𝑟2 Conversión de Unidades: Solución: 2 Se transforman los nanocoulomb 2𝑥10−9 𝐶 𝑥 5𝑥10−9 𝐶 9 𝑁𝑥𝑚 𝐹 = 9𝑥10 𝑥 12 (nC) en Coulomb ( C ), 𝐶2 (2 𝑚)2 -9 multiplicando por 10 C.Las 𝐹12 = 2,25𝑥10−8 𝑁 distancias no es necesario; ya 2 3𝑥10−9 𝐶𝑥 5𝑥10−9 𝐶 9 𝑁𝑥𝑚 𝐹32 = 9𝑥10 𝐶 2 𝑥 que están en la unidad del (4 𝑚)2 −9 sistema de medida M.K.S. 𝐹32 = 5,06𝑥10 𝐶 𝐹𝑅 = 2,25𝑥10−8 𝑁 + 5,06𝑥10−9 𝑁 𝐹𝑅 = 2,75𝑥10−9 𝑁 Los vectores: F12 y F32, tienen su origen en q2; ya que, sobre ella actúan las otras dos cargas y la fuerza resultante tiene sentido hacia la derecha. Debemos recordar que los signos de las cargas solo se utilizan para saber la naturaleza de cada fuerza; es decir, para el análisis vectorial. 24.- Se tienen tres cargas eléctricas cuyos módulos son: 𝑞1 = +4𝑥10−6 𝐶, 𝑞2 = −5𝑥10−6 𝐶 y 𝑞3 = −6𝑥10−6 𝐶, que estan en el vacío y separadas por las distancias que se indican en la figura. Calcular la fuerza resultante sobre 𝑞3 por efecto de las otras dos cargas. q1 q2 q3 ( ( ( ( ) -615 N; hacia la derecha ) -615 N; hacia la izquierda ) 615 N; hacia la izquierda ) 615 N; hacia la derecha Datos: −6 𝑞1 = +4𝑥10 𝐶 𝑞2 = −5𝑥10−6 𝐶 𝑞3 = −6𝑥10−6 𝐶 𝑟12 = 4𝑐𝑚 = 4𝑥10−2 𝑚 𝑟23 = 2𝑐𝑚 = 2𝑥10−2 𝑚 𝑟13 = 6𝑐𝑚 = 6𝑥10−2 𝑚 𝐹𝑅 =? 𝑠𝑜𝑏𝑟𝑒 𝑞3 4cm 2cm Diagrama: q1 q2 F13 q3 F23 4 cm 2 cm Como los vectores a sumar tienen igual dirección pero sentido contrario, la fuerza resultante “FR”, es: 𝐹𝑅 = 𝐹23 − 𝐹13 Para hallar las fuerzas: F13 y F23, aplicamos la ecuación de la Ley de Coulomb, para ambas fuerzas. 𝐹=𝐾 𝑞 𝑥 𝑞0 𝑟2 Conversión de Unidades: Solución: 2 Transformamos las distancias de 4𝑥10−6 𝑥6𝑥10−6 9 𝑁𝑥𝑚 𝐹 = 9𝑥10 𝑥 13 centímetros (cm) a metros (m), 𝐶2 (6𝑥10−2 𝑚)2 -2 multiplicando por 10 . Sumando las 𝐹13 = 60 𝑁 distancias r12 mas r23, hallamos la distancia 2 5𝑥10−6 𝐶𝑥6𝑥10−6 𝐶 9 𝑁𝑥𝑚 𝐹23 = 9𝑥10 𝐶 2 𝑥 r13. (2𝑥10−2 𝑚)2 𝐹23 = 675 𝑁 𝐹𝑅 = 675 𝑁 − 60𝑁 𝐹𝑅 = 615 𝑁 El vector resultante es hacia la derecha; ya que, la fuerza F23 es mayor que la fuerza F13, debido a las distancias de separación entre las cargas. 25.- Se tienen tres cargas eléctricas 𝑞𝐴 = +3𝑥10−6 𝐶, 𝑞𝐵 = −6𝑥10−6 𝐶 y 𝑞𝐶 = −8𝑥10−6 𝐶. Están en el vacío y en línea recta, separadas por las distancias que se indican en el dibujo. Calcular la fuerza resultante FR, sobre qA por efecto de las otras dos cargas. qA qB qC 3 cm ( ( ( ( 4 cm ) 224,08 N; Hacia la derecha ) 224,08 N; Hacia la izquierda ) -224,08 N; Hacia la derecha ) -224,08 N; Hacia la izquierda Datos: −6 𝑞𝐴 = +3𝑥10 𝐶 𝑞𝐵 = −6𝑥10−6 𝐶 𝑞𝐶 = −8𝑥10−6 𝐶 𝑟𝐴𝐵 = 3 𝑐𝑚 = 3𝑥10−2 𝑚 𝑟𝐵𝐶 = 4 𝑐𝑚 = 4𝑥10−6 𝑚 𝑟𝐴𝐶 = 7 𝑐𝑚 = 7𝑥10−2 𝑚 𝐹𝑅 =? 𝑆𝑜𝑏𝑟𝑒 𝑞𝐴 Diagrama: qA FCA FBA qB qC 3 cm 4 cm Realizado el análisis vectorial, podemos observar que los vectores, tienen la misma dirección y sentido, lo que implica que: 𝐹𝑅 = 𝐹𝐵𝐴 + 𝐹𝐶𝐴 Para hallar las fuerzas FBA y FCA, utilizamos la ecuación de la Ley de Coulomb, para ambos casos. 𝐹=𝐾 𝑞 𝑥 𝑞0 𝑟2 Conversión de unidades: Solución: 2 Transformamos los centímetros 6𝑥10−6 𝐶𝑥3𝑥10−6 𝐶 9 𝑁𝑥𝑚 𝐹 = 9𝑥10 𝑥 𝐵𝐴 (cm) a metros (m), 𝐶2 (3𝑥10−2 𝑚)2 -2 multiplicando por 10 m. Para 𝐹𝐵𝐴 = 180 𝑁 hallar la distancia “rAC”, 2 8𝑥10−6 𝐶𝑥3𝑥10−6 𝐶 9 𝑁𝑥𝑚 𝐹𝐶𝐴 = 9𝑥10 𝐶 2 𝑥 sumamos las distancias rAB mas (7𝑥10−2 𝑚)2 rBC. 𝐹𝐶𝐴 = 44,08 𝑁 𝐹𝑅 = 180 𝑁 + 44,08 𝑁 𝐹𝑅 = 224,08 𝑁 Los signos de las cargas solo se utilizan en el análisis vectorial o análisis de fuerzas y esta se dirige hacia la derecha. 26.- Se tienen tres cargas eléctricas: 𝑞1 = +3𝑥10−6 𝐶; 𝑞2 = +5𝑥10−6 𝐶 y 𝑞3 = −6𝑥10−6 𝐶. Que están en el vacío y en línea recta, separadas por las distancias que se indican en el dibujo. Calcular la fuerza resultante sobre q1 por efecto de q2 y q3. q1 q2 q3 3 cm ( ( ( ( 2 cm ) 85,2 N; Hacia la derecha ) 214,8 N; Hacia la derecha ) 214,8 N; Hacia la izquierda ) 85,2 N; Hacia la izquierda Datos: −6 𝑞1 = +3𝑥10 𝐶 𝑞2 = +5𝑥10−6 𝐶 𝑞3 = −6𝑥10−6 𝐶 𝑟12 = 3 𝑐𝑚 = 3𝑥10−2 𝑚 𝑟23 = 2 𝑐𝑚 = 2𝑥10−2 𝑚 𝑟13 = 5 𝑐𝑚 = 5𝑥10−2 𝑚 𝐹𝑅 =? 𝑠𝑜𝑏𝑟𝑒 𝑞1 Diagrama: F21 F31 q1 q2 q3 3 cm 2 cm Al realizar el análisis vectorial (fuerzas), observamos que los vectores: F21 y F31, tienen la misma dirección, pero sentidos contrarios; por ser 𝐹21 > 𝐹31 , nos queda que: 𝐹𝑅 = 𝐹21 − 𝐹31 Para hallar las fuerzas F21 y F31, aplicamos la ecuación de la Ley de Coulomb, para ambos casos. 𝐹=𝐾 𝑞 𝑥 𝑞0 𝑟2 Conversión de Unidades: Solución: 2 Transformamos los centímetros 5𝑥10−6 𝐶𝑥3𝑥10−6 𝐶 9 𝑁𝑥𝑚 𝐹 = 9𝑥10 𝑥 21 (cm) a metros (m), multiplicando 𝐶2 (3𝑥10−2 𝑚)2 -2 por 10 m. La distancia entre la 𝐹21 = 150 𝑁 carga 1 y la carga 3, la hallamos 2 6𝑥10−6 𝐶𝑥3𝑥10−6 𝐶 9 𝑁𝑥𝑚 𝐹31 = 9𝑥10 𝐶 2 𝑥 sumando las distancias r12 y r23. (5𝑥10−2 𝑚)2 𝐹31 = 64,8 𝑁 𝐹𝑅 = 150 𝑁 − 64,8 𝑁 𝐹𝑅 = 85,2 𝑁 La magnitud de la fuerza es de 85,2 N, hacia la izquierda; ya que el vector F21 es mayor que el vector F31 27.- Se tienen dos cargas eléctricas, cuyos módulos son: 𝑞𝑎 = +3𝑥10−6 𝐶 y 𝑞𝑏 = +4𝑥10−6 𝐶, están en el vacìo y en línea recta, separadas por una distancia de 9 cm, ¿En qué punto de la recta que las une, se debe colocar una tercera carga 𝑞𝑐 = +2𝑥10−6 𝐶; para, que la fuerza resultante sobre ella sea nula? ( ( ( ( ) 4,18 cm de qa ) 4,18 cm de qb ) 4,5 cm de qa ) 4,3 cm de qa Datos: 𝑞𝑎 = +3𝑥10−6 𝐶 𝑞𝑏 = +4𝑥10−6 𝐶 𝑞𝑐 = +2𝑥10−6 𝐶 𝑟𝑎𝑏 = 9 𝑐𝑚 𝐹𝑅 = 0; 𝑒𝑛 𝑞𝑐 Diagrama: qa Fbc qc Fac qb 9 cm (9 − 𝑋) X Solución: Para que FR= 0, qc debe estar ubicada entre qa y qb; además, las fuerzas Fac y Fbc deben ser iguales en dirección pero de sentidos contrarios. Para que se cumpla esta condición la carga qc, tiene que estar entre qa y qb. Entonces igualamos las fuerzas en magnitud. 𝐹𝑎𝑐 = 𝐹𝑏𝑐 Aplicamos la ecuación de la Ley de Coulomb, quedando que: 𝐾𝑥 𝑞𝑎 𝑥 𝑞𝑐 2 𝑟𝑎𝑐 =𝐾𝑥 𝑞𝑏 𝑥 𝑞𝑐 2 𝑟𝑏𝑐 /÷𝐾 Y como qc es igual en ambas ecuaciones, la simplificamos, quedando: 𝑞𝑎 𝑞𝑏 = 2 2 𝑟𝑎𝑐 𝑟𝑏𝑐 Agrupamos términos semejantes: 2 𝑟𝑏𝑐 𝑞𝑏 = 2 𝑟𝑎𝑐 𝑞𝑎 Para eliminar cuadrados de las distancias “r”, introducimos los términos restantes en una raíz cuadrada y sustituimos por sus valores: (9 − 𝑋) 4𝑥10−6 𝐶 =√ 𝑋 3𝑥10−6 𝐶 Extraemos raíz cuadrada y nos queda que: 9−𝑋 = 1,15 𝑋 Colocamos la ecuación de forma lineal: 9 − 𝑋 = 1,15 𝑋 Agrupamos términos semejantes nuevamente: 9 = 1,5 𝑋 + 𝑋 Operamos: 9 = 2,15 𝑋 Despejamos “X” 9 𝑋= 2,15 𝑋 = 4,18 𝑐𝑚 La fuerza resultante FR es nula a 4,18 cm de qa 28.-Se dispone de tres cargas eléctricas: 𝑞𝐴 = +3𝑥10−6 𝐶; 𝑞𝐵 = +2𝑥10−6 𝐶 y 𝑞𝐶 = 5𝑥10−6 𝐶, están en el vacío y en línea recta, separadas por las distancias que se indican en el dibujo. Calcular la fuerza resultante FR, con que qA y qB accionan a qC. qA qB qC 10 cm ( ( ( ( 5 cm )-42 N; hacia la derecha ) -42 N; hacia la izquierda ) 42 N; hacia la izquierda ) 42 N; hacia la derecha Datos: 𝑞𝐴 = +3𝑥10−6 𝐶 𝑞𝐵 = +2𝑥10−6 𝐶 𝑞𝐶 = +5𝑥10−6 𝐶 𝑟𝐴𝐵 = 10 𝑐𝑚 = 10𝑥10−2 𝑚 𝑟𝐵𝐶 = 5 𝑐𝑚 = 5𝑥10−2 𝑚 𝐹𝑅 =? 𝑠𝑜𝑏𝑟𝑒 𝑞𝐶 𝑟𝐴𝐶 = 15 𝑐𝑚 = 15𝑥10−2 𝑚 Diagrama: qA qB 10 cm qC FAC FBC 5 cm Realizado el análisis de fuerzas, podemos observar que, los vectores FAC y FBC, tienen la misma dirección y sentido, hacia la derecha; entonces: 𝐹𝑅 = 𝐹𝐴𝐶 + 𝐹𝐵𝐶 Para hallar la magnitud de la FAC y FBC, aplicamos la ecuación de la Ley de Coulomb, en ambos casos. 𝐹=𝐾 𝑞 𝑥 𝑞0 𝑟2 Conversión de Unidades: Solución: 2 Transformamos los 3𝑥10−6 𝐶𝑥5𝑥10−6 𝐶 9 𝑁𝑥𝑚 𝐹 = 9𝑥10 𝑥 𝐴𝐶 centímetros (cm) de las 𝐶2 (15𝑥10−2 𝑚)2 distancias a metros (m), 𝐹𝑎𝑐 = 6 𝑁 multiplicando por 10-2 m. La 2 2𝑥10−6 𝐶𝑥5𝑥10−6 𝐶 9 𝑁𝑥𝑚 𝐹 = 9𝑥10 𝑥 𝐵𝐶 distancia de separación entre 𝐶2 (5𝑥10−2 𝑚)2 qA y qC, la hallamos sumando 𝐹𝐵𝐶 = 36 𝑁 las distancias de separación 𝐹𝑅 = 6 𝑁 + 36 𝑁 rAB y rBC. 𝐹𝑅 = 42 𝑁 29.- Dos esferas A y B, están en el vacío separadas por una distancia de 10 cm. Tienen cargas eléctricas: 𝑞𝐴 = +3𝑥10−6 𝐶 y 𝑞𝐵 = −8𝑥10−6 𝐶. Con otra esfera C en estado neutro, primero se toca a A y después a B. Si la esfera C después de tocar a B, se separa del sistema, calcular la fuerza con que se accionan. ( ( ( ( ) Se atraen con una fuerza de 4,38 N ) Se repelen con una fuerza de 4,38 N ) Su fuerza es Nula (0) ) Se atraen con una fuerza de – 4,38 Datos: 𝑞𝐴 = +3𝑥10−6 𝐶 𝑞𝐵 = −8𝑥10−6 𝐶 𝑟𝐴𝐵 = 10 𝑐𝑚 = 10𝑥10−2 𝑚 𝐹𝐴𝐵 =? Diagrama: qA qB 10 cm Cuando dos esferas se ponen en contacto, las cargas se reparten en partes iguales; en tal sentido, debemos, calcular las cargas finales para la esfera A, como para la esfera B. Esto se logra sumando algebraicamente las cargas de cada esfera cuando entra en contacto con la esfera C. 𝑞𝐴 + 𝑞𝐶 = +3𝑥10−6 𝐶 + 0 𝑞𝐴 + 𝑞𝐶 = +3𝑥10−6 𝐶, como la carga es distribuida en partes iguales, se divide entre 2; quedando que: 𝑞𝐴 = 𝑞𝐶 = +1,5𝑥10−6 𝐶 Ahora la esfera C se toca con B. qC qB 𝑞𝐶 + 𝑞𝐵 = +1,5𝑥10−6 𝐶 − 8𝑥10−6 𝐶 𝑞𝐶 + 𝑞𝐵 = −6,25𝑥10−6 𝐶 Como ambas esferas después del contacto quedan con cargas iguales en magnitud; entonces: 𝑞𝐶 = 𝑞𝐵 = −3,25𝑥10−6 𝐶 Después el contacto la esfera C se separa del sistema; quedando la esfera A con una carga de: 𝑞𝐴 = +1,5𝑥10−6 𝐶 y la esfera B, con una carga de: 𝑞𝐵 = −3,25𝑥10−6 𝐶. Ahora procedemos a calcular la fuerza con que se accionan la esfera A y la esfera B, aplicando la ecuación de la Ley de Coulomb. 𝑞𝐴 𝑥 𝑞𝐵 2 𝑟𝐴𝐵 Sustituimos en la ecuación por sus valores: 𝐹𝐴𝐵 = 𝐾 2 𝐹𝐴𝐵 = 9𝑥109 𝑁𝑥𝑚 𝑥 𝐶2 1,5𝑥10−6 𝐶𝑥3,25𝑥10−6 𝐶 (10𝑥10−2 𝑚)2 𝐹𝐴𝐵 = 4,38 𝑁 La fuerza entre las esferas es de Atracción, por tener signos opuestos. 30.- Tres cargas eléctricas: 𝑞1 = +4𝑥10−8 𝐶; 𝑞2 = −10−7 𝐶; 𝑞3 = −5𝑥10−8 𝐶, están en el vacío y en línea recta. La distancia de separación entre 𝑞1 𝑦 𝑞2 es de 10 cm. Calcular la fuerza con que q1 acciona a q3, sabiendo que q1 y q2 se atraen con una fuerza de 40 dinas (din). ( ( ( ( ) q1 atrae a q3, con una fuerza de 112,5x10-6 N ) q1 repele a q3, con una fuerza de 112,5x10-6 N ) q1 atrae a q3, con una fuerza de -112,5x10-6 N ) q1 repele a q3, con una fuerza de -112,5x10-6 N Datos: 𝑞1 = +4𝑥10−8 𝐶 𝑞2 = −10−7 𝐶 𝑞3 = −5𝑥10−8 𝐶 𝑟23 = 10𝑐𝑚 = 10𝑥10−2 𝑚 𝐹12 = 40𝑑𝑖𝑛 = 40𝑥10−5 𝑁 𝐹13 =? 𝑟13 =? Diagrama: Realizamos un gráfico con las características, que tenemos en el enunciado del problema. q1 q2 q3 Conversión de unidades: Transformamos la unidad de fuerza que esta en dina (din) a Newton (N), multiplicando por 10-5 N y la unidad de distancia centímetros (cm) a metros (m), multiplicando por 10-2 m. Después de calculada la distancia entre q1 y q2, sabemos que la distancia entre las cargas 1 y 3, es de 0,3m o 30 cm, que sumado a los 10cm entre 2 y 3, nos da un valor de 0,4m que es igual a 40x10-2 m. Solución: Sabiendo el valor con que q1 acciona a q2, calculamos la distancia de separación entre ellas, aplicando la ecuación de la Ley de Coulomb: 𝑞1 𝑥 𝑞2 𝐹 10 cm 12=𝐾 𝑟2 Despejamos r12; como está elevada al cuadrado en la ecuación, para eliminar el cuadrado, introducimos dentro de una raíz cuadrada el resto de la ecuación. 𝑟 = √𝐾𝑥 𝑞1 𝑥 𝑞2 𝐹12 Sustituimos en la ecuación: 4𝑥10−8 𝐶 𝑥 10−7 𝐶 40𝑥10−5 𝑁 𝑟12 = 0,3 𝑚 = 30𝑐𝑚 Conocida esta distancia, ahora calculamos la fuerza con que q1 acciona a q3, utilizando la distancia de separación entre q1 y q3 y aplicando la ecuación de la Ley de Coulomb. 𝑟12 = √9𝑥109 𝑁𝑥𝑚2 𝑚2 𝑥 𝐹13 = 𝐾 𝑞1 𝑥 𝑞3 2 𝑟13 Sustituimos en la ecuación anterior: 4𝑥10−8 𝐶 𝑥 5𝑥10−8 𝐶 𝑁𝑥𝑚2 𝐹13 = 9𝑥109 𝐶 2 𝑥 (40𝑥10−2 𝑚)2 𝐹13 = 112,5𝑥10−6 𝑁 31.- Tres cargas eléctricas: 𝑞𝐴 ; 𝑞𝐵 𝑦 𝑞𝐶 , están en el vacío y en línea recta separadas por las distancias que se indica en el dibujo. 𝑞𝐴 𝑟𝑒𝑝𝑒𝑙𝑒 𝑎 𝑞𝐵 , con una fuerza de 4𝑥10−3 𝑁. Calcular la fuerza con que 𝑞𝐵 𝑟𝑒𝑝𝑒𝑙𝑒 𝑎 𝑞𝐶 . qA qB qC 5 cm ( ( ( ( 2 cm ) −24,95𝑥10−3 𝑁 ) −24,95 𝑁 ) 2495 𝑁 ) 24,95𝑥10−3 𝑁 Datos: 𝑞𝐴 = 𝑞𝐵 = 𝑞𝐶 = 𝑋 𝑟𝐴𝐵 = 5𝑐𝑚 = 5𝑥10−2 𝑚 𝐹𝐴𝐵 = 4𝑥10−3 𝑁 𝑟𝐵𝐶 = 2𝑐𝑚 = 2𝑥10−2 𝑚 Conversión de unidades: Transformamos los centímetros (cm) a metros (m), multiplicando por 10-2 m. Diagrama: No es necesaria la aplicación del diagrama, como tal. Solución: Se conoce la fuerza con que qA repele a qB, aplicamos la ecuación de la Ley de Coulomb, para hallar q. La cual es igual para las tres cargas. 𝑞𝐴 𝑥 𝑞𝐵 2 𝑟𝐴𝐵 Como: 𝑞𝐴 = 𝑞𝐵 = 𝑋 2 , nos queda que: 2 𝐹𝐴𝐵 𝑥 𝑟𝐴𝐵 2 𝑋 = 𝐾 Para eliminar el cuadrado de la “X”, introducimos los demás términos dentro de una raíz cuadrada: 𝐹𝐴𝐵 = 𝐾 𝑋= √ 𝐹12 𝑥 𝑟 2 𝐾 Entonces, al sustituir, nos queda que: 𝑋=√ 4𝑥10−3 𝑁 𝑥 (5𝑥10−2 𝑚)2 9𝑥109 𝑁 𝑥𝐶 2𝑚 2 𝑋 = 3,33𝑥10−8 𝐶 Como las cargas son iguales, decimos que: 𝑞𝐴 = 𝑞𝐵 = 𝑞𝐶 = 3,33𝑥10−8 𝐶 Conocido el valor de las cargas, ahora podemos calcular la fuerza con que se repelen B y C. Aplicamos la ecuación de la Ley de Coulomb para hallar el valor de FBC. 𝑞𝐵 𝑥 𝑞𝐶 2 𝑟𝐵𝐶 Sustituimos en la ecuación, por sus valores: 2 3,33𝑥10−8 𝐶 𝑥 3,33𝑥10−8 𝐶 9 𝑁𝑥𝑚 𝐹𝐵𝐶 = 9𝑥10 𝐶 2 𝑥 (2𝑥10−2 𝑚)2 𝐹𝐵𝐶 = 𝐾 𝐹𝐵𝐶 = 24,95𝑥10−3 𝑁 Problemas de Electrostática. Ley de Coulomb Nivel Alto (III) 32.- Se tienen tres cargas eléctricas cuyos módulos son: 𝑞𝐴 = −5𝑥10−6 𝐶; 𝑞𝐵 = −4𝑥10−6 𝐶 y 𝑞𝐶 = −4𝑥10−6 𝐶, ubicadas en los vértices de un triángulo rectángulo. Calcular la magnitud de la fuerza resultante sobre qB por efecto de qA y qC. qA 3 cm qB ( ( ( ( 6 cm qC ) 215 N ) 215,4 N ) 216 N ) -215 N Datos: 𝑞𝐴 = −5𝑥10−6 𝐶 𝑞𝐵 = −4𝑥10−6 𝐶 𝑞𝐶 = −8𝑥10−6 𝐶 𝑟𝐴𝐵 = 3 𝑐𝑚 = 3𝑥10−2 𝑚 𝑟𝐵𝐶 = 6𝑐𝑚 = 6𝑥10−2 𝑚 𝐹𝑅 =? 𝑠𝑜𝑏𝑟𝑒 𝑞𝐵 Diagrama: - qA 3 cm FCB - qB FR 6 cm - qC FAB Realizado el análisis vectorial, podemos observar que los vectores a sumar, tienen diferente dirección y sentidos, lo cual nos indica que en este caso en particular, que son perpendiculares; es decir, forman un ángulo de 90º, se aplica el teorema de Pitágoras, para hallar la magnitud de la fuerza resultante FR. 𝑎2 + 𝑏 2 = 𝑐 2 2 2 2 Donde: 𝑎 = 𝐹𝐶𝐵 ; 𝑏 2 = 𝐹𝐴𝐵 𝑦 𝐶 2 = 𝐹𝑅2 ; quedando que: 2 2 𝐹𝑅2 = 𝐹𝐶𝐵 + 𝐹𝐴𝐵 Para eliminar el cuadrado de FR, introducimos dentro de una raíz cuadrada los demás términos. 2 2 𝐹𝑅 = √𝐹𝐶𝐵 + 𝐹𝐴𝐵 Para hallar las fuerzas: FAB y FCB, aplicamos la ecuación de la Ley de Coulomb. Para cada uno de los casos: 𝐹=𝐾 𝑞 𝑥 𝑞0 𝑟2 Conversión de Unidades: Solución: 2 Transformamos las 5𝑥10−6 𝐶 𝑥4𝑥10−6 𝐶 9 𝑁𝑥𝑚 𝐹𝐴𝐵 = 9𝑥10 𝐶 2 𝑥 distancias de centímetros (3𝑥10−2 𝑚)2 (cm) a metros (m), multiplicando por 10-2m y 𝐹𝐴𝐵 = 200 𝑁 sustituimos en la ecuación. 8𝑥10−6 𝐶 𝑥 4𝑥10−6 𝐶 𝑁 𝑥 𝑚2 𝐹𝐶𝐵 = 9𝑥109 𝐶 2 𝑥 (6𝑥10−2 𝑚)2 𝐹𝐶𝐵 = 80 𝑁 𝐹𝑅 = √(80𝑁)2 + (200𝑁)2 𝐹𝑅 = 215,4 𝑁 Solo nos piden el cálculo de la magnitud o módulo de la fuerza resultante, en este caso, no hallamos ni dirección ni sentido. (Características). 33.- En los vértices del triángulo de la figura adjunta, hay cargas eléctricas: 𝑞𝐴 = −3𝑥10−7 𝐶, 𝑞𝐵 = +3𝑥10−6 𝐶 y 𝑞𝐶 = +3𝑥10−5 𝐶; ángulo en el vértice B es de 60º. Calcular la magnitud de la fuerza resultante que actúa sobre qC, por efecto de las otras dos cargas. - qA 6 cm +qC ( ( ( ( + qB ) Módulo de FR= 900 N ) Módulo de FR= - 900 N ) Módulo de FR= - 900,5 N ) Módulo de FR= 900,5 N Datos: 𝑞𝐴 = −3𝑥10−7 𝐶 𝑞𝐵 = +3𝑥10−6 𝐶 𝑞𝐶 = +3𝑥10−5 𝐶 𝑟𝐴𝐵 = 6𝑐𝑚 = 6𝑥10−2 𝑚 𝐹𝑅 =? 𝑠𝑜𝑏𝑟𝑒 𝑞𝐶 𝛼 = 60° Diagrama: - qA FAB 6cm +qB FCB +qC +qB Realizado el análisis vectorial, observamos que las fuerzas, son perpendiculares, lo que indica que se debe aplicar el teorema de Pitágoras, para hallar la fuerza resultante FR. 𝐶 2 = 𝑎2 + 𝑏 2 Donde c, es FR, a es FBC y b es FAB; Al sustituir a,b y c nos queda que: 2 2 𝐹𝑅2 = 𝐹𝐵𝐶 + 𝐹𝐴𝐶 Para eliminar el cuadrado de FR, introducimos el resto de los términos dentro de una raíz cuadrada: 2 2 𝐹𝑅 = √𝐹𝐵𝐶 + 𝐹𝐴𝐶 Ahora calculamos las fuerzas: FAC y FBC, aplicando la ecuación de la Ley de Coulomb. 𝑞 𝑥𝑞 𝐹𝐴𝐶 = 𝐾 𝐴 2 𝐶 y 𝑟𝐴𝐶 𝑞𝐵 𝑥 𝑞𝐶 𝐹𝐵𝐶 = 𝐾 2 𝑟𝐵𝐶 Conversión de Unidades: Transformamos los centímetros (cm) a metros (m), multiplicando por 10-2. Antes de sustituir en la ecuación de la Ley de Coulomb, debemos hallar las distancias “r”, aplicando las funciones trigonométricas sin 60° 𝑦 cos 60°. Para hallar la distancia “rAC”, la función seno del ángulo y la distancia “rBC” la función coseno del ángulo. Solución: 𝑐𝑜 𝑟 sin 60° = ℎ = 𝑟𝐴𝐶 ; despejamos rAC, quedando que: 𝐴𝐵 𝑟𝐴𝐶 = 𝑟𝐴𝐵 𝑥 sin 60° 𝑟𝐴𝐶 = 6𝑥10−2 𝑚 𝑥 sin 60° 𝑟𝐴𝐶 = 3√3 𝑥10−2 𝑚 𝑐𝑎 𝑟 cos 60° = ℎ = 𝑟𝐵𝐶 ; despejamos rBC, quedando que: 𝐴𝐵 𝑟𝐵𝐶 = 𝑟𝐴𝐵 𝑥 cos 60° 𝑟𝐵𝐶 = 6𝑥10−2 𝑚 𝑥 cos 60° 𝑟𝐵𝐶 = 3𝑥10−2 𝑚 Calculadas las distancias. Procedemos a calcular la fuerza ejercida por cada carga sobre qC. 2 3𝑥10−7 𝐶 𝑥 3𝑥10−5 𝐶 9 𝑁𝑥𝑚 𝐹𝐴𝐶 = 9𝑥10 𝐶 2 𝑥 (3√3 𝑥10−2 𝑚)2 𝐹𝐴𝐶 = 30 𝑁 3𝑥10−6 𝐶𝑥 3𝑥10−5 𝐶 (3𝑥10−2 𝑚)2 𝐹𝐵𝐶 = 900 𝑁 𝐹𝑅 = √(900 𝑁)2 + (30 𝑁)2 𝐹𝐵𝐶 = 9𝑥109 𝑁𝑥𝑚2 𝐶2 𝐹𝑅 = 900,5 𝑁 El módulo de FR es de 900,5 N 34.- En la figura se muestra un triángulo rectángulo, en sus vértices hay cargas eléctricas cuyos módulos son: q1= -6x10-6C; q2= - 3x10-6 C y q3= -3x10-6C. Calcular la magnitud de la fuerza resultante sobre q1 por efecto de las otras dos cargas. -q2 5 cm -q1 ( ( ( ( 3 cm -q3 ) 206,5 N ) 206 N ) -206,5 N ) 180 N Datos: 𝑞1 = −6𝑥10−6 𝐶 𝑞2 = −3𝑥10−6 𝐶 𝑞3 = −3𝑥10−6 𝐶 𝑟23 = 5𝑐𝑚 = 5𝑥10−2 𝑚 𝑟13 = 3𝑐𝑚 = 3𝑥10−2 𝑚 𝑟12 =? 𝐹𝑅 =? 𝑠𝑜𝑏𝑟𝑒 𝑞1 Diagrama: - q2 5 cm F21 -q1 3 cm -q3 FR F31 Como los vectores a sumar son perpendiculares, para hallar la magnitud de la fuerza resultante FR, aplicamos el Teorema de Pitágoras. 𝐶 2 = 𝑎2 + 𝑏 2 Donde c, es FR, a es F21 y b es F31; Al sustituir a,b y c nos queda que: 2 2 𝐹𝑅2 = 𝐹21 + 𝐹31 Para eliminar el cuadrado de FR, introducimos el resto de los términos dentro de una raíz cuadrada: 2 2 𝐹𝑅 = √𝐹31 + 𝐹21 Ahora calculamos las fuerzas: FAC y FBC, aplicando la ecuación de la Ley de Coulomb. 𝑞 𝑥𝑞 𝐹21 = 𝐾 2𝑟 2 1 y 12 𝑞3 𝑥 𝑞1 𝐹31 = 𝐾 2 𝑟13 Conversión de Unidades: Transformamos los centímetros (cm) a metros (m), multiplicando por 10-2. Solución: Antes de sustituir en la ecuación de la Ley de Coulomb, debemos hallar las distancias “r12”, aplicando el teorema de Pitágoras 𝐶 2 = 𝑎2 + 𝑏 2 Sabiendo que: 𝐶 = 𝑟23 ; 𝑎 = 𝑟13 𝑦 𝑏 = 𝑟12 . 2 2 2 𝑟23 = 𝑟13 + 𝑟12 Despejamos r12, que es la distancia que necesitamos, quedando que: 2 2 2 𝑟12 = 𝑟23 − 𝑟13 Para eliminar el cuadrado de la distancia r12, introducimos los demás términos dentro de una raíz cuadrada. 2 2 𝑟12 = √𝑟23 − 𝑟13 Sustituimos en la ecuación: 𝑟12 = √(5𝑥10−2 𝑚)2 − (3𝑥10−2 𝑚)2 𝑟12 = 4𝑥10−2 𝑚 Ahora procedemos a calcular las fuerzas ejercidas por cada carga sobre q1. 3𝑥10−6 𝐶 𝑥6𝑥10−6 𝐶 𝑁 𝑥 𝑚2 𝐹21 = 9𝑥109 𝐶 2 𝑥 (4𝑥10−2 𝑚)2 𝐹21 = 101,25 𝑁 2 3𝑥10−6 𝐶𝑥6𝑥10−6 𝐶 9𝑁 𝑥 𝑚 𝐹31 = 9𝑥10 𝐶 2 𝑥 (3𝑥10−2 𝑚)2 𝐹31 = 180 𝑁 𝐹𝑅 = √(180 𝑁)2 + (101,25 𝑁)2 𝐹𝑅 = 206,5 𝑁 35.- En los vértices del triángulo de la figura hay tres cargas eléctricas cuyos valores son: qA=+25x10-6C; qB=+9x10-6C y qC=+16x10-6C. Calcular el módulo de la fuerza resultante que actúa sobre qA por efecto de las otras dos cargas. Sabiendo que el ángulo en el vértice C es de 60º. +qB +qA ( ( ( ( 9 cm + qC ) 9,04 N )9N ) – 9,04 N )–9N Datos: 𝑞𝐴 = +25𝑥10−6 𝐶 𝑞𝐵 = +9𝑥10−6 𝐶 𝑞𝐶 = +16𝑥10−6 𝐶 𝑟𝐴𝐶 = 9𝑐𝑚 = 9𝑥10−2 𝑚 𝑟𝐴𝐵 =? 𝐹𝑅 =? 𝑠𝑜𝑏𝑟𝑒 𝑞𝐴 Diagrama: +qB FCA +qA FR 9 cm +qC FBA Como los vectores a sumar son perpendiculares, para hallar el módulo de la fuerza resultante FR, aplicamos el Teorema de Pitágoras: 𝐶 2 = 𝑎2 + 𝑏 2 Donde: Donde c, es FR, a es FCA y b es FBA; Al sustituir a,b y c nos queda que: 2 2 𝐹𝑅2 = 𝐹𝐶𝐴 + 𝐹𝐵𝐴 Para eliminar el cuadrado de FR, introducimos el resto de los términos dentro de una raíz cuadrada: 2 2 𝐹𝑅 = √𝐹𝐶𝐴 + 𝐹𝐵𝐴 Ahora calculamos las fuerzas: FCA y FBA, aplicando la ecuación de la Ley de Coulomb. 𝑞 𝑥𝑞 𝐹𝐵𝐴 = 𝐾 𝐵𝑟 2 𝐴 y 𝐴𝐵 𝑞𝐶 𝑥 𝑞𝐴 𝐹𝐶𝐴 = 𝐾 2 𝑟𝐴𝐶 Como no se conoce la distancia de separación entre las cargas A y B, la calculamos aplicando la función tangente del ángulo; ya que conocemos es el cateto adyacente al ángulo y necesitamos el opuesto: 𝐶𝑂 𝑟 tan 60° = 𝐶𝐴 = 𝑟𝐴𝐵 , despejamos rAB y nos queda que: 𝐴𝐶 𝑟𝐴𝐵 = 𝑟𝐴𝐶 𝑥 tan 60° Sustituimos en la ecuación: 𝑟𝐴𝐵 = 9𝑥10−2 𝑚 𝑥 tan 60° 𝑟𝐴𝐵 = 1,6𝑥10−1 𝑚 Conversión de Unidades: Solución: Los centímetros (cm) se Ahora procedemos a calcular las fuerzas: 2 transforman a metros (m), 9𝑥10−6 𝐶 𝑥 25𝑥10−6 9 𝑁𝑥𝑚 -2 𝐹 = 9𝑥10 𝑥 𝐵𝐴 multiplicando por 10 m. 𝐶2 (1,6𝑥10−1 𝑚)2 𝐹𝐵𝐴 = 7,9 𝑁 16𝑥10−6 𝐶𝑥25𝑥10−6 𝐶 (9𝑥10−2 𝑚)2 𝐹𝐶𝐴 = 4,4 𝑁 𝐹𝑅 = √(4,4 𝑁)2 + (7,9 𝑁)2 𝐹𝑅 = 9,04 𝑁 𝐹𝐶𝐴 = 9𝑥109 𝑁𝑥𝑚2 𝐶2 𝑥 36.- En cada uno de los vértices del triángulo de la figura hay cargas eléctricas cuyos valores son: qA=-4x10-6C; qB=-5x10-6C; qC=-2x10-6C y qD=+12x10-7C. Calcular el módulo de la fuerza resultante sobre qD por efecto de las otras cargas. El ángulo en el vértice A es igual a 30º y en el vértice C igual a 60º. -qB -qA ( ( ( ( 6 cm +qD -qC ) Sobre qD actúa una fuerza resultante de 61,55 N ) Sobre qD actúa una fuerza resultante de -61,55 N ) Sobre qD actúa una fuerza resultante de -61 N ) Sobre qD actúa una fuerza resultante de 61 N Datos: 𝑞𝐴 = −4𝑥10−6 𝐶 𝑞𝐵 = −5𝑥10−6 𝐶 𝑞𝐶 = −2𝑥10−6 𝐶 𝑟𝐴𝐷 = 6𝑐𝑚 = 6𝑥10−2 𝑚 𝑟𝐵𝐷 =? 𝑟𝐶𝐷 =? 𝐹𝑅 =? 𝑠𝑜𝑏𝑟𝑒 𝑞𝐷 𝛼 = 30° 𝛽 = 60° Diagrama: -qB -qA 6 cm +qD -qC FBD FAD FCD Se puede observar en la gráfica, que los vectores FAD y FCD, tienen la misma dirección y sentidos opuesto; lo que indica que habrá un vector resultante entre ellos, que tendrá dirección y sentido hacia la derecha; ya que, el sector FCD, es mayor que el vector FAD. Este vector resultante, se obtienen aplicando la suma de vectores. Y en la figura nos quedara: Conversión de Unidades: Transformamos los centímetros (cm) a metros (m), -2 multiplicando por 10 m. FBD FR (FCD – FAD) Obtenida la gráfica, observamos que los vectores a sumar son perpendiculares y para obtener el vector resultante, aplicamos el Teorema de Pitágoras. 𝐶 2 = 𝑎2 + 𝑏 2 Donde c, es FR, a es (FCD-FAD) y b es FBD; Al sustituir a,b y c nos queda que: 2 𝐹𝑅2 = (𝐹𝐶𝐷 − 𝐹𝐴𝐷 )2 + 𝐹𝐵𝐷 Para eliminar el cuadrado de la fuerza resultante, se introducen los demás términos dentro de una raíz cuadrada. 2 𝐹𝑅 = √(𝐹𝐶𝐷 − 𝐹𝐴𝐷 )2 + 𝐹𝐵𝐷 Ahora calculamos las fuerzas ejercidas por cada carga sobre qD, aplicando la ecuación de la Ley de Coulomb, para cada caso en específico y sustituyendo por los valores correspondientes. 𝑞 𝑥 𝑞0 𝑟2 4𝑥10−6 𝐶𝑥12𝑥10−7 𝐶 𝑁𝑥𝑚2 𝐹𝐴𝐷 = 9𝑥109 𝐶 2 𝑥 (6𝑥10−2 𝑚)2 𝐹𝐴𝐷 = 12 𝑁 Para calcular la FBD, necesitamos calcular la distancia rBD, esto aplicando la función trigonométrica tangente de 𝛼 = 30°. 𝐶𝑂 𝑟 tan 30° = 𝐶𝐴 = 𝑟𝐵𝐷; despejamos rBD y nos queda: 𝐹=𝐾 𝐴𝐷 𝑟𝐵𝐷 = 𝑟𝐴𝐷 𝑥 tan 30° Entonces: 𝑟𝐵𝐷 = 6𝑥10−2 𝑥 tan 30° 𝑟𝐵𝐷 = 3,46𝑥10−2 𝑚 Ahora calculamos la FBD. 5𝑥10−6 𝐶 𝑥 12𝑥10−6 𝐶 𝑁𝑥𝑚2 𝐹𝐵𝐷 = 9𝑥109 𝐶 2 𝑥 (3,46𝑥10−2 𝑚)2 𝐹𝐵𝐷 = 45 𝑁 Para calcular la fuerza FCD, necesitamos hallar primero la distancia de separación entre las cargas C y D. para hallar esta distancia, aplicamos la función trigonométrica tangente de 𝛽 = 60°. tan 60° = Despejamos rCD: 𝑟𝐶𝐷 = 𝐶𝑂 𝑟𝐵𝐷 = 𝐶𝐴 𝑟𝐶𝐷 𝑟𝐵𝐷 tan 60° Sustituimos en la ecuación: 3,46𝑥10−2 𝑚 tan 60° 𝑟𝐶𝐷 = 2𝑥10−2 𝑚 Procedemos ahora a calcular la fuerza FCD. 2𝑥10−6 𝐶𝑥12𝑥10−7 𝐶 𝑁𝑥𝑚2 𝐹𝐶𝐷 = 9𝑥109 𝐶 2 𝑥 (2𝑥10−2 𝑚)2 𝐹𝐵𝐶 = 54 𝑁 Se procede a calcular la fuerza resultante FR. 𝐹𝑅 = √(54 𝑁 − 12 𝑁)2 + (45 𝑁)2 𝐹𝑅 = 61,55 𝑁 𝑟𝐶𝐷 = 37.- En los vértices del triángulo de la figura adjunta hay cargas eléctricas cuyos módulos son: qA=+25x10-7C; qB=+9x10-6C y qC=+16x10-7C. Calcular el modulo de la fuerza resultante FR sobre qB por efecto de las otras dos cargas. El ángulo en el vértice C es de 60º +qB +qA +qC 9 cm ( ) Módulo de FR= -75,8 N ( ) Módulo de FR= 78,5 N ( ) Módulo de FR= 75,8 N ( ) Módulo de FR= -78,5 N Datos: 𝑞𝐴 = +25𝑥10−6 𝐶 𝑞𝐵 = +9𝑥10−6 𝐶 𝑞𝐶 = +16𝑥10−6 𝐶 𝑟𝐴𝐶 = 9𝑐𝑚 = 9𝑥10−2 𝑚 𝑟𝐴𝐵 =? 𝐹𝑅 =? 𝑠𝑜𝑏𝑟𝑒 𝑞𝐵 𝛼𝐶 = 60° 𝛽𝐴 = 30° Diagrama: Conversión de Unidades: Se transforman los centímetros (cm) a metros (m), multiplicando por 10-2 +qA 9 cm +qC Aquí se puede observar que los vectores a sumar forman un ángulo ≠ 90º, lo que indica que el vector resultante FR, se debe calcular aplicando el Teorema del Coseno, para hallar su módulo. 𝑐 2 = 𝑎2 + 𝑏 2 − 2𝑥𝑎𝑥𝑏𝑥 cos 𝜗 En este caso en particular, como los vectores se forman en el vértice A, entonces: cos 𝜗 = 180° − 𝛽 2 2 En el teorema del coseno 𝑐 2 = 𝐹𝑅 ; 𝑎2 = 𝐹𝐶𝐵 𝑦 𝑏 2 = 𝐹𝐴𝐵 ; al sustituir y eliminar el cuadrado de la fuerza resultante FR, introducimos el resto de los términos en una raíz cuadrada quedando: FR FAB FCB +qB β 2 2 𝐹𝑅 = √𝐹𝐶𝐵 + 𝐹𝐴𝐵 − 2𝑥𝐹𝐶𝐵 𝑥𝐹𝐴𝐵 𝑥 cos(180° − 𝛽) Los valores o módulos de las fuerzas FAB y FCB, los calculamos aplicando la ecuación de la Ley de Coulomb para cada caso en particular: 𝐹𝐴𝐵 = 𝐾 𝑞𝐴 𝑥 𝑞𝐵 2 𝑟𝐴𝐵 y 𝑞𝐶 𝑥 𝑞𝐵 2 𝑟𝐶𝐵 Para hallar el valor de la fuerza FAB, necesitamos la distancia de separación entre las cargas qA y qB, aplicando la función tangente del ángulo 𝛼 = 60°; podemos calcular la distancia rAB. 𝐶𝑂 𝑟 tan 60° = 𝐶𝐴 = 𝑟𝐴𝐶 ; despejamos rAB y 𝐹𝐶𝐵 = 𝐾 𝐴𝐵 nos queda: 𝑟𝐴𝐵 = 𝑟𝐴𝐶 tan 60° Sustituimos: 9𝑥10−2 𝑚 tan 60° 𝑟𝐴𝐵 = 5,2𝑥10−2 𝑚 Ahora calculamos la fuerza FAB: 2 25𝑥10−7 𝐶 𝑥 9𝑥10−6 𝐶 9 𝑁𝑥𝑚 𝐹𝐴𝐵 = 9𝑥10 𝐶 2 𝑥 (5,2𝑥10−2 𝑚)2 𝐹𝐴𝐵 ≅ 75 𝑁 Para hallar la fuerza FCB, necesitamos calcular la distancia rCB, esto lo hacemos aplicando la función coseno del ángulo 𝛼=60º. 𝐶𝐴 𝑟𝐴𝐶 cos 60° = = 𝐻 𝑟𝐶𝐵 Despejamos la distancia rCB. 𝑟𝐴𝐶 𝑟𝐶𝐵 = cos 60° Sustituimos: 9𝑥10−2 𝑚 𝑟𝐶𝐵 = cos 60° 𝑟𝐶𝐵 = 1,8𝑥10−1 𝑚 Calculamos la fuerza FCB: −7 −6 𝑁𝑥𝑚2 16𝑥10 𝐶𝑥9𝑥10 𝐶 𝐹𝐶𝐵 = 9𝑥109 𝐶 2 𝑥 (1,8𝑥10−1 𝑚)2 𝐹𝐶𝐵 = 4 𝑁 Cálculo de la fuerza resultante FR: 𝑟𝐴𝐵 = 𝐹𝑅 = √(4𝑁)2 + (75𝑁)2 − 2𝑥4𝑁𝑥75𝑁𝑥 cos(180° − 30°) 𝐹𝑅 = 78,5 𝑁 38.- En los vértices del triángulo de la figura adjunta hay cargas eléctricas cuyos módulos son: qA=+25x10-7C; qB=+9x10-6C y qC=+16x10-7C. Calcular el modulo de la fuerza resultante FR sobre qC por efecto de las otras dos cargas. El ángulo en el vértice C es de α=60º +qB +qA +qC 9 cm ( ( ( ( ) Su módulo es de 7,0 N ) Su módulo es de 7,4 N ) Su módulo es de 7,31 N ) Su módulo es de -7,31 N Datos: 𝑞𝐴 = +25𝑥10−7 𝐶 𝑞𝐵 = +9𝑥10−6 𝐶 𝑞𝐶 = +16𝑥10−7 𝐶 𝑟𝐴𝐶 = 9𝑐𝑚 = 9𝑥10−2 𝑚 𝑟𝐵𝐶 =? 𝐹𝑅 =? 𝑠𝑜𝑏𝑟𝑒 𝑞𝐶 Diagrama: +qB FAC +qA +qC 9 cm FR FBC En el análisis vectorial realizado, podemos observar que las fuerzas, tienen diferente dirección y sentido, formando un ángulo diferente a 90º; lo que indica, que para hallar el vector resultante o fuerza resultante, se debe aplicar el Teorema del coseno. Conversión de Unidades: Solución: Se transforman los 𝑐 2 = 𝑎2 + 𝑏 2 − 2𝑥𝑎𝑥𝑏𝑥 cos 𝜗 Donde:𝜗 = 180° − 𝛼, siendo alfa igual a 60º. centímetros (cm) a 2 2 En el teorema del coseno 𝑐 2 = 𝐹𝑅 ; 𝑎2 = 𝐹𝐴𝐶 𝑦 𝑏 2 = 𝐹𝐵𝐶 ; al metros (m), -2 multiplicando por 10 m. sustituir y eliminar el cuadrado de la fuerza resultante FR, introducimos el resto de los términos en una raíz cuadrada quedando: 2 2 𝐹𝑅 = √𝐹𝐴𝐶 + 𝐹𝐵𝐶 − 2𝑥𝐹𝐴𝐶 𝑥𝐹𝐵𝐶 𝑥 cos(180° − 𝛼) Para hallar las magnitudes de las fuerzas que actúan sobre qC, aplicamos la ecuación de la Ley de Coulomb, para cada caso en particular. 𝐹𝐴𝐶 = 𝐾 𝑞𝐴 𝑥 𝑞𝐶 2 𝑟𝐴𝐶 y 𝑞𝐵 𝑥 𝑞𝐶 2 𝑟𝐵𝐶 La distancia BC, la calculamos aplicando la función trigonométrica coseno del ángulo: (cos 𝛼). 𝐶𝐴 𝑟 cos 60° = 𝐻 = 𝑟𝐴𝐶 ; despejamos rBC, quedando que: 𝐵𝐶 𝑟𝐴𝐶 𝑟𝐵𝐶 = cos 60° 9𝑥10−2 𝑚 𝑟𝐵𝐶 = cos 60° 𝑟𝐵𝐶 = 1,8𝑥10−2 𝑚 Ahora procedemos a calcular las fuerzas ejercidas por cada carga sobre qC: −7 −6 𝑁𝑥𝑚2 25𝑥10 𝐶𝑥16𝑥10 𝐶 𝐹𝐴𝐶 = 9𝑥109 𝐶 2 𝑥 (9𝑥10−2 𝑚)2 𝐹𝐴𝐶 = 4,44 𝑁 −6 −7 𝑁𝑥𝑚2 9𝑥10 𝐶𝑥16𝑥10 𝐶 𝐹𝐵𝐶 = 9𝑥109 𝐶 2 𝑥 (1,8𝑥10−2 𝑚)2 𝐹𝐵𝐶 = 4 𝑁 2 2 𝐹𝑅 = √(4,44𝑁) + (4𝑁) − 2𝑥4,44𝑁𝑥4𝑁𝑥 cos(180° − 60°) 𝐹𝑅 = 7,31 𝑁 𝐹𝐵𝐶 = 𝐾 39.- ABC, es un triangulo equilátero de 6 cm de lado. En sus vértices hay cargas eléctricas cuyos valores son: 𝑞𝐴 = +3𝑥10−6 𝐶; 𝑞𝐵 = −6𝑥10−6 𝐶, tal y como se muestra en la figura. Calcular el modulo de la fuerza resultante, sobre una carga 𝑞𝐶 = +4𝑥10−6 𝐶 ubicada en el centro del triángulo. 6 cm +qA ( ( ( ( -qB ) 233,3 N ) 233,5 N ) -233,3 N ) 2,33 N Datos: 𝑞𝐴 = +3𝑥10−6 𝐶 𝑞𝐵 = −6𝑥10−6 𝐶 𝑞𝐶 = +4𝑥10−6 𝐶 𝐿 = 6𝑐𝑚 = 6𝑥10−2 𝑚 𝐹𝑅 = sobre 𝑞𝐶 Diagrama: FAC FR F +qA FBC -qB FAC FR FBC El análisis vectorial, nos indica que los vectores a sumar forman un ángulo diferente a 90º; entonces, ara hallar el valor de la fuerza resultante FR, debemos aplicar el Teorema del Coseno, donde, debido a los cortes en el triángulo y a la ubicación de q C el ángulo 𝜗 = 120°. Conversión de Solución: Unidades: Transformamos los 𝑐 2 = 𝑎2 + 𝑏 2 − 2𝑥𝑎𝑥𝑏𝑥 cos 𝜗 2 2 𝑦 𝑏 2 = 𝐹𝐵𝐶 ; al centímetros (cm) a En el teorema del coseno 𝑐 2 = 𝐹𝑅 ; 𝑎2 = 𝐹𝐴𝐶 metros (m), sustituir y eliminar el cuadrado de la fuerza resultante FR, -2 multiplicando X10 m introducimos el resto de los términos en una raíz cuadrada quedando: 2 2 𝐹𝑅 = √𝐹𝐵𝐶 + 𝐹𝐴𝐶 − 2𝑥𝐹𝐵𝐶 𝑥𝐹𝐴𝐶 𝑥 cos 120° Para hallar las magnitudes de las fuerzas que actúan sobre qC, aplicamos la ecuación de la Ley de Coulomb, para cada caso en particular. 𝐹𝐴𝐶 = 𝐾 𝑞𝐴 𝑥 𝑞𝐶 y 2 𝑟𝐴𝐶 𝑞𝐵 𝑥 𝑞𝐶 2 𝑟𝐵𝐶 Calculamos las distancias rAC y rBC, que son iguales; ya que, el triangulo es equilátero, a través de la función trigonométrica coseno, siendo el ángulo de 30º, debido a la ubicación de qC. 𝐹𝐵𝐶 = 𝐾 cos 30° = 𝐶𝐴 𝐻 =𝑟 𝑟 𝐴𝐶 , siendo r la distancia de la carga C al punto medio entre la carga A y B; despejamos rAC: 𝑟 𝑟𝐴𝐶 = cos 30° 3𝑥10−2 𝑚 𝑟𝐴𝐶 = cos 30° 𝑟𝐴𝐶 = 3,5𝑥10−2 𝑚 −6 −6 𝑁𝑥𝑚2 3𝑥10 𝐶 𝑥 4𝑥10 𝐶 𝐹𝐴𝐶 = 9𝑥109 𝐶 2 (3,5𝑥10−2 𝑚)2 𝐹𝐴𝐶 = 88,2 𝑁 2 6𝑥10−6 𝐶 𝑥 4𝑥10−6 𝐶 9 𝑁𝑥𝑚 𝐹𝐵𝐶 = 9𝑥10 𝐶 2 𝑥 (3,5𝑥10−2 𝑚)2 𝐹𝐵𝐶 = 176,3 𝑁 2 𝐹𝑅 = √(88,2 𝑁) + (176,3 𝑁)2 − 2𝑥88,2𝑁𝑥176,3𝑁𝑥 cos 120° 𝐹𝑅 = 233,3 𝑁 40.- Se dispone de un triangulo equilátero de 5 cm de lado, en sus vértices hay cargas eléctricas: 𝑞𝐴 = +8𝑥10−6 𝐶;𝑞𝐵 = +4𝑥10−6 𝐶 𝑦 𝑞𝐶 = +12𝑥10−7 𝐶. Calcular la magnitud de la fuerza resultante sobre qC por efecto de las otras dos cargas. +qC 5 cm +qA ( ( ( ( +qB ) 47,52 N ) 45,72 N ) 47,5 N ) 45,7 N Datos: 𝑞𝐴 = +8𝑥10−6 𝐶 𝑞𝐵 = +4𝑥10−6 𝐶 𝑞𝐶 = +12𝑥10−7 𝐶 𝐿 = 5 𝑐𝑚 = 5𝑥10−2 𝑚 𝐹𝑅 = Sobre 𝑞𝐶 𝑟𝐴𝐶 = 𝑟𝐵𝐶 = 𝐿 Diagrama: FR FBC FAC +qC 5 cm +qA +qB Como los vectores a sumar no son perpendiculares, se aplica el Teorema del Coseno, para hallar el valor de la fuerza resultante en la carga qC. Conversión de Solución: Unidades: Transformamos los 𝑐 2 = 𝑎2 + 𝑏 2 − 2𝑥𝑎𝑥𝑏𝑥 cos 𝜗 centímetros (cm) a metros (m), Como 𝛼 = 60°, entonces: 𝜗 = 180° − 60° -2 multiplicando X10 m. 2 2 En el teorema del coseno 𝑐 2 = 𝐹𝑅 ; 𝑎2 = 𝐹𝐴𝐶 𝑦 𝑏 2 = 𝐹𝐵𝐶 ; al sustituir y eliminar el cuadrado de la fuerza resultante FR, introducimos el resto de los términos en una raíz cuadrada quedando: 2 2 𝐹𝑅 = √𝐹𝐵𝐶 + 𝐹𝐴𝐶 − 2𝑥𝐹𝐵𝐶 𝑥𝐹𝐴𝐶 𝑥 cos 120° Para hallar las magnitudes de las fuerzas que actúan sobre qC, aplicamos la ecuación de la Ley de Coulomb, para cada caso en particular. 𝐹𝐴𝐶 = 𝐾 𝑞𝐴 𝑥 𝑞𝐶 2 𝑟𝐴𝐶 y 𝐹𝐵𝐶 = 𝐾 𝑞𝐵 𝑥 𝑞𝐶 2 𝑟𝐵𝐶 Sustituimos en las ecuaciones: 8𝑥10−6 𝐶 𝑥 12𝑥10−7 𝐶 𝐹𝐴𝐶 = 𝑥 (5𝑥10−2 𝑚)2 𝐹𝐴𝐶 = 34,56 𝑁 −6 2 4𝑥10 𝐶 𝑥12𝑥10−7 𝐶 9 𝑁𝑥𝑚 𝐹𝐵𝐶 = 9𝑥10 𝐶 2 (5𝑥10−2 𝑚)2 𝐹𝐵𝐶 = 17,28 𝑁 𝑁𝑥𝑚 9𝑥109 𝐶 2 2 Ahora calculamos la fuerza resultante FR: 𝐹𝑅 = √(34,56𝑁)2 + (17,28𝑁)2 − 2𝑥34,56𝑁𝑥17,28𝑁𝑥 cos 120° 𝐹𝑅 = 45,72 𝑁 41.- En los vértices del triangulo de la figura adjunta hay cargas eléctricas cuyos módulos son: 𝑞𝐴 = +16𝑥10−7 𝐶; 𝑞𝐵 = +10−5 𝐶 𝑦 𝑞𝐶 = +8𝑥10−7 𝐶. Calcular el modulo de la fuerza resultante que actúa sobre qC, por efecto de las otras dos cargas. El ángulo en el vértice C es igual a: 𝛼 = 60°. +qB +qA +qC 5 cm ( ( ( ( ) 74,4N ) 74 N ) 7,4 N ) -74,4 N Datos: 𝑞𝐴 = +16𝑥10−7 𝐶 𝑞𝐵 = +10−5 𝐶 𝑞𝐶 = +8𝑥10−7 𝐶 𝑟𝐴𝐶 = 5𝑐𝑚 = 5𝑥10−2 𝑚 𝑟𝐵𝐶 = 𝐹𝑅 = 𝑆𝑜𝑏𝑟𝑒 𝑞𝐶 Diagrama: +qB FAC +qA 5cm +qC FBC Conversión de Unidades: Transformamos los centímetros (cm) a metros (m), multiplicando X10-2 m. FR Solución: Como los vectores a sumar forman un ángulo diferente a 90º, se aplica el teorema del coseno, para hallar la fuerza resultante FR. 𝑐 2 = 𝑎2 + 𝑏 2 − 2𝑥𝑎𝑥𝑏𝑥 cos 𝜗 Como 𝛼 = 60°, entonces: 𝜗 = 180° − 60° 2 2 En el teorema del coseno 𝑐 2 = 𝐹𝑅 ; 𝑎2 = 𝐹𝐴𝐶 𝑦 𝑏 2 = 𝐹𝐵𝐶 ; al sustituir y eliminar el cuadrado de la fuerza resultante FR, introducimos el resto de los términos en una raíz cuadrada quedando: 2 2 𝐹𝑅 = √𝐹𝐴𝐶 + 𝐹𝐵𝐶 − 2𝑥𝐹𝐴𝐶 𝑥𝐹𝐵𝐶 𝑥 cos 120° Para hallar las magnitudes de las fuerzas que actúan sobre qC, aplicamos la ecuación de la Ley de Coulomb, para cada caso en particular. 𝐹𝐴𝐶 = 𝐾 𝑞𝐴 𝑥 𝑞𝐶 2 𝑟𝐴𝐶 y 𝐹𝐵𝐶 = 𝐾 𝑞𝐵 𝑥 𝑞𝐶 2 𝑟𝐵𝐶 Sustituimos en las ecuaciones: 16𝑥10−7 𝐶𝑥8𝑥10−7 𝐶 𝐹𝐴𝐶 = 𝑥 (5𝑥10−2 𝑚)2 𝐹𝐴𝐶 = 4,61 𝑁 Para hallar la FBC, necesitamos rimero calcular la distancia rBC, aplicando la función coseno de α= 60°. 𝑁𝑥𝑚 9𝑥109 𝐶 2 2 cos 60° = 𝐶𝐴 𝑟𝐴𝐶 = 𝐻 𝑟𝐵𝐶 Despejamos la distancia rBC: 𝐹𝐵𝐶 𝑟𝐴𝐶 5𝑥10−2 𝑚 𝑟𝐵𝐶 = = cos 60° cos 60° 𝑟𝐵𝐶 = 10−1 𝑁 −5 −7 𝑁𝑥𝑚2 10 𝐶𝑥8𝑥10 𝐶 = 9𝑥109 𝐶 2 𝑥 (10−1 𝑚)2 𝐹𝐵𝐶 = 72 𝑁 𝐹𝑅 = √(4,61𝑁)2 + (72𝑁)2 − 2𝑥4,61𝑁𝑥72𝑁𝑥 cos 120° 𝐹𝑅 = 74,4 𝑁 42.- En la figura se tienen tres cargas eléctricas cuyos módulos son: 𝑞𝐴 = +2𝑥10−6 𝐶; 𝑞𝐵 = +3𝑥10−6 𝐶 𝑦 𝑞𝐶 = +4𝑥10−6 𝐶. Calcular la fuerza resultante sobre qC, por efecto de las otras dos cargas. Angulo en el vértice C igual a 𝛼 = 60°. +qB 6 cm +qA ( ( ( ( +qC ) 98,5 N ) 98 N ) 110 N ) 120 N Datos: 𝑞𝐴 = +2𝑥10−6 𝐶 𝑞𝐵 = +3𝑥10−6 𝐶 𝑞𝐶 = +4𝑥10−6 𝐶 𝑟𝐵𝐶 = 6𝑐𝑚 = 6𝑥10−2 𝑚 𝑟𝐴𝐶 = 𝐹𝑅 𝑠𝑜𝑏𝑟𝑒 𝑞𝐶 Diagrama: +qB 6 cm FAC +qA +qC FBC Conversión de Unidades: Transformamos los centímetros (cm) a metros (m), multiplicando X10-2m. FR Solución: Se observa en el análisis que los vectores a sumar, forman un ángulo diferente a 90º, lo cual, nos indica que debemos aplicar el teorema del coseno, con el fin de hallar la fuerza resultante FR. 𝑐 2 = 𝑎2 + 𝑏 2 − 2𝑥𝑎𝑥𝑏𝑥 cos 𝜗 Como 𝛼 = 60°, entonces: 𝜗 = 180° − 60° 2 2 En el teorema del coseno 𝑐 2 = 𝐹𝑅 ; 𝑎2 = 𝐹𝐴𝐶 𝑦 𝑏 2 = 𝐹𝐵𝐶 ; al sustituir y eliminar el cuadrado de la fuerza resultante FR, introducimos el resto de los términos en una raíz cuadrada quedando: 2 2 𝐹𝑅 = √𝐹𝐴𝐶 + 𝐹𝐵𝐶 − 2𝑥𝐹𝐴𝐶 𝑥𝐹𝐵𝐶 𝑥 cos 120° Para hallar las magnitudes de las fuerzas que actúan sobre qC, aplicamos la ecuación de la Ley de Coulomb, para cada caso en particular. 𝐹𝐴𝐶 = 𝐾 𝑞𝐴 𝑥 𝑞𝐶 2 𝑟𝐴𝐶 y 𝑞𝐵 𝑥 𝑞𝐶 2 𝑟𝐵𝐶 Debemos hallar la distancia rAC, aplicando la función trigonométrica coseno de α y de esta forma calcular la fuerza FAC. 𝐹𝐵𝐶 = 𝐾 cos 60° = 𝐶𝐴 𝑟𝐴𝐶 = 𝐻 𝑟𝐵𝐶 Despejamos rAC: 𝐹𝐴𝐶 𝑟𝐴𝐶 = 𝑟𝐵𝐶 𝑥 cos 60° 𝑟𝐴𝐶 = 6𝑥10−2 𝑚 𝑥 cos 60° 𝑟𝐴𝐶 = 3𝑥10−2 𝑚 2𝑥10−6 𝐶 𝑥 4𝑥10−6 𝐶 𝑁𝑥𝑚2 = 9𝑥109 𝐶 2 𝑥 (3𝑥10−2 𝑚)2 𝐹𝐴𝐶 = 80 𝑁 𝐹𝐵𝐶 = 9𝑥109 𝑁𝑥𝑚2 𝐶2 𝐹𝐵𝐶 3𝑥10−6 𝐶 𝑥 4𝑥10−6 𝐶 (6𝑥10−2 𝑚)2 = 30 𝑁 𝑥 𝐹𝑅 = √(80𝑁)2 + (30)2 − 2𝑥80𝑁𝑥30𝑁𝑥 cos 120° 𝐹𝑅 ≅ 98,5 𝑁 43.- Una esfera esta suspendida de un dinamómetro que marca 1 pondio ( ). 5 cm debajo de ella se coloca una esfera cargada con +4x10-6C, con lo cual el dinamómetro marca 1,1 pondio. Calcular el signo y el valor de la carga que esta suspendida del dinamómetro. ( ( ( ( ) -6,8x10-11C ) +6,8x10-11C ) 4x10-6 C ) 9,8x10-4 C Procedimiento y Solución Como la carga suspendida aumenta en peso 0,1 pondio, significa que su aumento se debe a la fuerza de atracción que origina la otra carga. Debemos, transformar los pondios a Newton; ya que, el pondio es una unidad de fuerza (peso). 9,8 𝑁 F= 0,1 pondios x (1000 ) = 9,8𝑥10−4 𝑁 La distancia, también la transformamos de centímetros (cm) a metros (m), multiplicando X10-2 m o dividiendo entre 100. 5 𝑐𝑚 𝑟 = 100 𝑐𝑚 𝑥 1𝑚 = 0,05𝑚 ≡ 5𝑥10−2 𝑚 Aplicamos la ecuación de la Ley de Coulomb: 𝐹=𝐾 𝑞 𝑥 𝑞0 𝑟2 Y despejamos q2: 𝑞2 = 𝐹 𝑥 𝑟2 𝐾 𝑥 𝑞1 Sustituimos en la ecuación: 𝑞2 = 9,8𝑥10−4 𝑁 𝑥 (5𝑥10−2 𝑚)2 2 9𝑥109 𝑁 𝑥𝐶 2𝑚 𝑥 4𝑥10−6 𝐶 𝑞2 = 6,8𝑥10−11 𝐶 Conclusión: La carga es negativa, para que pueda existir una fuerza de atracción y des esta forma, el dinamómetro se desplace 0,1 pondio, de lo contrario no sucedería nada. 44.- Una esfera tiene una carga de −5𝑥10−8 𝐶 y esta suspendida del techo mediante un hilo de seda. Debajo de ella hay otra esfera que pesa 0,2 pondios (P) y tiene una carga de +𝑥10−10 𝐶. Calcular la distancia que las separa si esta segunda esfera esta en equilibrio. ( ( ( ( ) 1,35 cm ) -1,35 cm ) 1,35 m ) 13,5 m -q1 F +q2 P Procedimientos y Solución En la figura mostrada, se observa que sobre la esfera q2 actúan dos fuerzas opuestas; F que es la fuerza de atracción entre las esferas y P, que es el peso de la esfera. Como condición el problema nos dice que la segunda esfera q2, esta en equilibrio; en tal sentido, estas fuerzas son iguales en modulo pero de sentidos opuestos. F=P=0,2 P Transformamos los Pondios (P) a Newton (N) 9,8 𝑁 F= 0,2 P x 1000 𝑃 𝐹 = 1,96𝑥10−3 𝑁 Ahora se aplica la ecuación de la Ley de Coulomb y despejamos distancia r: 𝐹=𝐾 𝑞 𝑥 𝑞0 𝑟2 Al despejar “r” y eliminar el cuadrado, nos queda: 𝑟 = √𝐾𝑥 2 𝑁𝑥𝑚 𝑟 = √9𝑥109 𝐶 2 𝑥 𝑞1 𝑥 𝑞2 𝐹12 5𝑥10−8 𝐶 𝑥 8𝑥10−10 𝐶 1,96𝑥10−3 𝑁 𝑟 = 1,35𝑥10−2 𝑚 = 1,35𝑐𝑚 45.- Se dispone de dos esferas cargada de electricidad cuyas cargas son: q1= +4x10-5C y q2=-8x10-6C. Se les pone en contacto y después se les coloca a una distancia de 2 cm. Calcular el modulo e indicar la naturaleza de la fuerza con que se accionan. ( ( ( ( ) 5760 N; fuerza de repulsión ) 5760 N; fuerza de atracción ) 576,0 N; fuerza de repulsión ) 57,60 N; fuerza de repulsión Datos: 𝑞1 = +4𝑥10−5 𝐶 𝑞2 = −8𝑥10−6 𝐶 𝑟12 = 2𝑐𝑚 = 2𝑥10−2 𝑚 𝐹12 Diagrama: Conversión de Unidades: Transformamos los centímetros (cm) a metros (m), multiplicando X10-2m. Solución: Las cargas eléctricas son el déficit o exceso de electrones, cuando estas se ponen en contacto, los electrones son transferidos de una carga a la otra, quedando ambas con la misma carga y mismo signo. En tal sentido, sumamos algebraicamente ambas cargas: 𝑞1 + 𝑞2 = +4𝑥10−5 𝐶 − 8𝑥10−6 𝐶 +q1 F12 -q2 2 cm 𝑞1 + 𝑞2 = +32𝑥10−6 𝐶 Como son dos esferas y ambas quedan con cargas iguales; es decir, la mitad de la suma algebraica: 𝑞1 = 𝑞2 = 16𝑥10−6 𝐶 Ahora aplicamos la ecuación de la Ley de Coulomb, para calcular la fuerza entre las cargas. 𝐹 12=𝐾 𝑞1 𝑥 𝑞2 𝑟2 Sustituimos en la ecuación: 𝐹12 = 9𝑥109 𝑁𝑥𝑚2 𝐶2 𝑥 16𝑥10−6 𝐶𝑥 16𝑥10−6 𝐶 (2𝑥10−2 𝑚)2 𝐹12 = 5760 𝑁 Como las cargas son de igual signo después del contacto la fuerza entre ellas es de repulsión. 46.- Dos esferas A y B están en el vacio separadas por una distancia de 10 cm. Tienen cargas eléctricas qA=+3x10-6C y qB= - 8x10-6C. Con otra esfera C en estado neutro, primero se toca a A y después a B. Si la esfera C después de tocar a B se separa del sistema, calcular la fuerza con que se accionan. ( ( ( ( ) Se atraen con una fuerza de 4,38 N ) Se repelen con una fuerza de 4,38 N ) Se atraen con una fuerza de 43,8 N ) Se atraen con una fuerza de -4,38 N Datos: −6 𝑞𝐴 = +3𝑥10 𝐶 𝑞𝐵 = −8𝑥10−6 𝐶 𝑞𝐶 = 0 𝐹𝐴𝐵 𝑑𝑒𝑠𝑝𝑢é𝑠 𝑑𝑒𝑙 𝑐𝑜𝑛𝑡𝑎𝑐𝑡𝑜 𝑐𝑜𝑛 𝐶 Diagrama: + qA - qB 10 cm qC +qA -qB FAB 10 cm Conversión de Unidades: Solución: Los centímetros (cm) los Como la esfera C esta en estado neutro y toca a la transformamos a metros (m), esfera A, estas intercambian electrones, quedando multiplicando por 10-2 m. ambas con cargas de la misma magnitud y el mismo signo; posteriormente, después de cargada la esfera C se toca con B creando un intercambio de electrones nuevamente, quedando B y C con cargas iguales y del mismo signo. Para conocer el nuevo valor de las cargas A y B, sumamos algebraicamente, las cargas eléctricas: 𝑞𝐴 + 𝑞𝐶 = +3𝑥10−6 𝐶 + 0 𝐶 𝑞𝐴 + 𝑞𝐶 = +3𝑥10−6 𝐶, como quedan con cargas iguales después de la transferencia de electrones: 𝑞𝐴 = 𝑞𝐶 = +1,5𝑥10−6 𝐶 Ahora sumamos a la esferas C y B: 𝑞𝐶 + 𝑞𝐵 = 1,5𝑥10−6 𝐶 − 8𝑥10−6 𝐶 𝑞𝐶 + 𝑞𝐵 = −6,5𝑥10−6 𝐶 Lo cual nos dará una carga para ambas esferas de: 𝑞𝐶 = 𝑞𝐵 = −3,25𝑥10−6 𝐶 Ya conocidas las cargas de qA y qB, procedemos a calcular la fuerza con que se accionan las cargas después del contacto, aplicando la ecuación de la Ley de Coulomb. 𝐹𝐴𝐵 = 𝐾 𝑞𝐴 𝑥 𝑞𝐵 2 𝑟𝐴𝐵 Sustituimos: 𝐹𝐴𝐵 = 9𝑥109 𝑁𝑥𝑚2 𝐶2 𝑥 1,5𝑥10−6 𝐶 𝑥 3,25𝑥10−6 𝐶 (10𝑥10−2 𝑚)2 𝐹𝐴𝐵 = 4,38 𝑁 La fuerza es de atracción por ser las cargas de signos contrarios. 47.- Dos esferas iguales que pesan cada una 0,1 pondio (p), están en el vacio suspendidas de un mismo punto mediante hilos de seda de igual longitud. Por efecto de las cargas eléctricas iguales que poseen se repelen, quedando en equilibrio a una distancia de 9 cm. Calcular el valor de las cargas sabiendo que los hilos forman un ángulo de 90º. ( ( ( ( ) 𝑞𝐴 ) 𝑞𝐴 ) 𝑞𝐴 ) 𝑞𝐴 = 𝑞𝐵 = 𝑞𝐵 = 𝑞𝐵 = 𝑞𝐵 = 2,89𝑥10−8 𝐶 = 2,87𝑥10−8 𝐶 = 2,87𝑥10−7 𝐶 = 2,87𝑥10−6 𝐶 Datos: Diagrama: 𝑞𝐴 = 𝑞𝐵 , 𝑠𝑒 𝑑𝑒𝑠𝑐𝑜𝑛𝑜𝑐𝑒𝑛 𝑃 = 𝐹 = 0,1p 𝛼 = 90° F qA qB 9 cm Conversión de Unidades: Transformamos los centímetros (cm) a metros (m), multiplicando por 10-2m y los pondios (p) a Newton (N), multiplicando por 9,8 N y dividiendo entre 103p. FR P F es la fuerza de repulsión entre las cargas; ya que, son iguales y P es el eso de las esferas. Solución: La fuerza resultante debe tener la misma dirección que el hilo en el triangulo formado por el origen en qA, la fuerza resultante FR y el peso P. Calculamos el valor de F, aplicando la función trigonométrica tangente tan 𝛽, siendo β el ángulo entre Fr y P que es igual a 45º. 𝐶𝑂 𝐹 tan 45° = = 𝐶𝐴 𝑃 Despejamos F y nos queda: 𝐹 = 𝑃 𝑥 tan 45° Sustituimos y nos queda: 𝐹 = 0,1 𝑝 𝑥 tan 45° 𝐹 = 0,1 𝑝 Por lo tanto F=P. Transformamos los p a N: 0,1 𝑝 𝐹= 𝑥 9,8 𝑁 103 𝑝 𝐹 = 9,8𝑥10−4 𝑁 Realizada las transformaciones y hallado el valor de la fuerza de repulsión entre las cargas ya que son iguales en magnitud y signo, aplicamos la ecuación de la Ley de Coulomb y despejamos “q” como son iguales, decimos que: 𝑞𝐴 𝑥𝑞𝐵 = 𝑞 2 . 𝑞𝐴 𝑥 𝑞𝐵 2 𝑟𝐴𝐵 Como las “q” son iguales, decimos que: 𝑞𝐴 𝑥𝑞𝐵 = 𝑞 2 . 𝐹𝐴𝐵 = 𝐾 Al despejar “q” y eliminar el cuadrado de ella, introducimos el resto de los términos dentro de una raíz cuadrada: 𝑞= √ 𝐹𝐴𝐵 𝑥 𝑟 2 𝐾 Sustituimos: 𝑞=√ 9,8𝑥10−4 𝑁 𝑥 (9𝑥10−2 𝑚)2 9𝑥109 𝑁 𝑥𝐶 2𝑚 2 𝑞 = 2,87𝑥10−8 𝐶 𝑞 = 𝑞𝐴 = 𝑞𝐵 = 2,87𝑥10−8 𝐶 48.- Dos esferas iguales de masa 1 gr cada una, están suspendidas de un mismo punto por dos hilos de seda de 15 cm cada uno. Están cargadas con cargas iguales y debido a esto las cargas se repelen quedando en equilibrio cuando las separa una distancia de de 18 cm. Calcular el valor de las cargas. ( ( ( ( ) 𝑞𝐴 ) 𝑞𝐴 ) 𝑞𝐴 ) 𝑞𝐴 = 𝑞𝐵 = 𝑞𝐵 = 𝑞𝐵 = 𝑞𝐵 = 1,62𝑥10−7 𝐶 = 1,62𝑥10−6 𝐶 = 1,62𝑥10−5 𝐶 = 1,62𝑥10−8 𝐶 Datos: 𝑞𝐴 = 𝑞𝐵 𝑠𝑒 𝑑𝑒𝑠𝑐𝑜𝑛𝑜𝑐𝑒𝑛 𝑚 = 1 𝑔𝑟 = 10−3 𝐾𝑔 𝐿 = 15 𝑐𝑚 = 15𝑥10−2 𝑚 𝑟𝐴𝐵 = 18𝑐𝑚 = 18𝑥10−2 𝑚 Diagrama: O F C 15 cm q H A 18 cm FR P q E D F es la fuerza de repulsión y P es el peso. La resultante de la fuerza debe tener la misma dirección que el hilo. En la figura se observa que ΔAOH y el ΔEAD, son iguales, por tener sus lados paralelos. Conversión de Unidades: Transformamos los centímetros (cm) a metros (m), multiplicando por 102 m. Los gramos (gr) a kilogramos (Kg), -3 multiplicando por 10 . En este caso los Kg equivalen a Kilopondios (Kp) y ara transformar los Kp a Newton (N), multiplicamos por 9,8 N. 𝑃 = 10−3 𝐾𝑝 𝑥 9,8 𝑁 𝑃 = 9,8𝑥10−3 𝑁 Solución: Procedemos a calcular en el triangulo ΔAOH, el lado OH, aplicando el Teorema de Pitágoras: 𝐶 2 = 𝑎2 + 𝑏 2 Donde: 𝑐 = 𝑂𝐴; 𝑎 = 𝐴𝐻 𝑦 𝑏 = 𝑂𝐻 , quedando: 𝑂𝐴2 = 𝐴𝐻2 + 𝑂𝐻2 ; desejamos OH y para eliminar el cuadrado introducimos dentro de una raiz cuadrada, el resto de los terminos. 𝑂𝐻 = √(𝑂𝐴)2 − (𝐴𝐻)2 Sustituimos: 𝑂𝐻 = √(15𝑥10−2 𝑚)2 − (9𝑥10−2 )2 𝑂𝐻 = 12 𝑐𝑚 Procedemos ahora a calcular la funcion tangente del angulo (tan 𝛼); para poder hallar el valor de la fuerza y posteriormente las cargas electricas. 𝐶𝑂 𝐴𝐻 9𝑥10−2 𝑚 tan 𝛼 = = = 𝐶𝐴 𝑂𝐻 12𝑥10−2 𝑚 tan α = 0,75 Analizando las caracteristicas de los vectores, tenemos que: 𝐶𝑂 𝐹 = 𝐶𝐴 𝑃 tan 𝛼 = Despejando F, nos queda: 𝐹 = 𝑃 𝑥 tan 𝛼 = 9,8𝑥10−3 𝑁𝑥 0,75 𝐹 = 7,35𝑥10−3 𝑁 Ahora procedemos a calcular el valor de las cargas, aplicando la ecuacion de la Ley de Coulomb: 𝐹𝐴𝐵 = 𝐾 𝑞𝐴 𝑥 𝑞𝐵 2 𝑟𝐴𝐵 Como las “q” son iguales, decimos que: 𝑞𝐴 𝑥𝑞𝐵 = 𝑞 2 . Al despejar “q” y eliminar el cuadrado de ella, introducimos el resto de los términos dentro de una raíz cuadrada: 𝑞= √ 𝐹𝐴𝐵 𝑥 𝑟 2 𝐾 Sustituimos: 𝑞=√ 7,35𝑥10−3 𝑁 𝑥(18𝑥10−2 𝑚)2 9𝑥109 𝑁 𝑥𝐶 2𝑚 2 𝑞 = 1,62𝑥10−7 𝐶 𝑞𝐴 = 𝑞𝐵 = 𝑞 = 1,62𝑥10−7 𝐶 49.- Dos esferas A y B están en el vacio por una distancia de 9 cm. Tienen cargas eléctricas de qA=+6x10-6C y qB=-12x10-6C. Con otra esfera C en estado neutro, se toca primero a A y después a B. Si la esfera C después de tocar a B se separa del sistema. Calcular la fuerza con que se accionan. ( ( ( ( ) Se atraen con una fuerza de 15 N ) Se atraen con una fuerza de – 15 N ) Se repelen con una fuerza de 15 N ) Se repelen con una fuerza de 15 N Datos: 𝑞𝐴 = +6𝑥10−6 𝐶 𝑞𝐵 = −12𝑥10−6 𝐶 𝑞𝐶 = 0 𝐹𝐴𝐵 𝑑𝑒𝑠𝑝𝑢é𝑠 𝑑𝑒𝑙 𝑐𝑜𝑛𝑡𝑎𝑐𝑡𝑜 𝑐𝑜𝑛 𝐶 Diagrama: + qA - qB 9 cm qC +qA -qB FAB 9 cm Conversión de Unidades: Solución: Los centímetros (cm) los Como la esfera C esta en estado neutro y toca a la transformamos a metros (m), esfera A, estas intercambian electrones, quedando multiplicando por 10-2 m. ambas con cargas de la misma magnitud y el mismo signo; posteriormente, después de cargada la esfera C se toca con B creando un intercambio de electrones nuevamente, quedando B y C con cargas iguales y del mismo signo. Para conocer el nuevo valor de las cargas A y B, sumamos algebraicamente, las cargas eléctricas: 𝑞𝐴 + 𝑞𝐶 = +6𝑥10−6 𝐶 + 0 𝐶 𝑞𝐴 + 𝑞𝐶 = +6𝑥10−6 𝐶, como quedan con cargas iguales después de la transferencia de electrones: 𝑞𝐴 = 𝑞𝐶 = +3𝑥10−6 𝐶 Ahora sumamos a la esferas C y B: 𝑞𝐶 + 𝑞𝐵 = +3𝑥10−6 𝐶 − 12𝑥10−6 𝐶 𝑞𝐶 + 𝑞𝐵 = −9𝑥10−6 𝐶 Lo cual nos dará una carga para ambas esferas de: 𝑞𝐶 = 𝑞𝐵 = −4,5𝑥10−6 𝐶 Ya conocidas las cargas de qA y qB, procedemos a calcular la fuerza con que se accionan las cargas después del contacto, aplicando la ecuación de la Ley de Coulomb. 𝐹𝐴𝐵 = 𝐾 𝑞𝐴 𝑥 𝑞𝐵 2 𝑟𝐴𝐵 Sustituimos: 𝐹𝐴𝐵 = 9𝑥109 𝑁𝑥𝑚2 𝐶2 𝑥 3𝑥10−6 𝐶 𝑥 4,5𝑥10−6 𝐶 (9𝑥10−2 𝑚)2 𝐹𝐴𝐵 = 15 𝑁 La fuerza es de atracción por ser las cargas de signos contrarios. 50.- Dos esferas iguales de masa 0,6 gr cada una, están suspendidas de un mismo punto por hilos de seda de 12 cm de longitud cada uno. Están cargadas con cargas eléctricas iguales y debido a esto; estas cargas, se repelen quedando en equilibrio, cuando la distancia de separación entre ellas es de 16 cm. Calcular el valor de las cargas. ( ( ( ( ) qA=qB= 9,6x10-9 C ) qA=qB= 9,6x10-8 C ) qA=qB= 96x10-11 C ) qA=qB= 9,6x10-6 C Datos: 𝑞𝐴 = 𝑞𝐵 𝑠𝑒 𝑑𝑒𝑠𝑐𝑜𝑛𝑜𝑐𝑒𝑛 𝑚 = 0,6 𝑔𝑟 = 10−3 𝐾𝑔 𝐿 = 12 𝑐𝑚 = 12𝑥10−2 𝑚 𝑟𝐴𝐵 = 16𝑐𝑚 = 16𝑥10−2 𝑚 Diagrama: O F C 12 cm q H A 16 cm FR P q E D F es la fuerza de repulsión y P es el peso. La resultante de la fuerza debe tener la misma dirección que el hilo. En la figura se observa que ΔAOH y el ΔEAD, son iguales, por tener sus lados paralelos. Conversión de Unidades: Transformamos los centímetros (cm) a metros (m), multiplicando por 102 m. Los gramos (gr) a kilogramos (Kg), multiplicando por 10-3. En este caso los Kg equivalen a Kilopondios (Kp) y ara transformar los Kp a Newton (N), multiplicamos por 9,8 N. 𝑃 = 0,6𝑥10−3 𝐾𝑝 𝑥 9,8 𝑁 𝑃 = 5,88𝑥10−3 𝑁 Solución: Procedemos a calcular en el triangulo ΔAOH, el lado OH, aplicando el Teorema de Pitágoras: 𝐶 2 = 𝑎2 + 𝑏 2 Donde: 𝑐 = 𝑂𝐴; 𝑎 = 𝐴𝐻 𝑦 𝑏 = 𝑂𝐻 , quedando: 𝑂𝐴2 = 𝐴𝐻2 + 𝑂𝐻2 ; desejamos OH y para eliminar el cuadrado introducimos dentro de una raiz cuadrada, el resto de los terminos. 𝑂𝐻 = √(𝑂𝐴)2 − (𝐴𝐻)2 Sustituimos: 𝑂𝐻 = √(12𝑥10−2 𝑚)2 − (8𝑥10−2 )2 𝑂𝐻 = 14,4 𝑐𝑚 Procedemos ahora a calcular la funcion tangente del angulo (tan 𝛼); para poder hallar el valor de la fuerza y posteriormente las cargas electricas. 𝐶𝑂 𝐴𝐻 8𝑥10−2 𝑚 = = 𝐶𝐴 𝑂𝐻 14,4𝑥10−2 𝑚 tan α = 0,55 Analizando las caracteristicas de los vectores, tenemos que: 𝐶𝑂 𝑃 tan 𝛼 = = 𝐶𝐴 𝐹 Despejando F, nos queda: 𝐹 = 𝑃 𝑥 tan 𝛼 = 5,88𝑥10−3 𝑁 𝑥 0,55 𝐹 = 3,26𝑥10−3 𝑁 Ahora procedemos a calcular el valor de las cargas, aplicando la ecuacion de la Ley de Coulomb: tan 𝛼 = 𝐹𝐴𝐵 = 𝐾 𝑞𝐴 𝑥 𝑞𝐵 2 𝑟𝐴𝐵 Como las “q” son iguales, decimos que: 𝑞𝐴 𝑥𝑞𝐵 = 𝑞 2 . Al despejar “q” y eliminar el cuadrado de ella, introducimos el resto de los términos dentro de una raíz cuadrada: 𝑞= √ 𝐹𝐴𝐵 𝑥 𝑟 2 𝐾 Sustituimos: 𝑞=√ 3,26𝑥10−3 𝑁 𝑥(16𝑥10−2 𝑚)2 9𝑥109 𝑁 𝑥𝐶 2𝑚 2 𝑞 = 9,6𝑥10−8 𝐶 𝑞𝐴 = 𝑞𝐵 = 𝑞 = 9,6𝑥10−8 𝐶 El campo eléctrico es una magnitud física que viene dada, como la región del espacio, donde se ejercen fuerzas eléctricas. 𝐹 𝐸= 𝑞0 Es una magnitud vectorial; es decir posee modulo, dirección y sentido; el uso de los signos de las cargas solo es para el análisis vectorial (análisis del campo eléctrico creado por cada carga eléctrica). Cuando hablamos de la intensidad del campo eléctrico en un punto, se habla de la magnitud escalar, en otras palabras modulo o magnitud del campo eléctrico. En este caso como es en un punto, debemos tomar en cuenta que este punto, por convenio a nivel mundial, siempre es positivo. Expresándose de la siguiente forma: +q0 .P E r E -q0 . r P 𝑞0 𝑟2 Recordemos como el punto es positivo por convenios internacionales, si la carga es positiva, existirá una repulsión entre ellos, causando un alejamiento del vector campo eléctrico y si la carga es negativa existirá una atracción, causando un acercamiento del vector campo eléctrico hacia la carga. 𝐸=𝐾 Campo Eléctrico e intensidad del campo eléctrico en un punto: Problemas primer Nivel o Nivel bajo: 1.- Una carga eléctrica de +4x10-6C, esta situada en un campo eléctrico. Si sobre ella actúa una fuerza de 3x10-3 N, calcular la intensidad del campo en el punto donde esta situada la carga. ( ) 𝐸 = 750 𝑁𝐶 ( ) 𝐸 = 750 𝑁 𝑁 ( ) 𝐸 = 7,5 𝐶 ( ) 𝐸 = 75 𝑁 𝐶 Datos: 𝑞 = +4𝑥10−6 𝐶 𝐹 = 3𝑥10−3 𝑁 𝐸 =? Diagrama: No es Necesario Conversión de Unidades: Solución: No es necesario, ya que Aplicamos la ecuación de la definición de campo eléctrico: 𝐹 todas las unidades están 𝐸= en un mismo sistema de 𝑞0 medidas. Sustituimos en la ecuación: 3𝑥10−3 𝑁 𝐸= 4𝑥10−6 𝐶 𝑁 𝐸 = 750 𝐶 2.- Una carga eléctrica de -3x10-6 C esta situada en un campo eléctrico. Si sobre ella actúa una fuerza de 6x10-3N, calcular la intensidad del campo eléctrico en el punto donde esta situada la carga: ( ) 𝐸 = 20 𝑁 𝐶 ( ) 𝐸 = 200 ( )𝐸 =2 𝑁 𝑁 𝐶 𝐶 ( ) 𝐸 = 2000 𝑁 𝐶 Datos: 𝑞 = −3𝑥10−6 𝐶 𝐹 = 6𝑥10−3 𝑁 𝐸 =? Diagrama: No es necesario Conversión de Unidades: Solución: No es necesario, ya que Aplicamos la ecuación de la definición de campo eléctrico: 𝐹 todas las unidades están 𝐸= en un mismo sistema de 𝑞0 medida. Sustituimos en la ecuación: 6𝑥10−3 𝑁 𝐸= 3𝑥10−6 𝐶 𝑁 𝐸 = 2000 𝐶 Recordemos que los signos de las cargas solo es ara el análisis vectorial; del resto, en la ecuación no se utiliza. 𝑁 3.- En un punto de un campo eléctrico hay una intensidad de campo eléctrico de 25 𝐶 . Si sobre la carga se ejerce una fuerza de 5𝑥10−4 𝑁. Calcular el valor de la carga eléctrica. ( ( ( ( )𝑞 )𝑞 )𝑞 )𝑞 = 2𝑥10−6 𝐶 = −5𝑥10−6 𝐶 = 5𝑥10−6 𝐶 = 2𝑥10−5 𝐶 Datos: 𝐸 = 25 𝑁 𝐶 Diagrama: No es necesario realizar diagrama. 𝐹 = 5𝑥10−4 𝑁 𝑞 =? Conversión de Unidades: Solución: No es necesario, realizar Aplicamos la ecuación de la definición de campo eléctrico: 𝐹 conversión alguna. 𝐸= 𝑞0 Despejamos 𝑞0 , quedando: 𝐹 𝑞0 = 𝐸 Sustituimos en la ecuación: 𝑞0 = 5𝑥10−4 𝑁 25𝑁 𝐶 𝑞0 = 2𝑥10−5 𝐶 4.- En un punto de un campo eléctrico hay una intensidad de campo eléctrico de 35𝑁 𝐶 . Si −6 en ese punto colocamos una carga de +7𝑥10 𝐶, calcular la fuerza que actúa sobre la carga. ( ( ( ( )𝐹 )𝐹 )𝐹 )𝐹 = 2,45𝑥10−4 𝑁 = 2,45𝑥104 𝑁 = 2,45𝑥10−5 𝑁 = 2,54𝑥10−4 𝑁 Datos: Diagrama: No es necesario realizar diagrama. 𝐸 = 35𝑁 𝐶 −6 𝑞 = +7𝑥10 𝐶 𝐹 =? Conversión de Unidades: Solución: No es necesario, realizar Aplicamos la ecuación de la definición de campo eléctrico: 𝐹 conversión alguna. 𝐸= 𝑞0 Despejamos F, quedando: 𝐹 = 𝑞0 𝑥𝐸 Sustituimos en la ecuación: −6 𝐹 = 35𝑁 𝐶 𝑥7𝑥10 𝐶 𝐹 = 2,45𝑥10−4 𝑁 5.- Se dispone de una carga eléctrica de +4𝑥10−6 𝐶. Calcular la fuerza que actúa sobre ella si esta situada en un campo eléctrico de modulo igual a 50𝑁 𝐶. ( ( ( ( )𝐹 )𝐹 )𝐹 )𝐹 = 20 𝑁 = 20𝑁 𝐶 = 2𝑥10−4 𝑁 = −2𝑥10−4 𝑁 Datos: 50𝑁 𝐶 −6 Diagrama: No es necesario realizar diagrama. 𝐸= 𝑞 = +4𝑥10 𝐶 𝐹 =? Conversión de Unidades: Solución: No es necesario, realizar Aplicamos la ecuación de la definición de campo eléctrico: 𝐹 conversión alguna. 𝐸= 𝑞0 Despejamos F, quedando: 𝐹 = 𝑞0 𝑥𝐸 Sustituimos en la ecuación: −6 𝐹 = 50𝑁 𝐶 𝑥4𝑥10 𝐶 𝐹 = 2𝑥10−4 𝑁 6.- Una carga eléctrica de +8 𝑥10−6 𝐶 esta situada en un campo eléctrico. Si sobre ella actúa una fuerza de +6𝑥102 𝑑𝑖𝑛𝑎𝑠 (𝑑𝑖𝑛), calcular la intensidad del campo eléctrico en el punto donde se encuentra la carga. ( ( ( ( )𝐸 )𝐸 )𝐸 )𝐸 = 750𝑁 𝐶 = 75𝑁 𝐶 = 7,5𝑁 𝐶 = 0,75𝑁 𝐶 Datos: Diagrama: 𝑞 = +8𝑥10−6 𝐶 No es necesaria la realización de diagrama. 2 −3 𝐹 = 6𝑥10 𝑑𝑖𝑛 = 6𝑥10 𝑁 𝐸 =? Conversión de Unidades: Solución: Transformamos la unidad Aplicamos la ecuación de la definición de campo eléctrico: 𝐹 de fuerza del sistema c.g.s., 𝐸= dina (din) a a la unidad del 𝑞0 sistema M.K.S., Newton Sustituimos en la ecuación: (N), multiplicando por 10-5 6𝑥10−3 𝑁 𝐸 = N. 8𝑥10−6 𝐶 5 1 𝑁 = 10 𝑑𝑖𝑛 𝐸 = 750𝑁 1 𝑑𝑖𝑛 = 10−5 𝑁 𝐶 𝐹= 6𝑥102 𝑑𝑖𝑛 𝑥 10−5 𝑁 1 𝑑𝑖𝑛 𝐹 = 6𝑥10−3 𝑁 7.- Sobre una carga de +6𝑥10−6 𝐶, situada en un campo eléctrico, actúa una fuerza de 5𝑥10−3 𝐾𝑝 (Kilopondios), calcular la intensidad del campo eléctrico en el punto donde esta ubicada la carga. ( ( ( ( )𝐸 )𝐸 )𝐸 )𝐸 = 816𝑁 𝐶 = 8,16𝑁 𝐶 = 81,6𝑁 𝐶 = 0,816𝑁 𝐶 Datos: −6 𝑞 = +6𝑥10 𝐶 𝐹 = 5𝑥10−3 𝐾𝑝 = 4,9𝑥10−2 𝑁 𝐸 =? Conversión de Unidades: Transformamos la unidad de fuerza del sistema técnico, Kilopondios (Kp), a la unidad del sistema M.K.S., Newton (N), multiplicando por 9,8 N. 1𝐾𝑝 = 9,8 𝑁 5𝑥10−3 𝐾𝑝 𝑥9,8 𝑁 𝐹= 1 𝐾𝑝 𝐹 = 4,9𝑥10−2 𝑁 Diagrama: No es necesaria la realización de diagrama. Solución: Aplicamos la ecuación de la definición de campo eléctrico: 𝐹 𝐸= 𝑞0 Sustituimos en la ecuación: 4,9𝑥10−2 𝑁 𝐸= 6𝑥10−6 𝐶 𝐸 = 8,16𝑁 𝐶 8.- Se dispone de una carga eléctrica de +4𝑥10−6 𝐶. ¿Qué fuerza se aplica sobre dicha carga, cuando ella se encuentra en un punto de un campo eléctrico cuya intensidad es igual a 3,6𝑥106 𝑁𝐶? ( ( ( ( ) 144 N ) 1,44 N ) 14 N ) 14,4 N Datos: Diagrama: 6𝑁 No es necesario realizar diagrama. 𝐸 = 3,6𝑥10 𝐶 𝑞 = +4𝑥10−6 𝐶 𝐹 =? Conversión de Unidades: Solución: No es necesario, realizar Aplicamos la ecuación de la definición de campo eléctrico: 𝐹 conversión alguna. 𝐸= 𝑞0 Despejamos F, quedando: 𝐹 = 𝑞0 𝑥𝐸 Sustituimos en la ecuación: 𝑁 𝐹 = 4𝑥10−6 𝐶 𝑥 3,6𝑥106 𝐶 𝐹 = 14,4𝑁 9.- Una carga eléctrica crea una intensidad de campo eléctrico de 4𝑁 𝐶 en un punto, cuando sobre ella actúa una fuerza de 60 N. ¿Cuál es el valor de dicha carga? ( ( ( ( )𝑞 )𝑞 )𝑞 )𝑞 = 6,66𝑥10−2 𝐶 = 66,6𝑥10−2 𝐶 = 666𝑥10−2 𝐶 = 0,66𝑥10−2 𝐶 Datos: Diagrama: 𝑁 No es necesario realizar diagrama. 𝐸=4 𝐶 𝐹 = 60𝑁 𝑞 =? Conversión de Unidades: Solución: No es necesario, realizar Aplicamos la ecuación de la definición de campo eléctrico: 𝐹 conversión alguna. 𝐸= 𝑞0 Despejamos 𝑞0 , quedando: 𝐹 𝑞0 = 𝐸 Sustituimos en la ecuación: 𝑞0 = 60𝑁 4𝑁 𝐶 𝑞0 = 6,66𝑥10−2 𝐶 10.- Una carga eléctrica de 5 nanocoulomb (nC), esta situada en un punto de un campo eléctrico. Si sobre ella actúa una fuerza de 4𝑥10−6 𝑁, ¿Cuál es la intensidad del campo eléctrico en ese punto, donde esta ubicada la carga? ( ( ( ( ) 800𝑁 𝐶 ) 800 N ) 80𝑁 𝐶 ) 0,8𝑁 𝐶 Datos: 𝑞 = +5𝑛𝐶 = +5𝑥10−9 𝐶 𝐹 = 4𝑥10−6 𝑁 𝐸 =? Diagrama: No es necesaria la realización de diagrama. Conversión de Unidades: Transformamos la unidad de carga eléctrica de nanocoulomb (nC) a coulomb (C) que es la unidad del sistema M.K.S., de la carga eléctrica, multiplicando por 10-9C. Solución: Aplicamos la ecuación de la definición de campo eléctrico: 𝐹 𝐸= 𝑞0 Sustituimos en la ecuación: 4𝑥10−6 𝑁 𝐸= 5𝑥10−9 𝐶 𝐸 = 800𝑁 𝐶 11.- Se dispone de una carga eléctrica de +4𝑥10−6 𝐶. Calcular el modulo de la intensidad de campo eléctrico a 1 cm de ella y hacer un diagrama que indique el sentido de la intensidad del campo +q P E 6𝑁 ( ) 𝐸 = 3,6𝑥10 𝐶 ; +q P E ( ) 𝐸 = 36𝑥106 𝑁𝐶 ; +q P E 6𝑁 ( ) 𝐸 = 3,6𝑥10 𝐶 ; +q P E 6𝑁 ( ) 𝐸 = 3,6𝑥10 𝐶 ; Datos: 𝑞 = +4𝑥10−6 𝐶 𝑟 = 10 𝑐𝑚 = 10𝑥10−2 𝑚 𝐸 =? 𝑒𝑛 𝑒𝑙 𝑝𝑢𝑛𝑡𝑜 𝑃 Conversión de Unidades: Se transforman los centímetros (cm) a metros (m), multiplicando por 10-2 m. Diagrama: +q P E 10 cm Como la carga eléctrica es positiva y el punto por convenio es positivo, hay una repulsión; entonces, el campo eléctrico se aleja de la carga. Solución: Aplicamos la ecuación de la intensidad del campo eléctrico en un punto, situado a una distancia “r” de la carga eléctrica. 𝑞 𝐸=𝐾𝑥 2 𝑟 Sustituimos en dicha ecuación: 2 4𝑥10−6 𝐶 9 𝑁 𝑥𝑚 𝐸 = 9𝑥10 𝐶 2 𝑥 (10𝑥10−2 𝑚)2 𝑁 𝐸 = 3,6𝑥106 𝐶 12.- Se dispone de una carga eléctrica de −5𝑥10−6 𝐶. A esta a 18 cm de la carga, calcular el modulo de la intensidad del campo eléctrico y realice un diagrama que indique el sentido de dicha intensidad. -q P E 6𝑁 ( ) 𝐸 = 1,39𝑥10 𝐶 ; -q E P ( ) 𝐸 = 1,38𝑥106 𝑁𝐶 ; -q E P −6 𝑁 ( ) 𝐸 = 13,8𝑥10 𝐶 ; -q P E −6 𝑁 ( ) 𝐸 = 1,38𝑥10 𝐶 ; Datos: 𝑞 = −5𝑥10−6 𝐶 𝑟 = 18 𝑐𝑚 = 18𝑥10−2 𝑚 𝐸 =? 𝑒𝑛 𝑒𝑙 𝑝𝑢𝑛𝑡𝑜 𝑃 Conversión de Unidades: Se transforman los centímetros (cm) a metros (m), multiplicando por 10-2 m. Diagrama: q E P 18 cm Como la carga eléctrica es negativa y el punto por convenio es positivo, hay una atracción; entonces, el campo eléctrico se acerca a la carga. Solución: Aplicamos la ecuación de la intensidad del campo eléctrico en un punto, situado a una distancia “r” de la carga eléctrica. 𝑞 𝐸=𝐾𝑥 2 𝑟 Sustituimos en dicha ecuación: 5𝑥10−6 𝐶 𝑁 𝑥𝑚2 𝐸 = 9𝑥109 𝐶 2 𝑥 (18𝑥10−2 𝑚)2 𝑁 𝐸 = 1,38𝑥106 𝐶 13.- Una carga eléctrica crea una intensidad de campo eléctrico igual a 4𝑁 𝐶 , en un punto situado a 9 cm de ella. Calcular el valor de la carga. ( ( ( ( )𝑞 )𝑞 )𝑞 )𝑞 = 3,6𝑥10−12 𝐶 = 36𝑥10−12 𝐶 = 360𝑥10−12 𝐶 = 0,36𝑥10−12 𝐶 Datos: 4𝑁 𝐶 𝐸= 𝑟 = 9𝑐𝑚 = 9𝑥10−2 𝑚 𝑞 =? Diagrama: No es necesario realizarlo Conversión de Unidades: Solución: Se transforman los Aplicamos la ecuación de la intensidad del campo eléctrico en centímetros (cm) a un punto, situado a una distancia “r” de la carga eléctrica. 𝑞 metros (m), 𝐸 = 𝐾 𝑥 𝑟2 multiplicando por 10-2 Despejamos “q” m. 𝐸 𝑥 𝑟2 𝑞= 𝐾 Sustituimos: 𝑞= −2 2 4𝑁 𝐶 𝑥 (9𝑥10 ) 9𝑥109 𝑁 𝑥𝐶 2𝑚 2 𝑞 = 3,6𝑥10−12 𝐶 14.- Se dispone de una carga eléctrica +6𝑥10−6 𝐶. Calcular el modulo de la intensidad de campo eléctrico a 8 cm de ella y hacer un diagrama que indique el sentido de la intensidad del campo. +q ( ) 𝐸 = 8,44𝑥10−6 𝑁𝐶 ; +q 6𝑁 ( ) 𝐸 = 8,44𝑥10 𝐶 ; +q 𝑁 ( ) 𝐸 = 8,44 𝐶 ; +q ( ) 𝐸 = 8,44𝑥106 𝑁𝐶; Datos: 𝑞 = +6𝑥10−6 𝐶 𝑟 = 8𝑐𝑚 = 8𝑥10−2 𝑚 𝐸 =? 𝑒𝑛 𝑒𝑙 𝑝𝑢𝑛𝑡𝑜 𝑃 P E P E P E E P Diagrama: +q P E 10 cm Como la carga eléctrica es positiva y el punto por convenio es positivo, hay una repulsión; entonces, el campo eléctrico se aleja de la carga. Conversión de Unidades: Solución: Se transforman los Aplicamos la ecuación de la intensidad del campo eléctrico centímetros (cm) a metros en un punto, situado a una distancia “r” de la carga (m), multiplicando por 10-2 eléctrica. 𝑞 m. 𝐸=𝐾𝑥 2 𝑟 Sustituimos en dicha ecuación: 6𝑥10−6 𝐶 𝑁 𝑥𝑚2 𝐸 = 9𝑥109 𝐶 2 𝑥 (8𝑥10−2 𝑚)2 𝑁 𝐸 = 8,44𝑥106 𝐶 15.- Una carga eléctrica de +25𝑥10−6 𝐶, crea un campo eléctrico. Si en un punto de ese campo eléctrico la intensidad es de 16𝑥105 𝑁𝐶. Calcular la distancia del punto a la carga. ( ( ( ( ) 𝑟 = 3,75𝑥104 𝑚 ) 𝑟 = 3,75𝑥10−4 𝑚 ) 𝑟 = 3,75𝑥104 𝑐𝑚 ) 𝑟 = 3,75𝑥10−4 𝑐𝑚 Datos: 𝑞 = +25𝑥10−6 𝐶 𝑁 𝐸 = 16𝑥10−5 𝐶 𝑟 =? Diagrama: No es necesario realizar diagrama; ya que se va a calcular es la distancia de separación de la carga y el punto. Conversión de Unidades: No es necesaria. Solución: Aplicamos la ecuación de la intensidad del campo eléctrico en un punto, situado a una distancia “r” de la carga eléctrica. 𝑞 𝐸=𝐾𝑥 2 𝑟 Despejamos la distancia “r” y como esta elevada al cuadrado, para eliminar este. Introducimos dentro de una raíz cuadrada el resto de los términos. 𝑞 𝑟 = √𝑘 𝑥 𝐸 Sustituimos en la ecuación: 𝑟 = √9𝑥109 𝑁 𝑥 𝑚2 𝐶2 𝑥 25𝑥10−6 𝐶 16𝑥10−5 𝑁𝐶 𝑟 = 3,75𝑥104 𝑚 16.- Dos cargas eléctricas 𝑞1 = +4𝑥10−6 𝐶 y 𝑞2 = +3𝑥10−6 𝐶, están en el vacio separadas por una distancia de 12 cm. Calcular el campo eléctrico resultante en un punto P, situado a 5 cm de q1. ( ( ( ( )𝐸 )𝐸 )𝐸 )𝐸 = 8,89 𝑥106 𝑁𝐶 = 8𝑥106 𝑁𝐶 = −8,89𝑥10−6 𝑁𝐶 = 8,89𝑥103 𝑁 Datos: 𝑞1 = +4𝑥10−6 𝐶 𝑞2 = +3𝑥10−6 𝐶 𝑟12 12 𝑐𝑚 = 12𝑥10−2 𝑚 𝐸𝑅 =? 𝑒𝑛 𝑃 𝑟1𝑝 = 5𝑐𝑚 = 5𝑥10−2 𝑚 𝑟2𝑝 = 7𝑐𝑚 = 7𝑥10−2 𝑚 Diagrama: Conversión de Unidades: Se transforman los centímetros (cm) a metros (m), multiplicando por 10-2 m. Solución: Como los vectores a sumar tienen igual dirección pero sentidos contrarios, sumamos algebraicamente los campos creados por cada carga: 𝐸𝑅 = 𝐸1𝑝 − 𝐸2𝑝 Calculamos los campos E1p y E2p, aplicando la ecuación de la intensidad del campo eléctrico en un punto. 𝑞 𝑞 𝐸1𝑝 = 𝐾𝑥 𝑟 21 y 𝐸2𝑝 = 𝐾𝑥 𝑟 22 +q1 E2p P E1p +q2 12 cm 5 cm 7 cm Como las cargas eléctricas so positivas y por convenios internacionales el punto, también es positivo; entonces existe una repulsión entre el unto y las cargas, alejándose los campos eléctricos de las cargas 1𝑝 2𝑝 Sustituimos en las ecuaciones: 𝐸1𝑝 = 𝐸1𝑝 𝐸2𝑝 = 9𝑥109 4𝑥10−6 𝐶 𝑥 (5𝑥10−2 𝑚)2 𝑁 = 1,44𝑥107 𝐶 𝑁𝑥𝑚 9𝑥109 𝐶 2 𝑁 𝑥 𝑚2 𝐶2 𝑥 2 3𝑥10−6 𝐶 (7𝑥10−2 𝑚)2 𝐸2𝑝 = 5,51𝑥106 𝑁𝐶 𝑁 𝑁 𝐸𝑅 = 1,44𝑥107 𝐶 − 5,51𝑥106 𝐶 𝑁 𝐸𝑅 = 8,89𝑥106 𝐶 17.- Dos cargas eléctricas 𝑞1 = −5𝑥10−6 𝐶 y 𝑞2 = +3𝑥10−6 𝐶, están en el vacio separadas por una distancia de 15 cm. Calcular la intensidad del campo eléctrico resultante en un punto A, situado a 6 cm de q1. ( ( ( ( ) 1,58x106 𝑁𝐶 ) 1,58𝑥107 𝑁𝐶 ) 1,58𝑥105 𝑁𝐶 ) 1,58𝑥10−7 𝑁𝐶 Datos: 𝑞1 = −5𝑥10−6 𝐶 𝑞2 = +3𝑥10−6 𝐶 𝑟12 = 15 𝑐𝑚 = 15𝑥10−2 𝑚 𝐸𝑅 =? 𝑒𝑛 𝐴 𝑟1𝐴 = 6𝑐𝑚 = 6𝑥10−2 𝑚 𝑟2𝑝 = 9𝑐𝑚 = 9𝑥10−2 𝑚 Diagrama: Conversión de Unidades: Se transforman los centímetros (cm) a metros (m), multiplicando por 10-2 m. Solución: Como los vectores a sumar tienen igual dirección e igual sentido , sumamos algebraicamente los campos creados por cada carga: 𝐸𝑅 = 𝐸1𝐴 + 𝐸2𝐴 Calculamos los campos E1p y E2p, aplicando la ecuación de la intensidad del campo eléctrico en un punto. 𝑞 𝑞 𝐸1𝐴 = 𝐾𝑥 𝑟 21 y 𝐸2𝐴 = 𝐾𝑥 𝑟 22 +q1 E1A E2A A +q2 15 cm 6 cm 9 cm Como las cargas eléctricas son de diferentes signos y por convenios internacionales, el punto es positivo; entonces existe una repulsión entre la carga q2 el punto, alejándose el campo eléctrico de la carga y como la carga q1 es negativa existe una atracción entre ellos, acercándose el campo eléctrico a la carga. 1𝐴 2𝐴 Sustituimos en las ecuaciones: 5𝑥10−6 𝐶 (6𝑥10−2 𝑚)2 𝑁 = 1,25𝑥107 𝐶 𝐸1𝐴 = 9𝑥109 𝐸1𝑝 2 𝐸2𝐴 = 9𝑥109 𝑁 𝑥𝐶2𝑚 𝑥 𝑁 𝑥 𝑚2 𝐶2 𝑥 3𝑥10−6 𝐶 (9𝑥10−2 𝑚)2 𝐸2𝑝 = 3,33𝑥106 𝑁𝐶 𝑁 𝑁 𝐸𝑅 = 1,25𝑥107 𝐶 + 3,33𝑥106 𝐶 𝑁 𝐸𝑅 = 1,58𝑥107 𝐶 18.- Dos cargas eléctricas 𝑞1 = +4𝑥10−6 𝐶 y 𝑞2 = +8𝑥10−6 𝐶, están en el vacio separadas por una distancia de 8 cm. Calcular la intensidad del campo eléctrico en el punto medio de la recta que las une. ( ) 2,25𝑥106 𝑁𝐶 ( ) 2,25𝑥107 𝑁𝐶 ( ) 2,25𝑥10−6 𝑁𝐶 𝑁 ( ) 2,25𝑥10−7 𝐶 Datos: 𝑞1 = +4𝑥10−6 𝐶 𝑞2 = +8𝑥10−6 𝐶 𝑟12 = 8 𝑐𝑚 = 12𝑥10−2 𝑚 𝐸𝑅 =? 𝑒𝑛 𝑒𝑙 𝑝𝑢𝑛𝑡𝑜 𝑚𝑒𝑑𝑖𝑜 𝑟1𝑝 = 4𝑐𝑚 = 4𝑥10−2 𝑚 𝑟2𝑝 = 4𝑐𝑚 = 𝑥10−2 𝑚 Diagrama: Conversión de Unidades: Se transforman los centímetros (cm) a metros (m), multiplicando por 10-2 m. Solución: Como los vectores a sumar tienen igual dirección pero sentidos contrarios, sumamos algebraicamente los campos creados por cada carga: 𝐸𝑅 = 𝐸2𝑝 − 𝐸1𝑝 Calculamos los campos E1p y E2p, aplicando la ecuación de la intensidad del campo eléctrico en un punto. 𝑞 𝑞 𝐸1𝑝 = 𝐾𝑥 𝑟 21 y 𝐸2𝑝 = 𝐾𝑥 𝑟 22 +q1 E2p P E1p +q2 8 cm 4 cm 4 cm Como las cargas eléctricas son positivas y por convenios internacionales el punto, también es positivo; entonces existe una repulsión entre el unto y las cargas, alejándose los campos eléctricos de las cargas 1𝑝 2𝑝 Sustituimos en las ecuaciones: 4𝑥10−6 𝐶 (4𝑥10−2 𝑚)2 𝑁 = 2,25𝑥107 𝐶 𝐸1𝑝 = 9𝑥109 𝐸1𝑝 2 𝐸2𝑝 = 9𝑥109 𝑁 𝑥𝐶2𝑚 𝑥 𝑁 𝑥 𝑚2 𝐶2 𝑥 8𝑥10−6 𝐶 (4𝑥10−2 𝑚)2 𝐸2𝑝 = 4,5𝑥107 𝑁𝐶 𝑁 𝑁 𝐸𝑅 = 4,5𝑥107 𝐶 − 2,25𝑥107 𝐶 𝑁 𝐸𝑅 = 2,25𝑥107 𝐶 19.- Dos cargas eléctricas 𝑞1 = +5𝑥10−6 𝐶 y 𝑞2 = −9𝑥10−6 𝐶, están en el vacio separadas por una distancia de 10 m. Calcular la intensidad del campo eléctrico resultante, sobre el unto medio de la recta que las une. ( ( ( ( ) 5400𝑁 𝐶 ) 540𝑁 𝐶 ) 5040𝑁 𝐶 ) 540𝑁 𝐶 Datos: 𝑞1 = +5𝑥10−6 𝐶 𝑞2 = −9𝑥10−6 𝐶 𝑟12 = 10 𝑚 𝐸𝑅 =? 𝑒𝑛 𝐴 𝑟1𝐴 = 5 𝑚 𝑟2𝑝 = 5 𝑚 Diagrama: +q1 P E1A E2A -q2 10 m 5m 5m Como las cargas eléctricas son de diferentes signos y por convenios internacionales, el punto es positivo; entonces existe una repulsión entre la carga q1 el punto, alejándose el campo eléctrico de la carga y como la carga q2 es negativa existe una atracción entre ellos, acercándose el campo eléctrico a la carga. Conversión de Unidades: Solución: No es necesario, por estar la Como los vectores a sumar tienen igual dirección e igual distancia en metros (m) sentido , sumamos algebraicamente los campos creados por cada carga: 𝐸𝑅 = 𝐸1𝑝 + 𝐸2𝑝 Calculamos los campos E1p y E2p, aplicando la ecuación de la intensidad del campo eléctrico en un punto. 𝑞 𝑞 𝐸1𝑝 = 𝐾𝑥 𝑟 21 y 𝐸2𝑝 = 𝐾𝑥 𝑟 22 1𝑝 2𝑝 Sustituimos en las ecuaciones: 𝐸1𝐴 = 9𝑥109 𝑁 𝑥 𝑚2 𝐶2 5𝑥10−6 𝐶 (5𝑚)2 𝑥 𝑁 𝐸1𝑝 = 1800 𝐶 2 𝐸2𝐴 = 9𝑥109 𝑁 𝑥𝐶2𝑚 𝑥 9𝑥10−6 𝐶 (5 𝑚)2 𝐸2𝑝 = 3240𝑁𝐶 𝑁 𝑁 𝐸𝑅 = 1800 𝐶 + 3240 𝐶 𝑁 𝐸𝑅 = 5040 𝐶 20.- Se dispone de tres cargas eléctricas 𝑞1 = −3𝑥10−6 𝐶; 𝑞2 = +4𝑥10−6 𝐶 y 𝑞3 = +5𝑥10−6 𝐶., separadas por las distancias que se indican en la figura. Calcular la intensidad del campo eléctrico resultante sobre el punto P, ubicado a 3 cm de q3. -q1 +q2 2 cm ( ( ( ( +q3 P 4 cm 3 cm +q3 E1p A E2p ) 5,4𝑥106 𝑁𝐶 ) 5,4𝑥105 𝑁𝐶 )5,4𝑥10−7 𝑁𝐶 ) 5,4𝑥107 𝑁𝐶 Datos: 𝑞1 = −3𝑥10−6 𝐶 𝑞2 = +3𝑥10−6 𝐶 𝑞3 = +5𝑥10−6 𝐶 𝑟1𝑝 = 9𝑐𝑚 = 9𝑥10−2 𝑚 𝑟2𝑝 = 7𝑐𝑚 = 7𝑥10−2 𝑚 𝑟3𝑝 = 3𝑐𝑚 = 3𝑥10−2 𝑚 𝐸𝑅 =? 𝑠𝑜𝑏𝑟𝑒 𝑃 Diagrama: Conversión de Unidades: Los centímetros (cm) de las distancias, se transforman a metros (m), multiplicando por 10-2 m. Solución: Se puede observar en la figura que los vectores E2p y E3p, tienen igual dirección y sentido; pero, el vector E1p, tiene sentido contrario, al aplicar la suma de vectores, nos queda que: 𝐸𝑅 = 𝐸2𝑝 + 𝐸3𝑝 − 𝐸1𝑝 Para hallar los campos eléctricos creados por cada carga, aplicamos la ecuación de la intensidad del campo eléctrico en un punto. 𝑞1 𝐸1𝑝 = 𝐾𝑥 2 𝑟1𝑝 -q1 +q2 2 cm 4 cm E3p 3 cm Se puede observar en el análisis vectorial, que la carga q1 es negativa y el punto por convenios internacionales siempre será positivo, motivo por el cual el campo eléctrico creado por esa carga se acerca a ella, contrario a lo que sucede con q2 y q3; ya que ellas son positivas, entonces el campo eléctrico creado por ellas se aleja de las cargas. 𝐸2𝑝 = 𝐾 𝑥 𝑞2 2 𝑟2𝑝 𝑞3 2 𝑟3𝑝 Sustituimos en cada ecuación por sus valores: 𝐸3𝑝 = 𝐾 𝑥 𝑁 𝑥 𝑚2 3𝑥10−6 𝐶 𝑥 𝐶2 (9𝑥10−2 𝑚)2 𝑁 𝐸1𝑝 = 3,33𝑥106 𝐶 𝑁 𝑥 𝑚2 4𝑥10−6 𝐶 𝐸2𝑝 = 9𝑥109 𝐶 2 𝑥 (7𝑥10−2 𝑚)2 𝑁 𝐸2𝑝 = 7,35𝑥106 𝐶 𝑁 𝑥 𝑚2 5𝑥10−6 𝐶 𝐸3𝑝 = 9𝑥109 𝐶 2 𝑥 (3𝑥10−2 𝑚)2 𝐸1𝑝 = 9𝑥109 𝑁 𝐸3𝑝 = 5𝑥107 𝐶 𝑁 𝑁 𝑁 𝐸𝑅 = 7,35𝑥106 𝐶 + 5𝑥107 𝐶 − 3,33𝑥106 𝐶 𝑁 𝐸𝑅 = 5,4𝑥107 𝐶 21.- Se dispone de tres cargas eléctricas: 𝑞1 = −6𝑥10−6 𝐶 𝑞2 = −4𝑥10−6 𝐶 y 𝑞3 = −8𝑥10−6 𝐶, separadas por las distancias que se muestran en la figura. Calcular la magnitud de la intensidad del campo eléctrico en el punto A. indique el sentido del campo resultante. –q1 -q2 -q3 A 5 cm ( ( ( ( 2 cm 2 cm 8𝑁 ) 2,031𝑥10 𝐶 ; Hacia la izquierda ) 2,031𝑥107 𝑁𝐶; Hacia la izquierda ) 2,031𝑥108 𝑁𝐶; Hacia la derecha ) 2,031𝑥107 𝑁𝐶; Hacia la derecha Datos: 𝑞1 = −6𝑥10−6 𝐶 𝑞2 = −4𝑥10−6 𝐶 𝑞3 = −8𝑥10−6 𝐶 𝑟1𝑝 = 9𝑐𝑚 = 9𝑥10−2 𝑚 𝑟2𝑝 = 4𝑐𝑚 = 4𝑥10−2 𝑚 𝑟3𝑝 = 2𝑐𝑚 = 2𝑥10−2 𝑚 𝐸𝑅 =? 𝑠𝑜𝑏𝑟𝑒 𝐴 Diagrama: -q1 -q2 -q3 E3 E2 E1 A 5 cm 2 cm 2 cm Se puede observar en el análisis vectorial, que la carga q1, q2 y q3 son negativas y el punto por convenios internacionales siempre será positivo, motivo por el cual el campo eléctrico creado por esa carga se acerca a ellas, entonces el campo eléctrico creado por ellas se acerca a cada carga. Conversión de Unidades: Solución: Los centímetros (cm) de Se puede observar en la figura que los vectores a sumar las distancias, se tienen igual dirección y sentido, al aplicar la suma de transforman a metros (m), vectores, nos queda que: 𝐸𝑅 = 𝐸1𝐴 + 𝐸2𝐴 + 𝐸3𝐴 multiplicando por 10-2 m. Para hallar los campos eléctricos creados por cada carga, aplicamos la ecuación de la intensidad del campo eléctrico en un punto. 𝑞1 𝐸1𝐴 = 𝐾𝑥 2 𝑟1𝐴 𝐸2𝐴 = 𝐾 𝑥 𝑞2 2 𝑟2𝐴 𝐸3𝐴 = 𝐾 𝑥 𝑞3 2 𝑟3𝐴 Sustituimos en cada ecuación por sus valores: 𝑁 𝑥 𝑚2 6𝑥10−6 𝐶 𝑥 2 𝐶 (9𝑥10−2 𝑚)2 𝑁 𝐸1𝑝 = 6𝑥105 𝐶 𝑁 𝑥 𝑚2 4𝑥10−6 𝐶 𝐸2𝐴 = 9𝑥109 𝐶 2 𝑥 (4𝑥10−2 𝑚)2 𝑁 𝐸2𝑝 = 2,25𝑥107 𝐶 𝑁 𝑥 𝑚2 8𝑥10−6 𝐶 𝐸3𝐴 = 9𝑥109 𝐶 2 𝑥 (2𝑥10−2 𝑚)2 𝑁 𝐸3𝑝 = 1,8𝑥108 𝐶 𝑁 𝑁 𝑁 𝐸𝑅 = 6𝑥105 𝐶 + 2,25𝑥107 𝐶 + 1,8𝑥108 𝐶 𝐸1𝐴 = 9𝑥109 𝑁 𝐸𝑅 = 2,031𝑥108 𝐶 El vector ER, esta dirigido hacia la izquierda. 22.- Se dispone de tres cargas eléctricas 𝑞1 = +2𝑥10−6 𝐶; 𝑞2 = +4𝑥10−6 𝐶 y 𝑞3 = +6𝑥10−6 𝐶; separadas por las distancias indicadas en la figura. Calcular la intensidad del campo eléctrico resultante en el punto P e indique su sentido. +q1 +q2 3 cm ( ( ( ( +q3 2 cm P 3 cm ) 7,72𝑥107 𝑁𝐶 ) 7,72𝑥10−7 𝑁𝐶 )7,72𝑥108 𝑁𝐶 ) 7,72𝑥10−8 𝑁𝐶 Datos: 𝑞1 = −3𝑥10−6 𝐶 𝑞2 = +3𝑥10−6 𝐶 𝑞3 = +5𝑥10−6 𝐶 𝑟1𝑝 = 9𝑐𝑚 = 9𝑥10−2 𝑚 𝑟2𝑝 = 7𝑐𝑚 = 7𝑥10−2 𝑚 𝑟3𝑝 = 3𝑐𝑚 = 3𝑥10−2 𝑚 𝐸𝑅 =? 𝑠𝑜𝑏𝑟𝑒 𝑃 Diagrama: +q1 +q2 +q3 P E1 E2 E3 4 cm 2 cm 3 cm Se puede observar en el análisis vectorial, que la carga q1; q2 y q3 son positivas y el punto por convenios internacionales siempre será positivo, motivo por el cual el campo eléctrico creado por las cargas se aleja de ellas. Conversión de Unidades: Solución: Los centímetros (cm) de Se puede observar en la figura que los vectores a sumar las distancias, se tienen la misma dirección y sentido, al aplicar la suma de transforman a metros (m), vectores, nos queda que: 𝐸𝑅 = 𝐸1𝑝 + 𝐸2𝑝 + 𝐸3𝑝 multiplicando por 10-2 m. Para hallar los campos eléctricos creados por cada carga, aplicamos la ecuación de la intensidad del campo eléctrico en un punto. 𝑞1 𝐸1𝑝 = 𝐾𝑥 2 𝑟1𝑝 𝐸2𝑝 = 𝐾 𝑥 𝑞2 2 𝑟2𝑝 𝐸3𝑝 = 𝐾 𝑥 𝑞3 2 𝑟3𝑝 Sustituimos en cada ecuación por sus valores: 𝑁 𝑥 𝑚2 2𝑥10−6 𝐶 𝑥 𝐶2 (8𝑥10−2 𝑚)2 𝑁 𝐸1𝑝 = 2,81𝑥106 𝐶 𝑁 𝑥 𝑚2 4𝑥10−6 𝐶 𝐸2𝑝 = 9𝑥109 𝐶 2 𝑥 (5𝑥10−2 𝑚)2 𝑁 𝐸2𝑝 = 1,44𝑥107 𝐶 𝑁 𝑥 𝑚2 6𝑥10−6 𝐶 𝐸3𝑝 = 9𝑥109 𝐶 2 𝑥 (3𝑥10−2 𝑚)2 𝐸1𝑝 = 9𝑥109 𝑁 𝐸3𝑝 = 6𝑥107 𝐶 𝑁 𝑁 𝑁 𝐸𝑅 = 2,81𝑥106 𝐶 + 1,44𝑥107 𝐶 + 6𝑥107 𝐶 𝑁 𝐸𝑅 = 7,72𝑥107 𝐶 23.- Se dispone de dos cargas eléctricas 𝑞1 = +4𝑥10−6 𝐶 y𝑞2 = +9𝑥106 𝐶 están en el vacio separadas por una distancia de 10 m. Calcular en que punto de la recta que las une el campo eléctrico es nulo. ( ( ( ( ) El campo es nulo a 4 m de q1 ) El campo es nulo a 4 cm de q1 ) El campo es nulo a 4 m de q2 ) El campo es nulo a 4 m de q2 Datos: 𝑞1 = +4𝑥10−6 𝐶 𝑞2 = +9𝑥10−6 𝐶 𝑟12 = 10 𝑚 𝑋 =? 𝐸=0 Conversión de Unidades: No es necesario hacer transformación de unidades; ya que, todas las unidades de medidas están en un mismo sistema de medida. Diagrama: +q1 E2 X +q2 E1 (10-X) P 10 m Llamamos “X” a la distancia entre q1 y el punto “P” y (10-X) a la distancia entre q2 y el punto “P”. Solución: Para que el campo eléctrico sea nulo, es necesario que los campos creados por cada carga eléctrica, sean de la misma dirección pero de sentidos contrarios. Para cumplirse esta condición, el punto debe estar ubicado entre las cargas eléctricas; ya que, el punto por convenios internacionales siempre es positivo, creando una repulsión entre ellos y de esta forma los campos se alejan de las cargas. La otra condición es que deben ser iguales en magnitud, para eso igualamos los campos: 𝐸1= 𝐸2 Sustituimos por la ecuación de la intensidad de campo eléctrico: 𝑞1 𝑞2 𝐾𝑥 2 = 𝐾 𝑥 2 𝑟1𝑝 𝑟2𝑝 Simplificamos “K”, quedando: 𝑞1 𝑞2 2 = 2 𝑟1𝑝 𝑟2𝑝 Agrupamos términos semejantes: 2 𝑟2𝑝 𝑞2 = 2 𝑞1 𝑟1𝑝 Eliminamos cuadrados introduciendo dentro de una raíz cuadrada al resto de los términos: 𝑟2𝑝 𝑞2 =√ 𝑟1𝑝 𝑞1 Sustituimos por sus valores: (10 − 𝑋) 9𝑥10−6 𝐶 =√ 𝑋 4𝑥10−6 𝐶 10 − 𝑋 = 1,5 𝑋 Colocamos la ecuación de forma lineal: 10 − 𝑋 = 1,5 𝑋 Agrupamos nuevamente, términos semejantes: 10 = 1,5 𝑋 + 𝑋 10 = 2,5 𝑋 Despejamos “X”: 10 2,5 𝑋 =4𝑚 El campo eléctrico es nulo a 4 m de q1 y a 6 m de q2. 𝑋= 24.- Dos cargas eléctricas 𝑞1 = −25𝑥10−6 𝐶 y 𝑞1 = +16𝑥10−6 𝐶 están en el vacio separadas por una distancia de 18 cm. Calcular en que punto de la recta que las une el campo eléctrico, es nulo. ( ( ( ( ) El campo es nulo a 72 cm de q1 ) El campo es nulo a 72 m de q2 ) El campo es nulo a 72 m de q1 ) El campo es nulo a 72 cm de q2 Datos: 𝑞1 = −25𝑥10−6 𝐶 𝑞2 = +16𝑥10−6 𝐶 𝑟12 = 18𝑐𝑚 = 18𝑥10−2 𝑚 𝑋 =? 𝐸=0 Diagrama: -q1 +q2 P E1 18 cm X E2 La distancia entre q1 y q2, es de 18 cm y como desconocemos la distancia entre q2 y el punto P, la llamamos “X” Conversión de Unidades: Solución: Se transforman los Para que el campo eléctrico sea nulo, es necesario que centímetros (cm) a metros los campos creados por cada carga eléctrica, sean de la (m), multiplicando por 10-2 misma dirección pero de sentidos contrarios. Para m. cumplirse esta condición, el punto debe estar ubicado fuera de la línea que une las cargas eléctricas; ya que, el punto por convenios internacionales siempre es positivo, creando una repulsión con la carga q2 y una atracción con q1 de esta forma el campo E2 se aleja de la carga y el campo E1 se acerca a la carga. La otra condición es que deben ser iguales en magnitud, para eso igualamos los campos: 𝐸1 = 𝐸2 Sustituimos por la ecuación de la intensidad de campo eléctrico: 𝑞1 𝑞2 𝐾𝑥 2 = 𝐾 𝑥 2 𝑟1𝑝 𝑟2𝑝 Simplificamos “K”, quedando: 𝑞1 𝑞2 2 = 2 𝑟1𝑝 𝑟2𝑝 Agrupamos términos semejantes: 2 𝑟2𝑝 𝑞2 2 = 𝑞 𝑟1𝑝 1 Eliminamos cuadrados introduciendo dentro de una raíz cuadrada al resto de los términos: 𝑟2𝑝 𝑞2 =√ 𝑟1𝑝 𝑞1 Sustituimos por sus valores: 𝑋 16𝑥10−6 𝐶 =√ (18 + 𝑋) 25𝑥10−6 𝐶 𝑋 = 0,8 18 + 𝑋 Colocamos la ecuación de forma lineal: 𝑋 = 0,8(18 + 𝑋) Agrupamos nuevamente, términos semejantes: 𝑋 = 14,4 + 0,8𝑋 𝑥 − 0,8𝑋 = 14,4 Despejamos “X”: 0,2𝑋 = 14,4 14,4 𝑋= 0,2 𝑋 = 72 𝑐𝑚 El campo es nulo a 72 cm de q2. 25.-Se dispone de dos láminas metálicas paralelas con un área de 0,8 m2 cada una. La carga eléctrica que tiene cada lamina es de 5𝑥10−6 𝐶. Calcular el modulo del campo eléctrico que hay entre ellas. ( ( ( ( ) 7,02𝑥104 𝑁𝐶 ) 7,02𝑥10−4 𝑁𝐶 ) 7,02𝑥103 𝑁𝐶 ) 7,02𝑥105 𝑁𝐶 Datos: 2 𝑆 = 0,8 𝑚 𝑞 = 5𝑥10−6 𝐶 𝐶2 𝜀0 = 8,9𝑥10−12 𝑁 𝑥 𝑚2 𝐸 =? Conversión de Unidades: No es necesario. Diagrama: +q + + + + + -q - Cuando las láminas metálicas paralelas, están muy próximas, entre ellas se forma un campo eléctrico uniforme. Solución: Para hallar el valor de E, hacemos uso de la ecuación de campo eléctrico entre laminas paralelas: 𝑞 𝐸= 𝜀0 𝑥 𝑆 Siendo “S” el área y “𝛆0”, la constante sustituimos en la ecuación: 5𝑥10−6 𝐶 𝐸= 2 8,9𝑥10−12 𝑁 𝑥𝐶 𝑚2 𝑥 0,8 𝑚2 𝑁 𝐸 = 7,02𝑥105 𝐶 26.- El campo eléctrico en el interior de dos laminas metálicas paralelas es de 8𝑥106 𝑁𝐶. Si el área de cada lámina es de 04 m2, calcular la carga eléctrica que hay en cada lámina. ( ( ( ( ) 2,8𝑥10−6 𝐶 ) 48𝑥10−6 𝐶 ) 2,8𝑥10−5 𝐶 ) 28,48𝑥10−6 𝐶 Datos: 𝑆 = 0,4 𝑚2 𝑞 =? 𝐶2 𝜀0 = 8,9𝑥10−12 𝑁 𝑥 𝑚2 𝑁 𝐸 = 8𝑥106 𝐶 Conversión de Unidades: No es necesario. Diagrama: +q + + + + + -q - Cuando las láminas metálicas paralelas, están muy próximas, entre ellas se forma un campo eléctrico uniforme. Solución: Para hallar el valor de q, hacemos uso de la ecuación de campo eléctrico entre laminas paralelas y despejamos q : 𝑞 𝐸= 𝜀0 𝑥 𝑆 𝑞 = 𝐸𝑥𝑆𝑥𝜀0 Siendo “S” el área y “𝛆0”, la constante sustituimos en la ecuación: 2 𝑁 𝑞 = 8𝑥106 𝐶 𝑥 0,4 𝑚2 𝑥8,9𝑥10−12 𝑁 𝑥𝐶 𝑚2 𝑞 = 28,48𝑥10−6 𝐶 Como son láminas metálicas paralelas mantienen una carga eléctrica constante. 27.- Una carga eléctricas puntual de 8𝑥10−6 𝐶 tiene una masa de 0,2 gr y esta situada en un campo eléctrico uniforme de 16𝑥106 𝑁𝐶. Calcular con que aceleración se deslaza en dicho campo. ( ( ( ( ) 6,4𝑥103 𝑠𝑚2 ) 6,4𝑥105 𝑠𝑚2 ) 6,4𝑥106 𝑠𝑚2 ) 6𝑥105 𝑠𝑚2 Datos: Diagrama: −6 𝑞 = 8𝑥10 𝐶 No es necesario realizar diagrama. 𝑚 = 0,2 𝑔𝑟 = 2𝑥10−4 𝐾𝑔 𝑁 𝐸 = 16𝑥106 𝐶 𝑎 =? 𝐶2 𝜀0 = 8,9𝑥10−12 𝑁 𝑥 𝑚2 Conversión de Unidades: Transformamos los gramos (gr) a kilogramos (Kg), multiplicando por 10-3 Kg o dividiendo entre 1000 gr. Solución: Por las características del enunciado del problema, podemos inferir, que es una combinación de campo eléctrico con movimiento. Si aplicamos la 2da Ley de Newton, tenemos que: 𝐹 = 𝑚 𝑥 𝑎 (1) Y la ecuación del campo eléctrico por definición, nos dice que: 𝐹 𝐸= (2) 𝑞 Calculamos F, despejándola de la ecuación # 2, y nos queda: 𝐹=𝐸𝑥𝑞 Sustituimos: 𝑁 𝐹 = 16𝑥106 𝐶 𝑥 8𝑥10−6 𝐶 𝐹 = 128 𝑁 Ahora de la ecuación # 1, despejamos “a”: 𝐹 𝑎= 𝑚 Sustituimos: 128 𝑁 𝑎= 2𝑥10−4 𝐾𝑔 𝑚 𝑎 = 6,4𝑥105 𝑠2 28.- Una esfera cargada con 5𝑥10−6 𝐶, esta en un campo eléctrico uniforme de 2𝑥103 𝑁𝐶 accionada por una aceleración de 2𝑠𝑚2. Calcular la masa de la esfera. ( ( ( ( ) 0,05 Kg ) 0,005 Kg ) 0,005 gr ) 0,05 gr Datos: 𝑞 = 5𝑥10−6 𝐶 𝑚 =? 𝑁 𝐸 = 2𝑥103 𝐶 Diagrama: No es necesario realizar diagrama. 𝑚 𝑎 = 2 𝑠2 𝐶2 𝜀0 = 8,9𝑥10−12 𝑁 𝑥 𝑚2 Conversión de Unidades: No es necesario realizar Solución: Por las características del enunciado del problema, podemos inferir, que es una combinación de campo eléctrico con movimiento. Si aplicamos la 2da Ley de Newton, tenemos que: 𝐹 = 𝑚 𝑥 𝑎 (1) Y la ecuación del campo eléctrico por definición, nos dice que: 𝐹 𝐸= (2) 𝑞 Calculamos F, despejándola de la ecuación # 2, y nos queda: 𝐹=𝐸𝑥𝑞 Sustituimos: 𝑁 𝐹 = 2𝑥103 𝐶 𝑥 5𝑥10−6 𝐶 𝐹 = 0,01 𝑁 Ahora de la ecuación # 1, despejamos “m”: 𝐹 𝑚= 𝑎 Sustituimos: 0,01 𝑁 𝑚= 2𝑚 𝑠2 𝑚 = 0,005 𝐾𝑔 29.- En un campo eléctrico uniforme de 4𝑥106 𝑁𝐶, hay una esfera de 1 gr de masa cargada con una carga de 8𝑥10−6 𝐶. Calcular: a) ¿Qué rapidez lleva la esfera a los 4 segundos (s)?; b) ¿Qué distancia (X) ha recorrido a los 5 segundos (s), sabiendo que parte del reposo? ( ( ( ( )𝑉 )𝑉 )𝑉 )𝑉 = 1,28 = 1,28 = 12,8 = 1,28 𝑚⁄ 𝑠 𝑚⁄ 𝑠 𝑚⁄ 𝑠 𝑚⁄ 𝑠 𝑦𝑋 =4𝑚 𝑦 𝑋 = 4𝑥105 𝑚 𝑦 𝑋 = 4𝑥106 𝑚 𝑦 𝑋 = 40𝑥105 𝑚 Datos: Diagrama: −6 𝑞 = 8𝑥10 𝐶 No es necesario realizar diagrama. −4 𝑚 = 0,2 𝑔𝑟 = 2𝑥10 𝐾𝑔 𝑁 𝐸 = 16𝑥106 𝐶 𝑎 =? 𝐶2 𝜀0 = 8,9𝑥10−12 𝑁 𝑥 𝑚2 Conversión de Unidades: Transformamos los gramos (gr) a kilogramos (Kg), multiplicando por 10-3 Kg o dividiendo entre 1000 gr. Solución: Por las características del enunciado del problema, podemos inferir, que es una combinación de campo eléctrico con movimiento. Si aplicamos la 2da Ley de Newton, tenemos que: 𝐹 = 𝑚 𝑥 𝑎 (1) Y la ecuación del campo eléctrico por definición, nos dice que: 𝐹 𝐸= (2) 𝑞 Calculamos F, despejándola de la ecuación # 2, y nos queda: 𝐹=𝐸𝑥𝑞 Sustituimos: 𝑁 𝐹 = 4𝑥106 𝐶 𝑥 8𝑥10−6 𝐶 𝐹 = 32 𝑁 Ahora de la ecuación # 1, despejamos “a”: 𝐹 𝑎= 𝑚 Sustituimos: 32𝑁 𝑎 = −3 10 𝐾𝑔 𝑚 𝑎 = 3,2𝑥104 𝑠2 Posteriormente, calculamos la rapidez “V”, a los 4 s, aplicando la ecuación de la aceleración en el movimiento variado (M.V): 𝑉 − 𝑉0 𝑡 Como parte del reposo V0= 0, y despejamos “V”, nos queda que: 𝑉 = 𝑎𝑥𝑡 Sustituimos: 𝑉 = 3,2𝑥104 𝑚⁄𝑠 2 𝑥 4 𝑠 𝑉 = 1,28𝑥105 𝑚⁄𝑠 De la ecuación de la distancia “X” en el M:V, calculamos dicha magnitud: 𝑎 𝑥 𝑡2 𝑋 = 𝑉0 𝑥𝑡 − 2 Como V0=0, entonces: 𝑎 𝑥 𝑡2 𝑋= 2 Sustituimos: 3,2𝑥104 𝑚⁄𝑠 2 𝑥 (5 𝑠)2 𝑋= 2 𝑋 = 4𝑥105 𝑚 𝑎= 30.- Una esfera de 12 gr cargada con 90𝑥10−5 𝐶 está situada en un campo eléctrico uniforme y partiendo del reposo, recorre una distancia de 200 m en 10-4 s. Calcular la intensidad del campo eléctrico. ( ) 𝐸 = 5,33𝑥107 𝑁⁄𝐶 ( ) 𝐸 = 5,33𝑥10−7 𝑁⁄𝐶 ( ) 𝐸 = 53𝑥107 𝑁⁄𝐶 ( ) 𝐸 = 53𝑥10−7 𝑁⁄𝐶 Datos: 𝑚 = 12 𝑔𝑟 = 12𝑥10−3 𝐾𝑔 𝑞 = 90𝑥10−5 𝐶 𝑉0 = 0 𝑋 = 200 𝑚 𝑡 = 10−4 𝑠 𝐸 =? Diagrama: No es necesario Conversión de Unidades: Transformamos los gramos (gr) a kilogramos (Kg), multiplicando por 10-3 Kg o dividiendo entre 1000 gr. Solución: Ya se han resuelto problemas con características similares; donde hay una combinación de campo eléctrico y movimiento. Para tal fin, aplicaremos la ecuación de la distancia (X), en el movimiento variado (M.V): 𝑎 𝑥 𝑡2 𝑋 = 𝑉0 𝑥 𝑡 + 2 Como parte del reposo V0= 0, entonces: 𝑎 𝑥 𝑡2 𝑋= 2 Despejamos “a”: 2𝑥𝑋 𝑎= 2 𝑡 Sustituimos: 2 𝑥 200 𝑚 𝑎= (10−4 𝑠)2 𝑎 = 4𝑥106 𝑚⁄𝑠 2 Ahora con este valor de la aceleración y la masa, calculamos la fuerza “F”, aplicando la 2da Ley de Newton: 𝐹 =𝑚𝑥𝑎 Sustituimos: 𝐹 = 12𝑥10−3 𝐾𝑔 𝑥 4𝑥106 𝑚⁄𝑠 𝐹 = 4,8𝑥104 𝑁 Obtenida la fuerza, aplicamos la ecuación de la intensidad del campo eléctrico: 𝐸= 𝐹 𝑞0 Sustituimos: 𝐸= 4,8𝑥104 𝑁 90𝑥10−5 𝐶 𝐸 = 5,33𝑥107 𝑁⁄𝐶 31.- El campo eléctrico en el interior de dos láminas metálicas paralelas es de 5𝑥106 𝑁⁄𝐶 . Si el área de cada lámina es de 0,2 m2, calcular la carga eléctrica que hay en cada una de ellas. ( ( ( ( ) 8,9𝑥10−5 𝐶 ) 8,9𝑥10−6 𝐶 ) 9,8𝑥10−5 𝐶 ) 9,8𝑥10−6 𝐶 Datos: 𝑆 = 0,2 𝑚2 𝑞 =? 𝐶2 𝜀0 = 8,9𝑥10−12 𝑁 𝑥 𝑚2 𝑁 𝐸 = 5𝑥106 𝐶 Conversión de Unidades: No es necesario. Diagrama: +q + + + + + -q - Cuando las láminas metálicas paralelas, están muy próximas, entre ellas se forma un campo eléctrico uniforme. Solución: Para hallar el valor de q, hacemos uso de la ecuación de campo eléctrico entre laminas paralelas y despejamos q : 𝑞 𝐸= 𝜀0 𝑥 𝑆 𝑞 = 𝐸𝑥𝑆𝑥𝜀0 Siendo “S” el área y “𝛆0”, la constante sustituimos en la ecuación: 2 𝑁 𝑞 = 5𝑥106 𝐶 𝑥 0,2 𝑚2 𝑥8,9𝑥10−12 𝑁 𝑥𝐶 𝑚2 𝑞 = 8,9𝑥10−6 𝐶 Como son láminas metálicas paralelas mantienen una carga eléctrica constante. 32.- Se dispone de dos láminas metálicas paralelas con un área de 0,16 m2 cada una. La carga eléctrica que tiene cada lámina es 7x10-6C. Calcular el módulo de la intensidad del campo eléctrico que hay entre ellas. ( ( ( ( ) 49𝑥106 𝑁𝐶 ) −49𝑥106 𝑁𝐶 ) 4,9𝑥106 𝑁𝐶 ) 4,9𝑥10−6 𝑁𝐶 Datos: 2 𝑆 = 0,16 𝑚 𝑞 = 7𝑥10−6 𝐶 𝐶2 𝜀0 = 8,9𝑥10−12 𝑁 𝑥 𝑚2 𝐸 =? Conversión de Unidades: No es necesario. Diagrama: +q + + + + + -q - Cuando las láminas metálicas paralelas, están muy próximas, entre ellas se forma un campo eléctrico uniforme. Solución: Para hallar el valor de E, hacemos uso de la ecuación de campo eléctrico entre laminas paralelas: 𝑞 𝐸= 𝜀0 𝑥 𝑆 Siendo “S” el área y “𝛆0”, la constante sustituimos en la ecuación: 7𝑥10−6 𝐶 𝐸= 2 8,9𝑥10−12 𝑁 𝑥𝐶 𝑚2 𝑥 0,16 𝑚2 𝑁 𝐸 = 4,9𝑥106 𝐶 33.- Una esfera cargada con 8x10-6C, está en un campo eléctrico uniforme de 6x103𝑁⁄𝐶 , accionada por una aceleración de 4 𝑚⁄𝑠 2 . Calcular la masa de la esfera. ( ( ( ( ) 0,012 Kg ) 0,012 gr ) 12 Kg ) 12 gr Datos: 𝑞 = 8𝑥10−6 𝐶 𝑚 =? 𝑁 𝐸 = 6𝑥103 𝐶 Diagrama: No es necesario realizar diagrama. 𝑚 𝑎 = 4 𝑠2 𝐶2 𝜀0 = 8,9𝑥10−12 𝑁 𝑥 𝑚2 Conversión de Unidades: No es necesario realizar Solución: Por las características del enunciado del problema, podemos inferir, que es una combinación de campo eléctrico con movimiento. Si aplicamos la 2da Ley de Newton, tenemos que: 𝐹 = 𝑚 𝑥 𝑎 (1) Y la ecuación del campo eléctrico por definición, nos dice que: 𝐹 𝐸= (2) 𝑞 Calculamos F, despejándola de la ecuación # 2, y nos queda: 𝐹=𝐸𝑥𝑞 Sustituimos: 𝑁 𝐹 = 6𝑥103 𝐶 𝑥 8𝑥10−6 𝐶 𝐹 = 0,048 𝑁 Ahora de la ecuación # 1, despejamos “m”: 𝐹 𝑚= 𝑎 Sustituimos: 0,048 𝑁 𝑚= 4𝑚 𝑠2 𝑚 = 0,012 𝐾𝑔 34.- Una esfera de 3,2 gr cargada con 6x10-6C, está situada en un campo eléctrico uniforme y partiendo del reposo recorre 80 cm en 10-3s. Calcular la intensidad del campo eléctrico. ( ) 𝐸 = 8,53𝑥106 𝑁⁄𝐶 ( ) 𝐸 = 853𝑥106 𝑁⁄𝐶 ( ) 𝐸 = 8,53𝑥10−6 𝑁⁄𝐶 ( ) 𝐸 = 8,53𝑥108 𝑁⁄𝐶 Datos: 𝑚 = 32 𝑔𝑟 = 32𝑥10−3 𝐾𝑔 𝑞 = 6𝑥10−6 𝐶 𝑉0 = 0 𝑋 = 80 𝑐𝑚 = 80𝑥10−2 𝑚 𝑡 = 10−3 𝑠 𝐸 =? Diagrama: No es necesario Conversión de Unidades: Transformamos los gramos (gr) a kilogramos (Kg), multiplicando por 10-3 Kg o dividiendo entre 1000 gr. Solución: Ya se han resuelto problemas con características similares; donde hay una combinación de campo eléctrico y movimiento. Para tal fin, aplicaremos la ecuación de la distancia (X), en el movimiento variado (M.V): 𝑎 𝑥 𝑡2 𝑋 = 𝑉0 𝑥 𝑡 + 2 Como parte del reposo V0= 0, entonces: 𝑎 𝑥 𝑡2 𝑋= 2 Despejamos “a”: 2𝑥𝑋 𝑎= 2 𝑡 Sustituimos: 2 𝑥 80𝑥10−2 𝑚 𝑎= (10−3 𝑠)2 𝑎 = 1,6𝑥106 𝑚⁄𝑠 2 Ahora con este valor de la aceleración y la masa, calculamos la fuerza “F”, aplicando la 2da Ley de Newton: 𝐹 =𝑚𝑥𝑎 Sustituimos: 𝐹 = 3,2𝑥10−3 𝐾𝑔 𝑥 1,6𝑥106 𝑚⁄𝑠 𝐹 = 5120𝑁 Obtenida la fuerza, aplicamos la ecuación de la intensidad del campo eléctrico: 𝐹 𝐸= 𝑞0 Sustituimos: 5120𝑁 𝐸= 6𝑥10−6 𝐶 𝐸 = 8,53𝑥108 𝑁⁄𝐶 35.- Se dispone de dos láminas metálicas paralelas con un área común de 0,5 m2 y una carga eléctrica de 8x10-6C, cada lámina. Entre ellas hay una esfera de 10-2 gr que tiene una carga de 2x10-10C. Si parte del reposo, calcular cuanto tarda en recorrer 10-4 m. ( ( ( ( ) 2,35x10-3 s ) 2,35x103 s ) 2x103 s ) 0,23x10-3 s Datos: S = 0,5 m2 q = 8x10-6 C Diagrama: No es necesario realizarlo 𝐶2 𝜀0 = 8,9𝑥10−12 𝑁 𝑥 𝑚2 E =? Conversión de Unidades: No es necesario. Solución: Podemos observar que es un problema combinado de campo eléctrico entre láminas metálicas paralelas, movimiento y esfera. Aplicaremos la ecuación de la intensidad del campo eléctrico entre láminas paralelas: 𝑞 𝐸= 𝜀0 𝑥 𝑆 Sustituimos: 8𝑥10−6 𝐶 𝐸= 𝐶2 8,9𝑥10−12 𝑥0,5 𝑚2 𝑁 𝑥 𝑚2 𝐸 ≅ 1,8𝑥106 𝑁⁄𝐶 Obtenido el valor del campo eléctrico, procedemos a calcular la fuerza “F” y la aceleración “a”, de la esfera que se coloco entre las láminas metálicas. De la ecuación de la intensidad del campo eléctrico, despejamos “F”; Datos: 𝐸 = 1,8𝑥106 𝑁⁄𝐶 𝑚 = 10−2 𝑔𝑟 = 10−2 𝑥10−3 = 10−5 𝐾𝑔 𝑞𝑒 = 2𝑥10−10 𝐶 𝑋 = 10−4 𝑚 𝐹 𝑡 =? 𝐸= 𝑞0 𝑉0 = 0 Despejamos “F”: Se transformo los gramos (gr) a kilogramos (kg), 𝐹 = 𝑞0 𝑥𝐸 multiplicando por 10-3Kg. Sustituimos: 𝐹 = 1,8𝑥106 𝑁⁄𝐶 𝑥 2𝑥10−10 𝐶 𝐹 = 3,6𝑥10−4 𝑁 Ahora aplicamos la 2da Ley de Newton, para calcular la aceleración de la esfera: 𝐹 𝑎= 𝑚 Sustituimos: 3,6𝑥10−4 𝑁 𝑎= 10−5 𝐾𝑔 𝑎 = 36 𝑚⁄𝑠 2 Conocida la aceleración, haciendo uso de la ecuación de la distancia (X) en el movimiento variado (M.V), despejamos “t”: 𝑎 𝑥 𝑡2 𝑋 = 𝑉0 𝑥 𝑡 + 2 Como parte del reposo V0 = 0; entonces: 2𝑥𝑋 𝑡2 = 𝑎 Para eliminar el cuadrado de “t”, introducimos dentro de una raíz cuadrada, al resto de la ecuación: 𝑡=√ 2𝑥𝑋 𝑎 Sustituimos: 𝑡=√ 2 𝑥 10−4 𝑚 36 𝑚⁄𝑠 2 𝑡 = 2,35𝑥10−3 𝑠 36.- Un electrón se libera desde la placa inferior que se muestra en la figura, donde el campo eléctrico es de 1,5𝑥104 𝑁⁄𝐶 de magnitud. Si la distancia entre las placas es 1 cm. Calcular con respecto al electrón: a) la aceleración; b) la velocidad al alcanzar la laca positiva; c) el tiempo que tarda en recorrer la distancia entre las placas y d) la energía cinética al llegar a la laca superior. + + + + + d E - ( ( ( ( )𝑎 )𝑎 )𝑎 )𝑎 - - - - = 2,63𝑥1015 𝑠𝑚2; 𝑉 = 7,25𝑥106 𝑚𝑠; 𝑡 = 2,76𝑥10−9 𝑠 𝑦 𝐸𝑐 = 2,36𝑥10−17 𝐽 = 2,63𝑥10−15 𝑠𝑚2; 𝑉 = 7,25𝑥106 𝑚𝑠; 𝑡 = 2,76𝑥109 𝑠 𝑦 𝐸𝑐 = 2,36𝑥10−17 𝐽 = 2,63𝑥1015 𝑠𝑚2; 𝑉 = 7,25𝑥10−6 𝑚𝑠; 𝑡 = 2,76𝑥10−9 𝑠 𝑦 𝐸𝑐 = 2,36𝑥1017 𝐽 = 2,63𝑥10−15 𝑠𝑚2; 𝑉 = 7,25𝑥10−6 𝑚𝑠; 𝑡 = 2,76𝑥109 𝑠 𝑦 𝐸𝑐 = 2,36𝑥1017 𝐽 Datos: 𝑞 = 1,6𝑥10−19 𝐶 𝑁 𝐸 = 1,5𝑥104 𝐶 𝑎 =? 𝑡 =? 𝑚 = 9,11𝑥10−31 𝐾𝑔 𝑟 = 𝑌 = 1 𝑐𝑚 = 1𝑥10−2 𝑚 𝑉 =? 𝐸𝐶 =? Conversión de unidades: No es necesario Diagrama: No es necesario Solución: El electrón por tener una carga eléctrica negativa (-), se moverá desde la placa negativa a la positiva, por efecto de la fuerza “F” vertical hacia arriba. Como el campo es uniforme la fuerza es constante y para hallar su valor. Aplicamos la ecuación de la definición de intensidad de campo eléctrico: 𝐹 𝐸= 𝑞0 Despejamos “F” y nos queda: 𝐹 = 𝑞0 𝑥𝐸; (1) A su vez esta fuerza produce una aceleración hacia arriba, que de acuerdo con la 2da Ley de Newton, viene dada de la siguiente manera: 𝐹 , (2) 𝑚 Sustituimos la ecuación #1 en la ecuación #2: 𝐸𝑥𝑞 𝑎= 𝑚 Sustituimos: 1,5𝑥104 𝑁𝐶 𝑥 1,6𝑥10−19 𝐶 𝑎= 9,11𝑥10−31 𝐾𝑔 𝑎 = 2,63𝑥1015 𝑚⁄𝑠 2 Obtenida la aceleración, procedemos a calcular la velocidad del electrón; a través , de la ecuación de la velocidad en función de la distancia en el movimiento variado (M.V): 𝑉 2 = 𝑉02 + 2 𝑥 𝑎 𝑥 𝑌 Como el electrón es liberado desde la placa inferior asumimos, que parte del reposo 𝑉0 = 0 y para eliminar el cuadrado de la velocidad introducimos el resto de los términos dentro de una raíz cuadrada. 𝑉 = √2 𝑥 𝑎 𝑥 𝑌 Sustituimos: 𝑎= 𝑚 𝑉 = √2 𝑥 2,63𝑥1015 𝑠2 𝑥 102 𝑚 𝑉 = 7,25𝑥106 𝑚⁄𝑠 Ahora procedemos a calcular el tiempo que tarda en recorrer la distancia entre las placas, aplicando la ecuación de la distancia en el M.V: 𝑎 𝑥 𝑡2 𝑌 = 𝑉0 𝑥𝑡 − 2 Como V0= 0, entonces: 𝑎 𝑥 𝑡2 𝑌= 2 Despejamos “t” y eliminamos cuadrado introduciendo el resto de los términos en una raíz cuadrada: 𝑡=√ 2 𝑥𝑌 𝑎 Sustituimos: 𝑡=√ 2 𝑥 10−2 𝑚 2,63𝑥1015 𝑠𝑚2 𝑡 = 2,76𝑥10−9 𝑠 Ahora se calcula la energía cinética del electrón: 1 𝐸𝐶 = 𝑥 𝑚 𝑥 𝑉 2 2 𝐸𝐶 = 1 𝑚 𝑥 9,11𝑥10−31 𝐾𝑔𝑥(7,25𝑥106 𝑠 )2 2 𝐸𝐶 = 2,36𝑥10−17 𝐽 37.- Se tienen un campo eléctrico uniforme de modulo 3,5𝑥103 𝑁𝐶 . Calcular la magnitud del flujo eléctrico a través de un rectángulo de 0,35 m de ancho y 0,70 m de largo cuando las líneas de campo eléctrico están: a) perpendiculares al plano; b) paralelas al plano y c) formando un ángulo de 65º con la normal del plano. 2 2 2 ( ) 𝜙1 = 0𝑁 𝑥𝐶𝑚 ; 𝜙2 = 857,5𝑁 𝑥𝐶𝑚 ; 𝜙3 = 362,39 𝑁 𝑥𝐶𝑚 2 2 2 ( ) 𝜙1 = 57,5𝑁 𝑥𝐶𝑚 ; 𝜙2 = 0𝑁 𝑥𝐶𝑚 ; 𝜙3 = 2,39 𝑁 𝑥𝐶𝑚 2 2 2 ( ) 𝜙1 = 0𝑁 𝑥𝐶𝑚 ; 𝜙2 = 857,5𝑁 𝑥𝐶𝑚 ; 𝜙3 = 36,39 𝑁 𝑥𝐶𝑚 2 2 2 ( ) 𝜙1 = 87𝑁 𝑥𝐶𝑚 ; 𝜙2 = 0𝑁 𝑥𝐶𝑚 ; 𝜙3 = 362,39 𝑁 𝑥𝐶𝑚 Datos: Diagramas y Solución: 𝑁 3,5𝑥103 𝐶 𝐸= 𝑎 = 0,35 𝑚 𝐿 = 0,70 𝑚 𝜙𝐸 =? 𝑎) 𝛼 = 90° 𝑏)𝛼 = 0° 𝑐) 𝛼 = 65° L I plano 𝛼1 N E A Normal S Antes de proceder a calcular el flujo de campo eléctrico, hallamos el valor del área o superficie: 𝑆=𝐿𝑥𝑎 𝑆 = 0,70 𝑚 𝑥0,35 𝑚 𝑆 = 0,245 𝑚 Calculamos ahora el flujo (ϕ) en cada caso: 𝜙1 = 𝐸 𝑥 𝑆 𝑥 cos 𝛼 𝑁 𝜙1 = 3,5𝑥103 𝐶 𝑥 0,245 𝑚2 𝑥 cos 90° 𝜙1 = 0 Conversión de Unidades: Calculo del flujo (ϕ2): 𝑁 𝑥 𝑚2 𝐶 No es necesario. L I N E Normal A S Plano 𝑁 𝜙2 = 3,5𝑥103 𝐶 𝑥 0,245 𝑚2 𝑥 cos 0° 𝜙2 = 857,5 𝑁 𝑥 𝑚2 𝐶 Calculo del flujo (𝜙3 ): Plano L I N E 𝛼 = 65° A S Normal 𝑁 𝜙3 = 3,5𝑥103 𝐶 𝑥 0,245 𝑚2 𝑥 cos 65° 𝜙3 = 362,39 𝑁 𝑥 𝑚2 𝐶 38.- En la figura se muestra un triangulo rectángulo en A. En sus vértices hay cargas eléctricas 𝑞𝐵 = +3𝑥10−6 𝐶 y 𝑞𝐶 = +4𝑥10−6 𝐶. Calcular el modulo de la intensidad de campo eléctrico en el punto A creados por las cargas 𝑞𝐵 𝑦 𝑞𝐶 . ( ( ( ( ) 3327, 5 𝑁𝐶 ) 3327 𝑁 𝐶 ) 3327,7 𝑁𝐶 ) 3327,07 𝑁𝐶 +qB 3m A Datos: 𝛼𝐴 = 90° 𝑞𝐵 = +3𝑥10−6 𝐶 𝑞𝐶 = +4𝑥10−6 𝐶 𝑟𝐴𝐵 = 3 𝑚 𝑟𝐴𝐶 = 5 𝑚 𝐸𝐴 =? +qC Diagrama: +qB 3m ECA A Conversión de Unidades: Transformamos los centímetros (cm) a metros (m), multiplicando por 10-2 m o dividiendo entre 100 cm 5m 5m +qC EA EBA Como las cargas eléctricas son positivas y el punto por convenios internacionales es positivo; entonces existe una repulsión entre ellos, ocasionando que los vectores se alejen de las cargas. Solución: Como los vectores a sumar son perpendiculares, aplicamos el teorema de Pitágoras, ara hallar la intensidad del campo resultante en el punto A. 𝐶 2 = 𝑎2 + 𝑏 2 Donde: 𝑐 = 𝐸𝐴 ; 𝑎 = 𝐸𝐶𝐴 𝑦 𝑏 = 𝐸𝐵𝐴 ; quedando que: 2 2 𝐸𝐴2 = 𝐸𝐶𝐴 + 𝐸𝐵𝐴 Para eliminar el cuadrado de “EA” introducimos el resto de los términos dentro de una raíz cuadrada. 2 2 𝐸𝐴 = √𝐸𝐶𝐴 + 𝐸𝐵𝐴 Calculamos las magnitudes de los campos creados por cada carga, haciendo uso de la ecuación de la intensidad de campo eléctrico creado por cada carga: 𝑞𝐴 𝐸𝐵𝐴 = 𝐾 𝑥 2 𝑟𝐴𝐵 𝐸𝐶𝐴 = 𝐾 𝑥 𝑞𝐶 2 𝑟𝐶𝐴 Sustituimos: 𝐸𝐵𝐴 = 3𝑥10−6 𝐶 𝑥 (3 𝑚)2 𝑁 = 3000 𝐶 𝑁𝑥𝑚 9𝑥109 𝐶 2 𝐸𝐵𝐴 𝐸𝐶𝐴 = 9𝑥109 2 𝑁 𝑥 𝑚2 𝐶2 𝑥 𝐸𝐶𝐴 = 1440 4𝑥10−6 𝐶 (5 𝑚)2 𝑁 𝐶 𝑁 𝑁 𝐸𝐴 = √(1440 𝐶 )2 + (3000 𝐶 )2 𝑁 𝐸𝐴 = 3327,7 𝐶 39.- En la figura se muestra un triangulo rectángulo. En sus vértices hay cargas eléctricas 𝑞1 = +6𝑥10−6 𝐶 y 𝑞2 = +5𝑥10−6 𝐶. En el vértice inferior derecho hay un ángulo 𝛼 = 30° y la distancia entre q1 y q2 es de 20 cm. Calcular la magnitud de la intensidad de campo eléctrico en el punto P ubicado en el vértice del ángulo recto, creados por las cargas 𝑞1 𝑦 𝑞2 . ( ( ( ( )5,4𝑥106 𝑁𝐶 ) 1,56𝑥106 𝑁𝐶 ) 5,2𝑥106 𝑁𝐶 ) 5,62𝑥106 𝑁𝐶 +q1 20 cm α P Datos: 𝑟12 𝛼2 = 30° 𝑞1 = +6𝑥10−6 𝐶 𝑞2 = +5𝑥10−6 𝐶 = 20 𝑐𝑚 = 20𝑥10−2 𝑚 𝑟1𝑝 =? 𝑟2𝑝 =? 𝐸𝑅 =? +q2 Diagrama: +q1 20 cm E2p P +q2 ER E1p Como las cargas eléctricas son positivas y el punto, por convenios internacionales es positivo; entonces existe una repulsión entre ellos, ocasionando que los vectores se alejen de las cargas. Conversión de Unidades: Solución: Transformamos los Como los vectores a sumar son perpendiculares, aplicamos centímetros (cm) a metros el teorema de Pitágoras, ara hallar la intensidad del campo (m), multiplicando por 10-2 resultante en el punto A. m o dividiendo entre 100 𝐶 2 = 𝑎2 + 𝑏 2 Donde: 𝑐 = 𝐸𝑅 ; 𝑎 = 𝐸2𝑝 𝑦 𝑏 = 𝐸1𝑝 ; quedando que: cm 2 2 𝐸𝑅2 = 𝐸2𝑝 + 𝐸1𝑝 Para eliminar el cuadrado de “EA” introducimos el resto de los términos dentro de una raíz cuadrada. 2 2 𝐸𝑅 = √𝐸2𝑝 + 𝐸1𝑝 Calculamos las magnitudes de los campos creados por cada carga, haciendo uso de la ecuación de la intensidad de campo eléctrico creado por cada carga: 𝑞1 𝐸1𝑝 = 𝐾 𝑥 2 𝑟1𝑝 Hallamos la distancia 𝑟1𝑝 , aplicando la función sin 30°; ya que es el cateto opuesto al ángulo: 𝑟1𝑝 𝑐𝑜 sin 30° = = ℎ 𝑟12 Despejamos “r1p”: 𝑟1𝑝 = 𝑟12 𝑥 sin 30° 𝑟1𝑝 = 20𝑥10−2 𝑚 𝑥 cos 30° 𝑟1𝑝 = 10−1 𝑚 = 0,10 𝑚 Sustituimos en E1p: 𝐸1𝑝 = 6𝑥10−6 𝐶 𝑥 (0,1 𝑚)2 𝑁 = 5,4𝑥106 𝐶 𝑁𝑥𝑚 9𝑥109 𝐶 2 𝐸1𝑝 2 Ahora procedemos a calcular “E2p” 𝑞2 2 𝑟2𝑝 Debemos calcular previamente la distancia ”𝑟2𝑝 ", aplicando la función cos 30°: 𝐶𝐴 𝑟2𝑝 cos 30° = = 𝐻 𝑟12 Despejamos la distancia "𝑟2𝑝 ": 𝑟2𝑝 = 𝑟12 𝑥 cos 30° Sustituimos: 𝑟2𝑝 = 20𝑥10−2 𝑚 𝑥 cos 30° 𝑟2𝑝 = 1,7𝑥10−1 𝑚 = 0,17 𝑚 Sustituimos en E2p: 𝐸2𝑝 = 𝐾 𝑥 5𝑥10−6 𝐶 (0,17 𝑚)2 𝑁 = 1,56𝑥106 𝐶 𝐸𝐶𝐴 = 9𝑥109 𝐸𝐶𝐴 𝑁 𝑥 𝑚2 𝐶2 𝑥 𝑁 𝑁 𝐸𝐴 = √(1,56𝑥106 𝐶 )2 + (5,4𝑥106 𝐶 )2 𝐸𝐴 = 5,62𝑥106 𝑁 𝐶 40.- En la figura se muestra un triangulo rectángulo. En sus vértices hay cargas eléctricas 𝑞1 = −4𝑥10−6 𝐶 y 𝑞2 = +8𝑥10−6 𝐶. En el vértice inferior derecho hay un ángulo 𝛼 = 60° y la distancia entre q1 y P es de 3 cm. Calcular la magnitud de la intensidad de campo eléctrico en el punto P ubicado en el vértice del ángulo recto, creados por las cargas. ( ( ( ( )2,52𝑥106 𝑁𝐶 ) 2,52𝑥108 𝑁𝐶 ) 25,2𝑥109 𝑁𝐶 ) 25,2𝑥108 𝑁𝐶 -q1 3 cm α P Datos: 𝑟1𝑝 𝛼2 = 60° 𝑞1 = −4𝑥10−6 𝐶 𝑞2 = +8𝑥10−6 𝐶 = 3 𝑐𝑚 = 3𝑥10−2 𝑚 𝑟2𝑝 =? 𝐸𝑅 =? +q2 Diagrama: ER -q1 E1p 3 cm E2p P +q2 Como las cargas eléctricas son positivas y el punto, por convenios internacionales es positivo; entonces existe una repulsión entre q2 y el punto y una atracción entre q1 y el punto, ocasionando que el vector 2 se aleje y el 1 se acerque a la carga. Conversión de Unidades: Solución: Transformamos los Como los vectores a sumar son perpendiculares, aplicamos centímetros (cm) a metros el teorema de Pitágoras, ara hallar la intensidad del campo (m), multiplicando por 10-2 resultante en el punto A. m o dividiendo entre 100 𝐶 2 = 𝑎2 + 𝑏 2 Donde: 𝑐 = 𝐸𝑅 ; 𝑎 = 𝐸2𝑝 𝑦 𝑏 = 𝐸1𝑝 ; quedando que: cm 2 2 𝐸𝑅2 = 𝐸2𝑝 + 𝐸1𝑝 Para eliminar el cuadrado de “ER” introducimos el resto de los términos dentro de una raíz cuadrada. 2 2 𝐸𝑅 = √𝐸2𝑝 + 𝐸1𝑝 Calculamos las magnitudes de los campos creados por cada carga, haciendo uso de la ecuación de la intensidad de campo eléctrico creado por cada carga: 𝑞1 𝐸1𝑝 = 𝐾 𝑥 2 𝑟1𝑝 Sustituimos en E1p: 𝐸1𝑝 = 9𝑥109 4𝑥10−6 𝐶 (3𝑥10−2 𝑚)2 𝑁 = 4𝑥107 𝐶 𝑁 𝑥 𝑚2 𝐶2 𝐸1𝑝 𝑥 Ahora procedemos a calcular “E2p” 𝑞2 2 𝑟2𝑝 Debemos calcular previamente la distancia ”𝑟2𝑝 ", aplicando la función tan 30°: 𝐸2𝑝 = 𝐾 𝑥 𝐶𝑂 𝑟1𝑝 = 𝐶𝐴 𝑟2𝑝 tan 60° = Despejamos la distancia "𝑟2𝑝 ": 𝑟2𝑝 = Sustituimos: 𝑟2𝑝 𝑟1𝑝 tan 60° 3𝑥10−2 𝑚 𝑟2𝑝 = tan 60° = 1,7𝑥10−2 𝑚 = 0,017 𝑚 Sustituimos en E2p: 𝐸2𝑝 = 8𝑥10−6 𝐶 𝑥 (0,017 𝑚)2 𝑁 = 2,49𝑥108 𝐶 𝑁𝑥𝑚 9𝑥109 𝐶 2 𝐸2𝑝 2 𝑁 𝑁 𝐸𝑅 = √(2,49𝑥108 𝐶 )2 + (4𝑥107 𝐶 )2 𝐸𝑅 = 2,52𝑥108 𝑁 𝐶 41.- En la figura se muestra un triangulo rectángulo. En sus vértices hay cargas eléctricas 𝑞1 = −4𝑥10−6 𝐶 y 𝑞2 = +8𝑥10−6 𝐶. En el vértice inferior derecho hay un ángulo 𝛼 = 60° y la distancia entre q2 y P es de 3 cm. Calcular la magnitud de la intensidad de campo eléctrico en el punto P ubicado en el vértice del ángulo recto, creados por las cargas. ( ( ( ( )8,1𝑥106 𝑁𝐶 ) 2,52𝑥108 𝑁𝐶 ) 8,1𝑥107 𝑁𝐶 ) 25,2𝑥108 𝑁𝐶 -q1 α P Datos: 𝑟2𝑝 𝛼2 = 60° 𝑞1 = −4𝑥10−6 𝐶 𝑞2 = +8𝑥10−6 𝐶 = 3 𝑐𝑚 = 3𝑥10−2 𝑚 𝑟1𝑝 =? 𝐸𝑅 =? 3 cm +q2 Diagrama: -q1 E1p ER E2p P 3 cm +q2 Como las cargas eléctricas son positivas y el punto, por convenios internacionales es positivo; entonces existe una repulsión entre q2 y el punto. Una atracción entre q1 y el punto, ocasionando que el vector 1 se acerque y el 2 se aleje de la carga. Conversión de Unidades: Solución: Transformamos los Como los vectores a sumar son perpendiculares, aplicamos centímetros (cm) a metros el teorema de Pitágoras, ara hallar la intensidad del campo (m), multiplicando por 10-2 resultante en el punto A. m o dividiendo entre 100 𝐶 2 = 𝑎2 + 𝑏 2 Donde: 𝑐 = 𝐸𝑅 ; 𝑎 = 𝐸2𝑝 𝑦 𝑏 = 𝐸1𝑝 ; quedando que: cm 2 2 𝐸𝑅2 = 𝐸2𝑝 + 𝐸1𝑝 Para eliminar el cuadrado de “ER” introducimos el resto de los términos dentro de una raíz cuadrada. 2 2 𝐸𝑅 = √𝐸2𝑝 + 𝐸1𝑝 Calculamos las magnitudes de los campos creados por cada carga, haciendo uso de la ecuación de la intensidad de campo eléctrico creado por cada carga: 𝑞1 𝐸1𝑝 = 𝐾 𝑥 2 𝑟1𝑝 Sustituimos en E1p: Debemos calcular previamente la distancia ”𝑟2𝑝 ", aplicando la función tan 30°: 𝐶𝑂 𝑟1𝑝 = 𝐶𝐴 𝑟2𝑝 tan 60° = Despejamos la distancia "𝑟1𝑝 ": 𝑟1𝑝 = 𝑟2𝑝 𝑥 tan 60° Sustituimos: 𝑟1𝑝 = 3𝑥10−2 𝑚 𝑥 tan 60° 𝑟1𝑝 = 5,19𝑥10−2 𝑚 𝐸1𝑝 = 9𝑥109 4𝑥10−6 𝐶 (5,19𝑥10−2 𝑚)2 𝑁 = 1,33𝑥107 𝐶 𝑁 𝑥 𝑚2 𝐶2 𝐸1𝑝 𝑥 Ahora procedemos a calcular “E2p” 𝐸2𝑝 = 𝐾 𝑥 𝑞2 2 𝑟2𝑝 Sustituimos en E2p: 𝐸2𝑝 = 9𝑥109 𝑁 𝑥 𝑚2 𝐶2 𝑥 8𝑥10−6 𝐶 (3𝑥102 𝑚)2 𝐸2𝑝 = 8𝑥107 𝑁 𝐶 𝑁 𝑁 𝐸𝑅 = √(8𝑥107 𝐶 )2 + (1,33𝑥107 𝐶 )2 𝐸𝑅 = 8,1𝑥107 𝑁 𝐶 42.- ABC es un triangulo equilátero de 6 cm de lado. En los vértices hay cargas eléctricas cuyos valores son 𝑞𝐴 = +9𝑥10−6 𝐶; 𝑞𝐵 = −5𝑥10−6 𝐶 ; y 𝑞𝐶 = −18𝑥10−6 𝐶 . Calcular la intensidad del campo eléctrico resultante en el punto medio del lado AC. ( ( ( ( ) 2,7𝑥108 𝑁𝐶 ) 2,7𝑥107 𝑁𝐶 ) 2,7𝑥109 𝑁𝐶 ) 2,7𝑥105 𝑁𝐶 -qB 6 cm +qA Datos: 𝑞𝐴 = +9𝑥10−6 𝐶 𝑞𝐵 = −5𝑥10−6 𝐶 𝑞𝑐 = −18𝑥10−6 𝐶 𝐿 = 6 𝑐𝑚 = 6𝑥10−2 𝑚 𝐸𝑅 =? 𝑠𝑜𝑏𝑟𝑒 𝑃 𝑟𝐴𝑝 = 3 𝑐𝑚 = 3𝑥10−2 𝑚 𝑟𝐵𝑝 =? 𝑟𝐶𝑝 = 3 𝑐𝑚 = 3𝑥10−2 𝑚 P -qC Diagrama: -qB 6 cm +qA P -qC EB Conversión de Unidades: Se transforman los centímetros (cm) a metros (m), multiplicando por 10-2m o dividiendo entre 100 cm. EA EC Se puede observar que los vectores a sumar son perpendiculares; pero los vectores EA y EC, tienen la misma dirección y sentido, entre ellos habrá un vector resultante que tendrá esa misma dirección y el vector EB es perpendicular a ellos dos. Solución: Realizado el análisis vectorial y explicado los sentidos de los vectores anteriormente, hallamos el modulo del vector resultante, aplicando el teorema de Pitágoras. 𝐶 2 = 𝑎2 + 𝑏 2 Donde: 𝐶 = 𝐸𝑅 ; 𝑎 = (𝐸𝑎 + 𝐸𝐶 ) 𝑦 𝑏 = 𝐸𝐵 ; sustituimos en el teorema y eliminamos cuadrado de ER, introduciendo dentro de una raíz cuadrada el resto de los términos: 𝐸𝑅 = √(𝐸𝐴 + 𝐸𝐶 )2 + (𝐸𝐵 )2 Aplicando la ecuación de la intensidad del campo eléctrico, calculamos los campos creados por cada carga: 𝐸𝐴 = 𝐾 𝑥 𝑞𝐴 2 𝑟𝐴𝑝 Sustituimos: 9𝑥10−6 𝐶 𝐸𝐴 = 𝑥 (3𝑥10−2 𝑚)2 𝑁 𝐸𝐴 = 9𝑥107 𝐶 Para calcular el campo EB, debemos hallar la distancia de la carga B al punto P. 𝑞𝐵 𝐸𝐵 = 𝐾 𝑥 2 𝑟𝐵𝑝 Para calcular la distancia rBp, aplicamos la función seno de α: 𝑟𝐵𝑝 𝑐𝑜 sin 60° = = ℎ 𝑟𝐴𝐵 Despejamos distancia “𝑟𝐵𝑝 " 𝑟𝐵𝑝 = 𝑟𝐴𝐵 𝑥 sin 60° Sustituimos: 𝑟𝐵𝑝 = 6𝑥10−2 𝑚 𝑥 sin 60° 𝑟𝐵𝑝 = 5,19𝑥10−2 𝑚 2 5𝑥10−6 𝐶 9𝑁 𝑥 𝑚 𝐸𝐵 = 9𝑥10 𝐶 2 𝑥 (5,19𝑥10−2 𝑚)2 𝑁 𝐸𝐵 = 1,67𝑥107 𝐶 𝑁𝑥𝑚 9𝑥109 𝐶 2 2 Calculamos ahora el campo creado por la carga C: 𝑞𝐶 𝐸𝐶 = 𝐾 𝑥 2 𝑟𝐶𝑝 18𝑥10−6 𝐶 𝑁 𝑥 𝑚2 𝐸𝐶 = 9𝑥109 𝐶 2 𝑥 (3𝑥10−2 𝑚)2 𝑁 𝐸𝐶 = 1,8𝑥108 𝐶 𝑁 𝑁 𝑁 𝐸𝑅 = √(9𝑥107 𝐶 + 1,8𝑥107 𝐶 )2 + (1,67𝑥107 𝐶 )2 𝑁 𝐸𝑅 = 2,7𝑥108 𝐶 43.- ABC es un triangulo equilátero de 6 cm de lado. En los vértices hay cargas eléctricas cuyos valores son 𝑞𝐴 = +9𝑥10−6 𝐶; 𝑞𝐵 = +5𝑥10−6 𝐶 ; y 𝑞𝐶 = −18𝑥10−6 𝐶 . Calcular la intensidad del campo eléctrico resultante en el punto medio del lado AC. ( ( ( ( ) 1,51𝑥107 𝑁𝐶 ) 1,51𝑥108 𝑁𝐶 ) 1,51𝑥109 𝑁𝐶 ) 1,51𝑥105 𝑁𝐶 +qB 8 cm +qA Datos: 𝑞𝐴 = +9𝑥10−6 𝐶 𝑞𝐵 = +5𝑥10−6 𝐶 𝑞𝑐 = −18𝑥10−6 𝐶 𝐿 = 8𝑐𝑚 = 8𝑥10−2 𝑚 𝐸𝑅 =? 𝑠𝑜𝑏𝑟𝑒 𝑃 𝑟𝐴𝑝 = 4 𝑐𝑚 = 3𝑥10−2 𝑚 𝑟𝐵𝑝 =? 𝑟𝐶𝑝 = 4 𝑐𝑚 = 3𝑥10−2 𝑚 P -qC Diagrama: +qB 8 cm +qA P -qC EB EA EB Conversión de Unidades: Se transforman los centímetros (cm) a metros (m), multiplicando por 10-2m o dividiendo entre 100 cm. EC ER Se puede observar que los vectores a sumar son perpendiculares; pero los vectores EA y EC, tienen la misma dirección y sentido, entre ellos habrá un vector resultante que tendrá esa misma dirección y el vector EB es perpendicular a ellos dos. Solución: Realizado el análisis vectorial y explicado los sentidos de los vectores anteriormente, hallamos el modulo del vector resultante, aplicando el teorema de Pitágoras. 𝐶 2 = 𝑎2 + 𝑏 2 Donde: 𝐶 = 𝐸𝑅 ; 𝑎 = (𝐸𝑎 + 𝐸𝐶 ) 𝑦 𝑏 = 𝐸𝐵 ; sustituimos en el teorema y eliminamos cuadrado de ER, introduciendo dentro de una raíz cuadrada el resto de los términos: 𝐸𝑅 = √(𝐸𝐴 + 𝐸𝐶 )2 + (𝐸𝐵 )2 Aplicando la ecuación de la intensidad del campo eléctrico, calculamos los campos creados por cada carga: 𝐸𝐴 = 𝐾 𝑥 𝑞𝐴 2 𝑟𝐴𝑝 Sustituimos: 9𝑥10−6 𝐶 (4𝑥10−2 𝑚)2 𝑁 𝐸𝐴 = 5,06𝑥107 𝐶 Para calcular el campo EB, debemos hallar la distancia de la carga B al punto P. 𝑞𝐵 𝐸𝐵 = 𝐾 𝑥 2 𝑟𝐵𝑝 Para calcular la distancia rBp, aplicamos la función seno de α: 𝑟𝐵𝑝 𝑐𝑜 sin 60° = = ℎ 𝑟𝐴𝐵 Despejamos distancia “𝑟𝐵𝑝 " 𝑟𝐵𝑝 = 𝑟𝐴𝐵 𝑥 sin 60° Sustituimos: 𝑟𝐵𝑝 = 8𝑥10−2 𝑚 𝑥 sin 60° 𝑟𝐵𝑝 = 6,9𝑥10−2 𝑚 5𝑥10−6 𝐶 𝑁 𝑥 𝑚2 𝐸𝐵 = 9𝑥109 𝐶 2 𝑥 (6,9𝑥10−2 𝑚)2 𝑁 𝐸𝐵 = 9,45𝑥106 𝐶 𝐸𝐴 = 9𝑥109 𝑁 𝑥 𝑚2 𝐶2 𝑥 Calculamos ahora el campo creado por la carga C: 𝑞𝐶 𝐸𝐶 = 𝐾 𝑥 2 𝑟𝐶𝑝 2 18𝑥10−6 𝐶 9𝑁 𝑥 𝑚 𝐸𝐶 = 9𝑥10 𝐶 2 𝑥 (4𝑥10−2 𝑚)2 𝑁 𝐸𝐶 = 1,01𝑥108 𝐶 𝑁 𝑁 𝑁 𝐸𝑅 = √(5,06𝑥107 𝐶 + 1,01𝑥108 𝐶 )2 + (9,45𝑥106 𝐶 )2 𝑁 𝐸𝑅 = 1,51𝑥108 𝐶 44.- ABC es un triangulo equilátero de 6 cm de lado. En los vértices hay cargas eléctricas cuyos valores son 𝑞𝐴 = +9𝑥10−6 𝐶; 𝑞𝐵 = +5𝑥10−6 𝐶 ; y 𝑞𝐶 = +18𝑥10−6 𝐶 . Calcular la intensidad del campo eléctrico resultante en el punto medio del lado AC. ( ( ( ( ) 5,12𝑥107 𝑁𝐶 ) 5,12𝑥108 𝑁𝐶 ) 5,12𝑥106 𝑁𝐶 ) 5,12𝑥105 𝑁𝐶 +qB 8 cm +qA Datos: 𝑞𝐴 = +9𝑥10−6 𝐶 𝑞𝐵 = +5𝑥10−6 𝐶 𝑞𝑐 = −18𝑥10−6 𝐶 𝐿 = 8𝑐𝑚 = 8𝑥10−2 𝑚 𝐸𝑅 =? 𝑠𝑜𝑏𝑟𝑒 𝑃 𝑟𝐴𝑝 = 4 𝑐𝑚 = 3𝑥10−2 𝑚 𝑟𝐵𝑝 =? 𝑟𝐶𝑝 = 4 𝑐𝑚 = 3𝑥10−2 𝑚 P +qC Diagrama: +qB 8 cm +qA P -qC EB EC EA EC - EA EB Conversión de Unidades: Se transforman los centímetros (cm) a metros (m), multiplicando por 10-2m o dividiendo entre 100 cm. ER EB Se puede observar que los vectores a sumar son perpendiculares; pero los vectores EA y EC, tienen la misma dirección y sentido contrario, entre ellos habrá un vector resultante que tendrá esa misma dirección, pero sentido hacia el de mayor magnitud y el vector EB es perpendicular a ellos dos. Solución: Realizado el análisis vectorial y explicado los sentidos de los vectores anteriormente, hallamos el modulo del vector resultante, aplicando el teorema de Pitágoras. 𝐶 2 = 𝑎2 + 𝑏 2 Donde: 𝐶 = 𝐸𝑅 ; 𝑎 = (𝐸𝐶 − 𝐸𝐴 ) 𝑦 𝑏 = 𝐸𝐵 ; sustituimos en el teorema y eliminamos cuadrado de ER, introduciendo dentro de una raíz cuadrada el resto de los términos: 𝐸𝑅 = √(𝐸𝐶 − 𝐸𝐴 )2 + (𝐸𝐵 )2 Aplicando la ecuación de la intensidad del campo eléctrico, calculamos los campos creados por cada carga: 𝐸𝐴 = 𝐾 𝑥 𝑞𝐴 2 𝑟𝐴𝑝 Sustituimos: 9𝑥10−6 𝐶 (4𝑥10−2 𝑚)2 𝑁 𝐸𝐴 = 5,06𝑥107 𝐶 Para calcular el campo EB, debemos hallar la distancia de la carga B al punto P. 𝑞𝐵 𝐸𝐵 = 𝐾 𝑥 2 𝑟𝐵𝑝 Para calcular la distancia rBp, aplicamos la función seno de α: 𝑟𝐵𝑝 𝑐𝑜 sin 60° = = ℎ 𝑟𝐴𝐵 Despejamos distancia “𝑟𝐵𝑝 " 𝑟𝐵𝑝 = 𝑟𝐴𝐵 𝑥 sin 60° Sustituimos: 𝑟𝐵𝑝 = 8𝑥10−2 𝑚 𝑥 sin 60° 𝑟𝐵𝑝 = 6,9𝑥10−2 𝑚 5𝑥10−6 𝐶 𝑁 𝑥 𝑚2 𝐸𝐵 = 9𝑥109 𝐶 2 𝑥 (6,9𝑥10−2 𝑚)2 𝑁 𝐸𝐵 = 9,45𝑥106 𝐶 𝐸𝐴 = 9𝑥109 𝑁 𝑥 𝑚2 𝐶2 𝑥 Calculamos ahora el campo creado por la carga C: 𝑞𝐶 𝐸𝐶 = 𝐾 𝑥 2 𝑟𝐶𝑝 2 18𝑥10−6 𝐶 9𝑁 𝑥 𝑚 𝐸𝐶 = 9𝑥10 𝐶 2 𝑥 (4𝑥10−2 𝑚)2 𝑁 𝐸𝐶 = 1,01𝑥108 𝐶 𝑁 𝑁 𝑁 𝐸𝑅 = √(1,01𝑥108 𝐶 − 5,06𝑥107 𝐶 )2 + (9,45𝑥106 𝐶 )2 𝑁 𝐸𝑅 = 5,12𝑥107 𝐶 45.- En los extremos de la hipotenusa de un triangulo rectángulo se ubican cargas como las indicadas en la figura: q1=? y q2= +17,3 C, situadas a una distancia de 20 cm y 30 cm del ángulo recto respectivamente. Si la magnitud del campo eléctrico resultante en el vértice del ángulo recto es de 2,54𝑥1012 𝑁𝐶, calcular la magnitud de la carga q1. ( ( ( ( ) 8,25 C ) 8,35 C ) 8,26 C ) 8,36 C +q2 30 cm A 20 cm +q1 Datos: 𝑟1𝐴 𝑟2𝐴 Diagrama: 𝑞1 =? 𝑞2 = 17,3 𝐶 = 20 𝑐𝑚 = 20𝑥10−2 𝑚 = 30 𝑐𝑚 = 30𝑥10−2 𝑚 𝑁 𝐸𝐴 = 2,54𝑥1012 𝐶 +q2 30 cm E1 +q1 A 20 cm EA E2 Podemos observar que los vectores E1 y E2, son perpendiculares; ya que las cargas eléctricas son positivas y el punto por ser positivo según convenios, entonces hay una repulsión entre ellos y los vectores se alejan de las cargas. Conversión de Unidades: Transformamos los centímetros (cm) a metros (m), multiplicando por 10-2 m. Solución: E1 y E2, nos representan las magnitudes del campo eléctrico en el vértice del ángulo recto. Como ellos son perpendiculares ER, vienen a ser el campo resultante de la suma de estos y en modulo viene dado por la aplicación del teorema de Pitágoras. 𝐶 2 = 𝑎2 + 𝑏 2 Donde: 𝑐 = 𝐸𝐴 ; 𝑎 = 𝐸1 𝑦 𝑏 = 𝐸2 , quedando: 𝐸𝐴2 = 𝐸12 + 𝐸22 Despejamos E1 y para eliminar el cuadrado, introducimos dentro de una raíz cuadrada el resto de la ecuación: 𝐸1 = √𝐸𝐴2 + 𝐸22 Todo esto al conocimiento que tenemos de ER. Calculamos la magnitud del campo creado por q2. 𝑞2 𝐸2 = 𝐾 𝑥 2 𝑟2𝐴 Sustituimos: 17,3 𝐶 𝑁 𝑥 𝑚2 𝐸2 = 9𝑥109 𝐶 2 𝑥 (30𝑥10−2 𝑚)2 𝑁 𝐸2 = 1,73𝑥1012 𝐶 Ahora calculamos E1, con los valores que tenemos de los campos eléctricos: 𝑁 𝑁 𝐸1 = √(2,54𝑥1012 𝐶 )2 − (1,73𝑥1012 𝐶 )2 𝑁 𝐸1 = 1,86𝑥1012 𝐶 Calculado el campo creado por la carga q1, procedemos a calcular el valor de ella, aplicando la ecuación de la intensidad del campo eléctrico: 𝑞1 𝐸1 = 𝐾 𝑥 2 𝑟1 Des𝑝ejamos q1: 𝐸1 𝑥 𝑟12 𝑞1 = 𝐾 Sustituimos: 1,86𝑥1012 𝑁𝐶 𝑥 (20𝑥10−2 𝑚)2 𝑞1 = 2 9𝑥109 𝑁 𝑥𝐶 2𝑚 𝑞1 = 8,26 𝐶 46.- En la figura se tienen un cuadrado de 8 cm de lado. En cada uno de sus vértices hay cargas eléctricas cuyos valores son: 𝑞𝐴 = +4𝑥10−6 𝐶; 𝑞𝐵 = +5𝑥10−6 𝐶; 𝑞𝐶 = −6 −6 +6𝑥10 𝐶 𝑦 𝑞𝐷 = +8𝑥10 𝐶. Calcular el modulo de la intensidad del campo eléctrico resultante en el centro del cuadrado. ( ( ( ( ) 1,46𝑥108 𝑁𝐶 ) 1,48𝑥107 𝑁𝐶 ) 1,48𝑥108 𝑁𝐶 ) 1,46𝑥106 𝑁𝐶 +qA -qB 8 cm +qD Datos: 𝑞𝐴 = +4𝑥10−6 𝐶 𝑞𝐵 = −5𝑥10−6 𝐶 𝑞𝐶 = +6𝑥10−6 𝐶 𝑞𝐷 = +8𝑥10−6 𝐶 𝐿 = 8𝑐𝑚 = 8𝑥10−2 𝑚 𝐸𝑅 =? 𝑒𝑛 𝑒𝑙 𝑐𝑒𝑛𝑡𝑟𝑜 +qC Diagrama: +qA -qB P 8 cm +qD +qC O EB EA EC Conversión de Unidades: Se transformaron los centímetros (cm) a metros (m), multiplicando por 10-2 m o dividiendo entre 100 cm. EB+ED EA EC-EA Podemos observar que los campos eléctricos en el centro del cuadrado, se forman perpendicularmente; pero, debemos tomar en cuenta que los vectores formados por qA y qC, tienen la misma dirección y sentidos contrarios, mientras que los formados por qB y qD, tienen igual dirección y sentido. Solución: Como los vectores a sumar tienen las características mencionadas anteriormente, aplicamos el teorema de Pitágoras, con las variaciones que se tienen entre los vectores que actúan: 𝐶 2 = 𝑎2 + 𝑏 2 Donde: 𝑐 = 𝐸𝑅 ; 𝑎 = (𝐸𝐶 − 𝐸𝐴 )𝑦 𝑏 = (𝐸𝐵 + 𝐸𝐷 ); eliminando el cuadrado del vector resultante, introducimos dentro de una raíz el resto de la ecuación: 𝐸𝑅 = √(𝐸𝐶 − 𝐸𝐴 )2 + (𝐸𝐵 + 𝐸𝐷 )2 Calculamos los campos creados por cada carga, aplicando la ecuación de la intensidad de campo eléctrico en un punto: 𝑞 𝐸𝐴 = 𝐾 𝑥 𝑟 2𝐴 𝐴𝑝 𝑞𝐵 𝐸𝐵 = 𝐾 𝑥 2 𝑟𝐵𝑝 𝐸𝐶 = 𝐾 𝑥 𝑞𝐶 2 𝑟𝐶𝑝 𝑞𝐷 2 𝑟𝐷𝑝 Las distancias de las cargas al punto son iguales por ser un cuadrado y estar ubicado en su centro, aquí hacemos uso de un ángulo α= 45°, debido a las características de la figura; para hallar la distancia “r”, aplicamos la función coseno. 𝐶𝐴 𝑟𝑜𝑝 cos 45° = = 𝐻 𝑟𝐷𝑝 Despejamos “rDp”: 𝑟𝐷𝑝 = 𝑟𝑜𝑝 𝑥 cos 45° Sustituimos: 𝑟𝐷𝑝 = 4𝑥10−2 𝑚 𝑥 cos 45° 𝑟𝐷𝑝 = 2,83𝑥10−2 𝑚 Ahora calculamos los campos creados por cada carga: 4𝑥10−6 𝐶 𝑁 𝑥 𝑚2 𝐸𝐴 = 9𝑥109 𝐶 2 𝑥 (2,83𝑥10−2 𝑚)2 𝑁 𝐸𝐴 = 4,5𝑥107 𝐶 2 5𝑥10−6 𝐶 9𝑁 𝑥 𝑚 𝐸𝐵 = 9𝑥10 𝐶 2 𝑥 (2,83𝑥10−2 𝑚)2 𝑁 𝐸𝐵 = 5,6𝑥107 𝐶 6𝑥10−6 𝐶 𝑁 𝐸𝐶 = 9𝑥109 𝐶 𝑥 (2,83𝑥10−2 𝑚)2 𝑁 𝐸𝐶 = 6,7𝑥107 𝐶 8𝑥10−6 𝐶 𝑁 𝐸𝐷 = 9𝑥109 𝐶 𝑥 (2,83𝑥10−2 𝑚)2 𝑁 𝐸𝐷 = 9,05𝑥107 𝐶 𝐸𝑅 𝐸𝐷 = 𝐾 𝑥 𝑁 𝑁 𝑁 𝑁 = √(6,7𝑥107 𝐶 − 4,5𝑥107 𝐶 )2 + (5,6𝑥107 𝐶 +9,05𝑥107 𝐶 )2 𝑁 𝐸𝑅 = 1,48𝑥108 𝐶 47.- .- En la figura se tienen un cuadrado de 8 cm de lado. En cada uno de sus vértices hay cargas eléctricas cuyos valores son: 𝑞𝐴 = +4𝑥10−6 𝐶; 𝑞𝐵 = +5𝑥10−6 𝐶; 𝑞𝐶 = −6 −6 +6𝑥10 𝐶 𝑦 𝑞𝐷 = +8𝑥10 𝐶. Calcular el modulo de la intensidad del campo eléctrico resultante en el centro del cuadrado. ( ( ( ( ) 1,46𝑥108 𝑁𝐶 ) 1,48𝑥107 𝑁𝐶 ) 1,48𝑥108 𝑁𝐶 ) 1,46𝑥106 𝑁𝐶 +qA -qB 8 cm +qD Datos: 𝑞𝐴 = +4𝑥10−6 𝐶 𝑞𝐵 = −5𝑥10−6 𝐶 𝑞𝐶 = +6𝑥10−6 𝐶 𝑞𝐷 = +8𝑥10−6 𝐶 𝐿 = 8𝑐𝑚 = 8𝑥10−2 𝑚 𝐸𝑅 =? 𝑒𝑛 𝑒𝑙 𝑐𝑒𝑛𝑡𝑟𝑜 +qC Diagrama: +qA -qB P 8 cm +qD +qC O EB EA EC Conversión de Unidades: Se transformaron los centímetros (cm) a metros (m), multiplicando por 10-2 m o dividiendo entre 100 cm. EB+ED EA EC-EA Podemos observar que los campos eléctricos en el centro del cuadrado, se forman perpendicularmente; pero, debemos tomar en cuenta que los vectores formados por qA y qC, tienen la misma dirección y sentidos contrarios, mientras que los formados por qB y qD, tienen igual dirección y sentido. Solución: Como los vectores a sumar tienen las características mencionadas anteriormente, aplicamos el teorema de Pitágoras, con las variaciones que se tienen entre los vectores que actúan: 𝐶 2 = 𝑎2 + 𝑏 2 Donde: 𝑐 = 𝐸𝑅 ; 𝑎 = (𝐸𝐶 − 𝐸𝐴 )𝑦 𝑏 = (𝐸𝐵 + 𝐸𝐷 ); eliminando el cuadrado del vector resultante, introducimos dentro de una raíz el resto de la ecuación: 𝐸𝑅 = √(𝐸𝐶 − 𝐸𝐴 )2 + (𝐸𝐵 + 𝐸𝐷 )2 Calculamos los campos creados por cada carga, aplicando la ecuación de la intensidad de campo eléctrico en un punto: 𝑞 𝐸𝐴 = 𝐾 𝑥 𝑟 2𝐴 𝐴𝑝 𝑞𝐵 𝐸𝐵 = 𝐾 𝑥 2 𝑟𝐵𝑝 𝐸𝐶 = 𝐾 𝑥 𝑞𝐶 2 𝑟𝐶𝑝 𝑞𝐷 2 𝑟𝐷𝑝 Las distancias de las cargas al punto son iguales por ser un cuadrado y estar ubicado en su centro, aquí hacemos uso de un ángulo α= 45°, debido a las características de la figura; para hallar la distancia “r”, aplicamos la función coseno. 𝐶𝐴 𝑟𝑜𝑝 cos 45° = = 𝐻 𝑟𝐷𝑝 Despejamos “rDp”: 𝑟𝐷𝑝 = 𝑟𝑜𝑝 𝑥 cos 45° Sustituimos: 𝑟𝐷𝑝 = 4𝑥10−2 𝑚 𝑥 cos 45° 𝑟𝐷𝑝 = 2,83𝑥10−2 𝑚 Ahora calculamos los campos creados por cada carga: 4𝑥10−6 𝐶 𝑁 𝑥 𝑚2 𝐸𝐴 = 9𝑥109 𝐶 2 𝑥 (2,83𝑥10−2 𝑚)2 𝑁 𝐸𝐴 = 4,5𝑥107 𝐶 2 5𝑥10−6 𝐶 9𝑁 𝑥 𝑚 𝐸𝐵 = 9𝑥10 𝐶 2 𝑥 (2,83𝑥10−2 𝑚)2 𝑁 𝐸𝐵 = 5,6𝑥107 𝐶 6𝑥10−6 𝐶 𝑁 𝐸𝐶 = 9𝑥109 𝐶 𝑥 (2,83𝑥10−2 𝑚)2 𝑁 𝐸𝐶 = 6,7𝑥107 𝐶 8𝑥10−6 𝐶 𝑁 𝐸𝐷 = 9𝑥109 𝐶 𝑥 (2,83𝑥10−2 𝑚)2 𝑁 𝐸𝐷 = 9,05𝑥107 𝐶 𝐸𝑅 𝐸𝐷 = 𝐾 𝑥 𝑁 𝑁 𝑁 𝑁 = √(6,7𝑥107 𝐶 − 4,5𝑥107 𝐶 )2 + (5,6𝑥107 𝐶 +9,05𝑥107 𝐶 )2 𝑁 𝐸𝑅 = 1,48𝑥108 𝐶 47.- En la figura se tienen un cuadrado de 8 cm de lado. En cada uno de sus vértices hay cargas eléctricas cuyos valores son: 𝑞𝐴 = −4𝑥10−6 𝐶; 𝑞𝐵 = +5𝑥10−6 𝐶; 𝑞𝐶 = −6 −6 +6𝑥10 𝐶 𝑦 𝑞𝐷 = +8𝑥10 𝐶. Calcular el modulo de la intensidad del campo eléctrico resultante en el centro del cuadrado. ( ( ( ( ) 1,84𝑥108 𝑁𝐶 ) 1,48𝑥107 𝑁𝐶 ) 1,48𝑥108 𝑁𝐶 ) 1,84𝑥107 𝑁𝐶 -qA -qB 8 cm +qD Datos: 𝑞𝐴 = −4𝑥10−6 𝐶 𝑞𝐵 = −5𝑥10−6 𝐶 𝑞𝐶 = +6𝑥10−6 𝐶 𝑞𝐷 = +8𝑥10−6 𝐶 𝐿 = 8𝑐𝑚 = 8𝑥10−2 𝑚 𝐸𝑅 =? 𝑒𝑛 𝑒𝑙 𝑐𝑒𝑛𝑡𝑟𝑜 +qC Diagrama: -qA -qB P 8 cm +qD +qC O ER EB EA EB+ED EA Conversión de Unidades: Se transformaron los centímetros (cm) a metros (m), multiplicando por 10-2 m o dividiendo entre 100 cm. EC EC-EA Podemos observar que los campos eléctricos en el centro del cuadrado, se forman perpendicularmente; pero, debemos tomar en cuenta que los vectores formados por qA y qC, tienen la misma dirección y sentidos, al igual que los formados por qB y qD. Solución: Como los vectores a sumar tienen las características mencionadas anteriormente, aplicamos el teorema de Pitágoras, con las variaciones que se tienen entre los vectores que actúan: 𝐶 2 = 𝑎2 + 𝑏 2 Donde: 𝑐 = 𝐸𝑅 ; 𝑎 = (𝐸𝐶 + 𝐸𝐴 )𝑦 𝑏 = (𝐸𝐵 + 𝐸𝐷 ); eliminando el cuadrado del vector resultante, introducimos dentro de una raíz el resto de la ecuación: 𝐸𝑅 = √(𝐸𝐶 + 𝐸𝐴 )2 + (𝐸𝐵 + 𝐸𝐷 )2 Calculamos los campos creados por cada carga, aplicando la ecuación de la intensidad de campo eléctrico en un punto: 𝑞 𝐸𝐴 = 𝐾 𝑥 𝑟 2𝐴 𝐴𝑝 𝑞𝐵 𝐸𝐵 = 𝐾 𝑥 2 𝑟𝐵𝑝 𝐸𝐶 = 𝐾 𝑥 𝑞𝐶 2 𝑟𝐶𝑝 𝑞𝐷 2 𝑟𝐷𝑝 Las distancias de las cargas al punto son iguales por ser un cuadrado y estar ubicado en su centro, aquí hacemos uso de un ángulo α= 45°, debido a las características de la figura; para hallar la distancia “r”, aplicamos la función coseno. 𝐶𝐴 𝑟𝑜𝑝 cos 45° = = 𝐻 𝑟𝐷𝑝 Despejamos “rDp”: 𝑟𝐷𝑝 = 𝑟𝑜𝑝 𝑥 cos 45° Sustituimos: 𝑟𝐷𝑝 = 4𝑥10−2 𝑚 𝑥 cos 45° 𝑟𝐷𝑝 = 2,83𝑥10−2 𝑚 Ahora calculamos los campos creados por cada carga: 2 4𝑥10−6 𝐶 9𝑁 𝑥 𝑚 𝐸𝐴 = 9𝑥10 𝐶 2 𝑥 (2,83𝑥10−2 𝑚)2 𝑁 𝐸𝐴 = 4,5𝑥107 𝐶 5𝑥10−6 𝐶 𝑁 𝑥 𝑚2 𝐸𝐵 = 9𝑥109 𝐶 2 𝑥 (2,83𝑥10−2 𝑚)2 𝑁 𝐸𝐵 = 5,6𝑥107 𝐶 6𝑥10−6 𝐶 𝑁 𝐸𝐶 = 9𝑥109 𝐶 𝑥 (2,83𝑥10−2 𝑚)2 𝑁 𝐸𝐶 = 6,7𝑥107 𝐶 8𝑥10−6 𝐶 9𝑁 𝐸𝐷 = 9𝑥10 𝐶 𝑥 (2,83𝑥10−2 𝑚)2 𝑁 𝐸𝐷 = 9,05𝑥107 𝐶 𝐸𝑅 𝐸𝐷 = 𝐾 𝑥 𝑁 𝑁 𝑁 𝑁 = √(6,7𝑥107 𝐶 + 4,5𝑥107 𝐶 )2 + (5,6𝑥107 𝐶 + 9,05𝑥107 𝐶 )2 𝑁 𝐸𝑅 = 1,84𝑥108 𝐶 48.- ABC es un triangulo equilátero de 3 cm de lado. En los vértices hay cargas eléctricas: 𝑞𝐴 = +4𝑥10−6 𝐶; 𝑞𝐵 = +3𝑥10−6 𝐶; ubicadas en la base del triangulo. Calcular la magnitud de la intensidad del campo eléctrico resultante en el punto P, ubicado en el vértice superior del triangulo. P ( ) 6,1𝑥107 𝑁𝐶 ( ) 6,1𝑥106 𝑁𝐶 3 cm 8𝑁 ( ) 6,1𝑥10 𝐶 ( ) 6,1𝑥105 𝑁𝐶 +qA +qB Datos: 𝑞𝐴 = +4𝑥10−6 𝐶 𝑞𝐵 = +3𝑥10−6 𝐶 𝑟 = 3𝑐𝑚 = 3𝑥10−2 𝑚 𝐸𝑅 =? 𝑒𝑛 𝑃 Diagrama: ER EA EB P 3 cm +qA Conversión de Unidades: Transformamos los centímetros (cm) a metros (m), multiplicando por 10-2m o dividimos entre 100 cm +qB Solución: Como los vectores a sumar forman un ángulo diferente a 90º; es decir, no son perpendiculares, aplicamos el teorema del coseno para hallar la magnitud del campo eléctrico resultante en P. 𝑐 2 = 𝑎2 + 𝑏 2 − 2𝑥𝑎𝑥𝑏𝑥 cos 𝜗 Donde 𝜗 = 180° − 60° ; 𝑝orque el triangulo es equilátero. 𝑐 = 𝐸𝑅 ; 𝑎 = 𝐸𝐴 𝑦 𝑏 = 𝐸𝐵 Sustituimos y para eliminar el cuadrado del vector resultante, introducimos el resto de la ecuación en una raíz cuadrada: 2 2 𝐸𝑅 = √𝐸𝐴𝑝 + 𝐸𝐵𝑝 − 2𝑥𝐸𝐴𝑝 𝑥𝐸𝐵𝑝 𝑥 cos(180° − 60°) Calculamos los campos creados por cada carga, aplicando la ecuación de la intensidad de campo eléctrico en un punto: 𝑞 𝐸𝐴 = 𝐾 𝑥 𝑟 2𝐴 𝐴𝑝 𝑞𝐵 𝐸𝐵 = 𝐾 𝑥 2 𝑟𝐵𝑝 Sustituimos en la ecuación: 4𝑥10−6 𝐶 (3𝑥10−2 𝑚)2 𝑁 𝐸𝐴 = 4𝑥107 𝐶 𝐸𝐴 = 9𝑥109 𝑁 𝑥 𝑚2 𝐶2 𝑥 3𝑥10−6 𝐶 (3𝑥10−2 𝑚)2 𝑁 𝐸𝐵 = 3𝑥107 𝐶 𝐸𝐵 = 9𝑥109 𝑁 𝑥 𝑚2 𝐶2 𝑥 𝐸𝑅 𝑁 𝑁 𝑁 𝑁 = √(4𝑥107 𝐶 )2 + (3𝑥107 𝐶 )2 − 2𝑥4𝑥107 𝐶 𝑥3𝑥107 𝐶 𝑥 cos 120° 𝑁 𝐸𝑅 = 6,1𝑥107 𝐶 49.- ABC es un triangulo equilátero de 6 cm de lado. En los vértices A y C hay dos cargas eléctricas; 𝑞𝐴 = +9𝑥10−6 𝐶 y 𝑞𝐵 = −8𝑥10−6 𝐶. Calcular la intensidad del campo eléctrico resultante en el centro del triangulo. ( ( ( ( ) 1.1𝑥108 𝑁𝐶 ) 1,1𝑥109 𝑁𝐶 ) 1,1𝑥106 𝑁𝐶 ) 1,1𝑥108 𝑁𝐶 Datos: 𝑞𝐴 = +9𝑥10−6 𝐶 𝑞𝐵 = −8𝑥10−6 𝐶 𝑟 = 6𝑐𝑚 = 6𝑥10−2 𝑚 𝐸𝑅 =? 𝑒𝑛 𝑃 B 6 cm A C Diagrama: 6 cm +qA -qC EA P ER EC +qA 3 cm O 3 cm -qC Al hacer el análisis, nos queda un triangulo isósceles, donde en el vértice superior se forma un ángulo de 120º el cual se divide en dos de 60º, debido a la línea imaginaria que se traza para hacer el análisis de los vectores, por estar el punto en el medio del triangulo equilátero. Siendo los otros ángulos de 30º. Conversión de Unidades: Solución: Como los vectores a sumar forman un ángulo diferente a 90º; es decir, Transformamo s los centímetros (cm) a metros (m), multiplicando por 10-2m o dividimos entre 100 cm no son perpendiculares, aplicamos el teorema del coseno para hallar la magnitud del campo eléctrico resultante en P. 𝑐 2 = 𝑎2 + 𝑏 2 − 2𝑥𝑎𝑥𝑏𝑥 cos 𝜗 Donde 𝜗 = 180° − 60° ; 𝑝orque el triangulo es equilátero. 𝑐 = 𝐸𝑅 ; 𝑎 = 𝐸𝐴 𝑦 𝑏 = 𝐸𝐶 Sustituimos y para eliminar el cuadrado del vector resultante, introducimos el resto de la ecuación en una raíz cuadrada: 2 2 𝐸𝑅 = √𝐸𝐴𝑝 + 𝐸𝐶𝑝 − 2𝑥𝐸𝐴𝑝 𝑥𝐸𝐶𝑝 𝑥 cos(180° − 60°) Calculamos los campos creados por cada carga, aplicando la ecuación de la intensidad de campo eléctrico en un punto: 𝑞 𝐸𝐴 = 𝐾 𝑥 𝑟 2𝐴 𝐴𝑝 𝑞𝐶 𝐸𝐶 = 𝐾 𝑥 2 𝑟𝐶𝑝 Aplicando la función coseno, calculamos las distancias rAp y rCp, las cuales son iguales. 𝐶𝐴 𝑟0𝐴 cos 30° = = 𝐻 𝑟𝐴𝑝 Despejamos rAp: 𝑟𝑂𝐴 𝑟𝐴𝑝 = cos 30° Sustituimos: 3𝑥10−2 𝑚 𝑟𝐴𝑝 = cos 30° 𝑟𝐴𝑝 = 3,46𝑥10−2 𝑚 Sustituimos en la ecuación: 9𝑥10−6 𝐶 (3,46𝑥10−2 𝑚)2 𝑁 𝐸𝐴 = 6,77𝑥107 𝐶 𝐸𝐴 = 9𝑥109 𝐸𝐵 = 𝑁 𝑥 𝑚2 𝐶2 𝑥 8𝑥10−6 𝐶 𝑥 (3,46𝑥10−2 𝑚)2 𝑁 𝐸𝐵 = 6,01𝑥107 𝐶 𝑁𝑥𝑚 9𝑥109 𝐶 2 2 𝐸𝑅 𝑁 𝑁 𝑁 𝑁 = √(6,77𝑥107 𝐶 )2 + (6,01𝑥107 𝐶 )2 − 2𝑥6,77𝑥107 𝐶 𝑥6,01𝑥107 𝐶 𝑥 cos 120° 𝑁 𝐸𝑅 = 1,1𝑥108 𝐶 50.- Una carga 𝑞1 = +6 𝑛𝐶; esta ubicada sobre el eje “Y” e 𝑌 = +3 𝑐𝑚 y una carga 𝑞2 = −6 𝑛𝐶 ubicada sobre el eje “Y” en 𝑌 = −3 𝑐𝑚. Calcular: a) la magnitud del campo eléctrico en el punto 𝑋 = 4 𝑐𝑚. b) la fuerza que se ejerce sobre una carga de prueba 𝑞0 = 2 𝑛𝐶 colocada en 𝑋 = 4 𝑐𝑚. ( ( ( ( ) 𝐸𝑅 ) 𝐸𝑅 ) 𝐸𝑅 ) 𝐸𝑅 = 4,1𝑥104 𝑁𝐶; 𝐹 = 8,2𝑥10−7 𝑁 = 4𝑥104 𝑁𝐶; 𝐹 = 8𝑥10−7 𝑁 = 4,1𝑥10−4 𝑁𝐶; 𝐹 = 8,1𝑥10−7 𝑁 = 4,1𝑥10−4 𝑁𝐶; 𝐹 = −8,2𝑥10−7 𝑁 Datos: 𝑞1 = +6 𝑛𝐶 = +6𝑥10−9 𝐶 𝑌 = +3 𝑐𝑚 = +3𝑥10−2 𝑚 𝑞2 = −6 𝑛𝐶 = 6𝑥10−9 𝐶 𝑌 = −3 𝑐𝑚 = −3𝑥10−2 𝑚 𝑎) 𝐸𝑅 =? 𝑋 = 4 𝑐𝑚 = 4𝑥10−2 𝑚 𝑏) 𝐹 =? 𝑞0 = 2 𝑛𝐶 = 2𝑥10−9 𝐶 𝑋 = 4 𝑐𝑚 = 4𝑥10−2 𝑚 Diagrama: Conversión de unidades: Transformamos los centímetros (cm) a metros (m), multiplicando por 10-2 m y los nanocoulomb (nC) Solución: Como los vectores a sumar forman un ángulo ≠ 90°, aplicamos el teorema del coseno para hallar el modulo o magnitud de la intensidad del campo eléctrico resultante. +q1 + 3 cm O α 4 cm α - 3 cm α β E2 E1 -q2 ER Según las características del problema, debido a la ubicación de las cargas y el punto, los vectores, tienen la dirección y sentidos indicados en el diagrama. 𝑐 2 = 𝑎2 + 𝑏 2 − 2𝑥𝑎𝑥𝑏𝑥 cos 𝜗 Donde: 𝑐 = 𝐸𝑅 ; 𝑎 = 𝐸1 𝑦 𝑏 = 𝐸2 . También debemos tomar en cuenta que: 𝜗 = 180° − 𝛼; siendo α desconocido. a Coulomb, Para eliminar el cuadrado del vector resultante, introducimos dentro multiplicando por de una raíz cuadrada el resto de la ecuación: 10-9 C. 𝐸𝑅 = √𝐸12 + 𝐸22 − 2𝑥𝐸1 𝑥𝐸2 𝑥 cos(180° − 𝛼) Los campos creados por cada carga, los obtenemos aplicando la ecuación de la intensidad del campo eléctrico en un punto. 𝐸1 = 𝐾 𝑥 𝑞1 2 𝑟1𝑝 y 𝑞2 2 𝑟2𝑝 Las distancias de las cargas al punto se desconocen; pero las características de la figura nos indica que son iguales y la podemos calcular aplicando el teorema de Pitágoras, ya que se conocen los lados de los triángulos que se forman: 𝐸2 = 𝐾 𝑥 𝐶 2 = 𝑎2 + 𝑏 2 Donde 𝑐 = 𝑟; 𝑎 = 𝑋 𝑦 𝑏 = 𝑌, sustituimos y eliminamos el cuadrado de “r”, introduciendo dentro de una raíz cuadrada el resto de los términos. 𝑟 = √𝑋 2 + 𝑌 2 Sustituimos en la ecuación: 𝑟 = √(4𝑥10−2 𝑚)2 + (3𝑥10−2 𝑚)2 𝑟 = 0,05 𝑚 = 5𝑥10−2 𝑚 Ahora calculamos la intensidad de campo eléctrico creado por cada carga: 2 6𝑥10−6 𝐶 9𝑁 𝑥 𝑚 𝐸1 = 9𝑥10 𝐶 2 𝑥 (5𝑥10−2 𝑚)2 𝑁 𝐸1 = 21600 𝐶 Por tener características similares, los campos creados por cada carga son iguales: 𝐸1 = 𝐸2 Para hallar el valor de la intensidad del campo resultante, tenemos que calcular el valor del ángulo α, ara ello hacemos uso de la función sin 𝛼: 𝐶𝑂 𝑟01 sin 𝛼 = = 𝐻 𝑟1𝑥 Sustituimos: 3 𝑐𝑚 sin 𝛼 = 5 𝑐𝑚 sin 𝛼 = 0,6 Entonces: 𝛼 = 36°52′12" Ahora: 𝜗 = 180° − 36°52′12" 𝜗 = 143°7′48" para calcular ER, utilizamos el ángulo de 143º 𝐸𝑅 𝑁 𝑁 𝑁 = √(2,16𝑥104 𝐶 )2 + (2,16𝑥104 𝐶 )2 − 2 𝑥2,16𝑥104 𝐶 𝑥2,16𝑥104 𝑁𝐶𝑥 cos 143° 𝑁 𝐸𝑅 = 4,1𝑥104 𝐶 b) Hallamos la fuerza sobre la carga de prueba, aplicando la ecuación del campo eléctrico, por definición: 𝐸= 𝐹 𝑞0 Despejamos F: 𝐹 = 𝑞0 𝑥𝐸 Sustituimos: 𝑁 𝐹 = 4,1𝑥104 𝐶 𝑥 2𝑥10−9 𝐶 𝐹 = 8,2𝑥10−7 𝑁 Potencial Eléctrico (V): Se llama potencial eléctrico en un unto de un campo eléctrico al trabajo necesario realizado contra la fuerza eléctrica para transportar la unidad positiva de carga eléctrica desde fuera del campo eléctrico hasta dicho punto: 𝑊 𝑉= 𝑞0 Diferencia de Potencial (𝑉𝐵 − 𝑉𝐴 ): Se llama diferencia de potencial entre dos puntos A y B de un campo eléctrico, al trabajo por unidad de carga tiene que realizar un agente externo para llevar la unidad de carga positiva desde A hasta B sin que cambie la energía cinética. 𝑊𝐴𝐵 𝑉𝐵 − 𝑉𝐴 = 𝑞0 Energía Potencial Eléctrica (U): La energía potencial electrostática de un sistema de cargas eléctricas puntuales es el trabajo necesario para trasladar las cargas desde una separación infinita hasta sus posiciones finales sin aceleración. 𝑞1 𝑥 𝑞2 𝑈=𝐾𝑥 𝑟 La energía potencial eléctrica o trabajo eléctrico realizad (W). Existe una relación entre el electrón- voltio (eV) y el Joule (J): Sabemos que: 𝑊 = 𝑞0 𝑥 (𝑉𝐵 − 𝑉𝐴 ), si sustituimos en la ecuación q por 𝑒 = 1,6𝑥10−19 𝐶 𝑦 (𝑉𝐵 − 𝑉𝐴 )= 1 𝑉; nos queda que: 1𝑒𝑉 = 1,6𝑥10-19 C x 1 V, entonces: 1 𝑒𝑉 = 1,6𝑥10−19 𝐽 Diferencia de Potencial en un campo eléctrico uniforme: La diferencia de potencial entre dos placas con cargas opuestas es igual al producto de la magnitud del campo eléctrico (E) por la distancia (d) entre las placas. 𝑉𝐵 − 𝑉𝐴 = 𝐸 𝑥 𝑑 Potencial eléctrico debido a una carga puntual (V): 𝑊 Partiendo de la ecuación: 𝑉 = 𝑞 , y sabiendo que trabajo es 𝑊 = 𝐹 𝑥 𝑟, conociendo que 0 según la ley de Coulomb la fuerza F es: 𝐹=𝐾 𝑞 𝑥 𝑞0 𝑟2 Sustituimos en la ecuación anterior y nos queda que: 𝑞 𝑥 𝑞0 𝑊=𝐾 𝑥𝑟 𝑟2 Y: 𝑞 𝑥 𝑞0 𝑥𝑟 2 𝑉=𝐾 𝑟 𝑞0 Entonces: 𝑞 𝑉=𝐾𝑥 𝑟 Primer Nivel: (Bajo) 1.- Sobre una carga de +5x10-6 C, se realiza un trabajo de 6 joule. ¿Cuál es el potencial eléctrico creador por la carga?. ( ( ( ( ) 1,6x106 V ) 1,2x106 V ) 1,2x10-6 V ) 1,2x107 V Datos: 𝑞 = +5𝑥10−6 𝐶 𝑊 =6𝐽 𝑉 =? Conversión de Unidades: No es necesario. Diagrama: No es necesario Solución: Aplicamos la ecuación de la definición de potencial eléctrico: 𝑊 𝑉= 𝑞0 Sustituimos: 6𝐽 𝑉= 5𝑥10−6 𝐶 𝑉 = 1,2𝑥106 𝑉 2.- El potencial eléctrico creado por una carga eléctrica es de 25 voltios, cuando sobre ella se realiza un trabajo de 2x10-2 J. ¿Cuál es el valor de la carga? ( ( ( ( ) 3x10-4 C ) 8x104 C ) 8x10-4 C ) 3x104 C Datos: 𝑉 = 25 𝑉 𝑊 = 2𝑥10−2 𝐽 𝑞 =? Conversión de unidades: No es necesario. Diagrama: No es necesario Solución: Aplicamos la ecuación de la definición de potencial eléctrico: 𝑊 𝑉= 𝑞0 Despejamos “q”: 𝑊 𝑞0 = 𝑉 Sustituimos: 2𝑥10−2 𝐽 25 𝑉 𝑞0 = 8𝑥10−4 𝐶 𝑞0 = 3.- ¿Qué trabajo se debe realizar, para trasladar una carga eléctrica de +3x10-6 C en un campo eléctrico, cuando sobre ella actúa un potencial de 220 V? ( ( ( ( ) 66 J ) 660 J ) 6,6x10-6J ) 6,6x10-4 J Datos: 𝑊 =? 𝑞0 = +3𝑥10−6 𝐶 𝑉 = 220 𝑉 Conversión de Unidades: No es necesaria Diagrama: No es necesario Solución: Aplicamos la ecuación de la definición de potencial eléctrico: 𝑊 𝑉= 𝑞0 Despejamos “W”: 𝑊 = 𝑉 𝑥 𝑞0 Sustituimos: 𝑊 = 220 𝑉 𝑥 3𝑥10−6 𝐶 𝑊 = 6,6𝑥10−4 𝐽 4.- Sobre una carga de -8x10-6C, se realiza un trabajo de 2 J. ¿Cuál es el potencial eléctrico creado por la carga? ( ( ( ( ) −2,5𝑥105 𝑉 ) 2,5𝑥105 𝑉 ) 2,5𝑥10−5 𝑉 ) −2,5𝑥10−5 𝑉 Datos: 𝑞 = −8𝑥10−6 𝐶 𝑊 =2𝐽 𝑉 =? Conversión de Unidades: No es necesario. Diagrama: No es necesario Solución: Aplicamos la ecuación de la definición de potencial eléctrico: 𝑊 𝑉= 𝑞0 Sustituimos: 2𝐽 𝑉= (−8𝑥10−6 𝐶) 𝑉 = −2,5𝑥105 𝑉 5.- Para trasladar una carga de +5x10-6 C entre dos puntos de un campo eléctrico hay que realizar un trabajo de 4 joules. Calcular la diferencia de potencial entre dichos puntos. ( ( ( ( ) 5𝑥105 𝑉 ) 8𝑥105 𝑉 ) 8𝑥10−5 𝑉 ) −5𝑥108 𝑉 Datos: 𝑞0 = +5𝑥10−6 𝐶 𝑊𝐴𝐵 = 5𝐽 𝑉𝐵 − 𝑉𝐴 =? Diagrama: No es necesario Conversión de Unidades: No es necesaria. Solución: Aplicamos la ecuación de la definición de la diferencia de potencial: 𝑊𝐴𝐵 𝑉𝐵 − 𝑉𝐴 = 𝑞0 Sustituimos: 5𝐽 𝑉𝐵 − 𝑉𝐴 = 5𝑥10−6 𝐶 𝑉𝐵 − 𝑉𝐴 = 8𝑥105 𝑉 6.- La diferencia de potencial entre dos puntos de un campo eléctrico es de 4𝑥102 𝑉. Calcular el trabajo que hay que realizar ara transportar desde un punto a otro una carga de 6𝑥10−5 𝐶. ( ( ( ( ) 0,024 J ) 0,24 J ) -0,0024 J ) 0,02 J Datos: 𝑉𝐵 − 𝑉𝐴 = 4𝑥102 𝑊𝐴𝐵 =? 𝑞0 = +5𝑥10−6 𝐶 Diagrama: No es necesario Conversión de Unidades: No es necesaria. Solución: Aplicamos la ecuación de la definición de la diferencia de potencial: 𝑊𝐴𝐵 𝑉𝐵 − 𝑉𝐴 = 𝑞0 Despejamos “WAB” 𝑊𝐴𝐵 = 𝑞0 𝑥 (𝑉𝐵 − 𝑉𝐴 ) Sustituimos: 𝑊𝐴𝐵 = 6𝑥10−5 𝐶 𝑥 4𝑥102 𝑉 𝑊𝐴𝐵 = 0,024 𝐽 7.- La diferencia de potencial entre dos puntos de un campo eléctrico uniforme es 50 voltios. Calcular el valor de la carga eléctrica, cuando sobre ella se realiza un trabajo de 2,4x10-3 Joules. ( ( ( ( ) 4,8x10-5C ) 4,8x10-6C ) 4,8x10-3 C ) 4,8x10-9 C Datos: 𝑉𝐵 − 𝑉𝐴 = 50 𝑉 𝑞0 =? 𝑊𝐴𝐵 = 2,4𝑥10−3 𝐽 Diagrama: No es necesario Conversión de Unidades: Solución: No es necesario Aplicamos la ecuación de la diferencia de potencial entre dos puntos: 𝑉𝐵 − 𝑉𝐴 = 𝑊𝐴𝐵 𝑞0 Despejamos “q0” 𝑞0 = 𝑊𝐴𝐵 𝑉𝐵 − 𝑉𝐴 Sustituimos: 𝑞0 = 2,4𝑥10−3 𝐽 50 𝑉 𝑞0 = 4,8𝑥10−5 𝐶 8.- La distancia entre dos puntos de un campo eléctrico uniforme de 60 N/C es de 8 cm. Calcular la diferencia de potencial que hay entre ellos. ( ( ( ( ) 4,6 V ) 48 V ) 480 V ) 4,8 V Datos: 𝐸 = 60 𝑁⁄𝐶 𝑟 = 𝑑 = 8 𝑐𝑚 = 8𝑥10−2 𝑚 𝑉𝐵 − 𝑉𝐴 =? Conversión de Unidades: Se transforman los centímetros (cm) a metros (m), multiplicando por 10-2 m o dividiendo entre 100 cm Diagrama: No es necesario Solución: Aplicamos la ecuación de la diferencia de potencial en un campo eléctrico uniforme: 𝑉𝐵 − 𝑉𝐴 = 𝐸 𝑥 𝑑 Sustituimos: 𝑉𝐵 − 𝑉𝐴 = 60 𝑁⁄𝐶 𝑥8𝑥10−2 𝑚 𝑉𝐵 − 𝑉𝐴 = 4,8 𝑉 9.- La diferencia de potencial entre dos untos de un campo eléctrico uniforme es de 12 Voltios. Calcular la intensidad de dicho campo sabiendo que la distancia entre ambos untos es de 2 cm. ( ( ( ( ) 600 N/C ) 60 N/C ) 6 N/C ) -600 N/C Datos: 𝑉𝐵 − 𝑉𝐴 = 12 𝑉 𝐸 =? 𝑑 = 2 𝑐𝑚 = 2𝑥10−2 𝑚 Diagrama: No es necesario. Conversión de Unidades: Solución: Transformamos los Aplicamos la ecuación de la diferencia de potencial en un centímetros (cm) a campo eléctrico uniforme: 𝑉𝐵 − 𝑉𝐴 = 𝐸 𝑥 𝑑 metros (m), -2 multiplicando por 10 m o dividiendo entre 100 Despejamos “E” 𝑉𝐵 − 𝑉𝐴 cm. 𝐸= 𝑑 Sustituimos: 𝐸= 12 𝑉 2𝑥10−2 𝑚 𝐸 = 600 𝑁⁄𝐶 10.- Una carga eléctrica esta en un campo eléctrico uniforme de 25 N/C. Cuando se deslaza 4 cm realiza un trabajo de 5 joules. Calcular el valor de la carga. ( ( ( ( )5C ) 5x10-6 C ) 5x10-2 C ) -5 C Datos: 𝐸 = 25 𝑁⁄𝐶 𝑟 = 𝑑 = 4𝑐𝑚 = 4𝑥10−2 𝑚 𝑊𝐴𝐵 = 5 𝐽 𝑞0 =? Conversión de Unidades: Transformamos los centímetros (cm) a metros (m), multiplicando por 10-2 m o dividiendo entre 100 cm. Diagrama: No es necesario Solución: Aplicamos la ecuación de la diferencia de potencial en un campo eléctrico uniforme: 𝑉𝐵 − 𝑉𝐴 = 𝐸 𝑥 𝑑 Sustituimos: 𝑉𝐵 − 𝑉𝐴 = 25 𝑁⁄𝐶 𝑥 4𝑥10−2 𝑚 𝑉𝐵 − 𝑉𝐴 = 1 𝑉 Luego de calcular la diferencia de potencial (d.d.p), aplicamos la ecuación de la definición de diferencia de potencial y despejamos “q0”: 𝑉𝐵 − 𝑉𝐴 = 𝑊𝐴𝐵 𝑞0 Despejamos “q0” 𝑞0 = 𝑊𝐴𝐵 𝑉𝐵 − 𝑉𝐴 Sustituimos: 𝑞0 = 5𝐽 1𝑉 𝑞0 = 5 𝐶 11.- Una carga eléctrica de 8x10-6C esta situada en un campo eléctrico uniforme. Sobre ella actúa una fuerza de 4 dinas (din). Si la carga se deslaza del punto A al B distante 3 cm, calcular la diferencia de potencial entre dichos puntos. ( ( ( ( ) 0,16 V ) 15 V ) 1,5 V ) 0,15 V Datos: 𝑞0 = 8𝑥10−6 𝐶 𝐹 = 4 𝑑𝑖𝑛 = 4𝑥10−5 𝑁 𝑑 = 3 𝑐𝑚 = 3𝑥10−2 𝑚 𝑉𝐵 − 𝑉𝐴 =? Diagrama: No es necesario Conversión de Unidades: Transformamos los centímetros (cm) a metros (m), multiplicando por 10-2 m o dividiendo entre 100 cm. También en este caso se transforma la fuerza de dinas (din) a Newton (N), multiplicando por 10-5 N o dividiendo entre 100000 din. Solución: Calculamos el valor del campo eléctrico, aplicando la ecuación de la intensidad de campo eléctrico: 𝐹 𝐸= 𝑞0 Sustituimos: 4𝑥10−5 𝑁 𝐸= 8𝑥10−6 𝐶 𝐸 = 5 𝑁⁄𝐶 Ahora, aplicamos la ecuación de la diferencia de potencial en un campo eléctrico uniforme: 𝑉𝐵 − 𝑉𝐴 = 𝐸 𝑥 𝑑 Sustituimos: −2 𝑉𝐵 − 𝑉𝐴 = 5𝑁 𝐶 𝑥3𝑥10 𝑚 𝑉𝐵 − 𝑉𝐴 = 0,15 𝑉 12.- Calculemos el potencial eléctrico en un punto A, situado a 20 cm de una carga de 4x10-6C. ( ( ( ( ) 1,8x105 V ) 1,8x10-5 V ) 1,8 V ) 18 V Datos: 𝑉 =? 𝑟 = 20 𝑐𝑚 = 20𝑥10−2 𝑚 𝑞0 = 4𝑥10−6 𝐶 Diagrama: No es necesario Conversión de Unidades: Solución: Transformamos los Aplicamos la ecuación del potencial eléctrico en un punto: centímetros (cm) a metros 𝑞 (m), multiplicando por 10-2 𝑉=𝐾𝑥 𝑟 m o dividiendo entre 100 Sustituimos: cm. 2 4𝑥10−6 𝐶 𝑉 = 9𝑥109 𝑁 𝑥𝐶2𝑚 𝑥 20𝑥10−2 𝑚 𝑉 = 1,8𝑥105 𝑉 13.- Ubiquémonos en la figura y consideremos que 𝑞 = 3𝑥10−6 𝐶. Supóngase que las distancias desde la carga “q” a los untos A y B son respectivamente 𝑟𝐵 = 12 𝑐𝑚 y 𝑟𝐴 = 36 𝑐𝑚. Calcular la diferencia de potencial entre A y B. ( ( ( ( ) 15 V ) 1,5x105 V ) 15x105 V ) 1,5x10-5 V q Datos: −6 𝑞 = 3𝑥10 𝐶 𝑟𝐴 = 36 𝑐𝑚 = 36𝑥10−2 𝑚 𝑟𝐵 = 12 𝑐𝑚 = 12𝑥10−2 𝑚 𝑉𝐵 − 𝑉𝐴 =? Conversión de unidades: Transformamos los centímetros (cm) a metros (m), multiplicando por 10-2 m o dividiendo entre 100 cm. B . VB A . VA Diagrama: No es necesario; ya que, la diferencia de potencial es una magnitud escalar. No se trazan vectores. Solución: Calculamos los potenciales creados por cada carga sobre los puntos A y B, sumándolos algebraicamente posteriormente: Utilizamos la ecuación del potencial eléctrico en un punto, para hallar cada uno de los potenciales: 𝑞 𝑉𝐴 = 𝐾 𝑥 𝑟𝐴 Sustituimos: 3𝑥10−6 𝐶 𝑁 𝑥 𝑚2 𝑉𝐴 = 9𝑥109 𝐶 2 𝑥 36𝑥10−2 𝑚 𝑉𝐴 = 7,5𝑥104 𝑉 Ahora calculamos “VB” 𝑉𝐵 = 𝐾 𝑥 𝑞 𝑟𝐵 Sustituimos: 𝑉𝐵 = 9𝑥109 3𝑥10−6 𝐶 𝑁 𝑥 𝑚2 𝑥 𝐶2 12𝑥10−2 𝑚 𝑉𝐵 = 2,25𝑥105 𝑉 Obtenidos los potenciales en cada punto, calculamos la diferencia de potencial: 𝑉𝐵 − 𝑉𝐴 = 2,25𝑥105 𝑉 − 7,5𝑥104 𝑉 𝑉𝐵 − 𝑉𝐴 = 1,5𝑥105 𝑉 14.- Una carga eléctrica esta en un campo eléctrico uniforme de 100 N/C. Cuando se deslaza 8 cm realiza un trabajo de 35 joules. Calcular el valor de la carga. ( ( ( ( ) 4,3 C ) 4,35 C ) 4,375 C ) 4,735 C Datos: 100𝑁 𝐶 𝐸= 𝑟 = 8𝑐𝑚 = 8𝑥10−2 𝑚 𝑊 = 35 𝐽 𝑞0 =? Conversión de Unidades: Transformamos los centímetros (cm) a metros (m), multiplicando por 10-2 m o dividiendo entre 100 cm. Diagrama: No es necesario Solución: Aplicamos la ecuación de la diferencia de potencial en un campo eléctrico uniforme: 𝑉𝐵 − 𝑉𝐴 = 𝐸 𝑥 𝑑 Sustituimos: 𝑁 𝑉𝐵 − 𝑉𝐴 = 100 𝐶 𝑥 8𝑥10−2 𝑚 𝑉𝐵 − 𝑉𝐴 = 8 𝑉 Ahora calculamos la ecuación de la diferencia de potencial, por definición y despejamos “q”: 𝑊𝐴𝐵 𝑉𝐵 − 𝑉𝐴 = 𝑞0 Despejamos “q”: 𝑊𝐴𝐵 𝑞0 = 𝑉𝐵 − 𝑉𝐴 Sustituimos: 35 𝐽 𝑞0 = 8𝑉 𝑞0 = 4,375 𝐶 15.- Una carga eléctrica de 3x10-6 C, esta situada en un campo eléctrico uniforme. Sobre ella actúa una fuerza de 3 kilopondios (kp). Si la carga se desplaza del punto A al B distante 20 cm, calcular la diferencia de potencial (d.d.p) entre dichos puntos. ( ( ( ( ) 1,96x106 V ) 1,6x106 V ) 1,9x106 V ) 1,96x10-6 V Datos: 𝑞0 = 3𝑥10−6 𝐶 𝐹 = 3 𝐾𝑝 = 29,4 𝑁 𝑟 = 20 𝑐𝑚 = 20𝑥10−2 𝑚 𝑉𝐵 − 𝑉𝐴 =? Conversión de Unidades: Transformamos los centímetros (cm) a metros (m), multiplicando por 10-2 m o dividimos entre 100 cm. La fuerza la transformamos de kilopondios (Kp) a Newton (N), multiplicando por 9,8 N. Diagrama: No es necesario Solución: Calculamos el valor del campo eléctrico, aplicando la definición de intensidad del campo eléctrico: 𝐹 𝐸= 𝑞0 Sustituimos: 29,4 𝑁 𝐸= 3𝑥10−6 𝐶 𝑁 𝐸 = 9,8𝑥106 𝐶 Ahora aplicamos la ecuación de la d.d.p, en un campo eléctrico uniforme: 𝑉𝐵 − 𝑉𝐴 = 𝐸 𝑥 𝑑 Sustituimos: 𝑁 𝑉𝐵 − 𝑉𝐴 = 9,8𝑥106 𝐶 𝑥 20𝑥10−2 𝑚 𝑉𝐵 − 𝑉𝐴 = 1,96𝑥106 𝑉 16.- Calcular la energía potencial eléctrica creadas por dos cargas cuyos valores son: 𝑞1 = +4𝑥10−6 𝐶 y 𝑞2 = +6𝑥10−6 𝐶 Cuando se encuentran separadas a una distancia de 2 cm. ( ( ( ( ) 10 J ) 18 J ) 10,8 J ) 18,1 J Datos: 𝑈 =? 𝑞1 = +4𝑥10−6 𝐶 𝑞2 = +6𝑥10−6 𝐶 𝑟12 = 2 𝑐𝑚 = 2𝑥10−2 𝑚 Transformamos los centímetros (cm) a metros (m), multiplicando por 10-2 o dividiendo entre 100 cm. Diagrama: No es necesario Solución: Calculamos la energía potencial eléctrica, aplicando la ecuación de la definición: 𝑞1 𝑥 𝑞2 𝑈=𝐾𝑥 𝑟 Sustituimos: 4𝑥10−6 𝐶 𝑥 6𝑥10−6 𝐶 𝑁 𝑥 𝑚2 𝑈 = 9𝑥109 𝐶 2 𝑥 2𝑥10−2 𝑚 𝑈 = 10,8 𝐽 17.- Se tienen dos cargas eléctricas cuyos módulos son:𝑞1 = −5𝑥10−6 𝐶 y 𝑞2 = +3𝑥10−6 𝐶, separadas por una distancia de 5 cm. Calcular la energía potencial eléctrica de las dos cargas. ( ( ( ( ) -2,7 J ) 2,7 J ) -2,7 V ) 2,7 V Datos: Diagrama: No es necesario 𝑈 =? 𝑞1 = −5𝑥10−6 𝐶 𝑞2 = +3𝑥10−6 𝐶 𝑟12 = 5 𝑐𝑚 = 5𝑥10−2 𝑚 Transformamos los Solución: centímetros (cm) a Calculamos la energía potencial eléctrica, aplicando la metros (m), multiplicando ecuación de la definición: 𝑞1 𝑥 𝑞2 por 10-2 o dividiendo 𝑈=𝐾𝑥 𝑟 entre 100 cm. Sustituimos: (−5𝑥10−6 𝐶) 𝑥 (+6𝑥10−6 𝐶) 𝑁 𝑥 𝑚2 𝑈 = 9𝑥109 𝐶 2 𝑥 5𝑥10−2 𝑚 𝑈 = −2,7 𝐽 La energía potencial eléctrica es una magnitud escalar; es decir, puede ser negativa o positiva, lo que indica que tanto para ella como para el potencial eléctrico se deben utilizar los signos de las cargas. Donde las cargas eléctricas positivas generan potenciales y energía potencial eléctrica positivos, mientras que las cargas eléctricas negativas generan, potenciales y energía potencial eléctrica negativa. 18.- Calcular la energía potencial eléctrica creada por dos cargas cuyos valores son: 𝑞1 = −4𝑥10−6 𝐶 y 𝑞2 = −2𝑥10−6 𝐶, cuando se encuentran separadas a una distancia de 40 cm. ( ( ( ( ) 0,1 J ) 0,8 J ) 0,18 J ) 0,81 J Datos: 𝑈 =? 𝑞1 = −4𝑥10−6 𝐶 𝑞2 = −2𝑥10−6 𝐶 𝑟12 = 40 𝑐𝑚 = 40𝑥10−2 𝑚 Transformamos los centímetros (cm) a metros (m), multiplicando por 10-2 o dividiendo entre 100 cm. Diagrama: No es necesario Solución: Calculamos la energía potencial eléctrica, aplicando la ecuación de la definición: 𝑞1 𝑥 𝑞2 𝑈=𝐾𝑥 𝑟 Sustituimos: (−4𝑥10−6 𝐶) 𝑥 (−2𝑥10−6 𝐶) 𝑁 𝑥 𝑚2 𝑈 = 9𝑥109 𝐶 2 𝑥 40𝑥10−2 𝑚 𝑈 = 0,18 𝐽 La energía potencial eléctrica es una magnitud escalar; es decir, puede ser negativa o positiva, lo que indica que tanto para ella como para el potencial eléctrico se deben utilizar los signos de las cargas. Donde las cargas eléctricas positivas generan potenciales y energía potencial eléctrica positivos, mientras que las cargas eléctricas negativas generan, potenciales y energía potencial eléctrica negativa. 19.- La energía potencial eléctrica de dos cargas de 𝑞1 = +4𝑥10−6 𝐶 y 𝑞2 = +9𝑥10−6 𝐶 es de 0.25 J. ¿Qué distancia las separa? ( ( ( ( ) 1,296 m ) 1,296 cm ) 1,296 Km ) 1,2 m Datos: 𝑞1 = +4𝑥10−6 𝐶 𝑞2 = +9𝑥10−6 𝐶 𝑈 = 0,25 𝐽 𝑟12 =? Transformamos los centímetros (cm) a metros (m), multiplicando por 10-2 o dividiendo entre 100 cm. Diagrama: No es necesario Solución: Calculamos la energía potencial eléctrica, aplicando la ecuación de la definición: 𝑞1 𝑥 𝑞2 𝑈=𝐾𝑥 𝑟 Despejamos “r” 𝑞1 𝑥 𝑞2 𝑟12 = 𝐾 𝑥 𝑈 Sustituimos: 𝑟12 = 9𝑥109 𝑁 𝑥 𝑚2 𝐶2 𝑥 (+4𝑥10−6 𝐶) 𝑥 (+9𝑥10−6 𝐶) 0,25 𝐽 𝑟12 = 1,296 𝑚 20.- Un electrón y un protón, se encuentran separados por una distancia de 3x10 -5 m. ¿Cuál es su energía potencial eléctrica? ( ( ( ( ) -7,68x1024 J ) -7,68x10-24 J ) 7,68x10-24 J ) 7,68x1024 J Datos: 𝑞℮ = −1,6𝑥10−19 𝐶 𝑞𝑝 = +1,6𝑥10−19 𝐶 𝑟 = 3𝑥10−5 𝑚 𝑈 =? Conversión de unidades: No es necesario realizar Diagrama: No es necesario realizar Solución: Calculamos la energía potencial eléctrica, aplicando la ecuación de la definición: 𝑞1 𝑥 𝑞2 𝑈=𝐾𝑥 𝑟 Sustituimos: 2 (−1,6𝑥10−19 𝐶) 𝑥 (+1,6𝑥10−19 𝐶) 9𝑁 𝑥 𝑚 𝑈 = 9𝑥10 𝐶 2 𝑥 3𝑥10−5 𝑚 𝑈 = −7,68𝑥10−24 𝐽 La energía potencial eléctrica es una magnitud escalar; es decir, puede ser negativa o positiva, lo que indica que tanto para ella como para el potencial eléctrico se deben utilizar los signos de las cargas. Donde las cargas eléctricas positivas generan potenciales y energía potencial eléctrica positivos, mientras que las cargas eléctricas negativas generan, potenciales y energía potencial eléctrica negativa. En este caso en particular, estamos trabajando con partículas elementales del átomo, las cuales poseen masa y cargas constantes y donde el electrón y el protón, se diferencian en el signo de la carga, teniendo el electrón una carga eléctrica negativa y el protón una carga eléctrica positiva; pero, en magnitud son iguales. Nivel Medio: 21.- Se tienen dos cargas eléctricas ubicadas sobre una misma recta 𝑞1 = +6µ𝐶 y 𝑞2 = −6µ𝐶, separadas por 12 cm, como se muestra en la figura. Calcular: a) el potencial eléctrico en el punto A; b) el potencial eléctrico en el punto B y c) la diferencia de potencial (d.d.p). +q1 A -q2 B 4 cm ( ( ( ( ) 𝑉𝐴 ) 𝑉𝐴 ) 𝑉𝐴 ) 𝑉𝐴 = 6,75𝑥105 𝑉; 𝑉𝐵 = 6,75𝑥105 𝑉; 𝑉𝐵 = 6,75𝑥105 𝑉; 𝑉𝐵 = 6,75𝑥105 𝑉; 𝑉𝐵 8 cm = −1,01𝑥106 𝑉 y 𝑉𝐵 − 𝑉𝐴 = −1,01𝑥106 𝑉 y 𝑉𝐵 − 𝑉𝐴 = −1,01𝑥106 𝑉 y 𝑉𝐵 − 𝑉𝐴 = −1,01𝑥106 𝑉 y 𝑉𝐵 − 𝑉𝐴 Datos: 𝑞1 = +6 µ𝐶 = +6𝑥10−6 𝐶 𝑞2 = −6 µ𝐶 = −6𝑥10−6 𝐶 𝑎) 𝑉𝐴 =? 𝑟1𝐴 = 4𝑐𝑚 = 4𝑥10−2 𝑚 𝑟2𝐴 = 8𝑐𝑚 = 8𝑥10−2 𝑚 𝑏) 𝑉𝐵 =? 𝑟1𝐵 = 16𝑐𝑚 = 16𝑥10−2 𝑚 𝑟2𝐵 = 4𝑐𝑚 = 4𝑥10−2 𝑚 𝑐) 𝑉𝐵 − 𝑉𝐴 =? Conversión de unidades: Transformamos los centímetros (cm) a metros (m), multiplicando por 10-2m o dividiendo entre 100 cm. Además, se hizo la transformación de los microcoulomb (µC) a Coulomb (C), multiplicando por 10-6 C. 4 cm = −1,69𝑥106 𝑉 = 1,69𝑥106 𝑉 = 1,69𝑥106 𝑉 = 1,69𝑥106 𝑉 Diagrama: Solo es para visualizar las distancias de separación entre las cargas y los puntos. +q1 A -q2 B 4 cm 8 cm 4 cm Cargas eléctricas positivas crean potenciales positivos y cargas eléctricas negativas crean potenciales negativos, En el cálculo del potencial eléctrico creado por cada carga, si se utilizan los signos de las cargas por ser estas magnitudes escalares y existen potenciales positivos y negativos. Solución: Como el potencial es una magnitud escalar, el potencial creado por cada carga, es la suma algebraica de los potenciales en ese punto. Ara hallar los potenciales, aplicamos la ecuación del potencial eléctrico en un punto: 𝑉𝐴 = 𝑉1 + 𝑉2 𝑉1 = 𝐾 𝑥 Sustituimos: 𝑞1 𝑟1𝐴 𝑉1 = 9𝑥109 𝑁 𝑥 𝑚2 𝐶2 𝑥 (+6𝑥10−6 𝐶) 4𝑥10−2 𝑚 𝑉1 = 1,35𝑥106 𝑉 𝑉2 = 𝐾 𝑥 𝑞2 𝑟2𝐴 Sustituimos: 𝑉2 = 9𝑥109 𝑁 𝑥 𝑚2 𝐶2 𝑥 (−6𝑥10−6 𝐶) 8𝑥10−2 𝑚 𝑉2 = −6,75𝑥105 𝑉 𝑉𝐴 = 𝑉1 + 𝑉2 𝑉𝐴 = 1,35𝑥106 𝑉 + (−6,75𝑥105 𝑉) 𝑉𝐴 = 6,75𝑥105 𝑉 Ahora calculamos “VB”, de la misma manera que lo hicimos con “VA”: 𝑉𝐵 = 𝑉1 + 𝑉2 𝑉1 = 𝐾 𝑥 𝑞1 𝑟1𝐵 Sustituimos: 𝑉1 = 𝑁𝑥𝑚 9𝑥109 𝐶 2 2 (+6𝑥10−6 𝐶) 𝑥 16𝑥10−2 𝑚 𝑉1 = 3,37𝑥105 𝑉 𝑉2 = 𝐾 𝑥 𝑞2 𝑟2𝐵 Sustituimos: 𝑉2 = 9𝑥109 𝑁 𝑥 𝑚2 𝐶2 𝑥 (−6𝑥10−6 𝐶) 4𝑥10−2 𝑚 𝑉2 = −1,35𝑥106 𝑉 𝑉𝐵 = 𝑉1 + 𝑉2 𝑉𝐵 = 3,37𝑥105 𝑉 + (−1,35𝑥106 𝑉) 𝑉𝐵 = −1,01𝑥106 𝑉 Ahora se calcula la diferencia de potencial: 𝑉𝐵 − 𝑉𝐴 = −1,01𝑥106 𝑉 − (6,75𝑥105 𝑉) 𝑉𝐵 − 𝑉𝐴 = −1,69𝑥106 𝑉 22.- La energía cinética de una partícula es de 100 electrón voltio (℮V): calcular su velocidad si se trata de: a) electrón; b) protón. ( ( ( ( ) 𝑉℮ ) 𝑉℮ ) 𝑉℮ ) 𝑉℮ = 5,9𝑥10−6 𝑚𝑠 𝑦 𝑉𝑝 = 1,4𝑥105 𝑚𝑠 = 5,9𝑥106 𝑚𝑠 𝑦 𝑉𝑝 = 1,4𝑥105 𝑚𝑠 = 5,9𝑥106 𝑚𝑠 𝑦 𝑉𝑝 = 1,4𝑥10−5 𝑚𝑠 = 5,9𝑥10−6 𝑚𝑠 𝑦 𝑉𝑝 = 1,4𝑥10−5 𝑚𝑠 Datos: 𝐸𝐶 = 100 ℮𝑉 = 1.6𝑥10−17 𝐽 𝑣℮ =? 𝑣𝑝 =? 𝑚℮ = 9,11𝑥10−31 𝐾𝑔 𝑚𝑝 = 1,6725𝑥10−27 𝐾𝑔 𝑞℮ = −1,6𝑥10−19 𝐶 𝑞𝑝 = 1,6𝑥10−19 𝐶 Diagrama: No es necesario realizarlo Conversión de Unidades: Transformamos los electrón voltios (℮V) a Joules (J), multiplicando por 1,6𝑥10−19 𝐽 Solución: El electrón y el protón son partículas elementales del átomo, las cuales tienen una masa y una carga con valores constantes. Para hallar la velocidad o rapidez de las partículas, aplicamos la ecuación de la energía cinética: 1 𝐸𝑐 = 𝑥 𝑚 𝑥 𝑣 2 2 Despejamos “v” y para eliminar el cuadrado, introducimos dentro de una raíz el resto de los términos de la ecuación: 𝐸𝑐 = 100 ℮𝑉 𝑥 1,6𝑥10−19 1 ℮𝑉 𝐸𝑐 = 1,6𝑥10−17 𝐽 𝑣=√ 2 𝑥 𝐸𝑐 𝑚 Sustituimos para el electrón (℮− ): 𝑣=√ 2 𝑥 1,6𝑥10−17 𝐽 9,11𝑥10−31 𝐾𝑔 𝑣 = 5,9𝑥106 𝑚 𝑠 Ahora sustituimos para el protón (p): 𝑣=√ 2 𝑥 1,6𝑥10−17 𝐽 1,6725𝑥10−27 𝐾𝑔 𝑚 𝑣 = 1,4𝑥105 𝑠 23.- ¿Cuál es la energía potencial eléctrica de una carga de +6 nanocoulomb (nC) localizada a 0,05 m de otra carga de 80 nanocoulomb (nC)? ¿Cuál seria la energía potencial eléctrica si la misma carga de +6 nC, esta a 0,05 m de una carga de -80 nC? ( ( ( ( ) 8x10-3 J y -8x10-3 J ) 8,64x10-3 J y -8,64x10-3 J ) 8,6x10-3 J y -8,64x10-3 J ) 8,64x105 J y -8x105 J Datos: 𝑈 = 𝑊 =? 𝑞1 = +6 𝑛𝐶 = +6𝑥10−9 𝐶 𝑟12 = 0,05 𝑚 𝑞2 = +80 𝑛𝐶 = 80𝑥10−9 𝐶 𝑈 = 𝑊 =? 𝑞1 = +6𝑛𝐶 = +6𝑥10−9 𝐶 𝑞2 = −80𝑛𝐶 = −80𝑥10−9 𝐶 𝑟12 = 0,05 𝑚 Conversión de Unidades: Transformamos los nanocoulomb (nC) a Coulomb (C), multiplicando por 10-9 C. Diagrama: No es necesario realizar. Solución: Primero calculamos el potencial eléctrico (V), debido a la carga de +6 nC, aplicando la ecuación del potencial en un punto. 𝑞 𝑉=𝐾𝑥 𝑟 Sustituimos: 2 6𝑥10−9 𝐶 9𝑁 𝑥 𝑚 𝑉 = 9𝑥10 𝐶 2 𝑥 0,05 𝑚 𝑉 = 1080 𝑉 Ahora calculamos la energía potencial eléctrica, aplicando la ecuación de la definición del potencial eléctrico: 𝑊 𝑉= 𝑞0 Despejamos “W”: 𝑊 = 𝑞0 𝑥 𝑉 Sustituimos: 𝑊 = 80𝑥10−9 𝐶 𝑥 1080 𝑉 𝑊 = 8,64𝑥10−5 𝐽 Hacemos el mismo procedimiento; pero, para la carga de -80 nC. 𝑊 = −80𝑥10−9 𝐶 𝑥 1080 𝑉 𝑊 = −8,64𝑥10−5 𝐽 Ahora resolvemos el mismo problema, pero aplicando la ecuación de la energía potencial eléctrica por definición. Solución: para la carga de +80 nC. 𝑈=𝐾𝑥 Sustituimos: 𝑈 = 9𝑥109 𝑁 𝑥 𝑚2 𝐶2 𝑥 𝑞1 𝑥 𝑞2 𝑟 (+6𝑥10−9 𝐶)𝑥(+80𝑥10−9 𝐶) 0,05 𝑚 𝑈 = 8,64𝑥10−5 𝐽 Para la carga de -80 nC: 2 (+6𝑥10−9 𝐶)𝑥(−80𝑥10−9 𝐶) 9𝑁 𝑥 𝑚 𝑈 = 9𝑥10 𝐶 2 𝑥 0,05 𝑚 𝑈 = −8,64𝑥10−5 𝐽 En el primer caso solo se igualo el trabajo con la energía; esto, por el teorema del trabajo y la energía, donde todo trabajo se convierte en energía y toda energía en trabajo. En el segundo caso solo aplicamos directamente la ecuación de la energía potencial eléctrica. Y de esta forma queda demostrado la igualdad existente entre el trabajo y la energía. 𝑊=𝑈 24.- Calcular la diferencia de potencial, con la cual debe ser acelerado un electrón, que esta en reposo en un campo eléctrico uniforme, para que sea capaz de adquirir una rapidez de 3x107 m/s. ( ( ( ( ) 2,56x10-3 V ) 2,56x102 V ) 2,56x104 V ) 2,56x103 V Datos: 𝑞℮ = 1,6𝑥10−19 𝐶 𝑉 =? 𝑣0 = 0 𝑚 𝑣 = 3𝑥107 𝑠 𝑚℮ = 9,11𝑥10−31 𝐾𝑔 Diagrama: No es necesario realizarlo. Conversión de Unidades: No se realizan conversiones; todo, esta en un mismo sistema de medida. (M.K.S) Solución: Sea “q” la carga en movimiento, “m” su masa y “F” la fuerza electrostática que actúa sobre la carga cuando se somete a un campo eléctrico uniforme. La fuerza dinámica, según la 2da. Ley de Newton, viene dada: 𝐹 = 𝑚 𝑥 𝑎 (1) La fuerza electrostática. Según el campo eléctrico es: 𝐹 = 𝑞0 𝑥𝐸 (2) Para que el electrón (℮-), se mantenga en reposo dentro del campo eléctrico, debe cumplirse que la magnitud de la fuerza dinámica y la fuerza electrostática sean iguales; es decir: 𝑚 𝑥 𝑎 = 𝐸 𝑥 𝑞 (3) La aceleración según el movimiento variado (MV) es: 𝑣2 𝑎= (4) 2𝑥𝑑 El campo eléctrico uniforme entre placas viene dado por: 𝑉 (5) 𝐸= 𝑑 Sustituimos la ecuación (4) y la ecuación (5), en la ecuación (3): 𝑣2 𝑉 𝑚𝑥 =𝑞𝑥 2 𝑥𝑑 𝑑 Simplificamos y nos queda: 1 𝑥 𝑚 𝑥 𝑣2 = 𝑞 𝑥 𝑉 2 Como nos piden el potencial eléctrico “V”; despejamos: 1 𝑚 𝑥 𝑣2 𝑉= 𝑥 2 𝑞 La cual la podemos escribir así: 𝑚 𝑥 𝑣2 𝑉= 2𝑥𝑞 Sustituimos: 9,11𝑥10−31 𝐾𝑔 𝑥 (3𝑥107 𝑚 )2 𝑠 𝑉= 2 𝑥 1,6𝑥10−19 𝐶 𝑉 = 2,56𝑥103 𝑉 25.- Calcular la velocidad de un electrón, sabiendo que en un momento dado tiene una energía cinética de 150 ℮V. ( ( ( ( ) 7,26x106 m/s ) 7,26x10-6 m/s ) 7,26x107 m/s ) 7,26x10-7 m/s Datos: 𝐸𝐶 = 150 ℮𝑉 = 2,4𝑥10−17 𝐽 𝑣℮ =? 𝑚℮ = 9,11𝑥10−31 𝐾𝑔 𝑞℮ = −1,6𝑥10−19 𝐶 Diagrama: No es necesario realizarlo Conversión de Unidades: Transformamos los electrón voltios (℮V) a Joules (J), multiplicando por 1,6𝑥10−19 𝐽 Solución: El electrón y el protón son partículas elementales del átomo, las cuales tienen una masa y una carga con valores constantes. Para hallar la velocidad o rapidez del electrón, aplicamos la ecuación de la energía cinética: 1 𝐸𝑐 = 𝑥 𝑚 𝑥 𝑣 2 2 Despejamos “v” y para eliminar el cuadrado, introducimos dentro de una raíz, el resto de los términos de la ecuación: 𝐸𝑐 = 150 ℮𝑉 𝑥 1,6𝑥10−19 1 ℮𝑉 𝐸𝑐 = 2,4𝑥10−17 𝐽 𝑣=√ 2 𝑥 𝐸𝑐 𝑚 Sustituimos para el electrón (℮− ): 𝑣=√ 2 𝑥 2,4𝑥10−17 𝐽 9,11𝑥10−31 𝐾𝑔 𝑣 = 7,26𝑥106 𝑚 𝑠 26.- Dos cargas eléctricas 𝑞1 = +4𝑥10−6 𝐶 y 𝑞2 = −2,5𝑥10−6 𝐶 están ene el vacio separadas por una distancia de 20 cm. Calcular el potencial eléctrico resultante en el punto medio de la recta que las une. ( ( ( ( ) 1,35x105 V ) 1,1x105 V ) 1,3x105 V ) 1,35X103 V Datos: 𝑞1 = +4𝑥10−6 𝐶 𝑞2 = −2,5𝑥10−6 𝐶 𝑟12 = 20 𝑐𝑚 = 20𝑥10−2 𝑚 𝑉𝐴 =? Diagrama: +q1 A 20 cm 10 cm -q2 10 cm Solo se usa de referencia; recordemos, que el potencial eléctrico, es una magnitud escalar, no tiene ni dirección ni sentido. Conversión de Unidades: Solución: Transformamos los Por ser una magnitud escalar, el potencial resultante en el centímetros (cm) a metros punto A, es la suma algebraica de los potenciales creados (m), multiplicando por 10-2 por cada carga: 𝑉𝐴 = 𝑉1 + 𝑉2 m o dividiendo entre 100 Hallamos, los potenciales creados por cada carga, cm. aplicando la ecuación del potencial eléctrico en un punto. 𝑞 𝑉=𝐾𝑥 𝑟 Sustituimos en relación con cada caso en especifico: 𝑁 𝑥 𝑚2 (+4𝑥10−6 𝐶) 9 𝑉1 = 9𝑥10 𝑥 𝐶2 10𝑥10−2 𝑚 𝑉1 = 3,6𝑥105 𝑉 −6 𝑁 𝑥 𝑚2 (−2,5𝑥10 𝐶) 𝑉2 = 9𝑥109 𝐶 2 𝑥 10𝑥10−2 𝑚 𝑉2 = −2,25𝑥105 𝑉 𝑉𝐴 = 3,6𝑥10 𝑉 + (−2,25𝑥105 𝑉) 𝑉𝐴 = 1,35𝑥105 𝑉 Recordemos que en esta magnitud si usamos los signos de las cargas. 5 27.- Dos cargas eléctricas 𝑞1 = +6𝑥10−6 𝐶 y 𝑞2 = −12𝑥10−6 𝐶 están ene el vacio separadas por una distancia de 6 cm. Calcular el potencial eléctrico resultante en el punto medio de la recta que las une. ( ( ( ( ) 1,8x105 V ) 1,8x106 V ) -1,8x106 V ) 1,8X103 V Datos: 𝑞1 = +6𝑥10−6 𝐶 𝑞2 = −12𝑥10−6 𝐶 𝑟12 = 6 𝑐𝑚 = 6𝑥10−2 𝑚 𝑉𝐴 =? Diagrama: +q1 A 6 cm 3 cm -q2 3 cm Solo se usa de referencia; recordemos, que el potencial eléctrico, es una magnitud escalar, no tiene ni dirección ni sentido. Conversión de Unidades: Solución: Transformamos los Por ser una magnitud escalar, el potencial resultante en el centímetros (cm) a metros punto A, es la suma algebraica de los potenciales creados (m), multiplicando por 10-2 por cada carga: 𝑉𝐴 = 𝑉1 + 𝑉2 m o dividiendo entre 100 Hallamos, los potenciales creados por cada carga, cm. aplicando la ecuación del potencial eléctrico en un punto. 𝑞 𝑉=𝐾𝑥 𝑟 Sustituimos en relación con cada caso en especifico: 𝑁 𝑥 𝑚2 (+6𝑥10−6 𝐶) 9 𝑉1 = 9𝑥10 𝑥 𝐶2 3𝑥10−2 𝑚 𝑉1 = 1,8𝑥106 𝑉 −6 𝑁 𝑥 𝑚2 (−12𝑥10 𝐶) 𝑉2 = 9𝑥109 𝐶 2 𝑥 3𝑥10−2 𝑚 𝑉2 = −3,6𝑥106 𝑉 𝑉𝐴 = 1,8𝑥10 𝑉 + (−3,6𝑥106 𝑉) 𝑉𝐴 = −1,8𝑥106 𝑉 Recordemos que en esta magnitud si usamos los signos de las cargas. 6 28.- Dos cargas eléctricas 𝑞1 = +6𝑥10−6 𝐶 y 𝑞2 = +4𝑥10−6 𝐶 están ene el vacio separadas por una distancia de 8 cm. Calcular el potencial eléctrico resultante en un punto A ubicado a 3 cm de q1. ( ( ( ( ) 2,52x105 V )-2,52 x106 V ) 2,52x106 V ) 2,52X10-6 V Datos: 𝑞1 = +6𝑥10−6 𝐶 𝑞2 = +4𝑥10−6 𝐶 𝑟12 = 8 𝑐𝑚 = 8𝑥10−2 𝑚 𝑟1𝐴 = 3 𝑐𝑚 = 3𝑥10−2 𝑚 𝑟2𝐴 = 5𝑐𝑚 = 5𝑥10−2 𝑚 𝑉𝐴 =? Diagrama: +q1 A -q2 8 cm 3 cm 5 cm Solo se usa de referencia; recordemos, que el potencial eléctrico, es una magnitud escalar, no tiene ni dirección ni sentido. Conversión de Unidades: Solución: Transformamos los Por ser una magnitud escalar, el potencial resultante en el centímetros (cm) a metros punto A, es la suma algebraica de los potenciales creados (m), multiplicando por 10-2 por cada carga: 𝑉𝐴 = 𝑉1 + 𝑉2 m o dividiendo entre 100 Hallamos, los potenciales creados por cada carga, cm. aplicando la ecuación del potencial eléctrico en un punto. 𝑞 𝑉=𝐾𝑥 𝑟 Sustituimos en relación con cada caso en especifico: 𝑁 𝑥 𝑚2 (+6𝑥10−6 𝐶) 9 𝑉1 = 9𝑥10 𝑥 𝐶2 3𝑥10−2 𝑚 𝑉1 = 1,8𝑥106 𝑉 −6 𝑁 𝑥 𝑚2 (+4𝑥10 𝐶) 𝑉2 = 9𝑥109 𝐶 2 𝑥 5𝑥10−2 𝑚 𝑉2 = 7,2𝑥105 𝑉 𝑉𝐴 = 1,8𝑥10 𝑉 + 7,2𝑥105 𝑉 𝑉𝐴 = 2,52𝑥106 𝑉 Recordemos que en esta magnitud si usamos los signos de las cargas. 6 29.- Calcular la velocidad de un electrón, sabiendo que en un momento dado tiene una energía cinética de 2500 ℮V. ( ( ( ( ) 2,96x107 m/s ) 2,96x10-6 m/s ) 2.96x10-7 m/s ) 2,6x10-7 m/s Datos: 𝐸𝐶 = 2500 ℮𝑉 = 4𝑥10−16 𝐽 𝑣℮ =? 𝑚℮ = 9,11𝑥10−31 𝐾𝑔 𝑞℮ = −1,6𝑥10−19 𝐶 Diagrama: No es necesario realizarlo Conversión de Unidades: Transformamos los electrón voltios (℮V) a Joules (J), multiplicando por 1,6𝑥10−19 𝐽 Solución: El electrón y el protón son partículas elementales del átomo, las cuales tienen una masa y una carga con valores constantes. Para hallar la velocidad o rapidez del electrón, aplicamos la ecuación de la energía cinética: 1 𝐸𝑐 = 𝑥 𝑚 𝑥 𝑣 2 2 Despejamos “v” y para eliminar el cuadrado, introducimos dentro de una raíz, el resto de los términos de la ecuación: 𝐸𝑐 = 2500 ℮𝑉 𝑥 1,6𝑥10−19 1 ℮𝑉 𝐸𝑐 = 4𝑥10−16 𝐽 𝑣=√ 2 𝑥 𝐸𝑐 𝑚 Sustituimos para el electrón (℮− ): 𝑣=√ 2 𝑥 4𝑥10−17 𝐽 9,11𝑥10−31 𝐾𝑔 𝑣 = 2,96𝑥107 𝑚 𝑠 30.- Calcular la diferencia de potencial, con la cual debe ser acelerado un electrón, que esta en reposo en un campo eléctrico uniforme, para que sea capaz de adquirir una rapidez de 1,27x106 m/s. ( ( ( ( ) 2,59 V ) 4,56 V ) 4,59 V ) 4,59x103 V Datos: 𝑞℮ = 1,6𝑥10−19 𝐶 𝑉 =? 𝑣0 = 0 𝑚 𝑣 = 1,27𝑥106 𝑠 𝑚℮ = 9,11𝑥10−31 𝐾𝑔 Diagrama: No es necesario realizarlo. Conversión de Unidades: No se realizan conversiones; todo, esta en un mismo sistema de medida. (M.K.S) Solución: Sea “q” la carga en movimiento, “m” su masa y “F” la fuerza electrostática que actúa sobre la carga cuando se somete a un campo eléctrico uniforme. La fuerza dinámica, según la 2da. Ley de Newton, viene dada: 𝐹 = 𝑚 𝑥 𝑎 (1) La fuerza electrostática. Según el campo eléctrico es: 𝐹 = 𝑞0 𝑥𝐸 (2) Para que el electrón (℮-), se mantenga en reposo dentro del campo eléctrico, debe cumplirse que la magnitud de la fuerza dinámica y la fuerza electrostática sean iguales; es decir: 𝑚 𝑥 𝑎 = 𝐸 𝑥 𝑞 (3) La aceleración según el movimiento variado (MV) es: 𝑣2 𝑎= (4) 2𝑥𝑑 El campo eléctrico uniforme entre placas viene dado por: 𝑉 (5) 𝐸= 𝑑 Sustituimos la ecuación (4) y la ecuación (5), en la ecuación (3): 𝑣2 𝑉 𝑚𝑥 =𝑞𝑥 2 𝑥𝑑 𝑑 Simplificamos y nos queda: 1 𝑥 𝑚 𝑥 𝑣2 = 𝑞 𝑥 𝑉 2 Como nos piden el potencial eléctrico “V”; despejamos: 1 𝑚 𝑥 𝑣2 𝑉= 𝑥 2 𝑞 La cual la podemos escribir así: 𝑚 𝑥 𝑣2 𝑉= 2𝑥𝑞 Sustituimos: 9,11𝑥10−31 𝐾𝑔 𝑥 (1,27𝑥106 𝑚 )2 𝑠 𝑉= 2 𝑥 1,6𝑥10−19 𝐶 𝑉 = 4,59 𝑉 31.- ¿Cuál es la energía potencial eléctrica de una carga de +5 nanocoulomb (nC) localizada a 1,5 m de otra carga de +3 nanocoulomb (nC)? ¿Cuál seria la energía potencial eléctrica si la misma carga de +5 nC, esta a 1,5 m de una carga de -3 nC? ( ( ( ( ) 8x10-3 J y -8x10-3 J ) 8,64x10-3 J y -8,64x10-3 J ) 8,6x10-3 J y -8,64x10-3 J ) 8,64x105 J y -8x105 J Datos: 𝑈 = 𝑊 =? 𝑞1 = +5 𝑛𝐶 = +5𝑥10−9 𝐶 𝑟12 = 1,5 𝑚 𝑞2 = +3 𝑛𝐶 = +3𝑥10−9 𝐶 𝑈 = 𝑊 =? 𝑞1 = +5𝑛𝐶 = +5𝑥10−9 𝐶 𝑞2 = −3𝑛𝐶 = −3𝑥10−9 𝐶 𝑟12 = 1,5 𝑚 Conversión de Unidades: Transformamos los nanocoulomb (nC) a Coulomb (C), multiplicando por 10-9 C. Diagrama: No es necesario realizar. Solución: Primero calculamos el potencial eléctrico (V), debido a la carga de +5 nC, aplicando la ecuación del potencial en un punto. 𝑞 𝑉=𝐾𝑥 𝑟 Sustituimos: −9 𝑁 𝑥 𝑚2 5𝑥10 𝐶 𝑉 = 9𝑥109 𝐶 2 𝑥 1,5 𝑚 𝑉 = 30 𝑉 Ahora calculamos la energía potencial eléctrica, aplicando la ecuación de la definición del potencial eléctrico: 𝑊 𝑉= 𝑞0 Despejamos “W”: 𝑊 = 𝑞0 𝑥 𝑉 Sustituimos: 𝑊 = 3𝑥10−9 𝐶 𝑥 30 𝑉 𝑊 = 9𝑥10−10 𝐽 Hacemos el mismo procedimiento; pero, para la carga de -80 nC. 𝑊 = −3𝑥10−9 𝐶 𝑥 30 𝑉 𝑊 = −9𝑥10−10 𝐽 Ahora resolvemos el mismo problema, pero aplicando la ecuación de la energía potencial eléctrica por definición. Solución: para la carga de +3 nC. 𝑈=𝐾𝑥 Sustituimos: 𝑈 = 9𝑥109 𝑁 𝑥 𝑚2 𝐶2 𝑥 𝑞1 𝑥 𝑞2 𝑟 (+5𝑥10−9 𝐶)𝑥(+3𝑥10−9 𝐶) 1,5 𝑚 𝑈 = 9𝑥10−10 𝐽 Para la carga de -3 nC: (+5𝑥10−9 𝐶)𝑥(−3𝑥10−9 𝐶) 𝑁 𝑥 𝑚2 𝑈 = 9𝑥109 𝐶 2 𝑥 1,5 𝑚 𝑈 = 9𝑥10−10 𝐽 En el primer caso solo se igualo el trabajo con la energía; esto, por el teorema del trabajo y la energía, donde todo trabajo se convierte en energía y toda energía en trabajo. En el segundo caso solo aplicamos directamente la ecuación de la energía potencial eléctrica. Y de esta forma queda demostrado la igualdad existente entre el trabajo y la energía. 𝑊=𝑈 32.- Se tienen dos cargas eléctricas ubicadas sobre una misma recta 𝑞1 = +9µ𝐶 y 𝑞2 = −9µ𝐶, separadas por 36 cm, como se muestra en la figura. Calcular: a) el potencial eléctrico en el punto A; b) el potencial eléctrico en el punto B y c) la diferencia de potencial (d.d.p). +q1 A -q2 B 6 cm ( ( ( ( ) 𝑉𝐴 ) 𝑉𝐴 ) 𝑉𝐴 ) 𝑉𝐴 24 cm = 1,01𝑥106 𝑉; 𝑉𝐵 = −1,13𝑥106 𝑉 y 𝑉𝐵 − 𝑉𝐴 = 6,75𝑥105 𝑉; 𝑉𝐵 = −1,01𝑥106 𝑉 y 𝑉𝐵 − 𝑉𝐴 = −6,75𝑥105 𝑉; 𝑉𝐵 = 1,01𝑥106 𝑉 y 𝑉𝐵 − 𝑉𝐴 = 6,75𝑥105 𝑉; 𝑉𝐵 = −1,01𝑥106 𝑉 y 𝑉𝐵 − 𝑉𝐴 Datos: 𝑞1 = +9 µ𝐶 = +9𝑥10−6 𝐶 𝑞2 = −9 µ𝐶 = −9𝑥10−6 𝐶 𝑎) 𝑉𝐴 =? 𝑟1𝐴 = 6𝑐𝑚 = 6𝑥10−2 𝑚 𝑟2𝐴 = 24𝑐𝑚 = 24𝑥10−2 𝑚 𝑏) 𝑉𝐵 =? 𝑟1𝐵 = 36𝑐𝑚 = 66𝑥10−2 𝑚 𝑟2𝐵 = 6𝑐𝑚 = 6𝑥10−2 𝑚 𝑐) 𝑉𝐵 − 𝑉𝐴 =? Conversión de unidades: Transformamos los centímetros (cm) a metros (m), multiplicando por 10-2m o dividiendo entre 100 cm. Además, se hizo la transformación de los microcoulomb (µC) a Coulomb (C), multiplicando por 10-6 C. 6 cm = 2,14𝑥106 𝑉 = −1,69𝑥106 𝑉 = 1,69𝑥106 𝑉 = 1,69𝑥106 𝑉 Diagrama: Solo es para visualizar las distancias de separación entre las cargas y los puntos. +q1 A -q2 B 6 cm 24 cm 6 cm Cargas eléctricas positivas crean potenciales positivos y cargas eléctricas negativas crean potenciales negativos, En el cálculo del potencial eléctrico creado por cada carga, si se utilizan los signos de las cargas por ser estas magnitudes escalares y existen potenciales positivos y negativos. Solución: Como el potencial es una magnitud escalar, el potencial creado por cada carga, es la suma algebraica de los potenciales en ese punto. Ara hallar los potenciales, aplicamos la ecuación del potencial eléctrico en un punto: 𝑉𝐴 = 𝑉1 + 𝑉2 𝑉1 = 𝐾 𝑥 𝑞1 𝑟1𝐴 Sustituimos: 𝑉1 = 9𝑥109 𝑁 𝑥 𝑚2 𝐶2 𝑥 (+9𝑥10−6 𝐶) 6𝑥10−2 𝑚 𝑉1 = 1,35𝑥106 𝑉 𝑉2 = 𝐾 𝑥 𝑞2 𝑟2𝐴 Sustituimos: 𝑉2 = 9𝑥109 𝑁 𝑥 𝑚2 𝐶2 𝑥 (−9𝑥10−6 𝐶) 24𝑥10−2 𝑚 𝑉2 = −3,38𝑥105 𝑉 𝑉𝐴 = 𝑉1 + 𝑉2 𝑉𝐴 = 1,35𝑥106 𝑉 + (−3,38𝑥105 𝑉) 𝑉𝐴 = 1,01𝑥106 𝑉 Ahora calculamos “VB”, de la misma manera que lo hicimos con “VA”: 𝑉𝐵 = 𝑉1 + 𝑉2 𝑉1 = 𝐾 𝑥 𝑞1 𝑟1𝐵 Sustituimos: 𝑉1 = 𝑁𝑥𝑚 9𝑥109 𝐶 2 2 (+9𝑥10−6 𝐶) 𝑥 36𝑥10−2 𝑚 𝑉1 = 2,25𝑥105 𝑉 𝑉2 = 𝐾 𝑥 𝑞2 𝑟2𝐵 Sustituimos: 𝑉2 = 9𝑥109 𝑁 𝑥 𝑚2 𝐶2 𝑥 (−9𝑥10−6 𝐶) 6𝑥10−2 𝑚 𝑉2 = −1,35𝑥106 𝑉 𝑉𝐵 = 𝑉1 + 𝑉2 𝑉𝐵 = 2,25𝑥105 𝑉 + (−1,35𝑥106 𝑉) 𝑉𝐵 = −1,13𝑥106 𝑉 Ahora se calcula la diferencia de potencial: 𝑉𝐵 − 𝑉𝐴 = −1,13𝑥106 𝑉 − (1,01𝑥106 𝑉) 𝑉𝐵 − 𝑉𝐴 = −2,14𝑥106 𝑉 33.- Dos cargas eléctricas 𝑞𝐴 = +3𝑥10−6 𝐶 y 𝑞𝐵 = −9𝑥10−6 𝐶 están en el vacio separadas una distancia de 8 m. Calcular en que punto de la recta que las une el potencial eléctrico es nulo. ( ( ( ( ) – 2 m de qA ) 2 m de qA ) 4 m de qA ) – 4 m de qA Datos: 𝑞𝐴 = +3𝑥10−6 𝐶 𝑞𝐵 = −9𝑥10−6 𝐶 𝑟𝐴𝐵 = 8 𝑚 𝑋 =? 𝑉=0 Diagrama: Solo se utiliza de forma explicativa, con el fin de analizar el problema de forma más clara y sencilla. +qA P -qB 8m X (8-X) Para que el potencial eléctrico resultante sea nulo, se debe cumplir que los potenciales creados por cada carga, sean iguales en magnitud. Conversión de unidades: Solución: No es necesario, todas Partimos de la condición que los potenciales creados por cada están en un mismo carga sean iguales en magnitud. En tal sentido, aplicamos la sistema de unidades. ecuación del potencial eléctrico en un punto: 𝑉=𝐾𝑥 Igualamos los potenciales: 𝑞 𝑟 𝑉𝐴 = 𝑉𝐵 Sustituimos los potenciales por sus ecuaciones: 𝑞𝐴 𝑞𝐵 𝐾𝑥 =𝐾𝑥 𝑟𝐴𝑝 𝑟𝐵𝑝 Simplificamos “K” y agrupamos términos semejantes: 𝑟𝐵𝑝 𝑞𝐵 = 𝑟𝐴𝑝 𝑞𝐴 Sustituimos por sus valores: 8−𝑋 9𝑥10−6 𝐶 = 𝑋 3𝑥10−6 𝐶 8−𝑋 =3 𝑋 Colocamos la ecuación de forma lineal: 8 − 𝑋 = 3𝑋 Agrupamos términos semejantes, nuevamente: 8 = 3𝑋 + 𝑋 8 = 4𝑋 Despejamos “X”: 8 𝑋= 4 𝑋 =2𝑚 El potencial eléctrico (V), es nulo a 2 m de qA. 34.- Dos cargas eléctricas 𝑞1 = +4𝑥10−6 𝐶 y 𝑞2 = −8𝑥10−6 𝐶 están en el vacio separadas una distancia de 10 cm. Calcular en que punto de la recta que las une el potencial eléctrico es nulo. ( ( ( ( ) 3,33 cm de q1 ) -3,33 cm de q1 ) 3,33 m de q1 ) – 3,33 m de q1 Datos: 𝑞1 = +4𝑥10−6 𝐶 𝑞𝐵 = −8𝑥10−6 𝐶 𝑟𝐴𝐵 = 10 𝑐𝑚 = 10𝑥10−2 𝑚 𝑋 =? 𝑉=0 Diagrama: Solo se utiliza de forma explicativa, con el fin de analizar el problema de forma más clara y sencilla. +q1 P X -q2 10 cm (10-X) Para que el potencial eléctrico resultante sea nulo, se debe cumplir que los potenciales creados por cada carga, sean iguales en magnitud. Conversión de unidades: Solución: Transformamos los Partimos de la condición que los potenciales creados por centímetros (cm) a metros cada carga sean iguales en magnitud. En tal sentido, (m), multiplicando por 10-2 aplicamos la ecuación del potencial eléctrico en un punto: m o dividiendo entre 100 cm. 𝑉=𝐾𝑥 𝑞 𝑟 Igualamos los potenciales: 𝑉𝐴 = 𝑉𝐵 Sustituimos los potenciales por sus ecuaciones: 𝑞𝐴 𝑞𝐵 𝐾𝑥 =𝐾𝑥 𝑟𝐴𝑝 𝑟𝐵𝑝 Simplificamos “K” y agrupamos términos semejantes: 𝑟𝐵𝑝 𝑞𝐵 = 𝑟𝐴𝑝 𝑞𝐴 Sustituimos por sus valores: 10 − 𝑋 8𝑥10−6 𝐶 = 𝑋 4𝑥10−6 𝐶 10 − 𝑋 =2 𝑋 Colocamos la ecuación de forma lineal: 10 − 𝑋 = 2𝑋 Agrupamos términos semejantes, nuevamente: 10 = 2𝑋 + 𝑋 10 = 3𝑋 Despejamos “X”: 10 𝑋= 3 𝑋 = 3,33 𝑐𝑚 El potencial eléctrico (V), es nulo a 3,33 cm de q1. 35.- Dos esferas de R1 = 10 cm y R2 = 20 cm, poseen cargas eléctricas de 𝑞1 = +5𝑥10−6 𝐶 y 𝑞2 = −8𝑥10−6 𝐶. Se les pone en contacto. Calcular el potencial eléctrico en la superficie de cada una de ella. ( ( ( ( ) 𝑉1 ) 𝑉1 ) 𝑉1 ) 𝑉1 = −6,75𝑥104 𝑉 𝑦 𝑉2 = −1,35𝑥105 𝑉 = 6,75𝑥104 𝑉 𝑦 𝑉2 = 1,35𝑥105 𝑉 = 1,35𝑥105 𝑉 𝑦 𝑉2 = 6,75𝑥104 𝑉 = −1,35𝑥105 𝑉 𝑦 𝑉2 = −6,75𝑥104 𝑉 Datos: 𝑅1 = 10 𝑐𝑚 = 10𝑥10−2 𝑚 𝑅2 = 20𝑐𝑚 = 20𝑥10−2 𝑚 𝑞1 = +5𝑥10−6 𝐶 𝑞2 = −8𝑥10−6 𝐶 𝑉1 =? 𝑉2 =? Diagrama: No es necesario realizar. Conversión de Unidades: Transformamos los centímetros (cm) a metros (m), multiplicando por 10-2 m o dividiendo entre 100 cm. Solución: Como son esferas, hablamos de radios (R) de las esferas; además, debemos tomar en cuenta que al ponerlas en contacto las dos adquieren cargas iguales, que es igual a la mitad de la suma algebraica que poseen antes del contacto. 𝑞1 + 𝑞2 +5𝑥10−6 𝐶 + (−8𝑥10−6 𝐶) = 2 2 𝑞1 + 𝑞2 −3𝑥10−6 𝐶 = 2 2 𝑞1 = 𝑞2 = −1,5𝑥10−6 𝐶 Conocido el nuevo valor de las cargas, después del contacto, procedemos a calcular el potencial eléctrico en la superficie de cada una de las esferas, aplicando la ecuación del potencial eléctrico en la superficie de una esfera. 𝑞 𝑉=𝐾𝑥 𝑅 Sustituimos en la ecuación, para cada uno de los casos; es decir, para cada esfera con las cargas obtenidas después del contacto. 𝑁 𝑥 𝑚2 (−1,5𝑥10−6 𝐶) 9 𝑉1 = 9𝑥10 𝑥 𝐶2 10𝑥10−2 𝑚 𝑉1 = −1,35𝑥105 𝑉 𝑉2 = 9𝑥109 𝑁 𝑥 𝑚2 (−1.5𝑥10−6 𝐶) 𝑥 𝐶2 20𝑥10−2 𝑚 𝑉2 = −6,75𝑥104 𝑉 Nivel III. Alto 36.- En la figura se muestra un triangulo rectángulo en A, en los vértices B y C hay cargas eléctricas cuyos valores son 𝑞𝐵 = +3𝑥10−6 𝐶 y 𝑞𝐶 = −9𝑥10−6 𝐶. Calcular el potencial eléctrico resultante en A. ( ( ( ( ) -1,13x106 V ) -1,13x10-6 V ) +1,13x106 V ) -1,13x105 V +qB 3 cm A -qC 4 cm Datos: 𝑞𝐴 = +3𝑥10−6 𝐶 𝑞𝐵 = −9𝑥10−6 𝐶 𝑟𝐴𝐵 = 3𝑐𝑚 = 3𝑥10−6 𝐶 𝑟𝐴𝐶 = 4𝑐𝑚 = 4𝑥10−2 𝑚 𝑉𝐴 =? Diagrama: Solo se utiliza de muestra, para la realización del problema, no para análisis vectorial; ya que, el potencial eléctrico es una magnitud escalar. +qB 3 cm A -qC 4 cm Conversión de Unidades: Transformamos los centímetros (cm) a metros (m), multiplicando por 10-2 m o dividiendo entre 100 cm. Solución: Para hallar el potencial eléctrico resultante en A, debemos sumar algebraicamente, los potenciales creados por cada carga en ese punto. 𝑉𝐴 = 𝑉𝐴𝐵 + 𝑉𝐴𝐶 Calculamos los potenciales, aplicando la ecuación del potencial eléctrico en un punto, respecto a la carga “qB” y “qC”. 𝑞 𝑟 Sustituimos primero para “B” y luego para “C”: 2 (+3𝑥10−6 𝐶) 9 𝑁 𝑥𝑚 𝑉𝐴𝐵 = 9𝑥10 𝑐 2 𝑥 3𝑥10−2 𝑚 𝑉=𝐾𝑥 𝑉𝐴𝐵 = 9𝑥105 𝑉 𝑉𝐴𝐶 = 9𝑥109 𝑁 𝑥 𝑚2 𝐶2 𝑥 (−9𝑥10−6 𝐶) 4𝑥10−2 𝑚 𝑉𝐴𝐶 = −2,03𝑥106 𝑉 Conocidos los potenciales creados por cada carga, procedemos a calcular el potencial resultante en el punto A. 𝑉𝐴 = 9𝑥105 𝑉 + (−2,03𝑥106 𝑉) 𝑉𝐴 = −1,13𝑥106 𝑉 37.- En la figura se muestra un triangulo rectángulo en A, en los vértices B y C hay cargas eléctricas cuyos valores son 𝑞𝐵 = −5𝑥10−6 𝐶 y 𝑞𝐶 = −8𝑥10−6 𝐶. En el vértice “C” hay un ángulo de 30º. Calcular el potencial eléctrico resultante en A. ( ( ( ( ) 3,76x106 V ) -3,76x10-6 V ) -3,76x106 V ) -3,76x105 V +qB A -qC 4 cm Datos: 𝑞𝐴 = −5𝑥10−6 𝐶 𝑞𝐵 = −8𝑥10−6 𝐶 𝑟𝐴𝐶 = 4𝑐𝑚 = 4𝑥10−2 𝑚 𝑉𝐴 =? 𝛼𝐶 = 30° Diagrama: Solo se utiliza de muestra, para la realización del problema, no para análisis vectorial; ya que, el potencial eléctrico es una magnitud escalar. +qB A -qC 4 cm Conversión de Unidades: Transformamos los centímetros (cm) a metros (m), multiplicando por 10-2 m o dividiendo entre 100 cm. Solución: Para hallar el potencial eléctrico resultante en A, debemos sumar algebraicamente, los potenciales creados por cada carga en ese punto. 𝑉𝐴 = 𝑉𝐴𝐵 + 𝑉𝐴𝐶 Calculamos los potenciales, aplicando la ecuación del potencial eléctrico en un punto, respecto a la carga “qB” y “qC”. 𝑞 𝑟 Sustituimos primero para “B” y luego para “C”, no sin antes calcular la distancia “rAB”, aplicando la función tangente. tan 30°; ya que es conocido el ángulo y el cateto adyacente a este: 𝐶𝑎𝑡 𝑂𝑝 𝑟𝐴𝐵 tan 30° = = 𝐶𝑎𝑡 𝑎𝑑𝑦 𝑟𝐴𝐶 Despejamos la distancia “rAB”: 𝑟𝐴𝐵 = 𝑟𝐴𝐶 𝑥 tan 30° 𝑉=𝐾𝑥 Sustituimos: 𝑟𝐴𝐵 = 4𝑥10−2 𝑚 𝑥 tan 30° 𝑟𝐴𝐵 = 0,023 𝑚 = 2,3𝑥10−2 𝑚 𝑉𝐴𝐵 = 9𝑥109 𝑁 𝑥𝑚2 𝑐2 𝑥 (−5𝑥10−6 𝐶) 2, 3𝑥10−2 𝑚 𝑉𝐴𝐵 = −1,96𝑥106 𝑉 (−8𝑥10−6 𝐶) 𝑉𝐴𝐶 = 𝑥 4𝑥10−2 𝑚 𝑉𝐴𝐶 = −1,8𝑥106 𝑉 Conocidos los potenciales creados por cada carga, procedemos a calcular el potencial resultante en el punto A. 𝑉𝐴 = −1,96𝑥106 𝑉 + (−1,8𝑥106 𝑉) 𝑁𝑥𝑚 9𝑥109 𝐶 2 2 𝑉𝐴 = −3,76𝑥106 𝑉 38.- En la figura se muestra un triangulo rectángulo en A, en los vértices B y C hay cargas eléctricas cuyos valores son 𝑞𝐵 = +2𝑥10−6 𝐶 y 𝑞𝐶 = +4𝑥10−6 𝐶. En el vértice “C” hay un ángulo de 60º. Calcular el potencial eléctrico resultante en A. ( ( ( ( ) -7,73x105 V ) 7,73x10-6 V ) 7,73x106 V ) 7,73x105 V +qB 12 cm A Datos: 𝑞𝐴 = +2𝑥10−6 𝐶 𝑞𝐵 = +4𝑥10−6 𝐶 𝑟𝐵𝐶 = 12𝑐𝑚 = 12𝑥10−2 𝑚 𝑉𝐴 =? 𝛼𝐶 = 60° +qC Diagrama: Solo se utiliza de muestra, para la realización del problema, no para análisis vectorial; ya que, el potencial eléctrico es una magnitud escalar. +qB 12 cm A Conversión de Unidades: Transformamos los centímetros (cm) a metros (m), multiplicando por 10-2 m o dividiendo entre 100 cm. -qC Solución: Para hallar el potencial eléctrico resultante en A, debemos sumar algebraicamente, los potenciales creados por cada carga en ese punto. 𝑉𝐴 = 𝑉𝐴𝐵 + 𝑉𝐴𝐶 Calculamos los potenciales, aplicando la ecuación del potencial eléctrico en un punto, respecto a la carga “qB” y “qC”. 𝑞 𝑟 Sustituimos primero para “B” y luego para “C”, no sin antes calcular la distancia “rAB” y “rAC”, aplicando la función sin 60°, para la distancia (AB) y la función cos 60°, para la distancia (AC); ya que, es conocido el ángulo y la hipotenusa del triangulo : 𝐶𝑎𝑡 𝑂𝑝 𝑟𝐴𝐵 sin 60° = = 𝐻𝑖𝑝 𝑟𝐵𝐶 Despejamos la distancia “rAB”: 𝑉=𝐾𝑥 𝑟𝐴𝐵 = 𝑟𝐴𝐶 𝑥 sin 60° Sustituimos: 𝑟𝐴𝐵 = 12𝑥10−2 𝑚 𝑥 sin 60° 𝑟𝐴𝐵 = 0,104 𝑚 = 1,04𝑥10−1 𝑚 𝑉𝐴𝐵 = 𝑁 𝑥𝑚 9𝑥109 𝑐 2 2 (+2𝑥10−6 𝐶) 𝑥 0,104 𝑚 𝑉𝐴𝐵 = 1,73𝑥105 𝑉 Ahora calculamos la distancia (AC), aplicando la función cos 60°. 𝐶𝑎𝑡 𝑎𝑑𝑦 𝑟𝐴𝐶 cos 60° = = 𝐻𝑖𝑝 𝑟𝐵𝐶 Despejamos la distancia (AC): 𝑟𝐴𝐶 = 𝑟𝐵𝐶 𝑥 cos 60° Sustituimos: 𝑟𝐴𝐶 = 12𝑥10−2 𝑚 𝑥 cos 60° 𝑟𝐴𝐶 = 0,06 𝑚 = 6𝑥10−2 𝑚 (4𝑥10−6 𝐶) 6𝑥10−2 𝑚 5 𝑉𝐴𝐶 = 6𝑥10 𝑉 Conocidos los potenciales creados por cada carga, procedemos a calcular el potencial resultante en el punto A. 𝑉𝐴 = 1,73𝑥105 𝑉 + 6𝑥105 𝑉 𝑉𝐴𝐶 = 9𝑥109 𝑁 𝑥 𝑚2 𝐶2 𝑥 𝑉𝐴 = 7,73𝑥105 𝑉 39.- En la figura se muestra un triangulo rectángulo en A, en los vértices B y C hay cargas eléctricas cuyos valores son 𝑞𝐵 = +16𝑥10−6 𝐶 y 𝑞𝐶 = +24𝑥10−6 𝐶. En el vértice “C” hay un ángulo de 60º. Calcular el potencial eléctrico resultante en A. ( ( ( ( ) - 1,664x105 V ) 1,664x10-6 V ) 1,664x106 V ) 1,664x105 V +qB 36 cm A Datos: 𝑞𝐴 = +16𝑥10−6 𝐶 𝑞𝐵 = +24𝑥10−6 𝐶 𝑟𝐵𝐶 = 36𝑐𝑚 = 36𝑥10−2 𝑚 𝑉𝐴 =? 𝛼𝐶 = 60° +qC Diagrama: Solo se utiliza de muestra, para la realización del problema, no para análisis vectorial; ya que, el potencial eléctrico es una magnitud escalar. +qB 36 cm A Conversión de Unidades: Transformamos los centímetros (cm) a metros (m), multiplicando por 10-2 m o dividiendo entre 100 cm. -qC Solución: Para hallar el potencial eléctrico resultante en A, debemos sumar algebraicamente, los potenciales creados por cada carga en ese punto. 𝑉𝐴 = 𝑉𝐴𝐵 + 𝑉𝐴𝐶 Calculamos los potenciales, aplicando la ecuación del potencial eléctrico en un punto, respecto a la carga “qB” y “qC”. 𝑞 𝑟 Sustituimos primero para “B” y luego para “C”, no sin antes calcular la distancia “rAB” y “rAC”, aplicando la función sin 60°, para la distancia (AB) y la función cos 60°, para la distancia (AC); ya que, es conocido el ángulo y la hipotenusa del triangulo : 𝐶𝑎𝑡 𝑂𝑝 𝑟𝐴𝐵 sin 60° = = 𝐻𝑖𝑝 𝑟𝐵𝐶 Despejamos la distancia “rAB”: 𝑉=𝐾𝑥 𝑟𝐴𝐵 = 𝑟𝐴𝐶 𝑥 sin 60° Sustituimos: 𝑟𝐴𝐵 = 36𝑥10−2 𝑚 𝑥 sin 60° 𝑟𝐴𝐵 = 0,31 𝑚 = 3,1𝑥10−1 𝑚 𝑉𝐴𝐵 = 𝑁 𝑥𝑚 9𝑥109 𝑐 2 2 (+16𝑥10−6 𝐶) 𝑥 0,31 𝑚 𝑉𝐴𝐵 = 4,64𝑥105 𝑉 Ahora calculamos la distancia (AC), aplicando la función cos 60°. 𝐶𝑎𝑡 𝑎𝑑𝑦 𝑟𝐴𝐶 cos 60° = = 𝐻𝑖𝑝 𝑟𝐵𝐶 Despejamos la distancia (AC): 𝑟𝐴𝐶 = 𝑟𝐵𝐶 𝑥 cos 60° Sustituimos: 𝑟𝐴𝐶 = 36𝑥10−2 𝑚 𝑥 cos 60° 𝑟𝐴𝐶 = 0,18 𝑚 = 1,8𝑥10−1 𝑚 (24𝑥10−6 𝐶) 0,18𝑚 𝑉𝐴𝐶 = 1,2𝑥106 𝑉 Conocidos los potenciales creados por cada carga, procedemos a calcular el potencial resultante en el punto A. 𝑉𝐴 = 4,64𝑥105 𝑉 + 1,2𝑥106 𝑉 𝑉𝐴𝐶 = 9𝑥109 𝑁 𝑥 𝑚2 𝐶2 𝑥 𝑉𝐴 = 1,664𝑥106 𝑉 40.- En la figura se muestra un triangulo rectángulo en A, en los vértices B y C hay cargas eléctricas cuyos valores son 𝑞𝐵 = −7𝑥10−6 𝐶 y 𝑞𝐶 = −2𝑥10−6 𝐶. En el vértice “C” hay un ángulo de 30º. Calcular el potencial eléctrico resultante en A. ( ( ( ( ) -6,4x106 V ) 6,4x10-6 V ) 6,4x106 V ) -6,4x105 V +qB A -qC 2 cm Datos: 𝑞𝐴 = −7𝑥10−6 𝐶 𝑞𝐵 = −2𝑥10−6 𝐶 𝑟𝐴𝐶 = 2𝑐𝑚 = 2𝑥10−2 𝑚 𝑉𝐴 =? 𝛼𝐶 = 30° Diagrama: Solo se utiliza de muestra, para la realización del problema, no para análisis vectorial; ya que, el potencial eléctrico es una magnitud escalar. +qB A -qC 2 cm Conversión de Unidades: Transformamos los centímetros (cm) a metros (m), multiplicando por 10-2 m o dividiendo entre 100 cm. Solución: Para hallar el potencial eléctrico resultante en A, debemos sumar algebraicamente, los potenciales creados por cada carga en ese punto. 𝑉𝐴 = 𝑉𝐴𝐵 + 𝑉𝐴𝐶 Calculamos los potenciales, aplicando la ecuación del potencial eléctrico en un punto, respecto a la carga “qB” y “qC”. 𝑞 𝑟 Sustituimos primero para “B” y luego para “C”, no sin antes calcular la distancia “rAB”, aplicando la función tangente. tan 30°; ya que es conocido el ángulo y el cateto adyacente a este: 𝐶𝑎𝑡 𝑂𝑝 𝑟𝐴𝐵 tan 30° = = 𝐶𝑎𝑡 𝑎𝑑𝑦 𝑟𝐴𝐶 Despejamos la distancia “rAB”: 𝑟𝐴𝐵 = 𝑟𝐴𝐶 𝑥 tan 30° 𝑉=𝐾𝑥 Sustituimos: 𝑟𝐴𝐵 = 2𝑥10−2 𝑚 𝑥 tan 30° 𝑟𝐴𝐵 = 0,0115 𝑚 = 1,15𝑥10−2 𝑚 𝑉𝐴𝐵 = 9𝑥109 𝑁 𝑥𝑚2 𝑐2 𝑥 (−7𝑥10−6 𝐶) 1,15𝑥10−2 𝑚 𝑉𝐴𝐵 = −5,5𝑥106 𝑉 (−2𝑥10−6 𝐶) 𝑉𝐴𝐶 = 𝑥 2𝑥10−2 𝑚 5 𝑉𝐴𝐶 = −9𝑥10 𝑉 Conocidos los potenciales creados por cada carga, procedemos a calcular el potencial resultante en el punto A. 𝑉𝐴 = −5,5𝑥106 𝑉 + (−9𝑥105 𝑉) 𝑁𝑥𝑚 9𝑥109 𝐶 2 2 𝑉𝐴 = −6,4𝑥106 𝑉 41.- ABC es un triangulo equilátero de 9 cm de lado. En sus vértices hay cargas eléctricas cuyos módulos son 𝑞𝐴 = +2𝑛𝐶; 𝑞𝐵 = −8𝑛𝐶 y 𝑞𝐶 = +5𝑛𝐶. Calcular el potencial eléctrico resultante sobre el punto P, ubicado en el punto medio del lado AC. ( ( ( ( ) 976,9 V ) -976,9 V ) 2823,1 V ) -2823,1 V -qB 9 cm +qA +qC P Datos: Diagrama: −9 𝑞𝐴 = +2𝑛𝐶 = 2𝑥10 𝐶 𝑞𝐵 = −8𝑛𝐶 = −8𝑥10−9 𝐶 𝑞𝐶 = +5𝑛𝐶 = +5𝑥10−9 𝐶 𝐿 = 9𝑐𝑚 = 9𝑥10−2 𝑚 𝑉𝑅 =? en P -qB 9 cm +qA P +qC El diagrama es utilizado, solo de muestra, para un mejor análisis y resolución del problema. Conversión de Unidades: Transformamos los centímetros (cm) a metros (m), multiplicando por 10-2 m o dividiendo entre 100 cm. También transformamos los nanocoulomb (nC) a Coulomb (C), multiplicando por 10-9 C. Solución: El potencial eléctrico es una magnitud escalar, por tal motivo, el potencial resultante en el punto P, es la suma algebraica de los potenciales creados por cada carga en ese punto: 𝑉𝑅 = 𝑉𝐴 + 𝑉𝐵 + 𝑉𝐶 Antes, debemos hallar los potenciales creados por cada carga, aplicando la ecuación del potencial eléctrico en un punto. 𝑞 𝑉=𝐾𝑥 𝑟 Calculamos rimero el potencial creado por la carga “qA”, utilizando la distancia que hay entre A y P. 2 (+2𝑥10−9 𝐶) 9𝑁 𝑥 𝑚 𝑉𝐴 = 9𝑥10 𝐶 2 𝑥 4,5𝑥10−2 𝑚 𝑉𝐴 = 900 𝑉 Antes de calcular el potencial creado por “qB”, debemos calcular la distancia desde B hasta P, aplicando la función seno del ángulo (sin 60°): sin 60° = 𝑐𝑜 𝑟𝐵𝑃 = ℎ 𝑟𝐴𝐵 Despejamos “rBP”: 𝑟𝐵𝑃 = 𝑟𝐴𝐵 𝑥 sin 60° Sustituimos: 𝑟𝐵 = 9𝑥10−2 𝑚 𝑥 sin 60° 𝑟𝐵𝑃 = 0,078𝑚 = 7,8𝑥10−2 𝑚 Ahora utilizamos esta distancia para calcular el potencial creado por la carga “qB”: −9 𝑁 𝑥 𝑚2 (−8𝑥10 𝐶) 𝑉𝐵 = 9𝑥109 𝐶 2 𝑥 7,8𝑥10−2 𝑚 𝑉𝐵 = −923,1 𝑉 Calculamos el potencial creado por la carga “qC”, utilizando la distancia que hay de C al punto “P”: −9 𝑁 𝑥 𝑚2 (+5𝑥10 𝐶) 𝑉𝐶 = 9𝑥109 𝐶 2 𝑥 4,5𝑥10−2 𝑚 𝑉𝐶 = 1000 𝑉 Calculados los potenciales creados por cada carga, ahora procedemos a calcular el resultante en el unto P: 𝑉𝑅 = 900 𝑉 + (−923,1 𝑉) + 1000 𝑉 𝑉𝑅 = 976,9 𝑉 42.- ABC es un triangulo equilátero de 6 cm de lado. En sus vértices hay cargas eléctricas cuyos módulos son 𝑞𝐴 = −6µ𝐶; 𝑞𝐵 = −3µ𝐶 y 𝑞𝐶 = −4µ𝐶. Calcular el potencial eléctrico resultante sobre el punto P, ubicado en el punto medio del lado AC. ( ( ( ( ) 3,52x105 V ) -3,52x10-6 V ) -3,52x106 V ) 3,52x106 V -qB 6 cm -qA -qC P Datos: Diagrama: −6 𝑞𝐴 = −6µ𝐶 = −6𝑥10 𝐶 𝑞𝐵 = −3𝑛µ𝐶 = −3𝑥10−6 𝐶 𝑞𝐶 = −4µ𝐶 = −4𝑥10−6 𝐶 𝐿 = 6𝑐𝑚 = 6𝑥10−2 𝑚 𝑉𝑅 =? en P -qB 6 cm -qA P -qC El diagrama es utilizado, solo de muestra, para un mejor análisis y resolución del problema. Conversión de Unidades: Transformamos los centímetros (cm) a metros (m), multiplicando por 10-2 m o dividiendo entre 100 cm. También transformamos los nanocoulomb (nC) a Coulomb (C), multiplicando por 10-9 C. Solución: El potencial eléctrico es una magnitud escalar, por tal motivo, el potencial resultante en el punto P, es la suma algebraica de los potenciales creados por cada carga en ese punto: 𝑉𝑅 = 𝑉𝐴 + 𝑉𝐵 + 𝑉𝐶 Antes, debemos hallar los potenciales creados por cada carga, aplicando la ecuación del potencial eléctrico en un punto. 𝑞 𝑉=𝐾𝑥 𝑟 Calculamos rimero el potencial creado por la carga “qA”, utilizando la distancia que hay entre A y P. 2 (−6𝑥10−6 𝐶) 9𝑁 𝑥 𝑚 𝑉𝐴 = 9𝑥10 𝐶 2 𝑥 3𝑥10−2 𝑚 𝑉𝐴 = −1,8𝑥106 𝑉 Antes de calcular el potencial creado por “qB”, debemos calcular la distancia desde B hasta P, aplicando la función seno del ángulo (sin 60°): sin 60° = 𝑐𝑜 𝑟𝐵𝑃 = ℎ 𝑟𝐴𝐵 Despejamos “rBP”: 𝑟𝐵𝑃 = 𝑟𝐴𝐵 𝑥 sin 60° Sustituimos: 𝑟𝐵 = 6𝑥10−2 𝑚 𝑥 sin 60° 𝑟𝐵𝑃 = 0,0519𝑚 = 5,19𝑥10−2 𝑚 Ahora utilizamos esta distancia para calcular el potencial creado por la carga “qB”: −6 𝑁 𝑥 𝑚2 (−3𝑥10 𝐶) 𝑉𝐵 = 9𝑥109 𝐶 2 𝑥 5,19𝑥10−2 𝑚 𝑉𝐵 = −5,2𝑥105 𝑉 Calculamos el potencial creado por la carga “qC”, utilizando la distancia que hay de C al punto “P”: −6 𝑁 𝑥 𝑚2 (−4𝑥10 𝐶) 𝑉𝐶 = 9𝑥109 𝐶 2 𝑥 3𝑥10−2 𝑚 𝑉𝐶 = −1,2𝑥106 𝑉 Calculados los potenciales creados por cada carga, ahora procedemos a calcular el resultante en el unto P: 𝑉𝑅 = −1,8𝑥106 𝑉 + (−5,2𝑥10 5𝑉) + (−1,2𝑥106 𝑉) 𝑉𝑅 = −3,52𝑥106 𝑉 43.- Una esfera de 0,1 gr esta suspendida por medio de un hilo de seda entre dos laminas paralelas separadas por una distancia de 4 cm. La carga de de la esfera es de +5𝑥10−8 𝐶. Calcular la diferencia de potencial entre las láminas sabiendo que cuando la esfera queda en equilibrio el hilo forma un ángulo de 15º con la vertical. ( ( ( ( ) 209,6 V ) -209,6 V ) 206,9 V ) -206,9 V α 4 cm Datos: 𝑚 = 0,1𝑔𝑟 = 10−4 𝐾𝑔 𝑟 = 4𝑐𝑚 = 4𝑥10−2 𝑚 𝑞 = +5𝑥10−8 𝐶 𝛼 = 15° 𝑉𝐵 − 𝑉𝐴 =? Diagrama: α A F O α α P FR B C Conversión de Unidades: Transformamos los gramos (gr) a kilogramos (kg), multiplicando por 10-3 Kg o dividiendo entre 1000 gr. También se hizo la transformación de los centímetros (cm) a metros (m), multiplicando por 10-2 m o dividiendo entre 100 cm. Se hace el análisis de fuerzas que actúan sobre la esfera, las cuales son: F, que es la fuerza que actúa por efecto del campo eléctrico entre las placas y P que es el peso de la esfera. Solución: Calculamos en el triangulo 𝛥𝑂𝐵𝐶 𝑙𝑎 𝑓𝑢𝑒𝑟𝑧𝑎. Aplicando la función tangente: 𝐵𝐶 = 𝑂𝐴 = 𝐹 Entonces: 𝐶𝑎𝑡 𝑂𝑝 𝐵𝐶 𝐹 tan 15° = = = 𝐶𝑎𝑡 𝑎𝑑𝑦 𝑂𝐶 𝑃 Despejamos “F”: 𝐹 = 𝑃 𝑥 tan 15° De donde: 𝑚 𝑃 = 𝑚 𝑥 𝑔 = 10−4 𝐾𝑔𝑥9,8 𝑠2 𝑃 = 9,8𝑥10−4 𝑁 Ahora calculamos “F”: 𝐹 = 9,8𝑥10−4 𝑁 𝑥 tan 15° 𝐹 = 2,62𝑥10−4 𝑁 Obtenida la fuerza, calculamos ahora la intensidad del campo eléctrico, a través de la ecuación por definición: 𝐹 𝐸= 𝑞0 Sustituimos: 2,62𝑥10−4 𝑁 𝐸= 5𝑥10−8 𝐶 𝑁 𝐸 = 5240 𝐶 Ahora calculamos la diferencia de potencial, aplicando la ecuación de la diferencia de potencial entre laminas paralelas de un campo eléctrico: 𝑉𝐵 − 𝑉𝐴 = 𝐸 𝑥 𝑑 𝑉𝐵 − 𝑉𝐴 = 5240 𝑁𝐶 𝑥 4𝑥10−2 𝑚 𝑉𝐵 − 𝑉𝐴 = 209,6 𝑉 44.-En la figura se muestran tres cargas eléctricas 𝑞1 = +3𝑥10−6 𝐶; 𝑞2 = −3𝑥10−6 𝐶 y 𝑞3 = +3𝑥10−6 𝐶. Calcular la energía potencial eléctrica del sistema constituido por las tres cargas. +q3 ( ( ( ( )𝑈 )𝑈 )𝑈 )𝑈 = 4, 5 𝐽 = −4,05 𝐽 = −40,5 𝐽 = 40,5 𝐽 X +q1 -q2 1 cm Datos: 𝑞1 = +3𝑥10−6 𝐶 𝑞2 = −3𝑥10−6 𝐶 𝑞3 = +3𝑥10−6 𝐶 𝑟13 = 𝑟23 = 𝑋 =? 𝑟12 = 2𝑐𝑚 = 2𝑥10−2 𝑚 𝑈 =? X 1 cm 1 cm Diagrama: Solo de muestra ara especificar las condiciones del problema. +q3 X X 1 cm +q1 -q2 1 cm Conversión de Unidades: Transformamos los centímetros (cm a metros (m), multiplicando por 10-2 m o dividiendo entre 100 cm. 1 cm Solución: Se debe calcular la energía potencial eléctrica para cada par de cargas eléctricas. Sin embargo, debemos primero calcular la distancia de separación entre las cargas q1 y q3, la cual es la misma para las cargas q2 y q3. Si observamos la figura esa distancia la identificamos como X, la cual podemos hallarla, aplicando el teorema de Pitágoras: 𝐶 2 = 𝑎2 + 𝑏 2 Donde: C= X; a y b= 1 cm, para eliminar el cuadrado de C introducimos dentro de una raíz cuadrada el resto de la ecuación. 𝑋 = √𝑎2 + 𝑏 2 Sustituimos: 𝑋 = √(1 𝑐𝑚)2 + (1 𝑐𝑚)2 𝑋 = 1,4 𝑐𝑚 = 1,4𝑥10−2 𝑚 Ahora calculamos la energía potencial eléctrica para cada par de cargas: U12; U13 y U23. Utilizando la ecuación de la energía potencial eléctrica por definición: 𝑞 𝑥 𝑞0 𝑈=𝐾𝑥 𝑟 Sustituimos: 3𝑥10−6 𝐶 𝑥(−3𝑥10−6 𝐶) 𝑁 𝑥 𝑚2 𝑈12 = 9𝑥109 𝐶 2 𝑥 2𝑥10−2 𝑚 𝑈12 = −4,05 𝐽 2 3𝑥10−6 𝐶 𝑥3𝑥10−6 𝐶 9𝑁 𝑥 𝑚 𝑈13 = 9𝑥10 𝐶 2 𝑥 1,4𝑥10−2 𝑚 𝑈13 = 5,8 𝐽 −6 2 (−3𝑥10 𝐶) 𝑥 3𝑥10−6 𝐶 9𝑁 𝑥 𝑚 𝑈23 = 9𝑥10 𝐶 2 𝑥 1,4𝑥10−2 𝑚 𝑈23 = −5,8 𝐽 Ahora, como la energía es una magnitud escalar, sumamos algebraicamente los valores obtenidos anteriormente: 𝑈𝑇 = 𝑈12 + 𝑈13 + 𝑈23 Sustituimos: 𝑈𝑇 = −4,05 𝐽 + 5,8 𝐽 + (−5,8 𝐽) 𝑈𝑇 = −4,05 𝐽 Esto explica que ara construir esta estructura se ha realizado un trabajo negativo, si consideramos las tres cargas en el infinito y en reposo. 45.- En la figura se muestra un rectángulo cuyas longitudes son 5 cm y 15 cm y las cargas 𝑞1 = −5𝑥10−6 𝐶 y 𝑞2 = +2𝑥10−6 𝐶. Calcular: a) el potencial eléctrico en A; b) el potencial eléctrico en B; c) el trabajo que se debe realizar para trasladar una carga eléctrica de 𝑞0 = +6𝑥10−6 𝐶 desde B hasta A, a través de la diagonal del rectángulo. -q1 A 5 cm B ( ( ( ( ) 𝑉𝐴 ) 𝑉𝐴 ) 𝑉𝐴 ) 𝑉𝐴 15 cm +q2 = −6𝑥104 𝑉; 𝑉𝐵 = 7,8𝑥105 𝑉 y 𝑊𝐴𝐵 = −5,04 𝐽 = −6𝑥104 𝑉; 𝑉𝐵 = −7,8𝑥105 𝑉 y 𝑊𝐴𝐵 = −5,04 𝐽 = 6𝑥104 𝑉; 𝑉𝐵 = −7,8𝑥105 𝑉 y 𝑊𝐴𝐵 = 5,04 𝐽 = 6𝑥104 𝑉; 𝑉𝐵 = −7,8𝑥105 𝑉 y 𝑊𝐴𝐵 = −5,04 𝐽 Datos: 𝐴 = 5𝑐𝑚 = 5𝑥10−2 𝑚 𝐿 = 15𝑐𝑚 = 15𝑥10−2 𝑚 𝑞1 = −5𝑥10−6 𝐶 𝑞2 = +2𝑥10−6 𝐶 𝑎) 𝑉𝐴 =? 𝑏) 𝑉𝐵 =? 𝑐) 𝑊𝐴𝐵 =? 𝑞0 = +6𝑥10−6 𝐶 Conversión de Unidades: Transformamos los centímetros (cm) a metros (m), multiplicando por 10-2 m o dividiendo entre 100 cm. Diagrama: -q1 A 5 cm B +q2 15 cm Solo para indicar las condiciones del problema. Solución: a) Calculamos el potencial en A (VA), sumando algebraicamente los potenciales creados por cada carga en ese punto: 𝑉𝐴 = 𝑉1𝐴 + 𝑉2𝐴 Los potenciales V1A y V2A, los calculamos aplicando la ecuación del potencial eléctrico en un punto. 𝑞 𝑉=𝐾𝑥 𝑟 Sustituimos en cada uno de los casos que se requiera: (−5𝑥10−6 𝐶) 𝑁 𝑥 𝑚2 𝑉1𝐴 = 9𝑥109 𝐶 2 𝑥 15𝑥10−2 𝑚 𝑉1𝐴 = −3𝑥105 𝑉 2𝑥10−6 𝐶 𝑁 𝑥 𝑚2 𝑉2𝐴 = 9𝑥109 𝐶 2 𝑥 5𝑥10−2 𝑚 5 𝑉2𝐴 = 3,6𝑥10 𝑉 𝑉𝐴 = −3𝑥105 𝑉 + 3,6𝑥105 𝑉 𝑉𝐴 = 6𝑥104 𝑉 b) Calculamos el potencial en B (VB), sumando algebraicamente los potenciales creados por cada carga en ese punto: 𝑉𝐵 = 𝑉1𝐵 + 𝑉2𝐵 Los potenciales V1A y V2A, los calculamos aplicando la ecuación del potencial eléctrico en un punto. 𝑞 𝑉=𝐾𝑥 𝑟 Sustituimos en cada uno de los casos que se requiera: 2 (−5𝑥10−6 𝐶) 9𝑁 𝑥 𝑚 𝑉1𝐵 = 9𝑥10 𝐶 2 𝑥 5𝑥10−2 𝑚 5 𝑉1𝐵 = −9𝑥10 𝑉 2𝑥10−6 𝐶 𝑁 𝑥 𝑚2 𝑉2𝐵 = 9𝑥109 𝐶 2 𝑥 15𝑥10−2 𝑚 𝑉2𝐴 = 1,2𝑥105 𝑉 𝑉𝐵 = −9𝑥105 𝑉 + 1,2𝑥105 𝑉 𝑉𝐵 = −7,8𝑥105 𝑉 C) Ahora calculamos el trabajo para trasladar la carga de +6x10-6 C desde B hasta A, a través de la diagonal. Para eso utilizamos la ecuación de la diferencia de potencial entre dos puntos. 𝑊𝐴𝐵 𝑉𝐵 − 𝑉𝐴 = 𝑞0 Despejamos “WAB”: 𝑊𝐴𝐵 = 𝑞0 𝑥(𝑉𝐵 − 𝑉𝐴 ) Sustituimos: 𝑊𝐴𝐵 = 6𝑥10−6 𝐶𝑥(−7,8𝑥105 𝑉 − 6𝑥104 𝑉 𝑊𝐴𝐵 = −5,04 𝐽 46.- Se dispone de un cuadrado de 10 cm de lado. En cada uno de sus vértices hay cargas eléctricas cuyos valores son 𝑞𝐴 = +4𝑥10−6 𝐶 ;𝑞𝐵 = −3𝑥10−6 𝐶 ;𝑞𝐶 = +2,5𝑥10−6 𝐶 𝑞𝐷 = −7,5𝑥10−6 𝐶. Calcular el potencial eléctrico resultante en el centro del cuadrado. A D ( ( ( ( B α10 cm 10 cm C ) – 5,16x105 V ) + 5,16x105 V ) – 5,16x10-5 V ) + 5,16x10-5 V Datos: Diagrama: 𝐿 = 10𝑐𝑚 = 10𝑥10−2 𝑚 𝑞𝐴 = +4𝑥10−6 𝐶 𝑞𝐵 = −3𝑥10−6 𝐶 +qA -qB −6 𝑞𝐶 = +2,5𝑥10 𝐶 𝑞𝐷 = −7,5𝑥10−6 𝐶 P 𝑉𝑅 =? 𝛼 = 45° -qD 10 cm +qC Solo para ver las condiciones del problema. Conversión de unidades: Transformamos los centímetros (cm) a metros (m), multiplicando por 10-2 m o dividiendo entre 100 cm. Solución: Calculamos el potencial eléctrico resultante en el centro del cuadrado, como la suma algebraica de los potenciales creados por cada carga: 𝑉𝑅 = 𝑉𝐴 + 𝑉𝐵 + 𝑉𝐶 + 𝑉𝐷 Los potenciales creados por cada carga, lo obtenemos aplicando, la ecuación de la definición de potencial eléctrico en un punto: 𝑞 𝑉=𝐾𝑥 𝑟 Antes de sustituir en la ecuación, debemos calcular la distancia que desde las cargas hasta el centro del cuadrado, la cual será igual para todas; ya que, es un cuadrado y el ángulo en este caso es de 45º. Para eso hacemos uso de la función coseno. cos 45° = 𝐶𝑎𝑡 𝑎𝑑𝑦 𝐷𝐶 = 𝐻𝑖𝑝 𝐷𝐵 Despejamos “DB”: 𝑟𝐷𝐵 = Sustituimos: 𝑟𝐷𝐶 cos 45° 10𝑥10−2 𝑚 cos 45° 𝑟𝐷𝐵 = 0,14 𝑚 = 1,4𝑥10−1 𝑚 Pero como es en el centro del cuadrado; entonces, la distancia de separación entre las cargas y el centro del cuadrado es la mitad de lo calculado: 0,14 𝑚 𝑟𝐴𝑃 = 2 𝑟𝐴𝑃 = 0,07𝑚 = 7𝑥10−2 𝑚 Esta distancia es igual Para cada uno de los casos, procedemos ahora a calcular cada uno de los potenciales creados por cada carga eléctrica: −6 𝑁 𝑥𝑚2 4𝑥10 𝐶 𝑉𝐴 = 9𝑥109 𝑐 2 𝑥 7𝑥10−2 𝑚 𝑉𝐴 = 5,14𝑥105 𝑉 𝑟𝐷𝐵 = 𝑉𝐵 = 𝑁𝑥𝑚 9𝑥109 𝐶 2 2 (−3𝑥10−6 𝐶) 𝑥 7𝑥10−2 𝑚 𝑉𝐵 = −3,86𝑥105 𝑉 𝑉𝐶 = 9𝑥109 𝑁 𝑥 𝑚2 𝐶2 𝑥 2,5𝑥10−6 𝐶 7𝑥10−2 𝑚 𝑉𝐶 = 3,2𝑥105 𝑉 𝑉𝐷 = 9𝑥109 𝑁 𝑥 𝑚2 𝐶2 𝑥 (−7,5𝑥10−6 𝐶) 7𝑥10−2 𝑚 𝑉𝐷 = −9,64𝑥105 𝑉 𝑉𝑅 = 5,14𝑥105 𝑉 + (−3,86𝑥105 𝑉) + 3,2𝑥105 𝑉 + (−9,64𝑥105 𝑉) 𝑉𝑅 = −5,16𝑥105 𝑉 47.- .- En la figura se muestra un rectángulo cuyas longitudes son 3 cm y 9 cm y las cargas 𝑞1 = +2𝑥10−6 𝐶 y 𝑞2 = +8𝑥10−6 𝐶. Calcular: a) el potencial eléctrico en A; b) el potencial eléctrico en B; c) el trabajo que se debe realizar para trasladar una carga eléctrica de 𝑞0 = −5𝑥10−6 𝐶 desde B hasta A, a través de la diagonal del rectángulo. -q1 A 3 cm B ( ( ( ( ) 𝑉𝐴 ) 𝑉𝐴 ) 𝑉𝐴 ) 𝑉𝐴 9 cm +q2 = 2,6𝑥106 𝑉; 𝑉𝐵 = 1,4𝑥106 𝑉 y 𝑊𝐴𝐵 = 6 𝐽 = −2,6𝑥105 𝑉; 𝑉𝐵 = −1,4𝑥105 𝑉 y 𝑊𝐴𝐵 = −6 𝐽 = 2, 6𝑥106 𝑉; 𝑉𝐵 = −1,4𝑥10−6 𝑉 y 𝑊𝐴𝐵 = 6 𝐽 = 2,6𝑥10−6 𝑉; 𝑉𝐵 = 1,4𝑥10−5 𝑉 y 𝑊𝐴𝐵 = −6 𝐽 Datos: 𝐴 = 3𝑐𝑚 = 3𝑥10−2 𝑚 𝐿 = 9𝑐𝑚 = 9𝑥10−2 𝑚 𝑞1 = +2𝑥10−6 𝐶 𝑞2 = +8𝑥10−6 𝐶 𝑎) 𝑉𝐴 =? 𝑏) 𝑉𝐵 =? 𝑐) 𝑊𝐴𝐵 =? 𝑞0 = −5𝑥10−6 𝐶 Conversión de Unidades: Transformamos los centímetros (cm) a metros (m), multiplicando por 10-2 m o dividiendo entre 100 cm. Diagrama: -q1 A 3 cm B +q2 9 cm Solo para indicar las condiciones del problema. Solución: a) Calculamos el potencial en A (VA), sumando algebraicamente los potenciales creados por cada carga en ese punto: 𝑉𝐴 = 𝑉1𝐴 + 𝑉2𝐴 Los potenciales V1A y V2A, los calculamos aplicando la ecuación del potencial eléctrico en un punto. 𝑞 𝑉=𝐾𝑥 𝑟 Sustituimos en cada uno de los casos que se requiera: (2𝑥10−6 𝐶) 𝑁 𝑥 𝑚2 𝑉1𝐴 = 9𝑥109 𝐶 2 𝑥 9𝑥10−2 𝑚 5 𝑉1𝐴 = 2𝑥10 𝑉 2 (8𝑥10−6 𝐶) 9𝑁 𝑥 𝑚 𝑉2𝐴 = 9𝑥10 𝐶 2 𝑥 3𝑥10−2 𝑚 6 𝑉2𝐴 = 2,4𝑥10 𝑉 𝑉𝐴 = 2𝑥105 𝑉 + 2,4𝑥106 𝑉 𝑉𝐴 = 2,6𝑥106 𝑉 b) Calculamos el potencial en B (VB), sumando algebraicamente los potenciales creados por cada carga en ese punto: 𝑉𝐵 = 𝑉1𝐵 + 𝑉2𝐵 Los potenciales V1A y V2A, los calculamos aplicando la ecuación del potencial eléctrico en un punto. 𝑞 𝑉=𝐾𝑥 𝑟 Sustituimos en cada uno de los casos que se requiera: 2 (2𝑥10−6 𝐶) 9𝑁 𝑥 𝑚 𝑉1𝐵 = 9𝑥10 𝐶 2 𝑥 3𝑥10−2 𝑚 5 𝑉1𝐵 = 6𝑥10 𝑉 (8𝑥10−6 𝐶) 𝑁 𝑥 𝑚2 𝑉2𝐵 = 9𝑥109 𝐶 2 𝑥 9𝑥10−2 𝑚 5 𝑉2𝐴 = 8𝑥10 𝑉 𝑉𝐵 = 6𝑥105 𝑉 + 8𝑥105 𝑉 𝑉𝐵 = 1,4𝑥106 𝑉 C) Ahora calculamos el trabajo para trasladar la carga de +6x10-6 C desde B hasta A, a través de la diagonal. Para eso utilizamos la ecuación de la diferencia de potencial entre dos puntos. 𝑊𝐴𝐵 𝑉𝐵 − 𝑉𝐴 = 𝑞0 Despejamos “WAB”: 𝑊𝐴𝐵 = 𝑞0 𝑥(𝑉𝐵 − 𝑉𝐴 ) Sustituimos: 𝑊𝐴𝐵 = −5𝑥10−6 𝐶𝑥(1,4𝑥106 𝑉 − 2,6𝑥106 𝑉 𝑊𝐴𝐵 = 6 𝐽 48.- En la figura se tienen dos cargas dadas así: q1 = +40 nC y q2 = -30 nC, separadas 10 cm. Un punto A equidista de ellas y el punto B esta a 8 cm de q1 y a 6 cm de q2. Calcular: a) el potencial en el punto A; b) el potencial en el punto B; c) el trabajo necesario para transportar una carga de 0,026 µC desde el punto B hasta el punto A. B 8 cm 6 cm +q1 5 cm ( ( ( ( A 5 cm -q2 ) a) 1800 V; b) 0 V; c) 4,68x10-5 J ) a) 180 V; b) 10 V; c) 4,68x105 J ) a) -1800 V; b) 0 V; c)- 4,68x10-5 J ) a) 0 V; b) 1800 V; c) 4,68x10-5 J Datos: 𝑞1 = +40𝑛𝐶 = +40𝑥10−9 𝐶 𝑞2 = −30𝑛𝐶 = −30𝑥10−9 𝐶 𝑟12 = 10𝑐𝑚 = 10𝑥10−2 𝑚 𝑟1𝐴 = 𝑟2𝐴 = 5𝑐𝑚 = 5𝑥10−2 𝑚 𝑟1𝐵 = 8𝑐𝑚 = 8𝑥10−2 𝑚 𝑟2𝐵 = 6𝑐𝑚 = 6𝑥10−2 𝑚 a) 𝑉𝐴 =? b) 𝑉𝐵 =? c) 𝑊𝐴𝐵 =? 𝑞0 = 0,026µ𝐶 = 2,6𝑥10−8 𝐶 Diagrama: Conversión de Unidades: Transformamos los centímetros (cm) a metros (m), multiplicando por 10-2 m o dividiendo entre 100 cm. También se transformo los nanocoulomb (nC) a Coulomb (C), multiplicando por 10-9 C y los microcoulomb (µC) a coulomb (C), multiplicando por 10-6 C. Solución: a) Calculamos el potencial en A (VA), sumando algebraicamente los potenciales creados por cada carga en ese punto: 𝑉𝐴 = 𝑉1𝐴 + 𝑉2𝐴 Los potenciales V1A y V2A, los calculamos aplicando la ecuación del potencial eléctrico en un punto. 𝑞 𝑉=𝐾𝑥 𝑟 Sustituimos en cada uno de los casos que se requiera: (+40𝑥10−9 𝐶) 𝑁 𝑥 𝑚2 𝑉1𝐴 = 9𝑥109 𝐶 2 𝑥 5𝑥10−2 𝑚 𝑉1𝐴 = 7200 𝑉 B 8 cm 6 cm +q1 5 cm A 5 cm -q2 Solo para observar las condiciones del problema. 𝑉2𝐴 = 9𝑥109 (−30𝑥10−9 𝐶) 5𝑥10−2 𝑚 = −5400 𝑉 𝑁 𝑥 𝑚2 𝐶2 𝑉2𝐴 𝑥 𝑉𝐴 = 7200𝑉 + (−5400𝑉) 𝑉𝐴 = 1800 𝑉 b) Calculamos el potencial en B (VB), sumando algebraicamente los potenciales creados por cada carga en ese punto: 𝑉𝐵 = 𝑉1𝐵 + 𝑉2𝐵 Los potenciales V1A y V2A, los calculamos aplicando la ecuación del potencial eléctrico en un punto. 𝑞 𝑉=𝐾𝑥 𝑟 Sustituimos en cada uno de los casos que se requiera: 2 (40𝑥10−9 𝐶) 9𝑁 𝑥 𝑚 𝑉1𝐵 = 9𝑥10 𝐶 2 𝑥 8𝑥10−2 𝑚 𝑉1𝐵 = 4500 𝑉 2 (−30𝑥10−9 𝐶) 9𝑁 𝑥 𝑚 𝑉2𝐵 = 9𝑥10 𝐶 2 𝑥 6𝑥10−2 𝑚 𝑉2𝐴 = −4500 𝑉 𝑉𝐵 = 4500𝑉 + (−4500𝑉) 𝑉𝐵 = 0 𝑉 C) Ahora calculamos el trabajo para trasladar la carga de +6x10-6 C desde B hasta A, a través de la diagonal. Para eso utilizamos la ecuación de la diferencia de potencial entre dos puntos. 𝑊𝐴𝐵 𝑉𝐵 − 𝑉𝐴 = 𝑞0 Despejamos “WAB”: 𝑊𝐴𝐵 = 𝑞0 𝑥(𝑉𝐵 − 𝑉𝐴 ) Sustituimos: 𝑊𝐴𝐵 = 2,6𝑥10−8 𝐶𝑥(0𝑉 − 1800𝑉) 𝑊𝐴𝐵 = −4,68𝑥10−5 𝐽 49.- En la figura se muestra un triángulo en cuyos vértices C y D se ubican cargas 𝑞𝐶 = −3𝑥10−8 𝐶;𝑞𝐷 = +10−7 𝐶. Si la distancia AD es igual a 10 cm, calcular: a) el potencial en A; b) el potencial en B; c) 𝑉𝐵 − 𝑉𝐴 ; d) el trabajo que debe realizarse para trasladar una carga de 1,5 nC, desde A hasta B. ángulo en el vértice A igual a α=60º y el ángulo en el vértice B igual a β=30º. +qC -qD ( ( ( ( Α 10 cm β A B ) a) 7650 V; b) 1325 V; c) - 6325 V; d) -9,5x10-6 J ) a)- 7650 V; b) 1325 V; c) 6325 V; d) -9,5x10-5 J ) a) 7650 V; b) -1325 V; c) - 6325 V; d) -9,5x106 J ) a) 7650 V; b) -1325 V; c) 6325 V; d) 9,5x106 J Datos: 𝑞𝐶 = −3𝑥10−8 𝐶 𝑞𝐷 = +10−7 𝐶 𝑟𝐴𝐷 = 10𝑐𝑚 = 10𝑥10−2 𝑚 𝑉𝐴 =? 𝑉𝐵 =? 𝑉𝐵 − 𝑉𝐴 =? 𝑊𝐴𝐵 =? 𝑞0 = 1,5 𝑛𝐶 = 1,5𝑥10−9 𝐶 𝛼 = 60° 𝛽 = 30° Diagrama: +qC α -qD 10 cm β A B Solo para observar las condiciones del problema. Conversión de Unidades: Transformamos los centímetros (cm) a metros (m), multiplicando por 10-2 m o dividiendo entre 100 cm. También se transformo los nanocoulomb (nC) a Coulomb (C), multiplicando por 10-9 C. Solución: a) Calculamos el potencial en A (VA), sumando algebraicamente los potenciales creados por cada carga en ese punto: 𝑉𝐴 = 𝑉𝐶 + 𝑉𝐷 Los potenciales V1A y V2A, los calculamos aplicando la ecuación del potencial eléctrico en un punto. 𝑞 𝑉=𝐾𝑥 𝑟 Para hallar el potencial en A creado por C, debemos calcular la distancia de separación entre la carga y el punto, aplicando, la función coseno del ángulo, ya que, conocemos el cateto adyacente. 𝐶𝑎𝑡 𝑎𝑑𝑦 𝐴𝐷 cos 60° = = ℎ𝑖𝑝 𝐴𝐶 Despejamos “AC”: 𝐴𝐷 𝐴𝐶 = cos 60° Sustituimos: 10𝑥10−2 𝑚 𝐴𝐶 = cos 60° 𝐴𝐶 = 0,2 𝑚 Sustituimos en cada uno de los casos que se requiera: 2 (−3𝑥10−8 𝐶) 9𝑁 𝑥 𝑚 𝑉𝐶 = 9𝑥10 𝐶 2 𝑥 0,2𝑚 𝑉𝐶 = −1350 𝑉 2 (10−7 𝐶) 9𝑁 𝑥 𝑚 𝑉𝐷 = 9𝑥10 𝐶 2 𝑥 10𝑥10−2 𝑚 𝑉𝐷 = 9000 𝑉 𝑉𝐴 = −1350𝑉 + 9000𝑉 𝑉𝐴 = 7650 𝑉 b) Calculamos el potencial en B (VB), sumando algebraicamente los potenciales creados por cada carga en ese punto: 𝑉𝐵 = 𝑉𝐶 + 𝑉𝐷 Los potenciales V1A y V2A, los calculamos aplicando la ecuación del potencial eléctrico en un punto. 𝑞 𝑉=𝐾𝑥 𝑟 No sin antes calcular las distancias de separación entres las cargas y el punto B, haciendo uso de la función Seno y tangente de 30º: 𝐶𝑎𝑡 𝑜𝑝 𝐴𝐶 tan 30° = = 𝐶𝑎𝑡 𝑎𝑑𝑦 𝐴𝐵 Despejamos “AB”: 𝐴𝐶 𝐴𝐵 = tan 30° Sustituimos: 0,2 𝑚 𝐴𝐵 = tan 30° 𝐴𝐵 = 0,35 𝑚 Ahora calculamos la distancia de AD+AB, para obtener la distancia de BD: 𝐵𝐷 = 10𝑥10−2 𝑚 + 0,35𝑚 𝐵𝐷 = 0,45 𝑚 Calculamos la distancia CD, aplicando la función seno del ángulo de 30º: 𝐶𝑎𝑡 𝑂𝑝 𝐴𝐶 sin 30° = = 𝐻𝑖𝑝 𝐵𝐶 Despejamos “BC”: 𝐴𝐶 𝐵𝐶 = sin 30° Sustituimos: 0,2 𝑚 𝐵𝐶 = sin 30° 𝐵𝐶 = 0,4𝑚 Sustituimos en cada uno de los casos que se requiera: (−3𝑥10−8 𝐶) 𝑁 𝑥 𝑚2 𝑉𝐶 = 9𝑥109 𝐶 2 𝑥 0,4𝑚 𝑉𝐶 = −675 𝑉 (10−7 𝐶) 0,45𝑚 𝑉𝐷 = 2000 𝑉 𝑉𝐷 = 9𝑥109 𝑁 𝑥 𝑚2 𝐶2 𝑥 𝑉𝐵 = −675𝑉 + 2000𝑉 𝑉𝐵 = 1325 𝑉 c)Calculamos VB – VA: 𝑉𝐵 − 𝑉𝐴 = 1325 𝑉 − 7650 𝑉 𝑉𝐵 − 𝑉𝐴 = −6325 𝑉 d) Ahora calculamos el trabajo para trasladar la carga de 1,5x10-9 C desde A hasta B. Para eso utilizamos la ecuación de la diferencia de potencial entre dos puntos. 𝑊𝐴𝐵 𝑉𝐵 − 𝑉𝐴 = 𝑞0 Despejamos “WAB”: 𝑊𝐴𝐵 = 𝑞0 𝑥(𝑉𝐵 − 𝑉𝐴 ) Sustituimos: 𝑊𝐴𝐵 = 1,5𝑥10−9 𝐶𝑥(−6325 𝑉) 𝑊𝐴𝐵 = −9,5𝑥10−6 𝐽 50.- En la figura se tienen dos cargas dadas así: q1 = -4 µC y q2 = -3 µC, separadas 12 cm. Un punto A equidista de ellas y el punto B esta a 7 cm de q1 y a 5 cm de q2. Calcular: a) el potencial en el punto A; b) el potencial en el punto B; c) el trabajo necesario para transportar una carga de 1,27 µC desde el punto B hasta el punto A. B 7 cm 5 cm +q1 6 cm ( ( ( ( A 6 cm -q2 ) a) 1,05x106 V; b) 1,054x106 V; c) 508x10-3 J ) a) -1,05x106 V; b) +1,054x106 V; c) + 508x10-3 J ) a) -1,05x106 V; b) -1,054x106 V; c) - 508x10-3 J ) a) +1,05x106 V; b) +1,054x106 V; c) - 508x10-3 J Datos: 𝑞1 = −4µ𝐶 = −4𝑥10−6 𝐶 𝑞2 = −3µ𝐶 = −3𝑥10−6 𝐶 𝑟12 = 12𝑐𝑚 = 12𝑥10−2 𝑚 𝑟1𝐴 = 𝑟2𝐴 = 6𝑐𝑚 = 6𝑥10−2 𝑚 𝑟1𝐵 = 7𝑐𝑚 = 7𝑥10−2 𝑚 𝑟2𝐵 = 5𝑐𝑚 = 5𝑥10−2 𝑚 a) 𝑉𝐴 =? b) 𝑉𝐵 =? c) 𝑊𝐴𝐵 =? 𝑞0 = 1,27µ𝐶 = 1,27𝑥10−6 𝐶 Diagrama: Conversión de Unidades: Transformamos los centímetros (cm) a metros (m), multiplicando por 10-2 m o dividiendo entre 100 cm. También se transformo los microcoulomb (µC) a coulomb (C), multiplicando por 10-6 C. Solución: a) Calculamos el potencial en A (VA), sumando algebraicamente los potenciales creados por cada carga en ese punto: 𝑉𝐴 = 𝑉1𝐴 + 𝑉2𝐴 Los potenciales V1A y V2A, los calculamos aplicando la ecuación del potencial eléctrico en un punto. 𝑞 𝑉=𝐾𝑥 𝑟 Sustituimos en cada uno de los casos que se requiera: (−4𝑥10−6 𝐶) 𝑁 𝑥 𝑚2 𝑉1𝐴 = 9𝑥109 𝐶 2 𝑥 6𝑥10−2 𝑚 5 𝑉1𝐴 = −6𝑥10 𝑉 B 7 cm 5 cm +q1 6 cm A 6 cm -q2 Solo para observar las condiciones del problema. (−3𝑥10−6 𝐶) 6𝑥10−2 𝑚 = −4,5𝑥105 𝑉 𝑉2𝐴 = 9𝑥109 𝑉2𝐴 𝑁 𝑥 𝑚2 𝐶2 𝑥 𝑉𝐴 = −6𝑥105 𝑉 − 4,5𝑥105 𝑉 𝑉𝐴 = −1,05𝑥106 𝑉 b) Calculamos el potencial en B (VB), sumando algebraicamente los potenciales creados por cada carga en ese punto: 𝑉𝐵 = 𝑉1𝐵 + 𝑉2𝐵 Los potenciales V1A y V2A, los calculamos aplicando la ecuación del potencial eléctrico en un punto. 𝑞 𝑉=𝐾𝑥 𝑟 Sustituimos en cada uno de los casos que se requiera: (−4𝑥10−6 𝐶) 𝑁 𝑥 𝑚2 𝑉1𝐵 = 9𝑥109 𝐶 2 𝑥 7𝑥10−2 𝑚 𝑉1𝐵 = −5,14𝑥105 𝑉 2 (−3𝑥10−6 𝐶) 9𝑁 𝑥 𝑚 𝑉2𝐵 = 9𝑥10 𝐶 2 𝑥 5𝑥10−2 𝑚 𝑉2𝐴 = −5,4𝑥105 𝑉 𝑉𝐵 = −5,14𝑥105 𝑉 − 5,4𝑥105 𝑉 𝑉𝐵 = −1,054𝑥106 𝑉 C) Ahora calculamos el trabajo para trasladar la carga de +6x10-6 C desde B hasta A, a través de la diagonal. Para eso utilizamos la ecuación de la diferencia de potencial entre dos puntos. 𝑊𝐴𝐵 𝑉𝐵 − 𝑉𝐴 = 𝑞0 Despejamos “WAB”: 𝑊𝐴𝐵 = 𝑞0 𝑥(𝑉𝐵 − 𝑉𝐴 ) Sustituimos: 𝑊𝐴𝐵 = 1,27𝑥10−6 𝐶𝑥 ((−1,054𝑥106 𝑉) − (−1,05𝑥106 𝑉)) 𝑊𝐴𝐵 = −5,08𝑥10−3 𝐽
© Copyright 2026