1. No category

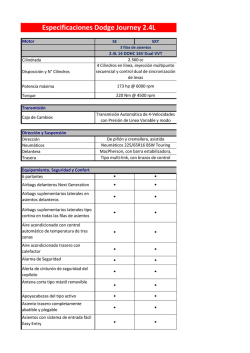
Cálculo de asientos mediante ensayos “in situ”. Aplicación a la Nueva Área Terminal
5. METODOLOGÍA DE CÁLCULO DE ASIENTOS MEDIANTE
DILATÓMETRO MARCHETTI Y PIEZOCONO
5.1. INTRODUCCIÓN
Como ya se ha comentado anteriormente, asociado a la problemática existente a la dificultad
de obtención de muestras representativas de suelos no cohesivos o sin capacidad de mantener
la succión (tensiones efectivas en meniscos), nace la utilización de los ensayos in situ como
método de predicción de asientos. En el caso del proyecto constructivo de la Modificación de la
carretera C-31 se escogieron el CPTu y el dilatómetro de Marchetti (DMT) para realizar dichas
predicciones. A continuación se presenta una breve explicación sobre los puntos más
importantes de la metodología utilizada.
5.2. METODOLOGÍA DE CÁLCULO.
La metodología utilizada en el cálculo de asientos del proyecto considera que el asiento total
(St) se calcula como la suma de asientos debidos a consolidación primaria (Sprim) más los
debidos a la consolidación secundaria (Ssec).
S t (t) = S prim (t) + S sec (t) (ec. 15)
Sin embargo, el los cálculos realizados para el estudio que aquí se presenta, se ha
considerado únicamente el asiento primario. Más adelante, en el capítulo OTROS ASPECTOS
se realizará una evaluación de la importancia del asiento secundario para un par de casos
representativos.
5.2.1. ASIENTOS PRIMARIOS
El asiento primario del terreno, que incluye el inmediato y el de consolidación primaria, se
estimó por el método dilatométrico (Marchetti, S.1997) que consiste en realizar una integral de
deformaciones a partir de un perfil de módulos elásticos.
H
∫
S prim (x) = ε(z)dz ≈
E
z i =H
∆σ v ' (z i , x)
·∆z
(z , x)
z =E DMT i
∑M
(ec. 16)
i
s
Perfil de M del
DMT
Δσ
Fig. 35. Esquema de cálculo del asiento
34
Cálculo de asientos mediante ensayos “in situ”. Aplicación a la Nueva Área Terminal
donde:
E:
H:
MDMT(z):
∆σ’v(z,x,t)
profundidad del plano de apoyo
profundidad de un eventual substrato indeformable
perfil de módulos dilatométricos
perfil de incrementos de tensión efectiva
El perfil de incrementos de tensión efectiva evoluciona con el tiempo según:
⎛ tC ⎞
∆σ' v (z, x, t) = ∆σ v (z, x, t)U(Tv) = ∆σ v (z, x, t)U⎜⎜ 2v ⎟⎟ (ec. 17)
⎝H ⎠
donde:
U:
grado de consolidación
coeficiente de consolidación vertical
cv:
H:
distancia hasta el borde drenante
perfil de incrementos de tensión total
∆σv(z,x,t)
El grado de consolidación se calcula mediante las siguientes expresiones (Jiménez Salas,
1981):
4·Tv
π
Si U < 60% ; Tv = ·U 2 ; luego
U=
(ec. 18)
π
4
Si U > 60% ; Tv = −0.9332·log (1− U) − 0.0851 ; luego
Donde Tv =
U = 1 − 10
−(Tv + 0.0851)
0.9332
(ec. 19)
Cv·t
, es el factor de tiempo. El valor de Cv es constante en los cálculos de
H2
consolidación (4x10-3 cm2/s para limos y arcillas) y, como se ha explicado antes, se obtuvo
interpretando conjuntamente ensayos edométricos y de disipación de cono.
H se obtiene de cada uno de los perfiles de los CPTu realizados. Se considera que H es la
distancia máxima que debe recorrer una gota de agua para salir de la capa. Entonces, se
considera que H = potencia de la capa impermeable/2. La complicación en muchas situaciones
es la de definir dentro de una capa limosa con intercalaciones arenosas, (como es el caso de la
capa intermedia del acuífero del delta), los diferentes subniveles drenantes. En ese caso, hay
que ir definiendo estas longitudes drenantes a partir de observar las caídas de presión de poros
de los registros de reconocimiento del CPTU. Observar
Fig. 36.
POTENCIA DE CAPA
NO DRENANTE
H
CAPAS DRENANTES
Fig. 36. Esquema de obtención del espesor drenante, H
Obsérvese un ejemplo de dicha evaluación (CPTu 2a) a partir de un registro típico de
piezocono.
35
Cálculo de asientos mediante ensayos “in situ”. Aplicación a la Nueva Área Terminal
H=0
2m
H=1
H=2
4m
5m
H=2.5
Fig. 37. Evaluación del espesor drenante mediante resultados de CPTu
Otro de los parámetros básicos para el cálculo de la integral de deformación es los incrementos
de tensión total provocados por la construcción de los terraplenes. Se obtienen a partir de las
soluciones para carga en banqueta o para carga rectangular sobre semiespacio elástico
(Jiménez Salas y otros, 1981 “Geotecnia y Cimientos”). La selección de una u otra forma de
carga viene determinada por la situación y la forma en planta de cada unidad.
La primera de las aproximaciones será válida cuando se observa el efecto de la carga desde
una sección transversal al eje de un terraplén suficientemente largo. No todos los casos a
estudiar se pudieron aproximar a esta situación, con lo que, para este trabajo, se ha modificado
el programa de cálculo asumiendo el cálculo de tensión bajo carga rectangular.
5.3. PROGRAMA DE CALCULO
5.3.1. INTRODUCCIÓN
El programa de predicción de asientos fue desarrollado por el proyectista con el objetivo de
tener una idea de las magnitudes y distribuciones de movimientos esperables.
Se programaron las funciones externas necesarias en macros de Visual Basic y se enlazaron
con Excel para preparar una serie de hojas de resultados sistemáticos.
La idea principal del programa es introducir los datos de terreno, geometría del terraplén y
reconocimiento oportunos, para obtener resultados de deformación vertical por capa, asiento
dilatométrico final por capa y acumulado, y mediante el grado de consolidación, el asiento en
diferentes etapas del proceso a definir por el usuario.
El trabajo relacionado con el propio programa de cálculo que se ha realizado en el desarrollo
de la tesina ha sido revisarlo a fondo, depurando algunos errores e incluyendo las
modificaciones que oportunamente se señalan.
A continuación, se presenta a modo de ejemplo, la apariencia del programa de cálculo:
36
Cálculo de asientos mediante ensayos “in situ”. Aplicación a la Nueva Área Terminal
DEFINICIÓN DE
LA DENSIDAD
DEL TERRENO
DEFINICIÓN DE LA
GEOMETRÍA DEL
TERRAPLÉN
DEFINICIÓN DEL
RECONOCIMIENTO
DEFINICIÓN DEL INSTANTE DE
CÁLCULO
DEFINICIÓN DEL PUNTO CÁLCULO
DENTRO DE LA SECCIÓN
MACROS
RESULTADOS
Fig. 38. Esquema de funcionamiento del programa de cálculo
Cada uno de los recuadros descritos, representa información básica del modelo.
37
Cálculo de asientos mediante ensayos “in situ”. Aplicación a la Nueva Área Terminal
5.3.2. DEFINICIÓN DE LAS CARACTERÍSTICAS DEL TERRENO
INPUTS GENERALES
H(z), espesor drenante
MDMT, Módulo dilatométrico
Cv, Coeficiente de consolidación vertical
FUNCIONES ASOCIADAS A LOS INPUTS DEL TERRENO
• FUNCIÓN Uconsol. Grado de consolidación
INPUTS
H, espesor drenante
T, tiempo
Cv, coeficiente de consolidación vertical
OUTPUT
U, grado de consolidación
(Jiménez Salas, 1981):
Tv =
Cv·t
H2
Si U < 60%
Si U > 60%
; Tv =
π 2
·U ;
4
luego
U=
4·Tv
π
; Tv = −0.9332·log (1− U) − 0.0851 ; luego
−(Tv + 0.0851)
U = 1 − 10 0.9332
• FUNCIÓN buscaE
A partir de la serie de datos resultado de un DMT y de la profundidad busca el módulo
correspondiente.
INPUTS
Indentificador DMT (Clave E)
z, profundidad
OUTPUT
MDMT, módulo dilatométrico en z
• FUNCIÓN buscaH
A partir de la serie de espesores drenantes obtenidos del CPTu y de la profundidad busca
el valor correspondiente de H
38
Cálculo de asientos mediante ensayos “in situ”. Aplicación a la Nueva Área Terminal
INPUTS
Identificador CPTu (Perfil H)
Z, profundidad
OUTPUT
H, espesor drenante en z
5.3.3. DEFINICIÓN DE LAS CARGAS
La definición de las cargas se puede realizar de dos formas:
•
CARGA INSTANTÁNEA.
Suponiendo que la carga se coloca toda de golpe, de forma instantánea. Se obtiene de
multiplicar la densidad del terraplén por la altura máxima.
q = ρ·h (ec. 1)
•
HISTORIA DE CARGAS.
Aplicado en aquellas situaciones donde el proceso constructivo se prolonga durante un
tiempo comparable al de la consolidación. La forma de aproximar esta situación es
dividiendo el periodo de construcción del terraplén en diversas etapas instantáneas y
considerando en cada periodo de cálculo solo la carga existente hasta dicho momento.
El cálculo de los asientos en este caso se explica mediante la siguiente figura. Se
representan tres etapas de carga, la primera se inicia en el momento t=t1 y llega hasta
una cota de H=H1. La segunda, cuyo inicio de carga está en t=t2, llega hasta H=H2. Sin
embargo, los asientos producidos por esta etapa, solo son los correspondientes a la
carga necesaria para pasar H1 a H2, luego se restan los asientos producidos por H1 en
el periodo de construcción de H2. En la etapa 3, se realiza exactamente la misma
operación; t3 es el momento en que empieza este escalón de carga y llega a tener una
altura = H3. De la misma forma que en la etapa anterior, se tienen que sustraer los
asientos producidos por el terraplén de altura H2 en este periodo.
En el proyecto solo se consideró carga instantánea debido a la falta de datos de obra. En el
presente trabajo, gracias a la cantidad de datos obtenidos en obra respecto a la historia de
se ha podido aplicar
cargas, y siguiendo el ejemplo de Arroyo y Mateos, 2006
sistemáticamente el segundo método
39
Cálculo de asientos mediante ensayos “in situ”. Aplicación a la Nueva Área Terminal
Fig. 39. Procedimiento de cálculo de asientos considerando la historia de cargas.
40
Cálculo de asientos mediante ensayos “in situ”. Aplicación a la Nueva Área Terminal
A continuación, se da un ejemplo de cómo se ha aplicado la historia de cargas de un terraplén.
En primer lugar, se ha construido la aproximación a la historia de carga real mediante diversos
escalones, como se observa en la figura siguiente
TD-8
15
ALTURA DE TIERRAS (m)
12
9
6
3
ALTURA TIERRAS
APROXIM ALTURA
0
0
150
300
450
600
TIEMPO (DÍAS)
Fig. 40. Aproximación a la altura del terraplén en escalones de carga
Una vez realizado el esquema anterior se definen los intervalos de tiempo en los que se
construyen los diferentes escalones.
DÍAS
h(m)
t0
0
1.2
H1
t1
125
1.2
H2
t1
125
3.7
H3
t2
220
3.7
H4
t2
220
9
H5
t3
370
9
H6
t3
370
12.4
H7
t4
641
12.4
Tabla 3. Definición escalones de carga
A continuación, se calculan los días de actuación de cada etapa de carga para evaluar los
asientos en cada instante de tempo (Tabla 4 y Tabla 5).
Notar que se toman los valores de asientos para todos los instantes (términos positivos), y a
posteriori se restan los que no actúan en la etapa correspondiente (términos negativos).
41
Cálculo de asientos mediante ensayos “in situ”. Aplicación a la Nueva Área Terminal
Dias de actuación de cada etapa de carga
Puesta en carga
0
125
220
370
Dias a origen
ti
ti - t1
ti - t2
ti-t3
t0
0
t1
0
0
0
0
125
125
0
0
0
t2
220
220
95
0
0
t3
370
370
245
150
0
t4
641
641
516
421
271
Tabla 4. Días de actuación de cada etapa de carga
TÉRMINOS POSITIVOS
H1
H1
ti
rho
t0
0
H2
H2
ti - t1 rho
H3
H3
H4
H4
ti - t2
rho
ti - t3
rho
SUMA
13
13
t1
125 124
0
41
165
t2
220 127
95
376
0
100
t3
370 128
245
391
150
921
0
137
1577
t4
641 130
516
393
421
940
271
1270
2733
SUMA
603
TÉRMINOS NEGATIVOS
H1
H1
ti - t1
rho
H2
H2
ti - t2 rho
H3
H3
H4
H4
ti - t3
rho
ti-t4
rho
t0
0
t1
0
13
13
t2
95
123
0
41
t3
245
127
150
385
0
100
612
t4
516
128
421
393
271
936
1457
164
Días a origen
ASIENTO
t0
0
13
t1
60
152
t2
120
439
t3
365
965
t4
641
1276
Tabla 5. Cálculos de asiento considerando la historia de cargas
42
Cálculo de asientos mediante ensayos “in situ”. Aplicación a la Nueva Área Terminal
5.3.4. DEFINICIÓN GEOMÉTRICA DE LOS TERRAPLENES.
Para la mayoría de casos estudiados, la forma de calcular la tensión debida a la construcción
de los terraplenes se basa en la superposición de dos banquetas infinitas cuya sección
transversal acabe resultando la deseada:
Fig. 41. Sección transversal tipo de los terraplenes de cálculo.
Este proceso requiere la utilización de las siguientes funciones:
• TENSIÓN VERTICAL BAJO BANQUETA. SZB
INPUTS: (parámetros geométricos del terraplén)
z, profundidad
x, distancia desde el pie del talud
a, base del talud
b, base total
p, carga máxima
OUTPUT:
σZ, tensión vertical
(Jiménez Salas, 1980)
Fig. 42. Esquema geométrico de la banqueta
Radios característicos
R 0 = x 2 + z 2 R 1 = (x − a) 2 + z 2 R 2 = (x − b) 2 + z 2
Ángulos característicos
aux = cosα =
R 02 + R 12 − a 2
2·R 0 ·R 1
43
Cálculo de asientos mediante ensayos “in situ”. Aplicación a la Nueva Área Terminal
aux = cosb =
α = acos·aux
R 12 + R 22 − (b − a) 2
, por el teorema del coseno
2·R 1·R 2
β = acos·aux
Entonces sv,
SZB = σ Z =
⎞
p ⎛⎜
x
z
β + α − 2 ·(x − b) ⎟ (ec. 212)
⎟
π ⎜⎝
a
R2
⎠
• TENSIÓN VERTICAL BAJO TERRAPLÉN. SZT
Como ya se ha comentando anteriormente, la tensión bajo el terraplén se obtiene como
superposición de dos casos particulares de tensión bajo banqueta (SZB), a partir de la función
SZT
Fig. 43. Superposición de dos banquetas
SZT = SZB (z, x, a, b+a, p) + SZB (z,x2, a, a, -p) ; x2=x-b ; siendo b la base total – base del
talud
INPUTS: Resultados de la SZB en las dos situaciones descritas
OUTPUT: Tensión bajo el terraplén
• TENSIÓN VERTICAL BAJO CARGA RECTANGULAR. FUNCIÓN Qrectall
En los casos donde la hipótesis de deformación plana no es válida por la geometría del
terraplén, ha sido necesario realizar un cambio de la formulación del modelo para asimilar las
tierras del terraplén a una carga rectangular repartida uniformemente. La solución general de
tensiones bajo el vértice del rectángulo cargado fue dada por Holl (1940), y se basa en la figura
siguiente:
44
Cálculo de asientos mediante ensayos “in situ”. Aplicación a la Nueva Área Terminal
a
y
b
x
z
z
Fig. 44. Carga rectangular repartida uniformemente, Holl (1940)
Los parámetros que intervienen en los cálculos se resumen a continuación:
INPUTS:
L, lado mayor del rectángulo
b, lado menor del rectángulo
x, coordenada x del punto de evaluación de la tensión (paralelo a L)
y, coordenada y del punto de evaluación de la tensión (paralelo a b)
z, profundidad del punto de evaluación de la tensión
número 1, 2, 3 en función de la componente de la tensión a evaluar
p, carga
OUTPUTS:
Sigmax
Sigmay
Sigmaz
Las fórmulas analíticas de las tensiones obtenidas por Holl son (Jiménez Salas, 1980):
σz =
⎡
⎤
p ⎢
ab
abz 1
1 ⎥
Atag
·(
+
+
) (ec. 223)
2π ⎢
zR 3 R 3 R 2 R 2 ⎥
1
2 ⎦
⎣
⎡
⎤
abz ⎥
ab
⎢
σx =
Atag
−
(ec. 234)
2π ⎢
zR 3 R 2 ·R ⎥
⎣⎢
1 3 ⎦⎥
p
⎡
⎤
abz ⎥
ab
⎢
σy =
Atag
−
(ec. 245)
2π ⎢
zR 3 R 2 ·R ⎥
⎢⎣
2 3 ⎥⎦
p
Donde, R 1 = a 2 + z 2
R2 = b2 + z2
45
R3 = a2 + b2 + z2
Cálculo de asientos mediante ensayos “in situ”. Aplicación a la Nueva Área Terminal
5.3.5. DISCUSIÓN DE LA VALIDEZ DEL MÉTODO PARA SUELOS NO ELÁSTICOS
Consideranando todo el planteamiento del modelo de cálculo de asientos, surge una cuestión
importante. ¿Puede esperarse que el método de predicción funcione, si sus bases son a partir
de la teoría de la elasticidad, y como sabemos, los suelos, en general, se comporta
básicamente de forma plástica?
Sabemos que el método dilatométrico de cálculo de asiento predice asientos lineales, partiendo
de la elasticidad (ver ec.16), lo que da un asiento proporcional a la carga (en condiciones de
trabajo)
El módulo MDMT proviene de trazar la recta tangente en un punto concreto de la curva tensióndeformación de la curva edométrica. Si dicha curva tiene un cambio de pendiente abrupto,
normalmente en la zona cercana a la fluencia puede llegar a ser un módulo inadecuado del
suelo, porque la aproximación tangente no es correcta.
Este comportamiento se da en algunas arcillas muy estructuradas, pero como en general, la
mayoría de suelos, arcillas blandas y arenas tienen este cambio mucho más suave, así, MDMT
representa mejor la media edométrica en esa zona.
Por otra parte, se han planteado dudas acerca de la validez del propio módulo edométrico para
cálculos elásticos en otros casos, en particular en arcillas sobreconsolidadas. Diversos autores
como por ejemplo, Marchetti, 2001, han estudiado el tema, y han concluido que:
En problemas de arcillas sobreconsolidadas, se puede aplicar la corrección de SkemptonBjerrum (1957) entre otras. Esta corrección tiene un rango de 0.2-15 (<<1). A partir de esto
podemos decir que la corrección de Skempton-Bjerrum produce una reducción del S1-DMT en
un factor de 2 to 5.
Por otro lado, en el libro de Terzaghi y Peck (Soil Mechanics in Engineering Practice, 1996) se
puede encontrar que en arcillas sobreconsolidadas "el módulo proveniente de un buen
edómetro puede ser de 2 a 5 veces menor que los módulos “in situ”. "
Luego, estos dos factores aproximadamente se pueden llegar a compensar.
En el caso de estudio, el suelo está constituido por arcillas blandas con una curva tensióndeformación suave y en principio el módulo dilatométrico se ajusta bien en todo el rango de
tensiones.
46