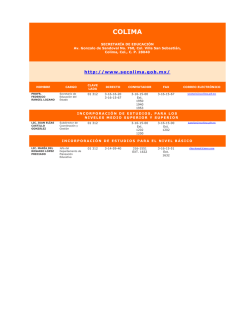
Guía de autoestudio de matemática 2017 - UNAN
Managua septiembre 2016 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] INTRODUCCION Estimados estudiantes: Dentro del actual proceso de globalización y de la modernización de la enseñanza de la matemática, el Consejo Nacional de las Universidades (CNU) y el Ministerio de Educación, Se han dado a la tarea de presentarles un material de ejercicios y problemas introductorios, con el objetivo que tengan la oportunidad de consolidar sus conocimientos mediante un entrenamiento matemático que les permita fortalecer sus capacidades cognitivas e intelectuales referidas al campo de las ciencias matemáticas. Este material reúne ciertas características entre las cuales se pueden destacar las siguientes: 1. Tiene como fuente primaria los temas que tradicionalmente ofrecen grandes dificultades para los estudiantes de secundaria; por ello, se hace énfasis en los aspectos teóricos de los conceptos matemáticos 2. Se han insertado problemas de lógica matemática, semejantes a situaciones objetivas de fenómenos de la vida cotidiana. 3. El enfoque se ha centrado por un lado, en la proposición de problemas donde intervienen conceptos, teoremas y propiedades de las distintas áreas matemáticas, por el otro, ejercicios de cálculo para desarrollar destrozas y habilidades. 4. Algunos problemas han sido seleccionados de revistas matemáticas, de exámenes de entrenamiento y de concursos matemáticos. 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] COMISIÓN DE MATEMÁTICA INTEGRANTES: 1. Humberto Antonio Jarquín López (MINED) 2. Francisco Emilio Díaz Vega (MINED) Coordinador 3. Héctor Benito Flores Guido (UNAN- LEÓN) 4. Fredy José González Martínez (UNAN- LEÓN) 5. Francisco Rutilio Zelaya (UNAN- LEÓN) 6. Primitivo Herrera Herrera (UNAN –MANAGUA) 7. Armando José Huete Fuentes (UNAN –MANAGUA) 8. María auxiliadora Rosales ( UNA) 9. María Lisseth Valdivia ( UNA) 10. Mauricio Alexander Gonzalez Salazar(UNA) 11. Hank Espinoza (UNI) 12. Roberto Ruiz ( UNI) 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] Aritmética 1. La expresión 212 + 212 + 212 + 212 equivale a : a) 212 b) 214 c) 248 d) 433 2. Al número de tres dígitos 2a3 se le suma el número 326 y da el número de tres dígitos 5b9. Si sabemos que el número 5b9 es divisible entre 9, entonces a + b es: a) 2 b) 4 c) 6 d) 8 3. Al simplificar [(9 - 4) + (-10 + 3)] ×(6 × (-5))÷[(-12 + 8) (6 - 9) (95 - 90)] el resultado es: a) 1 b) -1 c) 2 d) -2 4. ¿Cuántos divisores diferentes tiene el número 2000? a) 15 b) 18 c) 17 d) 20 5. Al simplificar 4 (3)2 ÷6 - 3 4 + 2 [5 (7) - 15 × 3] 4 ÷ 12 - 9. El resultado es a) 19 b) -11 c) 11 d) 29 2 3 de los hombres están casados con los de las mujeres. Si 3 5 nunca se casan con forasteros, ¿Cuál es la proporción de solteros en dicha ciudad? 6. En una ciudad 1 7 1 5 b) c) d) 7 19 5 12 7. Un corredor ha dado cinco y media vueltas a una pista de 300 m,¿Cuántos km recorrió? a) a)15 km b) 165 km c)16.5 km d)1650 km 8. El resultado de efectuar – 4(2 - 3 ) + 2(5 - 3 ) es : 5 a) 7 5 b) 17 4 4 c) 29 10 d) – 2 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] 9. El resultado de x n1 x n es: a) x n 2 1 b) x 2 n 1 xn c) x n 1 d) x 1 10. La expresión decimal 2. 9 es equivalente a : a) 2 b) 3 c) 29 9 10 10 2 d) 27 9 1 4 3 11. El resultado de la operación 8 3 81 4 625 corresponde a : a) 27 b) 4 c) 26 d) 30 12. El resultado de a) 4 15 2 4 6 , es: 3 5 7 4 7 b) c) 35 45 d) 13. ¿Cuánto gano o pierdo si vendo por los 4 30 3 7 de los del costo de un juguete 5 2 que me ha costado C$40.00? a) gano C$24 b) pierdo C$24 c) gano C$140 d) gano C$44 1 2 1 2 14. La solución de 5 4 es: 1 1 2 a) 2 c) 1 b) -2 d) -1 1 2 15. El valor de la expresión, a) – 2 16. Los 2 2 23 b) 2 4 de 1 000 son: 5 a) 800 2 es: d) – 1 c) 1 b) 250 c) 200 d) 850 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] 17. La fracción generatriz de la siguiente fracción decimal: 0.333... es: 1 33 33 333 a) b) c) d) 3 100 10 1000 1 1 1 18. El resultado de efectuar: (0,3) es: 0,1 0,01 0,001 a) 33 b) 333 c) 3 d) 0.3 19. El resultado de dividir: 0.27 0.0009 es: a) 3 b) 30 c) 3000 d) 300 2 3 20. Al resolver la operación siguiente: 5 el resultado es: 6 5 1 3 5 7 a) b) c) d) 4 4 4 4 RAZONES Y PROPORCIONES 21. El 25% del semiperímetro de una circunferencia mide 3 cm. Su diámetro mide: A) B) C) D) E) 12 cm 6 cm 24 cm 18 cm Ninguna de las anteriores 22. Cuarenta y seis obreros se demoran 6 días en construir una casa. ¿Cuántos días se demorarán 69 obreros? A) B) C) D) E) 9 días 8 días 4 días 3,3 días Ninguna de las anteriores 23. Pedro se demora tres horas en cortar el pasto y su hermano menor se demora el doble. Si trabajan juntos el tiempo empleado en realizar la labor es de: 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] A) 1 hora B) 2 horas C) 3 horas D) 4 horas E) 6 horas F) 24. Si Carlos midiera un 26% menos, su estatura sería de 1,40 m. ¿Cuánto mide Carlos? A. 1,60 m B. 1,70 m C. 1,75 m D. 1,80 m E. 1,89 m 25. Si a : b = 2 : 3, ¿cuál expresión da igual a cero? A) B) C) D) E) 3a + 2b -3a - 2b 3a - b 3a -2b a-2b 26. ¿Cuál es el 75% de 2 horas? A) B) C) D) E) 70 min 80 min 90 min 56 min 50 min 27. Juan pinta una casa en sólo 6 horas. Diego pintará la misma casa en 9 horas. ¿Cuánto demoran en pintarla si trabajan los dos juntos? A) 3,6 horas B) 4,8 horas C) 6,3 horas D) 7,5 horas E) 7,8 horas 28. ¿Qué altura tendría una pila de 1 000 000 de hojas de cuaderno si se necesitan 10 hojas para tener 1 mm? Compare esta altura con su casa de habitación. 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] a) 1 000 mm mm b) 10 000 mm c) 1 000 000 mm d) 100 000 mm e) 100 29. ¿Cuántos rieles de 15 m se necesitan para enlazar a una fábrica con la estación que dista 765 m? a) 95 rieles rieles b) 85 rieles c) 55 rieles d) 75 rieles e) 45 30. ¿Cuántos alfileres de 3.5 cm de largo pueden fabricarse con un alambre de latón de 152.07 m, sabiendo que hay una pérdida de 2 mm de alambre por alfiler? a) 46 alfileres 49 alfileres b) 43 alfileres c) 48 alfileres d) 50 alfileres e) 31. Para ir a clase, Pedro tiene que andar por término medio 1,520 pasos de 62 cm. ¿Cuántos km habrá recorrido durante un año escolar de 210 días si va al colegio dos veces al día? a) 20.2 km 18.8 km b) 18.6 km c) 17.9 km d) 19.7 km e) 32. Dos contratistas han reparado un camino de 5 km 4 hm 5 dam. El primero ha hecho la mitad más 3 hm 25 m y ha cobrado 86400 córdobas. ¿Cuánto cobró el segundo? a) 74 637 78 000 b) 75 637 c) 74 000 d) 75 000 e) 33. La alcaldía de cierto municipio tiene una extensión de 1008 hm2 y otra alcaldía en otro municipio 1683750 m2 ¿Cual es mayor y en cuantos kilómetros supera una de la otra? a) La 1ra y la supera en 1.58 b) La 2da y la supera en 1 c) La 2da y la supera en 1,58 d) La 1ra y la supera en 1,5 e) La 2da y son iguales. 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] 34. Un terreno de 26 000 m2 se ha dividido en lotes de 32,5 dam2. Halla el número de lotes obtenidos. a) 8 lotes 80000 lotes b) 80 lotes c) 800 lotes d) 8000 lotes e) 35. Se ha necesitado 54,000 losetas para pavimentar los 2,430 m 2 que miden las aceras de una calle. ¿Cuál es en mm2 la superficie de una loseta? a) 2 222 mm2 222,222 mm2 b) 2 2222 mm2 c) 222 222 mm2 d) 2 222 222 mm2 e) 22 36.Si el m2 de terreno vale 2 euros, ¿Cuántos euros vale comprar un campo de 7 ha? a) 40 000 euros b) 10 000 euros c) 35 000 euros d) 14 000 euros e) 120 000 euros 37. La isla mayor de la Tierra es Groenlandia y mide 2 180 000 km2 y una de las más pequeñas es Cabrera, con 2 000 ha. ¿Cuántas veces cabe Cabrera en Groenlandia? a) 100 000 veces b) 200 000 veces c) 109 000 vces d) 108 000 veces e) 110 000 veces. 38.En una caja de 0,696 dam3, ¿cuántos cubos de 12 m3 caben? a) 60 cubos cubos b) 25 cubos c) 30 cubos d) 44 cubos e) 58 39. Una tinaja que contiene 0,4 m3 de aceite ha costado 800 euros ¿a cuántos euros resulta el litro? a) 6 euros euros b) 2 euros c) 3 euros d) 4 euros e) 5 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] 40. Un caramelo tiene un volumen de 1,3 cm3. ¿Cuántos caramelos caben en una caja de 0,4498 dm3? a) 346 caramelos b) 246 caramelos c) 156 caramelos d) 220 caramelos e) 356 caramelos. 41. Los trozos cúbicos de jabón de 5 cm de arista se envían en cajas cúbicas de 60 cm de arista. ¿Cuántos trozos puede contener la caja? a) 1 628 trozos trozos b) 1 528 trozos c) 1 428 trozos d) 1 728 trozos e) 1 828 42. ¿Cuántas botellas de 750 cm3 se necesitan para envasar 300 litros de refresco. a) 200 botellas botellas b) 300 botellas c) 400 botellas d) 500 botellas e) 280 43. Una bodega vende vino al por mayor a 1,45 €/l. ¿Cuál es el coste de un camión cisterna que transporta 5 m3de ese vino? a) 7 520 € e) 7 500 € b) 7 025 € c) 7 050 € d) 7 250 € 44. ¿Cuántos vasos de 0,25 l se podrán llenar con el refresco de una botella de 0,25 dal? a) 10 vasos vasos b) 20 vasos c) 30 vasos d) 15 vasos e) 25 45. La capacidad de un depósito de gasolina es 1500 litros. ¿Cuál es su volumen en cm3? a) 150 000 c3 100,000 c3 b) 15 000 c3 c) 1 500 c3 d) 1 500,000 c3 e) 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] 46. Un camión transporta 50 cajas con botellas llenas de agua. Cada caja contiene 20 botellas de litro y medio. Una caja vacía pesa 1 500 g, y una botella vacía, 50 g. ¿Cuál es el peso total de la carga? a) 1 625 kg kg b) 1 620 kg c) 1 605 kg d) 1 525 kg e) 1 655 47. Si para construir un muro necesito 2 toneladas de cemento, ¿cuántos sacos de 25 kilos de cemento tendré que comprar? a) 60 sacos sacos b) 70 sacos c) 50 sacos d) 75 sacos e) 80 48.Un barco transporta 2800 toneladas de mercancía. ¿Cuántos vagones harán falta para transportar esa mercancía si cada vagón carga 1400 kg? a) 2 100 vagones b) 2 010 vagones c) 2 000 vagones 200 vagones d) 2 020 vagones e) 2 ALGEBRA 1 1 3 1. Dado el polinomio lineal 𝑓(𝑥) = 𝑥 − 2, la suma de 𝑓(𝑥) + 𝑓 (𝑥 + 4) + 𝑓 (𝑥 + 4) es igual a: 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] A. 4x B. 4x+1 1 4𝑥 + 2 C. 1 4𝑥 − 2 D. 2. Si x + y = 1 y xy=1, ¿Cuál es el valor de la expresión 𝑥 3 + 𝑦 3 ? A. -1 B. -2 C. -3 3. Si a = -1, b = 3, c = 5, entonces A. − 1 C. 4. El valor numérico de la expresión -4 𝑎+𝑏−|𝑎−𝑏| |𝑎|+|𝑏|+|𝑐| B. 1 9 D. 1 − D. 9 2 9 a 2 (a b2 ) (a 3 b3 ) (a 2 b) para a = 1 (a 2 b2 ) (2a 3b2 ) y b = – 2 es: A. 27 10 B. 27 10 C. 18 35 D. 15 17 5. Las raíces de la ecuación 𝑎𝑥 2 + 𝑏𝑥 + 𝑐 = 0, serán recíprocas si: A. a = b B. a = bc 6. El resultado de b 5 y 2 2 A. bn 25y m n m 5 y m C. c = a D. c=b bn es 2n 2m B. b 25y 2 2 C. bn 25y m 2n 2m D. b 25y E. 0 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] 7. La descomposición en factores de la expresión 3x2 – 2x – 8 es: A. (3x +4) (x + 2) B. (3x + 4) (x - 2) C. (3x – 4) (x - 2) D. (3x – 4) (x + 2) 8. La descomposición en factores de la expresión x3 – 64y3 es: A. (x – 4y) C. (x + 4y) (4xy + x2 + 16y2 ) B. (4xy + x2 + 16y2) D. (x – 4y) (4xy + x2 +16y2) a 2 4 b2 3a 2 5ab 2 b2 9. La simplificación de es: ab 2 b2 3a 2 a b A. a b (3a b) B. b a C. a b D. 1 E. a(3a b) b (3a b) 1 1 a a se obtiene 10. Al simplificar la expresión 1 1 a a 2 A. (1 a ) a 2 B. (1 a ) a 1 2 C. (1 a ) 1 a 11. El resultado de la siguiente operación 4 x2 1 A. (4 x 1)(x 1) 2 D. ( a 1) 4 x2 1 B. (4 x 1)(x 1) a 1 E. (1 a ) 2 a 1 12 x 2 4 x 1 3 x 2 8 x 3 x 1 4 x 2 11x 3 x2 9 C. 4 x2 1 (4 x 1)(x 1) D. es: 4 x2 1 (4 x 1)(x 1) 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] 2 x y 12. Al desarrollar se obtiene y x A. x4 2 x2 y2 y4 x 2 y2 B. x 4 2 x 2 y 2 y4 x 2 y2 C. x 4 2 x 2 y2 y 4 13. Al racionalizar el denominador de la fracción A. 2 x 5 3 4 B. 2 x 5 3 2 14. El conjunto solución de la ecuación A. -5 B. 15 x 2 y2 x 2 3 2 x 5 2 x 5 3 2 C. D. D. x 4 x 2 y2 y4 x 2 y2 se obtiene 2 x 5 3 2 3x 15 1 es x 5 x 5 C. 10 D. -15 15. El valor de k que proporciona sólo una solución real de la ecuación x 2 kx k 2 3x es : A. 5 B. 1 C. 0 D. – 1 16. El valor de la variable y al resolver el sistema de ecuaciones 4 2 3 x y 3 x y 3 2 4 1 3 x y 3 x y 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] A. 3 2 17 .Al efectuar A. B. x2 4 (x 2) 2 2(x 2) x 2 3 2 C. (x 2) 2 x2 4 B. 18. Al resolver la ecuación 8 7 D. 7 8 se obtiene: 2(x 2) x2 C. 2(x 2) x 2 D. 2(x 2) x 2 x 1 2 x 1 4 se obtiene que la diferencia entre la x 1 x 1 mayor y la menor de las raíces es: A. -5 B. 5 C. 1 19. Al resolver el sistema de ecuaciones 2x 3 y 2x 3 y D. -1 2 5 2 6 xy 1 se obtiene que el valor de la variable y es: A. 2 3 B. 3 2 C. 2 3 D. 7 8 20. El conjunto solución de la desigualdad x3 + x2 – 2x > 0 es: A. (– 2; 1) (1;+) B. [– 2;0) [1; +) C. (– 2; 0) [1, +) D. [– 2, 0) (1, +) 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] 21. El valor de k de manera que la ecuación 2x2 + kx + 4 = 0 tenga una raíz igual a – 3 es: A. 12 13 B. 12 13 C. 22. El conjunto solución de la desigualdad | x + A. – 4 8 x 3 3 B. 8 4 <x 3 3 C. – 22 3 D. 2 | 2 es 3 8 4 < x< 3 3 D. 23. El conjunto solución de la desigualdad 1 7x 3 es: 2 A. [1; 5] D. [1; 2] B. [– 1; 5] C. [–1; 0] 22 3 8 4 x 3 3 24. El conjunto solución de la desigualdad |5 – 2x| < 7 está dado por el intervalo A. (–1; 0) B. (1, 6) C. (-1, 6) 25. El conjunto solución de la desigualdad D. (–1; 2) (x 10)(x 2) 0 es: x2 7 x 8 A. [– 10; –1] [2; 8] B. [–10;0) [2;8) C. (-10;-1) (3; 8) D. [–10; 1] [2;8) 26. El conjunto solución de la ecuación A. {-3; 11} B. {3; 11} C. {3;-11} 2x 3 x 2 2 es: D. {-3;-11} 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] 27. Si |2x – 1| > 3, el valor de x que no pertenece al conjunto solución es: A. – 3 1 28. Si x x A. 2 B. 3 2 D. – 1 C. 1 3 , entonces x 3 1 es igual a: 3 x B. -1 C. 0 D. 1 29. El conjunto solución de 3x + | x | = – 8 es: A. -2 B. -1 C. -4 D. 1 30. Al factorizar la expresión −12x 3 + 36x 2 − 27x, uno de los factores es: B) (2x − 3)2 A) -2 31. El resultado simplificado de 4 A) 𝑦 3 √4𝑥 2 𝑦 4 C) 5𝑥 2 3𝑦 4 √8𝑥 3 𝑦 7 2 B) 𝑦 2 √4𝑥𝑦 2 D) (2x + 3)2 1 4 ∙ 3𝑥 √8𝑥 2 𝑦 3 , es: 3 C) 𝑦 3 √4𝑥𝑦 2 D) 𝑦 3 4√4𝑥𝑦 32. Si x, y, z, son números positivos que satisfacen las siguientes expresiones 1 1 1 7 x 4, y 1, z , entonces el valor de xyz es: y z x 3 A. -1 B. -2 C. 1 D. 2 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] 33. Si n > 1, entonces A. n1/27 3 n3 n 3 n es igual a: 13/27 B. n13/21 D. n131/127 C. n 34. Si (𝑥 + 𝑦)2 = 2(𝑥 2 + 𝑦 2 ) entonces el valor de la expresión E dado por 𝐸= A. 3 3𝑥 3 −𝑦 3 𝑥2 𝑦 + 3𝑥+2𝑦 5𝑥 + 6𝑦 2𝑥+𝑦 , es igual a: C. 5 B. 2 D. 6 35. Si el polinomio 𝑃(𝑥) = 𝑥 4 + 𝑎𝑥 3 − 𝑏𝑥 2 + 𝑐𝑥 − 1 es divisible por (𝑥 − 1)(𝑥 + 1)(𝑥 − 1), el valor de (𝑎 + 𝑏 + 𝑐)2 es: A. 8 B. 64 36. Si el cociente notable 𝑥 30 −𝑦 𝑚 𝑥 𝑛 −𝑦 2 C. 27 D. 1 tiene 10 términos, entonces el valor de (m + n) es: A. 23 B. 25 C. 35 D. 50 37. Si 264 = a𝑎 𝑦 (√3)54 = (3𝑏)𝑏 , al determinar el valor de 3ª + b se obtiene: A. 66 B. 48 C. 99 D. 44 1 38. Si (2𝑎 + 𝑏)−𝑐 = 5 , entonces el valor de (b2 + 4ab + 4a2 es: A. 25 B. 125 C. 1 25 D. 1 125 39. Un barril contiene 120 litros de alcohol y 180 litros de agua; un segundo barril contiene 90 litros de alcohol y 30 litros de agua. ¿Qué cantidad de litros deberán 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] sacársele a cada uno de los barriles para obtener una mezcla homogénea que contenga 70 litros de agua y 70 litros de alcohol? 40. Si x 4 − y 4 = z 3 ; x 2 − y 2 = 8 ; entonces A. (𝑥 + 𝑦)(𝑦 − 𝑥) A. x y6 z4 8 es igual a ∶ C. (𝑥 − 𝑦)2 B. (𝑥 + 𝑦)(𝑥 − 𝑦) 23 43 4 41. Al simplificar x 1 y 2 z 7 3 3 3 x y z z3 D. (𝑥 + 𝑦)2 3 resulta: B. x y3 z5 C. x y6 z5 D. x2 y6 z5 42. Si 2x 3 x 2 p x 2 p 2 es divisible entre x + 1, siendo p un entero, entonces el valor de p es: A. 5 2 B. 5 2 C. 43. El conjunto solución de la desigualdad A. ( – ; 3 ) 2 B. (2; 9) C. ( – ; 1 2 D. 1 2 3 1 es: 2 x 3 x 2 3 3 ) (2;9) D. ( – ; ) ∩ (2; 9) 2 2 44. Dos enteros 𝑎 > 1 𝑦 𝑏 > 1 𝑠𝑎𝑡𝑖𝑠𝑓𝑎𝑐𝑒𝑛 𝑎𝑏 + 𝑏 𝑎 = 57 , determinar la suma a+b A. 4 B. 6 45. Si 𝑥 + 𝑦 = 1 ; 𝑥𝑦 = 1 C. 5 D. 7 ¿Cuál será el valor de x3 + y3? 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] A. -1 B. -2 C. -3 D. -4 46. El polinomio 𝑝(𝑥) = 𝑥 3 − 𝑥 2 + 𝑥 + 1 se anula en 1, luego p(x) es divisible por: A. 𝑥 − 4 B. 𝑥 − 3 C. 𝑥 − 2 D. 𝑥 − 1 47. La suma de dos números es 666 y si se divide el mayor entre el menor el cociente es 5 y el residuo 78. Dichos números son: A. {548; 118} B. {568; 98} C. {558; 108} D. {538; 128} 48. Si suponemos que el cociente intelectual de Einstein era 170 y si éste se calcula al dividir la edad mental por la edad cronológica multiplicado por 100. La edad mental de Einstein cuando publicó en 1905 su teoría sobre el efecto fotoeléctrico era: A. 44,2 B) 45,2 C) 47,2 D) 49,2 49. Mi hijo es ahora tres veces más joven que yo, pero hace cinco años era cuatro veces más joven. ¿Cuántos años tiene? A. 10 B. 5 C. 25 D. 15 50. Un grupo de amigos fue a tomar unos refrescos y unas empanadas, y lo pusieron todo en una cuenta que ascendió a 36 córdobas. Todos iban a pagar por igual, pero tres de ellos se habían ido, por lo que a cada uno le tocó pagar 1 córdobas más. ¿Cuántas personas conformaban el grupo original? A. 5 B. 10 C. 15 D. 12 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] 51. El producto de tres enteros positivos consecutivos es 3360 y su suma es 45. ¿Cuál es el mayor de esos tres números? A. 27 B. 16 C. 15 D. 14 52. Un autobús comienza su trayecto con un cierto número de pasajeros. En la primera parada descienden descienden 1 2 1 3 de los pasajeros y suben 8. En la segunda parada de los pasajeros y suben 2 nuevos. En este momento, el autobús lleva la mitad del número de pasajeros de los que llevaba al principio del trayecto. ¿Cuántos pasajeros había al principio? A 18 B 36 C 30 D 42 53. Halla tres números sabiendo que el segundo es mayor que el primero en la misma cantidad que el tercero es mayor que el segundo, que el producto de los dos más pequeños es 85 y que el producto de los dos mayores es 115. A. 23 2 ; 10; 17 2 B. 23 2 ; 15; 17 2 C. 3 2 ; 10; 1 2 D. 23 2 ; 1; 17 2 54. Marlene en su bicicleta calcula que si avanza a 10 km/hora llegará a su destino a la 1p.m., y si avanza a 15 km/hora llegará a su destino a las 11 a.m. ¿a qué velocidad, en km/hora, tiene que avanzar para llegar a las 12m.? A. 8 B. 6 C. 18 D. 12 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] 55. Un camino puede recorrerse en “t” horas con una cierta velocidad en km/hr. El mismo camino se puede hacer en una hora menos aumentando en un kilómetro por hora la velocidad. Hallar la longitud del camino en km. A. t B. t 3 t C. t2 1 D. t2 t 56. De un depósito de 100 litros de capacidad, lleno de alcohol puro, se saca una cierta cantidad de alcohol y se le reemplaza por agua. Se saca después la misma cantidad de mezcla y se reemplaza por agua, quedando ésta última mezcla con un 49% de alcohol. Determinar la cantidad de líquido que se ha sacado cada vez. A. 30 litros B. 15 litros C. 25 litros D. 35 litros 57. La suma de tres números es 21. El cociente de dos de ellos es 2.5 y la suma de estos dividida entre el tercero da como cociente 2. ¿Cuál es el menor de los tres números? A. 5 B. 6 C. 4 D. 3 58. Un padre actualmente tiene el triple de la edad de su hijo; si hace 6 años la edad del padre era el quíntuple de la edad de su hijo. ¿Cuánto es la suma de las cifras de edad del padre? A. 8 B. 6 C. 10 D. 9 59. Dos tuberías abiertas simultáneamente llenan un depósito en 1 hora 12 minutos. Si una de ellas tarda 1 hora más que la otra, en llenar el mismo depósito ¿en qué tiempo lo llenará la tubería de mayor caudal? A. 3 horas B. 1 hora C. 2 horas D. 4 horas 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] 60. Por Navidad, en cierta empresa todos los empleados se ofrecen regalos. En esta ocasión las mujeres se han dado mutuamente un regalo, pero los hombres lo han repartido: la mitad han dado un regalo a sus compañeros y la otra mitad lo han ofrecido a cada una de sus compañeras. Sabemos que el doble del número de mujeres excede en 6 al número de hombres. Si en total se han dado 318 regalos, ¿cuántos empleados laboran en la empresa? A. 37 B. 16 C. 11 D. 27 61. Determinar un entero positivo con los datos siguientes: si se añade un 5 a la derecha el número resultante es divisible exactamente por un número que sobrepasa en 3 el buscado, siendo el cociente igual al divisor menos 16. A. 32 B. 12 C. 22 D. 44 62. Hallar un número de dos cifras sabiendo que el número de unidades excede en dos el número de decenas y que el producto del número deseado por la suma de sus dígitos es 144. A. 24 B. 46 C. 13 D. 57 63. Si n es un entero positivo, la igualdad (𝑚4 − 𝑘𝑚2 𝑛 + 𝑛2 )𝑛 = (𝑚2 − 𝑛) 2𝑛 se cumple si k toma el valor: A. 2 B. -2 C. 4 D. -4 64. Un factor de 5𝑡 − 12 + 2𝑡 2 es (t + 4) y el otro es: 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] A. (t + 4) B. (2t - 3) 65. El sistema de ecuaciones A. k = 1 C. (3 - 2t) D. (2t + 3) kx y 1 tiene solución única si: x k y 2 B. k = -1 C. k = 1 y k = -1 D. k ≠ -1 y k ≠ 1 66. Encontrar la solución real del siguiente sistema de ecuación 67. Sean 𝑎 𝑦 𝑏 números reales distintos tales que 2𝑎2 + 2𝑏 2 = 5𝑎𝑏. (𝑎+𝑏) ¿Cuántos son los posibles valores de (𝑎−𝑏)? a) 1 b) 2 c) 3 d) 4 e) 5 68. ¿Cuántas ternas 𝑥, 𝑦, 𝑧 de números reales satisfacen el sistema? 𝑥(𝑥 + 𝑦 + 𝑧) = 26 {𝑦(𝑥 + 𝑦 + 𝑧) = 27 𝑧(𝑥 + 𝑦 + 𝑧) = 28 a) 1 b) 2 c) 3 d) 4 e) Ninguna FUNCIONES REALES Y TRIGONOMETRÍA 1. Escriba el producto cartesiano de los conjuntos dados. a. 𝐴 = {−2, −1,0,1,2}, 𝐵 = {3,5,7} b. 𝐴 = {𝑎, 𝑒, 𝑖, 𝑜, 𝑢}, 𝐵 = {𝑐, 𝑑, ℎ}. 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] 2. A partir de los productos cartesianos del ejercicio anterior defina 2 relaciones y 2 funciones. 3. Determine cuáles de las siguientes relaciones representan funciones y cuáles no. Justifique su respuesta. a. 𝑓 = {(2, 6), (−3, 6), (4, 9), (2, 10)} b. 𝑔 = {(𝑎, 2), (𝑏, 3), (𝑐, 5), (𝑎, 7)} c. ℎ = {(𝑎, 1), (𝑏, 2), (𝑐, 1), (𝑑, 2)} d. 𝑝 = {(−2, 4), (−1, 1), (0, 0), (1, 1)} e. 𝑀 = { (𝑥, 𝑦 ) | 𝑦 = 5𝑥 − 3, con 𝑥, 𝑦 ∈ ℝ } f. 𝑁 = { (𝑥, 𝑦 ) | 𝑦 2 = −𝑥 2 − 1, con 𝑥, 𝑦 ∈ ℝ } g. 𝑓: ℝ ⟶ ℝ si 𝑓(𝑥) = 𝑥 2 + 𝑥 − 6 h. ℎ: 𝑥 ⟼ 𝑦 mediante 𝑦 = ±√𝑥 + 4 si 𝑥, 𝑦 ∈ ℝ. 4. Dadas las siguientes leyes de asignación, determine el dominio y el rango de su función correspondiente. a. 𝑓 = {(0, −1), (3, −2), (1, 0), (−3, 5), (2, 6)} b. 𝑦 = 3𝑥 2 + 5𝑥 − 1 c. 𝑓(𝑥) = 2𝑥 − 6 d. 𝑔(𝑥) = √2𝑥 + 4 e. 𝑦 = ℎ(𝑥) = f. 𝑦 = 𝑥 𝑥 2 −16 𝑥2 𝑥 2 +1 5. Efectúe las evaluaciones indicadas para cada función real. a. 𝑓(𝑥) = 2𝑥 2 + 5𝑥 − 3; 𝑓(0), 𝑓(−1), 𝑓(𝑥 2 − 3), 𝑓(𝑥 + ℎ) b. 𝑔(𝑥) = √𝑥 + 9 ; 𝑔(7), 𝑔(−5), 𝑔(𝑥 + 9), 𝑔(𝑥 4 − 2) c. 𝑦 = 𝐻(𝑥) = 3𝑥 𝑥+1 ; 𝐻(2), 𝐻(0), 𝐻(−3), 𝐻(ℎ + 3). 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] 6. Determine dominio, rango y trace la gráfica de las funciones dadas por las leyes de asignación siguientes: a. 𝑓(𝑥) = 3𝑥 − 2 −2, i. 𝑟(𝑥) = {√𝑥 2 −𝑥 , b. 𝑔(𝑥) = 4 j. 𝑠(𝑥) = 2|𝑥 + 6| c. 𝑦 = −(𝑥 + 5)2 + 1 k. 𝑦 = −(𝑥 + 2)3 + 5 d. ℎ(𝑥) = 𝑥 2 + 6𝑥 − 2 l. 𝑓(𝑥) = { e. 𝑔(𝑥) = −5𝑥 + 1 f. 𝑦 = 𝑥 3 − 1 g. 𝑝(𝑥) = { 𝑥≥2 𝑥<2 |𝑥 − 2| + 3, 𝑥 < 0 𝑥 + 5, 𝑥≥0 m. 𝑦 = −√4 − 𝑥 −2𝑥, 𝑥≤2 −𝑥 2 − 4𝑥 + 1, 𝑥 > 2 h. 𝑓(𝑥) = 3√𝑥 − 1 + 8 𝑥2, n. 𝑔(𝑥) = { 𝑥 3 , 2𝑥, 𝑥 < −1 |𝑥| < 1 𝑥≥1 7. Se desea elaborar una caja sin tapa partiendo de una pieza rectangular de cartón, cuyas dimensiones son 20 × 30 centímetros, cortando en las esquinas cuadrados idénticos de área 𝑥 2 , y doblando los lados hacia arriba. El volumen 𝑉, de la caja en función de 𝑥 es: a) 4𝑥 3 − 100𝑥 2 + 600𝑥 b) −4𝑥 3 − 20𝑥 2 + 600𝑥 c) −4𝑥 3 + 20𝑥 2 + 600𝑥 d) −4𝑥 3 + 100𝑥 2 − 600𝑥 8. La tasa de crecimiento 𝑦, de un niño, en libras por mes, se relaciona con su peso actual 𝑥 en libras, mediante la fórmula 𝑦 = 𝑐𝑥(21 − 𝑥), donde 𝑐 es una constante positiva y 0 < 𝑥 < 21. ¿A qué peso se tiene la tasa máxima de crecimiento? a) 21 libras b) −21 libras c) 10.5 libras d) 10 libras 9. Hace 5 años se compró una casa en $ 16,000, este año fue valorada en $ 19,000. Suponiendo que el valor de la casa está relacionado linealmente con el tiempo. La fórmula que indica el valor de la casa en cualquier tiempo 𝑡 (en años) después de la fecha de compra es: a) 𝑓(𝑡) = 600𝑡 + 19,000 b) 𝑓(𝑡) = 60𝑡 − 1,900 c) 𝑓(𝑡) = −60𝑡 − 1,900 d) 𝑓(𝑡) = −600𝑡 + 19,000 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] 10. Un objeto se lanza verticalmente hacia arriba desde la azotea de un edificio, con velocidad inicial de 144 𝑚/𝑠. Su distancia 𝑠(𝑡) en metros sobre el piso a los 𝑡 segundos de ser lanzado está dada por 𝑠(𝑡) = 6𝑡 2 + 144𝑡 + 100. La altura máxima sobre el piso y la altura del edificio son respectivamente: a) 42.4 𝑚 y 10.0 𝑚 b) 10.0 𝑚 y 42.4 𝑚 c) 424.0 𝑚 y 100.0 𝑚 d) 100.0 𝑚 y 424.0 𝑚 11. El pago diario de una cuadrilla de trabajadores es directamente proporcional al número de trabajadores. Si una cuadrilla de 12 trabajadores gana 𝐶$ 5,400 diario. El pago diario en función del número de trabajadores 𝑥 está dado por la expresión: a) 𝑓(𝑥) = 450𝑥 b) 𝑓(𝑥) = c) 𝑓(𝑥) = −450𝑥 1 450 d) 𝑓(𝑥) = − 𝑥 1 450 𝑥 12. Una fábrica de lámparas tiene costos fijos de $ 3,000 y el costo de la mano de obra y de materiales es de $ 15 por lámpara, encuentre la función de costo total del número de lámparas producidas. Si cada lámpara se vende a $ 25, la función de utilidad está dada por: a) 𝑈(𝑥) = 10𝑥 − 3,000 c) 𝑈(𝑥) = −10𝑥 + 3,000 b) 𝑈(𝑥) = 10𝑥 + 3,000 d) 𝑈(𝑥) = −10𝑥 − 3,000 13. Para cada pareja de funciones dadas, halle 𝑓 ± 𝑔, 𝑓 ∙ 𝑔 y 𝑓 𝑔 . Determine el dominio de las funciones resultantes. a. 𝑓(𝑥) = 1 + 1 𝑥 , 𝑔(𝑥) = b. 𝑓(𝑥) = √𝑥 − 2 , c. 𝑓(𝑥) = 2𝑥+3 3𝑥−2 1 𝑥 𝑔(𝑥) = √4 − 𝑥 , 𝑔(𝑥) = 4𝑥 3𝑥−2 d. 𝑓(𝑥) = 𝑥 2 + 2, 𝑔(𝑥) = 2𝑥 2 − 1 e. 𝑓(𝑥) = 2𝑥 𝑥−4 , 𝑔(𝑥) = 𝑥 𝑥+5 . 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] 14. Sean las funciones reales 𝑓, 𝑔 dadas por las leyes de asignación 𝑓(𝑥) = 𝑥 + 𝑓 3, 𝑔(𝑥) = 𝑥 2 , respectivamente. Calcule (𝑓 + 𝑔)(3), (𝑓 − 𝑔)(3), (𝑓𝑔)(3) y ( ) 𝑔 (3). 15. Dadas las funciones reales, 𝑝 + 𝑚 y 𝑝, mediante (𝑝 + 𝑚)(𝑥) = 6 − 1 2 𝑥 y 𝑝(𝑥) = 3𝑥 + 1, respectivamente. Halle la ley de asignación para la función 𝑚. 𝑓 16. Dadas las funciones reales, 𝑓 y 𝑔 , mediante 𝑓(𝑥) = 1 𝑥 𝑓 𝑥+1 𝑔 𝑥 2 −𝑥 y ( ) (𝑥) = , respectivamente. Halle 𝑔(𝑥). 17. Dadas las funciones 𝑓, 𝑔 mediante las leyes de asignación siguientes, calcule (𝑓 ∘ 𝑔)(𝑥) y (𝑔 ∘ 𝑓)(𝑥). 1 a. 𝑓(𝑥) = 4𝑥 2 − 3, 𝑔(𝑥) = 3 − 2 𝑥 2 b. 𝑓(𝑥) = √𝑥 + 1 , 𝑔(𝑥) = 3𝑥 c. 𝑓(𝑥) = 𝑥 2 + 1, 𝑔(𝑥) = √𝑥 − 1 d. 𝑓(𝑥) = 3 𝑥+1 , 3 𝑔(𝑥) = √𝑥 e. 𝑓(𝑥) = 𝑥 2 − 3𝑥, 𝑔(𝑥) = √𝑥 + 2 . 18. Sean las funciones 𝑓, 𝑔 dadas por 𝑓(𝑥) = 3𝑥 2 + 4 respectivamente, halle (𝑓 ∘ 𝑔)(𝑥), (𝑔 ∘ 𝑓)(𝑥) y (𝑓 ∘ 𝑔)(−2). y 𝑔(𝑥) = 5𝑥, 19. Verifique que (𝑓 ∘ 𝑔)(𝑥) = (𝑔 ∘ 𝑓)(𝑥) = 𝑥 para los casos siguientes: 1 a. 𝑓(𝑥) = 2𝑥 − 6, 𝑔(𝑥) = 2 𝑥 + 3 3 b. 𝑓(𝑥) = 𝑥 3 , 𝑔(𝑥) = √𝑥 . 20. Un incendio en un campo abierto seco, se propaga en forma circular. Si el radio de este círculo aumenta a una velocidad de 6 𝑚/𝑚𝑖𝑛. Exprese el área total incendiada 𝐴 (en 𝑚2 ) como una función del tiempo 𝑡 (en minutos). a) 𝐴(𝑡) = 36𝜋𝑡 2 b) 𝐴(𝑡) = 6𝜋 2 𝑡 2 c) 𝐴(𝑡) = 6𝜋𝑡 2 d) 𝐴(𝑡) = 36𝜋 2 𝑡 2 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] 21. Dos barcos parten de un puerto a la misma hora, uno viaja al oeste con una velocidad de 17 𝑚𝑖/ℎ, y el otro hacia el sur a 12 𝑚𝑖/ℎ. Si 𝑡 es el tiempo en horas que ha transcurrido desde sus partidas, exprese la distancia 𝑑 entre los barcos como una función del tiempo. a) 𝑑(𝑡) = 433𝑡 2 b) 𝑑(𝑡) = 20.81𝑡 2 c) 𝑑(𝑡) = 20.81𝑡 d) 𝑑(𝑡) = 433𝑡 22. Se desea construir un tanque de acero para almacenar gas propano. Su forma debe ser la de un cilindro recto circular de 10 𝑚 de altura con una semiesfera unida en cada extremo. Su radio 𝑟 debe determinarse, exprese el volumen 𝑉 del tanque (medido en pies cúbicos) en función de 𝑟. 2 a) 𝑉(𝑟) = 2𝜋𝑟 2 (5 − 3 𝑟) 2 c) 𝑉(𝑟) = 2𝜋𝑟 2 (3 𝑟 + 5) 4 b) 𝑉(𝑟) = 3 𝜋𝑟 3 − 10𝜋𝑟 2 d) 𝑉(𝑟) = 34 3 𝜋𝑟 3 23. Determine si las funciones reales dadas por las siguientes leyes de asignación son biyectivas. a. 𝑔(𝑥) = 3𝑥 + 5 b. ℎ(𝑥) = 𝑥 2 c. 𝑔(𝑥) = 2𝑥 d. 𝑓(𝑥) = 𝑥 3 − 6 e. 𝑔(𝑥) = √𝑥 + 7 f. ℎ(𝑥) = 5𝑥 2 − 𝑥 + 1 24. Para cada una de las funciones dadas por las leyes de asignación siguientes (a) verifique que son biyectivas (b) halle su inversa 𝑓 −1 (c) compruebe que se cumple la igualdad (𝑓 ∘ 𝑓 −1 )(𝑥) = (𝑓 −1 ∘ 𝑓)(𝑥) = 𝑥, (d) trace las gráficas de cada pareja de funciones (𝑓, 𝑓 −1 ) en un mismo plano cartesiano de manera que se evidencie la simetría respecto a la recta 𝑦 = 𝑥. a. 𝑓(𝑥) = 3𝑥 + 5 b. 𝑓(𝑥) = 2𝑥 3 − 5 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] c. 𝑓(𝑥) = √3 − 𝑥 d. 𝑓(𝑥) = √4 − 𝑥 2 , con dom𝑓 = [0, 2] e. 𝑓(𝑥) = −𝑥 2 + 3, con dom𝑓 = {𝑥 ∈ ℝ | 𝑥 ≥ 0} 3 f. 𝑓(𝑥) = √𝑥 + 1. 25. Transforme de forma exponencial a logarítmica y viceversa, según el caso. a. 43 = 643 b. 10−3 = 0.001 c. log 3 1 243 = −5 d. log 7 1 = 0 26. Reescriba las siguientes expresiones como combinación de logaritmos en 𝑥, 𝑦, 𝑧. √𝑥 𝑧2 3 b. log 𝑎 √𝑥√𝑦𝑧 3 a. log 𝑎 𝑦4 c. log [√ 𝑥2 𝑦𝑧 5 ∙ 𝑧] 27. Reescriba los siguientes logaritmos como uno solo en función de 𝑥, 𝑦 y 𝑧. 1 a. 2 log 𝑎 𝑥 + 3 log 𝑎 (𝑥 − 2) − 5 log 𝑎 (2𝑥 + 3) b. log 𝑥 3 𝑦 2 − 2 log 𝑥 3√𝑦 + 3 log 𝑥 𝑦 28. La cantidad de radio puro 𝑞 que queda después de inicialmente se tenía 𝑞0 miligramos es 𝑡 años, cuando 𝑡 𝑞 = 𝑞0 ∙ 2−1600 . El tiempo 𝑡 expresado en términos de log 2 es: a. 𝑡 = 1600 log 2 𝑞0 − 1600 log 2 𝑞 b. 𝑡 = 1600 log 2 𝑞0 + 1600 log 2 𝑞 c. 𝑡 = 1600 log 2 𝑞 − 1600 log 2 𝑞0 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] d. 𝑡 = −1600 log 2 𝑞 + 1600 log 2 𝑞0 29. El número 𝑁 de bacterias en un cierto cultivo en un tiempo 𝑡, está dado por 𝑁 = 104 ∙ 3𝑡 . El tiempo 𝑡 en función de 𝑁 utilizando logaritmos de base 3 es: a. 𝑡 = log 3 𝑁 − 4 log 3 10 b. 𝑡 = 4 log 3 𝑁 − log 3 10 c. 𝑡 = 4 log 3 𝑁 + log 3 10 d. 𝑡 = 4 log 3 (𝑁 − 10) 30. Trace la gráfica de las funciones reales dadas por las reglas de asignación siguientes: c. ℎ(𝑥) = 2|𝑥| a. 𝑓(𝑥) = 4𝑥 b. 𝑔(𝑥) = 3−𝑥 4 d. 𝑓(𝑥) = {log 𝑥 1/5 𝑥 ≥ 25 0 < 𝑥 < 25 e. 𝑔(𝑥) = { f. 𝑔(𝑥) = 3𝑥 + 3−𝑥 g. ℎ(𝑥) = log1/10 𝑥 h. 𝑦 = log 4 𝑥 i. 𝑦 = log 2 (𝑥 + 2) j. 𝑦 = log 2 𝑥 + 3 k. 𝑦 = log 2 √𝑥 l. 𝑦 = 2𝑥+3 m. 𝑦 = (3) 2 𝑥 1 𝑥 (2) 𝑥≤3 −(𝑥 − 3)2 𝑥 > 3 n. 𝑦 = log 5 (𝑥 − 2) 31. El número de bacterias de cierto cultivo incrementó de 600 a 1800 entre las 7: 00 𝑎𝑚 y las 9: 00 𝑎𝑚. Suponiendo que el crecimiento es exponencial, se puede mostrar, usando métodos de cálculo, que 𝑡 horas después de las 1 7: 00 𝑎𝑚 el número 𝑓(𝑡) de bacterias está dado por 𝑓(𝑡) = 600 (3 2 𝑡 ). a. Calcule el número de bacterias en el cultivo a las 8: 00 𝑎𝑚, a las 10: 00 𝑎𝑚 y a las 11: 00 𝑎𝑚. b. Trace la gráfica de 𝑓 desde 𝑡 = 0 hasta 𝑡 = 4. 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] 32. Si 1,000 dólares se invierten al 12 % anual y se capitalizan los intereses mensualmente, ¿cuál es el monto acumulado después de (a) 1 mes, (b) 2 meses, (c) 6 meses, y (d) 1 año? 33. Si cierta marca de automóvil se compra por 𝐶 dólares, su valor comercial 𝑣(𝑡) al final de t años está dado por 𝑣(𝑡) = 0.78𝐶(0.85)𝑡−1 . Si el costo original es de $ 10 000, calcule (redondeando a unidades) el valor después de (a) 1 año, (b) 4 años, y (c) 7 años. 34. Resuelva las siguientes ecuaciones: a. 105𝑥−2 = 348 b. log 2 (9𝑥+1 + 7) = 2 log 2 (3𝑥+1 + 1) c. log(𝑥 − 9) + log 100𝑥 = 3 d. 103𝑥−7𝑥 = e. 2 𝑥+2+√𝑥−3 1 100 − (5)2𝑥+√𝑥−3 + 8 = 0 f. 49𝑥 − 50(7𝑥 ) + 49 = 0 35. Resuelva los siguientes sistemas de ecuaciones: 𝑥 a. { √𝑥 + 𝑦 = 2 (𝑥 + 𝑦)3𝑥 = 279,936 53𝑥−2𝑦 = 3,125 b. { 6𝑥−7𝑦 11 = 14,641 36. Escriba cada ángulo en notación decimal en grados: a. 40° 10′ 25′′ b. 61° 42′ 21′′ c. 98° 22′ 45′′ d. 1° 2′ 3′′ 37. Escriba cada ángulo en notación de grados, minutos y segundos: a. 18.255° 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] b. 29.411° c. 44.01° d. 61.24° 38. Convertir los ángulos en grados a radianes y viceversa según el caso. a. 630° d. − 7 2 b. 𝜋 e. 11 6 15 4 𝜋 c. 720° 𝜋 f. −135° 39. Halle el ángulo complementario de 𝜃 si a. 𝜃 = 5° 17′ 34′′ b. 𝜃 = 32.5° c. 𝜃 = 63° 4′ 15′′ d. 𝜃 = 82.73° 40. Halle el ángulo suplementario de 𝛽 si a. 𝛽 = 48° 51′ 37′′ b. 𝛽 = 152° 14′ 4′′ c. 𝛽 = 136.42° d. 𝛽 = 1 6 𝜋 41. Calcule funciones trigonométricas restantes si sen 𝜃 = √5 5 y cos 𝜃 = 2√5 5 . 42. Si 𝜃 es un ángulo agudo, halle las seis funciones trigonométricas si: a. sec 𝜃 = 6 5 b. csc 𝜃 = 4 c. cot 𝜃 = d. tan 𝜃 = 7 24 5 12 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] 43. Calcule el valor de cada expresión 𝜋 𝜋 𝜋 𝜋 a. sen2 6 + cos2 6 b. sec 2 3 − tan2 3 44. Sea 𝑃(𝑥, 𝑦) el lado terminal de 𝜃. Calcule las seis funciones trigonométricas de 𝜃. a. 𝑃(−6, 2) b. 𝑃(−4, −3) 3 c. 𝑃(5, −2) d. 𝑃 (−1, 8) 45. Un ángulo central 𝜃 intercepta un arco de 7 𝑐𝑚 de largo en una circunferencia de radio de 4 𝑐𝑚. Aproxime la medida de 𝜃 en: (a) radianes, y, (b) grados. 46. La distancia entre dos puntos 𝐴 y 𝐵 en la Tierra, se mide sobre un círculo con centro 𝐶 en el centro de la Tierra y radio igual a la distancia de 𝐶 a la superficie. Si el diámetro terrestre es de 8 000 millas aproximadamente, calcule la distancia entre 𝐴 y 𝐵 cuando el ángulo 𝐴𝐶𝐵 mide (a) 60°, (b) 45°, (c) 30°, (d) 10°. 47. Trace la gráfica de las funciones dadas por las leyes de asignación siguientes: a. 𝑦 = sen 𝑥 𝜋 b. 𝑦 = 3 cos (𝑥 − 4 ) 1 c. 𝑓(𝑥) = 2 1 𝜋 cot (2 𝑥 − 4 ) d. 𝑔(𝑥) = − cos(3𝑥 + 𝜋) 1 e. ℎ(𝑥) = 2 cos 3𝑥 48. Demostrar las siguientes identidades: a. tan4 𝜃 − sec 4 𝜃 = 1 − 2 sec 2 𝜃 b. c. 1 cos2 𝑥 +1 + tan2 𝑥 = 2 + 2 tan2 𝑥 1+cos 𝛼 sen 𝛼 2 + sen 𝛼 cos 𝛼 = cos 𝛼+1 sen 𝛼 cos 𝛼 2 d. sec 𝜆 + tan 𝜆 = (1 − sen2 𝜆) sec 4 𝜆 49. Si 𝛼 y 𝛽 son ángulos agudos tales que cos 𝛼 = 4 5 y tan 𝛽 = 8 15 . Halle: 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] a. sen(𝛼 + 𝛽) b. cos(𝛼 + 𝛽) c. sec(𝛼 + 𝛽) d. sen(𝛼 − 𝛽) 50. Halle el conjunto solución de las siguientes ecuaciones en el intervalo dado: a. sen 𝑥 − 2 sen 𝑥 = 0 b. 2 tan2 𝑥 − sec 2 𝑥 = 0 𝜋 c. cos (2𝑥 − 4 ) 𝑥 d. sen 2 + cos 𝑥 = 1 51. Se da una circunferencia de radio 10 𝑚. El coseno del ángulo que forman las tangentes a dicha circunferencia, trazadas por los extremos de una cuerda de 15 𝑚 de longitud es: a. b. c. d. √2 3 5 8 2 3 1 8 52. Resuelvan el triángulo 𝐴𝐵𝐶 si: a. 𝑎 = 15 𝑐𝑚, 𝑏 = 18 𝑐𝑚 y 𝛼 = 33° 30′. b. 𝑎 = 40 𝑐𝑚, 𝑏 = 50 𝑐𝑚 y 𝑐 = 60 𝑐𝑚. c. 𝑎 = 11.8 𝑐𝑚, 𝑏 = 15.6 𝑐𝑚 y 𝛾 = 34° 20′. 53. La altura de un árbol que está situado sobre un terreno llano, sabiendo que desde un punto del suelo se observa su copa bajo un ángulo de elevación de 45° y, desde un punto 15 metros más cerca del árbol, a un ángulo de 60° es: a. 30.5 𝑚 b. 45 𝑚 c. 31.7 𝑚 d. 35.49 𝑚 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] Geometría Euclidiana I. EJERCICIOS SOBRE CONCEPTOS BÁSICOS 1. En la figura, el ángulo COB mide 120º y el ángulo COD mide la mitad del ángulo BOA. Entonces, la medida del BOA es: C B A. 20º D O B. 30º C. 40º D. 60º E. 80º A 2. Si dos planos diferentes se intersecan, su intersección es: A. Un punto. D. Dos rectas diferentes B. Dos puntos E. Falta información C. Una única recta 3. En la figura, m 1 m 4 , m 2 m 3 ¿cuál de las siguientes expresiones es siempre verdadera? A. m 1 || m 2 B. m1 m 3 C. m 3 || m 4 D. m 2 m 4 E. NDLA 4. R, S y T son tres puntos colineales como se muestran en la figura. Si ST = 4x + 4 y RS es la mitad de ST, entonces la longitud de RT es A. 3x – 4 5. R S B. 3x – 6 C. 3x + 2 xº 50º T D. 6x – 12 A partir de la información indicada en la figura, el valor de y es: 120º A. 170º yº E. 6x + 6 B. 130º C. 120º D. 100º E. 50º 130º 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] xº 6. A En la figura, si B 90º A. 50º 140º C 7. , el valor de x es: 70º C. 130º D. 140º E. 230º D D y En la figura, , entonces el valor de y es: E 130º x B C A 8. A. 30º x B. 40º C. 45º D. 50º E. 60º D. 65 E. 75º En la figura, el valor de x es 115º A. 25º B. 40º C. 45º 140º 9. En la figura, el valor de x es xº A. 30º 150º B. 40º C. 45º D. 50º E. 60º 10. A – B – C – D; E y F son puntos medios de AB y CD respectivamente; Si AC = 10 y BD = 12, entonces EF = ? A. 5 B. 6 C. 9 D. 11 E. 22 A 11. En la figura º + º = 255º, entonces ¿m A = ? A. 75º B B. 105º C. 127.5º D. 30º E. 45º C 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] 12. Para qué valor de x, los segmentos AB y CD son paralelos? C 25º A D xº A. 25 B B. 50 C. 65 D. 75 13. E. 130 A Si B 120º , ¿Cuál es el valor de x? E A. 170º B. 150º C. 120º D. 100º xº E. 80º C D 14. Si la medida de un ángulo es tres veces la medida de su suplemento, ¿cuál es la medida de dicho ángulo? A. 30º B. 60º C. 90º D. 120º E. 135º 15. Dos veces la medida de un ángulo es 30° menos que cinco veces la medida de su complemento, ¿cuál es la medida de dicho ángulo? A. 30º B. 60º C. 90º D. 120º E. 135º 16 60º En la figura las rectas y son paralelas. Entonces el valor de x es 110º A. 170 xº B. 50 C. 85 D. 25 E. 30 17. En la figura las rectas y 84° son paralelas. Entonces el valor de x es (x – 6)° A. 170 B. 50 C. 85 D. 25 E. 20 (3x + 10)° 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] 18. P Q 2 S 1 Si m P = 90º, 1 2, 3 4, entonces m R es 3 4 R A. 30º B. 45º C. 60º D. 90º E. Falta información. __ 19. En una recta se toman los puntos A, B y C, de manera que B es punto medio de AC . Se toma otro punto O, tal que B – O – C. Encuentre el valor numérico de A. 2 B. 1 C. 1 2 D. AO OC . OB 3 2 E. Falta información. II. TRIÁNGULOS Y CUADRILÁTEROS 1. ÁREAS DE TRIÁNGULOS Y CUADRILÁTEROS RECTÁNGULO PARALELOGRAMO TRAPECIO ROMBO b d b A=bh h h D b A=bh h B d A= Dd B’ A= (B + b)h = B’h TRIÁNGULOS 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] c a h b b A= base x altura A= h a ab A= ah Fórmula de Herón: (Área de un triángulo en función de sus lados) A= x A= TRIÁNGULO EQUILÁTERO , donde s 2. RELACIONES MÉTRICAS EN LOS TRIÁNGULOS RECTÁNGULOS Dado un triángulo rectángulo ABC, con ángulo recto en C, las longitudes de sus lados (a, b, c), la altura correspondiente a la hipotenusa (h) y las proyecciones de los catetos sobre la hipotenusa (m, n), se cumplen las siguientes relaciones métricas: C i) h = ii) b = iii) a = iv) m + n = c a b h n A m D c B EJERCICIOS PROPUESTOS SOBRE TRIÁNGULOS Y CUADRILÁTEROS 1. Un poste cercano a un árbol mide 2 m y su sombra en un momento dado mide 1.8 m, entonces si la sombra del árbol en ese momento mide 11 m, la altura del árbol es A. 11 m B. 11.22 m C. 12. D. 12.22 E. 13 m 2. Una varilla clavada en el piso y cercana a un árbol mide 3 m y su sombra mide 1.5 m, entonces si el árbol mide 36 m, su sombra mide A. 36 m B. 30 m C. 18 m D. 15 m E. 9 m 3. El perímetro de un triángulo rectángulo isósceles con hipotenusa igual a 10 redondeado a dos decimales es 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] A. 7.07 B. 14.14 C. 24.14 D. 24.99 E. 50 En el triángulo rectángulo de la figura, los valores de x e y, respectivamente son 4. y 8 4 A. 11 y 13 x B. 15 y 16 D. 16 y 8.94 C. 9 y 8 E. 12 y 8.94 5. Un método para encontrar la altura de un edificio es colocar un espejo en el suelo y después situarse de manera que la parte más alta del edificio pueda verse en el espejo ¿qué altura tiene un edificio si una persona cuyos ojos están a 1.5 m del piso observa la parte superior del edificio cuando el espejo está a 120 m del edificio y la persona está a 6 m del espejo? A. 20 m B. 30 m C. 31.5 m D. 120 m E. 126 m 6. La altura respecto a la hipotenusa de un triángulo rectángulo mide 10 m y los segmentos que determina sobre la hipotenusa son entre sí como 7 es a 14. Entonces la longitud del cateto menor es A. 4 m B. 7.07 m C. 12.25 m D. 14 m E. 15.5 m 7. El perímetro de un rectángulo es 85 m y su diagonal mide 32.5 m. Por lo tanto los lados del rectángulo miden: A. 15 m y 27.5 m B. 20 m y 22.5 m C. 7.5 m y 25 m D. 30m y 12.5 m E. 40m y 2.5 m 8. El perímetro de un triángulo mide 50 y sus lados son proporcionales a 4, 6 y 8. Entonces su lado mayor mide A. 50/3 B. 25/9 C. 100/9 D. 25 E. 200/9 9. En un triángulo rectángulo, un lado mide 2 106 , otro 5 15 . Si el lado desconocido es el menor, ¿cuánto mide? A. 7 B. 8 C. 9 D. 10 E. 11 10. 7 6 El área del triángulo de la figura, redondeada al entero más cercano, mide: A. 21 9 11. B. 22 C. 27 D. 31 E. 54 ¿Cuál es el área del triángulo de la figura? 6 A. 20 B. 24 C. 30 D. 48 E. 60 10 12. Si un rectángulo de 3 m de ancho y 10 m de largo tiene la misma área que un triángulo rectángulo isósceles, entonces la longitud de cada cateto del triángulo es A. 7.5 B. 2 15 C. 15 D. 15 3 E. 10 13. El área de un trapecio isósceles de bases 22 m y 10 m y cuyos lados congruentes miden 10 es A. 2220 m2 B. 160 m2 C. 128 m2 D. 80 m2 E. 64 m2 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] 14. La siguiente figura consta de siete cuadrados congruentes. El área total de esta figura es 63 cm 2. Entonces el perímetro de la figura es: A. 16 cm A 15. B C H F C. 24 cm D. 48 cm E. 84 cm Si ACEG es un cuadrado y el área del cuadrilátero BDFH mide 162 ¿cuánto mide AC? (las marcas iguales representan partes congruentes) D G B. 21 cm A. 9 B. 12.72 C. 18 D. 25.44 E. 81 E __ 16. Se tiene un trapecio ABCD donde BC es la base menor. BC = 10 cm. y CD = 20 cm. Las medidas de los ángulos A, B y C son 30°, 150° y 120° respectivamente, entonces AD = ? A. 60 cm. B. 50 cm. C. 40 cm. D. 30 cm. E. 20 cm. 17. Si las medianas en un triángulo rectángulo, trazadas a partir de los vértices de los ángulos agudos miden 40 cm, entonces la medida de la hipotenusa del triángulo rectángulo es 5 cm y 5 40 cm 2 A. B. 2 13 cm C. 45 cm D. 11.32 cm E. 5.66 cm 18. En la figura, los cuadrados ABCD y EFGH son congruentes. AB = 10 cm y G es el centro del cuadrado ABCD. Entonces el área total cubierta por el polígono AHEFBCDA es D C G A B H A. 100 cm2 B. 120 cm2 C. 150 cm2 D. 175 cm2 E. 200 cm2 F E 19. ABCD es un cuadrado, el ABE es isósceles, CF = FB. Entonces, la medida del ángulo EFB es igual a D E C F A B A. 150° B. 135° D. 60° E. 45° C. 90° 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] 20. B C D En la figura, ABCF es un paralelogramo. B, C y D son colineales. Si AB = 18, AD = 30 y FE = 12. ¿Cuánto mide AE? E A A. 10 F B. 12 C. 15 D. 20 E. 25 21. En un trapecio isósceles, la diferencia de las bases es de 10 m. La altura mide 12 m. y el perímetro 76 m. Entonces su área es: A. 86 m2 B. 176 m2 C. 226 m2 D. 288 m2 E. 300 m2 22. En la figura ABCD es un cuadrado de lado 1 cm. y CE = 2 cm., entonces el área del triángulo ADF en cm2 es igual a D A A. 1 2 B. 1 3 D. 1 6 E. 1 8 F B E C C. 1 4 23. Sea ABC un triángulo isósceles con AB = BC = 10 y AC = 16. Sea BD la mediana trazada sobre el lado AC y sea G el baricentro. Entonces el área del triángulo ADG es A. 6 B. 8 C. 10 D. 12 E. 24 24. Sea ABC un triángulo isósceles con AB = AC = 17 cm y P un punto cualquiera del lado BC, diferente de los puntos extremos. Por P se trazan una paralela a AC que corta a AB en Q y una paralela a AB que corta a AC en R. El perímetro del cuadrilátero AQPR es A Q R B P A. 8.5 cm B. 17 cm C. 34 cm D. 51 cm E. 68 cm C 25. De acuerdo a la información que se proporciona en la figura, el segmento de mayor longitud es B A 70° 55° 60° A. AB 60° D B. BC C. CD D. DA E. BD C 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] 26. En la figura ABCD es un cuadrado de lado 1, CMN es equilátero, El área de CMN es igual a D C M A N B A. 0.866 B. 0.7071 D. 0.5 E. 0.4641 C. 0.75 27. La siguiente figura muestra dos cuadrados de lado 1 cm., donde AEFG se ha obtenido de ABCD al girar este cuadrado 45° sobre el vértice A. Entonces el área sombreada es F C B E G A. D. A 2 –1 B. 0.5 2 C. 0.451 E. 0.375 D 28. Los ángulos agudos de un triángulo rectángulo, que también es isósceles, miden A. 30° B. 45° C. 35° D. 75° E. 60° 29. En la figura ABCD es un cuadrilátero con AD || BC . La diagonal AC es perpendicular al lado CD . mBAC = 30°, AC = 4 B 3 y AB = BC. Entonces el área de ABCD es igual a C A. 6 A B. 12 C. 12 3 D. 24 E. 30 D 30. Se tiene un trapecio ABCD donde BC es la base menor. BC = 10 cm y CD = 20 cm . Las medidas de los ángulos A, B y C son 30°, 150° y 120° respectivamente, entonces el área del trapecio mide A. 300 3 cm2. B. 400 cm2. C. 300 cm2. D. 200 cm2. E. 200 3 cm2. 31. En la figura, mBAC = , mBPC = mBQC = 90°. Entonces la medida de BHC es 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] A P H Q B C A. 180 – B. C. 90 – D. 2 E. 3 32. Si las medianas en un triángulo rectángulo, trazadas a partir de los vértices de los ángulos agudos miden 20 cm, entonces la medida en cm de la hipotenusa del triángulo rectángulo es 5 cm y A. 5 B. 6 C. 8 D. 9 E. 10 33. En la figura, los dos cuadrados tienen el mismo centro. La razón entre el lado del cuadrado menor y el lado del cuadrado mayor es 2/5. Entonces la razón entre el área sombreada y el área del cuadrado mayor es A. 1/6 B. 21/100 D. 2/5 E. 4/9 C. 1/3 34. En la figura, AB = AC = 4, BD = DC = 3 y mBAC = 60°, entonces la longitud del segmento AD es A A. 2 3 – 5 D. 2 D B. 2 3 + 5 C. 1 E. 3.5 C B 35. En la figura el cuadrilátero ACDE es un trapecio tal que ED = 15 cm , AC = 24 cm y la altura es 12 cm. Sabiendo que B es el punto medio del lado AC, el área del cuadrilátero OBCD es E D O A B A. 112 cm 2 B. 117 cm 2 D. 140 cm 2 E. 360 cm 2 C. 120 cm 2 C 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] 36. En la figura, ABCD es un cuadrado de lado 6 cm. y CE = DE = 5 cm., entonces la longitud de es E A cm D. 30 B. 15 cm C D B A C. E. 37 132 52.8 En la figura, a partir de la información dada, ¿cuál es el valor de x? x A. 76 66 B. 25 C. 13.2 D. 5.28 E. 5 10 38. ABCD es un paralelogramo. P es un punto de la diagonal AC . Trazamos por P paralelas a los lados del paralelogramo. Estas paralelas intersecan a los lados del paralelogramo en los puntos indicados en la figura. Sabiendo que el área de ABCD es 40 cm2 , entonces el área del cuadrilátero RQMN es igual a A R N B P D M 39 Q A. 10 cm 2 B 20 cm2 C. 30 cm 2 D. 40 cm 2 E. 50 cm 2 C A En el triángulo rectángulo ABC ¿cuál es la longitud del segmento BC? 6 A. 15 3 B. 12 C. 10 D. 9 E. 7.5 C B x 40. Sea ABCD un cuadrado. Por el vértice A se traza un segmento que corta a la prolongación del lado BC en E, al lado DC en F y a la diagonal BD en G. Si AG = 3 y GF = 1 ¿cuál es la longitud de FE? A D G F A. 12 B C B. 10 C. 9 D. 8 E. 6 E 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] III. CIRCUNFERENCIA Y POLÍGONOS EJERCICIOS PROPUESTOS B 1. A. 40° D A 2. En la figura de la derecha si la medida de los arcos AD y BC son 140º y 80° respectivamente, entonces el valor de es C B. 50° C. 60° D. 70° E. 80° C El triángulo ABC está inscrito en un semicírculo de diámetro AB. Si AC = 8 y BC = 6, el área de la región sombreada tiene un valor de B A A. 15.27 C 3. B. 24 C. 36.37 D. 61.07 E. 48 El triángulo ABC está inscrito en un semicírculo de diámetro AB. Si AC = 8 y CD = 4.8, el área de la región sombreada tiene un valor de A D B A. 15.27 B. 24 C. 36.37 D. 61.07 E. 48 . 4. Y X Z La circunferencia de la figura tiene radio 2 y el arco XYZ tiene longitud . ¿Cuánto mide la cuerda XZ? A. B. 2 C. 2 E. D. 5. En la figura el área del círculo mayor es 1 m 2. El círculo menor es tangente internamente al círculo mayor y también es tangente a los lados del ángulo inscrito que mide 60°. Entonces el área del círculo menor es A. 1 2 B. 4 9 C. D. 2 E. 1 2 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] Q 6. C En la figura C es el centro de la circunferencia de radio r y es un segmento tangente en T, de longitud 2r, entonces PC mide 7. A. r P T 10 B. r C. 3r D. r E. 5r Los extremos de la figura son semicírculos, ¿Cuál es el área de la región sombreada? 8 A. 80 8. B. 8 C. 10 D. 16 E. 16 + 80 C B es un diámetro. Si m AB = 50°, entonces m BAC = ? En la figura O A. 25° B. 50° C. 65° D. 90° E. 130° A 9. 10. En la figura, los círculos son tangentes y tienen radio igual a 10. Si se unen los centros de los círculos se forma un cuadrado. ¿Cuál es el área de la región sombreada? D A. (400 – 100) B. 400 – 100 D. 400 – 100 E. 400 – 400 B C. 100 – 400 En la figura, la medida del arco AB es 30°, y la medida del BPA es 35°. Los medidas del arco CD y el ángulo DAC (en grados) son respectivamente P A C A. 100 y 25 B. 50 y 50 D. 50 y 25 E. 25 y 50 C. 100 y 50 11. La expresión (p + q) p = (r + s) r, se cumple en la situación representada por r r s q s p A r q B p r q p s p s q C D 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] 12. En la figura se dan tres semicircunferencias mutuamente tangentes. CD y DA son diámetros de las circunferencias menores. El punto B está en la semicircunferencia mayor. BD CA . Si BD = 2, entonces el área sombreada es igual a B B. A. 1 C D C. 2 D. A 3 4 9 4 E. 13. Las medidas de los arcos AB y AC se indican en la figura. La medida del BAC es A 110° 130° C A. 55° B B. 60° C. 65° D. 110° E. 130° 14. En la figura, BC une los centros de los círculos tangentes. AB BC , BC = 8 y AC = 10, entonces la longitud de la circunferencia pequeña es igual a A B A. C 15. B. 2 C. 3 D. 4 E. 5 La figura representa un hexágono regular, ¿cuál es el valor de x? x A. 3 3 16. B. 6 3 C. 6 D. 18 E. 9 3 A B C 0.4 La figura representa un círculo inscrito en un cuadrado que a su vez está inscrito en otro cuadrado. B es punto medio de AC ¿Cuál es el área de la región sombreada? A. 0.025 B. 0.048 C. 0.1428 D. 0.153 E. 0.1582 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] 17. A Los segmentos AC y BD se cortan en P y son tangentes a las circunferencias en los puntos A, C, B y D. B P Si AC = 31, PB = 19 ¿Cuál es el valor de AP? C D A. 6 B. 12 C. 15 D. 25 E. 50 18. Seis triángulos equiláteros de 1 cm. de lado se unen para formar un hexágono como se muestra en la figura. Se circunscribe un círculo alrededor del hexágono ¿cuál es el área de la región sombreada? 3 ) cm2 2 A. ( D. B. ( 3 cm2 3 3 3 ) cm2 2 C. (2 3 ) cm2 2 E. (2 3 3 ) cm2 19. Un triángulo ABC está inscrito en una circunferencia como se muestra en la figura. Se tiene m A = 50º y m C = 60º. Se trazan tangentes por A, B y C de manera que se forma el triángulo circunscrito A’B’C’. Entonces la medida del ángulo A’ es: C’ B A’ A. 40º B. 60º C. 80º D. 100º E. 120º C A B’ 20. El triángulo ABC es equilátero y sus lados AC y BC son tangentes a la circunferencia con centro en O y radio 3 . El área del cuadrilátero AOBC es A C O 6 A. 3 B. D. 6 E. 12 C 3 3 B 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] 21. Si un ángulo central de 30° en una circunferencia intercepta un arco de 6 m de longitud, entonces el radio de la circunferencia mide A. /36 B. /6 C. D. 36/ E. 180 22. En la figura se tiene una circunferencia de radio 1 y un hexágono regular de lado 1. Si O es el centro de la circunferencia, entonces el área de la región sombreada es O A. 0.5 23 B. 0.866 C. 1 D. 1.5 E. 2 Los arcos AB y BC son semicírculos cuyos centros están sobre un diámetro del círculo que se muestra en la figura. A B C Si BC = 2 AB, entonces la razón entre el área de la región sombreada y el área de la región no sombreada es: A. 2 B. C. 1 D. E. 24. Una moneda circular de radio 1, está sobre una mesa. Si ponemos cuatro monedas más grandes de igual tamaño alrededor de ella, ¿cuál es el radio de las monedas grandes que permite que cada una sea tangente a las dos adyacentes y a la de radio 1? B. 1 + 2 A. 1 C. 2 2 D. 2 + E. 2.5 25. En la siguiente figura ABC y AEB son semicírculos, F es el punto medio del diámetro AC, B es punto medio del arco AC y AF = 1¿Cuál es el área de la región sombreada? B E A A. 1/2 B. 2 C. /4 F D. 3/4 C E. /4 – 1/2 26. Si el radio de un círculo aumenta en unidades, ¿cuánto aumenta su perímetro? A. B. 2 C. 3 D. 2 E. 22 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] 27. Dos semicírculos de radio 3 están inscritos en un semicírculo de radio 6 como se muestra en la figura. Un círculo de radio r es tangente a los tres semicírculos. ¿Cuánto vale r ? r A. 1 B. 1.5 C. 2 D. 2.5 E. 3 28. En la figura los círculos adyacentes son tangentes y tienen radio 1. ¿Cuánto vale el área de la región sombreada? A 29. B O C A. 6 – 3 B. 3 – 2 D. 6 –1 E. 6 – 3 C. 2 – 1 En la figura, m BCA = 90º, BA = 5 y AC = 3. ¿Cuál es el área del círculo con centro en O? A. 16 B. 8 C. 6 D. 5 E. 4 30. El lado mayor del rectángulo de la figura mide 20. La curva trazada en su interior está formada por cinco semicircunferencias ¿cuál es la longitud de la curva? A. 25 B. 20 C. 15 D. 10 E. 5 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] 31 La figura muestra dos segmentos perpendiculares tangentes a ambas circunferencias, las cuales son tangentes entre sí. Si el radio de la circunferencia pequeña mide 1, entonces el radio de la circunferencia más grande mide A. 3 + 2 B. 4 C. 6 D. 4 + 2 E. 8 32. Tres círculos de radio 1, con sus centros colineales son tangentes como se muestra en la figura. ¿Cuál es el área de la región sombreada? B. 4 – A. 8 – 2 C. 12 – 3 D. 8 – 3 E. 4 + 33. La figura muestra un hexágono regular inscrito en un círculo. Si el área del círculo es 1, ¿cuánto mide el área del triángulo ABC? O A C A. B. C. D. E. B 34. ¿Qué polígono regular tiene la misma cantidad de diagonales que de lados? A. Pentágono B. Hexágono C. Octógono D. Decágono E. Dodecágono 35. Sean O el centro de una circunferencia de radio r y ED = r. Si mDEC = k (m BOA), entonces el valor de k es: B D A O C E A. B. C. 1 D. 2 E. 3 36 . Si se aumenta el radio de un círculo en un 100%, ¿en qué porcentaje aumenta su área? A. 50% B. 100% C. 200% D. 100% E. 300% 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] 37. Se tienen tres círculos concéntricos de radios 1, 2 y 3 respectivamente. ¿Cuál es la razón entre el área de la región cuadriculada y el área de la región oscura? A. B. C. D. E. 2 38. El segmento AB es diámetro de una circunferencia de radio 1 y lado del triángulo equilátero ABC. Si la circunferencia corta a AC y BC en los puntos D y E respectivamente, entonces la longitud AE es: A. 1 B. 3 C. 3 2 D. 5 3 E. 2 3 2 39. En una circunferencia se tienen dos cuerdas paralelas de longitudes 10 y 14 que distan 6 entre sí. Entonces la longitud de la cuerda paralela a ambas y que equidista de ellas mide: A. 11 B. 12 C. 13 D. 184 E. 192 40. Un triángulo equilátero y un hexágono regular están inscritos en el mismo círculo. Si se divide el área del hexágono entre el área del triángulo se obtiene: A. 1.5 B. 2 C. 2.5 D. 3 E. 3 IV. VOLUMEN CUERPOS SÓLIDOS EJERCICIOS PROPUESTOS 1. En el prisma recto de la figura, las bases son triángulos equiláteros, con perímetros de 30 cm.. Si la altura del prisma es 10 cm. ¿cuál es el área total de la superficie del prisma? A. 100 B. C. 100 D. 300 E. 50 + 300 2. Tres vértices de un cubo, de los cuales no hay dos que estén en la misma arista, se unen para formar un triángulo. Si la arista del cubo tiene longitud 1, ¿Cuál es el área del triángulo formado? A. 6 2 B. 3 2 C. 2 2 D. 6 4 E. 3 4 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] B 3. A D C La figura representa un cubo. La intersección del plano ABG y el plano BCE es la recta G E F 4. De un cubo de 5” de arista se forma un cilindro circular recto de 3” de diámetro, entonces el volumen de la parte sobrante del cubo, en pulgadas cúbicas, es aproximadamente A. 8 B. 10 C. 80 D. 90 E. 100 5. La altura de un prisma rectangular es un tercio de su longitud y el ancho es la mitad de su longitud. Si la diagonal del prisma mide 30 cm., su volumen es A. 900 cm3 B. 1688.25 cm3 C. 2833.8 cm3 D. 4583.5 cm3 E. 9000 cm3 6. Al introducir un trozo de metal en un tanque rectangular con agua, de dimensiones 50 cm. x 37 cm., el nivel del agua subió 1 cm. ¿cuál es el volumen del trozo de metal? A. 13 cm3 B. 87 cm3 C. 88 cm3 D. 1850 cm3 E. 9250 cm3 7. ¿Cuál es el número máximo de diagonales que pueden trazarse sobre las caras de un cubo de manera que no hayan dos diagonales que tengan un punto en común? A. 2 B. 3 C. 4 D. 5 E. 6 c 8. En la figura se muestra un paralelepípedo rectangular. Si a = 2b y b = , ¿Cuál es el volumen en términos 2 de c? a c b 2 A. c 2 B. 2c 2 C. c 3 D. c3 2 E. c3 4 9. El área de la base de una pirámide es 45 y el área de una sección transversal es 20. Si la altura de la pirámide es 6 ¿a qué distancia de la sección transversal está el vértice? A. 1.5 B. 2.25 C. 4 D. 4.75 E. 5 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] 10. El área de la base de una pirámide es 45 y el área de una sección transversal es 20. Si la altura de la pirámide es 6 ¿cuál es la razón entre los volúmenes de la pirámide mayor y la menor? A. 3/2 B. 2 C. 9/4 D. 3 E. 27/8 11. La base de una pirámide es un triángulo equilátero cuyo perímetro es 12. Si la altura es 10, el volumen de la pirámide es 40 3 40 C. D. 40 3 E. 120 3 3 12. En un tronco de pirámide, la altura mide 10 m y las bases son cuadradas de 5 m y 9 m de lado respectivamente. Hallar la diferencia (en m3 ) entre su volumen y la de un prisma recto de igual altura y de base igual a la sección del tronco paralela a las bases y equidistante de ellas. A. 40 B. A. 4 B. 7 C. 40 D. 40 3 E. 70 13. En una pirámide cuadrada, en la que el lado de la base mide 8 cm y la altura mide 20 cm, se traza una sección paralela a la base a 14 cm de ésta. Entonces el área de dicha sección es A. 2.14 cm2 B. 5.76 cm2 C. 16.32 cm2 D. 31.36 cm2 E. 44.08 cm2 14. Los diámetros de dos cilindros circulares rectos concéntricos son 12 y 6 pulgadas respectivamente y la generatriz común es de 20 pulgadas, entonces el volumen del espacio que queda entre ambos cilindros es A. 270 pulg3 B. 270 pulg3 C. 540 pulg3 D. 540 pulg3 E. 2160 pulg3 15. El volumen de una cisterna cilíndrica es 1200 m3 y su altura es igual al diámetro, por lo tanto su área total es A. 190.98 m2 B. 576.25 m2 C. 600 m2 625.13 m2 D. E. 712 m2 16. Un cono de revolución tiene 13 cm. de generatriz y el radio de la base es de 5 cm. Se corta por un plano paralelo a la base que corta a la generatriz en un punto distante 5.2 cm. del vértice. Entonces el volumen del tronco de cono formado es A. 351.52 cm3 B. 294.05 cm3 C. 202.8 cm3 D. 135.2 cm3 E. 67.6 cm3 17. Dado un cono circular recto con radio 3 m y generatriz 5 m, entonces su área lateral es A. 2 B. 12 C. 15 D. 16 E. 30 18. El área lateral de un tronco de cono que se forma cuando se corta un cono recto de 6 cm. de radio y 8 cm. de altura, por medio de un plano paralelo a la base del cono y que lo corta a una altura de 4.5 cm. es A. 304.84 m2 B. 216 m2 C. 152.42 m2 D. 84.82 m2 E. 28.27 m2 19. Dos esferas de metal de radios 2a y 3a se funden juntos para hacer una esfera mayor. El radio de la nueva esfera es A. 2.5a B. 5a C. 6.5a D. 3 35 a E. 5a 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] 20. Un cono tiene una altura igual al doble de su radio. Una esfera tiene un radio igual al radio de la base del cono. La razón entre el volumen del cono y el volumen de la esfera es A. 1/2 B. 1 C. 3/2 D. 2 E. 4 21. Un cono tiene una altura igual al triple de su radio. Una esfera tiene un radio igual al radio de la base del cono. La razón entre el volumen del cono y el volumen de la esfera es A. 1/2 B. 1 C. 3/2 D. 3/4 E. 3 22. La altura de un cono es 5 cm. Un plano a 2 cm. del vértice es paralelo a la base del cono. Si el volumen del cono más pequeño es 24 cm3 , el volumen del cono más grande es A. 750 cm3 B. 375 cm3 C. 240 cm3 D. 120 cm3 E. 48 cm3 23. Un cubo está inscrito en una esfera. Si el área de la superficie total del cubo es 40 2 m , entonces el área de la superficie de la esfera es A. 10 m2 B. 15 m2 C. 20 m2 D. 30 m2 E. 40 m2 24. La base de una pirámide hexagonal tiene un área de 26 m 2. Si el volumen de dicha pirámide es 78 m3, entonces su altura mide A. 3 m B. 4 m C. 6 m D. 9 m E. 12 m C 25 Si el cono de la figura tiene un volumen de 1000 3 3 cm , C es el 9 vértice, AB un diámetro y mACB = 120°, entonces el diámetro de la base, en centímetros, es A B A. 5 B. 10 C. 15 D. 20 E. 30 26. El área de la superficie total de un cubo es 12 m 2. Entonces la longitud de su diagonal es A. 2 B. 3 C. 2 D. 5 E. 6 27. Si la generatriz de un cono mide 25 m y el diámetro de su base es 8 m, su volumen mide A. 200 m3 B. 400 m3 C. 413.48 m3 D. 418.88 m3 E. 1587.4 m3 28. En una esfera de radio 2, se tiene inscrito un cilindro de manera que el diámetro del cilindro es igual al radio de la esfera. Entonces el área lateral del cilindro es A. 4 B. 8 C. 2 3 D. 4 3 E. 8 3 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] UNIDAD DE GEOMETRÍA ANALÍTICA 1. El triángulo de vértices 𝐴(−5, −1), 𝐵(2, 3) y 𝐶(3, −2) es: a) Isósceles b) Equilátero c) Rectángulo d) Rectángulo isósceles 2. El perímetro 𝑃 y el área 𝐴 del cuadrilátero cuyos vértices son 𝐴(−3, −1), 𝐵(0,3), 𝐶(3,4) y 𝐷(4, −1) son: a) 𝑃 = 20 𝑢, 𝐴 = 22 𝑢2 b) 𝑃 = 22 𝑢, 𝐴 = 22 𝑢2 c) 𝑃 = 20 𝑢, 𝐴 = 22 𝑢 d) 𝑃 = 20 𝑢2 , 𝐴 = 22 𝑢2 3. Los vértices de un triángulo son 𝐴(3,8), 𝐵(2, −1), 𝐶(6, −1). La longitud de la ̅̅̅̅ es: mediana trazada al lado 𝐵𝐶 b) 28 a) √28 d) 82 c) √82 4. Los vértices de un cuadrado son (−1,3), (3, −1), (−1, −1) y (3,3). La longitud de sus diagonales es: a) 2 b) 4 c) 4√2 d) 3√2 5. Dos vértices opuestos de un cuadrado son (5,1) y (−1,3). El área del cuadrado es: a) 40 𝑢² b) 20 𝑢² c) 10 𝑢² d) 16 𝑢² 6. Uno de los extremos de un segmento de longitud 5 es el punto (3, −2). Si la abscisa del otro extremo es 6, su ordenada es: a) 3 b) 2 c) −6 d) b y c son verdaderos 7. Sea un segmento cuyos extremos son los puntos 𝐴(−2,3) y 𝐵(6, −3). Los puntos de trisección del segmento son: 2 10 a) (3 , 1), ( 3 , −1) 2 10 c) (− 3 , 1), ( 3 , −1) 2 10 b) (3 , −1), ( 3 , 1) 2 10 d) (3 , 1), ( 3 , 1) 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] 8. Uno de los extremos de un segmento es el punto (7,8) y su punto medio es (4,3). El otro extremo es: a) (1,2) b) (−1, −2) c) (−1,2) d) (1, −2) 9. Una recta de pendiente 3 pasa por el punto (3,2). Si la abscisa de otro punto de la recta es 4, su ordenada es: a) −5 b) 5 c) −4 d) 4 10. Dados los puntos 𝐴(3,2) y 𝐵(5,4) halla un punto 𝐶, alineado con 𝐴 y 𝐵, de manera que se obtenga 21 16 a) ( 5 , 5 ) 𝐶𝐴 𝐶𝐵 = b) (− 3 2 21 16 5 , 5) 21 16 c) ( 5 , − 5 ) d) (2, 3) 11. Dado el segmento de extremos 𝑃₁(3, −2) y 𝑃₂(−4,1), encuentre las coordenadas del punto 𝑃 que lo divide en la razón −2 a) (11,4) b) (−11,4) c) (5,4) d) (11, −4) 12. En un triángulo el baricentro 𝐵(𝑥, 𝑦) es tal que las distancias de este punto al vértice 𝑀(2,4) y al punto medio 𝑁(1, −1) del lado opuesto están en la relación 𝑀𝐵 𝑀𝑁 = 2. Las coordenadas del punto 𝐵 son: 4 2 a) (3 , 3) 4 2 b) (− 3 , 3) 2 4 c) (− 3 , 3) d) (2, 1) 13. Las coordenadas del punto que divide al segmento con extremos 𝐴(−1,4) y 1 𝐵(−5, −8) en la razón − 3 son: a) (1, −2) b) (2, −1) c) (1,10) d) (−1,10) 14. Las coordenadas del punto que divide al segmento con extremos 𝐴(3,2) y 𝐵(−1, −1) en la razón a) (2,1) 1 2 son: b) (−1,2) 5 c) (− 3 , −1) 5 d) (3 , 1) 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] 15. Encontrar el punto medio del segmento cuyos extremos son 𝐴(5,4); 𝐵(−3,8) a) (1,6) b) (6, 1) c) (−1,6) d) (1, −6) 16. El punto medio de un segmento es (2,2). Si uno de sus extremos es (−2,3), el otro es: a) (6,1) b) (6,3) c) (6, −3) d) (6, −1) 17. Encuentre los extremos del segmento cuyo punto medio es (2,1), si la abscisa de uno de ellos es 𝑥 = 6 y la ordenada del otro es 𝑦 = −1. a) (6,1); (−2, −1) b) (6,3); (−2, −1) c) (6, −3); (−2; −1) d) (6, −1); (2; −1) 18. Una recta 𝑙₁ pasa por los puntos 𝐴(3,2) y 𝐵(−4, −6) y otra recta 𝑙₂ pasa por los puntos 𝐶(−7,1) y el punto 𝐷(𝑥, −6). Sabiendo que 𝑙₁ es perpendicular a 𝑙₂, el valor de 𝑥 es: a) −1 b) 3 c) −3 d) 1 19. Dados los vértices de un triángulo 𝐴(2,0), 𝐵(1, −3) y 𝐶(2, −5), el otro extremo de la mediana correspondiente a 𝐵 es: 5 a) (2, − 2) 1 b) (0, 2) 5 c) (2 , 0) 3 d) (2 , 0) 20. La mediatriz del segmento determinado por los puntos 𝐴(−2,3) y 𝐵(4,1) pasa por el punto: a) (2,3) b) (3,4) c) (−2,1) d) (1,2) 21. Determine la pendiente de la recta que pasa por los puntos (−4, −1) y (5,2). a) 2 b) 1 2 c) 1 3 d) 3 22. Determine la pendiente de la recta que pasa por los puntos (−3,3) y (4, −4). a) 2 b) 1 c) 3 d) −1 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] 23. Determine la pendiente de la recta que pasa por los puntos (−5,2) y (−5, −4). a) No existe b) 0 c) 6 d) −2 24. La pendiente de la recta que pasa por los puntos (𝑥, −3) y (−2,6) es 3, el valor de 𝑥 es: a) 2 b) 5 c) 6 d) −5 25. La pendiente de la recta que pasa por los puntos (−3,4) y (1, 𝑦) es cero, entonces el valor de la ordenada es: a) 3 b) 0 c) No existe d) 4 26. Una recta de pendiente −2 pasa por el punto 𝐴(−1,4). Hallar su ecuación en la forma simétrica. 𝑦 a) 𝑥 + 3 = 1 𝑦 b) 𝑥 + 2 = 2 𝑥 c) 𝑦 + 2 = 2 𝑦 d) 𝑥 + 2 = 1 27. Hallar la ecuación de la recta cuya pendiente es −4 y que pasa por el punto de intersección de las rectas 2𝑥 + 𝑦 − 8 = 0 y 3𝑥 − 2𝑦 + 9 = 0. a) 4𝑥 + 3𝑦 − 10 = 0 b) 4𝑥 + 𝑦 − 9 = 0 c) 𝑥 − 2𝑦 − 8 = 0 d) 4𝑥 + 𝑦 − 10 = 0 28. Hallar la ecuación de la mediatriz del segmento cuyos extremos son 𝑃₁(−3,2) y 𝑃₂(1,6). a) 𝑥 + 𝑦 + 3 = 0 b) 𝑥 − 𝑦 + 3 = 0 c) 𝑥 + 𝑦 − 3 = 0 d) 𝑥 + 2𝑦 − 3 = 0 29. Una recta pasa por el punto 𝐴(7,8) y es paralela a la recta que pasa por los puntos 𝐶(−2,2) y 𝐷(3, −4). Su ecuación es: a) 𝑥 + 𝑦 − 82 = 0 b) 6𝑥 + 5𝑦 − 82 = 0 b) c) 𝑥 + 6𝑦 − 82 = 0 d) 6𝑥 − 5𝑦 + 82 = 0 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] 30. Hallar el valor de 𝑘 para que la recta 𝑘²𝑥 + (𝑘 + 1)𝑦 + 3 = 0 sea perpendicular a la recta 3𝑥 − 2𝑦 − 11 = 0. a) 2±√7 3 b) 1+√3 c) 2 31. Sean las rectas paralelas 3𝑥 − 4𝑦 + 8 = 0 y entre ellas es: a) 10 b) 10 1±√2 7 1±√7 3 6𝑥 − 8𝑦 + 9 = 0. La distancia 7 c) 7 7 d) d) 10 32. Hallar los ángulos interiores del triángulo cuyos vértices son los puntos (−2,1), (3,4) y (5, −2). a) 77°28′16′′, 54°9′44′′ y 49°12′59′′ b) 50°28′16′′, 54°9′44′′ y 48°21′59′′ c) 77°28′16′′, 54°9′44′′ y 48°21′59′′ d) 72°28′16′′, 59°9′44′′ y 48°21′59′′ 33. Dos rectas se cortan formando un ángulo de 45°. La recta inicial pasa por los puntos (−2,1) y (9,7) y la recta final pasa por los puntos (3,9) y 𝐴 cuya abscisa es −2. La ordenada de 𝐴 es: a) −3 b) 8 c) −8 d) 0 34. Una recta 𝑙₁ pasa por los puntos (3,2) y (−4, −6) y la otra recta pasa por el punto (−7,1) y el punto 𝐴 cuya ordenada es −6. Hallar la abscisa del punto 𝐴, sabiendo que 𝑙₁ es perpendicular a 𝑙₂. a) 1 b) 5 c) −1 d) −5 35. Encuentre la pendiente y el ángulo de inclinación de una recta paralela a la recta que pasa por los puntos (1, −2) y (3,8). a) 5 y 78°41′24′′ b) 4 y 41°78′24′′ c) 5 y 24°41′78′′ d) 4 y 78°41′24′′ 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] 36. Hallar los ángulos agudos del triángulo rectángulo cuyos vértices son 𝐴(2,5), 𝐵(8, −1) y 𝐶(−2,1). a) 59°18′31′′ y 30°41′20′′ b) 56°18′35′′ y 33°41′24′′ b) c) 24°18′35′′ y 65°41′24′′ d) 56°38′35′′ y 33°21′24′′ 37. La ecuación de una circunferencia es 𝑥² + 𝑦² = 50. El punto medio de una cuerda de esta circunferencia es el punto (−2,4). La ecuación de la cuerda es: a) 𝑥 − 2𝑦 − 10 = 0 b) 𝑥 − 2𝑦 + 10 = 0 b) c) 𝑥 + 2𝑦 + 10 = 0 d) 2𝑥 − 2𝑦 + 10 = 0 38. Un espejo parabólico tiene una profundidad de 12 𝑐𝑚 en el centro y un diámetro en la parte superior de 32 𝑐𝑚. ¿Cuál es la distancia del vértice al foco? a) 16 16 b) − 3 3 c) 3 d) 4 16 39. La ecuación de la hipérbola de centro en el origen, longitud del eje transverso 12 y pasa por el punto (8, 14) es: a) 𝑥² 252 − 𝑦² 36 =1 b) 𝑥² 36 − 𝑦² 252 =1 c) y² 252 − x² 36 =1 d) 𝑥² 252 + 𝑦² 36 =1 40. En una elipse, los radios focales son los segmentos que unen los focos con un punto cualquiera de ella. Las ecuaciones de las rectas que contienen los radios focales correspondientes al punto (2, 3) de la elipse 3𝑥² + 4𝑦 = 48 son: a) 𝑥 − 2 = 0; 3𝑥 − 4𝑦 + 6 = 0 c) 𝑥 − 2 = 0; 3𝑥 + 4𝑦 + 6 = 0 b) 𝑥 + 2 = 0; 3𝑥 − 4𝑦 + 6 = 0 d) 𝑥 + 2 = 0; 3𝑥 + 4𝑦 − 6 = 0 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] 41. La ecuación de una hipérbola con centro en el origen, longitud del eje transverso 8, excentricidad a) 7𝑥² + 9𝑦² = 112 c) 7𝑦² − 9𝑥² = 112 4 3 y con focos sobre el eje 𝑋 es b) 9𝑥² − 7𝑦² = 112 d) 7𝑥² − 9𝑦² = 112 42. El filamento de una lámpara de flash está a 3 8 de pulgadas del vértice del reflector parabólico y se encuentra en su foco. La ecuación del reflector, suponiendo que está dirigido hacia la derecha y su vértice en el origen es a) 3𝑥 − 2𝑦² = 0 b) 3𝑥 + 2𝑦² = 0 c) 2𝑥 − 3𝑦² = 0 d) −3𝑥 − 2𝑦² = 0 43. Una parábola cuyo foco es 𝐹(0, 6) y la ecuación de la directriz es 𝑦 = −6, tiene por ecuación: a) 𝑥² = 24𝑦 b) 𝑦² = 24𝑥 c) 𝑥² = −24𝑦 44. Si la excentricidad de una cónica es a) Parábola b) Elipse d) 𝑦² = −24𝑥 5 , entonces se trata de una 2 c) Circunferencia d) Hipérbola 45. La ecuación de la circunferencia con centro en el origen y que pasa por (−3, 4) es a) 𝑥² + 𝑦² = 16 b) 𝑥² + 𝑦² = 25 c) 𝑥² + 𝑦² = 9 d) 𝑥² − 𝑦² = 25 46. De los siguientes puntos el único que se encuentra sobre la circunferencia 𝑥² + 𝑦² = 1 es a) (√2, −1) 1 √3 ,− ) 2 2 b) ( c) (1, 1) d) (−1, −1) 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] 47. Si los extremos de un diámetro de una circunferencia con centro en el origen son (√5, 2) y (−√5, −2), la ecuación de dicha circunferencia es a) 𝑥² + 𝑦² = 9 b) 𝑥² + 𝑦² = 3 c) 𝑥² + 𝑦² = 16 d) 𝑥² − 𝑦² = 9 48. Si (2, 2) es el punto medio de una cuerda en la circunferencia 𝑥² + 𝑦² = 16, la ecuación de dicha cuerda es a) 2𝑥 + 𝑦 − 4 = 0 b) 𝑥 + 𝑦 − 4 = 0 c) 𝑥 − 𝑦 − 4 = 0 d) 𝑥 − 𝑦 + 4 = 0 49. La ecuación de la circunferencia con centro en el origen y que pasa por el punto de intersección de las rectas 3𝑥 + 3𝑦 = 15 y 2𝑥 − 2𝑦 = −2 es a) 𝑥² − 𝑦² = 13 b) 𝑥² + 𝑦² = 13 c) 𝑥² + 𝑦² = 9 d) 𝑥² + 𝑦² = 11 50. La ecuación de una elipse con focos en (±√5, 0) y longitud del eje mayor igual a 6 es a) 9𝑦² − 4𝑥² = 36 b) 4𝑥² + 9𝑦² = 36 c) 9𝑥² + 4𝑦² = 36 d) 4𝑥² − 9𝑦² = 36 51. La ecuación de una parábola que tiene su foco en el punto 𝐹(2, 0) y su directriz es la recta de ecuación 𝑥 = −2 es a) 𝑦² = −8𝑥 b) 𝑦² = 8𝑥 1 1 c) 𝑦² = − 8 𝑥 d) 𝑦² = 8 𝑥 52. Dada la parábola que tiene por ecuación 𝑥² = −6𝑦, encontrar las coordenadas del foco y la ecuación de la directriz 3 3 a) 𝐹 (0, − 2) y 𝑦 = − 2 3 3 c) 𝐹 (2 , 0) y 𝑥 = − 2 3 b) 𝐹 (0, − 2) 3 3 y 𝑦=2 3 d) 𝐹 (− 2 , 0) y 𝑥 = 2 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] 53. Las coordenadas del foco y la ecuación de la directriz de la parábola 𝑥 = 1 − 4 𝑦² son respectivamente a) (1, 0) y 𝑥 = 1 c) (0, −1) y 𝑥 = −1 b) (−1, 0) y 𝑥 = 1 d) (1, 0) y 𝑥 = −1 54. La ecuación de la parábola con vértice en el origen y foco (−√2, 0) es a) 𝑦 2 = 4√2𝑥 c) 𝑦² = −4√2𝑥 b) 𝑥 2 = 4√2𝑦 d) 𝑥² = −4𝑦 55. El foco y la directriz de la parábola 2𝑦 − 𝑥² = 0 son respectivamente 1 c) ( , 2 1 1 a) (0, 2) 1 ) y 𝑦= 2 1 b) ( , 0) y 𝑦 = 2 y 𝑦 = −2 2 1 −2 1 1 d) (0, 2) y 𝑦 = − 2 56. La ecuación de la parábola cuyo foco es (4, 0) y directriz 𝑥 = −4 es a) 𝑦² = 16𝑥 b) 𝑦² = −4𝑥 c) 𝑦² = 4𝑥 d) 𝑦² = −16𝑥 57. La ecuación de la parábola cuyo eje de simetría es el eje 𝑌, vértice en el origen y que pasa por (−2, −2) es a) 𝑥 2 = 2𝑦 b) 2𝑥 2 = −𝑦 c) 𝑥 2 = −2𝑦 d) 𝑥 2 = −𝑦 58. Si la longitud del eje mayor es 16 y la distancia focal es 8, entonces la ecuación de la elipse con eje focal en el eje 𝑌 es a) 𝑥² 48 − 𝑦² 64 =1 b) 𝑥² 48 + 𝑦² 64 =1 c) 𝑥² 64 + 𝑦² 48 =1 d) 𝑥² 64 − 𝑦² 48 =1 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] 4 59. Si la excentricidad es 5 y la distancia focal es 16, la ecuación de la elipse con eje focal en el eje 𝑋 es a) 𝑥² 100 + 𝑦² 36 =1 b) 𝑥² 36 + 𝑦² 100 =1 c) 𝑥² 𝑦² − 100 36 =1 𝑥² d) 16 + 𝑦² 36 =1 60. La excentricidad de la elipse 2𝑥² + 4𝑦² = 8 es a) √2 2 b) √3 2 c) √3 3 √2 d) − 2 61. El único punto que no pertenece a la elipse con focos sobre el eje 𝑋, eje mayor 20 y eje menor 10 es: 5√ 3 ) 2 a) (−5, b) (5, 5√ 3 ) 2 2 √3 ) 2 c) (5, 5√ 3 d) (5, − 2 ) 62. La ecuación de la elipse que pasa por (3, 2√3), con vértice correspondiente al eje menor (0, 4) es a) 𝑥² 16 + 𝑦² 36 =1 b) 𝑥² 36 − 𝑦² 16 =1 c) 𝑥² 36 𝑦² + 16 = −1 d) 𝑥² 9 + 𝑦² 36 =1 63. Los focos de la hipérbola 4𝑥² − 9𝑦² = 36 son a) (0, ±√13) b) (±13, 0) c) (0, ±13) d) (±√13, 0) 64. Las asíntotas de la hipérbola 25𝑦² − 16𝑥² = 400, son: 4 a) 𝑦 = ± 5 𝑥 4 5 b) 𝑥 = ± 5 𝑦 5 c) 𝑦 = ± 4 𝑥 d) 𝑥 = ± 4 𝑦 3 65. La ecuación de la hipérbola con asíntotas 𝑦 = ± 2 𝑥, es a) 𝑥² 4 − 𝑦² 9 =1 b) 𝑥² 2 − 𝑦² 3 =1 c) 𝑥² 4 + 𝑦² 9 =1 d) 𝑥² 9 − 𝑦² 4 =1 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] 66. Las coordenadas de los vértices de una hipérbola son (±1, 0) y sus focos (±2, 0). Entonces su ecuación es a) 𝑥² 1 − 𝑦² 3 =1 b) 𝑥² 1 + 𝑦² 3 =1 c) 𝑥² 3 − 𝑦² 1 =1 d) 𝑥² 1 − 𝑦2 3 = −1 67. La excentricidad de la hipérbola 𝑦² − 4𝑥² = 4 es √5 a) − 2 b) 2 5 2 c) − √ √2 d) √5 2 68. El foco y la directriz de una parábola cuya ecuación es 𝑦² = 36𝑥 son respectivamente: a) 𝐹(−9,0) y 𝑥 = 9 c) 𝐹(0, −9) y 𝑦 = 9 b) 𝐹(9, 0) y 𝑥 = −9 d) 𝐹(0,9) y 𝑦 = −9 MINISTERIO DE EDUCACIÓN DOSIFICACIÓN DE CONTENIDOS DE MATEMÁTICA CURSO DE REFORZAMIENTO ESCOLAR A ESTUDIANTES DE QUINTO AÑO ENCUENTRO 1 2 3 4 CONTENIDO ANALÍTICO UNIDAD I: ARITMETICA. Operaciones con fracciones aritméticas: Suma, Resta, Multiplicación, División y Potenciación. Problemas de aplicación. Notación Científica. Definición. Operaciones con expresiones numéricas en notación científica. Conversión de los diferentes sistemas de Medidas: Longitud, superficie, capacidad, volumen y peso. Problemas de aplicación. Razones y Proporciones .Porcentajes, Interés simple. Interés compuesto. Regla de tres simple y compuesta (Directa e Inversa). Problemas de aplicación. UNIDAD II: ALGEBRA. Productos Notables y Factorización (de acuerdo al programa vigente del MINED) 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] Simplificación algebraicas. y operaciones con fracciones 5 Potenciación y radicación de expresiones algebraicas: Propiedades, Operaciones usando potencias y radicales y Racionalización de fracciones algebraicas 6 Resolución de ecuaciones en una variable: Lineales, Cuadráticas y reducibles a ellas. 7 Relación entre las raíces y los coeficientes de la ecuación cuadrática (Teorema de Vieta, uso del discriminante). Sistemas de ecuaciones lineales en dos y tres variables. Problemas de aplicaciones Definición y propiedades de desigualdades: Intervalos, Desigualdades lineales, Desigualdades cuadráticas y cúbicas (factorizable), Desigualdades racionales y Desigualdades con valor absoluto 8 9 UNIDAD III: GEOMETRIA EUCLIDIANA Conceptos generales: puntos, rectas, plano, relación “estar entre”, segmento, rayo, semirrecta, ángulo, perpendicularidad, paralelismo, rectas paralelas cortadas por una secante Polígonos regulares e irregulares. Problemas de aplicación. 10 Puntos y rectas notables de un triángulo. Congruencia de triángulos. Criterios de Congruencia 11 Teorema fundamental de la proporcionalidad y teorema de Thales, Semejanza de triángulos y Criterios fundamentales Relaciones métricas en un triángulo rectángulo (Teoremas: Pitágoras, Altura y de los Catetos) Problemas de aplicación 12 Circunferencia: Radio, diámetro, cuerda, arco, rectas tangentes y secantes, ángulos (Central, Inscritos, semi inscritos, circunscritos, interiores y exteriores). Relaciones métricas en una 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] circunferencia. Problemas de aplicación. Área de regiones planas: triángulo, cuadrilátero, círculo y polígono regular. Área de sectores circulares y sectores sombreados. Problemas de aplicación 13 14 Definición y propiedades de cuerpos sólidos, áreas laterales, totales y volúmenes de cuerpos sólidos: Prisma, cono, cilindro, pirámide y esfera. (No truncados). Problemas de aplicación. UNIDAD IV: FUNCIONES DE UNA VARIABLE REAL Definición y propiedades de las funciones en general. Comportamiento analítico y grafico de funciones Función constante. Función lineal. Función cuadrática, Función valor absoluto. Función raíz cuadrada. Función seccionada. Problemas de aplicación. 15 Definición y propiedades de las Funciones exponenciales y logarítmicas. Ecuaciones exponenciales y logarítmicas. Problemas de aplicación. 16 Razones trigonométricas. Conceptos, definiciones, dominio, recorrido y gráficas de las tres funciones trigonométricas fundamentales (Seno, coseno y tangente). Identidades y ecuaciones trigonométricas. (Ángulos medios, sencillos y dobles, potencia hasta grado dos). 17 Resolución de triángulos rectángulos y oblicuángulos. Problemas de aplicación UNIDAD V: GEOMETRIA ANALITICA PLANA Elementos básicos de la geometría analítica en el plano cartesiano: Distancia entre dos puntos. División de un segmento en una razón dada. Coordenadas del punto medio de un segmento. 18 19 La recta: Pendiente de una recta. Ecuaciones de la recta: Punto-pendiente, cartesiana, pendienteordenada, simétrica y general. Ángulo entre rectas. Condiciones de paralelismo y perpendicularidad. Distancia de un punto a una recta. Distancia entre dos rectas paralelas. 20 Estudio y determinación de los elementos, tipos de 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected] ecuaciones y gráficas de las cónicas con centro en el origen: Circunferencia, Parábola, Elipse e Hipérbola. Problemas de aplicación Nota: Se recomienda realizar una evaluación al finalizar cada unidad desarrollada. El tipo de prueba deberá simular la estructura de un examen de admisión (Selección múltiple). En la unidad de Funciones se recomienda abordar los conceptos, definiciones y propiedades. Características de las funciones de todos los tipos (algebraicas y transcendentes) según su comportamiento (Dominios, intercepto con los ejes coordenados, paridad, monotonía (Creciente y decreciente), asíntotas, recorridos y gráficas). 2016: VAMOS ADELANTE!EN BUENA ESPERANZA,EN BUEN CORAZÓN EN VICTORIAS CRISTIANA, SOCIALISTA, SOLIDARIA! Ministerio de Educación Dirección General de Educación Secundaria - Teléf:22538490 Ext:167 y 149 EMAIL: [email protected]
© Copyright 2026