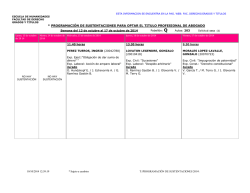
Modelo de asignación de costos para la expansión de la
Pontificia Universidad Católica de Chile
Escuela de Ingeniería
Departamento Ingeniería Eléctrica
Modelo de asignación de
costos para la expansión de la
transmisión: aproximación a la
teoría del kernel
Alumno: Francisco J. Evans M.
Profesor Guía: Hugh Rudnick V. D.W.
Profesor Supervisor: Juan Zolezzi C.
INTRODUCCIÓN
l Características de la Transmisión
l Asignación de Costos de Transmisión
n
Problema
lNo existe un método preferido
l Teoría de Juegos
n
Kernel
Interacción entre agentes
Asignación de Costos de la Expansión
Medio centralizado
1
TEORÍA DE JUEGOS
n
n
Función Característica V (_)
Racionalidades
lGrupal
N
lIndividual
lColectiva
v(N) = ∑Xi
i=1
Xi ≥V ({}
i)
∑X
i
Imputación
≥ V (S) ∀i∈ S ∀S ⊂ N
l Teoría del Exceso
e( S ) =
Núcleo
∀i ∈ N
∑X
∀ i∈S
i
Kernel
− V (S )
KERNEL
l Máximo Excedente
S AB = MaxS / A∈S , B∉Se(S)
l Equilibrio
S AB = S BA
S AB > S BA
S AB > S BA
y X B = V (B)
y X A = V (A)
l Fases de Comunicación
n
n
Centralizado
Descentralizado
Asimetrías de Información
2
KERNEL
lVentajas
n
n
n
n
El Kernel pertenece al núcleo (si existe), cumpliendo
así con las 3 racionalidades de coalición.
Si no existe núcleo, el Kernel no involucra al agente
que no se coaliciona, asignándole el costo de
participar solo en la expansión (Stand
(Stand Alone Costs
Costs).
).
La asignación del Kernel, corresponde a un equilibrio
de fuerzas, entre los agentes pertenecientes a una
coalición, por lo tanto, es justa desde el punto de
vista de la negociación.
El Kernel posee una estructura de formación de
coaliciones, que es transparente en un medio de
información perfecta.
KERNEL
l Desventajas
n
n
n
En el Kernel, las asignaciones de costos dependen de la
estructura de coalición que se realice. Por lo tanto, es
dependiente del proceso de formación de coaliciones.
Del punto anterior, se deduce además que en un juego con
núcleo, el Kernel no es único.
La formación de coalición en el Kernel, requiere de una
información perfecta entre los agentes, pues depende del
exceso que tengan las distintas coaliciones. Si dicha información
no es perfecta (asimetría de información), la asignación es
sesgada. Transformándose la información en una ventaja
competitiva, dentro de un medio de cooperación (idea del dilema
del prisionero).
l ¿Qué sucede en una Transmisión Centralizada?
3
MODELO DE ASIGNACIÓN DE
COSTOS
l Orígenes del modelo
n
n
n
Expansión óptima
¿Cómo distribuir los Costos?
Diversos intereses de los agentes
Uso económico de la red
lPotencia
lEnergía
n
Esta se eligió
Se afirma
lManera más equitativa de distribuir costos
n
n
Uso económico por potencia
Los usos máximos no coincidentes
MODELO DE ASIGNACIÓN DE
COSTOS
l Desarrollo del modelo
n
Cálculo Flujo DC
lCond. Físicas de la Red
lConsumo
lGeneración
n
Cálculo Parámetros GGDF
lCada línea de expansión
Cada
hora
del
día
Espectro
de
Flujos
de
cada
coalición
4
MODELO DE ASIGNACIÓN DE
COSTOS
l Desarrollo del modelo (cont.
(cont.))
n
Se define concepto de $/MW
lCada línea de expansión
Costo _ línea
Flujo _ max_ real _ linea
$ / MW =
n
n
Obtención de condiciones de juego
Cálculo del Kernel
lBeneficios a agentes en contraflujo
Menor asignación de Costos
No pago de la expansión (mejor caso)
n
n
EJEMPLO INTUITIVO
l Sean dos agentes (A y B), que utilizan dos líneas de
expansión (1 y 2), cuyo costos es de $ 50 cada una.
Linea expansión 1
60
40
Flujo Máx (MW)
22
20
18
16
14
12
8
10
2
0
6
0
4
MW
20
-20
-40
-60
CoaIición
Exp. 1
Exp. 2
C(1)
50
60
C(2)
50
50
C(1;2)
30
90
Horas del dia
Flujo Agente A
Flujo Agente B
Flujo Total
Linea expansión 2
100
MW
80
60
40
20
0
1
3
5
7
9
11
13
15
17
19
21
23
Horas del dia
Flujo Agente A
Flujo Agente B
Flujo Total
5
EJEMPLO INTUITIVO
l Se determinan los $/MW para cada línea
de expansión.
n
Línea expansión 1
$ / MW
→
n
Costo _ línea
50 5
=
=
Flujo _ max_ linea _ real 30 3
Línea expansión 2
$ / MW
→
Costo_ línea
50 5
=
=
Flujo _ max_ linea _ real 90 9
EJEMPLO INTUITIVO
l Condiciones de juego
Costo ($) Stand Alone
Costs
Exceso ($)
Ahorro de Costos
Coalición
Exp. 1
Exp. 2
Exp. 1
Exp. 2
C(1)
-83.33
-33.33
0
0
C(2)
-83.33
-27.77
0
0
C(1;2)
-50
-50
116.66
11.11
6
EJEMPLO INTUITIVO
l Prorrata utilizando Kernel
Única coalición {A,B
{A,B}}
n Análisis de Máximos Excesos
S AB : e({A}) = X { A} − V ({ A}) = X { A} − 0
n
S AB = Max (e ({ A})) = X { A } − 0
S BA : e ({B}) = X { B } − V ({B}) = X {B } − 0
S BA = Max ( e ({ B})) = X { B} − 0
EJEMPLO INTUITIVO
Expansión 1
n
n
(i) S AB = S BA
→ X A = X B
(iiii)) X + X = 116.66
A
B
Expansión 2
S AB = S BA
→ X A = X B
X A + X B = 11.11
7
EJEMPLO INTUITIVO
SX
Costo Stand Alone
($)
Asig. Ahorro de
Costos ($)
Asig. Indiv. ($)
Exp. 1
Exp. 2
Exp. 1
Exp. 2
Exp. 1
Exp. 2
- 83.33
- 33.33
58.33
5.55
- 25
- 27.78
- 83.33
- 27.77
58.33
5.55
- 25
- 22.22
S
{1}
{2}
X
- 52.78
- 47.22
CONCLUSIONES
l El modelo presenta un conjunto de variables
económicas y técnicas, que se pueden ajustar a la
problemática de expansión de cualquier sistema
eléctrico.
l El desarrollo del modelo para cada línea de expansión,
involucra un mini juego cooperativo con características
de juego independientes de otras expansiones.
l Se “premia” a los agentes que aportan contraflujos en un
tramo de expansión cualquiera.
l La forma de determinar las condiciones de juego,
contempla un análisis dinámico del uso de las líneas
expandidas
8
CONCLUSIONES
l La asignación de costos presenta características de
equilibrio y transparencia en un sistema de transmisión
centralizado.
l La asignación de costos, puede ser realizada a cualquier
agente que hace uso del sistema de transmisión.
l El modelo es transparente y justo en la medida en que
los agentes involucrados tengan información perfecta de
sus pares.
Modelo de asignación de
costos para la expansión de la
transmisión: aproximación a la
teoría del kernel
9
© Copyright 2026