1. 2. 3. 4. Elimine signos de agrupación y resuelva: 5.
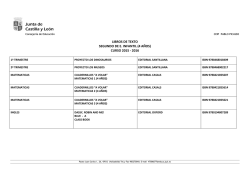
COLEGIO COLOMBO BRITANICO DEPARTAMENTO DE MATEMATICAS REPASO GENERAL MATEMATICAS GRADO 9 1. 2. 3. 4. Elimine signos de agrupación y resuelva: 5. COLEGIO COLOMBO BRITANICO DEPARTAMENTO DE MATEMATICAS REPASO GENERAL MATEMATICAS GRADO 9 6. 7. 8. Escriba una ecuación y resuélvala como solución del siguiente problema: 9. 10. Clasifique cada número en uno o más de los conjuntos dados. Para ello coloque una marca en la casilla que corresponda. N Z Q I R 2.555… 4.2 0 11. Escriba en cada caso dos números que cumplan la condición, si es posible: No. 1 Racional entre 0 y 1 Racional natural Real no positivo Irracional negativo No. 2 COLEGIO COLOMBO BRITANICO DEPARTAMENTO DE MATEMATICAS REPASO GENERAL MATEMATICAS GRADO 9 12. Indique falso (F) o verdadero (V) según considere: Proposición Consideración 13. Indique el número racional que se representa en la posición dada: Posición en la recta 14. Escriba el símbolo Número correspondiente , o entre los corchetes según sea el caso. 15. Resuelva la siguiente operación: 16. Elimina signos de agrupación y opera términos semejantes: 17. Resuelva cada uno de los siguientes problemas: a. Uno de los lados de un rectángulo mide – y el otro lado mide ¿Cuánto mide su perímetro? b. A la suma de de con con réstele el producto COLEGIO COLOMBO BRITANICO DEPARTAMENTO DE MATEMATICAS REPASO GENERAL MATEMATICAS GRADO 9 18. Utilice el triángulo de Pascal para expandir: a. b. 19. Encuentre un polinomio que represente el volumen de la figura: 20. Encuentre el cuarto término en el desarrollo . 21. Encuentre el tercer término en el desarrollo de 22. Represente todos los números racionales dados en una misma recta numérica. 23. Ordene de mayor a menor: 24. Resuelva y simplifique: a. b. c. COLEGIO COLOMBO BRITANICO DEPARTAMENTO DE MATEMATICAS REPASO GENERAL MATEMATICAS GRADO 9 25. Elimina signos de agrupación y opera términos semejantes: 1 3 3 3 a. 2 4 5 4 1 1 1 b. 7 x y 2 z 5 x 9 y 5 z 3 z 2 3 2 26. Resuelva cada uno de los siguientes problemas: a. El lado de un cuadrado viene representado por el polinomio . Encuentre un polinomio que represente su perímetro y otro que represente el área del cuadrado. b. A la suma de con réstele el producto de con 27. Encuentre un polinomio que represente el área de la figura: 28. Usando el método largo resuelva la siguiente división: 29. Factorice cada expresión: a. b. c. d. e. f. 30. Simplifique: x y 2 2 x -y xy - y 2 1+ a. a+b a-b b. a+b 1a-b 1+ c. 2 3 x + 6x + 5 x - 2 x - 2x · + 2 2 2 x - 5x + 4 x - 4 x - 4x COLEGIO COLOMBO BRITANICO DEPARTAMENTO DE MATEMATICAS REPASO GENERAL MATEMATICAS GRADO 9 31. Resuelva las siguientes ecuaciones: a. x2 4 x 3 0 b. c. x3 x 2 4 x 4 0 x3 4 x 0 d. x(x+1)=2 32. Resuelva los siguientes problemas: a. Determine dos números impares consecutivos cuyo producto sea 195. b. Un lado de un triángulo rectángulo es 3 pies más largo que el otro lado. La hipotenusa es de 15 pies. Encuentra las dimensiones del triángulo. c. El producto de dos números positivos es 60. Encuentra los dos números, siendo uno de ellos mayor por 4. d. Un rectángulo tiene lados de una longitud de x+5 y x−3 . ¿Qué número es xsi el área del rectángulo es 48? De acuerdo al siguiente dibujo (L1 // L2) completa lo que se solicita: L1 L2 m q n r p u s t Ángulos internos: ............................ Ángulos externos: ............................ Alternos Internos: ............................ Alternos Externos: ............................ Conjugados Internos: .......................... Conjugados Externos: ......................... 33. A partir del gráfico que a continuación se muestra relaciona las columnas de forma conveniente: (L1 // L2) L1 c d b a L2 g f h e COLEGIO COLOMBO BRITANICO DEPARTAMENTO DE MATEMATICAS REPASO GENERAL MATEMATICAS GRADO 9 a) a y b ( ) Ángulos alternos Externos b) f y d ( ) Ángulos Conjugados Internos c) b y g ( ) Ángulos Internos ( ) Ángulos Conjugados Externos d) c y f 34. Calcular “x” a partir del gráfico mostrado (L1 // L2). Si: m∢AOB = 2m∢BOC. B a) 50º b) 60º L1 A O C c) 120º d) 130º x+ 10º e) 115º L2 35. Una pareja de ángulos conjugados entre paralelas están en la relación de 3 a 7 Calcular el complemento del que se pueda. a) 19º d) 36º b) 18º e) 72º c) 54º 36. Dos ángulos alternos entre paralelas miden: 2x+20º y 3x 10º. Calcular el suplemento de la suma de las medidas de ambos. a) 100º d) 120º 37. b) 20º e) 130º c) 150º Calcular “x” a partir del gráfico mostrado. x + 10º a) 150º L1 b) 130º c) 30º d) 120º e) 140º 38. 10º L2 20º Del gráfico, calcular “x” (L1 // L2).. a) 55º 45º L1 b) 115º c) 120º d) 65º e) 125º L2 70º xº COLEGIO COLOMBO BRITANICO DEPARTAMENTO DE MATEMATICAS REPASO GENERAL MATEMATICAS GRADO 9 39. Conteste verdadero o falso: a. Dos rectas perpendiculares a una tercera son paralelas entre sí. b. Dos rectas paralelas a una tercera son perpendiculares entre sí. c. Si una recta es paralela a un plano, entonces la recta es paralela a todas las rectas del plano. d. Si y son tres rectas tales que y e. Si y son tres rectas coplanarias tales que , entonces . y , entonces . f. Si dos rectas son coplanarias, entonces son paralelas. g. Si dos segmentos son coplanarios y no tienen ningún punto común, entonces son paralelos. h. Si un plano contiene una de dos rectas paralelas, entonces el plano contiene la otra recta. i. Si se cortan dos rectas mediante una secante, entonces los ángulos alternos externos son congruentes. j. Si se cortan dos rectas mediante una secante, se forman exactamente cuatro parejas de ángulos alternos internos. 40. Determine el valor de x en cada proporción: a. b. c. d. 41 . C a l c ul ar l a al t ura d e un edi fi cio q ue p ro yec ta una so mb ra de 6 .5 m a la m i s ma hor a q ue un pos te de 4 .5 m de alt ura d a una so mb ra de 0. 90 m.
© Copyright 2026