1. No category

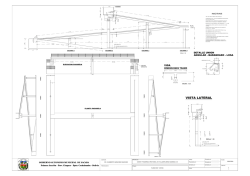
Diseño en Concreto II
2.
2.1
LOSAS EN DOS DIRECCIONES
INTRODUCCIÓN
La historia de las losas se remonta a los romanos, grandes constructores empíricos, pues no se
conoce a la fecha memorias de cálculo o diseño. Trabajaron mucho el arco, y se sabe que
incluso usaron varillas de hierro en la losa del techo de los baños de Caracalla, también usaron
concreto con agregado liviano para construir el domo del Panteón. Sozen y Siess, dicen que la
primera losa plana moderna fue construida por Turner en1906 en Minneapolis, en el mismo año
Maillart construyo una en Suiza. La losa Turner tenía las columnas anchas en el nudo y
refuerzo de acero en direcciones ortogonales diagonales. Turner baso su diseño en el análisis
incompleto de la teoría de placas de H.T. Eddy. En este período se uso la teoría de la viga
análoga cruzada, lo que causo un error, ya que solo parte de la carga era llevada en cada
dirección. En 1914 J.R. Nichols, uso la estática para calcular el momento total en la losa. Esta
es la forma básica del diseño actual de losas.
Las losas pueden estar apoyadas sobre vigas de concreto reforzado, en muros de mampostería o
de concreto reforzado, en elementos de acero estructural, en forma directa por columnas o
sobre el terreno. Si se apoyan en dos lados opuestos, se dice que la losa trabaja en una
dirección. Si la losa se apoya en los cuatro lados, se dice que trabaja en dos direcciones.
Las losas de concreto se pueden sostener directamente por columnas, y se utilizan cuando las
luces no son muy largas y las cargas no son pesadas. La construcción del tipo losa plana,
tampoco incluye vigas pero incorpora una región con un sobreespesor de losa alrededor de la
columna (drop-panel o ábacos) y emplea con frecuencia columnas con forma acampanada en la
parte superior, ambos son mecanismos para reducir los esfuerzos generados por cortante y
flexión negativa alrededor de las columnas. Por lo general se llaman paneles con ábacos o
sobreespesores y capiteles de columna. También se puede usar la losa con viguetas en dos
direcciones o losa reticular, conocida como reticular celulado se parece a la losa con ábacos.
Con el fin de reducir la carga muerta de la construcción con losas macizas, se forman vacíos
mediante la utilización de casetones, construidos en metal, fibra de vidrio, bloque de cemento,
esterilla o icopor. Se obtiene así una construcción nervada en dos direcciones. Generalmente,
los aligeramientos se omiten cerca de las columnas de manera que se forme una losa maciza o
ábaco, para resistir mejor los momentos y cortantes en estas áreas.
Muchas losas están apoyadas continuamente sobre el terreno, como las de carreteras, pistas de
aeropuerto y pisos de bodega. En general se construye sobre una base de rocamuerta o de grava
bien compactada para asegurar un apoyo uniforme y permitir un drenaje adecuado del subsuelo.
El acero de refuerzo de las losas se coloca principalmente en dirección paralela a la superficie
de la losa. Las losas de concreto reforzado se diseñan casi siempre para cargas uniformemente
distribuidas sobre la losa, limitados por las vigas de apoyo o por los ejes entre centros de
columnas. Las grandes cargas concentradas requieren vigas de apoyo.
Javier Fajardo
59
Diseño en Concreto II
2.2
LOSAS MACIZAS
Placa sólida de concreto de espesor constante con o sin drop-panel (Ábaco) para mejorar
cortante y/o con capiteles en las columnas. Si no tiene drop-panel se llama losa plana. El
espesor varía entre 10 y 25 cm. Es utilizada para luces entre 5 y 6 m. Si se postensiona, las
luces se pueden aumentar hasta en un 50%.
Ventajas:
− Es el sistema de mínimo espesor, reduciendo la altura del edificio, menor costo y se puede
poner un piso adicional donde la altura del edificio este restringida.
− Se adapta a cualquier localización de los apoyos, ya sean columnas o muros.
− El cielo raso puede ser pintado directamente.
− Su mayor utilidad es en edificios de apartamentos
Desventajas:
− Luces muy cortas, lo que implica muchos apoyos.
− Produce estructuras pesadas aumentando el costo de las columnas y la edificación.
− Presentan deflexiones grandes debido a la relación h/l baja, el creep es un problema.
− Es sensible al tamaño y localización de los huecos.
2.3
LOSAS ALIGERADAS
Placa delgada fundida simultáneamente con viguetas de poco espesor, espaciadas a corta
distancia, pueden ir en una o dos direcciones. Se puede considerar como una losa maciza a la
que se le quita el concreto por debajo del eje neutro. Los huecos se pueden hacer de cualquier
material permanente o removible, como casetones de esterilla, metálicos, bloque de cemento o
esterilla recubiertos de plástico, polipropileno, etc. para aumentar los reusos. Dependiendo del
material puede dar de una vez el acabado del cielo. La mano de obra es costosa por la
carpintería de la formaletería, encareciendo la obra. Se usa para luces de 7 a 14 m máximo, con
postensando se aumentan las luces en 50%. Se usa mucho en edificios de oficinas y comercio.
Ventajas:
− Sistema para luces medianas a grandes
− Es relativamente liviano
Desventajas.
− No es apropiado para distribuciones no ortogonales de columnas y muros.
− Hay que instalar cielo raso.
− El aligeramiento es costoso
− Hay dificultad para el paso de ductos grandes o buitrones.
2.4
VIGA Y PLACA
Losa de 10 a 15 cm de espesor soportado por vigas fundidas monolíticamente con la placa,
espaciadas entre 3 y 6 m. El sistema esta limitado por la altura que se le pueda dar a las vigas,
de 1/15 a 1/20 de la luz.
Javier Fajardo
60
Diseño en Concreto II
Ventajas:
− Sistema para luces grandes
− Se adapta fácilmente a huecos grandes como los de escaleras, ascensores, etc.
− Se adapta a cualquier planta del edificio
− Pesa relativamente poco
Desventajas:
− Necesita mucha altura
− No hay formaleta estándar, aunque la que se utilice puede tener reusos bajando el costo.
Fuente: Reinforced Concrete. MacGregor, James, G.
Javier Fajardo
61
Diseño en Concreto II
2.5
LOSAS EN DOS DIRECCIONES APOYADAS EN LOS BORDES
Son losas rectangulares que guardan ciertas proporciones y están sostenidas de tal forma que se
obtiene una acción en dos direcciones. Cuando se aplica la carga, estas losas se deflectan para
conformar una superficie cóncava en forma de plato. La losa tiene curvatura en las dos
direcciones principales y, como los momentos son proporcionales a las curvaturas, también hay
momentos en las dos direcciones. Para resistir estos momentos, la losa debe reforzarse en las
dos direcciones con barras de acero para tomar una parte de la carga en cada dirección.
El tipo más simple de losa en dos direcciones es la que esta soportada en sus cuatro bordes por
vigas monolíticas de concreto relativamente altas y rígidas (C13.9 del NSR-98), por muros o
por vigas de acero. Esta losa está formada por franjas paralelas en cada una de las dos
direcciones perpendiculares. Parte de la carga es tomada por una de estas franjas ortogonales y
se transmite a los bordes, y el resto de la carga lo toma el otro conjunto.
Fuente: Diseño de Estructuras de Concreto. Nilson, Arthur H.
la: luz corta
lb: luz larga
w: carga uniformemente distribuida por unidad de área
Cada una de las dos franjas actúa como una viga simple cargada uniformemente por la parte de
la carga w que le corresponde. Ya que las franjas son parte de la misma losa monolítica, la
deflexión en los puntos de intersección debe ser la misma.
4
5w a l a4 5w b l b
=
384EcI 384EcI
wa: Fracción de la carga w que se transmite en la dirección corta
wb: Fracción de la carga w que se transmite en la dirección larga
4
w a lb
=
4
w
b la
Javier Fajardo
La mayor parte de la carga se transmite en la dirección corta.
62
Diseño en Concreto II
En la figura anterior las franjas cerca de los bordes tienden a torcerse, y la torsión absorbe parte
de la carga, por esto los momentos flectores en losas elásticas son menores que las losas con
franjas independientes. El alabeo de las franjas produce esfuerzos ocasionados por la torsión y
flexión, los cuales son mayores cerca de las esquinas, es decir que la carga de la losa la absorben
los momentos y el torque, por eso los momentos son menores cerca a los bordes en losas en dos
direcciones.
Para una losa cuadrada wa = wb = w/2, el momento máximo será:
(w/2)l 2
= 0.0625wl 2
8
Este momento se ha medido en una losa real y tiene un valor de 0.048wl2, que es menor que el
calculado con estática, por lo tanto la torsión toma el 23% del momento.
Los mayores momentos ocurren donde la curvatura es mayor, ya que k = M/EI. El acero de la
franja central por lo tanto llegará primero a la fluencia, y cuando esta ya no pueda soportar carga,
las franjas adyacentes lo harán. Esta redistribución inelástica continuará hasta que en un área
relativamente grande de la porción central de la losa, todos los aceros en ambas direcciones estén
en fluencia, entonces se presentará la falla.
Por lo tanto las losas no necesitan diseñarse para el máximo momento absoluto en cada una de
las dos direcciones (como en el valor de 0.048w12), sino para un momento promedio menor en
cada una de las dos direcciones en la porción central de la losa.
La curvatura y por lo tanto el momento en la franja corta cerca al borde, es menor que en la franja
central. En consecuencia, se presenta una variación del momento de la luz corta en la dirección
larga de la luz, siendo mayor el momento en la franja central de la dirección corta. En conclusión
la losa ideal para armado en dos direcciones es la losa cuadrada, y no es conveniente cuando
tiende a volverse rectangular, cuando la relación lado largo a corto m>2.0, lo mejor es hacer una
losa en una dirección.
2.6
ANÁLISIS MEDIANTE EL MÉTODO DE LOS COEFICIENTES.
Desarrollado por Marcus en 1963 y según el C.13.9.1 del NSR-98:
C.13.9.1- ALCANCE - El procedimiento de la presente sección solo es aplicable a losas cuyos paneles están
apoyados en sus cuatro bordes sobre muros o sobre vigas rígidas ante deflexiones verticales. Una viga se considera
rígida ante deflexiones verticales, para efectos de la aplicación del presente método, cuando el parámetro α es mayor
o igual a 0.50, o en losas macizas cuando la altura de la viga es mayor o igual a tres veces el espesor de la losa.
Cuando se trate de losas nervadas, el mínimo número de nervaduras en cada dirección debe ser mayor o igual a seis,
para poder aplicar el método de esta sección.
El método debe usarse en vigas cuya altura total no sea menor que aproximadamente 3 veces el
espesor de la losa. Todos los sistemas de losas de concreto reforzado en dos direcciones deben
analizarse y diseñarse de acuerdo con un método unificado o Método de Diseño Directo según el
Javier Fajardo
63
Diseño en Concreto II
C.13.6 del NSR-98. Para sistemas que no cumplen los requisitos que permiten realizar el análisis
mediante el método de diseño directo, los ingenieros utilizan el método 3 del Código ACI 318 de
1963 o según el NSR-98 diseñarse con el C.13.9 LOSAS EN DOS DIRECCIONES APOYADOS
SOBRE MUROS O VIGAS RÍGIDAS y el C13.4 – DEFINICIONES Y PROCEDIMIENTO DE
DISEÑO PARA LOSAS EN DOS DIRECCIONES.
El método utiliza tablas de coeficientes basados en análisis elásticos pero también tienen en
cuenta la redistribución inelástica. En consecuencia, el momento de diseño en cada dirección es
menor en cierta cantidad que el momento máximo elástico en esa dirección. Los momentos en las
franjas centrales en las dos direcciones se calculan según el C13.9.6
w l2
a, j j a
Mb = C w l 2
b, j j b
Ma = C
Ci,j: Coeficientes que se aplican a los momentos de losas en dos direcciones según el método
C.13.9. El subíndice i indica la dirección corta o larga (la o lb) y el subíndice j indica si es
aplicable a la carga mayorada viva (wl), muerta (wd) o total (wt).
w:
Carga uniforme
la:
Longitud de la luz libre en la dirección corta
lb:
Longitud de la luz libre en la dirección larga
El panel se divide en ambas direcciones, en una franja central cuyo ancho es igual a la mitad del
panel y en dos franjas de borde o franjas de columna con un ancho igual a un cuarto del ancho del
panel (C.13.4.1). La franja central se diseña para el momento total. En las franjas de borde, este
momento se supone que disminuye de su valor máximo en el borde de la franja central a un tercio
de su valor en el borde del panel según C.13.9.7- MOMENTOS DE DISEÑO EN LA FRANJA
DE COLUMNAS.
Fuente: Diseño de Estructuras de Concreto. Nilson, Arthur H. Distribución de momentos en la luz corta.
Javier Fajardo
64
Diseño en Concreto II
Fuente: NSR-98
El método tiene las siguientes limitaciones:
− Supone que hay vigas muy rígidas o muros en todos los bordes C.13.9.1
− Cuando m = la/lb < 0.5, se considera como una losa en una dirección, debe colocarse refuerzo
para momento negativo a lo largo del lado corto para retracción de fraguado y temperatura,
como el correspondiente para m = 0.5. C13.9.3
Javier Fajardo
65
Diseño en Concreto II
Fuente: NSR-98
− En los bordes discontinuos debe utilizarse un momento negativo equivalente a 1/3 del
positivo.
− Las secciones críticas están localizadas en M(-) en los bordes del panel y M(+) en las líneas
centrales del panel. C13.9.5
Javier Fajardo
66
Diseño en Concreto II
Fuente: NSR-98
− Los momentos en la franja de columnas, deben reducirse del valor total de Ma o Mb en el
límite de la franja central a 1/3 del borde.
− Cuando el momento negativo de un lado del apoyo sea menos del 80% del valor en el otro
lado del apoyo, la diferencia debe distribuirse de acuerdo a las rigideces relativas de las losas.
C13.9.8
Javier Fajardo
67
Diseño en Concreto II
Fuente: NSR-98
− El cortante en la losa debe calcularse de acuerdo a lo que da la tabla C.13.8 del NSR-98
− Las vigas de apoyo del panel tienen cargas de acuerdo a la tabla C.13.8. En ningún caso la
carga sobre la viga del lado corto, debe ser menor de la del área aferente limitada por líneas a
45° de las esquinas y la carga equivalente uniformemente repartida para la viga corta es wla/3
Javier Fajardo
68
Diseño en Concreto II
Problema: La siguiente placa tiene cargas w cv = 300 kgf/m 2 y w cm = 400 kgf/m 2 .
Encontrar los momentos de diseño para los paneles I, II, III
m=
4.80
= 0.80
6.00
Diseñar como losa en dos direcciones.
Se mayoran las cargas:
wu cm = 1.4 * 0.400 = 0.56 T/m 2
wu cv = 1.7 * 0.300 = 0.51 T/m 2
1.070 T/m 2
Los momentos en las franjas centrales en las dos direcciones se calculan con:
2
Ma = C
w l
a, i j a
2
Mb = C
w l
b, i j b
Panel I (Caso 2): Franja de columnas 0.25 l2 y 0.25l1.
Para la tabla C.13.8
wa: Porcentaje de carga del panel soportada en la dirección corta.
wb: Porcentaje de carga del panel soportada en la dirección larga
Javier Fajardo
69
Diseño en Concreto II
Las Cargas sobre las vigas de apoyo se calculan con la Tabla C.13.8.
Javier Fajardo
70
Diseño en Concreto II
Carga sobre la viga del lado corto:
4.80 * 2.40
* 1.07 = 6.16 T
2
Pu = 0.93 * 4.80 = 4.46 T
wla 1.07 * 4.80
wu =
=
= 1.71 T
m
3
3
Pu = 1.71 * 4.8 = 8.21 T
Usar
Pu =
Panel II: (Caso 8)
Javier Fajardo
71
Diseño en Concreto II
Las Cargas sobre las vigas de apoyo se calculan con la Tabla C.13.8.
4.80 * 2.40
* 1.07 = 6.16 T
2
Pu = 01.44 * 4.80 = 6.93 T
wla 1.07 * 4.80
wu =
=
= 1.71 T
m
3
3
Pu = 1.71 * 4.8 = 8.21 T
Usar
Pu =
Panel III. (Caso 4)
Javier Fajardo
72
Diseño en Concreto II
Las Cargas sobre las vigas de apoyo se calculan con la Tabla C.13.8.
4.80 * 2.40
* 1.07 = 6.16 T
2
Pu = 0.93 * 4.80 = 4.46 T
wla 1.07 * 4.80
wu =
=
= 1.71 T
m
3
3
Pu = 1.71 * 4.8 = 8.21 T
Usar
Pu =
2.7
REFUERZO PARA TEMPERATURA Y RETRACCIÓN DE FRAGUADO
El concreto se retrae a medida que fragua y se debe curar a más de 10°C (C.5.11) durante 7 días.
Una losa por lo general está rígidamente unida a otras partes de la estructura y no puede
contraerse libremente como una losa simplemente apoyada, lo que genera esfuerzos de retracción
de fraguado.
Como el concreto es débil a tensión, estos esfuerzos de temperatura y de retracción de fraguado
pueden producir agrietamiento. Las grietas pueden controlarse colocando refuerzo en la losa para
distribuir uniformemente las grietas. A medida que el concreto tiende a contraerse, este refuerzo
resiste la contracción sometido a compresión.
Para losas armadas en una dirección, el refuerzo suministrado para resistir los momentos flectores
tiene el efecto de reducir la retracción de fraguado. Debido a que la contracción ocurre en todas
las direcciones, es necesario proporcionar refuerzo para limitar la contracción por retracción de
fraguado y temperatura en dirección perpendicular a la del refuerzo principal.
El acero exigido por el Código NSR-98 en el capítulo C.7.12 y el C.13.5 para control de grietas
de retracción de fraguado y temperatura también representa el refuerzo mínimo admisible en la
dirección de la luz para losas armadas en una dirección; la cuantía mínima de 0.0020.
2.8
REFUERZO PARA LOSAS ARMADAS EN DOS DIRECCIONES Y APOYADAS
EN LOS BORDES
El refuerzo principal a flexión se coloca en un patrón ortogonal con barras paralelas
perpendiculares a los bordes apoyados. El refuerzo de la losa debe cumplir con lo especificado en
el C.13.5. El espaciamiento del refuerzo a flexión en las secciones críticas no debe exceder 2
veces el espesor de la losa, excepto las áreas que sean de construcción nervada, además se debe
cumplir con el C.7.6
El área de refuerzo en cada dirección no debe ser menor que lo requerido en C.7.12
Javier Fajardo
73
Diseño en Concreto II
El refuerzo para momento positivo perpendicular a un borde discontinuo debe extenderse hasta el
borde de la losa y anclarse mínimo 150 mm.
El refuerzo para momento negativo perpendicular a un borde discontinuo debe anclarse en las
vigas de borde, columnas o muros según el C.12
Para una losa en voladizo el refuerzo debe anclarse dentro de esta.
Para losas macizas con vigas entre apoyos y α>1.0, debe proporcionarse refuerzo especial,
superior e inferior, en las esquinas exteriores como se indica en el C13.5.6.
El refuerzo especial debe colocarse a una distancia igual a 1/5 de la luz mayor, en ambas
direcciones a partir de la esquina.
Fuente: Diseño de Estructuras de Concreto. Nilson, Arthur H.
Los momentos torsionantes tienden a agrietar la losa en las esquinas en la parte inferior a lo largo
de la diagonal del panel, y en la parte superior en la dirección perpendicular a la diagonal.
Cuando se utilicen sobrespesores para reducir el refuerzo negativo sobre la columna de la losa, el
tamaño del sobrespesor debe darse según el C.13.5.7.
El sobrespesor debe extenderse en cada dirección a una distancia mayor de 1/6 de la luz en cada
dirección medida al eje de los apoyos.
El saliente del sobrespesor debe tener al menos ¼ del espesor de la losa.
El refuerzo en losas sin vigas debe tener los puntos de doblamiento y extensiones indicadas en la
figura C.13.1.
Javier Fajardo
74
Diseño en Concreto II
Para luces adyacentes desiguales debe cumplirse la figura C.13.1 para la luz mayor.
Las barras inferiores en la franja de columnas deben ser continuas o empalmarse por traslapo
Tipo A. (C.12.15). Dos de las barras inferiores deben ser continuas, empalmarse en el apoyo y
pasar a través de la columna.
Para aberturas en un sistema de losas debe mantenerse la cantidad total de refuerzo requerida para
losa sin abertura.
No se puede interrumpir el refuerzo con aberturas de más de 1/8 del ancho de la franja de
columna en cualquiera de las luces. Debe añadirse una cantidad de refuerzo equivalente al
interrumpido.
Fuente: NSR-98
Javier Fajardo
75
Diseño en Concreto II
2.9
ESPESOR MÍNIMO DE LOSAS
El NSR-98, en el capitulo C.9.5, especifica los limites máximos de altura de vigas y las deflexiones
máximas permisibles. La Tabla C9.1(a) y C9.1(b) del NSR-98, muestra un conjunto de espesores
mínimos que deben usarse en vigas y losas no preesforzadas que trabajan en una dirección, a menos
que un calculo cuidadoso de las deflexiones permita obtener espesores menores sin efectos
perjudiciales. En el C.9.5.3 se dan los espesores mínimos para losas sin vigas que trabajen en dos
direcciones.
Según el C.9.5.3.2 del NSR-98, el espesor mínimo de la losa con vigas entre apoyos en todos sus
lados debe ser:
a) Para α m ≤ 0.2 se deben cumplir los requisitos del C.9.5.3.2
b) Para 2.0 ≥ α m ≥ 0.2 el espesor debe ser menor que :
fy
)
1500
h=
≥ 120 mm
36 + 5β (α − 0.2)
m
ln (0.8 +
c) Para α m > 0.2 el espesor debe ser menor que :
fy
ln (0.8 +
)
1500 ≥ 90 mm
h=
36 + 9 β
d) Si en los bordes discontinuos no se coloca una viga de borde con una relación de rigidez
α mayor a 0.8, hay necesidad de aumentar en un 10% el espesor requerido por las
ecuaciones C.9.4 o C.9.7 en el panel con borde discontinuo.
ln: Luz libre en la longitud larga en losas que trabajan en dos direcciones, medida de la cara a la
cara de los apoyos en losas sin vigas, y de la cara a la cara de las vigas u otros apoyos en los otros
casos. En mm
b: relación de la luz libre larga a la corta, para losas que trabajan en dos direcciones
α: Relación de la rigidez a flexión de la sección de viga con respecto a la rigidez de un sector de
losa definido lateralmente por lo ejes centrales de los paneles adyacentes (en caso de que existan)
a ambos lados de la viga. Véase el Capítulo C.13.
αm. Valor promedio de a para todas las vigas existentes en los bordes del panel.
Problema: Diseñar el panel mostrado como losa maciza en dos direcciones. Se considera
continuo en los 4 lados y con Vigas de borde de 30X50 cm.
m=
5.70
= 0.85
6.70
Javier Fajardo
76
Diseño en Concreto II
1. Predimensionamiento: Inicialmente se debe predimensionar un espesor inicial de la losa, para
lo cual se puede usar la tabla C.9.3 del NSR-98.
h=
ln 6.70
=
= 0.20 m
33
33
También se puede usar lo que recomienda el ACI para calcular el espesor mínimo de la losa.
perímetro libre del panel
≥ 0.09
180
2 * (5.70 + 6.70)
h=
= 0.138 m ≈ 0.14 m
180
Tomando un espesor h promedio
h=
h=
(C.9.5.3.2) > 120 mm Bien
0.20 + 0.14
= 0.17 m
2
2. Evaluación de cargas. (El panel no soporta particiones):
Carga Muerta
Peso propio:
2.4*0.17
Alistado:
2.2*0.04
Cielo raso:
2.2*0.02
Piso en baldosa de cemento.
wucm
Carga Viva (Vivienda)
wucv
wu
Javier Fajardo
0.41 T/m2
0.09 T/m2
0.04 T/m2
0.10 T/m2
0.64 T/m2*1.4*9.81 = 8.79 kN/m2
1.80 kN/m2*1.7 = 3.06 kN/m2
11.85 kN/m2
=
=
=
=
=
=
=
77
Diseño en Concreto II
3. Momentos de diseño:
4. Refuerzo longitudinal en franjas centrales
ρ ⋅ fy 

2
Mu = φ ⋅ ρ ⋅ fy1 − 0.59
 ⋅ bd
f´c 

Despejo ρ
f´c
ρ=
−
2 * 0.59 * fy
Javier Fajardo
2


f´c
Mu * f´c

 −
2
 2 * 0.59 * fy 
bd φ * 0.59 * fy 2
78
Diseño en Concreto II
1.4
[MPa]
fy
ρmin = 0.0033
ρ≥
Asmin T = ρbh = 0.0020 * 100 * 17 = 3.4 cm 2
= ρbd = 0.0033 * 100 * 15 = 5.0 cm 2
flex
s max ≤ 2h = 34 cm
smax ≤ 500 mm
Asmin
Luz Corta: b = 1.0 m, d = 0.15 m
LuzLarga: b = 1.0 m, d = 0.14 m
Javier Fajardo
79
Diseño en Concreto II
5. Refuerzo en la franja de Columnas
El momento se reduce a 1/3 en el borde del panel y se colocará a un espaciamiento uniforme,
usando un momento promedio igual a 2/3 del de las franjas centrales. Por lo tanto el área de
refuerzo será 2/3 de la colocada en la franja central, aunque para este caso se debe usar el
mínimo, es decir, se debe continuar con #3@16 hasta el borde en ambas direcciones.
6. Cortante
m=
5.70
= 0.85
6.70
De la Tabla C.13-8 del NSR-98, se encuentra que el coeficientes de transmisión de carga en la
dirección corta es wa = 0.66, esto quiere decir que el 66% de la carga se transmite en la dirección
corta, y el coeficiente en la dirección larga es wb = 0.34 o el 34% de la carga se transmite en la
dirección larga. La suma de los dos coeficientes debe ser igual a 1.0.
5.70 * 2.85
* 11.85 = 96.25 kN
2
Pu = 13.5 * 5.70 = 77 kN
wla 11.85 * 5.70
wu =
=
= 22.52 kN
m
3
3
Pu = 22.52 * 5.70 = 128.36 kN
Usar
Pu =
6.1 Losa Dirección Corta (d = 0.15 m)
38.48
Vd
=
2.85
2.70
Vd = 36.45 kN
Javier Fajardo
80
Diseño en Concreto II
Vd 36.45 * 10 3
=
= 243.0 kPa
bd
1.0 * 0.15
f´c
21.1
φvc = φ
= 0.85 *
= 650.53 kPa ≥ 243.0 kPa
6
6
vu =
Bien
6.2 Losa Dirección Larga. (d = 0.14 m)
Vu = 22.29*6.70 / 2 = 74.67 kN
74.67
Vd
=
3.35
3.21
Vd = 71.55 kN
Vd 71.55 * 10 3
=
= 511.07 kPa
bd
1.0 * 0.14
f´c
21.1
φvc = φ
= 0.85 *
= 650.53 kPa ≥ 511.07 kPa
6
6
vu =
Bien
Esto quiere decir que toda la fuerza cortante la absorbe el concreto. El espesor es suficiente para
resistir los esfuerzos cortantes mayorados. Aunque se puede reducir un poco más el espesor, se
deben revisar las deflexiones según el NSR-98.
6.3 Vigas de apoyo Dirección corta (d = 0.45 m)
wu =
wla 11.85 * 5.70
=
= 22.52 kN
m
3
3
Vu = 22.52*5.70 / 2 = 64.18 kN
64.18 Vd
=
2.85
2.4
Vd = 54.05 kN
Vd 54.05 * 10 3
=
= 400 .34 kPa
bd
0.3 * 0.45
f´c
21.1
φvc = φ
= 0.85 *
= 650.53 kPa ≥ 400 .34 kPa
6
6
vu =
Bien
Usar estribos φ3/8” dos ramas en la viga cada d/4 = 11 cm durante 2d = 90 cm desde la cara del
apoyo, después cada d/2 = 22.5 cm.
Javier Fajardo
81
Diseño en Concreto II
6.4 Vigas de apoyo Dirección larga (d = 0.45 m)
Vu = 22.29*6.70 / 2 = 74.67 kN
74.67 Vd
=
3.35
2.9
Vd = 64.64 kN
Vd 64.64 * 10 3
=
= 478 .81 kPa
bd
0.3 * 0.45
f´c
21.1
φvc = φ
= 0.85 *
= 650.53 kPa ≥ 478 .81 kPa
6
6
vu =
Bien
Usar estribos φ3/8” dos ramas en la viga cada d/4 = 11 cm durante 90 cm desde la cara del apoyo,
después cada 22.5 cm.
Problema: Diseñar el panel mostrado como losa aligerada en dos direcciones, es continuo en los
4 lados y esta apoyado sobre vigas de borde de 30x50 cm.
Se construirá una placa aligerada con casetón reutilizable. Para que cumpla con el C.13.9-1 del
NSR-98, se deben colocar mínimo 6 nervios o viguetas en cada dirección de 0.10 m de ancho,
cada 0.81 m en la dirección corta y cada 0.84 m en la dirección larga. A continuación se
transcribe lo que dice el código respecto al dimensionamiento geométrico que deben tener las
losas aligeradas.
Javier Fajardo
82
Diseño en Concreto II
C.13.2 - LOSAS CON NERVADURAS O ALIGERADAS
C.13.2.1 - DEFINICIÓN - La construcción con nervaduras consiste en una combinación monolítica, o prefabricada,
de nervios espaciados regularmente, en una o en dos direcciones, y de una loseta superior que actúa también en una o
en dos direcciones de acuerdo con la acción de las viguetas. La loseta puede ser parcialmente prefabricada, pero
como mínimo una parte de su espesor debe ser vaciado en sitio.
C.13.2.2- LIMITACIONES DIMENSIONALES - Las losas con nervaduras deben cumplir las condiciones
dimensionales dadas a continuación:
(a) Los nervios no deben tener menos de 100 mm de ancho en su parte superior, y su ancho promedio no puede ser
menor de 80 mm. Su altura libre no debe ser mayor de 5 veces el espesor promedio del alma.
(b) La porción vaciada en sitio de la loseta superior debe tener al menos 45 mm de espesor, pero ésta no debe ser
menor de 1/20 de la distancia libre entre los nervios. Cuando se utilicen bloques de aligeramiento permanentes de
concreto o de arcilla cocida, o plaquetas prefabricadas, estos elementos pueden considerarse como parte del
recubrimiento de concreto que prescribe C.7.7 y la parte vaciada en sitio del espesor mínimo de la loseta superior
puede reducirse a 40 mm. La loseta superior debe tener como mínimo el refuerzo de repartición y temperatura que
prescribe el Capítulo C.7, y deben tenerse en cuenta los requerimientos propios para diafragmas sísmicos cuando la
losa en general actúa como tal.
(c) Para losas nervadas en una dirección, la separación máxima entre nervios, medida centro a centro, no puede ser
mayor que 2.5 veces el espesor total de la losa, sin exceder 1.20 m. Para losas nervadas en dos direcciones, la
separación máxima entre nervios, medida centro a centro, no puede ser mayor que 3.5 veces el espesor total de la
losa, sin exceder 1.50 m.
(d) Cuando se trate de losas en una dirección, deben colocarse viguetas transversales de repartición con una
separación libre máxima de 10 veces el espesor total de la losa, sin exceder 4.0 m.
C.13.2.3 - SISTEMAS DE NERVADURAS COMO CONJUNTO DE VIGAS - Cuando se excede la separación
máxima entre viguetas dada en el ordinal (c) de C.13.2.2, o cuando el mínimo número de nervaduras en la dirección
bajo consideración dentro del panel es menor de 4, las nervaduras deben considerarse como elementos aislados y su
análisis y diseño no puede regirse por los procedimientos del presente Capítulo. La losa entre nervaduras en este caso
debe analizarse diseñarse como una losa en una o dos direcciones, según sea el caso, cumpliendo los requisitos
correspondientes.
Javier Fajardo
83
Diseño en Concreto II
1. Predimensionamiento: Aunque se debe determinar el espesor h de la losa según el C.9.5.3.2 del
NSR-98, este método se usará después, por el momento se usará la Tabla C.9.1(b).
h=
ln 6.70
=
= 0.32 m
21
21
Usar h = 0.35 m
2. Evaluación de cargas. (El panel no soporta particiones):
Peso de la losa = (6.70*5.70*0.35-56*0.71*0.74*0.30)*2.4*1.10 = 12.0 T/m2
Carga Muerta
Peso propio:
12.0/(5.70*6.70)
Alistado:
2.2*0.04
Cielo raso:
2.2*0.02
Piso en baldosa de cemento.
wucm
Carga Viva (Vivienda)
wucv
wu
Javier Fajardo
0.31 T/m2
0.09 T/m2
0.04 T/m2
0.10 T/m2
0.54 T/m2*1.4*9.81 = 7.42 kN/m2
1.80 kN/m2*1.7 = 3.06 kN/m2
10.48 kN/m2
=
=
=
=
=
=
=
84
Diseño en Concreto II
3. Momentos de Diseño
4. Refuerzo longitudinal en franjas centrales
ρ ⋅ fy 

2
Mu = φ ⋅ ρ ⋅ fy1 − 0.59
 ⋅ bd
f´c 

Despejo ρ
f´c
ρ=
−
2 * 0.59 * fy
2


f´c
Mu * f´c

 −
 2 * 0.59 * fy 
bd 2 φ * 0.59 * fy 2
Asmin T = ρbh = 0.0020 * 10 * 35 = 0.7 cm 2
Asmin
flex
= ρbd = 0.0033 * 10 * 31 = 1.023 cm 2
Javier Fajardo
85
Diseño en Concreto II
Luz Corta: b = 0.10 m, d = 0.31 m
LuzLarga: b = 0.10 m, d = 0.31 m
5. Refuerzo longitudinal en la franja de Columnas
El momento se reduce a 1/3 en el borde del panel y se usará un momento promedio igual a 2/3
del de las franjas centrales. Si se toma el momento máximo de 17.16 kN.m en la dirección corta,
el momento promedio en la franja de columnas será de 11.44 kN.m, obteniendo una cuantía de
0.0033, que es igual a la mínima. Se debe colocar 1#4 arriba y abajo en ambas direcciones.
Javier Fajardo
86
Diseño en Concreto II
6. Cortante
m=
5.70
= 0.85
6.70
De la Tabla C.13-8 del NSR-98, se encuentra que el coeficientes de transmisión de carga en la
dirección corta es wa = 0.66, esto quiere decir que el 66% de la carga se transmite en la dirección
corta, y el coeficiente en la dirección larga es wb = 0.34 o el 34% de la carga se transmite en la
dirección larga. La suma de los dos coeficientes debe ser igual a 1.0.
5.70 * 2.85
* 10.48 = 85.12 kN
2
Pu = 11.94 * 5.70 = 68 .04 kN
wla 10.48 * 5.70
wu =
=
= 19.91 kN
m
3
3
Pu = 19.91 * 5.70 = 113.5 kN
Usar
Pu =
6.1 Nervios Dirección Corta (d = 0.31 m)
34.03
Vd
=
2.85
2.54
Vd = 30.33 kN
Vd 30.33 * 10 3
vu =
=
= 978.31 kPa
bd
0.1 * 0.31
f´c
21.1
φvc = φ
= 0.85 *
= 650.53 kPa ≤ 978.31 kPa
6
6
Javier Fajardo
87
Necesita estribos
Diseño en Concreto II
Av ⋅ fy
bw ⋅ vs
vu ≤ φvn + φvc
vu
vs =
− vc
φ
s=
φ = 0.85
f´c
6
vu
f´c
vs =
−
φ
6
978.31 650.53
vs =
−
= 385.62 kPa
0.85
0.85
71*10 − 6 * 420 *106
s=
= 0.77 m
0.10 * 385.62 *103
d 31
smax = =
= 7.8 cm
4 4
vc =
Usar estribos φ3/8” en S cada 7.5 cm durante 90 cm y después cada 15.5 cm.
6.2 Nervios Dirección Larga. (d = 0.31 m)
Vu = 17.91*6.70 / 2 = 60.0 kN
60
Vd
=
3.35 3.04
Vd = 54.45 kN
Vd 54.45 * 10 3
=
= 1756.38 kPa
bd
0.1 * 0.31
f´c
21.1
φvc = φ
= 0.85 *
= 650.53 kPa ≤ 1756.38 kPa
6
6
1756.38 650.53
vs =
−
= 1301 kPa
0.85
0.85
71 * 10 − 6 * 420 * 10 6
s=
= 0.23 m
3
0.10 * 1301 * 10
d 31
smax = =
= 7.8 cm
4 4
vu =
Requiere estribos
Usar estribos φ3/8” en S cada 7.5 cm durante 90 cm y después cada 15.5 cm.
Javier Fajardo
88
Diseño en Concreto II
6.3 Vigas de apoyo en la dirección Corta (d = 0.45 m)
wla 10.48 * 5.70
=
= 19.91 kN
m
3
3
Pu = 19.91 * 5.70 = 113.5 kN
Usar
wu =
56.75
Vd
=
2.85
2.40
Vd = 30.33 kN
Vd 47.79 * 10 3
=
= 354 kPa
bd
0.3 * 0.45
f´c
21.1
φvc = φ
= 0.85 *
= 650.53 kPa ≥ 354 kPa
6
6
vu =
Bien
Usar estribos φ3/8” de dos ramas cada 11 cm durante 90 cm y después cada 22.5 cm.
6.4 Vigas de apoyo en la dirección Larga(d = 0.45 m)
Vu = 17.91*6.70 / 2 = 60.0 kN
60
Vd
=
3.35 2.90
Vd = 51.94 kN
Vd 51.94 * 10 3
=
= 384 .74 kPa
bd
0.3 * 0.45
f´c
21.1
φvc = φ
= 0.85 *
= 650.53 kPa ≥ 384 .74 kPa
6
6
vu =
Bien
Usar estribos φ3/8” de dos ramas cada 11 cm durante 90 cm y después cada 22.5 cm.
2.10
CONTROL DE DEFLEXIONES
El Código ACI de 1963 que introdujo el método de los coeficientes, establece que el espesor de
la losa no debe ser menor que 3.5” y no menor que el perímetro total del panel dividido por 180.
En el NSR-98 se establece el espesor mínimo de losas sin vigas interiores en el C.9.5.3.2 y la
Tabla C.9.3 y en el C.9.5.3.3 el espesor mínimo para losas en general, cuyas ecuaciones tienen en
cuenta la rigidez relativa de la losa y de las vigas de borde, la relación de las dimensiones de los
lados largo y corto del panel y las condiciones de restricción a lo largo de los bordes
Javier Fajardo
89
Diseño en Concreto II
Se puede calcular la deflexión en el centro de un panel de losa y comparar los resultados con los
de la Tabla C.9.2. Las deflexiones de losas se ven afectadas por la restricción rotacional variable
en los bordes, la influencia de distribuciones alternas de aplicación de las cargas, las relaciones
variables de las longitudes de los lados, los efectos del agrietamiento, la retracción de fraguado y
el flujo plástico.
La deflexión de una losa apoyada en los bordes puede estimarse con base en los coeficientes de
momento. La deflexión que interesa son las de largo plazo ocasionado por cargas permanentes y
las deflexiones inmediatas generadas por carga viva. En el cálculo de deflexiones es conservador
usar la luz corta.
Los coeficientes de las tablas C13.5, C.13.6 y C.13.7 se desarrollaron teniendo en cuenta
condiciones de cargas alternas, tomando cargas muerta y viva completas sobre dos paneles
adyacentes a un borde y lograr el máximo momento negativo y para los cálculos de momento
positivo, se incluyen dos patrones de carga: carga muerta en ambos paneles y carga viva
únicamente en el panel donde se va a determinar el máximo momento positivo.
Las deflexiones máximas que genera la carga viva, se obtendrán cuando la carga viva actúa sobre
un panel pero no sobre los paneles adyacentes, es decir, con una distribución en forma de tablero
de ajedrez. La deflexión que produce la carga viva debe basarse en los máximos momentos
positivos encontrados con la tabla C.13.7, y con los momentos negativos estáticamente
consistentes en los bordes apoyados.
La variación del momento en la dirección larga del panel para una carga uniformemente
distribuida es parabólica y la suma de los momentos positivos y del promedio de los negativos de
acuerdo con la estática, es:
w l2
M= b b
8
wb: Fracción de carga transmitida en la dirección larga del panel.
Para empotramiento en los apoyos:
Mneg =
1
2
w l2 = M
12 b b 3
El momento positivo será:
Mpos =
1
1
w l2 = M
b
b
24
3
Los coeficientes para momento positivo se obtuvieron suponiendo un 50% de empotramiento.
Las deflexiones se calculan usando el diagrama parabólico de momentos con momento máximo
positivo Mb en el centro de la luz, y momentos negativos en los extremos iguales a la mitad de
este valor.
Javier Fajardo
90
Diseño en Concreto II
Fuente: Diseño de Estructuras de Concreto. Nilson, Arthur H.
La deflexión en el centro de la luz de la franja central, de una losa para carga viva con bordes
continuos, será:
3M l 2
b b
∆ =
l 32E I
c e
Mb: Máximo momento positivo y obtenido mediante la utilización de los coeficientes apropiados.
Ec: es el módulo elástico del concreto.
Ie: Momento efectivo de inercia de la sección transversal de concreto con ancho unitario.
En el método de los coeficientes, los momentos negativos en los bordes discontinuos de las losas
se suponen iguales a un tercio del momento positivo en la misma dirección (C.13.9.4.a).
Para el caso especial en que los bordes están completamente libres de restricciones, como en el
caso de losas apoyadas en muros de mampostería, la deflexión en el centro de la luz que genera la
carga viva es:
Javier Fajardo
91
Diseño en Concreto II
5M l 2
b b
∆ =
l 48E I
c e
La deflexión por carga muerta debe basarse en el diagrama de momentos encontrado utilizando
los máximos momentos positivos, con base en la tabla C.13.6, que supone que todos los paneles
están cargados. Los bordes continuos se consideraron empotrados para la deducción de los
coeficientes. La deflexión en el centro de la luz por carga muerta, para el caso con los dos
extremos continuos es:
M l2
b b
∆D =
16E c I e
Cuando ambos extremos están libres de restricciones, la deflexión en el centro de la luz por carga
muerta es:
5M l 2
b b
∆D =
48E c I e
Las deflexiones anteriores se dedujeron para una franja unitaria en la dirección larga del panel,
los cálculos también pueden basarse en una franja en la dirección corta. La deflexión resultante
en el centro del panel debe ser la misma en cualquiera de las dos direcciones, aunque debido a la
naturaleza aproximada de los cálculos se pueden esperar pequeñas diferencias.
Un procedimiento razonable consiste en calcular la deflexión en cada una de las direcciones y
luego promediar los resultados. El Código NSR-98 sugiere que se utilice el momento de inercia
Ie para tener en cuenta la influencia del agrietamiento del concreto en la reducción de la rigidez.
(C.9.5.3.4)
Las deflexiones de la losa, calculadas con las ecuaciones anteriores, son las deflexiones elásticas
iniciales que se produjeron inmediatamente después de la aplicación de las cargas. Para cargas
sostenidas, el Código recomienda que el aumento de la deflexión a largo plazo puede
determinarse con el C.9.5.2.4. La experiencia indica que un valor de 2.0 subestima las
deflexiones dependientes del tiempo en losas, probablemente porque las losas tienen relaciones
de espesor/luz menores que las de las vigas, que sirvieron de base para la determinación de los
multiplicadores a largo plazo. Branson sugiere la utilización de un valor ξ = 3.0 para losas.
Problema: La siguiente losa maciza, va a soportar particiones susceptibles de daño por
deflexiones, las cuales se instalan 3 meses después de retirada la obra falsa. Calcular las
deflexiones a largo plazo por la carga muerta y viva de servicio con 25% permanente. f´c = 21
MPa
Javier Fajardo
92
Diseño en Concreto II
Ec = 3900 21 ≈ 18 GPa
Ig = se calcula para una franja de 1.0 m de ancho
Ig =
1.0 * 0.17 3
= 4.094 * 10 −4 m 4
12
Como h≥hmin según C.9.5.3.2 y C.9.5.3.3, se puede usar Ie = Ig, y el error será mínimo, además
de conservativo. Si se desea usar un espesor menor que el especificado en el código, se debe usar
Ie. La deflexión a largo plazo será:
∆
LP
=∆
L
+λ
∆ +λ
∆
(to,∞) D
(∞) LS
Luz Larga:
∆ D : Deflexión instantánea en el centro del panel por carga muerta
M l2
b b
∆D =
16E c I e
4.73
Mb =
= 3.38 * 1.0 = 3.38 kN.m
1.4
3.38 * 10 3 * 6.70 2
∆D =
= 1.29 * 10 − 3 m = 1.29 mm
9
−
4
16 * 18 * 10 * 4.094 * 10
Javier Fajardo
93
Diseño en Concreto II
Luz Corta:
∆D =
M a l a2
16E c I e
6.85
= 4.89 * 1.0 = 4.89 kN.m
1.4
4.89 * 10 3 * 5.70 2
∆D =
= 1.35 * 10 − 3 m = 1.35 mm
16 * 18 * 10 9 * 4.094 * 10 − 4
Ma =
∆ : Deflexión inmediata por carga viva
l
3M l 2
b b
∆ =
l 32E I
c e
Luz Larga:
2.61
Mb =
= 1.54 * 1.0 = 1.54 kN.m
1.7
3 * 1.54 * 10 3 * 6.70 2
∆ =
= 8.79 * 10 − 4 m = 0.88 mm
l
9
−
4
32 * 18 * 10 * 4.094 * 10
Luz Corta:
3.68
Ma =
= 2.16 * 1.0 = 2.16 kN.m
1.7
3 * 2.16 * 10 3 * 5.70 2
∆ =
= 8.92 * 10 − 4 m = 0.89 mm
l
32 * 18 * 10 9 * 4.094 * 10 − 4
La deflexión por Creep se halla multiplicando por:
λ=
ξ
1 + 50 ρ´
ρ´ : Refuerzo a compresión en el centro de la luz
2.0 − 1.0
λ
=
= 1.0
λ ∞ = 2.0
(to=3m,∞) 1 + 50(0)
Ya que las vigas tiene una relación espesor/luz menor que una viga, la experiencia indica que se
debe usar un valor de ξ = 3.0 (Branson – ACI).
∆ = 0.89 + 3.0 * 1.35 + 1.0 * 0.25 * 0.89 = 5.16 mm <
Javier Fajardo
94
l
930
=
= 1.40 cm
480 480
Bien