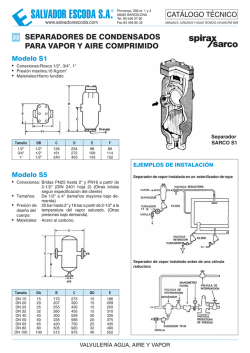
DERECHOS RESERVADOS
REPÚBLICA BOLIVARIANA DE VENEZUELA UNIVERSIDAD RAFAEL URDANETA FACULTAD DE INGENIERÍA ESCUELA DE INGENIERÍA QUÍMICA D R SE E R S O H C E ER S O D VA PROPUESTA DE UNA HERRAMIENTA DIDÁCTICA PARA EVAPORADORES DE UN SOLO EFECTO Trabajo Especial de Grado presentado ante la Universidad Rafael Urdaneta para optar al título de: INGENIERO QUÍMICO Autor: Br. María José Mata Tutor: Ing. Gladys Quevedo. MSc Maracaibo, octubre de 2014 PROPUESTA DE UNA HERRAMIENTA DIDÁCTICA PARA EVAPORADORES DE UN SOLO EFECTO R SE E R Mata Martínez, SMaría José O H REC C.I 21.356.078 _________________________ DEUrb. Monte Bello, calle: M-N. #11-66 Telf. :(0424) 6166617 [email protected] _________________________ Ing. Quevedo Gladys. MSc Tutor Académico S O D VA DEDICATORIA D R SE E R S O H C E ER S O D VA A mis padres, por apoyarme a lo largo de mi vida, brindándome su amor incondicional. A mis abuelos, por guiarme y educarme. A mis hermanos por confiar en mí desde el inicio. AGRADECIMIENTOS En primer lugar quiero agradecer a Dios, por acompañarme siempre, brindándome su amor incondicional y dándome la perseverancia para lograr las metas que me propongo. S O D VA A mis padres, José Luis Mata y Mary Martínez, por brindarme todo su amor y ER S E A mis hermanos, Eduardo I, Jorge M. y José M.R por confiar en mí y cuidarme durante S O Hcosa que necesitara. C toda mi vida, ayudándome E en cada DER acompañarme en cada momento, Amándome incondicionalmente. A el Ing. Pedro Aponte, por ayudarme. Le doy gracias a todos aquellos amigos y familiares que bien sea directa o indirectamente me apoyado durante todos mis años de estudio, y durante la realización de este trabajo especial de grado. Gracias a la Ing. Quevedo Gladys MSc, por proporcionarme el tema de investigación y haber aportado sus conocimientos para guiarme, ayudándome a llevar a cabo éste Trabajo de Investigación. Finalmente a la Universidad Rafael Urdaneta y a todo el profesorado por ser los facilitadores de nuestro aprendizaje, en especial a aquellos profesores que transformaron mi pensar mostrándome una nueva perspectiva; Gracias por transmitir algo tan invaluable como lo es el conocimiento. María Mata (2014) ÍNDICE GENERAL RESUMEN ABSTRACT Pág. INTRODUCCIÓN………………………………………………………………….. 19 21 S O D 21 A 1.1. Planteamiento del problema………………………………………………... V ER S 1.2. Objetivos……………………………………………………………………… 24 E R S 1.2.1. Objetivo General…………………………………………………………… 24 O H C E 1.2.1. Objetivos Específicos……………………………………………………… 24 R E D 1.3. Justificación………………………………………………………………….. 24 1. CÁPITULO I. EL PROBLEMA………………………………………………... 1.4. Delimitación………………………………………………………………….. 26 1.4.1. Delimitación espacial……………………………………………………… 26 1.4.2. Delimitación temporal……………………………………………………... 27 1.4.3. Delimitación científica……………………………………………………... 27 2. CÁPITULO II. MARCO TEÓRICO….………………………………………... 28 2.1. Antecedente………………………………………………………………….. 28 2.2. Bases teóricas……………………………………………………………….. 32 2.2.1. Sistemas de Unidades…………………………………………………… 32 2.2.1.1. El sistema de unidades SI……………………………………………... 33 2.2.1.2. El sistema de unidades CGS………………………………………….. 34 2.2.3.3. El sistema inglés de unidades (PLS)…………………………………. 34 2.2.2. Principios fundamentales en la ingeniería química……………………. 35 2.2.2.1. Conservación de la masa………………………………………………. 35 2.2.2.2. Conservación de la energía……………………………………………. 35 2.2.2.3. Balance de masa o materiales…………………………………………. 36 6 2.2.2.4. Balance de Energía……………………………………………………... 37 2.2.3. Operaciones Unitarias…………………………………………………….. 37 2.2.3.1. Clasificación de las Operaciones Unitarias…………………………… 39 2.2.4. Evaporación………………………………………………………………… 39 2.2.4.1. Definición de Evaporación……………………………………………… 39 2.2.4.2. Operación de un sistema de evaporación para simple efecto……… 2.2.4.2.1. Variables determinantes en el procedimiento matemático del diseño de sistemas de evaporación…………………………………………….. 2.2.4.2.2. Especificaciones de la solución a concentrar………………………. 41 42 S DO 47 S RE A V R SE 2.2.4.2.3. Evaporación mediante represión de vapor………………………… 2.2.4.2.4. Efectos de las variables de proceso en la operación de sistemas de evaporación de efecto simple……………………………………………….. 2.2.4.2.4. Efectos de las variables de procesos en la operación de sistemas de evaporación de efecto simple……………………………………………….. 2.2.5. Errores Sistemáticos……………………………………………………… 54 2.2.5.1. Error relativo…………………………………………………………….. 58 2.2.6. Microsoft Excel……………………………………………………………. 58 2.2.7. Microsoft Visual Basic…………………………………………………….. 59 2.3. Sistema de Variables……………………………………………………….. 60 3. CAPÍTULO III. MARCO METODOLÓGICO………………………………… 3.1. Tipo de Investigación……………………………………………………….. 62 62 3.2. Diseño de la investigación…………………………………………………. 63 3.3. Técnicas de recolección de datos………………………………………… 65 3.4. Instrumentos de recolección de datos…………………………………… 67 3.5. Fases de la investigación………………………………………………… 3.5.1. Fase 1: Establecimiento del procedimiento matemático para evaporadores de un solo efecto………………………………………………… 3.5.2. Fase 2: Programación del procedimiento matemático………………... 70 3.5.3. Fase 3: Desarrollo de las ventanas de usuario………………………... 73 3.5.4. Fase 4: Elaboración del manual de usuario…………………………… 73 O H C E ER D 56 56 57 70 71 7 4. CAPÍTULO IV. ANALISIS DE RESULTADOS………………………………. 4.1. Fase 1: Establecimiento del procedimiento matemático para evaporadores de un solo efecto…………………………………………………. 4.1.1. Posibles soluciones a concentrar………………………………………… 4.1.2. Identificación de los posibles casos en el procedimiento matemático para evaporadores de un solo efecto…………………………………………… 4.1.3. Resultados en el establecimiento del procedimiento matemático de la herramienta didáctica para evaporadores de un solo efecto…………………. 4.2. Fase 2: Programación del procedimiento matemático de la herramienta didáctica para evaporadores de un solo efecto………………………………… 4.2.1. Primicias a la programación del procedimiento matemático de la herramienta didáctica para evaporadores de un solo efecto………………… 4.2.2. Desarrollo del procedimiento matemático de la herramienta didáctica, mediante Microsoft Office Excel©………………………………………………. 4.2.2.1. Resultados………………………………………………………………... 4.2.3. Desarrollo de la calculadora de propiedades de vapor de agua haciendo uso de Microsoft Office Excel© y Visual Basic 2010………………. 4.3. Fase 3: Desarrollo de las ventanas de usuario…………………………… O H C E ER D 75 75 85 S97 O D VA R SE E R S 75 107 107 108 123 141 152 4.4. Fase 4: Elaboración del manual de usuario……………………………… 164 CONCLUSIONES………………………………………………………………….. 167 RECOMENDACIONES……………………………………………………………. 169 REFERENCIAS BIBLIOGRÁFICAS……………………………………………... 171 ANEXOS…………………………………………………………………...……….. 174 APENDICE………………………………………………………………………….. 215 8 ÍNDICE DE TABLAS Pág. Tabla 2.1. Sistema de Variables…………………………………………………. Tabla 3.1. Reporte de datos de los problemas planteados en la herramienta didáctica para evaporadores de un solo efecto………………………………… Tabla 3.2. Reporte de resultados determinados mediante la herramienta didáctica de evaporadores de un solo efecto para diferentes casos y tipo de solución…………………………………………………………………………….. Tabla 3.3. Comparación entre el método tradicional y los resultados arrojados por la herramienta didáctica para evaporadores de un solo efecto…………… Tabla 4.1. Reporte de datos del primer ejercicio planteado para elaborar el procedimiento matemático de la herramienta didáctica……………………….. Tabla 4.2. Reporte de datos del segundo ejercicio planteado para elaborar el procedimiento matemático de la herramienta didáctica……………………….. Tabla 4.3. Reporte de datos del tercer ejercicio planteado para elaborar el procedimiento matemático de la herramienta didáctica……………………….. Tabla 4.4. Reporte de datos del cuarto ejercicio planteado para elaborar el procedimiento matemático de la herramienta didáctica……………………….. Tabla 4.5. Reporte de datos del quinto ejercicio planteado para elaborar el procedimiento matemático de la herramienta didáctica……………………….. Tabla 4.6. Reporte de datos del sexto ejercicio planteado para elaborar el procedimiento matemático de la herramienta didáctica……………………….. Tabla 4.7. Reporte de datos del séptimo ejercicio planteado para elaborar el procedimiento matemático de la herramienta didáctica……………………….. Tabla 4.9. Reporte de resultados obtenidos por medio de la herramienta didáctica de evaporadores para el ejemplo propuesto 4.6……………………. Tabla 4.10. Comparación entre los resultados obtenidos por medio de la herramienta didáctica y el método tradicional para el ejemplo 4.6…………… Tabla 4.11. Reporte de resultados obtenidos por medio de la herramienta didáctica de evaporadores para el ejemplo propuesto 4.7……………………. Tabla 4.12. Comparación entre los resultados obtenidos por medio de la herramienta didáctica y el método tradicional para el ejemplo 4.7…………… Tabla 4.13. Reporte de resultados obtenidos por medio de la herramienta didáctica de evaporadores para el ejemplo propuesto 4.8……………………. DE REC 68 69 S DO A V R SE E R S HO 60 70 99 100 101 102 103 104 105 124 125 126 127 128 9 Tabla 4.14. Comparación entre los resultados obtenidos por medio de la herramienta didáctica y el método tradicional para el ejemplo 4.8…………… Tabla 4.15. Reporte de resultados obtenidos por medio de la herramienta didáctica de evaporadores para el ejemplo propuesto 4.9……………………. Tabla 4.16. Comparación entre los resultados obtenidos por medio de la herramienta didáctica y el método tradicional para el ejemplo 4.9…………… Tabla 4.17. Reporte de resultados obtenidos por medio de la herramienta didáctica de evaporadores para el ejemplo propuesto 4.10……………………. Tabla 4.18. Comparación entre los resultados obtenidos por medio de la herramienta didáctica y el método tradicional para el ejemplo 4.10…………… Tabla 4.19. Reporte de resultados obtenidos por medio de la herramienta didáctica de evaporadores para el ejemplo propuesto 4.11……………………. Tabla 4.20. Comparación entre los resultados obtenidos por medio de la herramienta didáctica y el método tradicional para el ejemplo 4.11…………… Tabla 4.21. Reporte de resultados obtenidos por medio de la herramienta didáctica de evaporadores para el ejemplo propuesto 4.12……………………. Tabla 4.22. Comparación entre los resultados obtenidos por medio de la herramienta didáctica y el método tradicional para el ejemplo 4.12…………… Tabla 4.23. Reporte de resultados obtenidos por medio de la herramienta didáctica de evaporadores para el ejemplo propuesto 4.13……………………. Tabla 4.24. Comparación entre los resultados obtenidos por medio de la herramienta didáctica y el método tradicional para el ejemplo 4.13…………… Tabla 6.1.1. Reporte de resultados obtenidos por el método tradicional, para el ejemplo 4.6. CASO I, Solución diluida………………………………………….. Tabla 6.1.2. Reporte de resultados obtenidos por el método tradicional, para el ejemplo 4.7. CASO II, Solución diluida………………………………………….. Tabla 6.1.3. Reporte de resultados obtenidos por el método tradicional, para el ejemplo 4.8. CASO III, Solución diluida………………..……………………….. Tabla 6.1.4. Reporte de resultados obtenidos por el método tradicional, para el ejemplo 4.9. CASO IV, Solución diluida…………………..…………………….. Tabla 6.2.1. Reporte de resultados obtenidos por el método tradicional, para el ejemplo 4.10. CASO I, Solución concentrada………………………………….. Tabla 6.2.2. Reporte de resultados obtenidos por el método tradicional, para el ejemplo 4.11. CASO II, Solución concentrada………………………………….. Tabla 6.2.3. Reporte de resultados obtenidos por el método tradicional, para el ejemplo 4.12. CASO III, Solución concentrada……………………………….. Tabla 6.2.4. Reporte de resultados obtenidos por el método tradicional, para el ejemplo 4.13. CASO IV, Solución concentrada……………………………….. D C E R E 130 131 133 134 S O AD V R E ES R S HO 129 135 136 137 138 139 140 224 226 227 228 240 242 243 244 ÍNDICE DE FIGURAS Pág. Figura 2.1. Diagrama simplificado de un evaporador de efecto simple..…… 41 Figura 2.2. Diagrama de entalpía-concentración para el sistema NaOHH2O…………………………………………………………………………..…….. 50 Figura 2.3. Diagrama de Duhring para el sistema NaOH-H2O.……………… 52 Figura 2.4. Curvas de solubilidad de algunas sales típicas en el agua……... Figura 2.5. Diagrama ilustrativo de los fundamentos de recompresión mecánica del vapor………………................................................................... Figura 4.1.1. Diagrama de un sistema de evaporación de un solo efecto….. Figura 4.1.2. Diagrama de Duhring representativo al cálculo de la temperatura de ebullición de la mezcla para soluciones concentradas…….. Figura 4.1.3. Diagrama de entalpía-concentración representativo al cálculo de la temperatura de ebullición para soluciones concentradas……………… Figura 4.1.4. Diagrama de un sistema de evaporación de efecto simple. Señalando como incógnita principal el área superficial de evaporador…….. Figura 4.1.5. Diagrama de un sistema de evaporación de efecto simple. Señalando el coeficiente global de transferencia de calor como incógnita principal…………………………………………………………………………….. Figura 4.1.6. Diagrama de un sistema de evaporación de efecto simple. Señalando la composición del soluto en la corriente final del evaporador, como incógnita principal…………………………………………………………... Figura 4.1.7. Diagrama de un sistema de evaporación de efecto simple. Señalando el flujo de alimentación al evaporador, como incógnita principal……………………………………………………………………………. Figura 4.2.1. Ingreso a un documento nuevo en Microsoft Excel…………… 54 Figura 4.2.2. Hoja de datos compartidos por los casos……………………… 111 Figura 4.2.3. Introducción de datos a la herramienta didáctica por caso….. 112 Figura 4.2.4. Identificación de la opción ‘Validación de datos’……………… 114 Figura 4.2.5. Selección del criterio de validación de datos………………….. 114 Figura 4.2.6. Selección de los datos a mostrar en la lista desplegable……. 115 Figura 4.2.7. Elaboración de la lista desplegable…………………………….. 115 DER R SE E R S O ECH S55 O D 78 VA 83 84 87 90 92 95 111 Figura 4.2.8. Convirtiendo unidades a kilogramo…………………………….. 116 Figura 4.2.9. Cambio de valor en la celda E11con respecto a la unidad proporcionada por la lista desplegable………………………………………… 117 11 Figura 4.2.10. Cambio de unidades para el flujo de alimentación en el caso1……………………………………………………………………………… 117 Figura 4.2.11. Determinación de los resultados, mediante el procedimiento 118 matemático recreado en las hojas de cálculo de Excel 2013………………. Figura 4.2.12. Reporte de resultados en la herramienta didáctica, Caso I.. 119 Figura 4.2.13. Cálculos respectivos a la sección de comparación………… 119 Figura 4.2.14. Tabla comparativa entre los resultados del ejercicio original, con los resultados obtenidos mediante la modificación de una variable especificada previamente………………………………………………………. 121 Figura 4.2.15. Opción ‘Proteger Hojas’ en Microsoft Excel 2013………….. 122 S O D VA ER S E R Figura 4.2.16. Ocultar hojas de cálculos……………………………………… S HO obtenidos del ejemplo 4.6 de Figura 4.2.17. Reporte de C resultados E soluciones diluidasE deR la herramienta didáctica para evaporadores de un D solo efecto………………………………………………………………………… Figura 4.2.18. Reporte de resultados obtenidos del ejemplo 4.7 de soluciones diluidas de la herramienta didáctica para evaporadores de un solo efecto………………………………………………………………………… Figura 4.2.19. Reporte de resultados obtenidos del ejemplo 4.8 de soluciones diluidas de la herramienta didáctica para evaporadores de un solo efecto………………………………………………………………………… Figura 4.2.20. Reporte de resultados obtenidos del ejemplo 4.9 de soluciones diluidas de la herramienta didáctica para evaporadores de un solo efecto………………………………………………………………………… Figura 4.2.21. Reporte de resultados obtenidos del ejemplo 4.10 de soluciones concentradas de la herramienta didáctica para evaporadores de un solo efecto…………………………………………………………………. Figura 4.2.22. Reporte de resultados obtenidos del ejemplo 4.11 de soluciones concentradas de la herramienta didáctica para evaporadores de un solo efecto…………………………………………………………………. Figura 4.2.23. Reporte de resultados obtenidos del ejemplo 4.12 de soluciones concentradas de la herramienta didáctica para evaporadores de un solo efecto…………………………………………………………………. Figura 4.2.24. Reporte de resultados obtenidos del ejemplo 4.13 de soluciones concentradas de la herramienta didáctica para evaporadores de un solo efecto…………………………………………………………………. 122 124 126 128 131 132 135 137 139 12 Figura 4.2.25. Seleccionando la opción ‘Complementos’, en Microsoft 142 Excel……………………………………………………………………………… Figura 4.2.26. Seleccionando la herramienta de análisis VBA……………. 143 Figura 4.2.27. Activar Macros para la herramienta de análisis VBA……… Figura 4.2.28. Incorporación de las tablas de vapor a la herramienta didáctica para evaporadores de un solo efecto……………………………... Figura 4.2.29. Creación de la hoja de cálculo donde tendrá lugar la calculadora de propiedades de vapor……………………………………...... Figura 4.2.30. Cálculos internos de la calculadora de propiedades de vapor…………………………………………………………………………….. Figura 4.2.31. Macro definido para el cálculo de propiedades del vapor de agua mediante la especificación de la presión en estado saturado………. Figura 4.2.32. Macro definido para el cálculo de las propiedades de vapor mediante el ingreso de condiciones de sobresaturación………………....... Figura 4.2.33. Macro definido para el cálculo de las propiedades de vapor mediante el uso de métodos de interpolación entre los valores reportados en la tabla de vapor……………………………………………………………... Figura 4.2.34. Especificando los comandos destinados a la ejecución de la calculadora……………………………………………………………………….. Figura 4.2.35. Ingreso de la presión saturada a la calculadora de propiedades del agua…………………………………………………………... Figura 4.2.36. Cálculo de las propiedades del vapor, a la presión de saturación introducida…………………………………………………………… Figura 4.2.37. Ingreso de la presión y la temperatura a la calculadora de propiedades del agua…………………………………………………………… Figura 4.2.38. Calculo de las propiedades del vapor, a la presión de saturación…………………………………………………………………………. Figura 4.2.39. Abriendo Visual Basic 2010 desde Microsoft Excel 2013….. 143 Figura 4.2.40. Creación de Ventana Auxiliar………………………………….. 154 Figura 4.2.41. Configuración del botón en la ventana creada……………... 155 Figura 4.2.42. Insertando botón de comando………………………………… 156 Figura 4.2.43. Modificando propiedades del botón insertado………………. 156 O H C E ER D 145 S 146 O D VA R SE E R S 144 147 147 148 149 150 150 151 151 153 Figura 4.2.44. Configurando botones en hojas de cálculo………………….. 157 Figura 4.2.45. Configuración del botón para redirigir a la hoja 2 del documento……………………………………………………………………….. 157 Figura 4.2.46. Selección de la hoja2 mediante el botón insertado en la hoja1 del documento…………………………………………………………….. 158 13 Figura 4.2.46. Página de inicio de la herramienta didáctica para evaporadores de un solo efecto………………………………………………… Figura 4.2.48. Convertidor de unidades básico……………………………….. Figura 4.2.49. Ventana auxiliar de selección de las propiedades del vapor de agua a mostrar………………………………………………………………… Figura 4.2.50. Ventana auxiliar configurada para mostrar las tablas de capacidades caloríficas del agua………………………………………………. Figura 4.2.51. Ventana auxiliar configurada para la selección del tipo de solución a tratar…………………………………………………………………… Figura 4.2.52. Ventana auxiliar configurada para la selección del tipo de caso a ejecutar……………………………………………………………………. Figura 4.2.53. Ventana auxiliar configurada para especificar las condiciones del vapor de agua destinado a calefacción en el evaporador… Figura 4.2.54. Ventana auxiliar destinada a proporcionar información al usuario…………………………………………………………………………..... Figura 4.2.55. Ventana auxiliar destinada a proporcionar información al usuario con respecto a los diagramas de entalpía vs concentración y el uso apropiado de ellos………………………………………………………….. Figura 5.1. Página de inicio….…………………………………………………. E R E D 160 161 S O D VA 161 161 R SE E R S CHO 159 159 162 163 163 177 Figura 5.2. Selección del tipo de solución a tratar ………………………….. 178 Figura 5.3. Ventanas de ayuda ………………………………………………… 179 Figura 5.4. Selección del caso a ejecutar ……………………………………. 180 Figura 5.5. Ingreso de datos para el CASO I diluido ………………………… Figura 5.6. Definiendo la temperatura del evaporador para soluciones diluidas.......................................................................................................... Figura 5.7. Definir la temperatura del evaporador para soluciones diluidas, mediante el uso de la calculadora de propiedades del agua ..……………… Figura 5.8. Especificando la presión del evaporador en la calculadora de propiedades del agua para determinar la temperatura de la solución……… Figura 5.9. Introduciendo valores en la ventana auxiliar correspondiente a la temperatura del evaporador para soluciones diluidas……………………... Figura 5.10. Definiendo entalpías de la solución……………………………… 182 Figura 5.11. Introducir entalpías de la solución. Para soluciones diluidas…. 187 182 183 184 185 186 Figura 5.12. Diagrama de entalpías…………………………………………… 187 Figura 5.13. Definiendo capacidades caloríficas de las soluciones de entrada y salida en soluciones diluidas………………………………………… 188 14 Figura 5.14. Introducir valores para especificar las condiciones de la corriente de vapor de agua al evaporador, para el ejemplo de solución diluida………………………………………………………………………………. 189 Figura 5.15. Procedimiento del CASO I………………………………………... 190 Figura 5.16. Reporte de resultados para solución diluida y CASO I………... 192 Figura 5.17. Ventana e ayuda referente al tipo de caso a seleccionar…….. 194 Figura 5.18. Ingreso de datos del caso seleccionado………………………… Figura 5.19. Definir temperatura del evaporador. Soluciones Concentradas……………………………………………………………………… Figura 5.20. Introducir el incremento del punto de ebullición. Para definir la temperatura del evaporador……………………………………………………... Figura 5.21. Explicación del diagrama de Duhring……………………………. 195 196 S O D A V R E ES R S HdelOevaporador…………………………... Figura 5.22. Introducir temperatura C E Figura 5.23. Reporte DEdeRla temperatura del evaporador……………………… 197 198 198 199 Figura 5.24. Definiendo entalpías de la solución……………………………… 199 Figura 5.25. Introducir entalpías. Solución concentrada……………………... Figura 5.26. Definiendo entalpía de la corriente de vapor para vapor sobrecalentado……………………………………………………………………. Figura 5.27. Introduciendo valores calculados mediante la calculadora de las propiedades del agua………………………………………………………… Figura 5.28. Definir método de especificación de la corriente S…………….. 200 Figura 5.29. Procedimiento del CASO III………………………………………. 205 Figura 5.30. Reporte de resultados para el CASO III………………………… 207 Figura 5.31. Selección de la variable a modificar…………………………….. 208 Figura 5.32. Introducir el nuevo valor de la variable a modificar……………. 208 Figura 5.33. Tabla comparativa de resultados………………………………… 208 Figura 5.34. Propiedades de vapor de agua………………………………….. 210 Figura 5.35. Tabla de capacidades caloríficas del agua…………………….. 211 Figura 5.36. Tabla de propiedades de vapor de agua……………………….. 211 201 202 204 Figura 5.37. Calculadora de propiedades de vapor………………………….. 212 Figura 5.38. Determinación de propiedades a través de la calculadora de vapor………………………………………………………………………………. 213 Figura 6.1.1. Aplicación de las tablas de vapor para determinar la temperatura del evaporador de soluciones diluidas………………………….. 220 15 Figura 6.1.2. Tabla de vapor de agua saturado, para determinar las condiciones de saturación de la corriente S…………………………………… Figura 6.2.1. Ubicación de la temperatura de saturación para el solvente puro en las tablas de vapor saturado…………………………………………… Figura 6.2.2. Identificación temperatura de la solución concentrada, del ejemplo 4.12. Mediante el diagrama de Duhring……………………………… Figura 6.2.3 Identificación de las entalpías de la solución para el ejemplo 4.10, en el diagrama de entalpía vs concentración para el sistema NaOHH2O………………………………………………………………………………... Figura 6.2.4. Ubicación de la entalpía del vapor de agua sobrecalentado generado en el evaporador……………………………………………………… Figura 6.2.5. Tabla de vapor de agua saturado, para determinar las condiciones de saturación en la corriente S, para el ejemplo 4.10…………. D 232 234 S O D 237 VA 235 R SE E R S O H C E ER 222 238 LISTA DE SIMBOLOS Y ABREVIATURAS Símbolos y abreviaturas utilizados para diseñar la herramienta didáctica para evaporadores de un solo efecto. Nombre de la variable Velocidad o flujo de alimentación Temperatura de la alimentación R S Velocidad o flujo de la corriente concentrada HO C E Composición del soluto enE corriente concentrada D la R Entalpía de la alimentación Unidad (SI) F kg/h SK O D A kJ/kg.K V Cpf R ESEhf kJ/kg Composición del soluto en la alimentación Capacidad Calorífica de la alimentación Nomenclatura Xf -- Tf P kg/h Xp -- Cpp kJ/kg.K hp kJ/kg V kg/h Hv kJ/kg S kg/h Ts K Pvap kPa hs kJ/kg Hs kJ/kg λ kJ/kg Incremento del punto de ebullición IPE K/°C Temperatura de ebullición de la solución T1 K Tref K U kJ/m².h.K A m² q kJ/h Psist kPa Capacidad Calorífica de la corriente concentrada Entalpía de la corriente concentrada Velocidad o Flujo de la corriente de salida del vapor evaporado Entalpía de la corriente de salida del vapor evaporado Flujo de la corriente de vapor destinado a calefacción Temperatura de saturación de la corriente de calefacción Presión de vapor de la corriente de calefacción Entalpía del líquido saturado en la corriente de calefacción Entalpía del vapor saturado en corriente de calefacción Calor latente Temperatura de referencia Coeficiente global de transferencia de calor Área Superficial de transferencia de calor en el evaporador Flujo de Calor en el evaporador Presión del Evaporador Mata M, María J. “Propuesta de una herramienta didáctica para evaporadores de un solo efecto” Trabajo Especial de Grado a ser presentado para optar al título de Ingeniero Químico. Universidad Rafael Urdaneta. Facultad de Ingeniería. Escuela de Ingeniería Química. Maracaibo, Venezuela. 2014. RESUMEN S O D VA R El presente trabajo especial de grado tuvo como objetivo proponer una herramienta didáctica para evaporadores de un solo efecto, dentro de la cátedra de Operaciones Unitarias II, impartida en la escuela de Ingeniería Química de la Universidad Rafael Urdaneta. Con la finalidad de incluir modelos de simulaciones de perspectiva didáctica durante el tiempo de desarrollo de la materia, los cuales permitirán mostrar cómo influyen hoy en día estos programas en la Ingeniería Química, así mismo, ayudará a optimizar el tiempo que se maneja para impartir la cátedra en cuestión e igualmente servirá de complemento a los docentes que opten por introducirla en su metodología de enseñanza. Esta investigación fue de tipo descriptivo, basada en un diseño de fuente mixta, ya que, para el cumplimiento del objetivo general se utilizó tanto la revisión bibliográfica como programas donde se recrearon los cálculos especificados para el diseño de evaporadores de simple efecto. Igualmente al desarrollar el procedimiento matemático para llevar a cabo la herramienta, se definieron ciertos criterios básicos. Posteriormente, recreados mediante el uso de Microsoft Excel 2013© en su modalidad ‘programador’. A continuación, se diseñaron y vincularon a la herramienta, ventanas auxiliares que tendrían como objetivo proporcionarle información al usuario sobre cada especificación del diseño de sistemas de evaporadores. Finalmente se elaboró un manual de usuario que explica el manejo adecuado del programa de perspectiva didáctica. Ahora bien, mediante los resultados obtenidos se comprobó la veracidad de la herramienta comparando dichos valores con los respectivos al método tradicional. Esta investigación presenta ciertas limitantes que fueron especificadas a lo largo del desarrollo de la misma, por lo que se recomienda realizar investigaciones complementarias en pro de ampliar el alcance de esta. O H C E ER D SE E R S Palabras claves: Herramienta didáctica, diseño de sistemas de evaporación, un solo efecto, modelo de simulación de perspectiva didáctica, manual del usuario. Correo electrónico: [email protected] Mata M, María J. “Proposal for a single effect evaporator teaching tool” Degree Thesis presented to opt for Bachelor of Science in Chemical Engineering Degree. Rafael Urdaneta University. Faculty of Engineering. School of Chemical Engineering. Maracaibo, Venezuela. 2014. ABSTRACT S O D VA R This degree thesis aimed to propose a teaching tool for single effect evaporators, within the Unit Operations II subject, taught at the School of Chemical Engineering, at Rafael Urdaneta University, in order to include didactic perspective simulation models during the time of development of the subject , which will allow to show how these programs influence chemical engineering nowadays, also, it will help to optimize the time it takes to impart the given subject and also will complement the works of those teachers who choose to implement it in their teaching methodology. This research was descriptive, based on a design of mixed source, since, for the fulfillment of the overall objective, both, literature review and software programs where the specified calculations for the design of single-effect evaporators were recreated, were used. Similarly while developing the mathematical procedure to implement the tool, certain basic criteria were defined which were subsequently recreated in Microsoft Excel 2013 © in the ' programmer ' mode. Then auxiliary windows were designed and liked to the tool, whose purpose would be to provide information to the user about each design specification of the evaporator design. Finally a user manual explaining the proper operation of the didactic perspective tool was crafted. To conclude, the results obtained proved the accuracy of the tool, when compared with the values obtained by using the traditional method. This research has certain limitations that were specified during the development of it , so it is recommended that additional research for expanding the scope of this. H C E ER O D SE E R S Keywords: teaching tool, evaporation systems design, single effect, didactic perspective simulation model, user manual. Email: [email protected] INTRODUCCIÓN En la actualidad existe un alto grado de desarrollo tecnológico, a medida que pasa el tiempo la humanidad va mejorando las herramientas mediante las cuales se puede trabajar de manera más eficiente para maximizar el aprendizaje. Al hablar de Operaciones Unitarias; nos encontramos en un amplio campo de procesos y etapas S O D VA que se llevan a cabo en la industria química, la cuales han sido siempre un tema muy extenso. R SE E R S Entre todos estos procesos se encuentra la Evaporación, la cual depende de O H C E es simple pero su entendimiento se dificulta de cierta forma, de modo que los ER D estudiantes buscan la mayor cantidad de herramientas disponibles para facilitar su muchos factores, ya sean sus propiedades físicas como químicas, esta operación comprensión, es por esto que este trabajo especial de grado contiene todo lo referido a la Evaporación de efecto simple, a sus diferentes funciones y utilidades. El propósito de este proyecto es desarrollar una herramienta didáctica para evaporadores de un solo efecto de manera que pueda ayudar significativamente a los estudiantes proporcionándoles los recursos necesarios para ampliar la obtención de sus conocimientos. Por tal motivo se procedió a: identificar las herramientas disponibles para los estudiantes; definir las bases y criterios para el desarrollo del proyecto; desarrollar el programa para la evaluación de los evaporadores de un solo efecto y por ultimo validar los resultados obtenidos por la herramienta con los obtenidos a través de la literatura. Así mismo, se puede decir que hoy en día existen diversas herramientas que pueden utilizarse para especificar el diseño de los sistemas de evaporación de un solo efecto, pero estas suelen ser muy costosas para ser utilizadas en estudios académicos e independientes, igualmente que no proporcionan un área de enseñanza a la persona que las utilice, por lo tanto se propone generar una herramienta didáctica que parte de modelos de simulación de perspectiva didácticos 20 los cuales le proporcionan al usuario a través de ventanas auxiliares, la información y descripción de las etapas que se requieren para diseñar un sistema de evaporación de efecto simple. En tal sentido el estudio se estructuró en cuatro capítulos. El capítulo I contiene el planteamiento del problema y su formulación, los objetivos de la investigación, la justificación, y finaliza con la delimitación del problema. El capítulo II, hace S O D VA referencia al marco teórico que comprende la revisión de la literatura, la cual abarca R SE E R S la descripción de los antecedentes que se especificaron para esta investigación, las bases teóricas y otros aspectos que sustentan teóricamente el estudio. O H C E ER D Así mismo el capítulo III, corresponde al marco metodológico, el cual constituye la guía para obtener los datos necesarios para la verificación del problema estudiado, y abarca los siguientes aspectos: tipo y diseño de investigación, técnicas e instrumentos de recolección de datos y culmina con las fases de investigación. Posteriormente, el capítulo IV, trata de los resultados de la investigación donde se describe el procedimiento utilizado para desarrollar las fases del trabajo especial de grado, al igual que se reportan los resultados obtenidos, el análisis y la comparación de los datos de la investigación con los datos de la literatura. Para finalizar se presentan las conclusiones, las recomendaciones, las referencias bibliográficas utilizadas y se finaliza con la inclusión de los anexos. CAPÍTULO I EL PROBLEMA Se desarrollan en este capítulo, los factores que motivan a la ejecución de este Trabajo S O D A V se comenta sobre la justificación y delimitación de la presenteR investigación. SE E R S O H 1.1. Planteamiento del problema C E R E D Los procesos de las industrias químicas se pueden ver fraccionados por partes, estas, Especial de Grado, abordando la problemática que dio lugar a su creación, junto con las propuestas planteadas para hacer frente al problema enunciado. De igual forma, podrían estudiarse y operarse de forma individual, algunas de las etapas que conforman el proceso en cuestión pueden consistir en reacciones químicas, mientras que otras se encargan de los cambios físicos de la solución a producir; calentamiento, absorción, concentración, cambios de fases, mezclado, pulverización, entre otros. La ingeniería química se considera versátil en lo que se refiere a la descomposición de los procesos en las industrias; subdividiéndolos en etapas físicas individuales, y de esta forma ampliar los conocimientos y entrenamientos prácticos por cada una de ellas, para favorecer el funcionamiento del proceso en general. Estas etapas físicas, se denominan operaciones unitarias. A lo largo de los estudios que se requieren para optar por el título de ingeniero químico, se imparten ciertas materias referentes a estas etapas físicas ya mencionadas anteriormente, donde se busca proporcionar los conocimientos y características de las principales operaciones unitarias en los procesos de la industria química. En el caso de la Universidad Rafael Urdaneta, forma parte del plan de estudio de la escuela de ingeniería química; la cátedra Operaciones Unitarias II. La cual abarca los procesos de separación física de la materia o purificación de la misma. En esta, se 22 hacen los estudios pertinentes de los equipos principales de dichos procesos, como lo son los evaporadores, evaporadores flash, destilación binaria y destilación multicomponentes. Al enfocase en los sistemas de evaporación, se podría concluir que este tipo de Operación Unitaria se encarga de la concentración de soluciones, las cuales se conforman por solutos no volátiles y solventes volátiles. La concentración se origina S O D VA haciendo pasar dicha solución por una cámara en donde ocurre una transferencia ER S E R ambas corrientes; el vapor que pasa porS los tubos sede su calor transmitiéndoselo O H C a la solución y elevando su temperatura, lo que a continuación, generará la E R E en el producto a concentrar. Dsolvente evaporación del de calor; la misma es iniciada, por el contacto de esta solución con una corriente de vapor que transcurre a través de un serpentín de forma que al entrar en contacto Para el caso específico del diseño de un sistema de evaporadores, se detecta en la práctica, que la unificación de la enseñanza de este tema, en conjunto con sistemas de simulación de perspectiva didáctica, ayudará a la comprensión de esta operación unitaria enfocada en los procesos de separación. Este planteamiento busca demostrar la necesidad de implementar una herramienta que permita simplificar la comprensión de esta Operación Unitaria fundamental de la Ingeniería Química. En el diseño de un sistema de evaporadores se debe tomar en cuenta que al momento de recolectar los datos necesarios para llevar a cabo el objetivo, se presentan ciertas dificultades que al impartir la materia, aumentarán las complicaciones del tema, generando confusiones y disminuyendo la compresión y el rendimiento por parte de los alumnos. Para la recolección de datos en el diseño de un sistema de evaporadores, lo primero y lo más relevante que se deberá tomar en cuenta es que las soluciones capacitadas para ser incluidas en este tipo de procesos, deben estar conformadas por solutos no volátiles, de forma que no se evapore con el solvente en la solución, y permita lograr la concentración del producto deseado. Por otro lado, se deben buscar ciertas 23 variables indispensables en el desarrollo del diseño de un sistema de evaporadores como podrán ser; las entalpias y la elevación del punto de ebullición de la mezcla, las cuales podrían estar regidas e igualmente limitadas por diagramas particulares y académicos. Así mismo, los cálculos por los que se establece el diseño de un sistema de evaporación, suelen implicar múltiples consideraciones y en algunos casos confusos a la hora de distinguir las variables que se desean obtener. S O D VA Igualmente, es necesario resaltar el factor tiempo. Si bien es cierto, al momento de ER S E simulación de un sistema de evaporadores. AlR implementar la herramienta didáctica S O H se busca optimizar el tiempo que se maneja C de evaporadores de un solo efecto, E ER para impartir laD cátedra en cuestión, favoreciendo de esta forma tanto al alumnado comprender las diferentes operaciones unitarias, se requiere de un tiempo de aprendizaje gradual; de cada uno de los pasos a seguir para armar el modelo de como a los docentes encargados de dicha labor. Así mismo, estos factores representarían parte importante del diseño de los sistemas de evaporadores en la materia de Operaciones Unitarias II, de manera que se busca implementar una herramienta que automatice los pasos que resultan comunes a los procesos de solución, orientando a su vez en la recolección de los valores obtenidos por las variables mencionadas anteriormente, y aplicarlos a los cálculos propios del diseño, junto con una sección de comparación en donde el aspirante a ingeniero químico pueda observar cómo afecta la manipulación de algunas variables en comparación con los resultados originales. De esta forma, se colabora en agilizar y optimizar el proceso de enseñanza, incluyendo simulaciones en simultáneo que permitirán mostrar como introducción a los alumnos la importancia y los beneficios que estos programas proporcionan a la Ingeniería Química. 24 1.1. Objetivos de la investigación 1.1.1. Objetivo general: Proponer una herramienta didáctica para evaporadores de un solo efecto. 1.1.2. 1. Objetivos específicos: Programar el procedimiento matemático de la herramienta didáctica para O H C E ER evaporadores de un solo efecto. 3. R SE E R S evaporadores de un solo efecto. 2. S O D VA Establecer el procedimiento matemático de la herramienta didáctica para D Desarrollar las ventanas de usuario de la herramienta didáctica para evaporadores de un solo efecto. 4. Elaborar el manual de usuario de la herramienta didáctica para evaporadores de un solo efecto. 1.2. Justificación de la investigación Este trabajo de investigación busca implementar una herramienta didáctica que complemente y facilite la explicación paso a paso que se debe llevar a cabo para diseñar un sistema de evaporadores de simple efecto, en donde se beneficiarán no solo los docentes que opten por este complemento, sino también, los alumnos o usuarios que la utilicen para ampliar sus conocimientos sobre la cátedra de Operaciones Unitarias específicamente el área de los sistemas de evaporadores de un solo efecto. Es de considerar, que en el diseño de sistemas de evaporadores, es necesario hacer uso de graficas que complementan el cálculo de las entalpías de la solución, e igualmente favorecen a la determinación de la elevación del punto de ebullición de la mezcla a concentrar. Así mismo, al hablar de evaporación utilizando como medio de calentamiento vapor de agua en condiciones de saturación, es 25 fundamental especificar las condiciones de esta corriente a través de las tablas de vapor de agua saturación. De la misma forma, en caso de que la solución sea acuosa, las propiedades que presente el solvente evaporado, deben determinarse a partir de la información termodinámica tabulada para este compuesto. Al percatarse de estos factores dentro del procedimiento matemático del diseño de evaporadores desde la perspectiva académica, es necesario incluir en la S O D VA herramienta didáctica para evaporadores de un solo efecto, una descripción de las ER S E R se adaptaron a una hoja de cálculo, en donde con simples instrucciones señaladas, S O Hdidáctico, pueda calcular las condiciones de C el complemento de simulación E ER saturación o D sobrecalentamiento para la corriente de vapor, especificando gráficas, junto con una explicación de la manera que deben utilizarse. Por otra parte, cuenta con las tablas de vapor dentro de su estructura, e igualmente dichas tablas únicamente dos variables. Igualmente, con la finalidad de verificar los efectos de la modificación de las variables de proceso en estos sistemas, la herramienta debe incluir una sección de comparación de resultados, en donde los usuarios que hagan uso de ella, podrían manipular ciertas variables del sistema y comparar los resultados obtenidos con los originales, dándole una perspectiva diferente en lo que se refiere a las variables del diseño de sistemas de evaporadores de un solo efecto, explorando de esta forma, los efectos que esta modificación genera en el desempeño del sistema. Por otro lado, encontramos que esta herramienta dará inicio a la incorporación del método de simulación de perspectiva didáctica dentro de la cátedra de Operaciones Unitarias, la cual es de gran relevancia ya que uno de los complementos más comunes e importantes dentro de la Ingeniería Química es precisamente el uso de los simuladores de procesos en sus estudios de verificación y diseño. Igualmente busca motivar la indagación referente al tema de simuladores con perspectiva didáctica, de forma que se sigan realizando investigaciones en esta área. 26 Además, esta herramienta podría servir como base para que nuevas investigaciones puedan ampliar este sistema, desarrollando más áreas de estudio, como podría ser; incluir el área de optimización de los sistemas de evaporadores o ampliar este mismo trabajo de investigación para sistemas de múltiples efectos, también puede servir de guía para la elaboración de procesos similares dentro de la misma cátedra, como por ejemplo, realizar una propuesta para sistemas de destilación. S O D VA ER S E R incluyendo en su estructura simulaciones que en conjunto con la bibliografía S O Hde la forma en la cual se ingresen y se ubiquen C adecuada orienten la comprensión E ER los datos, paraD lograr así el objetivo de simplificar el entendimiento de este tema. Por otra parte, mediante esta investigación se pretende generar una propuesta sobre el desarrollo de una herramienta para impartir el tema de evaporadores, Este sistema busca elevar el rendimiento académico en esta área, a partir del desarrollo de dicha herramienta didáctica, contemporánea y automatizada que servirá como complemento para dictar la materia Operaciones Unitarias II. 1.3. Delimitación de la investigación 1.3.1. Espacial Esta investigación se realizó en la República Bolivariana de Venezuela, dentro del Estado Zulia, específicamente en la Universidad Rafael Urdaneta, ubicada en la avenida El Milagro, Vereda del Lago dentro de la ciudad de Maracaibo. 1.3.2. Temporal Esta investigación se realizó en el periodo comprendido entre septiembre del 2013 y octubre de 2014. 27 1.3.3. Científica El modelo que se desarrolló está orientado a la simulación de sistemas de evaporadores de un solo efecto, para el cual será necesario tomar como base conocimientos previamente adquiridos en las diferentes áreas impartidas durante la carrera Ingeniería Química, como el área de Operaciones Unitarias, Fisicoquímica y Programación. S O D Apleno dominio más relevantes de la escuela de Ingeniería Química, deberán V tener R SyEBalances de Energía y de los estudios de Termodinámica, Fisicoquímica E R S O Materiales los cuales serán esenciales en el desarrollo del diseño de los sistemas H C E R de evaporadores de un solo efecto. DE Específicamente al hacer referencia de los conocimientos impartidos en las áreas A su vez, el área de Programación se ve reflejada en gran parte durante el desarrollo de la herramienta didáctica para evaporadores de un solo efecto, ya que a lo largo de sus objetivos fue necesario acudir a estos conocimientos, para darle forma a los procesos matemáticos que conforman los sistemas de evaporación, de igual forma, fue necesario desarrollar la interfaz de usuario por donde la persona que haga uso de la herramienta pueda introducir los datos adecuados y calcular los resultados de acuerdo a las condiciones previamente definidas. CAPÍTULO II MARCO TEÓRÍCO Cada investigación presenta consigo ciertas incertidumbres que revelan el interés S O D A del Trabajo Especial De Grado se incluirán las investigaciones yaV realizadas que se R SseEincluyó una exhaustiva E presentarán como antecedentes del mismo. Además, R Sa estudiar, esto con el propósito de O H revisión bibliográfica sobre las variables C E R E sumergirnos en D el componente teórico, emplearlo de manera eficaz, y generar a su en un tema en especial, y en muchas ocasiones estas incógnitas nacen de trabajos de investigaciones que han marcado precedentes; razón por la cual en esta sección vez una propuesta de una herramienta didáctica para evaporadores de un solo efecto que sirva de la manera más adecuada en el campo de estudio. 2.1. Antecedentes Los estudios anteriores representan la información que sirve de base para establecer, descubrir o plantear nuevos esquemas. En este orden de ideas, se ha hecho la debida recolección de documentación histórico - teórica de proyectos anteriores relacionados con la presente investigación. Rincón (2013). Desarrollo de herramienta de cálculo para la eficiencia de las calderas generadoras de vapor. Trabajo especial de grado para optar por el título de Ingeniero Químico en la Universidad Rafael Urdaneta, Maracaibo Edo. Zulia, Venezuela. El presente trabajo especial de grado tuvo como objetivo desarrollar una herramienta de cálculo para evaluar la eficiencia de las calderas generadoras de vapor empleando el método indirecto propuesto por la norma ASME PTC 4-2008. 29 Con el fin de alcanzar lo propuesto, se identificaron las calderas existentes en planta eléctrica del área de servicios industriales del complejo petroquímico Ana María Campos. El presente trabajo especial de grado tuvo como objetivo desarrollar una herramienta de cálculo para evaluar la eficiencia de las calderas generadoras de vapor empleando el método indirecto propuesto por la norma ASME PTC 4-2008. S O D A Ana María eléctrica del área de servicios industriales del complejo petroquímico V R SE Campos. E R S O H C y criterios para el desarrollo de la herramienta, E R Así mismo, se definieron las bases E D según lo dispuesto por la norma, además se determinaron los parámetros Con el fin de alcanzar lo propuesto, se identificaron las calderas existentes en planta necesarios para la evaluación de la eficiencia, es decir las propiedades del combustible, agua, vapor y aire. Luego, aplicando la norma propuesta, se desarrolló el programa utilizando Excel en conjunto con Visual Basic. Posteriormente, se verificó el programa con los datos de diseño de las calderas identificadas, obteniendo como resultado una desviación con respecto a la eficiencia de 0,45% y 0,12% respectivamente para las calderas 1 y 2. Finalmente se validó la herramienta de cálculo creada con los valores promedios obtenidos de los datos operacionales. Dicha investigación sirve como guía para llevar a cabo el segundo objetivo específico dentro de este trabajo especial de grado, ya que el procedimiento utilizado para diseñar la herramienta de simulación sobre la eficiencia de las calderas, es similar a la metodología empleada para desarrollar la herramienta didáctica del diseño de los sistemas de evaporadores. Sirviendo de gran ayuda en el desarrollo de este proyecto. 30 García, Peña y López (2010). Desarrollo De Un Sistema De Evaporación Y Concentración De Jugos De Múltiple Efecto Para Mejorar La Eficiencia Térmica Y Productividad Y Disminuir El Impacto Ambiental En La Producción De Panela. Artículo de Investigación; elaborado por la Corporación Colombiana de Investigación Agropecuaria CORPOICA, Bogotá, Colombia. Colombia es el primer productor de panela en América y el segundo, a nivel mundial, S O D desarrollándose en el país para este sector agroindustrial, V aúnA se presentan R E Sel proceso de producción problemas tecnológicos que afectan directamente E R S O panelera, la rentabilidad y sostenibilidad económica del mismo. Entre los principales H C eficiencia energética, que incrementa los costos E R problemas se encuentran la baja E D de producción y los problemas ambientales por emisiones de gases y calor al después de la India. Sin embargo y pese al adelanto tecnológico que ha venido ambiente. Por estos motivos CORPOICA propuso diseñar, construir y optimizar un sistema de evaporación de múltiple efecto, que busca aprovechar el vapor generado en la producción de panela y así mejorar la eficiencia térmica del proceso. Con el desarrollo de un prototipo elaborado a través de programadores, donde se pueda recrear el sistema de evaporación destinado a la producción de la panela, de forma que ayude a mejorar el funcionamiento real del sistema. Esta investigación realizada por la Corporación Colombiana De Investigación Agropecuaria, sirvió soporte a lo largo de la elaboración de este trabajo especial de grado, especialmente duran el desarrollo del objetivo 2; el cual se enfocó en diseñar un sistema de evaporación con perspectiva didáctica valiéndose de herramientas de programación. 31 Báez y Salas (2014). Dimensionamiento de equipos en procesos de absorción química para endulzamiento de gas natural. Trabajo especial de grado para optar por el título de Ingeniero Químico en la Universidad Rafael Urdaneta, Maracaibo Edo. Zulia, Venezuela. El presente trabajo especial de grado tuvo como objetivo proponer un modelo de simulación en una hoja de cálculo de Excel para el dimensionamiento de equipos S O D A rápida y plantear un instrumento de cálculo que permita obtener de una manera V R E de endulzamiento Sproceso precisa, las dimensiones de los equipos principales del E R S mediante la absorción química. HO C E R DE en procesos de absorción química para endulzamiento de gas natural, con el fin de Para la realización del modelo de simulación, se definieron los procesos y equipos comprendidos en los sistemas de endulzamiento mediante absorción química con aminas y con carbonato de potasio, a los cuales posteriormente se les estableció un procedimiento de cálculo; que abarca, el dimensionamiento de torres de absorción, regeneración, separadores y calentadores que se consideraron los más relevantes para el desarrollo del proceso. Finalmente se elaboró un manual de usuario para el manejo adecuado del programa. A través de los resultados obtenidos del modelo de simulación, cálculos manuales y el contraste entre ellos, se concluyó que el modelo de simulación logra cubrir ciertas limitantes de los simuladores comerciales; sin embargo el mismo modelo cuenta con sus propias limitantes en base a la información bibliográfica. A su vez, este modelo permite comparar los diferentes sistemas de absorción para evaluar factores de eficiencia; fundamental en el desarrollo de proyectos de ingeniería. Éste trabajo de investigación sirvió de complemento para la elaboración de la herramienta didáctica para evaporadores de un solo efecto. Así mismo, formo parte 32 fundamental del desarrollo del manual de usuario; tomando toda la información con respecto a procedimiento de este objetivo para posteriormente aplicarlo durante la ejecución del cuatro objetivo de este trabajo especial de grado. 2.2. Bases teóricas Las bases teóricas forman parte esencial de la investigación, las mismas dan el S O D VA aporte necesario para el completo entendimiento del problema y su solución ER S E comprenden un Sistema de Evaporación yS sus R fundamentos teóricos, así mismo, se O H de los antecedentes ya mencionados para abrirá́ camino a la investigación partiendo C E ERde la herramienta didáctica para evaporadores de un solo llevar a cabo la D práctica respectiva. De esta manera, se pueden diagnosticar mediante estas, las variables que componen el problema. En este sentido, se definirán los conceptos básicos que efecto. 2.2.1. Sistemas de Unidades Para Geankoplis (1998), Existen tres sistemas de unidades fundamentales empleados actualmente en la ciencia y la ingeniería. El primero y lo resalta como el más importante; es el sistema SI (Systeme International d’unités), cuyas tres unidades básicas son el metro (m), el kilogramo (kg) y el segundo (s). Así mismo, Geankoplis (1998), identifica los otros sistemas como; el sistema INGLES: pie (ft) - libra (Ib) - segundo (s) o sistema PLS (FPS). Y en último lugar el sistema centímetro (cm) - gramo (g) - segundo (s), o sistema CGS. En la actualidad se ha adoptado ya el sistema SI de manera oficial para usarse en ingeniería y las ciencias. Para Geankoplis (1998), los sistemas INGLES y CGS todavía tienen bastante aceptación. Muchos de los datos químicos y físicos, así como las ecuaciones empíricas, están expresados en estos dos sistemas. Por tanto, el ingeniero no sólo debe conocer a la perfección el sistema SI, sino además poseer cierto grado de familiarización con los otros dos sistemas. 33 2.2.1.1. El sistema de unidades SI Geankoplis (1998), Explica que las unidades fundamentales del sistema SI son: la unidad de longitud es el metro (m); la de tiempo es el segundo (s); la de masa es el kilogramo (kg); la de temperatura es el Kelvin (K); y la de un elemento es el kilogramo mol (kg mol). Las unidades restantes se derivan de estas cantidades. La unidad de fuerza es el newton (N), que se define como 1 newton (N) = 1 kg·m2/s2 S O D VA R SE E R S La unidad básica de trabajo, energía o calor es el newton-metro, o joule (J): O H C E ER 1 joule (J) = 1 newton·m (N·m) = 1 kg·m2/s2 D La potencia se mide en joule/s o watts (W): 1 joule/s (J/s) = 1 watt (W) La unidad de presión es el newton/m2 o Pascal (Pa): 1 newton/m2 (N/m2) = 1 Pascal (Pa) El Sistema SI de unidades fundamentales usado en este texto y otros sistemas de unidades La presión en atmósferas (atm) no es una unidad estándar del sistema SI, pero se usa en la etapa de transición. La aceleración de la gravedad se define como: 1 g = 9,80665 m/s2 Algunos de los prefijos para múltiplos de las unidades básicas son: Giga (G) = 109; mega (M) = 106; kilo (k) =103, centi (c) = 10-2 ; mili (m) = 10-3; micro (p) = 10-6 y nano (n) = 10-9. El prefijo c es poco usual. Las temperaturas se definen en Kelvin (K), como unidad estándar del sistema SI. Sin embargo, en la práctica se usa mucho la escala Celsius (⁰C) que se define como T °C = T(K) – 273,15 34 Nótese que 1 °C = 1 K cuando se trata de diferencias de temperatura, ∆T⁰C = ∆TK La unidad estándar de tiempo preferible es el segundo (s), pero también puede expresarse en unidades no decimales de minutos (min), horas (h) o días (d). 2.2.1.2. El sistema de unidades CGS S O D VA R SE E R S El sistema CGS se relaciona con el sistema SI como Geankoplis (1998) a HO C E 1 g masa (g) = 1 x 10 ER continuación lo describe: D -3 kg masa (kg) 1 cm = 1 x 10-2 m 1 dina = 1 g · cm/s2 = 1 x 10-5 newton (N) 1 erg = 1 dina · cm = 1 x 10-7 joule (J). La aceleración estándar de la gravedad es: g = 980,665 cm/s 2.2.1.3. El sistema inglés de unidades (PLS) A continuación Geankoplis (1998), muestra la equivalencia entre el sistema inglés y el SI: 1 Ib masa = 0,45359 kg 1 pie = 0,30480 m 1 Ib fuerza (lbf) = 4,4482 newton (N) 1 pie · lbf = 1,35582 newton · m (N · m) = 1,35582 joules (J) 1 lb/pulg2 abs = 6,89476 x 103 newton/m2 (N/m2) 1,8 °F = 1 K = 1 °C (centígrado o Celsius) g = 32,174 pie/s 35 2.2.2. Principios fundamentales en la ingeniería química 2.2.2.1. Conservación de la masa Para definir la ley de conservación de la masa, Geankoplis (1998, p13.), expresa: Una de las leyes básicas de física es la ley de la conservación de la masa. Esta ley, expresada en forma simple, enuncia que la masa no puede crearse ni destruirse (excluyendo, por supuesto, las reacciones nucleares o atómicas). Por consiguiente, la masa (o el peso) total de todos los materiales que intervienen en el proceso debe ser igual a la de todos los materiales que salen del mismo, más la masa de los materiales que se acumulan o permanecen en el proceso. S O D VA E(Ec.R2.1) S E SR O Entradas = salidas + acumulación H C E ER Según Geankoplis (1998). En la mayoría de los casos no se presenta acumulación D de materiales en el proceso, por lo que las entradas son iguales a las salidas. A este tipo de sistema se le llama proceso en estado estacionario. Entradas = salidas (estado estacionario) 2.2.2.2. (Ec. 2.2) Conservación de la Energía Para llevar a cabo los balances de materiales basándonos en el argumento de Geankoplis (1998), se utiliza la ley de conservación de la masa, la cual indica que la masa que entra al sistema es igual a la que sale más la acumulada en el proceso. De manera similar Geankoplis (1998) explica sobre la ley de conservación de la energía. La cual postula que toda la energía que entra a un proceso es igual a la que sale más la que queda en el proceso. La energía puede manifestarse de varias maneras, Geankoplis (1998) define qué; Algunas de sus formas más comunes son la entalpía, la energía eléctrica, la energía química (en términos de la ∆H de la reacción), la energía cinética, la energía potencial, el trabajo y el flujo de calor. 36 2.2.2.3. Balance de masa o materiales Según Geankoplis (1998), en la dinámica de fluidos se estudia el movimiento de éstos. Por lo general, se transfieren de un lugar a otro por medio de dispositivos mecánicos tales como bombas o ventiladores por carga de gravedad o por presión, y fluyen a través de sistemas de tuberías o equipo de proceso. Basándose en las publicaciones de Geankoplis (1998) el primer paso en la S O D A del mismo. de conservación de la masa a la totalidad del sistema o a unaV parte R E S Considerando primero un balance elemental para una geometría simple, para E R S de masa. O deducir después la ecuación general de balance H C E R E = Salida + Acumulación (Ec. 2.3) DEntrada resolución de los problemas de flujo casi siempre consiste en aplicar los principios a. Volumen de control para balances Geankoplis (1998 p52) se refiere al volumen de control para los balances de la siguiente manera: Las leyes de conservación de la masa, la energía y el momento lineal se refieren siempre a un sistema y gobiernan la interacción de dicho sistema con sus alrededores. El sistema se define como una cierta cantidad de fluido de identidad conocida. Sin embargo, en el flujo de fluidos no es fácil identificar las partículas individuales. Así mismo Geankoplis (1998), continúa argumentando que la atención de estos, se centra en un cierto espacio a través del cual fluye la solución en vez de hacerlo con una cierta masa del fluido. El método empleado que resulta más conveniente consiste en seleccionar un volumen de control que es una región constante en el espacio a través de la cual fluye el compuesto. 37 b. Ecuación global para el balance de masa Geankoplis (1998), explica que al deducir la ecuación general para el balance total de masa (Ec. 2.17), la ley de la conservación de la masa puede enunciarse como sigue para un volumen de control donde no se genera masa: ( + ( 2.2.2.4. S O D VA Velocidad de salida Velocidad de Entada ) ( ) de masa de masa del volumen de control al volumen de control R SE E R S O H C E ER Velocidad de acumulación Velocidad de generación )= 0 ( ) (Ec 2.4) de masa de masa en el volumen de control D Balance de Energía Para la elaboración del balance de energía según Geankoplis (1998), se aplica el principio de conservación de la energía a un volumen de control fijo en el espacio de manera similar al caso de conservación de la masa, para obtener los balances generales de masa. La ecuación de conservación de la energía se combina con la primera ley de la termodinámica, a fin de obtener la ecuación global final de balance de energía. La primera ley de la termodinámica puede escribirse como: ∆E = Q – W (Ec. 2.5) Geankoplis (1998) continúa describiendo la reseña de la ecuación 2.19, donde especifica: E: es la energía total por unidad de masa de fluido. Q: es el calor absorbido por unidad de masa de fluido W: es el trabajo de cualquier clase realizado por unidad de masa de fluido sobre los alrededores. 38 Por otro lado Geankoplis (1998), describe el balance para una cantidad que se conserva, como en el caso de la energía. Es similar a la ecuación 2.18 y se expresa como sigue para un volumen de control. Velocidad de salida - velocidad de entrada + velocidad de acumulación = 0 (Ec. 2.6) 2.2.3. Operaciones Unitarias S O D VA Para definir este concepto, McCabe (2007, p4), compara las operaciones unitarias como operaciones individuales, enunciando lo siguiente: R O SE E R S Las operaciones individuales tienen técnicas comunes y se basan en los mismos principios científicos. Por ejemplo, en la mayoría de los procesos es preciso mover los sólidos y los fluidos; transferir calor u otras formas de energía de una sustancia a otra, y realizar operaciones como el secado, reducción del tamaño, destilación y evaporación. El concepto de operación unitaria es el siguiente: mediante el estudio sistemático de estas operaciones en sí mismos, operaciones que evidentemente constituyen la trama de la industria y las líneas de producción, se unifica y simplifica el tratamiento de todos los procesos. H C E ER D De la misma forma, McCabe (2007), argumenta que aunque las operaciones unitarias son una rama de la ingeniería, se basan de igual manera en la ciencia y la experiencia. Él asegura que las mismas deben combinar la teoría y la práctica para diseñar el equipo, construirlo, ensamblarlo, hacerlo operar y darle mantenimiento. Por otro lado, el autor Foust, (2006 p17), define las operaciones unitarias como las etapas de un proceso, como se cita a continuación: El proceso puede ser cualquier conjunto de etapas que impliquen modificaciones de la composición química o ciertos cambios físicos en el material que se va a preparar, procesar, separar o purificar. El trabajo de muchos ingenieros químicos involucra la selección de las etapas adecuadas en el orden apropiado para formular un proceso capaz de conducir a la elaboración de un producto químico, una separación o una purificación. Ya que cada una de las etapas que constituyen un proceso se encuentra sujeta a variaciones, el ingeniero de proceso debe especificar también las condiciones exactas bajo las cuales debe llevarse a cabo cada etapa. 39 Para Geankoplis (1998), los procesos químicos y físicos, así como los biológicos y alimenticios, presentan semejanzas en cuanto a la forma en que los materiales de entrada o de alimentación se modifican o se procesan para obtener los productos finales. Este autor considera que estos procesos químicos, físicos o biológicos, aparentemente distintos se pueden clasificar en una serie de etapas individuales y diferentes entre ellas; llamadas Operaciones Unitarias, las mismas se encuentran en todos los tipos de industrias de proceso. S O D VA ER S E R Para Geankoplis (1998, p313), las Operaciones Unitarias se pueden clasificar de la S O H siguiente forma: C E R E Estudia los principios que determinan el flujo y transporte 1. Flujo de Dfluidos: 2.2.3.1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. Clasificación de las Operaciones Unitarias de cualquier fluido de un punto a otro. Transferencia de calor: Esta operación unitaria concierne a los principios que gobiernan la acumulación y transferencia de calor y de energía de un lugar a otro. Evaporación: Éste es un caso especial de transferencia de calor, que estudia la evaporación de un disolvente volátil (como el agua), de un soluto no volátil como la sal o cualquier otro tipo de material en solución. Secado: Separación de líquidos volátiles casi siempre agua de los materiales sólidos. Destilación: Separación de los componentes de una mezcla líquida por medio de la ebullición basada en las diferencias de presión de vapor. Absorción: En este proceso se separa un componente gaseoso de una corriente por tratamiento con un líquido. Separación de membrana: Este proceso implica separar un soluto de un fluido mediante la difusión de este soluto de un líquido o gas, a través de la barrera de una membrana semipermeable, a otro fluido. Extracción líquido-líquido: En este caso, el soluto de una solución líquida se separa poniéndolo en contacto con otro disolvente líquido que es relativamente inmiscible en la solución. Adsorción: En este proceso, un componente de una corriente líquida o gaseosa es retirado y adsorbido por un adsorbente sólido. Lixiviación líquido-sólido: Consiste en el tratamiento de un sólido finamente molido con un líquido que disuelve y extrae un soluto contenido en el sólido. Cristalización: Se refiere a la extracción de un soluto, como la sal, de una solución por precipitación de dicho soluto. 40 12. Separaciones físico-mecánicas: Implica la separación de sólidos, líquidos o gases por medios mecánicos, tales como filtración, sedimentación o reducción de tamaño, que por lo general se clasifican como operaciones unitarias individuales. Así mismo, Geankoplis (1998), explica que las operaciones unitarias comparten entre ellas ciertos principios básicos, toma como ejemplo; el mecanismo de difusión o de transferencia de masa presentes en el secado, absorción, destilación y S O D VA cristalización. La transferencia de calor es común al secado, la destilación, la evaporación, etc. 2.2.4.1. O H C E ER 2.2.4. Evaporación D R SE E R S Definición de Evaporación Para Foust (2006). La evaporación es la operación unitaria que se encarga de concentrar una solución mediante la eliminación del disolvente por ebullición. Él mismo explica; que por lo general la concentración se detiene antes que el soluto comience a precipitarse de la solución. En consecuencia, un evaporador debe consistir básicamente de un intercambiador de calor capaz de hervir la solución y un dispositivo para separar la fase vapor del líquido en ebullición. Así mismo, Martínez (2004 p120), concluye refiriéndose a la descripción de los evaporadores, lo siguiente: Un evaporador de transmisión indirecta de calor, no es más que un intercambiador de calor modificado. Puesto que la evaporación implica una ebullición, la subcapa gaseosa en contacto con la fase líquida en la interfase líquido-vapor, estará constituida por vapor generado y por consiguiente no habrá resistencia a la transferencia de materia en la fase gaseosa, de ahí que esta operación esté controlada por la velocidad de transferencia de calor y no por la correspondiente de transferencia de materia McCabe (2007) define el objetivo de la evaporación como el de concentrar una solución consistente compuesta por un soluto no volátil y un solvente volátil. De la misma forma, argumenta que en la mayor parte de las evaporaciones, el solvente es agua. En la evaporación, por lo general, el producto valioso es el líquido 41 concentrado mientras que el vapor se condensa y se desecha. Sin embargo, en un caso específico es probable que ocurra lo contrario. Para la obtención de agua mineral, esta es la que se evapora obtener un vapor exento de sólidos el cual posteriormente se condensara para la alimentación de calderas, para procesos con requerimientos especiales o para el consumo humano. Por otra parte, McCabe (2007 p511), realiza una comparación de la evaporación con respecto a otras Operaciones Unitarias. S O D VA La evaporación difiere del secado en que el residuo es un líquido, (algunas veces altamente viscoso) en vez de un sólido; se diferencia de la destilación en que el vapor es generalmente un solo componente y, aun cuando el vapor sea una mezcla, en la evaporación no se intenta separar el vapor en fracciones; difiere de la cristalización en que su interés reside en concentrar una solución y no en formar cristales. En ciertas situaciones, por ejemplo, en la evaporación de salmuera para producir sal común, la frontera entre evaporación y cristalización dista mucho de ser nítida. O H C E ER D 2.2.4.2. R SE E R S Operación de un sistema de evaporación para efecto simple Geankoplis (1998), con la finalidad de resumir el método de operación de los evaporadores de efecto simple. Realiza una reseña de las variables que afectan el evaporador, tomando como ejemplo la figura 2.2 en donde se muestra un diagrama simplificado del evaporador de una sola etapa o de efecto simple. Figura 2.1. Diagrama simplificado de un evaporador de efecto simple. Geankoplis (1998) específica para figura 2.2. Que la alimentación entra a Tf y en la sección de intercambio de calor entra vapor saturado a Ts. El vapor condensado 42 sale en forma de pequeños chorros. Puesto que se supone que la solución del evaporador está completamente mezclada, el producto concentrado y la solución del evaporador tienen la misma composición y temperatura T1, que corresponde al punto de ebullición de la solución. La temperatura del vapor también es T1, pues está en equilibrio con la solución en ebullición. La presión es Psist, que es la presión de vapor de la solución a T1. S O D VA Geankoplis (1998 p549), toma como ejemplo: R Si se supone que la solución que se va a evaporar es bastante diluida y parecida al agua, 1 kg de vapor de agua producirá aproximadamente 1 kg de vapor al condensarse. Esto ocurrirá siempre que la alimentación tenga una temperatura Tf cercana al punto de ebullición. En el cálculo de la velocidad de transferencia de calor en un evaporador se emplea el concepto de un coeficiente total de transferencia de calor. Se establece entonces la ecuación: O H C E ER D SE E R S q = U∙ A ∙ (Ts-T1) (Ec. 2.7) De la misma forma, Geankoplis (1998 p 549) continúa explicando la ecuación 2.7. Donde q es la velocidad de transferencia de calor en q, U es el coeficiente total de transferencia de calor, A es el área de transferencia de calor, Ts es la temperatura del vapor que se condensa y T1 es el punto de ebullición del líquido. 2.2.4.2.1. Variables determinantes en el procedimiento matemático del diseño de sistemas de evaporación a. Entalpía Van Ness (1997), resume la definición de la entalpía mediante la siguiente ecuación: H=U+PV (Ec. 2.8) De la misma forma (Van Ness 1997), explica que las unidades de todos los términos de esta ecuación deben ser iguales. Así mismo, el producto PV tiene unidades de energía, al igual que U; por consiguiente, H también deber especificarse con 43 unidades de energía. En el sistema SI la unidad básica de presión es el Pascal, y, para el volumen, el m3. Por tanto, el producto PV tiene la unidad Joule. b. Capacidades Caloríficas Van Ness (1997 p51), explica este concepto de la siguiente forma: El calor es visto a menudo como una relación con el efecto que tiene sobre el objeto hacia o desde el cual se transfiere. Lo anterior constituye el origen de la idea de que un cuerpo tiene una capacidad para el calor. Entre más pequero sea el cambio de temperatura en un cuerpo provocado por la transferencia de una cantidad de calor dada, mayor es su capacidad. Por otra parte, la capacidad calorífica puede definirse como R SE E R S dQO C C =H E dT ER D S O D VA (Ec. 2.8) Van Ness (1997), expresa que la dificultad principal con esta expresión; es que hace que C, al igual que Q, sea una cantidad que dependa del proceso más que una función de estado. Sin embargo, para él lo expresado anteriormente sugiere la posibilidad de definir más de una capacidad calorífica útil. De hecho, para Van Ness (1997), existen dos capacidades caloríficas de uso muy común para fluidos homogéneos: Capacidad calorífica a volumen constante Cv= ( ∂U )v ∂T (Ec. 2.9) Capacidad calorífica a presión constante Cp= ( ∂H )p ∂T (Ec. 2.10) Así mismo Van Ness (1997), argumenta que estas definiciones acomodan tanto capacidades caloríficas molares como específicas (las que usualmente se conocen como calores específicos), lo que depende del hecho de que el coeficiente de transferencia de calor y la entalpía sean propiedades molares o específicas. Aunque 44 las definiciones de Cv y Cp no hacen referencia a ningún proceso. Para él cada una de ellas permite realizar una descripción especialmente sencilla de un proceso en particular. Para un proceso a presión constante: dH = Cp dT (Ec. 2.11) S O D VA (Presión constante) ER S E ∆H = ∫ Cp dT S R (Ec. 2.12) O H C E ER (Presión constante) De esta manera Van Ness (1997) dice que: T1 T2 D Igualmente, para un proceso a presión constante y mecánicamente reversible describe que Q=m*∆H. de forma que: T1 Q= m∙∆H = m∙ ∫ Cp dT (Ec. 2.13) T2 c. Transferencia de Calor Martínez (2004) explica que como en un cambiador de calor, el caudal de calor transmitida q, en el evaporador puede darse a través de la ecuación de transmisión de calor, que se puede expresar de la forma siguiente: q=U∙A∙∆T (Ec. 2.14) Basándose en los criterios de Martínez (2004), U es el coeficiente global de transmisión de calor en el evaporador, que puede tomar la forma coeficiente aparente, o coeficiente corregido, dependiendo de cual fuese el criterio que se siga en la determinación de la temperatura de ebullición de la disolución en el evaporador y A es el área para la transmisión de calor. 45 Así mismo Martínez (1004) señala que el valor de delta de temperatura para la forma aparente, viene dado por la diferencia entre la temperatura de condensación del vapor de calefacción Ts y la temperatura de ebullición del líquido en la cámara de evaporación, medida a través de la presión existente en dicha cámara, lo que implica la no consideración de la elevación del punto de ebullición por efecto del soluto en la disolución o la debida a cualquier gradiente hidráulico. Análogamente para el cálculo de del delta de temperatura en la forma corregida habría que S O D A temperatura de ebullición del líquido en la cámara de evaporación. V R SE E R S O d. Coeficiente de transferencia de calor H C E R DEde la ecuación 2.14 estableciendo que el flujo de calor a través McCabe (2007) para considerar todas las posibles correcciones ya indicadas, en la determinación de la de las capas de sólidos en serie es proporcional a la fuerza impulsora y a la diferencia de temperatura global ΔT. Esto se aplica también al flujo de calor a través de capas líquidas y sólidas en serie. En un intercambiador de calor la fuerza impulsora se toma como Th – Tc, donde Th es la temperatura media del fluido caliente y Tc la del fluido frío. McCabe (2007), Finalmente resume el cálculo del coeficiente de transferencia de calor, realizando un despeje de la ecuación 2.14 de la variable en cuestión de forma que pueda determinarse mediante los valores medidos de q, A y ΔT: U= q A∙∆T (Ec. 2.15) Calor Sensible Van Ness (1997 p56) define el calor sensible de la siguiente forma: La transferencia de calor a un sistema en el que no existen transiciones de fase, reacciones químicas y ningún cambio en la composición, pero aun así hace que la temperatura del sistema cambie. Se denomina calor sensible. Cuando el sistema es una sustancia homogénea de composición constante, la 46 regla de las fases indica que el estado del sistema queda establecido al fijar los valores de las propiedades intensivas. Calor Latente Foust (2006) explica que cuando una sustancia pura se vaporiza a partir de un estado líquido, a presión constante, no existe ningún cambio en la temperatura; sin embargo, el proceso requiere la transferencia de una cantidad finita de calor a la S O D A V Así mismo, Foust (2006) continúa la definición del calor latente, argumentando que R E S la característica principal de este proceso esR laE coexistencia de dos fases. Un S Osola especie es univariante y su estado Huna sistema de dos fases formado por C E intensivo está determinado DER por la especificación de una sola propiedad intensiva. sustancia. Este efecto calorífico se conoce como calor latente de vaporización. Por tanto, el calor latente que acompaña a un cambio de fase; es una función exclusiva de la temperatura, y está relacionado con las demás propiedades del sistema por una ecuación termodinámica exacta: ∆H=T ∙ ∆V dPsat dT (Ec. 2.16) Donde; Foust (2006) explica que para una especie pura a temperatura T: ∆H: Calor Latente ∆V: Cambio de volumen que acompaña al cambio de fase Psat: Presión de vapor Así mismo, Foust (2006) continua argumentando; que cuando se aplica la ecuación (2.16) a la vaporización de un líquido puro, dPsat/dT es la pendiente de la curva de presión de vapor contra la curva de temperatura en la temperatura de interés, ∆V es la diferencia entre los volúmenes molares del vapor y el líquido en condiciones de saturación y ∆H es el calor latente de vaporización. Por tanto, los valores de ∆H pueden calcularse a partir de datos de presión de vapor y volumétricos. 47 e. Economía McCabe (1997 p525), explica la economía de la siguiente manera: El factor principal que influye sobre la economía de un sistema de evaporadores es el número de efectos. Mediante un diseño adecuado, la entalpía de vaporización del vapor de calentamiento que entra en el primer efecto se utiliza una o más veces dependiendo del número de efectos. La economía también se ve afectada por la temperatura de la alimentación. S O D A la carga de de la alimentación es inferior a la de ebullición en el primer efecto, para V R SE del vapor y sólo calentamiento se utiliza una parte de la entalpía de vaporización E R S De igual forma, si la alimentación O una parte queda disponible para la evaporación. H Ca la de ebullición de la solución, la vaporización E R está a una temperatura superior E D súbita que se produce contribuye a generar una evaporación adicional a la Así mismo McCabe (1997), continúa la definición añadiendo que si la temperatura producida por la entalpía de vaporización en el vapor de calentamiento. Desde el punto de vista cuantitativo, la economía del evaporador es totalmente una cuestión de balances de entalpía. 2.2.4.2.2. Especificaciones de la Solución a Concentrar Basándose en los criterios de McCabe (1997), La principal condición que deben presentar las soluciones a ser incorporadas en los sistemas de evaporación, es la de estar conformadas por solutos no volátiles y solventes volátiles. Así mismo, para este autor; es la gran variedad de características de soluciones (que demanda criterio y experiencia en el diseño y operación de evaporadores) lo que amplía esta operación desde una sencilla transferencia de calor hasta un arte separado. A continuación, se hace referencia mediante varios autores a algunas de las propiedades más importantes que deben presentar las soluciones. 48 a. Concentración McCabe (1997), Especifica que aunque la solución de alimentación que entra a evaporador pueda estar suficientemente diluida teniendo muchas de las propiedades físicas del agua, a medida que aumenta la concentración la solución adquiere cada vez un carácter más individualista. Obteniendo como resultado que la densidad y la viscosidad aumenten con el contenido de sólidos presentes hasta S O D VA que la solución se transforme en saturada o se vuelva demasiado viscoso para una transferencia de calor adecuada. R SE E R S HO C E separar, pues de lo contrario ER los tubos se obstruyen. Igualmente, La temperatura de D ebullición de la solución puede también aumentar en forma considerable al De igual forma, McCabe (1997) continúa argumentando que la ebullición continua de una solución saturada da lugar a la formación de cristales, que es preciso incrementar el contenido de sólidos, de modo que la temperatura de ebullición de una solución concentrada puede ser mucho mayor que la del agua a la misma presión. Balance de Energía para soluciones Diluidas McCabe (1997), Define el balance de energía para disoluciones cuyos calores de disolución son despreciables, en un evaporador de simple efecto; se calculan a partir de los calores específicos y las temperaturas de las soluciones. La velocidad de transferencia de calor (q) del lado de la solución incluye (qf), el calor transferido hacia la solución diluida necesario para variar su temperatura desde (Tf) hasta la temperatura de ebullición (T), y (qv), calor necesario para realizar la evaporación. q = qf + qv (Ec. 2.17) Así mismo, McCabe (1997), continúa especificando que si el calor específico de la solución diluida se supone constante para el intervalo de temperatura comprendido entre (Tf) y (T), se puede obtener entonces: 49 qf = mf Cpf (T − Tf ) (Ec. 2.18) Igualmente para el calor necesario para realizar la evaporación: qv = (mf − m)·λv (Ec. 2.19) Donde: Cpf = calor específico de la solución diluida S O D VA λv = calor latente de vaporización procedente de la solución concentrada R SE E R S De la misma forma, McCabe (1997 p528) finaliza la descripción del balance de entalpía para soluciones diluidas de la siguiente forma: O H C E ER Si la elevación del punto de ebullición de la solución concentrada es despreciable, λv = λ, el calor latente de vaporización del agua a la presión del espacio de vapor. Cuando la elevación del punto de ebullición es considerable, el vapor que abandona la solución es sobrecalentado en una cantidad, en grados, igual a la elevación del punto de ebullición, y λυ difiere ligeramente de λ. Sin embargo, en la práctica casi siempre resulta suficientemente exacto utilizar λ, que se obtiene directamente a partir de las tablas del vapor de agua D Balances de energía para soluciones concentradas Basándose en McCabe (1997). Si el calor de dilución de la mezcla que se concentra es demasiado grande para ser despreciado, se usa un diagrama de entalpíaconcentración para valores de hf y h. Para este diagrama; la entalpía, en joules por gramo de solución, se grafica contra la concentración, en fracción de masa o porcentaje en peso de soluto. Las isotermas del diagrama muestran la entalpía como una función de la concentración a temperatura constante. Igualmente tomando como referencia a McCabe (1997). Se extrajo la figura 2.2. La cual representa un diagrama de entalpía-concentración para soluciones de hidróxido de sodio y agua. Las concentraciones están en fracción masa de hidróxido de sodio, las temperaturas en grados Fahrenheit y las entalpías en Btu por libra de solución. 50 De esta forma, McCabe (1997 p528) hace referencia a la recopilación de las entalpías para la solución. Se toman los valores de Hf y H del diagrama, y la entalpía Hv respectiva al vapor que sale del evaporador se obtiene a partir de las tablas del vapor de agua. Las líneas curvas límite sobre las que terminan las isotermas del diagrama, representan condiciones de temperatura y concentración para las que se forman fases sólidas Las entalpías de todas las soluciones de una sola fase están situadas por encima de esta línea límite. D R SE E R S O H C E ER S O D VA Figura 2.2. Diagrama de entalpía-concentración para el sistema NaOH-H2O. McCabe (1997) 51 Elevación del punto de ebullición McCabe (1997) Explica que la presión de vapor de la mayor parte de las soluciones acuosas son menores que la del agua, a la misma temperatura. En consecuencia, para una presión dada, la temperatura de ebullición de las soluciones es mayor que la del agua pura. El aumento del punto de ebullición sobre el del agua se conoce con el nombre de elevación del punto de ebullición IPE, (boiling point elevation S O D VA BPE). R SE E R S IPE = T⁰ - T1 (Ec. 2.20) O H C E T⁰: Temperatura del solvente puro en ebullición a la presión del sistema. DER Donde: T1: Temperatura del solvente presente en la solución a la presión del sistema. Así mismo, McCabe (1997) argumenta que esta diferencia resulta pequeña para soluciones diluidas, pero puede alcanzar un valor de hasta 80 °C para soluciones concentradas de sales inorgánicas. Como se observa en la ecuación 2.20, se calcula mediante la resta de la temperatura de vaporización del solvente puro (en la mayoría de los casos es el agua) con la temperatura de ebullición de la solución. Basándose en McCabe (1997). Para las soluciones muy concentradas, el IPE se obtiene mejor a partir de una regla empírica conocida como regla de Dühring, según la cual la temperatura de ebullición de una determinada solución es una función lineal de la temperatura de ebullición del agua pura a la misma presión. Por lo tanto, si se grafica la temperatura de ebullición de la solución contra la del agua pura a la misma presión, se obtiene una línea recta. Para diferentes concentraciones resultan diferentes rectas. Para amplios intervalos de presión la regla no es exacta; pero para un intervalo moderado, las líneas son casi rectas aunque no necesariamente paralelas. 52 D R SE E R S O H C E ER S O D VA Figura 2.3. Diagrama de Dühring para el sistema NaOH-H2O. McCabe (1997). 53 La figura 2.3. Representan un conjunto de líneas de Dühring para soluciones de hidróxido de sodio en agua. La utilización de esta figura se ilustra mediante el siguiente problema que toma como ejemplo McCabe (1997 p519); Si la presión sobre una solución de hidróxido sódico a 40% es tal que el agua hierve a 200 °F (93.3 °C), leyendo desde el eje X para 200 °F a la línea de la solución de 40% y después horizontalmente al eje y, se encuentra que la temperatura de ebullición de la solución con esta presión es 250 °F (121.1 °C). La IPE para esta solución con esta presión es por lo tanto 50 °F (27.8 °C). S O D VA ER S E Geankoplis (1998), explica que muchos productos, en especial los alimentos y otros R S HaOla temperatura y se degradan cuando ésta materiales biológicos, son sensibles C E sube o el calentamiento DERes muy prolongado. Entre ellos están los materiales b. Sensibilidad térmica de los materiales farmacéuticos; productos alimenticios como leche, jugo de naranja y extractos vegetales; y materiales químicos orgánicos delicados. La cantidad de degradación está en función de la temperatura y del tiempo. c. Incrustaciones McCabe (1997) “Algunas soluciones depositan costras sobre la superficie de calentamiento. En estos casos, el coeficiente global disminuye progresivamente hasta que llega un momento en que es preciso interrumpir la operación del evaporador y limpiar los tubos”. (p546) d. Presión y temperatura Geankoplis (1998), explica que el punto de ebullición de la solución está relacionado con la presión del sistema. Cuanto más elevada sea la presión de operación del evaporador, mayor será la temperatura de ebullición. Además, la temperatura de ebullición también se eleva a medida que aumenta la concentración del material disuelto por la acción de la evaporación. Para mantener a un nivel bajo la 54 temperatura de los materiales termosensibles suele ser necesario operar a presiones al vacío. D R SE E R S O H C E ER S O D VA Figura 2.4. Curvas de solubilidad de algunas sales típicas en el agua. Procesos de Transportes y Operaciones Unitaria, Geankoplis (1998). e. Formación de espuma Para McCabe (1997). “Algunos materiales, en especial las sustancias orgánicas, forman espuma durante la vaporización. Una espuma estable acompaña al vapor que sale del evaporador, causando un fuerte arrastre”. (p546) 2.2.4.2.3. Evaporación mediante represión de vapor En su libro McCabe (1997) explica que la energía del vapor formado en la ebullición de una solución puede utilizarse para vaporizar más agua siempre que exista una caída de temperatura en la dirección deseada para la transferencia de calor. En un evaporador de múltiple efecto, esta caída de temperatura se crea mediante una disminución progresiva del punto de ebullición de la solución en una serie de evaporadores que operan con presiones absolutas más bajas. 55 Así mismo, McCabe (1997 p540), declara: La fuerza impulsora deseada también se puede obtener aumentando la presión (y, por lo tanto, la temperatura de condensación) del vapor formado, utilizando una recompresión mecánica o térmica. El vapor comprimido se condensa después en la cámara de vapor del evaporador del que procede. f. Recompresión mecánica S O D A temperatura mecánica del vapor. La alimentación fría se precalienta hasta una V R SdeE calor con la solución próxima a la de la ebullición mediante intercambio E R S O concentrada y se bombea a través de un calentador como en el caso de un H C forzada. E R evaporador convencional de circulación DE (McCabe 1998). En la figura 2.6, se ilustra el fundamento de la recompresión Sin embargo para McCabe (1997), el vapor formado no se condensa directamente sino que se comprime hasta una presión algo más elevada por medio de un compresor centrífugo o de desplazamiento positivo, transformándose así en “vapor” de calentamiento que entra como alimentación en el calentador. Puesto que la temperatura de saturación del vapor comprimido es superior a la de ebullición de la alimentación, el calor fluye desde el vapor hacia la solución generando más vapor. Figura 2.5. Diagrama ilustrativo de los fundamentos de recompresión mecánica del vapor. McCabe (1997). 56 g. Recompresión térmica McCabe (1997), describe el sistema de recompresión térmica, como el vapor que se comprime utilizando vapor de alta presión en un eyector de chorro. Esto da lugar a más vapor de calentamiento del que se requiere para la ebullición de la solución, de forma que el exceso de vapor se purga o se condensa. La relación entre el vapor de calentamiento y el vapor procedente de la solución depende de la presión de S O D VA evaporación; para muchas operaciones a baja temperatura, con vapor de R calentamiento de 8 a 10 atm de presión, la relación entre el vapor de calentamiento SE E R S que se requiere y la masa de agua evaporada es del orden de 0.5. HO C E manejar grandes volúmenes ER de vapor de baja densidad, la recompresión térmica D resulta más adecuada que la recompresión mecánica para la evaporación a vacío. Así mismo, McCabe (1997), argumenta que como los chorros de vapor pueden Los eyectores son más baratos y de más fácil mantenimiento que los compresores y los sopladores. Las principales desventajas de la recompresión térmica son la baja eficiencia mecánica y la falta de flexibilidad del sistema frente a variaciones en las condiciones de operación. 2.2.4.2.4. Efectos de las variables de proceso en la operación de sistemas de evaporación de efecto simple Geankoplis (1998), expresa en diferentes oportunidades dentro del contenido de sus publicaciones; referentes a sistemas de evaporación. La importancia de los efectos que generan las variables del proceso en los evaporadores. Por lo que a continuación se inserta la conceptualización del comportamiento al que él hace referencia, de las variables más resaltantes en la operación de los evaporadores de simple efecto. 57 (Geankoplis, 1998, p555) Efecto de la temperatura de alimentación: La temperatura de entrada de la alimentación tiene un gran efecto sobre la operación del evaporador. Si esta entra a una temperatura fría al evaporador, en comparación con el punto de ebullición de la solución a las condiciones de operación. Aproximadamente una cuarta parte del vapor de agua utilizado en el proceso para calentar la misma, se consume al elevar la temperatura de la alimentación hasta el punto de ebullición. Por tanto, sólo quedan ¾ del vapor de agua para la vaporización de la alimentación. Si la alimentación en cambio, está a presión y temperatura superiores al punto de ebullición del evaporador, se logra una vaporización adicional por medio de la evaporación instantánea de una parte de la alimentación caliente. El precalentamiento de la alimentación reduce el tamaño del evaporador y el área de transferencia de calor que se requiere. Efecto de la presión. La presión del evaporador es la responsable de definir la temperatura de ebullición de la solución, afectando la transferencia de vapor que se genera desde la sección de calefacción a la solución. Originando un ∆T para el cálculo del calor transferido. En muchos casos es deseable contar con un valor alto de ∆T, pues a medida que ∆T aumenta, el área de la superficie de calentamiento A y el costo del evaporador disminuyen. Para reducir la presión abajo del evaporador (esto es, para operar el vacío), debe usarse un condensador y una bomba de vacío. Efecto de la presión del vapor de agua. Cuando se usa vapor de agua saturado a presión más alta, el valor de ∆T aumenta, con lo cual disminuye el tamaño y el costo del evaporador. Sin embargo, el vapor de alta presión cuesta más y suele ser más valioso como fuente de potencia en otros equipos. Por consiguiente, la presión óptima del vapor de agua se determina mediante un balance económico general. D R SE E R S O H C E ER S O D VA 2.2.5. Errores Sistemáticos Según Skoog (2001), los errores sistemáticos tienen un valor definido y una causa asignable, y son de la misma magnitud y medidas que se efectúan de la misma manera. Para este autor, existen tres tipos de errores sistemáticos los cuales se citan a continuación (Skoog, 2001, p96): 58 Los errores instrumentales, causados por el comportamiento no ideal de los instrumentos, las calibraciones deficientes o el uso en condiciones no apropiadas causan los errores instrumentales. Los errores de método, que derivan del comportamiento químico o físico no ideal de los sistemas analíticos Los errores personales, que resultan del descuido, falta de atención o limitaciones personales del experimentador. 2.2.5.1. Error relativo S O D VA ER S E R que en general el error relativo O es S ineludible y depende básicamente del CH disponible para realizar la medición o calculo. E procedimiento elegido yR la tecnología DE Matemáticamente define la siguiente expresión por donde se puede determinar un Para Skoog (2001), el error relativo es una desviación del valor medido de una magnitud física respecto al valor real de dicha magnitud. Skoog (2001) considera, porcentaje de error relativo: Valor medio-Valor real %Erelativo= | | *100 Valor real (Ec. 2.21) Donde Skoog (2001), explica que el valor medido es el valor que se obtuvo del resultado del experimento y el valor real es el dato con el que se va a comparar. 2.2.6. Microsoft Excel (Centro de ayuda de Excel, 2013). Excel es una herramienta muy eficaz para obtener información con significado a partir de grandes cantidades de datos. También funciona muy bien con cálculos sencillos y para realizar el seguimiento de casi cualquier tipo de información. La clave para desbloquear todo este potencial es la cuadrícula de las celdas. Las celdas pueden contener números, texto o fórmulas. Los datos se escriben en las celdas y se agrupan en filas y columnas. Esto permite sumar datos, ordenarlos y filtrarlos, ponerlos en tablas y crear gráficos muy visuales. 59 2.2.7. Microsoft Visual Basic (Centro de ayuda, Microsoft Visual Basic©, 2008). Visual Basic es un lenguaje de programación dirigido por eventos, desarrollado por Alan Cooper para Microsoft. Este lenguaje de programación es un dialecto de BASIC, con importantes agregados. Su primera versión fue presentada en 1991. D H C E ER O SE E R S R S O D VA 60 2.3. Sistema de variables OBJETIVO GENERAL: PROPONER UNA HERRAMIENTA DIDÁCTICA PARA EVAPORADORES DE UN SOLO EFECTO Objetivos Especifico Variable Indicadores Dimensiones Establecer el procedimiento matemático de la D evaporadores de un solo efecto. E R S O H C E ER herramienta didáctica para SER S O D VA Procedimiento matemático Definición de las soluciones a tratar. Identificación de los posibles casos dedicados a la resolución de los problemas académicos. Elaboración del Balance de materiales y energía para cada caso preseleccionado. Herramienta didáctica para Metodología para la recolección de las variables evaporadores de un necesarias en cada caso. solo efecto Determinación de las incógnitas requeridas para Programar el procedimiento cada caso preseleccionado. matemático de la Programación del herramienta didáctica para procedimiento evaporadores de un solo matemático Asignar las variables de entrada para cada caso efecto. Recrear el procedimiento matemático para cada uno de los casos. Especificar parámetros constantes. Determinar las incógnitas por cada caso. 61 Objetivos Específicos Variable Indicadores Dimensiones Identificar el material a Desarrollar la ventana de exponer en las ventanas. usuario de la herramienta didáctica para evaporadores Desarrollo de las de un solo efecto. ventanas de usuario Desarrollar la interfaz de cada ventana de acuerdo a S O D VA la etapa donde se desee Herramienta didáctica un solo efecto Elaborar el manual de didáctica para evaporadores de un solo efecto HO C E R DE usuario de la herramienta R SE E R S para evaporadores de Iniciar Sesión en la herramienta Especificar El caso y el tipo de solución. Elaboración del manual de usuario ubicar. Introducción de los datos. Reporte de Resultados. Comparación de variables. CAPÍTULO III MARCO METODOLÓGICO En este capítulo se desarrollan una serie de procesos sistemáticos y metodológicos, técnicas e instrumentos para medir las variables que intervinieron en la investigación S O D proyecto el cual genera una alternativa de solución al problema antes Adescrito en la V R Universidad Rafael Urdaneta. La metodología incluye SelEtipo de investigación, el E R S diseño, las técnicas, instrumentos, y los procedimientos que fueron utilizados en la O H C E investigación. R E D al mismo tiempo. Su uso permitió confirmar la hipótesis que se propuso en el 3.1. Tipo de Investigación Rodriguez y Valldeoriola (2009, p.29) describen la investigación descriptiva: Como una investigación de mayor profundidad dado que va más allá de la exploración, porque con ella se debe medir las variables que intervienen en el estudio; las características, las actitudes, el comportamiento de las unidades investigadas. Responde ¿a cuánto?, ¿en qué medida?, ¿cómo?, ¿dónde? Arias (2006) explica el marco metodológico como un conjunto de pasos, técnicas y procedimientos que se emplean para formular y resolver problemas; este método se basa en la formulación de hipótesis las cuales pueden ser confirmadas o descartadas por medios de investigaciones relacionadas al problema de investigación para seleccionar el que mejor describa el presente trabajo y así fundamentar el estudio en cuestión. Por otro lado, Hurtado. (2007) plantea que es el conjunto de acciones destinadas a describir y analizar a fondo el problema descrito, a través de procedimientos 63 específicos que incluye las técnicas de observación y recolección de datos, determinando el “cómo” se realizará el estudio, esta tarea consiste en hacer operativo los conceptos y elementos del problema que se va a estudiar. Basándose en las descripciones anteriores, el presente trabajo especial de grado se podría considerar como una investigación descriptiva, ya que a través de ella se busca optimizar el modelo de enseñanza de la cátedra Operaciones Unitarias II en S O D VA la escuela de Ingeniería Química de la Universidad Rafael Urdaneta, mediante la ER S E R la materia, beneficiando igualmente a los docentes que incorporen a su metodología S O H Cperspectiva didáctica. este programa de simulación con E R DE elaboración de una herramienta didáctica para evaporadores de un solo efecto. De forma que favorezca el rendimiento académico de la población estudiantil que cursa 3.2. Diseño de la investigación Altuve y Rivas (1998) aseguran que el diseño de una investigación, “…es una estrategia general que adopta el investigador como forma de abordar un problema determinado, el cual permite identificar los pasos que se deben seguir para efectuar su estudio”. (p.75) Por su parte, Arias (2006) afirma que “El diseño de investigación es la estrategia general que adopta el investigador para responder al problema planteado”. (p.93) (Hernández, Fernández y Baptista, 2006), Cada tipo de diseño posee características particulares por lo que cada uno es diferente a cualquier otro y no es lo mismo seleccionar un tipo de diseño que otro. La eficacia de cada uno de ellos depende de si se ajusta realmente a la investigación que se esté realizando. Acerca de la investigación experimental Hernández et al., (2006), explica que dicha investigación se refiere a un estudio en el que se manipulan intencionalmente una o más variables independientes, para analizar los efectos que la manipulación 64 realizada tiene sobre una o más variables dependientes, dentro de una situación de control para el investigador. Según Ramírez, Bravo y Méndez, (1987). El diseño documental, es una variable de la investigación científica, cuyo objetivo fundamental es el análisis de diferentes fenómenos (de orden histórico, psicológico, etc.) de la realidad a través de la indagación exhaustiva, sistemática y rigurosa, utilizando técnica muy precisas; de S O D VA la documentación existente que directa o indirectamente, aporte la información R E S E Según Arias (2006) “La investigación documental es un proceso basado en la R S O H búsqueda, recuperación, análisis, crítica e interpretación de datos secundarios, es C E R por otros investigadores en fuentes documentales: decir, los obtenidos DyEregistrados atinente al fenómeno que estudiaremos. impresas, audiovisuales o electrónicas”. (p101) Dentro del diseño experimental González, YII y Curiel (2003), definen el diseño estadístico de experimentos; este consiste en el modelado matemático del fenómeno físico que se pretende estudiar, de tal manera que se reduce al mínimo el número de corridas de experimentos que se realizan en la realidad solo ejecutando los necesarios para preparar el modelo. A su vez “se debe considerar como una herramienta a utilizar en el análisis de procesos”. Sobre la simulación González et al. (2003, p.83) expresan: Es un comportamiento para la realización de experimentos por medio de una computadora digital y con la ayuda de modelos matemáticos, con el fin de obtener información sobre el comportamiento del sistema… En general, mediante las técnicas de simulación se pueden analizar el efecto de las interrelaciones de una sistema o proceso dado determinar las recirculaciones (de materiales, energía o información), hacer estudios de capacidad, detectar cuellos de botella, definir las condiciones límites de operación y otras aplicaciones más. 65 De acuerdo con las definiciones de estos autores se concluyó, que la investigación desarrollada tuvo un diseño documental y experimental, dado que la fuente de información utilizada para desarrollar el procedimiento matemático de la herramienta didáctica para evaporadores de un solo efecto. Fue la determinada mediante la bibliografía seleccionada previamente, que ya ha sido evaluada y constatada, de manera que se consideran fuentes confiables de información. S O D A recreación de los ejercicios propuestos en la herramienta didáctica para V R E Scon el método tradicional de evaporadores de un solo efecto fueron comparados E R Sson los posibles métodos para llevar a O cálculo. Donde las variables independientes H C y las variables dependientes son los resultados E R cabo el desarrollo del procedimiento E D arrojados por los métodos. Así mismo, se considera experimental ya que, los resultados obtenidos mediante la 3.3. Técnicas de recolección de datos Haciendo referencia al concepto de técnicas para la recolección de datos que plantea Arias (2006) se tiene que las técnicas de recolección de datos son las formas o maneras de obtener la información. Arias (2006), indica que la observación directa consiste “en visualizar o captar mediante la vista, en forma sistemática, cualquier hecho, fenómeno o situación que se produzca en la naturaleza o en la sociedad, en función de unos objetivos de investigación pre-establecidos” (p.67). Rodríguez y Valldeoriola (2009) afirman que “la observación directa es aquella técnica en la cual el investigador puede observar y recoger datos mediante su propia observación, apoyado en sus sentidos (conocimiento empírico)” (p.56). La observación directa se utilizó para determinar los factores que generan la necesidad de implementar la herramienta didáctica para evaporadores de un solo efecto; en la metodología de enseñanza de la cátedra Operaciones Unitarias II. 66 Siendo una de las materias más relevantes en el plan de estudio de la escuela de ingeniería química en la Universidad Rafael Urdaneta. Partiendo de esta técnica, se consideró que al unificar la enseñanza referente a los sistemas de evaporación, en conjunto con modelos de simulación de perspectiva didáctico, beneficiaria el rendimiento académico de los alumnos, e igualmente serviría como introducción a las tan importantes herramientas de simulación S O D Así mismo, se identificó mediante la técnica de observación directa que Aimplementar V R la herramienta didáctica serviría un complemento metodológico, SE que igualmente E R Sel procedimiento matemático para llevar beneficiaría al docente a la hora de explicar O H C E a cabo el diseño de sistemas de evaporación para efectos simples, optimizando el R DE tiempo gradual que se requiere para impartir esta catedra. profesional que van de la mano de la ingeniería química. La técnica de observación documental según Altuve y Rivas (1998, p.69): Constituye la vía más expedita de obtener datos sobre ellos, sin embargo, no siempre es posible efectuarla porque se requiere, primero, la existencia del fenómeno para el momento de la observación y segundo, la coincidencia del observador con el momento exacto de producción del hecho. Si no fuera posible observarlo, seguramente el fenómeno dejo huellas y estas deben reflejarse en cualquiera de las diversas formas documentales que existen, su análisis da lugar a la observación documental. Además, la observación documental la define Hurtado (2007) como “una técnica en la cual se recurre a información escrita, ya sea bajo la forma de datos que pueden haber sido producto de mediciones hechas por otros, o como textos que en sí mismos constituyen los eventos de estudio” (p.427). Sirviendo como argumento lo descrito anteriormente, se puede concluir que este trabajo especial de grado se vio regido por la técnica de observación documental y la técnica de observación directa. 67 Durante la elaboración de la herramienta didáctica para evaporadores de un solo efecto, se llevó a cabo una búsqueda previa mediante la técnica de observación documental. Esta se centró en encontrar proyectos que se hubiesen realizado en la misma área, de forma que sirvieran de respaldo al contenido de la investigación. Así mismo, tomando en cuenta la bibliografía recomendada, la cual fue parte crucial en el desarrollo de cada objetivo planteado. S O D VA ER S E R S Hurtado (2007, p.29) define los instrumentos de recolección de datos de la siguiente O H C E manera: R DE 3.4. Instrumentos de recolección de datos Instrumentos que representan la herramienta con la cual se va a recoger, filtrar y codificar la información. Los instrumentos, pueden estar ya elaborados e incluso normalizados, como es el caso de los test y algunas escalas. Sin embargo, si se trata de eventos poco estudiados puede ser necesario que el investigador elabore sus propios instrumentos. Los instrumentos están en correspondencia con las técnicas de recolección de datos; junto con los tipos de indicios que permiten captar el evento de estudio. Para esta investigación, se realizó el diseño de la tabla 3.1, de forma que ayudara a especificar los valores de las variables que proporcionan los problemas académicos extraídos previamente de la bibliografía especificada. Mediante la cual se reportaron los datos descritos por cada ejercicio planteado, y posteriormente identificar la forma de resolverlos mediante los datos proporcionados, de esta forma se llevó a cabo el procedimiento matemático para la herramienta didáctica de evaporadores de simple efecto. Donde se especificaron las limitaciones y alcances que la herramienta presenta y de qué forma se procedería a recrear el diseño de los sistemas de evaporación de un solo efecto. 68 Tabla 3.1. Reporte de datos de los problemas planteados en la herramienta didáctica para evaporadores de un solo efecto. Corriente Variable ALIMENTACIÓN Flujo de Alimentación Temperatura de Entrada Concentración Capacidad Calorífica Entalpía PRODUCTO CALEFACCIÓN Capacidad Calorífica O D H C E ER Unidad S O D VA R SE E R S Concentración SISTEMA Valor Entalpía Área Coeficiente de Transferencia de Calor Presión Sistema Incremento del Punto de Ebullición Temperatura de Saturación Presión de vaporización Posteriormente, con ayuda de la Tabla 3.1, se clasificaron los problemas planteados; según el tipo de disolución que se requería concentrar y las incógnitas a determinar. Ya que estos eran los principales factores que afectaban el procedimiento de los ejercicios al momento de calcular los resultados. Así mismo, luego de desarrollar el procedimiento matemático para cada uno de los casos especificados según el tipo de solución a trabajar, se inició el desarrollo de la herramienta didáctica para evaporadores de un solo efecto. Posteriormente generó los resultados para etapa configurada. Utilizando la tabla 3.2, se resumieron los valores de estos resultados arrojados por la herramienta. 69 Tabla 3.2. Reporte de resultados determinados mediante la herramienta didáctica de evaporadores de un solo efecto para los diferentes casos y tipo de solución. Solución Tipo: CASO: Resultados de la Herramienta Corriente Variable Flujo Temperatura Concentración Capacidad Calorífica Entalpía Alimentación Producto Vapor Sistema Corriente de Vapor como Calefacción Unidad kg/h K O H C E ER Flujo Temperatura de Saturación Presión de vaporización Entalpía del Líquido Entalpía del Vapor Calor Latente S O D VA R SE E R S Flujo Concentración Temperatura Capacidad Calorífica Entalpía Flujo Temperatura Entalpía Estado Área Calor Temperatura Coeficiente de Transferencia de Calor Incremento del Punto de Ebullición Presión Sistema Economía D Valor kJ/kg.K kJ/kg kg/h K kJ/kg.K kJ/kg kg/h K kJ/kg m² kJ/h K kJ/h.m².K °C kPa kg/h K kPa kJ/kg kJ/kg kJ/kg Adicionalmente, y con la finalidad de validar los resultados obtenidos por el simulador de perspectiva didáctica; se elabora la tabla 3.3, donde a continuación muestra las deviaciones y porcentajes de errores entre los resultados obtenidos mediante la herramienta didáctica de evaporadores de un solo efecto y los valores determinados mediante el procedimiento tradicional. 70 Tabla 3.3. Comparación entre el método tradicional y los resultados arrojados por la herramienta didáctica para evaporadores de un solo efecto. Variable Determinada Resultado Método Tradicional Resultado Herramienta Didáctica % Error Variable Determinada POR CASO Flujo de producto concentrado (P) Flujo de vapor de agua para calefacción (S) D R SE E R S O H C E ER S O D VA Flujo de Solvente Evaporado (V) 3.5. Fases de la investigación Con el propósito de cumplir los objetivos planteados en este trabajo de investigación, fueron estructuradas las actividades y tareas del mismo en múltiples fases o etapas, como se muestra a continuación: 3.5.1. Fase 1: Establecimiento del procedimiento matemático para evaporadores de un solo efecto Para establecer el procedimiento matemático de la herramienta didáctica para evaporadores de un solo efecto, en primera instancia se realizó una investigación de observación documental. A través del uso de dicha técnica; se identificaron los factores necesarios para especificar la bibliografía a utilizar. Esta última, debió caracterizarse por presentar versatilidad al momento de plantear problemas académicos; referentes al diseño de evaporadores de simple efecto. Y explicar de una forma sencilla y detallada el desarrollo de cada ejercicio, sirviendo como principal apoyo a lo largo de la investigación. 71 Posteriormente, se realizó una preselección de los ejercicios plasmados en los libros acogidos, para determinar factores cruciales que pudiesen regir el procedimiento. Al comenzar a analizar los enunciados propuestos y agrupar las variables proporcionadas en el enunciado del problema; se observó que por lo general los ejercicios se dividían en cuatro posibles casos; donde cada uno tenía un enfoque diferente con respecto a las incógnitas a determinar. Partiendo de los datos descritos por el mismo problema. S O D VA ER S E R ser tratados como disoluciones diluidas o disoluciones concentradas. Por lo tanto, S O H Cla comprensión y recreación del procedimiento con la intención de facilitar E R E matemático, los D casos resaltados anteriormente; se subdividieron de acuerdo al tipo Finalmente, al proceder a realizar la resolución de los problemas propuestos; se observó que dependiendo de las variables proporcionadas, los ejercicios podrían de disolución a trabajar. El procedimiento matemático fue desarrollado a partir de los balances definidos para el sistema de evaporación de efecto simple, estos preceden de los principios de conservación de masa y energía desarrollados en el capítulo II de esta investigación. Para la elaboración del procedimiento matemático de los evaporadores de un solo efecto se utilizó como instrumento de recolección de datos la tabla 3.1, la cual tuvo como objetivo identificar por medio de la agrupación de los valores descritos en los ejemplos seleccionados mediante la observación documental, previa al desarrollo de las fases de la investigación. Determinar, los posibles casos y tipos de soluciones existentes, que especificaran las condiciones del proceso en cada ejemplo propuesto. 3.5.2. Fase 2: Programación del procedimiento matemático Una vez definidos los criterios y las fórmulas necesarias para desarrollar el procedimiento matemático en cada caso y por cada tipo de disolución especificada anteriormente. Se procedió a recrearlo en Microsoft Excel 2013. Este programa 72 resulta muy versátil para el objetivo principal de esta investigación, ya que cuenta con hojas de cálculos de fácil manejo donde se pueden reportar y configurar el procedimiento descrito, realizando modificaciones al documento. El programa Microsoft office Excel, es una herramienta accesible pues no necesita de instaladores secundarios, códigos de acceso, o compra de patentes, solo un ordenador que tenga instalado el paquete Microsoft office. La estructura regular de S O D VA una hoja de cálculo es una matriz matemática, con dos elementos fundamentales: R SE E R S las columnas verticales y las filas horizontales; la intersección entre ambos elementos se denomina celda. HO C E didáctica para evaporadores DER de un solo efecto, ya que a través de él se pueden Igualmente, se seleccionó este programa como base para desarrollar la herramienta vincular accesos directos a Microsoft Visual Basic; por medio de la activación de ciertos complementos, sin necesidad de remitirse a la instalación del programador en el servidor donde se ejecutará la herramienta. Por otra parte, la incorporación de estos complementos en el documento principal de Microsoft Excel; facilitaron más aun el desarrollo del programa de simulación con fines didácticos, ya que a través de comandos sencillos y el uso de macros generales se pueden transitar e identificar valores entre las hojas de cálculos sin realizar selecciones manuales. Finalmente se obtuvieron los resultados de los ejercicios propuestos, calculados luego de configurar el procedimiento matemático para cada uno de los casos en la herramienta didáctica para evaporadores de un solo efecto, los cuales se reportaron haciendo uso de la tabla 3.2. Adicional a esto, se realizó una comparación la cual se reportó utilizando la tabla 3.3, entre los valores de mayor relevancia arrojados por el simulador de perspectiva didáctica y el método tradicional de cálculo, donde se reportó el porcentaje de error relativo existente entre ambos. 73 3.5.3. Fase 3: Desarrollo de las ventanas de usuario Luego de estructurar el procedimiento matemático en el documento de Microsoft Excel 2013, se realizó la activación de los complementos mencionados anteriormente, para vincular el documento con ventanas auxiliares creadas en Visual Basic, mediante el empleo de la función desarrollador. Utilizando un lenguaje dirigido por eventos, el cual se maneja en el dialecto BASIC cuyas siglas refieren Beginner's All-purpose Symbolic Instruction Code, (Código de S DO Simbólico A V R SE Instrucciones de Propósito General para Principiantes). E R S HO auxiliares, las cuales permiten al usuario hojas de cálculos modificadas C y ventanas E ajustar las condiciones, DERintroducir los valores y unidades requeridas por la Aunado a esto, se creó una interfaz gráfica dentro del documento conformado por herramienta; para llevar a cabo el diseño de los evaporadores de simple efecto desde una perspectiva didáctica. Por último, se crearon secciones por donde se le proporciona al operador información correspondiente a la etapa en donde se encuentre dentro de la herramienta, ayudándolo y aportando información complementaria del tema. 3.5.4. Fase 4: Elaboración del manual de usuario Se elaboró un manual para el uso correcto de la herramienta didáctica para evaporadores de un solo efecto, con la finalidad de facilitar al usuario las instrucciones básicas mediante las cuales se podrá llevar a cabo la simulación del proceso desde una perspectiva didáctica. Estas instrucciones le proporcionarán los conocimientos requeridos para el total manejo del programa. Dicho manual contiene ejemplos ilustrativos paso a paso de forma apropiada en que se deben introducir los datos para complementar el cálculo de las variables a determinar por el simulador de evaporadores de efecto simple con perspectiva didáctica. 74 Dicho manual fue elaborado en un documento de formato Microsoft Office Word; y al ser finalizado fue llevado a un formato PDF, contando con dos presentaciones, una digital a la cual se tendrá acceso desde el modelo de simulación y una impresa anexada como a esta investigación. D H C E ER O SE E R S R S O D VA CAPITULO IV ANALISIS DE RESULTADOS Este capítulo tiene como finalidad dar a conocer de forma detallada de los resultados obtenidos, presentándolos de manera gráfica y a través de tablas y figuras, que permiten un mejor entendimiento de los mismos. S O D A para 4.1. Fase 1: Establecimiento del procedimiento matemático V R SE evaporadores de un solo efecto E R S O H C Esta fase principalmente se concentró en dividir el enfoque de la solución del E R E D al tipo de disolución con la que se pretende trabajar e problema, con respecto igualmente, separando cada tipo en diferentes casos de acuerdo a las incógnitas que se quisieran determinar. De forma que al incorporar estos parámetros en la herramienta didáctica para evaporadores de un solo efecto, le facilite al usuario recrear el problema planteado en el programa de perspectiva didáctica. 4.1.1. Posibles soluciones a concentrar Recordando la bibliografía seleccionada de la cual se extrajeron los conceptos básicos que fundamentaron esta investigación, establecidos en el capítulo 2. Se Hace referencia a la definición que especifica McCabe en Operaciones Unitarias en la Ingeniería Química (1997 p512), Donde habla de la concentración, como especificación de las soluciones a concentrar por los evaporadores. Primeramente, McCabe (1997), hace referencia a que las soluciones para este tipo de operación unitaria deben estar conformadas por un soluto no volátil en presencia de un solvente volátil, de forma que al alcanzar el punto de ebullición de la mezcla 76 dentro del evaporador, sea el solvente el único que se evapore aumentando la concentración del soluto en la solución Igualmente, la concentración de la solución afecta de acuerdo al porcentaje que en se encuentre, los cálculos para determinar variables como temperatura o la cantidad de vapor introducido como calefacción al evaporador. Ya que, mientras más concentrada este la solución a la entrada del evaporador más elevado será el punto S O D Aunque la solución de alimentación que entra como mezcla aA un evaporador V R puede estar suficientemente diluida teniendo muchas de las propiedades E S E físicas del agua, pero a medida que aumenta la concentración; la solución R S adquiere cada vez un carácter más individualista. La densidad y la viscosidad O H C aumentan con el contenido E de sólidos hasta que la solución se transforma en saturada oD el E licorR se vuelve demasiado viscoso para una transferencia de calor adecuada. de ebullición de la mezcla. McCabe (1997 p512), hace referencia a esta condición: Igualmente, Geankoplis (1998 p545), redacta lo siguiente: El punto de ebullición de la solución está relacionado con la presión del sistema. Cuanto más elevada sea la presión de operación del evaporador, mayor será la temperatura de ebullición. Además, la temperatura de ebullición también se eleva a medida que aumenta la concentración del material disuelto por la acción de la evaporación. Este fenómeno se llama elevación del punto de ebullición. Basándose en el criterio de estos dos autores, se separó el procedimiento matemático para diseñar un sistema de evaporadores, en dos categorías principalmente las cuales desarrollaban el problema partiendo desde la perspectiva de que la solución fuera diluida o concentrada. Estas condiciones afectaban principalmente el balance de energía del evaporador, ya que al hablar de soluciones concentradas, las entalpías tendrían que calcularse partiendo de gráficas entalpia/concentración. De la misma forma, la temperatura del evaporador iba a estar dada por el incremento del punto de ebullición de la mezcla con respecto al solvente puro. 77 Para la elaboración del balance de energía considerando la solución como diluida. Las propiedades de esta se pudieron asumir como las propiedades del agua a las condiciones del sistema, ya que para fines didácticos; la concentración es tan pequeña que el incremento en las propiedades con respecto al solvente puro, pueden descartarse. De esta forma, se hizo referencia a la ecuación 2.17 expresada en el capítulo 2 de S O D VA esta investigación, en donde McCabe (1997), define el balance de energía para soluciones diluidas, con la siguiente expresión: q=qf + qv Donde: O D H C E ER R SE E R S (Ec. 2.17) La velocidad de transferencia de calor (q) del lado de la solución incluye (qf), el calor transferido hacia la solución diluida necesario para variar su temperatura desde (Tf) hasta la temperatura de ebullición (T), y (qv), calor necesario para realizar la evaporación. Así mismo define a qf y qv a continuación: qf = mf Cpf (T − Tf ) qv = (mf − m)·λv (Ec. 2.18) (Ec. 2.19) Donde, (mf) representa el flujo de líquido de la solución a evaporar, (Cpf) la capacidad calorífica que presenta la solución para realizar el cambio de estado desde (Tf) hasta (T), (m) representa el flujo de vapor generado luego de la vaporización y (λv), representa el calor latente que genera la solución a las condiciones del sistema para cambiar de estado. Tomando como ejemplo un evaporador de efecto simple, que dispone de una solución acuosa la cual se encuentra diluida. Esta es introducida al evaporador con la finalidad de aumentar su concentración, la solución entra a un flujo (F) con una temperatura (Tf), de la misma forma se tiene vapor de agua como medio de 78 calefacción, el cual se encuentra a una temperatura de saturación (Ts) entrando a una velocidad (S). La vaporización se realiza a la presión atmosférica (Psist) originando la evaporación del solvente en la solución; a una velocidad (V). Así mismo, la solución ahora con mayor concentración de soluto, sale del evaporador a una velocidad (P); como el vapor generado por la evaporación del solvente y la solución concentrada se encuentran en equilibrio dentro del evaporador, ambas corrientes salen a la temperatura de ebullición de la mezcla (T1). R SE E R S O H C E ER D S O D VA Figura 4.1.1. Diagrama de un sistema de evaporación de un solo efecto. Continuando con el principio para soluciones diluidas planteado anteriormente junto con la ley de conservación de la energía. Se especificó que el balance de energía en un evaporador con las condiciones señaladas en la figura 4.1.1; y considerando solución diluida estaba dado por la expresión: q absorbido = F·hf – [P·hp + V·(Hv-hv)] q generado = S·λ (Ec. 4.1) (Ec. 4.2) Donde q(absorbido) y q(generado) son iguales, por lo tanto: F·hf + S·λ = P·hp + V·Hv Partiendo de la ecuación 2.18: hf = Cpf·(Tf – T1) (Ec. 4.4) hp = Cpp·(T1 – Tref) (Ec. 4.5) (Ec. 4.3) 79 Para la corriente de vapor de agua que se utilizó como calefacción en la evaporación, se hablaba de un diferencial de entalpías denominado calor latente; el cual se representó como (λ). Esto se debe a que el vapor de agua que ingresa al evaporador se encuentra en estado saturado, posteriormente a la transferencia de calor este se condensa saliendo como liquido saturado. Por lo tanto, no se origina ningún incremento o descenso de la temperatura o la presión en la corriente; el cambio de estado ocurre gracias al calor latente generado. Este se determinó haciendo uso de las tablas de vapor saturado para el agua. S O D VA ER S E temperatura de referencia para el cálculo S de laR entalpía de la solución concentrada, O H del evaporador. Por lo tanto, y tomando en C la misma, se igualo a la temperatura E DEdeRuna solución acuosa, la corriente de vapor generado en la cuenta que se trataba Por otro lado, al hablar de la solución a evaporar, se debió especificar una vaporización del solvente se considera en estado saturado, de manera que se repiten las características de la corriente de calefacción. Al hacer referencia al balance de energía para soluciones concentradas, las propiedades de la solución no son iguales a las del agua, puesto que presentaban un porcentaje de soluto apreciable. Dicho porcentaje debió ser considerado al calcular la temperatura de ebullición del evaporador, igualmente al determinar la cantidad requerida de vapor de agua como calefacción para dar origen a la transferencia de calor dentro del evaporador. De la misma forma, fue necesario hacer uso de diagramas específicos para determinados compuestos; los cuales complementaron el procedimiento matemático de los sistemas de evaporación de un solo efecto que trabajan con soluciones concertadas. Tomando en cuenta las referencias bibliográficas de las cuales se basó esta investigación, se trajo a colación la sección de balances de energía para soluciones concentradas plasmada en el capítulo 2, la cual fue tomada del McCabe (1997). Si el calor de dilución de la mezcla que se concentra es demasiado grande para ser despreciado, se usa un diagrama de entalpía-concentración para 80 valores de hf y h. Para este diagrama; la entalpía, en joules por gramo de solución, se grafica contra la concentración, en fracción de masa o porcentaje en peso de soluto. Las isotermas del diagrama muestran la entalpía como una función de la concentración a temperatura constante. Igualmente tomando como referencia a McCabe (1997). Se extrajo la figura 2.3. La cual representa un diagrama de entalpía-concentración para soluciones de hidróxido de sodio y agua. Las concentraciones están en fracción masa de hidróxido S O D VA de sodio, las temperaturas en grados Fahrenheit y las entalpías en Btu por libra de R E S E De esta forma, McCabe (1997 p528) hace R referencia a la recopilación de las S entalpías para la solución. HO C E ER de Hf y H del diagrama, y la entalpía Hv respectiva al Dvalores Se toman los solución. vapor que sale del evaporador se obtiene a partir de las tablas del vapor de agua. Las líneas curvas límite sobre las que terminan las isotermas del diagrama, representan condiciones de temperatura y concentración para las que se forman fases sólidas Las entalpías de todas las soluciones de una sola fase están situadas por encima de esta línea límite. Figura 2.3. Diagrama de entalpía-concentración para el sistema NaOH-H2O. Operaciones Unitarias en Ingeniería Química, McCabe (1997). 81 De la misma forma McCabe (1997), señala que la presión de vapor de la mayor parte de las soluciones acuosas es menor que la del agua a la misma temperatura. En consecuencia, para una presión dada, la temperatura de ebullición de las soluciones es mayor que la del agua pura. El aumento del punto de ebullición sobre del agua se conoce con el nombre de elevación del punto de ebullición IPE, boiling point elevation of solution. Es pequeño para soluciones diluidas, pero puede alcanzar un valor de hasta 80 °C (144 °F) para soluciones concentradas de sales inorgánicas. S O D VA R SE E R S HO C E la cual la temperatura de ebullición de una determinada solución es una función DER Basándose en McCabe (1997). Para las soluciones muy concentradas, el IPE se obtiene mejor a partir de una regla empírica conocida como regla de Dühring, según lineal de la temperatura de ebullición del agua pura a la misma presión. Por lo tanto, si se grafica la temperatura de ebullición de la solución contra la del agua pura a la misma presión, se obtiene una línea recta. Para diferentes concentraciones resultan diferentes rectas (Figura 2.4). Para amplios intervalos de presión la regla no es exacta; pero para un intervalo moderado, las líneas son casi rectas aunque no necesariamente paralelas. La ecuación que representa el incremento del punto de ebullición IPE es la siguiente: IPE = T⁰ - T1 (Ec. 2.20) Donde: T⁰: Temperatura del solvente puro en ebullición a la presión del sistema. T1: Temperatura del solvente presente en la solución a la presión del sistema. 82 D R SE E R S O H C E ER S O D VA Figura 2.4. Diagrama de Dühring para el sistema NaOH-H2O. Operaciones Unitarias en la Ingeniería Química, McCabe (1997). Ahora bien, partiendo de estos conocimientos se tomó el ejemplo anterior modificando el criterio de concentración de la solución el cual se consideró como solución concentrada de forma que pudiese utilizarse para representar el procedimiento matemático; este ejemplo se refiere a la figura 4.1.1. Igualmente se utilizó la ecuación 4.3, descrita a partir de la ley de conservación de la masa: F·hf + S·λ = P·hp + V·Hv (Ec. 4.3) Donde, para el caso de soluciones concentradas; la temperatura de ebullición tuvo el primer lugar en lo referente a la determinación de las propiedades de la solución, ya que la misma es requerida para lograr introducirse en los diagramas entalpías – concentración (figura 2.3), de donde posteriormente se extrajeron los valores para (hf) y (hp), la temperatura de la solución se determinó mediante la regla de Dühring explicada por McCabe (1997) anteriormente. En primer lugar se determinó la 83 temperatura de ebullición del agua pura a la presión del evaporador (Psist) y con este valor y el porcentaje de soluto presente en la solución, se introdujo en el diagrama de Dühring para determinar la temperatura de ebullición de la mezcla, como se ilustra en la figura 4.1.2. D R SE E R S O H C E ER S O D VA Figura 4.1.2. Diagrama de Dühring representativo al cálculo de la temperatura de ebullición de la mezcla para soluciones concentradas. Luego de obtener la temperatura de ebullición de la mezcla se procedió a determinar las entalpías de la solución ingresando al diagrama de entalpías vs concentración del sistema respectivo con la concentración del soluto y la temperatura de la solución como se ilustra en la figura 4.1.3. 84 D R SE E R S O H C E ER S O D VA Figura 4.1.3. Diagrama de entalpía-concentración representativo al cálculo de la temperatura de ebullición de la mezcla para soluciones concentradas. Por otro lado, al hablar del vapor producido por la evaporación del solvente en solución, se describe para el caso de soluciones acuosas concentradas como vapor sobrecalentado, ya que dicha corriente, como se describió anteriormente; esta en equilibrio con la fase liquida dentro del evaporador, de esta forma la temperatura que alcanza el evaporador es la misma en las corrientes de salidas; por lo tanto esta temperatura es igual a al punto de ebullición de la mezcla especificado a la presión del sistema. De esta forma se dice que la corriente (V) esta unos grados por encima de su punto de ebullición normal, de manera que se considera vapor sobrecalentado. Igualmente por tratarse de soluciones acuosas, la entalpía del vapor generado se ubicó en las tablas de vapor de agua sobrecalentadas a la presión y temperatura del sistema. Si bien es cierto la corriente (S) no sufre modificaciones con respecto 85 al tipo de solución que se utiliza en el evaporador. Por lo que se mantienen las especificaciones descritas para el caso de soluciones diluidas. Luego de realizar el procedimiento anterior para la elaboración del procedimiento matemático de la herramienta didáctica para evaporadores de un solo efecto, se puntualizó que para el desarrollo de esta investigación solo se tomarían en consideración las soluciones de base acuosa, de forma que pudiesen facilitar los cálculos del simulador de perspectiva académica. S O D VA ER S E R para evaporadores de un solo efecto S HO C E R E D Posteriormente a realizar el procedimiento para llevar a cabo el balance de energía 4.1.2. Identificación de los posibles casos en el procedimiento matemático en el evaporador, de acuerdo al tipo de solución con el que se lleve a cabo la evaporación, se identificaron las incógnitas que los problemas de perspectiva académicos podrían presentar de acuerdo a su descripción. De esta manera, se consideró separar los ejercicios planteados por casos, valiéndose de las variables que se requerían especificar; de esta forma se determinaron que por lo general los problemas redactados en la bibliografía se centraban en determinar cuatro alternativas para diferentes soluciones: El primer caso (CASO I), buscaba hallar el área superficial del evaporador (A), a partir de las variables proporcionadas; flujo o velocidad en la alimentación, concentración del soluto en la disolución, la temperatura a la entrada del evaporador, las condiciones del evaporador; presión, temperatura, coeficiente global de transferencia de calor, la temperatura del evaporador. Así mismo, las entalpias de la solución y por último, las condiciones de la corriente de vapor de agua, utilizado como iniciador de la transferencia de calor. Para especificar el diseño de un evaporador de simple efecto, partiendo de lo descrito anteriormente, fue llevado a cabo un procedimiento que tomo como 86 fundamentos la descripción del balance de masa que parte de la ley de conservación de masa, estos términos fueron especificados en el capítulo 2 de esta investigación. Basándose en las publicaciones de Geankoplis (1998) el primer paso en la resolución de los problemas de flujo casi siempre consiste en aplicar los principios de conservación de la masa a la totalidad del sistema o a una parte del mismo. S O D VA Considerando primero un balance elemental para una geometría simple, para deducir después la ecuación general de balance de masa. R SE E R S Se trajo a colación la ecuación 2.17 descrita por Geankoplis (1997) para establecer O H C E ER las bases del procedimiento matemático para diseñar un sistema de evaporación de efecto simple: D Entrada = Salida + Acumulación (Ec. 2.3) Así mismo, se utilizó el siguiente ejemplo para determinar el balance de masa para evaporadores de un solo efecto: Ejemplo 4.2 Un evaporador de efecto simple, dispone de una solución acuosa. Esta es introducida al evaporador con la finalidad de aumentar su concentración, la solución entra a un flujo (F) con una temperatura (Tf) y una concentración inicial (Xf), de la misma forma se tiene vapor de agua como medio de calefacción, el cual se encuentra a una temperatura de saturación (Ts) entrando a una velocidad (S). La vaporización se realiza a la presión atmosférica (Psist) y con un coeficiente de transferencia de calor (U), originando la evaporación del solvente en la solución; a una velocidad (V). Así mismo, la solución ahora con mayor concentración de soluto (Xp), sale del evaporador a una velocidad (P) a la temperatura de ebullición de la mezcla (T1). Se desea determinar el área del evaporador representado en la figura 4.1.4. 87 S O D VA Figura 4.1.4. Diagrama de un sistema de evaporación de efecto simple. Señalando como R E S E Tomando en cuenta la ley de conservación deR la masa, la cual enuncia: “la masa S O en el proceso debe ser igual a la de H total de todos los materiales que intervienen C E todos los materiales DEqueRsalen del mismo, más la masa de los materiales que se incógnita principal, el área superficial del evaporador. acumulan o permanecen en el proceso”, y considerando la ecuación 2.17 se tiene que para el evaporador representado en la figura 4.1.4. F+S=s+V+P (Ec. 4.5) De igual forma, para un balance por componentes: F·Xf = P·Xp (Ec. 4.6) Ya que las únicas corrientes que poseen en su composición porcentajes de soluto son la corriente de alimentación (F) y la corriente de salida del evaporador (P). Por otra parte, se hizo uso de la ecuación 2.14 la cual describe Martínez (2004) para la transferencia de calor en un evaporador: q=U∙A∙∆T (Ec. 2.14) Donde, ∆T es la diferencia de temperaturas entre el calor suministrado como calefacción (Ts) y la temperatura de ebullición de la mezcla (T1). Igualmente se trajeron a colación las ecuaciones; 4.2 que fue desarrollada al principio de este capítulo para el cálculo del calor generado en la corriente de calefacción, y la ecuación 4.3 que hace referencia al balance de energía previamente explicado. 88 q = S.λ (Ec. 4.2) F·hf + S·λ = P·hp + V·Hv (Ec. 4.3) De esta manera, se desarrolló el procedimiento matemático para determinar el área superficial de transferencia de calor en un evaporador de simple efecto. Despejando en primer lugar de la ecuación 4.6 el flujo o velocidad de la corriente de salida del evaporador (Xp), ya que se conoce como datos la concentración inicial (Xf) y la concentración final, junto con el flujo de la alimentación (F). P= F∙Xf Xp O H C E ER D R E (Ec. S4.7) E R S P S O D VA Luego de determinar el flujo de la corriente de salida del evaporador (P), de procedió a calcular el flujo de vapor de solvente evaporado sustituyendo el valor de P y F en la ecuación 4.5 y despejando el flujo de vapor (V). V=F–P V (Ec. 4.8) El flujo de la corriente de calefacción (S), se hizo 0 en la ecuación 4.5 ya que resulta el mismo a la entrada y a la salida. Así mismo, se procedió a calcular los valores de las entalpías de la solución y del vapor como se explicó para el balance de energía. Posteriormente se despeja de la ecuación 4.3, el flujo de vapor de agua saturado destinado a la calefacción del evaporador dando lugar a la ecuación 4.9. S= (P ∙hp)+ (V ∙Hv)- (F ∙hf) λ S (Ec. 4.9) Luego de haber obtenido el flujo de la corriente destinada a la calefacción en el evaporador, se calculó el flujo de calor partiendo de la ecuación 4.2, como a continuación se muestra: q=S·λ q (Ec. 4.2) Por último, utilizando el calor (q), el coeficiente de transferencia de calor, la temperatura de la corriente de calefacción y la temperatura de ebullición de la 89 solución se determina el área de transferencia de calor, despejando ésta misma; de la ecuación 2.14. A= q U∙(Ts-T1) A (Ec. 4.10) De esta forma, se identificó como el caso uno (1), el destinado a calcular el área de un evaporador de simple efecto, para cada tipo de solución a concentrar. La S O D VA concentración de la solución afecta únicamente la determinación de las entalpías y el cálculo de la temperatura de ebullición. R SE E R S Así mismo, se asignó un segundo caso (CASO II), encargado de determinar el O H C E en el primer caso, aR excepción del área superficial del evaporador que a E D continuación, sería especificada como dato al inicio. El procedimiento del caso dos coeficiente global de transferencia de calor (U), a partir de las variables señaladas (2) es similar al del primer caso. Como ya se dijo anteriormente el diseño de los sistemas de evaporación de un solo efecto se apoyó en la ley de conservación de la masa y la ley de conservación de la energía. De esta forma, tomando el siguiente ejemplo como guía se procedió a elaborar el procedimiento para determinar el coeficiente global de transferencia de calor (U). Ejemplo 4.3. Un evaporador de efecto simple, dispone de una solución acuosa. Esta es introducida al evaporador con la finalidad de aumentar su concentración, la solución entra a un flujo (F) con una temperatura (Tf) y una concentración inicial (Xf), de la misma forma se tiene vapor de agua como medio de calefacción, el cual se encuentra a una temperatura de saturación (Ts) entrando a una velocidad (S). La vaporización se realiza a la presión atmosférica (Psist) y con un área superficial de transferencia de calor (A), originando la evaporación del solvente en la solución; a una velocidad (V). Así mismo, la solución ahora con mayor concentración de soluto (Xp), sale del evaporador a una velocidad (P) a la temperatura de ebullición 90 de la mezcla (T1). Se desea determinar el coeficiente global de transferencia de calor en el evaporador representado en la figura 4.1.5. R SE E R S O H C E ER S O D VA Figura 4.1.5. Diagrama de un sistema de evaporación de efecto simple, señalando el coeficiente de transferencia de calor como incógnita principal. D Para el evaporador de la figura 4.1.5, se pueden resumir las ecuaciones expresadas en el caso uno de la siguiente forma: Balance General de Masa: F = V+P (Ec. 4.5) Balance por Componente: F·Xf = P·Xp (Ec. 4.6) Balance de Energía: F·hf + S·λ = P·hp + V·Hv q=U∙A∙∆T (Ec. 4.3) (Ec. 2.14) q = S.λ (Ec. 4.2) En primer lugar se despejó de la ecuación 4.6 el flujo o velocidad de la corriente de salida del evaporador (Xp), ya que se conoce como datos la concentración inicial (Xf) y la concentración final, junto con el flujo de la alimentación (F). P= F∙Xf Xp P (Ec. 4.7) 91 Luego de determinar el flujo de la corriente de salida del evaporador (P), se procedió a calcular el flujo de vapor de solvente evaporado sustituyendo el valor de P y F en la ecuación 4.5 y despejando el flujo de vapor (V). V=F–P V (Ec. 4.8) Así mismo, se procedió a calcular los valores de las entalpías de la solución y del vapor como se explicó anteriormente, posterío al cálculo de las entalpías y la S O D A lugar a la vapor de agua saturado destinado a la calefacción del evaporador, dando V R SE ecuación 4.9. E R S O H (P ∙hp)+ (V C∙Hv)- (F ∙hf) S (Ec. 4.9) E S= R λ DE temperatura de ebullición de la mezcla. Se despeja de la ecuación 4.3, el flujo de Luego de haber obtenido el flujo de la corriente destinada a la calefacción en el evaporador, se calculó el flujo de calor partiendo de la ecuación 4.2, como a continuación se muestra: q=S·λ q (Ec. 4.2) Por último, utilizando el calor (q), el área superficial del evaporador, la temperatura de la corriente de calefacción y la temperatura de ebullición de la solución se determinó el coeficiente global de transferencia de calor para el evaporador descrito en el ejemplo 4.3; despejándolo de la ecuación 2.14. U= q A∙(Ts-T1) U (Ec. 4.11) De esta forma se determinó el coeficiente global de transferencia de calor, siguiendo el procedimiento que posteriormente se identificó como caso dos (2), el cual será recreado en la herramienta didáctica para evaporadores de un solo efecto. Es importante resaltar que en los procedimientos de la identificación de los casos no se hace referencia al cálculo de las entalpías ni de la forma de definir la temperatura de ebullición de acuerdo a la concentración en que se presente el 92 soluto en la solución. Ya que al principio de este capítulo se hizo referencia paso a paso de la forma correcta para elaborar el balance de energía de acuerdo al tipo de solución a concentrar. Por otro lado, el caso tres (CASO III), se limita en encontrar la composición del soluto en la corriente de producto o corriente final (Xp), a partir de las variables especificadas por el problema planteado. De esta forma, se consideró el siguiente S O D Ejemplo 4.4. Un evaporador de efecto simple, dispone de una solución Aacuosa. Esta V R es introducida al evaporador con la finalidad deE aumentar SE su concentración, la R S (Tf) y una concentración inicial solución entra a un flujo (F) con unaO temperatura H C (Xf), de la misma formaR se E tiene vapor de agua como medio de calefacción, el cual DE se encuentra a una temperatura de saturación (Ts) entrando a una velocidad (S). ejemplo para desglosar el procedimiento matemático que respecta al caso tres (3). La vaporización se realiza a la presión atmosférica (Psist), con un coeficiente de transferencia de calor (U) y para un área superficial de transferencia de calor (A), originando la evaporación del solvente en la solución; a una velocidad (V). Así mismo, la solución sale del evaporador a una velocidad (P) con una concentración desconocida, a la temperatura de ebullición de la mezcla (T1). Se desea determinar la concentración final de la solución en el evaporador representado en la figura 4.1.6. Figura 4.1.6. Diagrama de un sistema de evaporación de efecto simple, señalando la composición del soluto en la corriente final, como incógnita principal. 93 Para el evaporador de la figura 4.1.6, se pueden resumir las siguientes ecuaciones en lo que corresponde al balance de masa y energía: Balance General de Masa: F = V+P (Ec. 4.5) Balance por Componente: F·Xf = P·Xp Balance de Energía: HO C E R q = S.λ DE R SE E R S F·hf + S·λ = P·hp + V·Hv (Ec. 4.3) q=U∙A∙∆T S O D VA (Ec. 4.6) (Ec. 2.14) (Ec. 4.2) En primer lugar se debió especificar mediante los cálculos correspondientes al tipo de solución que se desea concentrar, la temperatura de la mezcla; junto con las entalpías para la corriente de alimentación y de producto final, al igual que para las corrientes de vapor de agua. Luego de definir estas variables se procede a calcular la concentración final del soluto de la siguiente forma: Partiendo de la ecuación 2.14, y tomando los valores del coeficiente global de transferencia de calor, el área superficial del evaporador y el diferencial de temperaturas entre el evaporador y la corriente de calefacción, se determinó el flujo de calor que existe en el evaporador. q = U · A · (Ts – T1) q (Ec. 2.14) Luego de determinar el flujo de calor en el evaporador (q), se procedió a calcular el flujo de vapor de agua destinado a calefacción, a partir de la ecuación 4.2, en la que se realizó un despeje de la corriente S, dando lugar a la ecuación 4.12. S= q λ S (Ec. 4.12) 94 Posteriormente, se realizó un despeje de la variable V en la ecuación 4.5; la cual representa el flujo de vapor del solvente evaporado. Asi mismo, se sustituye el la ecuación 4.3 originando ecuación 4.13 de la siguiente forma: V=F–P (Ec. 4.8) F·hf + S·λ = P·hp + V·Hv (Ec. 4.3) Sustituyendo Ec. 4.8 en Ec. 4.3. F·hf + S·λ = P·hp + (F – P)·Hv S O D VA R (Ec. 4.13) SE E R S A continuación, se despejó de la ecuación anterior la variable P que representa el HO C E R- Hv)+ (S ∙λ) F∙(hf E flujo de la corriente ya concentrada a la salida del evaporador. D P= P (hp - Hv) (Ec. 4.14) Luego de calcular la velocidad de la solución concentrada a la salida del evaporador (P), se calculó por medio de la ecuación 4.8, el flujo de vapor evaporado. V=F–P V (Ec. 4.8) Por último, partiendo del balance por componentes se despejó la composición del soluto en la salida del evaporador. Xp= F∙Xf P Xp (Ec. 4.15) Por último, se identificó el caso cuatro (CASO IV), el cual se designó con el objetivo de calcular el flujo o velocidad de alimentación (F) a la entrada de un evaporador de simple efecto, a partir de los conceptos básicos que se han venido haciendo referencia. De esta manera se modificó el ejemplo propuesto en el caso tres (3), de forma que colaborará con la elaboración del procedimiento matemático en lo que corresponde a este caso. Ejemplo 4.5. Un evaporador de efecto simple, dispone de una solución acuosa. Está es introducida al evaporador con la finalidad de aumentar su concentración, la 95 solución entra a una temperatura (Tf) y una concentración inicial (Xf), de la misma forma se tiene vapor de agua como medio de calefacción, el cual se encuentra a una temperatura de saturación (Ts) entrando a una velocidad (S). La vaporización se realiza a la presión atmosférica (Psist), con un coeficiente de transferencia de calor (U) y para un área superficial de transferencia de calor (A), originando la evaporación del solvente en la solución; a una velocidad (V). Así S O D VA mismo, la solución sale del evaporador a una velocidad (P) con una composición R final (Xp), a la temperatura de ebullición de la mezcla (T1). Se desea determinar la SE E R S concentración final de la solución en el evaporador representado en la figura 4.1.7. O H C E ER D Figura 4.1.7. Diagrama de un sistema de evaporación de efecto simple, señalando la alimentación, como incógnita principal. Para el evaporador de la figura 4.1.7, se definen las siguientes ecuaciones en lo que corresponde al balance de masa y energía: Balance General de Masa: F = V+P (Ec. 4.5) Balance por Componente: F·Xf = P·Xp (Ec. 4.6) Balance de Energía: F·hf + S·λ = P·hp + V·Hv (Ec. 4.3) 96 q=U∙A∙∆T (Ec. 2.14) q = S.λ (Ec. 4.2) En primer lugar se debió especificar mediante los cálculos correspondientes al tipo de solución que se desea concentrar, la temperatura de la mezcla; junto con las entalpías para la corriente de alimentación, de producto final y para las corrientes de vapor de agua. Luego de definir estas variables se procede a calcular la S O D A global de V Partiendo de la ecuación 2.14, y tomando los valores delR coeficiente SE E transferencia de calor, el área superficial del evaporador y el diferencial de R S de calefacción, se determinó el flujo O H temperaturas entre el evaporador y la corriente C E R de calor que existe DenEel evaporador. concentración final del soluto de la siguiente forma: q = U · A · (Ts – T1) q (Ec. 2.14) Luego de determinar el flujo de calor en el evaporador (q), se procedió a calcular el flujo de vapor de agua destinado a calefacción, a partir de la ecuación 4.2, en la que se realizó un despeje de la corriente S, dando lugar a la ecuación 4.12. S= q λ S (Ec. 4.12) Posteriormente, se realizó un despeje de la variable V en la ecuación 4.5; la cual representa el flujo de vapor del solvente evaporado. Asi mismo, se sustituye el la ecuación 4.3 originando ecuación 4.13 de la siguiente forma: V=F–P (Ec. 4.8) F·hf + S·λ = P·hp + V·Hv (Ec. 4.3) Sustituyendo Ec. 4.8 F·hf + S·λ = P·hp + (F – P)·Hv (Ec. 4.13) 97 A continuación, se despejó del balance por componentes la variable P para sustituirla en la ecuación anterior de forma que quede en función de la alimentación. P= F∙Xf Xp (Ec. 4.7) F∙Xf F∙Xf F ∙ hf + S ∙ λ = ( ) ∙ hp + [F∙Hv- ( ) ∙Hv] Xp Xp Realizando el despeje de la variable F en la ecuación 4.16: F= (Ec 4.16) S O D VA R 4.17) E(Ec. F S E SR (- S ∙λ) Xf ∙hp Xf ∙Hv [(hf)- ( ) -(Hv)+ ( )] Xp Xp HO C E R el flujo de alimentación del evaporador (F), se sustituye Asi mismo, luego deE D obtener junto a las composiciones a la entrada (Xf) y a la salida (Xp) en la ecuación 4.7 para optener el valor de P: P= F∙Xf Xp P (Ec. 4.7) Por ultimo se sustituye en la ecuación 4.8 para obtener la velocidad del vapor originado por la evaporación del solvente en la solución. V=F–P V (Ec. 4.8) 4.1.3. Resultados en el establecimiento del procedimiento matemático de la herramienta didáctica para evaporadores de un solo efecto. Previamente a la elaboración del procedimiento matemático de la herramienta didáctica, se realizó una investigación documental donde tuvo lugar la selección de la bibliografía en que se sustentó este objetivo específico del dicho trabajo especial de grado, extrayendo los criterios principales que debían tomarse en cuenta en conjunto con ejercicios de perspectiva académica, los cuales servirían como ejemplos para diseñar el programa propuesto. 98 De manera, que luego de establecer los criterios principales que se debían seguir, se tomaron ocho (8) ejercicios planteados; donde cuatro eran bajo la caracterización de soluciones diluidas y los otros cuatro de soluciones concentradas. Cada uno de los ejercicios se centraba en determinar una incógnita diferente; como se explicó en la parte de identificación de los casos, según las variables a calcular. Así mismo, los datos de los ejercicios seleccionados fueron agrupados en la tabla S O D VA 3.1, para facilitar la identificación de las características especificadas en cada R enunciado. A continuación, se especifican los ejercicios que fueron seleccionados SE E R S reportando conjuntamente la tabla de datos que responde a cada uno. O H C E ER D SOLUCIONES DILUIDAS Tomando como ejemplo 4.6. (Geankoplis 1998 p554). Área de transferencia de calor en un evaporador de un solo efecto. Un evaporador continuo de efecto simple concentra 9072 kg/h de una solución de sal al 1% en peso que entra a 311 K, hasta una concentración final de 1.5% en peso. El vapor en el evaporador está a 101.325 kPa y el vapor de agua que se introduce está saturado a 143.3 kPa. El coeficiente total U = 1704 W/(m 2.K). Calcule las cantidades de vapor y de producto de líquido, así como el área de transferencia de calor que se requiere. Puesto que se trata de una solución diluida, suponga que su punto de ebullición es igual al del agua. 99 Tabla 4.1. Reporte de datos del primer ejercicio planteado para elaborar el procedimiento matemático de la herramienta didáctica. Corriente ALIMENTACIÓN PRODUCTO SISTEMA Variable Flujo de Alimentación Temperatura de Entrada Concentración Capacidad Calorífica Entalpía Concentración Capacidad Calorífica Entalpía Área Coeficiente de Transferencia de Calor Presión Sistema Incremento del Punto de Ebullición Temperatura de Saturación Presión de vaporización CALEFACCIÓN 9072 311 0,01 4,14 -0,015 4,14 -? 1704 101,325 0 -143,325 Unidad kg/h K kJ/kg.K S O D VA R SE E R S O ECH DER Valor kJ/kg.K W/m².K kPa kPa En la Tabla 4.1 se resumieron los datos proporcionados por el ejercicio descrito anteriormente. De esta forma se resaltó en color amarillo; la variable que se deseaba calcular; para este caso es el área superficial de transferencia de calor (A). De tal forma bajo los criterios especificados anteriormente, se abordó el ejercicio mediante el procedimiento matemático desglosado para el caso uno (1). Por otro lado, a continuación se describe el ejemplo 4.7. (Geankoplis 1998 p574). Coeficiente de transferencia de calor en un evaporador de efecto simple. Una alimentación de 4535 kg/h de solución de sal al 2% en peso a 311 K, entra continuamente a un evaporador para concentrarse a 3%. La evaporación se lleva a presión atmosférica y el área del evaporador es 69,7 m 2. El calentamiento se logra con vapor de agua saturado a 383,2 K. Puesto que la solución es diluida, se puede suponer que tiene el mismo punto de ebullición del agua. Se estima que la capacidad calorífica de la alimentación es Cp = 4,10 kJ/kg.K. Calcule las cantidades de vapor y de líquido producido y el coeficiente total de transferencia de calor. 100 Tabla 4.2. Reporte de datos del segundo ejercicio planteado para elaborar el procedimiento matemático de la herramienta didáctica. Corriente ALIMENTACIÓN PRODUCTO SISTEMA Variable Flujo de Alimentación Temperatura de Entrada Concentración Capacidad Calorífica Entalpía Concentración Capacidad Calorífica Entalpía Área Coeficiente de Transferencia de Calor Presión Sistema Incremento del Punto de Ebullición Temperatura de Saturación Presión de vaporización 4535 311 0,02 4,1 -0,03 4,1 -69,7 ? 101,325 0 383,2 -- Unidad kg/h K kJ/kg.K S O D VA R SE E R S HO C E R DE CALEFACCIÓN Valor kJ/kg.K m² kPa K En la tabla 4.2 se resumieron los datos proporcionados por el ejemplo dos. De esta forma se resaltó en color amarillo; la variable que se deseaba calcular; para este caso es el coeficiente global de transferencia de calor (U). De tal forma bajo los criterios especificados anteriormente, se abordó el ejercicio mediante el procedimiento matemático desglosado para el caso dos (2). De manera que sirviera de ejemplo, el desarrollo del problema para soluciones diluidas. De la misma forma se toma como ejemplo 4.8 (Geankoplis 1998 p574). El siguiente enunciado el cual es la continuación del ejercicio anterior: Efectos de una alimentación más rápida en el evaporador. Con los mismos valores del área, U, presión del vapor de agua, presión del evaporador y temperatura de la alimentación del problema anterior. Calcule las cantidades de líquido y de vapor que salen y la concentración del líquido de salida cuando la velocidad de alimentación se aumenta a 6804 kg/h. 101 Tabla 4.3. Reporte de datos del tercer ejercicio planteado para elaborar el procedimiento matemático de la herramienta didáctica. Corriente Variable ALIMENTACIÓN SISTEMA 6804 kg/h Temperatura de Entrada Concentración Capacidad Calorífica Entalpía 311 K 0,02 4,1 kJ/kg.K -- CALEFACCIÓN Área Coeficiente de Transferencia de Calor Presión Sistema Incremento del Punto de Ebullición Temperatura de Saturación Presión de vaporización S O D VA R ESE R S HO C E R E D Unidad Flujo de Alimentación Concentración Capacidad Calorífica Entalpía PRODUCTO Valor ? 4,1 kJ/kg.K -- 69,7 m² 6520,2 kJ/m².h.K 101,325 kPa 0 383,2 K -- En la tabla 4.3 se reportaron los datos proporcionados por el ejercicio anterior el cual es una combinación del ejemplo dos. De esta forma se resaltó en color amarillo; la variable que se deseaba calcular; para este caso es la composición final del soluto (Xp). De tal forma bajo los criterios especificados anteriormente, se abordó el ejercicio mediante el procedimiento matemático desglosado para el caso tres (3). De manera que sirviera de ejemplo, el desarrollo del problema para soluciones diluidas. Igualmente. Se tomó como ejemplo 4.9 el siguiente (Geankoplis 1998 p574): Una alimentación de solución de sal al 2% en peso a 311 K, entra continuamente a un evaporador para concentrarse a 3%. La evaporación se lleva a una presión del evaporador de 41,4 kPa y el área del evaporador es 69,7 m2. El calentamiento se logra con vapor de agua saturado a 383,2 K. Puesto que la solución es diluida, se puede suponer que tiene el mismo punto de ebullición del agua. Se estima que la capacidad calorífica de la alimentación es Cp = 4,10 kJ/kg.K. Determine la capacidad o velocidad de la alimentación en estas condiciones. 102 Tabla 4.4. Reporte de datos del cuarto ejercicio planteado para elaborar el procedimiento matemático de la herramienta didáctica. Corriente Variable ALIMENTACIÓN PRODUCTO SISTEMA Flujo de Alimentación Temperatura de Entrada Concentración Capacidad Calorífica Entalpía Concentración Capacidad Calorífica Entalpía Área Coeficiente de Transferencia de Calor Presión Sistema Incremento del Punto de Ebullición Temperatura de Saturación Presión de vaporización ? 311 0,02 4,1 -0,03 4,1 -69,7 6520,2 41,4 0 Unidad K kJ/kg.K S O D VA SER E R S HO C E R DE CALEFACCIÓN Valor kJ/kg.K m² kJ/m².h.K kPa 383,2 K -- En la tabla 4.4 se reportaron los datos proporcionados por el ejercicio descrito anteriormente. De esta forma se resaltó en color amarillo; la variable que se deseaba calcular; para este caso es la alimentación a la entrada del evaporador (F). De tal forma bajo los criterios especificados anteriormente, se abordó el ejercicio mediante el procedimiento matemático desglosado para el caso tres (3). De manera que sirviera de ejemplo, el desarrollo del problema para soluciones diluidas. SOLUCIONES CONCENTRADAS Así mismo, tomando como ejemplo 4.10 para soluciones concentradas el siguiente (Ocon y Tojo, s.f. p172): En un evaporador simple se tratan 15000 kg/h de una disolución de NaOH al 10% que ha de concentrarse hasta el 50% en peso. El vapor empleado como medio de calefacción es vapor saturado a 3,5 atm, y una vez condensado sale a la temperatura de condensación. El vacío mantenido en la cámara de evaporación es de 620 mmHg, referido a la presión atmosférica normal. El coeficiente integral de transmisión de calor vale 1600 kcal/m².h.⁰C. Si la 103 alimentación entra a 40⁰C y no se pierde calor con el exterior, determine; la superficie de calefacción. Tabla 4.5. Reporte de datos del quinto ejercicio planteado para elaborar el procedimiento matemático de la herramienta didáctica. Corriente Variable ALIMENTACIÓN PRODUCTO SISTEMA Flujo de Alimentación Temperatura de Entrada Concentración Concentración O ECH CALEFACCIÓN Unidad S O D VA R SE E R S Área Coeficiente de Transferencia de Calor Presión Sistema Incremento del Punto de Ebullición Temperatura de Saturación Presión de vaporización DER Valor 15000 kg/h 40 °C 0,1 0,5 ? 1600 kcal/m².h.°C 620 mmHg (vacío) --3,5 atm En la tabla 4.5 se reportaron los datos proporcionados por el ejercicio descrito anteriormente. El cual se considera solución concentrada, ya que al no hacer referencia en esto ni especificar las capacidades caloríficas o el incremento del punto de ebullición, se asume como solución concentrada para el sistema NaOH– H2O. De esta forma se resaltó en color amarillo; la variable que se deseaba calcular; para este caso es el área de transferencia de calor (A). De tal forma bajo los criterios especificados anteriormente, se abordó el ejercicio mediante el procedimiento matemático desglosado para el caso uno (1). De manera que sirviera de ejemplo, el desarrollo del problema para soluciones concentradas. De la misma forma, se identifica el ejemplo 4.11, (Geankoplis 1998 p575): Coeficiente de transferencia de calor para evaporar NaOH. Para concentrar 4536 kg/h de una solución de NaOH al 10% en peso hasta 20% en peso, se usa un evaporador de efecto simple con área de 37,6 m 2. La alimentación entra a 21,1 ˚C. Se usa vapor de agua saturado a 110 ˚C como medio de calentamiento y la presión en el evaporador es 51,7 kPa. Calcule los kg/h de vapor de agua utilizado y el coeficiente total de transferencia de calor. 104 Tabla 4.6. Reporte de datos del sexto ejercicio planteado para elaborar el procedimiento matemático de la herramienta didáctica. Corriente Variable ALIMENTACIÓN PRODUCTO SISTEMA CALEFACCIÓN Valor Flujo de Alimentación Temperatura de Entrada Concentración Concentración Área Coeficiente de Transferencia de Calor Presión Sistema Incremento del Punto de Ebullición C E R DE kg/h K S O D VA R ESE R S HO Temperatura de Saturación Presión de vaporización 4536 294,3 0,1 0,2 37,6 ? 51,7 -- Unidad m² kPa 383,15 K -- En la tabla 4.6 se reportaron los datos proporcionados por el ejercicio descrito anteriormente. El cual se considera solución concentrada, ya que al no hacer referencia en esto ni especificar las capacidades caloríficas o el incremento del punto de ebullición, se asume como solución concentrada para el sistema NaOH– H2O. De esta forma se resaltó en color amarillo; la variable que se deseaba calcular; para este caso es el coeficiente global de transferencia de calor (U). De tal forma bajo los criterios especificados anteriormente, se abordó el ejercicio mediante el procedimiento matemático desglosado para el caso dos (2). De manera que sirviera de ejemplo, el desarrollo del problema para soluciones concentradas. El ejemplo 4.12. Es una modificación del ejemplo 4.10 de Ocon y Tojo, (s.f. p172): En un evaporador simple se tratan 15000 kg/h de una disolución de NaOH al 10% que ha de concentrarse. El vapor empleado como medio de calefacción es vapor saturado a 3,5 atm, y una vez condensado sale a la temperatura de condensación. El vacío mantenido en la cámara de evaporación es de 620 mmHg, referido a la presión atmosférica normal. El coeficiente integral de transmisión de calor vale 1600 kcal/m².h.⁰C y la superficie de transferencia de calor es igual a 120 m². Si la 105 alimentación entra a 40⁰C y no se pierde calor con el exterior, determine; la composición final del soluto a la salida del evaporador. Considere un IPE de 40,98 y un valor de entalpía para la corriente final de 790kJ/kg. En la tabla 4.7 se muestran las variables proporcionadas por el ejemplo 4.12. El cual se considera solución concentrada, ya que al no hacer referencia en esto ni especificar las capacidades caloríficas o el incremento del punto de ebullición, se S O D VA asume como solución concentrada para el sistema NaOH–H2O. De esta forma se ER S E R anteriormente, se abordó el ejercicio S mediante el procedimiento matemático O H C desglosado para el caso tres (3). De manera que sirviera de ejemplo, el desarrollo E R E concentradas. Dsoluciones del problema para resaltó en color amarillo; la variable que se deseaba calcular; para este caso es la composición final del evaporador (Xp). De tal forma bajo los criterios especificados Tabla 4.7. Reporte de datos del séptimo ejercicio planteado para elaborar el procedimiento matemático de la herramienta didáctica. Corriente ALIMENTACIÓN PRODUCTO SISTEMA CALEFACCIÓN Variable Flujo de Alimentación Temperatura de Entrada Concentración Concentración Área Coeficiente de Transferencia de Calor Presión Sistema Incremento del Punto de Ebullición Temperatura de Saturación Presión de vaporización Valor Unidad 15000 kg/h 40 °C 0,1 ? 120 m² 1600 kcal/m².h.°C 620 mmHg(vacío) 40,98 -3,5 atm 106 De la misma forma, Se redacta el ejemplo 4.13 (Geankoplis 1998, p575): Producción en un evaporador de efecto simple. Un evaporador concentra F kg/h a 311 K de una solución de NaOH al 20% en peso hasta 50% en peso. El vapor de agua saturado para el calentamiento está a 399,3 K. la presión en el evaporador es de 13,3 kPa abs. El coeficiente total es 1420 W/m2.K y el área es 86,4 m2. Calcule la velocidad de alimentación F del evaporador. S O D VA R SE E R S Tabla 4.8. Reporte de datos del octavo ejercicio planteado para elaborar el procedimiento matemático de la herramienta didáctica. Corriente D HO Variable C E ER ALIMENTACIÓN PRODUCTO SISTEMA CALEFACCIÓN Flujo de Alimentación Temperatura de Entrada Concentración Concentración Área Coeficiente de Transferencia de Calor Presión Sistema Temperatura de Saturación Presión de vaporización Valor Unidad ? kg/h 311 K 0,2 0,5 86,4 1420 13,3 399,3 m² W/m².K kPa K -- En la tabla 4.8, se muestran las variables proporcionadas por el ejercicio anterior. El cual se considera solución concentrada, ya que al no hacer referencia en esto ni especificar las capacidades caloríficas o el incremento del punto de ebullición, se asume como solución concentrada para el sistema NaOH–H2O. De esta forma se resaltó en color amarillo; la variable que se deseaba calcular; para este caso es la alimentación de entrada al evaporador (F). De tal forma bajo los criterios especificados anteriormente, se abordó el ejercicio mediante el procedimiento matemático desglosado para el caso cuatro (4). De manera que sirviera de ejemplo, el desarrollo del problema para soluciones concentradas. 107 4.2. Fase 2: Programación del procedimiento matemático de la herramienta didáctica para evaporadores de un solo efecto Una vez establecidos los procedimientos de cálculos a ser utilizados en la herramienta didáctica para evaporadores de un solo efecto. Se procedió a la estructuración de este procedimiento en un documento Microsoft Office Excel©, versión 2013 y Visual Basic, versión 2010. S O D 4.2.1. Primicias a la programación del procedimiento matemático A de la V R herramienta didáctica para evaporadoresE deS unE solo efecto R S O H Antes de recrear el procedimiento C matemático mediante el uso de Microsoft Excel y E R E ciertas características relevantes que el usuario debía Visual Basic, se D especificaron tomar en cuenta, los cuales se denominarían posteriormente como limitaciones del programa. Si bien esta investigación busca proponer un simulador básico con fines académicos, el cual tiene la capacidad de reproducir el comportamiento de evaporadores bajo ciertos criterios, con la finalidad de facilitar o ayudar a la compresión del tema de evaporación en la cátedra de Operaciones Unitarias II, impartida en la Universidad Rafael Urdaneta. Por lo tanto, se limitó su funcionamiento a ciertas restricciones que a continuación se enumeran: 1. Solo reproduce ejercicios de evaporación para efecto simple o un solo efecto. 2. Las soluciones a trabajar deben ser acuosas, es decir, que el solvente que conforma la solución debe ser el agua. 3. El sistema de unidades es el sistema internacional (SI), donde los flujos son requeridos y proporcionados exclusivamente en másicos. 4. Se restringieron los cálculos a cuatro tipos de casos; donde el caso 1 determina el área superficial del evaporador, el caso 2 busca hallar el coeficiente de transferencia de calor, el caso 3 pretende determinar la 108 concentración del producto final y el caso 4 busca calcular el flujo o velocidad de la alimentación. 5. En la sección de comparación, solo se pueden manipular las variables bajo el mismo caso seleccionado anteriormente y el mismo tipo de solución. 6. En las ventanas alternas a las hojas de cálculo se deben especificar los valores decimales con punto (.). Así mismo, en las hojas de cálculo se deben especificar los valores decimales con coma (,). S O D VA 7. El convertidor de unidades incluido en la herramienta solo convierte unidades R SE E R S básicas del sistema internacional al sistema inglés. O 8. El vapor de la corriente que entra al evaporador para llevar a cabo la H C E ER evaporación, debe ser vapor de agua a condiciones de saturación. D De la misma forma; con la finalidad de ayudar a la comprensión de la herramienta, se asignaron colores y letras representativas a cada una de las corrientes del evaporador: La alimentación del evaporador se representó en color verde y con la letra (F). La corriente de salida de la solución o producto se clasifico de color naranja, con la letra (P). Los datos referentes al sistema, como; temperatura, área, calor, coeficiente global de transferencia de calor y economía adoptaron el color rojo. Las corrientes de vapor de solvente evaporado y vapor de agua destinado a calefacción se denominaron (V) y (S) respectivamente, junto con la asignación del azul claro para la corriente V y azul oscuro para corriente S. 4.2.2. Desarrollo del procedimiento matemático de la herramienta didáctica; mediante Microsoft Office Excel© Si bien es cierto, el procedimiento de la herramienta didáctica para evaporadores de un solo efecto, es bastante extenso. Para recrearlo fue necesario utilizar 109 complementos que facilitaran la selección de los criterios principales y la introducción de los datos básicos que se describen en los ejercicios académicos. Por este motivo fue seleccionado Microsoft Office Excel 2013 como programa base, debido a la versatilidad que presenta para desarrollar cálculos matemáticos con las modalidades y complementos que lo caracterizan. Así mismo, para comparar la veracidad del simulador de perspectiva didáctica; se S O D VA desarrolló el procedimiento matemático por la forma tradicional. Basándose en ER S E R para comparar los valores arrojados por la herramienta. S HO C E Una de las modalidades DERo complementos de Microsoft Office Excel© es la opción ejemplos extraídos de la bibliografía seleccionada; aplicando la técnica de observación documental. Los resultados obtenidos mediante este método sirvieron de vincularse con el lenguaje de programación Visual Basic 2010. A través del cual, mediante un dialecto BASIC se pueden generar comandos básicos que reproduzcan funciones y operaciones específicas. Igualmente por medio de esta herramienta, se pueden crear ventanas auxiliares al documento que faciliten al usuario el ingreso de datos y manejo del programa. La estructura básica de una hoja de cálculo en Excel, es una matriz matemática; con dos elementos fundamentales: las columnas (encabezadas por letras: A, B, C.) y las filas (encabezadas por números: 1, 2, 3.). La intersección entre ambos elementos se denominan celdas (nombradas por letras y números: A1, B5, D32.) y es el elemento más importante desde el punto de vista de la información. Debido a la versatilidad de las hojas de cálculo, se utilizan a veces para hacer pequeñas bases de datos, informes, gráficos estadísticos, clasificaciones de datos, entre otros usos. Las operaciones más frecuentes se fundamentan en cálculos entre celdas, las cuales son referenciadas respectivamente mediante la letra de la columna y el número de la fila, por ejemplo =B1*C1. 110 Los principales elementos de trabajo son: Fila: Es un conjunto de varias celdas dispuestas en sentido horizontal. Título de fila: Está siempre a la izquierda y nombra a las filas mediante números. Columna: Es un conjunto de varias celdas dispuestas en sentido vertical. Título de columna: Está siempre arriba y nombra a las columnas mediante S O D VA letras, que en el caso de Excel© 2013 van desde la A hasta la IV. Luego de ER S E R Celda: Es la intersección de una fila y una columna y en ella se introducen S O H C los gráficos, ya se trate de texto, números, fecha u otros datos. Una celda se E R E D el nombre de la columna, seguido del nombre de la fila. Por nombra mediante la columna Z viene la AA, AB, AC…, luego de la AZ viene la BA, la BB, la BC, y así sucesivamente. ejemplo, la celda que es la intersección de la fila 29 con la columna F, se denomina F29. Rango: Los rangos son una referencia a un conjunto de celdas de una planilla de cálculos. Se definen mediante letras y números. Se denomina mediante la celda de una esquina del rango (generalmente la superior izquierda), luego dos puntos y la esquina opuesta. Por ejemplo, al rango que comprende las celdas C4, C5, C6, C7, D4, D5, D6, D7, E4, E5, E6 y E7 se lo denomina C4:E7. A continuación se describe paso a paso, como se llevó a cabo la recreación del procedimiento matemático para elaborar la herramienta didáctica para evaporadores de un solo efecto. En primer lugar se procedió a entrar en Microsoft Excel 2013 y crear un documento nuevo, como se ilustra en la figura 4.2.1. 111 D R SE E R S O H C E ER S O D VA Figura 4.2.1. Ingreso a un documento nuevo en Microsoft Excel. Figura 4.2.2. Hoja de datos compartidos por los caso. 112 Posteriormente la hoja1 se denominó, “DATOS INTRODUCIDOS EN LAS VENTANAS COMPARTIDAS”, la cual tiene como finalidad agrupar los datos que el usuario introducirá, a través de ventanas auxiliares programas en Visual Basic. En esta hoja; se especificarían las variables requeridas manejar, junto con el valor de cada una de ellas. Las variables se encuentran agrupadas por tablas, donde cada tabla responde a una corriente específica diferenciadas por colores, como se muestra en la figura 4.2.2. S O D VA ER S E R concentradas fue necesario diseñar ocho tipos de casos diferentes. Dichas hojas S O H C del usuario, donde se deberán ingresar el valor están destinadas a la manipulación E R E de las variablesD básicas del evaporador, haciendo uso de una lista desplegable Así mismo, se identificaron hojas de cálculo para la especificación de los datos en cada caso. Es importante resaltar que al tratar con soluciones diluidas y donde pueda seleccionar las unidades respectivas dentro del sistema internacional. (Figura 4.2.3). Figura 4.2.3. Introducción de datos a la herramienta didáctica por caso. 113 En esta parte, se indicó al operador, los datos requeridos por el programa de perspectiva didáctica, para llevar a cabo el procedimiento según el caso y el tipo de solución a trabajar. Posteriormente, se vinculó la hoja con ventanas auxiliares; a las que se accederá por medio de botones que más a delante se configuraron, como se muestra en la figura 4.2.3. Mediante el uso de ventanas auxiliares el usuario tendrá la tarea de especificar las condiciones requeridas para el cálculo de entalpías e igualmente definir la temperatura de la solución. S O D VA ER S E R necesario realizar conversiones de unidades internas cuando el caso lo ameritará, S O H y de esta manera mantener la C concordancia entre las variables, para no afectar los E R E D cálculos posteriormente. Si bien es cierto, los datos de los problemas académicos pueden encontrarse especificados de varias formas. En consecuencia, para calcular los resultados fue Así mismo, para realizar esta operación fue necesario especificar listas de datos en donde se identificaron las unidades respectivas para cada variable. Estas, se ubicaron del lado derecho de cada celda que contendría el valor numérico de la variable proporcionada en la hoja, como se resalta en color rojo en la figura 4.2.3. La elaboración de la lista de unidades fue bastante sencilla, en primer lugar se accedió a una hoja en blanco donde se reportaría en una columna las unidades a mostrar para cada variable; En este caso, se colocaron en la parte inferior de la hoja de datos compartidos representada en la figura 4.2.2. Posteriormente se accedió a la pestaña de “DATOS” ubicada en la parte superior de la hoja de cálculo, en esta pestaña se ubicó la opción “validación de datos”, como se especifica en la figura 4.2.4. 114 D R SE E R S O H C E ER S O D VA Figura 4.2.4. Identificación de la opción ‘Validación de datos’. Así mismo, al identificar la opción se especificó el criterio de validación a escoger, como se muestra en la figura 4.2.5. El cual, se indicó como una lista desplegable. Posterior a esto, se selecciona las celdas que contienen los datos a mostrar por la lista creada como se aprecia en la figura 4.2.6. Figura 4.2.5. Selección del criterio de validación de datos. 115 R SE E R S O H C E ER S O D VA Figura 4.2.6. Selección de los datos a mostrar en la lista desplegable. D Finalmente obteniendo una lista desplegable con los datos resaltados en la figura 4.2.6 en rojo, la cual se posicionaría en la celda donde se ubicó el puntero previo a todos estos pasos, que en este caso sería la celda J11. (Figura 4.2.7). Figura 4.2.7. Elaboración de la lista despegable. 116 Así mismo, la lista sola no realiza los cambios de unidades precisados en la recreación del procedimiento matemático de la herramienta didáctica, partiendo de esto, se hizo uso del comando “SI”, para las conversiones de unidades respectivas al seleccionar cualquier unidad de la lista: por ejemplo. Para este caso en específico la lista hace referencia a las posibles unidades en el sistema internacional para identificar el peso o masa. Si se quisiera trabajar solamente en la unidad de kilogramo (kg), utilizando el comando “SI” se realizarían los cambios respectivos para todas las demás unidades. S O D VA ER S E R se ejecutaría de la siguiente forma (figura 4.2.8): SI(J11=”g”;I11*1000;I11), siendo S O H C la lista desplegable, y la celda I11 en donde se la celda J11 en la que se posicione E R DE Es decir. Si el peso o masa se posee identificado en gramos (g), el comando “SI”, ubique el valor de la variable. De esta manera, si se traduce el comando planteado en la figura 4.2.8. Sería; si en la celda J11 aparece el dato “g”, entonces; Multiplica la celda I11 por 1000 para llevarlo a kilogramo, sino coloca el valor de I11. Por lo tanto, cuando el usuario introduzca el valor en gramos internamente se convertirá a kilogramos para ejecutar los cálculos manteniendo concordancia en las unidades (figura 4.2.9). Figura 4.2.8. Convirtiendo unidades a kilogramo. 117 D R SE E R S O H C E ER S O D VA Figura 4.2.9. Cambio de valor en la celda E11 con respecto a la unidad proporcionada. Siguiendo con lo antes planteado, se identificaron para cada caso una hoja de reporte de datos, en la que se ejecutarían los cambios de unidades para las variables que lo requirieran; Introducidas tanto en las ventanas auxiliares, como en la hoja de ingreso de datos por caso. En la figura 4.2.10, se resalta en color rojo la conversión de unidades respectiva para el flujo de la alimentación conforme lo defina el usuario en la hoja del caso 1 y en color azul la celda donde se ejecutara el cambio especificado. Figura 4.2.10. Cambio de unidades para el flujo de alimentación en el caso 1. 118 Posteriormente se crearon las hojas de cálculos denominadas “SOLUCIÓN”, en la que se ejecutarían los cálculos respectivos para el procedimiento matemático de la herramienta didáctica por caso, estas hoja se diseñaron de acuerdo al caso seleccionado, para separar así un procedimiento del otro. Igualmente separando cada calculo por tablas especificando las corrientes pertenecientes a los valores. Así mismo, se representaron las ecuaciones descritas S O D VA en la fase uno para cada caso, determinando así los resultados, valiéndose de los R SE E R S datos y especificaciones introducidos por el operador de la herramienta. O H C E ER D Figura 4.2.11. Determinación de los resultados, mediante el procedimiento matemático recreado en las hojas de cálculo de Excel 2013. Luego de recrear el procedimiento matemático de cada caso en el simulador de perspectiva didáctica, se procedió a identificar la tabla donde se reporten los resultados obtenidos, la cual especifica todos los valores que definen el diseño de un evaporador de efecto simple, junto con el tipo de solución con que se trabajó y el caso seleccionado. Las variables se encuentran, separadas por tablas las cuales responden a colores de acuerdo a la corriente que describiera, identificando cada variable y el nombre de la corriente con las unidades respectivas. 119 Igualmente, se resaltó en la hoja de reporte de resultado la incógnita principal para el caso seleccionado. Por otro lado, se incluyeron ciertos botones los cuales posteriormente se configurarían para redirigir la pantalla del programa a otras áreas del mismo. Igualmente, se creó en la herramienta didáctica de evaporadores de un solo efecto, una sección de comparación de resultados; donde permitiera, manipular una variable, manteniendo el caso y el tipo de solución. De forma que el usuario pudiera comprobar posteriormente como afectara la manipulación de esta S O D A cálculo respectiva a cada caso, como se ilustra en la figura (2.4.13). V R SE E R S O H C E R DE propiedad en el diseño del evaporador. Para esta sección se configuró otra hoja de Figura 4.2.12. Reporte de resultados en la herramienta didáctica CASO I. Figura 4.2.13. Cálculos respectivos a la sección de comparación. 120 Nuevamente, se ejecutó el comando “SI”, pero en este caso con la finalidad de identificar el nuevo valor manipulado. La variable modificada se ubicaría en la hoja de datos compartidos (figura 4.2.2), en la parte de “COMPARACIÓN”. Para de esta forma, indicarle al programa el valor que ha de seleccionar. Como se resalta en la figura anterior. Por ejemplo, al manipular la temperatura de la alimentación; está se introduce en S O D VA una ventana auxiliar que posteriormente redirigirá el valor indicado a la hoja de datos ER S E R (CeldaY). Donde la “CeldaX” sería el nuevo valor introducido, el cual posteriormente S O H C se modificará a grados kelvin (de ser introducido en otras unidades), así mismo, la E R DE especificada en el caso original. “CeldaY” es la temperatura compartidos. Una vez introducida la temperatura, el programa tomará a través del comando “SI”, el nuevo dato de la siguiente manera: SI(CeldaX)>273,15; (CeldaX); Por último, luego de calcular los nuevos valores se procedió a reportarlos, en conjunto con los originales en una hoja de cálculo de Excel. La cual al igual que la “hoja de reporte de resultados”, se conformó de tablas donde cada una representa una corriente; mediante un color y las variables que la condicionan con sus respectivas unidades. En esta página se pueden observar todas las variables que determinan el diseño de un evaporador de efecto simple. Así mismo, se hace referencia a la propiedad alterada; Resaltando, la incógnita principal, respectiva a cada caso tanto en la solución original, como luego de modificar la variable manipulada. De la misma forma que en la hoja de reporte de resultados, se incluyeron a la página ciertos botones que posteriormente se configurarían de forma que el usuario pudiese redirigirse a otras áreas del programa si así lo desea. Es importante señalar que para condiciones de la herramienta didáctica, los valores no se guardan como variables, una vez que desee redirigirse al inicio el programa borrará los datos introducidos anteriormente para comenzar el procedimiento matemático otra vez. 121 D R SE E R S O H C E ER S O D VA Figura 4.2.14. Tabla comparativa entre los resultados del ejercicio original, con los resultados obtenidos mediante la modificación de la variable especificada previamente. Para finalizar, se procedió a proteger las hojas de cálculo en donde no se necesitará introducir información; como fueron las tablas de reporte de resultados, y la tabla de comparación entre el ejercicio original y el ejercicio modificado. Como se muestra en la figura 2.4.15, se accedió a la opción “Proteger Hoja” ubicada en la pestaña “REVISAR”. De esta forma, lo que se busca es que el usuario no pueda modificar por error las características de las hojas protegidas. Así mismo, se ocultaron las páginas destinadas al cálculo y agrupación de datos para llevar a cabo el procedimiento matemático, tal cual se muestra en la figura 2.4.16. Donde, posteriormente fue protegido el libro completo al igual que se hiso con las hojas, de manera que se evitara el acceso del usuario a estas secciones. Previendo que pudiese modificar los cálculos internos y afectara la configuración de la herramienta didáctica para evaporadores de un solo efecto. 122 D R SE E R S O H C E ER S O D VA Figura 4.2.15. Opción ‘Proteger Hojas’ en Microsoft Excel 2013. Figura 4.2.16. Ocultar hojas de cálculos. 123 4.2.2.1. Resultados Luego de recrear el procedimiento matemático desarrollado previamente para elaborar la herramienta didáctica de evaporadores de un solo efecto. Se continuó con la verificación del funcionamiento de la misma, mediante la ejecución de ejercicios extraídos de la bibliografía seleccionada en la primera fase de esta investigación. A continuación se presentan, los ejemplos establecidos en la fase S O D didáctica para evaporadores de un solo efecto. Igualmente resumiendo A el reporte V R SunaEtabla donde se ilustran de los resultados arrojado por el programa, se generó E R S el caso y se resaltó en color amarillo estos valores identificando el tipo de solución, O H C E la variable determinada (tabla R DE 3.2). anterior, junto con la figura donde se ilustra los datos arrojados por la herramienta Así mismo, se realizaron ciertos cálculos para determinar el porcentaje de error y la desviación estándar que presenta la herramienta didáctica de evaporadores de un solo efecto con respecto al método de cálculo tradicional, reportando estos valores igualmente en un tabla representativa (tabla 3.3). SOLUCIONES DILUIDAS Tomando como ejemplo 4.6. (Geankoplis 1998 p554). Área de transferencia de calor en un evaporador de un solo efecto. Un evaporador continuo de efecto simple concentra 9072 kg/h de una solución de sal al 1% en peso que entra a 311 K, hasta una concentración final de 1.5% en peso. El vapor en el evaporador está a 101.325 kPa y el vapor de agua que se introduce está saturado a 143.3 kPa. El coeficiente total U = 1704 W/(m 2.K). Calcule las cantidades de vapor y de producto de líquido, así como el área de transferencia de calor que se requiere. Puesto que se trata de una solución diluida, suponga que su punto de ebullición es igual al del agua. 124 Tabla 4.9. Reporte de resultados obtenidos por medio de la herramienta didáctica de evaporadores para el ejemplo propuesto 4.6. Solución: Diluida CASO: I Resultados de la Herramienta Corriente Alimentación Producto Vapor de Agua Sistema Calefacción Variable Valor Flujo (F) Temperatura (Tf) Concentración (Xf) Capacidad Calorífica (Cpf) Entalpía (hf) Flujo (P) Concentración (Xp) Temperatura (T1) Capacidad Calorífica (Cpp) Entalpía (hp) Flujo (V) Temperatura (T1) Entalpía (Hv) Estado Área (A) Calor (q) Temperatura (T1) Coeficiente de Transferencia de Calor (U) Incremento del Punto de Ebullición (IPE) Presión Sistema (Psist) Economía Flujo (S) Temperatura de Saturación (Ts) Presión de vaporización (Pvap) Entalpía del Líquido (hs) Entalpía del Vapor (Hs) Calor Latente (λ) D S O D VA R SE E R S O H C E ER Unidad 9072 kg/h 311 K 0,01 4,14 kJ/kg.K -257,301 kJ/kg 6048 kg/h 0,015 373,15 K 4,14 kJ/kg.K 0 kJ/kg 3024 kg/h 373,15 K 2257 kJ/kg SATURADO 150,3917 m² 9159209,136 kJ/h 373,15 K 6134,4 kJ/h.m².K 0 101,325 kPa 0,736314754 4106,9393 kg/h 383,07 K 143 kPa 461,0236 kJ/kg 2691,202 kJ/kg 2230,178 kJ/kg Figura 4.2.17. Reporte de resultados obtenidos del ejemplo 4.6 de soluciones diluidas de la herramienta didáctica para evaporadores de un solo efecto. 125 Adicionalmente, y con la finalidad de validar los resultados obtenidos por el simulador de perspectiva didáctica; se elabora la tabla 4.10, donde a continuación se muestran el porcentaje de error entre los resultados obtenidos mediante la herramienta didáctica de evaporadores de un solo efecto y los valores determinados mediante el procedimiento tradicional; para el ejemplo 4.6 de soluciones diluidas. Tabla 4.10. Comparación entre los resultados obtenidos por medio de la herramienta S O D VA didáctica y el método tradicional para el ejemplo 4.6. Variable Determinada R SE E R S Resultado Método Tradicional Resultado Herramienta Didáctica % Error 149,3 m² 150,391 m² 0,73074347 6048 kg/h 6048 kg/h 0 Flujo de vapor de agua para calefacción (S) 4108 kg/h 4106,9393 kg/h 0,02582035 Flujo de Solvente Evaporado (V) 3024 kg/h 3024 kg/h 0 Área superficial del evaporador D Flujo de producto concentrado (P) O H C E ER Por otro lado, a continuación se describe el ejemplo 4.7. (Geankoplis 1998 p574). Coeficiente de transferencia de calor en un evaporador de efecto simple. Una alimentación de 4535 kg/h de solución de sal al 2% en peso a 311 K, entra continuamente a un evaporador para concentrarse a 3%. La evaporación se lleva a presión atmosférica y el área del evaporador es 69,7 m 2. El calentamiento se logra con vapor de agua saturado a 383,2 K. Puesto que la solución es diluida, se puede suponer que tiene el mismo punto de ebullición del agua. Se estima que la capacidad calorífica de la alimentación es Cp = 4,10 kJ/kg.K. Calcule las cantidades de vapor y de líquido producido y el coeficiente total de transferencia de calor. 126 S O D VA Figura 4.2.18. Reporte de resultados obtenidos del ejemplo 4.7 de soluciones diluidas de la herramienta didáctica para evaporadores de un solo efecto. O H C E ER R SE E R S Tabla 4.11. Reporte de resultados obtenidos por medio de la herramienta didáctica de para el ejemplo propuesto 4.7. D de la Herramienta Resultados Corriente Alimentación Producto Vapor de Agua Sistema Calefacción Variable Flujo (F) Temperatura (Tf) Concentración (Xf) Capacidad Calorífica (Cpf) Entalpía (hf) Flujo (P) Concentración (Xp) Temperatura (T1) Capacidad Calorífica (Cpp) Entalpía (hp) Flujo (V) Temperatura (T1) Entalpía (Hv) Estado Área (A) Calor (q) Temperatura (T1) Coeficiente de Transferencia de Calor (U) Incremento del Punto de Ebullición (IPE) Presión Sistema (Psist) Economía Flujo (S) Temperatura de Saturación (Ts) Presión de vaporización (Pvap) Entalpía del Líquido (hs) Entalpía del Vapor (Hs) Calor Latente (λ) Solución: Diluida CASO: II Valor Unidad 4535 kg/h 311 K 0,02 4,1 kJ/kg.K -254,815 kJ/kg 3023,33 kg/h 0,03 373,15 K 4,1 kJ/kg.K 0 kJ/kg 1511,666 kg/h 373,15 K 2257 kJ/kg SATURADO 69,7 m² 4567320,945 kJ/h 373,15 K 6424,3409 kJ/h.m².K 0 101,325 kPa 0,737888309 2048,63796 kg/h 383,35 K 145 kPa 462,174 kJ/kg 2691,616 kJ/kg 2229,4427 kJ/kg 127 Adicionalmente, y con la finalidad de validar los resultados obtenidos por el simulador de perspectiva didáctica; se elabora la tabla 4.12, donde a continuación se muestran el porcentaje de error entre los resultados obtenidos mediante la herramienta didáctica de evaporadores de un solo efecto y los valores determinados mediante el procedimiento tradicional; para el ejemplo 4.7 de soluciones diluidas. S O D VA Tabla 4.12. Comparación entre los resultados obtenidos por medio de la herramienta didáctica y el método tradicional para el ejemplo 4.7. Variable Determinada R SE E R S Resultado Método Tradicional Resultado Herramienta Didáctica % Error 6520,225 kJ/m2.h.K 6424,34 kJ/m2.h.K 1,47057809 Flujo de producto concentrado (P) 3023,33 kg/h 3023,33 kg/h 0 Flujo de vapor de agua para calefacción (S) 2048,639 kg/h 2048,63796 kg/h 5,0765E-05 Flujo de Solvente Evaporado (V) 1511,667 kg/h 1511,666 kg/h 6,6152E-05 O H C E ER D Coeficiente de transferencia de calor De la misma forma se toma como ejemplo 4.8 (Geankoplis 1998 p574). El siguiente enunciado el cual es la continuación del ejercicio anterior: Efectos de una alimentación más rápida en el evaporador. Con los mismos valores del área, U, presión del vapor de agua, presión del evaporador y temperatura de la alimentación del problema anterior. Calcule las cantidades de líquido y de vapor que salen y la concentración del líquido de salida cuando la velocidad de alimentación se aumenta a 6804 kg/h. 128 S O D VA R SE E R S Figura 4.2.19. Reporte de resultados obtenidos del ejemplo 4.8 de soluciones diluidas de la herramienta didáctica para evaporadores de un solo efecto. O H C E ER Tabla 4.13. Reporte de resultados obtenidos por medio de la herramienta didáctica para el ejemplo propuesto 4.8. D Resultados de la Herramienta Corriente Alimentación Producto Vapor de Agua Sistema Calefacción Variable Flujo (F) Temperatura (Tf) Concentración (Xf) Capacidad Calorífica (Cpf) Entalpía (hf) Flujo (P) Concentración (Xp) Temperatura (T1) Capacidad Calorífica (Cpp) Entalpía (hp) Flujo (V) Temperatura (T1) Entalpía (Hv) Estado Área (A) Calor (q) Temperatura (T1) Coeficiente de Transferencia de Calor (U) Incremento del Punto de Ebullición (IPE) Presión Sistema (Psist) Economía Flujo (S) Temperatura de Saturación (Ts) Presión de vaporización (Pvap) Entalpía del Líquido (hs) Entalpía del Vapor (Hs) Calor Latente (λ) Solución: Diluida CASO: III Valor Unidad 6520 kg/h 311 K 0,02 4,1 kJ/kg.K -254,815 kJ/kg 5232,4459 kg/h 0,02492 373,15 K 4,1 kJ/kg.K 0 kJ/kg 1287,554 kg/h 373,15 K 2257 kJ/kg SATURADO 69,7 m² 4567320,919 kJ/h 373,15 K 6424,3409 kJ/h.m².K 0 101,325 kPa 0,628494846 2048,63096 kg/h 383,35 K 145 kPa 462,1741 kJ/kg 2691,6167 kJ/kg 2229,44254 kJ/kg 129 Adicionalmente, y con la finalidad de validar los resultados obtenidos por el simulador de perspectiva didáctica; se elabora la tabla 4.14, donde a continuación se muestran el porcentaje de error entre los resultados obtenidos mediante la herramienta didáctica de evaporadores de un solo efecto y los valores determinados mediante el procedimiento tradicional; para el ejemplo 4.8 de soluciones diluidas. Tabla 4.14. Comparación entre los resultados obtenidos por medio de la herramienta S O D VA didáctica y el método tradicional para el ejemplo 4.8. Variable Determinada R SE E R S Resultado Método Tradicional Resultado Herramienta Didáctica % Error Composición de el soluto a la salida 0,0245 0,02492 1,71428571 Flujo de producto concentrado (P) 5548,51 kg/h 5232,445 kg/h 5,69639417 Flujo de vapor de agua para calefacción (S) 2048,638 kg/h 2048,63996 kg/h 9,5673E-05 Flujo de Solvente Evaporado (V) 1255,49 kg/h 1287,554 kg/h 2,55390326 O H C E ER D Igualmente. Se tomó como ejemplo 4.9 el siguiente (Geankoplis 1998 p574): Una alimentación de solución de sal al 2% en peso a 311 K, entra continuamente a un evaporador para concentrarse a 3%. La evaporación se lleva a una presión del evaporador de 41,4 kPa y el área del evaporador es 69,7 m2. El calentamiento se logra con vapor de agua saturado a 383,2 K. Puesto que la solución es diluida, se puede suponer que tiene el mismo punto de ebullición del agua. Se estima que la capacidad calorífica de la alimentación es Cp = 4,10 kJ/kg.K. Determine la capacidad o velocidad de la alimentación en estas condiciones. 130 Tabla 4.15. Reporte de resultados obtenidos por medio de la herramienta didáctica para el ejemplo propuesto 4.9. Solución: Diluida CASO: IV Resultados de la Herramienta Corriente Alimentación Producto Variable Flujo (F) Temperatura (Tf) Concentración (Xf) Capacidad Calorífica (Cpf) Entalpía (hf) Flujo (P) Concentración (Xp) Temperatura (T1) Capacidad Calorífica (Cpp) Entalpía (hp) Flujo (V) Temperatura (T1) Entalpía (Hv) Estado Área (A) Calor (q) Temperatura (T1) Coeficiente de Transferencia de Calor (U) Incremento del Punto de Ebullición (IPE) Presión Sistema (Psist) Economía Flujo (S) Temperatura de Saturación (Ts) Presión de vaporización (Pvap) Entalpía del Líquido (hs) Entalpía del Vapor (Hs) Calor Latente (λ) D Vapor de Agua Sistema Calefacción Unidad 16368,5618 kg/h 311 K 0,02 4,1 kJ/kg.K -159,08 kJ/kg 10912,3746 kg/h 0,03 349,8 K 4,1 kJ/kg.K 0 kJ/kg 5456,187 kg/h 349,8 K 2317 kJ/kg SATURADO 69,7 m² 15247037,3 kJ/h 349,8 K 6520,2275 kJ/h.m².K 0 41,4 kPa 0,79781121 6838,945 kg/h 383,35 K 144,563 kPa 462,17416 kJ/kg 2691,6167 kJ/kg 2229,4425 kJ/kg S O D VA R SE E R S O H C E ER Valor 131 S O D VA R Figura 4.2.20. Reporte de resultados obtenidos del ejemplo 4.9 de soluciones diluidas de la herramienta didáctica para evaporadores de un solo efecto. SE E R S HO C E se muestran el porcentaje DER de error entre los resultados obtenidos mediante la Adicionalmente, y con la finalidad de validar los resultados obtenidos por el simulador de perspectiva didáctica; se elabora la tabla 4.16, donde a continuación herramienta didáctica de evaporadores de un solo efecto y los valores determinados mediante el procedimiento tradicional; para el ejemplo 4.9 de soluciones diluidas. Tabla 4.16. Comparación entre los resultados obtenidos por medio de la herramienta didáctica y el método tradicional para el ejemplo 4.9. Variable Determinada Resultado Método Tradicional Resultado Herramienta Didáctica % Error Flujo de Alimentación 16283,1 kg/h 16368,5618 kg/h 0,52484969 Flujo de producto concentrado (P) 10855,4 kg/h 10912,3745 kg/h 0,52484938 Flujo de vapor de agua para calefacción (S) 6808,44 kg/h 6838,945 kg/h 0,44804684 Flujo de Solvente Evaporado (V) 5427,7 kg/h 5456,187 kg/h 0,52484478 132 SOLUCIONES CONCENTRADAS Así mismo, tomando como ejemplo 4.10 para soluciones concentradas el siguiente (Ocon y Tojo, s.f. p172): En un evaporador simple se tratan 15000 kg/h de una disolución de NaOH al 10% que ha de concentrarse hasta el 50% en peso. El vapor empleado como medio de calefacción es vapor saturado a 3,5 atm, y una vez condensado sale a la temperatura de condensación. El vacío mantenido en la cámara de evaporación es de 620 mmHg, referido a la presión atmosférica normal. El coeficiente integral de transmisión de calor vale 1600 kcal/m².h.⁰C. Si la alimentación entra a 40⁰C y no se pierde calor con el exterior, determine; la superficie de calefacción. D R SE E R S O H C E ER S O D VA Figura 4.2.21. Reporte de resultados obtenidos del ejemplo 4.10 de soluciones concentradas de la herramienta didáctica para evaporadores de un solo efecto 133 Tabla 4.17. Reporte de resultados obtenidos por medio de la herramienta didáctica para el ejemplo propuesto 4.10. Solución: Concentrada CASO: I Resultados de la Herramienta Corriente Variable Alimentación Producto Vapor de Agua Sistema Calefacción Flujo (F) Temperatura (Tf) Concentración (Xf) Capacidad Calorífica (Cpf) Entalpía (hf) Flujo (P) Concentración (Xp) Temperatura (T1) Capacidad Calorífica (Cpp) Entalpía (hp) Flujo (V) Temperatura (T1) Entalpía (Hv) Estado Área (A) Calor (q) Temperatura (T1) Coeficiente de Transferencia de Calor (U) Incremento del Punto de Ebullición (IPE) Presión Sistema (Psist) Economía Flujo (S) Temperatura de Saturación (Ts) Presión de vaporización (Pvap) Entalpía del Líquido (hs) Entalpía del Vapor (Hs) Calor Latente (λ) Unidad 15000 kg/h 313,15 K 0,1 -- kJ/kg.K 160 kJ/kg 3000 kg/h 0,5 372,32 K -- kJ/kg.K 548,10 kJ/kg 12000 kg/h 372,32 K 2685 kJ/kg SOBRECALENTADO 116,72342 m² 31395499,2 kJ/h 372,32 K 6698,88 kJ/h.m².K 40,984 18,665 kPa 0,820231 14630,0249 kg/h 412,472 K 355 kPa 586,2114 kJ/kg 2732,17 kJ/kg 2145,9635 kJ/kg S O D VA R SE E R S O H C E ER D Valor 134 Adicionalmente, y con la finalidad de validar los resultados obtenidos por el simulador de perspectiva didáctica; se elabora la tabla 4.18, donde a continuación se muestran el porcentaje de error entre los resultados obtenidos mediante la herramienta didáctica de evaporadores de un solo efecto y los valores determinados mediante el procedimiento tradicional; para el ejemplo 4.10 de soluciones concentradas. S O D VA Tabla 4.18. Comparación entre los resultados obtenidos por medio de la herramienta R didáctica y el método tradicional para el ejemplo 4.10. SE E R S O ECH Variable Determinada Resultado Método Tradicional Resultado Herramienta Didáctica % Error Área Superficial del Evaporador 116,753 m2 116,7234 m2 0,0025335 Flujo de producto concentrado (P) 3000 kg/h 3000 kg/h 0 Flujo de vapor de agua para calefacción (S) 14630 kg/h 14630,0249 kg/h 0,0001701 Flujo de Solvente Evaporado (V) 12000 kg/h 12000 kg/h 0 DER De la misma forma, se identifica el ejemplo 4.11, (Geankoplis 1998 p575): Coeficiente de transferencia de calor para evaporar NaOH. Para concentrar 4536 kg/h de una solución de NaOH al 10% en peso hasta 20% en peso, se usa un evaporador de efecto simple con área de 37,6 m 2. La alimentación entra a 21,1 ˚C. Se usa vapor de agua saturado a 110 ˚C como medio de calentamiento y la presión en el evaporador es 51,7 kPa. Calcule los kg/h de vapor de agua utilizado y el coeficiente total de transferencia de calor. 135 S O D VA R SE E R S Figura 4.2.22. Reporte de resultados obtenidos del ejemplo 4.11 de soluciones concentradas de la herramienta didáctica para evaporadores de un solo efecto O H C E ER Tabla 4.19. Reporte de resultados obtenidos por medio de la herramienta didáctica para el ejemplo propuesto 4.11. D Resultados de la Herramienta Corriente Alimentación Producto Vapor de Agua Sistema Calefacción Variable Flujo (F) Temperatura (Tf) Concentración (Xf) Entalpía (hf) Flujo (P) Concentración (Xp) Temperatura (T1) Entalpía (hp) Flujo (V) Temperatura (T1) Entalpía (Hv) Estado Área (A) Calor (q) Temperatura (T1) Coeficiente de Transferencia de Calor (U) Incremento del Punto de Ebullición (IPE) Presión Sistema (Psist) Economía Flujo (S) Temperatura de Saturación (Ts) Presión de vaporización (Pvap) Entalpía del Líquido (hs) Entalpía del Vapor (Hs) Calor Latente (λ) Solución: Concentrada CASO: II Valor Unidad 4536 kg/h 567,45 K 0,1 98,47 kJ/kg 2268 kg/h 0,2 370,65 K 351,05 kJ/kg 2268 kg/h 370,65 K 2677 kJ/kg SOBRECALENTADO 37,6 m² 6421773,96 kJ/h 370,65 K 13663,3489 kJ/h.m².K 15,47 52 kPa 0,787571128 2879,7399 kg/h 383,15 K 144 kPa 461,327 kJ/kg 2691,311 kJ/kg 2229,984 kJ/kg 136 Adicionalmente, y con la finalidad de validar los resultados obtenidos por el simulador de perspectiva didáctica; se elabora la tabla 4.20, donde a continuación se muestran el porcentaje de error entre los resultados obtenidos mediante la herramienta didáctica de evaporadores de un solo efecto y los valores determinados mediante el procedimiento tradicional; para el ejemplo 4.11 de soluciones concentradas. S O D VA Tabla 4.20. Comparación entre los resultados obtenidos por medio de la herramienta R didáctica y el método tradicional para el ejemplo 4.11. SE E R S CHO Variable Determinada Resultado Método Tradicional Resultado Herramienta Didáctica % Error Coeficiente de transferencia de calor 13663,4 kJ/m2.h.K 13663,3489 kJ/m2.h.K 0,00037399 Flujo de producto concentrado (P) 2268 kg/h 2268 kg/h 0 Flujo de vapor de agua para calefacción (S) 2879,75 kg/h 2879,7399 kg/h 0,00035072 Flujo de Solvente Evaporado (V) 2268 kg/h 2268 kg/h 0 E R E D Tomando como ejemplo 4.12 para soluciones concentradas el siguiente (Ocon y Tojo, s.f. p172): En un evaporador simple se tratan 15000 kg/h de una disolución de NaOH al 10% que ha de concentrarse. El vapor empleado como medio de calefacción es vapor saturado a 3,5 atm, y una vez condensado sale a la temperatura de condensación. El vacío mantenido en la cámara de evaporación es de 620 mmHg, referido a la presión atmosférica normal. El coeficiente integral de transmisión de calor vale 1600 kcal/m².h.⁰C y la superficie de transferencia de calor es igual a 120 m². Si la alimentación entra a 40⁰C y no se pierde calor con el exterior, determine; la composición final del soluto a la salida del evaporador. 137 S O D VA R SE E R S Figura 4.2.23. Reporte de resultados obtenidos del ejemplo 4.12 de soluciones concentradas de la herramienta didáctica para evaporadores de un solo efecto. O H C E ER Tabla 4.21. Reporte de resultados obtenidos por medio de la herramienta didáctica para el ejemplo propuesto 4.12. Solución: Concentrada CASO: III D Resultados de la Herramienta Corriente Alimentación Producto Vapor de Agua Sistema Calefacción Variable Flujo (F) Temperatura (Tf) Concentración (Xf) Entalpía (hf) Flujo (P) Concentración (Xp) Temperatura (T1) Entalpía (hp) Flujo (V) Temperatura (T1) Entalpía (Hv) Estado Área (A) Calor (q) Temperatura (T1) Coeficiente de Transferencia de Calor (U) Incremento del Punto de Ebullición (IPE) Presión Sistema (Psist) Economía Flujo (S) Temperatura de Saturación (Ts) Presión de vaporización (Pvap) Entalpía del Líquido (hs) Entalpía del Vapor (Hs) Calor Latente (λ) Valor Unidad 15000 kg/h 313,15 K 0,1 160 kJ/kg 2953,3728 kg/h 0,5078 372,32 K 790 kJ/kg 12046,6271 kg/h 372,32 K 2685 kJ/kg SOBRECALENTADO 120 m² 32276811,57 kJ/h 372,32 K 6698,88 kJ/h.m².K 40,98 18,665 kPa 0,800934811 15040,7086 kg/h 412,472 K 354,637 kPa 586,2114 kJ/kg 2732,1749 kJ/kg 2145,96348 kJ/kg 138 Adicionalmente, y con la finalidad de validar los resultados obtenidos por el simulador de perspectiva didáctica; se elabora la tabla 4.22, donde a continuación se muestran el porcentaje de error entre los resultados obtenidos mediante la herramienta didáctica de evaporadores de un solo efecto y los valores determinados mediante el procedimiento tradicional; para el ejemplo 4.12 de soluciones concentradas. S O D VA Tabla 4.22. Comparación entre los resultados obtenidos por medio de la herramienta R didáctica y el método tradicional para el ejemplo 4.12. SE E R S CHO Variable Determinada Resultado Método Tradicional Resultado Herramienta Didáctica % Error Composición del soluto en la salida 0,5078 0,5078 0 Flujo de producto concentrado (P) 2953,41 kg/h 2953,3728 kg/h 0,00125956 Flujo de vapor de agua para calefacción (S) 15040,7 kg/h 15040,7086 kg/h 5,3189E-5 Flujo de Solvente Evaporado (V) 12046,6 kg/h 12046,6271 kg/h 0,00022496 E R E D De la misma forma, Se redacta el ejemplo 4.13 (Geankoplis 1998, p575): Producción en un evaporador de efecto simple. Un evaporador concentra F kg/h a 311 K de una solución de NaOH al 20% en peso hasta 50% en peso. El vapor de agua saturado para el calentamiento está a 399,3 K. la presión en el evaporador es de 13,3 kPa abs. El coeficiente total es 1420 W/m2.K y el área es 86,4 m2. Calcule la velocidad de alimentación F del evaporador. 139 S O D VA R SE E R S Figura 4.2.24. Reporte de resultados obtenidos del ejemplo 4.13 de soluciones O H C E ER concentradas de la herramienta didáctica para evaporadores de un solo efecto. D Tabla 4.23. Reporte de resultados obtenidos por medio de la herramienta didáctica para el ejemplo propuesto 4.13. Resultados de la Herramienta Corriente Alimentación Producto Vapor de Agua Sistema Variable Flujo (F) Temperatura (Tf) Concentración (Xf) Entalpía (hf) Flujo (P) Concentración (Xp) Temperatura (T1) Entalpía (hp) Flujo (V) Temperatura (T1) Entalpía (Hv) Estado área (A) Calor (q) Temperatura (T1) Coeficiente de Transferencia de Calor (U) Incremento del Punto de Ebullición (IPE) Presión Sistema (Psist) Economía Flujo (S) Temperatura de Saturación (Ts) Calefacción Presión de vaporización (Pvap) Entalpía del Líquido (hs) Entalpía del Vapor (Hs) Calor Latente (λ) Solución: Concentrada CASO: IV Valor Unidad 8546,9373 kg/h 311 K 0,2 140 kJ/kg 3418,774 kg/h 0,5 367,15 K 490 kJ/kg 5128,16243 kg/h 367,15 K 2676 kJ/kg SOBRECALENTADO 86,4 m² 14199909,12 kJ/h 367,15 K 5112 kJ/h.m².K 43,47 13 kPa 0,78899015 6499,6533 kg/h 399,3 K 241 529,896 2714,6139 2184,7179 kPa kJ/kg kJ/kg kJ/kg 140 Adicionalmente, y con la finalidad de validar los resultados obtenidos por el simulador de perspectiva didáctica; se elabora la tabla 4.24, donde a continuación se muestran el porcentaje de error entre los resultados obtenidos mediante la herramienta didáctica de evaporadores de un solo efecto y los valores determinados mediante el procedimiento tradicional; para el ejemplo 4.13 de soluciones concentradas. S O D VA Tabla 4.24. Comparación entre los resultados obtenidos por medio de la herramienta R didáctica y el método tradicional para el ejemplo 4.13. SE E R S O ECH Variable Determinada Resultado Método Tradicional Resultado Herramienta Didáctica % Error Flujo de la Alimentación 8546,93 kg/h 8546,9373 kg/h 8,5411E-05 Flujo de producto concentrado (P) 3418,67 kg/h 3418,774 kg/h 0,00304212 Flujo de vapor de agua para calefacción (S) 6499,64 kg/h 6499,6533 kg/h 0,00020463 Flujo de Solvente Evaporado (V) 5128,16 kg/h 5128,1643 kg/h 8,3851E-05 DER Análisis de los resultados El porcentaje de error obtenido para cada ejemplo. Fue calculado de siguiente manera: Valor medido-Valor real %Erelativo= | | *100 Valor real (Ec. 2.25) Donde el valor calculado representa el resultado arrojado por la herramienta didáctica para evaporadores de un solo efecto, y el valor original es sustituido por el resultado calculado por el método tradicional. 141 Así mismo, se puede considerar que los resultados obtenidos por medio de la herramienta didáctica, son fiables ya que en comparación con los cálculos realizados de la manera ordinaria no presentan un porcentaje de error significativo. En promedio el error obtenido por los resultados es 0,4380%. Sin embargo, se puede observar que los ejemplos de soluciones concentradas recreados en el programa de perspectiva académica presentan un porcentaje de error menor que los de soluciones diluidas. Siendo el promedio de porcentajes de error para S O D VA soluciones diluidas igual a 0,88% y el promedio para soluciones concentradas ER S E R Esto se debe a que para el caso de las soluciones concentradas, el cálculo de las S O Hser suministrado por el usuario a partir de las entalpías no se realiza, ya E queC debe DER gráficas de concentración-entalpía, de manera que resulta exactamente el mismo 0,000433%. valor para el método tradicional. En cambio en las soluciones diluidas, el simulador de perspectiva didáctica, calcula el valor de la entalpía y dispone de dicho valor con todos los decimales que este genere. Por el contrario, al realizar el procedimiento por el método tradicional solo se toman los que la persona considere adecuados, esto a su vez genera un porcentaje de error en los resultados. 4.2.3. Desarrollo de la calculadora de propiedades de vapor de agua haciendo uso de Microsoft Office Excel© y Visual Basic 2010 Para facilitar la especificación de las propiedades de vapor de agua en la herramienta didáctica para evaporadores de un solo efecto, se llevaron a cabo varias secuencias de comandos básicos; lo cuales permitieron automatizar la selección de datos en las tablas de vapor de agua. De manera que, el usuario que opte por utilizar el programa de perspectiva académica, pudiese determinar dichas condiciones en las corrientes que lo ameriten, sin necesidad de entrar manualmente a las tablas. Únicamente, especificando una o dos variables (si se trata de vapor 142 saturado (1) y si se habla de vapor sobrecalentado (2)), en una hoja de cálculos que se denominó “Calculadora de propiedades de vapor”. Para el desarrollo de esta sección de la herramienta didáctica, se hizo uso de la modalidad de “Programador” que dispone Microsoft Excel en sus complementos. A través de la cual se conecta con el lenguaje de programación Visual Basic, (este como se ha explicado anteriormente), trabaja mediante comandos básicos definidos S O D Para la activación de este complemento en el documento donde Ase recreó el V R procedimiento matemático descrito anteriormente, SseEingresó a la pestaña E R S “DESARROLLADOR”, ubicada en la barra de herramientas del documento de Excel. O H C E la opción “Complementos” (figura 4.2.17), la cual A continuación, se seleccionó R E D por el dialecto BASIC. abrirá una ventana con las modalidades que trae a disposición Microsoft Excel 2013. Figura 4.2.25. Seleccionando la opción ‘Complementos’, en Microsoft Excel. Posteriormente, se activa la el complemento para vincular la hoja de cálculo con Visual Basic 2010, seleccionando la casilla correspondiente a esta opción, como se muestra a continuación. 143 R SE E R S O H C E ER S O D VA D Así mismo, fue necesario la creación de macros incorporados en la herramienta. Figura 4.2.26. Seleccionando la herramienta de análisis VBA. Estos últimos se podrían definir como sistemas de comandos ejecutables para una determinada función. Excel tiene opción de grabar macros, donde al seleccionarla se realizan las funciones que se desean grabar y estas se guardaran internamente con comandos que posteriormente al asignarle un ejecutable se reproduzcan. A los cuales se pueden acceder o grabar mediante las opciones sugeridas en la pestaña “DESARROLLADOR”, donde se encuentran ubicados en la esquina superior izquierda. Figura 4.2.27. Activar Macros para la herramienta de análisis VBA. 144 A continuación, se introdujeron las tablas propiedades del vapor de agua, (Termodinámica, Cengel ,2011), a una hoja de cálculo nueva en el documento donde se recreó el procedimiento matemático explicado anteriormente, con la finalidad de reportar las propiedades de las corrientes partiendo de dicha tabla. (Figura 4.2.20). D R SE E R S O H C E ER S O D VA Figura 4.2.28. Incorporación de las tablas de vapor a la herramienta didáctica para evaporadores de un solo efecto. De la misma forma, se identificó una hoja de cálculo nueva con la denominación “DATA”, en donde se introducirían las variables que definan las condiciones del vapor. Igualmente; en dicha hoja se mostrarían las propiedades especificadas por las variables previamente introducidas. En esta hoja se diseñó una especie de tabla que define la variables, el valor de esta y la unidad en se deben introducir y como se reportan los datos. 145 D R SE E R S O H C E ER S O D VA Figura 4.2.29. Creación de la hoja de cálculo donde tendrá lugar la calculadora de propiedades de vapor. Si bien es cierto, las tablas de vapor reportan las propiedades tabuladas para ciertos valores de presión y temperatura, por lo que es necesario realizar interpolaciones cuando la presión o la temperatura designada se encuentran entre dos valores. De esta manera fue importante definir los límites de temperatura y de presión para estos cálculos, de manera que al introducir presiones o temperaturas fuera del rango especificado para la fase en que se encuentra el vapor, la calculadora emita un mensaje identificando el problema. Para llevar a cabo estos cálculos y limitaciones fue necesario diseñar una hoja de cálculo donde se separaran por tablas las posibles variables a introducir, igualmente tomando los valores proporcionados por el usuario en la calculadora, y de esta manera reproducirlos en los cálculos en los cálculos de interpolación y extrapolación. 146 D R SE E R S O H C E ER S O D VA Figura 4.2.30. Cálculos internos de la calculadora de propiedades de vapor Estos cálculos se ejecutaron gracias a la reproducción de ciertos macros que fueron diseñados para cada función específica de la calculadora. Como se explicó, mediante la opción “grabar macros” en la pestaña “DESARROLLADOR” (figura 4.2.19) se procedió al diseño de estos complementos en la herramienta didáctica para evaporadores de un solo efecto. Para lograr programar las especificaciones de cada macro se realizaron varios ejercicios de acuerdo a las variables que se desearan especificar. Por ejemplo, para el caso de la determinación de propiedades de vapor saturado, mediante la presión del vapor; se introdujo el valor correspondiente en la hoja de cálculo denominada “DATA”, la cual contiene la calculadora de propiedades. Donde posteriormente se ubicaría dicho dato en la tabla de vapor de agua a condiciones de saturación. 147 R SE E R S O H C E ER S O D VA Figura 4.2.31. Macro definido para el cálculo de propiedades del vapor de agua mediante la especificación de la presión en estado saturado. D Este procedimiento se repitió para la determinación de propiedades mediante el ingreso de la temperatura saturada. Igualmente se especificó un macro que definiera las propiedades mediante la incorporación de temperatura y presión, ubicando estas; en la tabla de vapor y de coincidir con las condiciones de saturación reportarlas de esta forma. De no ser así, redirigir la búsqueda al área de sobresaturación. Figura 4.2.32. Macro definido para el cálculo de las propiedades de vapor mediante el ingreso condiciones de sobresaturación. 148 De la misma manera, se crearon los macros de Ejecución y Limpieza. Repitiendo el procedimiento anterior, seleccionando “grabar macros”; pero esta vez para tomar los valores identificados en las tablas de vapor y ubicarlos en la hoja de cálculos, donde se definirían las propiedades mediante la interpolación de los datos extraídos de la tabla, y posteriormente mostrar los cálculos obtenidos en las celdas seleccionadas dentro de la hoja denominada “DATA”. (Figura 4.2.21). S O D VA Así mismo, se repitió el procedimiento, para crear el macro de limpieza, el cual tuvo ER S E R modificar ciertos criterios en ellos de forma que optimizara la ejecución de la S O H C calculadora. E DER como objetivo borrar los valores de las variables para volver a utilizar la calculadora. Luego de grabar cada uno de los macros anteriormente explicados, se procedió a Figura 4.2.33. Macro definido para el cálculo de las propiedades de vapor mediante el uso de métodos de interpolación entre los valores reportados en la tabla de vapor. Por otra parte, a los últimos dos macros creados se les asigno un “ejecutable”; este se puede definir como el un comando generado por la combinación de dos teclas (Ctrl + otra tecla), que al presionarlas al mismo tiempo se ejecute la función especificada en el macro. De manera que a través de la opción “Macros” situada en la pestaña “DESARROLLADOR”, se redirigirá la pantalla a una ventana donde se muestran todos los macros creados para Microsoft Excel 2013, presionando 149 igualmente el botón “Opciones”, se visualiza otra ventana donde se introduce la tecla que junto con control reproducirá el macro. Para este caso se identificó el macro de ejecución de la calculadora con (“Ctrl + O”), de la misma forma para el macro de limpieza (“Ctrl + M”). D R SE E R S O H C E ER S O D VA Figura 4.2.34. Especificando los comandos destinados a la ejecución de la calculadora. Por ultimo luego de hacer las modificaciones pertinentes en la hoja donde tiene lugar la calculadora de vapor, de forma que luzca agradable para el usuario. E igualmente indicando en un cuadro de texto los comandos ejecutables para calcular las propiedades de vapor y para limpiar la calculadora, se procedió a probar la misma con la incorporación de dos ejemplos sencillos. Ejemplo 4.14. Calcular las propiedades de saturación del agua para una presión de vapor de 101,325 kPa. En la figura 4.2.35, se puede observar cómo se ingresa el valor de la presión, así mismo en la figura 4.2.36, se visualiza la obtención de los resultados luego de presionar las teclas Ctrl + “O” en conjunto. 150 D R SE E R S O H C E ER S O D VA Figura 4.2.35. Ingreso de la presión saturada a la calculadora de propiedades del agua. Figura 4.2.36. Calculo de las propiedades del vapor, a la presión de saturación introducida. 151 Ejemplo 4.15. Calcular las propiedades del agua para una presión de 85 kPa y una temperatura de 120°C. En la figura 4.2.37, se puede observar cómo se ingresan los valores de presión y la temperatura, así mismo en la figura 4.2.38, se visualiza la obtención de los resultados luego de presionar las teclas Ctrl + “O” en conjunto. D R SE E R S O H C E ER S O D VA Figura 4.2.37. Ingreso de la presión y la temperatura a la calculadora de propiedades del agua. Figura 4.2.38. Calculo de las propiedades del vapor, a la presión de saturación 152 4.3. Fase 3: Desarrollo de las ventanas de usuario Como se ha venido describiendo en la fase de recreación del procedimiento matemático, definido para la herramienta didáctica de evaporadores de un solo efecto. Se seleccionó como programa base Microsoft Excel 2013©, el mismo presenta en sus características la opción de vincularse con el lenguaje de programación Visual Basic 2010. A través del cual, mediante un dialecto BASIC se S O D VA pueden generar comandos básicos que reproduzcan funciones y operaciones R específicas. Igualmente por medio de esta herramienta de análisis, se pueden crear SE E R S ventanas auxiliares al documento que faciliten al usuario el ingreso de datos y HO C E Así mismo, en las figuras ER4.2.25 y 4.2.26, se indicó la forma correcta de activar este D complemento a partir de la pestaña “DESARROLLADOR”. Ahora bien, para el llevar manejo del programa. a cabo este objetivo, se diseñaron ventanas auxiliares al documento de Excel. Que a continuación, partiendo de comandos básicos en el dialecto BASIC se configuraron a los botones introducidos en las hojas de cálculos. Y de esta manera, proporcionarle el acceso más fácil al usuario por las etapas de la herramienta didáctica para evaporadores de un solo efecto. Igualmente suministrándole la información necesaria para ayudarle a comprender el procedimiento de los evaporadores de simple efecto. Para ingresar en la modalidad de programación dentro del documento de Microsoft Excel, luego de activar la herramienta de análisis VBA. Se procede a acceder a la pestaña “DESARROLLADOR”, donde se encuentra la opción “Modo de diseño”, posteriormente en la misma pestaña del lado izquierdo, se accede a la parte interna de Visual Basic, con la opción respectiva. 153 D R SE E R S O H C E ER S O D VA Figura 4.2.39. Abriendo Visual Basic 2010 desde Microsoft Excel 2013. Como se puede observar en la imagen anterior, donde se resalta la opción “Visual Basic” que redirige la pantalla a este programa en cuestión. Se muestra la forma en que se crearon las ventanas auxiliares o Formularios. En la parte superior del lado izquierdo de la ventana que hace referencia la figura 4.2.39, se enlistan los proyectos que se tienen especificados en el documento. Es decir, las ventanas auxiliares, los módulos o macros, y las hojas de Excel. Igualmente en la parte de color gris, al seleccionar algún proyecto, se muestran los comandos de programación que el mismo contiene en su configuración. Así mismo, más abajo en el mismo lado de la ventana. Se visualiza la lista de propiedades, en donde se hace referencia a las características que puede presentar los proyecto seleccionado, como son; el color, dimensiones, nombre a mostrar, nombre configurado, entre otras. Las ventanas auxiliares fueron las protagonistas en el desarrollo de esta fase, ya que las mismas pueden presentar diversas características de diseño y herramientas como; botones, listas desplegables, cuadros de textos, opciones de selección entre 154 otros. Lo que contribuyó de manera significativa al diseño de la herramienta didáctica para evaporadores de un solo efecto. A continuación, se muestra cómo se diseñaron estas ventanas multifuncionales. En primer lugar se situó en la parte de “proyectos” indicada anteriormente, haciendo clic derecho al mouse y seleccionando “insertar” seguido de “UserForm”, enseguida se mostró la ventada creada. D R SE E R S O H C E ER S O D VA Figura 4.2.40. Creación de Ventana Auxiliar. En la figura 4.2.40, se muestra la ventana creada y adicionalmente la incorporación de un botón de comando como. Al seleccionar el botón se muestra sus características en la parte izquierda inferior, donde se puede modificar el nombre, color, tipo de letra, entre otras cosas. Así mismo, al hacer doble clic en él, se redirige a la programación interna del mismo. Para el caso de la figura 4.2.41. Se insertaron dos opciones de selección a la ventana, donde posteriormente y utilizando el comando “If”. (El cual funciona igual que el comando “SI” utilizado para realizar los cambios de unidades respectivos en la recreación del procedimiento matemático en la hoja de caculo de Microsoft Excel). 155 Se configuro el botón de modo que al seleccionar la opción 1 se abriera una ventana representativa de dicha opción y de la misma manera para la alternativa 2. D R SE E R S O H C E ER S O D VA Figura 4.2.41. Configuración del botón en la ventana creada. Igualmente para el caso de las hojas de cálculo, se pueden configurar botones que al seleccionarlos, redirija al usuario a una ventana auxiliar o a otra hoja a través de comandos básicos. Las figura 4.2.42, 4.2.43 y 4.2.44 muestran la manera en que se introdujo y se configuraron los botones dentro de las hojas de cálculo diseñadas para la herramienta didáctica de evaporadores de un solo efecto. En la figura 4.2.42, se seleccionó la opción “insertar” en la pestaña “DESARROLLADOR”, donde se desglosa una lista de las posibles opciones. En la parte “ActiveX” se seleccionan los botones de comandos, los cuales se pueden configurar de la misma manera que se explicó para los botones en las ventanas auxiliares. Al seleccionarlo se abre una ventana de propiedades (figura 4.2.43), en donde se puede modificar la apariencia del botón. 156 D R SE E R S O H C E ER S O D VA Figura 4.2.42. Insertando botón de comando. Figura 4.2.43. Modificando propiedades del botón insertado. 157 D R SE E R S O H C E ER S O D VA Figura 4.2.44. Configurando botones en hojas de cálculo. Los botones insertados en las hojas de cálculo, además de activar las ventanas auxiliares que se configuren, puede redirigir a otras páginas de acuerdo al comando que se le especifique. Como se muestra en las figuras 4.2.45 y 4.2.46. Figura 4.2.45. Configuración del botón insertado para redirigir a la hoja 2 del documento. 158 D R SE E R S O H C E ER S O D VA Figura 4.2.46. Selección de la hoja2 mediante el botón insertado en la hoja1 del documento. Ahora bien, con la ejecución de estos pasos sencillos se desarrollaron las ventanas y botones de la herramienta didáctica para evaporadores de un solo efecto. Con la finalidad de ayudar al operador a transitar por las secciones que conforman el simulador de perspectiva académica, igualmente proporcionándole la información referente al área donde se encuentre y requiriendo de ser el caso; suministrar los valores de ciertas variables para llevar a cabo el procedimiento matemático. En la figura 4.2.47. Se ilustra la página principal a la que el usuario tendrá acceso al entrar a la herramienta. En donde se encuentran los datos de la universidad a la que pertenece esta investigación, junto con el logotipo representativo. Igualmente, se le configuraron cuatro botones a la hoja de cálculo, donde cada uno de ellos guía al usuario por las distintas secciones que tiene el programa: El botón especificado con el nombre “Manual de usuario”. Fue destinado a abrir el manual elaborado en la fase cuatro de esta investigación, el cual explica por medio de ilustraciones la forma adecuada de utilizar la herramienta para obtener los mejores resultados. 159 D R SE E R S O H C E ER S O D VA Figura 4.2.47. Página de inicio de la herramienta didáctica para evaporadores de un solo efecto Así mismo, la opción “convertidor de unidades”, dirige la pantalla hacia un convertidor básico de unidades que se le proporcionó al operador como herramienta de ayuda en la resolución de los ejercicios (figura 4.2.48). Figura 4.2.48. Convertidor de unidades básico. 160 Por otra parte, se configuró a la opción “Propiedades del agua” una ventana donde el usuario puede escoger entre dirigirse a las tablas de vapor reproducidas en una hoja de Excel, la tabla de capacidades caloríficas para el agua o la calculadora de vapor diseñada para calcular las propiedades del agua sin necesidad de introducirse manualmente en las tablas de vapor (figura 4.2.49). D R SE E R S O H C E ER S O D VA Figura 4.2.49. Ventana auxiliar de selección de las propiedades de vapor de agua a mostrar. Figura 4.2.50. Ventana auxiliar configurada para mostrar las tablas de capacidades caloríficas del agua. 161 Por último, se indicó con el nombre “Tipo de Solución” el botón que guiará al usuario a introducirse en la recreación de ejercicios propuestos en el programa. A este botón se le configuro una ventana auxiliar. Donde se le requiere al usuario especificar el tipo de solución a manejar en el problema (figura 4.2.51), para posteriormente seleccionar el caso a desarrollar (figura 4.2.52). D R SE E R S O H C E ER S O D VA Figura 4.2.51. Ventana auxiliar configurada para la selección del tipo de solución a tratar. Figura 4.2.52. Ventana auxiliar configurada para la selección del tipo de caso a ejecutar. 162 A continuación, se redirige la pantalla a la hoja de ingreso de datos de acuerdo al caso seleccionado, en donde se encuentran 3 botones destinados a definir la temperatura del evaporador (T1), las entalpías (Cp/H) y la corriente de vapor de agua destinado a calefacción (Ts/Pvap). Al seleccionar alguno de estos botones se configuraron en su programación ventanas respectivas en donde el usuario pudiese ingresar los datos especificados con sus respectivas unidades (figura 4.2.53). D R SE E R S O H C E ER S O D VA Figura 4.2.53. Ventana auxiliar configurada para especificar las condiciones del vapor de agua destinado a calefacción en el evaporador. Por otro lado, se crearon ventanas de información, las cuales se ejecutan mediante botones denominados “Debes Saber”, estos se encuentran en ciertas ventanas u hojas a lo largo de todas las secciones de la herramienta didáctica para evaporadores de un solo efecto. Dichas ventanas tienen como función suministrar información al operador sobre la etapa del procedimiento en que se encuentra, para de esta forma, colaborar a la compresión del tema (figura 4.2.54). Igualmente, al especificar la temperatura del evaporador y las entalpías de la solución, se configuraron las opciones de mostrar los diagramas respectivos para la determinación de estas variables en dónde. A continuación se ejecutan ventanas 163 que contienen el diagrama como imagen y describen la forma en que se deben manipular, para posteriormente introducir los valores en la herramienta (4.2.55). D R SE E R S O H C E ER S O D VA Figura 4.2.54. Ventana auxiliar destinada a proporcionar información al usuario. Figura 4.2.55. Ventana auxiliar destinada a proporcionar información al usuario con respecto a los diagramas de Entalpía vs Concentración y el uso apropiado de ellos 164 4.4. Fase 4: Elaboración del manual de usuario Finalmente, luego de que los resultados fueron contrastados con los cálculos manuales y estos se consideraron consistentes, se prosiguió a la elaboración de un manual de uso del modelo de simulación en la hoja de cálculo Excel©, el cual contiene los pasos a seguir para el funcionamiento adecuado del modelo de simulación y tiene la ventaja de organizar y concretar cada uno de los S O D V Este manual cumple la función de guiar al usuario durante laA ejecución del R E E programa, para que éste haga el uso adecuado de laS herramienta didáctica. En el R S manual se incluyeron los parámetros y unidades que intervienen en la elaboración HO C E de la hoja de cálculo, ejemplos de llenado de cada fase, requerimientos para la DER procedimientos realizados. utilización del programa, entre otros. Para la elaboración del manual de usuario se llevaron a cabo los siguientes pasos: Portada Se identificó en esta parte el manual, indicando el nombre del programa que explica, el año en que fue elaborado, la investigación a la que pertenece, los autores, institución, entre otros. Índice Este fue elaborado luego de la realización del manual, en él se encuentra la ubicación de cada una de las partes del manual, en orden de aparición. Introducción En ella se indica la importancia del manual y una breve explicación para describir la utilización del mismo. 165 Inicio de sesión En esta parte se hizo referencia a la página principal de la herramienta didáctica para evaporadores de un solo efecto y modo de apertura de las diferentes opciones contenidas en el modelo de simulación de perspectiva académica. Selección de la solución S O D VA En esta parte del manual se describió el tipo de solución a posible a seleccionar con R SE E R S la que se quiere realizar la recreación del problema planteado. O H C E ER Selección del caso D Igualmente, en esta parte se identificó la forma adecuada de realizar la seleccionar del caso según las incógnitas a determinar, acorde al tipo de solución con el que se vaya a trabajar en el problema. A continuación se recreó un ejemplo para el caso uno y otro para el caso dos, explicando detalladamente la forma de ingresar los datos en cada sección de la herramienta. A través del uso de figuras donde se mostró cada sección descrita de la herramienta didáctica para evaporadores de un solo efecto. Sección de Comparación De la misma forma, tomando uno de los ejemplos anteriores, se explicó el procedimiento para manipular las variables, de forma que posteriormente se compararan los resultados alterados con los originales del ejercicio. Botones “Debes Saber” En esta sección, se hizo referencia a las ventanas destinadas a proporcionar información concreta al usuario de manera que colaborara a la compresión del diseño de evaporadores de simple. 166 Tablas de Vapor de Agua En esta parte se habló brevemente de como introducirse a las tablas de vapor agua, recreadas en una hoja de cálculo perteneciente a la herramienta, igualmente se hizo referencia a las capacidades caloríficas del agua. Y se explicó detalladamente el uso de la calculadora de propiedades del agua. Limitaciones Por último, en esta sección se definieron los alcances o E S E R en forma impresa en el anexo 1 de esta investigación. S O H C E R DE R S O D VA límites referentes al simulador de perspectiva didáctica. El manual de usuario elaborado se encuentra CONCLUSIONES Se identificó como principal criterio de especificación al diseñar el procedimiento para los sistemas de evaporación de efecto simple, la cantidad de soluto presente en la solución destinada a concentrarse. De manera que, dependiendo S O D Ade definir la ebullición de la mezcla generando básicamente dos formas V R SE temperatura de la solución dentro del evaporador. E R S O H EC Comúnmente enE losR ejercicios planteados en la bibliografía referida a sistemas D lo diluida que esta se encuentre, producirá un incremento en el punto de de evaporación para simple efecto, las soluciones designadas a alimentar estos equipos entran de forma diluida de manera que se consideran muchas de las propiedades físicas del agua. Así mismo, por lo general son de base acuosa para simplificar especificaciones de las corrientes. Igualmente, se identificaron cuatro procedimientos diferentes de cálculos posibles de acuerdo a las variables que se deseen determinar, en conjunto con los datos especificados en la descripción del ejercicio, cada caso se enfoca en determinar una variable diferente partiendo de los balances de masa y energía generales del evaporador. Previo a desarrollar la interfaz de la herramienta didáctica para evaporadores de un solo efecto, es fundamental tener completo manejo de los factores que afectan el procedimiento matemático para el diseño de los sistemas de evaporación. De la misma forma, que es necesario tener conocimientos básicos de programación. 168 Durante el desarrollo de la herramienta didáctica fue necesario la incorporación de ventanas auxiliares que le proporcionaran al usuario información acerca de la etapa en donde se encontrara. El modelo de simulación de perspectiva académica desarrollado; permite el procesamiento de datos a estudiantes, profesores, investigadores, ingenieros químicos, que laboran en la industria química en la ejecución del proceso y, así S O D VA mismo, a aquellos que imparten la metodología de las operaciones unitarias en las instituciones educacionales. R SE E R S O H C E evaporadores de unR solo efecto, haciendo uso de Microsoft Office Excel 2013© E D en conjunto con el lenguaje de programación Visual Basic 2010. Se obtuvieron Tras recrear el procedimiento matemático de la herramienta didáctica para resultados satisfactorios. Los cuales posteriormente se compararon con los valores obtenidos por el método tradicional, determinando en forma general un error expresado de manera porcentual que en promedio fue 0,45% para resultados. El manual de usuario elaborado para el uso de la herramienta didáctica, tiene que como objetivo orientar la participación del operador a través de la misma, de forma que guíe a la persona por las áreas que la conforman, de manera que, pueda obtener los resultados esperados. RECOMENDACIONES Ampliar la utilidad de la herramienta didáctica para evaporadores de un solo efecto, con la finalidad de incorporar otros tipos de soluciones distintas a las de base acuosa. S O D VA Realizar una investigación más a fondo de otros posibles casos que se puedan R presentar en la literatura, e incluirlos en la herramienta didáctica para evaporadores de un solo efecto. SE E R S HO C E ERtrabajo de grado la utilización de las hojas de cálculo para fue crucial para Deste Tener conocimientos básicos y avanzados de la hoja de cálculo Excel, ya que los diferentes procedimientos matemáticos. Tener dominio básico del área de termodinámica y operaciones unitarias, ya que estas áreas son necesarias para llevar a cabo el procedimiento del diseño de sistemas de evaporación de efecto simple. Validar los resultados obtenidos mediante la herramienta didáctica para evaporadores de un solo efecto, ya que por lo general presentan un porcentaje de error que por muy pequeño que sea este, se debe considerar. Expandir los evaporadores a dos y tres efectos, para así abarcar todo el campo de esta operación unitaria. Leer detalladamente el manual de usuario previo a introducirse en la herramienta, de manera que puedan hacer mejor uso de esta y obtener los resultados deseados. REFERENCIAS BIBLIOGRÁFICAS Arias, F. (2006). El proyecto de investigación. 5 Ed. Caracas, Venezuela: Editorial Episteme. S O D VA Altuve y Rivas (1998). Metodología de la investigación. Modulo instruccional III. Caracas Venezuela: Editorial Orial Ediciones. R SE E R S Báez M. y Salas E. (2014). Dimensionamiento de equipos en procesos de absorción O H C E optar por el título Rde Ingeniero Químico). E D Maracaibo Edo. Zulia, Venezuela. química para endulzamiento de gas natural. (Trabajo especial de grado para Universidad Rafael Urdaneta, Bersanelli M. y Gargantini M. (2006). Solo el asombro conoce la aventura de la investigación científica. Madrid Barcelona: Editorial Encuentro S.A, Madrid. Cengel Y. (2012). Termodinamica. 7 Ed. Ciudad de México, México: Editorial McGRAW-HILL. Foust A. (2006). Principios de Operaciones Unitarias. 2 Ed. México: Editorial Continental, S.A. García H. Peña A. y Lopez R. (2010). Desarrollo de un Sistema de Evaporación y Concentración de Jugos de Múltiple Efecto para Mejorar la Eficiencia Térmica y Productiva y Disminuir El Impacto Ambiental en la Producción De Panela. Revista Colombiana de Investigación Agropecuaria, p25; p38. 171 Geankoplis C. (1998). Procesos de Transporte y Operaciones Unitarias. 3 Ed. Mexico: Editorial Continental, S.A. Gomez, M. (2006). Introducción a la metodología de la investigación cientifica.1 Ed. Cordoba. Editorial Brujas. Gonzalez, R. Yii,M. y Curriel, L. (2003). Metodología de la investigación científica para las ciencias técnicas. Cuba. Editorial Quaderna S O D A V 4 Ed. Iztapalapa, México: Editorial McGraw-Hill Interamericana. R SE E R S 5 Ed. Caracas. Venezuela: Editorial Hurtado, J. (2007). El proyecto de investigación. O H C E Quiron. R DE Hernández, R. Fernández, C. y Baptista, P. (2006). Metodología de la investigación. Martínez P. (2004). Operaciones de Separación en Ingeniería Química. Madrid, España: Editorial: PEARSON EDUCACIÓN S,A. McCabe W.(2007). Operaciones unitarias en ingeniería química. 7 Ed. México: Editorial McGRAW-HILL Microsoft Corporation© (2013), Microsoft Office Excel© Centro de Ayuda de Excel. http://office.microsoft.com/es-es/excel-help Microsoft Visual Basic. (2008). Visual Basic Centro de Ayuda Microsoft Visual Basic para Aplicaciones. http://msdn.microsoft.com Ocon J. Tojo G. Problemas de Ingenieria Quimica. TOMO I. México: Editorial Aguilar. Ramírez, T. Bravo, L. y Méndez, P. (1987). La investigación documental y bibliográfica. Edición original. Rodríguez, D. y Valldeoriola, J. (2009). Metodología de la investigación Barcelona, Madrid: Editorial Eureca Media, SL. Rincón E. (2013). Desarrollo de herramienta de cálculo para la eficiencia de las Calderas generadoras de vapor. (Trabajo especial de grado para optar por el título de Ingeniero Químico). Universidad Rafael Urdaneta, Maracaibo Edo. Zulia, Venezuela. Skoog D. (2001). Fundamentos de Química Analítica. México: Editorial Thomsom. S O D VA Van Ness H. (1996) Introducción a la Termodinámica en la Ingeniería Química. 5 Ed. Ciudad de México, México: Editorial McGRAW-HILL. O D H C E ER R SE E R S ANEXO 1 REPÚBLICA BOLIVARIANA DE VENEZUELA UNIVERSIDAD RAFAEL URDANETA. FACULTAD DE INGENIERÍA. ESCUELA DE INGENIERÍA QUÍMICA. D R SE E R S O H C E ER S O D VA HERRAMIENTA DIDACTICA PARA EVAPORADORES DE UN SOLO EFECTO MANUAL DE USUARIO Elaborado por: Maracaibo, Septiembre, 2014 Br. Mata María José ÍNDICE Pag. INTRODUCCIÓN……………………………………………………………… 3 1. INICIAR SECIÓN………………………………………………………. 4 2. SELECCIÓN DE LA SOLUCIÓN…………………………………….. 5 S 2.1. Solución Diluida………………………………………………………... DO 6 A V 2.1.1. Selección del caso…………………………………………………….. 7 ER S E R 2.2. Solución Concentrada………………………………………………… 20 S O H C 2.2.1. Selección del caso…………………………………………………….. 20 E R E D 2.3. Comparación…………………………………………………………… 34 3. PROPIEDADES DEL VAPOR DE AGUA………………………………. 37 4. LIMITACIONES……………………………………………………………. 41 INTRODUCCIÓN Cuando se habla de propuestas de simuladores o programas que se encarguen de reproducir problemas de ingeniería, es necesario crear un manual al finalizar el diseño de dichos programas, en donde se explique detalladamente como debe ejecutarse. En este caso, el manual de usuario de la herramienta didáctica para evaporadores de un solo efecto busca impartir una guía de cómo se debe manejar S O D en cuestión, durante toda la explicación, y de esta forma el A usuario pueda V R desenvolverse mejor a la hora de utilizar el simulador. SE E R S que no poseen los conocimientos O Este manual es ideal para aquellos usuarios H C E R E de las diferentes aplicaciones en la herramienta didáctica necesarios para D el manejo el simulador en sus distintas áreas; colocando imágenes referentes a la herramienta de evaporadores de un solo efecto. Cabe destacar que este modelo de cálculo puede ser utilizado en varias versiones de Microsoft Office Excel © ya que fue realizado en el mismo. A continuación se encuentran una serie de pasos necesarios para el correcto funcionamiento de la herramienta didáctica para evaporadores de un solo efecto, que consta de una metodología básica que ayuda a realizar el dimensionamiento conceptual de los diferentes tipos de opciones que presenta el simulador. El Manual de Usuarios de la Herramienta Didáctica para Evaporadores de un solo efecto, se divide en seis secciones que abarcan cada etapa del programa: la primera titulada “Iniciar Sesión”; donde se explica cómo introducirse al programa, posteriormente menciona la selección del tipo de solución con la que se trabajará a lo largo del ejercicio; en esta parte explica detalladamente como se introducen los datos de los problemas y cómo funciona en general la ventana de usuario creada para manipular la herramienta. Así mismo, realiza una breve explicación de la forma en que se realizaron los cálculos internamente, para luego dar a conocer la parte de conversión de unidades y propiedades de vapor de agua. Dejando en último lugar las limitaciones que presenta el programa. INICIAR SESIÓN Al dar inicio a la Herramienta Didáctica para Evaporadores de un solo efecto aparece una página principal, donde se muestra el encabezado y logo de la Universidad Rafael Urdaneta, junto con cuatro (4) opciones para que el usuario decida entre cada una de forma que comience a utilizar la herramienta (Figura 1.1). S O D A vincula se va a trabajar en el ejercicio. La segunda opción; “Manual deV Usuario”, R E conocer cómo utilizar Spueda dicho archivo mostrándolo en PDF, para que elR usuario E S de Vapor de Agua” como opción O el programa. A continuación se tiene “Propiedades H Cse muestra una ventana de decisión donde se E R tres, al escoger dicha opción E D selecciona la tabla a redirigir ya sean las tablas de vapor o las tablas de las La primera; “Tipo de Solución” en donde se selecciona el tipo de solución con que capacidades caloríficas. Por último, como cuarta opción, el “Convertidor de Unidades”, esta última opción redirige a una hoja de cálculo donde funciona un convertidor de unidades básicos en el sistema internacional para facilitarle los cálculos al usuario. Figura 5.1. Página de inicio. SELECCIÓN DE LA SOLUCIÓN Luego de iniciar sesión en la herramienta didáctica para evaporadores de un solo efecto, se procede a seleccionar el tipo de solución con la que se va a trabajar (Figura I.2.); Teniendo en cuenta que para fines del programa solo se trabajará con soluciones acuosas. Las soluciones se pueden dividir en Concentradas y Diluidas. D R SE E R S O H C E ER S O D VA Figura 5.2. Selección del tipo de solución a tratar. Al hablar de soluciones diluidas se considera en la mayoría de los casos que el incremento del punto de ebullición (IPE) es igual a 0 por lo que la temperatura del evaporador pasa a ser igual que la Temperatura de ebullición del solvente puro a la presión del evaporador. Por otro lado, cuando se trabaja soluciones concentradas, el Incremento del punto de ebullición es mayor a 0 y esto a su vez significa que la temperatura del evaporador sea distinta a la temperatura de ebullición del solvente puro, lo que hace más riguroso el cálculo de las propiedades necesarias para hallar los resultados requeridos. La herramienta didáctica para evaporadores de un solo efecto con la opción “Tipo de Solución” busca simplificar los cálculos y argumentaciones de forma que durante el uso del programa el usuario pueda aprender más sobre las soluciones diluidas o concentradas (de acuerdo a cual sea su elección) para evaporadores. A continuación, de describe como seleccionar el tipo de solución en la herramienta. 2.1. Solución Diluida S O D A V los botones “Debes Saber”, estos se encuentran a lo largo deR todo el programa con E S E la finalidad de proporcionarle pequeños consejos o información al usuario de R S O H manera que pueda guiarlo durante C la ejecución del ejercicio dentro de la herramienta E R E de la selección de la solución (Figura I.3), se abre una didáctica, para D el caso En busca de ayudar al usuario por las diferentes secciones del programa, se idearon ventana donde muestra una pequeña información de lo que son soluciones diluidas y concentradas y porque es relevante seleccionar entre ambas. Figura 5.3. Ventanas de Ayuda. Al seleccionar “Solución diluida” de la ventana que abre la opción “tipo de solución” (figura 5.2) y presionar el botón “Siguiente” de la misma ventana, el programa te redirige a la selección del caso. El procedimiento de este caso va a estar limitado para soluciones diluidas y de base acuosa. Las soluciones se consideran diluidas cuando el soluto entra en proporciones muy pequeñas de forma que pueda descartar el incremento del punto de ebullición con respecto al solvente, igualando las condiciones de ebullición de la mezcla a las condiciones de saturación del solvente puro. S O D VA ER S E En un intento de facilitar la manipulación y diseño de la herramienta didáctica para R S O por separar en cuatro posibles casos a Hoptó evaporadores de un solo efecto se C E ejecutar el procedimiento DERmatemático, simplificando así los cálculos y objetivos del 2.1.1. Selección del Caso programa. De esta forma, cada caso se diferencia básicamente por la variable o a determinar con sus respectivos datos de entrada. (Figura 5.4.) Figura 5.4. Selección del caso a ejecutar. De esta manera, las variables a determinar o incógnitas; se resaltan en cada recuadro con diferentes colores representativos para cada uno de los casos a evaluar, mientras que las variables que deben ser introducidas como datos se señalan en color negro. En general, las variables que se requieren para llevar a cabo el procedimiento matemático con la finalidad de definir el diseño de los sistemas de evaporación para efecto simple, son; el área superficial de transferencia de calor (A), el coeficiente global de transferencia de calor (U), la concentración del soluto a la entrada y a la S O D VA salida del evaporador (Xf; Xp), el flujo de entrada o alimentación al evaporador (F), ER S E R Cada uno de los casos ilustrados en la figura 5.4, se encarga de determinar alguna S O Hespecificadas, partiendo del valor numérico de C de estas variables que no han sido E ER Dfueron. las otras que si lo La presión del sistema (Psist), las condiciones de la corriente de vapor de agua destinada a la calefacción (Ts; Pvap), y las entalpías de la solución (hp; hf; Hv). El primer caso (CASO I), busca hallar el área superficial del evaporador (A), Así mismo, El segundo caso (CASO II), busca determinar el coeficiente global de transferencia de calor (U), Por otro lado, el caso tres (CASO III), refiere su búsqueda a encontrar la composición final del soluto en la corriente de producto o corriente concentrada (Xp), Por ultimo para el caso cuatro (CASO IV) en soluciones diluidas, se busca hallar el flujo o velocidad de alimentación (F), Ingresar Datos Para explicar el uso adecuado de la herramienta en soluciones diluidas, se escogió previamente un ejemplo a desarrollar del caso uno (CASO I), donde se desea determinar el área superficial del evaporador (A). A continuación en la figura 5.5. Se procede a ingresar los datos de un ejercicio modelo tomado del libro: Procesos de transporte de operaciones unitaria. Geankoplis (1998). Ejemplo (8.4-1) Como se alcanza a observar, en la celda de unidades al lado del valor de la variable, se puede seleccionar las diferentes unidades del sistema internacional (SI) para especificar la variable introducida. Se introducen en primer lugar los datos de la corriente de alimentación (identificando la concentración inicial en fracción, y no en porcentaje), producto y sistema (Presión y Coeficiente Global de transferencia de calor). Posteriormente se procede a definir la temperatura del evaporador figura 5.5. D R SE E R S O H C E ER S O D VA Figura 5.5 Ingreso de datos para el caso 1 diluido. Figura 5.6. Definiendo la temperatura del evaporador para soluciones diluidas. Para definir de la temperatura de ebullición de la solución fue necesario valerse de las tablas de vapor del agua a la presión del evaporador, ya que como se ha venido explicando, por tratase de una solución diluida con base acuosa, se pueden igualar sus propiedades a la del agua pura. Así mismo, en la figura 5.6 luego de presionar el botón ubicado en medio del evaporador con el nombre ‘Tsat’ se muestra una ventana auxiliar, mediante la cual se especifica como que se desea definir la temperatura del evaporador; ya sea suministrando los datos directamente S O D VA calculados a partir del ingreso de las tablas de vapor manualmente o, mediante la ER S E Seleccionando la primera opción se obtiene la R figura 5.7. S O H C E DER utilización de la calculadora de propiedades del agua. Figura 5.7. Definir la temperatura del evaporador para soluciones diluidas, mediante el uso de la calculadora de propiedades del agua. Donde a continuación, se redirige la pantalla hacia la calculadora antes menciona, igualmente ejecutando una ventana donde posteriormente se identificaran las propiedades de vapor. Introduciendo los valores obtenidos de temperatura, presión y entalpía para definir las condiciones dentro del evaporador. La herramienta didáctica para evaporadores de un solo efecto, cuenta con una calculadora de propiedades del agua, donde siguiendo unos pequeños pasos se pueden determinar las propiedades del vapor de agua a condiciones saturadas y sobrecalentadas sin necesidad de dirigirse a las tablas de vapor manualmente. Para condiciones de saturación basta con especificar la temperatura o presión de la solución para que la calculadora arroje los demás valores, así mismo, para S O D VA condiciones de sobrecalentamiento o sobresaturación del vapor es necesario R especificar 2 variables (no más de dos variables), para que la herramienta calcule SE E R S las propiedades del vapor correspondientes a la temperatura y presión O H C E ER especificadas. (Figura 5.8, figura 5.9). D Figura 5.8. Especificando la presión del evaporador en la calculadora de propiedades del agua para determinar la temperatura de la solución. D R SE E R S O H C E ER S O D VA Figura 5.9. Introduciendo valores en la ventana auxiliar correspondiente a la temperatura del evaporador para soluciones diluidas. Es importante señalar que para los valores introducidos dentro de las hojas de cálculo de Excel, (como se muestra el ejemplo de la figura 2.1.5), se debe utilizar coma (,) para especificar los decimales en caso de que la variable los posea. Por el contrario si el dato o variable va a ser especificada en una ventana alterna los decimales que el valor contenga se deben especificar con punto (.). Así mismo, se debe argumentar que los resultados arrojados por la herramienta didáctica para evaporadores de un solo efecto reflejan un porcentaje de error con respecto a los valores reales, se recomienda utilizar la herramienta como apoyo en el área de evaporación pero tomando en cuenta el porcentaje de error que presenta. Posterior a la especificación de la temperatura del evaporador, se procede a definir las entalpías de la solución en la entrada, salida del producto y salida del vapor del evaporador, seleccionando la opción “Cp/H” (ver Figura 5.10). D R SE E R S O H C E ER S O D VA Figura 5.10. Definiendo entalpias de la solución. En la Figura 5.10. hizo selección del botón “Cp/H” mediante el cual se abrió la ventana representada en la figura anterior, mediante la cual se procede a indicar de qué manera se desea elaborar el cálculo de las entalpías para la solución, esta sección te brinda tres posibles opciones para definir dichas variables. Como se puede observar en la Figura 5.11, la cual corresponde a la opción uno (“Introducir Entalpías”), el programa redirige al usuario hacia una ventana alterna donde se pueden introducir directamente las entalpías de la corriente de alimentación y la corriente del producto final en caso de que el ejercicio proporcione, mientras que la entalpía de la corriente de vapor del solvente evaporado, por tratarse de una solución diluida se define como el calor latente a las condiciones de saturación para la presión del sistema. D R SE E R S O H C E ER S O D VA Figura 5.11. Introducir entalpías de la solución. Para soluciones diluidas. Por otro lado (Ver Figura 5.12.), la opción dos (“Diagrama de Entalpías”), introduce al usuario al diagrama de entalpías para soluciones acuosas (tomando de ejemplo el diagrama para sistema NaOH-Agua, en donde explica la forma correcta de utilizar esas herramientas y cuales datos son los requeridos para extraer la información adecuada. Generalmente, los diagramas de entalpía son utilizados para soluciones concentradas, pero en esta sección de soluciones diluidas se incluyó, en caso de que el usuario quisiera saber un poco de este tipo de complementos para el diseño de los sistemas de evaporación de un simple efecto. Figura 5.12. Diagrama de entalpías. Así mismo, en la opción 3 (“Introducir Capacidades Caloríficas”), la herramienta didáctica proporciona al usuario la posibilidad de introducir las capacidades caloríficas de cada corriente en caso de que este las posea (Ver Figura 5.13.). Se especificó como limitante que la temperatura de referencia dirigida al cálculo de la entalpía mediante por medio de las capacidades caloríficas fuese la misma que la S O D VA de la solución en el evaporador, para facilitar de esta manera los cálculos internos del programa de perspectiva académico. O H C E ER D R SE E R S Figura 5.13. Definiendo capacidades caloríficas de las soluciones de entrada y salida. Así mismo, por tratarse de soluciones diluidas no es necesario especificar la entalpia de la corriente de vapor de agua evaporado, ya que por tratarse de una solución diluida y habiendo especificado la temperatura de referencia como igual a la temperatura del sistema, se considera que la entalpía de la corriente de vapor es el calor latente requerido para que el solvente (en este caso el agua), cambie de fase de líquido a vapor. Ya por último, luego de especificarse las entalpías de la solución y la temperatura del sistema junto con las variables principales de concentración, flujo, presión, área y/o coeficiente de transferencia, se requiere definir las condiciones a la que trabaja el vapor de agua introducido en el evaporador como medio de calefacción (corriente S). Para la herramienta didáctica de evaporadores de un solo efecto se tomó como limitación que la corriente de vapor de agua destinada como método de calefacción, siempre estuviese en condiciones de saturación. Independientemente del tipo de solución o del caso seleccionado. S O D representado en la página de ingreso de datos. Se mostrará una ventana A similar a V R E si se desea definir la representada en la figura 5.6, a través de la cualE se S selecciona R Spropiedades del agua o directamente, la corriente por medio de la calculadora de O H CPara este caso se utilizó la segunda opción, puesto E en la ventana auxiliar respectiva. R DE Seleccionando el botón “Ts/Pvap”, el cual se sitúa debajo del evaporador que se conocían los valores de la corriente S desde otros ejercicios anteriores. . Figura 5.14. Introducir valores para especificar las condiciones de la corriente de vapor de agua al evaporador para el ejemplo de solución diluida. Procedimiento Luego de introducir todos los datos que el ejercicio proporciona al usuario y este a su vez a la herramienta didáctica para evaporadores de un solo efecto, se procede a mostrar un resumen de lo que sería el procedimiento para calcular las incógnitas manualmente, empezando por los balances de masa y energía y una imagen representativa del evaporador resaltando el caso en que se encuentra el usuario S O D A V La finalidad de esta sección es explicarle al usuario la manera de desarrollar el R SE E ejercicio en caso de que lo quiera realizar a su vez de forma manual, muestra las R S con la explicación paso a paso de lo O H ecuaciones y los despejes respectivos junto C E R que realiza la herramienta DE internamente. En esta sección el usuario no debe (ver Figura 5.15). introducir ninguna variable ni hace modificaciones, solo se le mostrará el procedimiento respectivo para que lo pueda desarrollar. Figura 5.15. Procedimiento del CASO I. Luego de revisar el procedimiento, se selecciona la opción “Tabla de Resultados”, la cual redirige el programa a la tabla de resultados que se determinaron siguiendo el procedimiento posteriormente planteado. Es importante señalar que en la sección de procedimientos no se especifica la forma de calcular las entalpías de la solución solo muestra el paso a paso de la solución del problema refiriéndose a las ecuaciones a utilizar y que variables calcular primero, para llegar al resultado que se desea obtener. S O D VA R SE E R S HO C E Para dar por finalizado ERel ejercicio, se muestran los resultados obtenidos por los D valores introducidos previamente en la herramienta. El reporte de resultados se Resultados divide por corriente, teniendo un total de cuatro corrientes más los resultados de las variables del sistema (ver Figura 5.16), este reporte muestra todos los valores introducidos junto con los calculados posteriormente basándose en el procedimiento descrito anteriormente, especificando igualmente el tipo de solución con que se trabajó, el caso y resaltando en amarillo la incógnita principal a determinar. El reporte muestra los resultados en las unidades reflejadas sin posibilidad de cambiar a otras unidades. Es importante señalar que la herramienta didáctica para evaporadores de un solo efecto trabaja solamente en sistema internacional (SI). Por otro lado, la herramienta cuenta con una sección comparativa la cual manteniendo el caso y el tipo de solución, se pueden realizar manipulaciones a ciertas variables, para posterior ver una tabla comparativa, entre los resultados del ejercicio original, y los calculados luego de la alteración de la variable seleccionada (Ver Sección Comparar). D R SE E R S O H C E ER S O D VA Figura 5.16. Reporte de resultados para solución diluida y CASO I. 2.2. Solución Concentrada Al seleccionar “Solución Concentrada” en la ventana que se abre luego de presionar el botón “Tipo de solución”, como se muestra en la figura 5.1 el programa te redirige a la selección del caso, que en este caso por tratarse de solución concentrada de base acuosa, todos los casos se rigen por este criterio. Las soluciones se consideran concentradas cuando hay una composición apreciable del soluto en la solución de manera que exista una elevación o incremento en el punto de ebullición de esta con respecto al solvente puro (en este caso es el agua) lo que afectará posteriormente la definición de las entalpías de la solución a la entrada y a la salida del evaporador. 2.2.1. Selección del Caso En un intento de facilitar la manipulación y diseño de la herramienta didáctica para evaporadores de un solo efecto se optó por separar en cuatro posibles casos a ejecutar el procedimiento matemático, simplificando así los cálculos y objetivos del programa. De esta forma, cada caso se diferencia básicamente por la variable o a determinar con sus respectivos datos de entrada. (Figura 5.4.) D R SE E R S O H C E ER S O D VA Figura 5.4. Selección del caso a ejecutar para soluciones concentradas. De esta manera, las variables a determinar o incógnitas; se resaltan en cada recuadro con diferentes colores representativos para cada uno de los casos a evaluar, mientras que las variables que deben ser introducidas como datos se señalan en color negro. En general, las variables que se requieren para llevar a cabo el procedimiento matemático con la finalidad de definir el diseño de los sistemas de evaporación para efecto simple, son; el área superficial de transferencia de calor (A), el coeficiente global de transferencia de calor (U), la concentración del soluto a la entrada y a la salida del evaporador (Xf; Xp), el flujo de entrada o alimentación al evaporador (F), La presión del sistema (Psist), las condiciones de la corriente de vapor de agua destinada a la calefacción (Ts; Pvap), y las entalpías de la solución (hp; hf; Hv). Cada uno de los casos ilustrados en la figura 5.4, se encarga de determinar alguna de estas variables que no han sido especificadas, partiendo del valor numérico de las otras que si lo fueron. El primer caso (CASO I), busca hallar el área superficial del evaporador (A), Así mismo, El segundo caso (CASO II), busca determinar el coeficiente global de transferencia de calor (U), Por otro lado, el caso tres (CASO III), refiere su búsqueda a encontrar la composición final del soluto en la corriente de producto o corriente concentrada (Xp), Por ultimo para el caso cuatro (CASO IV) en soluciones diluidas, se busca hallar el flujo o velocidad de alimentación (F), S O D VA En busca de ayudar al usuario por las diferentes secciones del programa, se idearon los botones “Debes Saber”, estos se encuentran a lo largo de todo el programa con ER S E R manera que pueda guiarlo durante la ejecución del ejercicio dentro de la herramienta S O H en la figura 5.17; la información que se C didáctica. Para la ventanaE representada DEa R muestra es referente los tipos de casos y la diferencia que existe entre ellos. la finalidad de proporcionarle pequeños consejos o información al usuario de Figura 5.17. Ventana de ayuda referente al tipo de caso a seleccionar. Ingresar Datos Para explicar el uso adecuado de la herramienta en soluciones concentradas, se escogió previamente un ejemplo a desarrollar del caso tres (CASO III), donde se desea determinar la composición final del soluto en la corriente de salida (Xp). A continuación en la figura 5.18. Se procede a ingresar los datos del ejercicio. D R SE E R S O H C E ER S O D VA Figura 5.18. Ingreso de Datos del caso seleccionado. Como se alcanza a observar, en la celda de unidades al lado del valor de la variable, se puede seleccionar las diferentes unidades del sistema internacional (SI) para especificar la variable introducida. Se introducen en primer lugar los datos de la corriente de alimentación (identificando la concentración inicial en fracción, y no en porcentaje), producto y sistema (Presión y Coeficiente Global de transferencia de calor). Posteriormente se procede a definir la temperatura del evaporador figura 5.19. D R SE E R S O H C E ER S O D VA Figura 5.19. Definir Temperatura del Evaporador. Soluciones Concentradas. Al definir la temperatura del evaporador para soluciones concentradas, se da a escoger entre tres opciones dependiendo de la forma que se desee especificar la temperatura del evaporador; La primera opción “Calcular Temperatura de Saturación del agua pura a la Presión del sistema”. Esta opción envía la pantalla de la herramienta hasta la calculadora de propiedades del agua, para determinar la temperatura del agua saturada a la presión del sistema. La misma fue configurada previendo que se requiriera de este valor para entrar a los diagramas de Duhring o para calcular la temperatura de la solución mediante el la ecuación de incremento de punto de ebullición. Así mismo, como se representa en la figura 5.20, la opción dos permite calcular la temperatura de la solución por medio del incremento del punto de ebullición junto con la temperatura de ebullición del agua pura. D R SE E R S O H C E ER S O D VA Figura 5.20. Introducir el incremento del punto de ebullición. Para definir la temperatura del evaporador. Así mismo, la herramienta le suministra al usuario una explicación de cómo utilizar el diagrama de Duhring para soluciones acuosas (tomando como ejemplo el sistema NaOh-Agua), al seleccionar el botón “diagrama” en la ventana del incremento del punto de ebullición, aparece una ventana alterna donde se muestra la figura representativo de este y la explicación de cómo utilizar dicha herramienta para conseguir los valores que se requieren (ver Figura 5.21), de igual forma le permite al usuario introducir el valor de temperatura obtenida a través del diagrama. Es importante señalar que para los valores introducidos dentro de las hojas de cálculo de Excel, (como se muestra el ejemplo de la figura 5.18), se debe utilizar coma (,) para especificar los decimales en caso de que la variable los posea. Por el contrario si el dato o variable va a ser especificada en una ventana alterna los decimales que el valor contenga se deben especificar con punto (.). S O D VA R SE E R S HO C E R“Temperatura del Evaporador”, se utiliza cuando el usuario Por último, la opciónE tres D ya posee un valor de temperatura o cuando lo extrae de algún diagrama y decide Figura 5.21. Explicación del diagrama de Duhring. introducirlo directamente en la herramienta didáctica para evaporadores de un solo efecto (figura 5.22). Luego de definir la temperatura de la solución por cualquiera de estas opciones, automáticamente en la página de ingreso de datos se modificará el valor de T1 como se muestra en la figura 5.23. Con el objetivo de identificarla al definir las entalpías. Figura 5.22. Introducir temperatura del evaporador. S O D VA R SE E R S HO C E Rlos resultados arrojados por la herramienta didáctica para Es importante señalar Eque D evaporadores de un solo efecto refleja un porcentaje de error con respecto a los Figura 5.23. Reporte de la temperatura del evaporador. valores reales, se recomienda utilizar la herramienta como apoyo en el área de evaporación pero tomando en cuenta el porcentaje de error que presenta. Posterior a la especificación de la temperatura del evaporador, se procede a definir las entalpías de la solución en la entrada, salida del producto y salida del vapor del solvente evaporado, seleccionando la opción “Cp/H” (ver Figura 5.24). Figura 5.24. Definiendo entalpias de la solución. En la Figura 5.24 se procede a seleccionar la forma en que se desea definir el cálculo de las entalpias de la solución, esta sección te brinda cuatro posibles opciones para definir dichas variables: Seleccionando la opción uno (“Introducir Entalpías”), a continuación el programa redirige al usuario hacia una ventana alterna donde se pueden introducir directamente las entalpías de la corriente de alimentación y la corriente del producto S O D VA final en caso de que el ejercicio las proporcione, mientras que la entalpía de la ER S E R ventana se le proporciona al usuario la S posibilidad de elegir entre introducir los O H C valores previamente identificados en las tablas de vapor del agua para condiciones E R E sobrecalentadasD de la forma manual, introducir los valores haciendo uso de la corriente de vapor del solvente evaporado por tratarse de una solución concentrada de base acuosa, se debe definir por mediante las tablas de vapor, en esta misma calculadora de propiedades de vapor del agua. Figura 5.25. Introducir entalpias. Solución Concentrada. De ser seleccionada la opción,”Calculadora de propiedades de vapor” definiendo así el vapor que sale por la corriente V (corriente de vapor evaporado); se redirige a la sección donde se ubica la calculadora de propiedades del agua, donde se abrirá una ventana para introducir los resultados obtenidos de las tablas de vapor sobresaturado a la presión y temperatura del sistema (Figura 5.26). D R SE E R S O H C E ER S O D VA Figura 5.26. Definiendo entalpía de la corriente de vapor para vapor sobrecalentado La herramienta didáctica para evaporadores de un solo efecto, cuenta con una calculadora de propiedades del agua, donde siguiendo unos pequeños pasos se pueden determinar las propiedades del vapor de agua a condiciones saturadas y sobrecalentadas sin necesidad de dirigirse a las tablas de vapor manualmente. Para condiciones de saturación basta con especificar la temperatura o presión de la solución para que la calculadora arroje los demás valores, así mismo, para condiciones de sobrecalentamiento o sobresaturación del vapor es necesario especificar 2 variables (no más de dos variables), para que la herramienta calcule las propiedades del vapor correspondientes a la temperatura y presión especificadas (ver figura 5.27). D R SE E R S O H C E ER S O D VA Figura 5.27. Introduciendo valores calculados mediante la calculadora de las propiedades del agua. Por otro lado (Ver Figura 5.12.), la opción dos (“Diagrama de Entalpías”), introduce al usuario al diagrama de entalpías para soluciones acuosas (tomando de ejemplo el diagrama para sistema NaOH-Agua), en donde explica la forma correcta de utilizar esas herramientas y cuales datos son los requeridos para extraer la información adecuada, para a continuación redirigir a la opción uno y que el usuario introduzca el mismo las entalpías de la solución Figura 5.12. Explicación del diagrama de entalpías. Así mismo, en la opción 3 (“Introducir Capacidades Caloríficas”), la herramienta didáctica proporciona al usuario la posibilidad de introducir las capacidades caloríficas de cada corriente; en caso de que las posea (Ver Soluciones diluidas “Ingreso de datos”, definición de entalpía). Ya por último, tras especificarse las entalpías de la solución y la temperatura del sistema junto con las variables principales de flujo, concentración, presión, área y/o S O D VA coeficiente de transferencia, se requiere definir las condiciones a la que trabaja el R vapor de agua destinado a la calefacción del evaporador, para realizar la SE E R S trasferencia de calor que de origen a la concentración de la solución (corriente S). O H C E limitación que la corriente ERde vapor de agua destinada como método de calefacción, D siempre estuviese en condiciones de saturación. Independientemente del tipo de Para la herramienta didáctica de evaporadores de un solo efecto se tomó como solución o del caso seleccionado. Seleccionando el botón “Ts/Pvap”, el cual se sitúa debajo del evaporador representado en la página de ingreso de datos. Se mostrará una ventana representada en la figura 5.28, a través de la cual se selecciona si se desea definir la corriente por medio de la calculadora de propiedades del agua o directamente, en la ventana auxiliar respectiva. Para este caso se utilizó la segunda opción, puesto que se conocían los valores de la corriente S desde otros ejercicios anteriores. D R SE E R S O H C E ER S O D VA Figura 5.28. Definir el método de especificación de la corriente S. Figura 5.13. Introducir valores para especificar las condiciones de la corriente de vapor de agua al evaporador para el ejemplo de solución diluida. Procedimiento Luego de introducir todos los datos que el ejercicio proporciona al usuario y este a su vez a la herramienta didáctica para evaporadores de un solo efecto, se procede a mostrar un resumen de lo que sería el procedimiento para calcular las incógnitas manualmente, empezando por los balances de masa y energía y una imagen representativa del evaporador resaltando el caso en que se encuentra el usuario S O D Adesarrollar el La finalidad de esta sección es explicarle al usuario la manera de V R E manual, muestra las Sforma ejercicio en caso de que lo quiera realizar a su vez de E R S con la explicación paso a paso de lo O ecuaciones y los despejes respectivos junto H C E R que realiza la herramienta internamente. En esta sección el usuario no debe E D introducir ninguna variable ni hace modificaciones, solo se le mostrará el (ver Figura 5.29). procedimiento respectivo para que lo pueda desarrollar. Figura 5.29. Procedimiento del CASO III. Luego de revisar el procedimiento, se selecciona la opción “Tabla de Resultados”, la cual redirige el programa a la tabla de resultados que se determinaron siguiendo el procedimiento posteriormente planteado. Es importante señalar que en la sección de procedimientos no se especifica la forma de calcular las entalpías de la solución solo muestra el paso a paso de la solución del problema refiriéndose a las ecuaciones a utilizar y que variables calcular primero, para llegar al resultado que se desea obtener. S O D VA ER S E R Para dar por finalizado el ejercicio, se muestran los resultados obtenidos por los S O H C en la herramienta. El reporte de resultados se valores introducidos previamente E R DE divide por corriente, teniendo un total de cuatro corrientes más los resultados de las Resultados variables del sistema (ver Figura 5.30), este reporte muestra todos los valores introducidos junto con los calculados posteriormente basándose en el procedimiento descrito anteriormente, especificando igualmente el tipo de solución con que se trabajó, el caso y resaltando en amarillo la incógnita principal a determinar. El reporte muestra los resultados en las unidades reflejadas sin posibilidad de cambiar a otras unidades. Es importante señalar que la herramienta didáctica para evaporadores de un solo efecto trabaja solamente en sistema internacional (SI). Por otro lado, la herramienta cuenta con una sección comparativa la cual manteniendo el caso y el tipo de solución, se pueden realizar manipulaciones a ciertas variables, para posterior ver una tabla comparativa, entre los resultados del ejercicio original, y los calculados luego de la alteración de la variable seleccionada (Ver Sección Comparar). R SE E R S O H C E Comparación DER S O D VA Figura 5.30. Reporte de resultados para el CASO III. 2.3. La herramienta didáctica para evaporadores de un solo efecto, le proporciona al usuario la posibilidad de realizar alteraciones en ciertas variables (dependiendo del caso), con la finalidad de comparar los resultados originales con los resultados obtenidos luego de manipular dicha variable, manteniendo el caso y el tipo de solución original. Luego de reportar los resultados, la herramienta en la misma hoja donde se muestran los resultados presenta la opción de “comparar”, la cual al seleccionarla, se puede visualizar una ventana con una lista de variables pasibles a modificar (figura 5.31). De igual forma al seleccionar alguna de las variables se abre una ventana alterna para que se introduzca el nuevo valor de dicha variable (figura 5.32). Tomando el ejemplo de solución diluida se procedió a manipular el flujo de la alimentación (F), aumentando su valor para observar cómo podría afectar los resultados del ejercicio original. S O D VA R SE E R S Figura 5.31. Selección de la variable a modificar. O H C E ER D Figura 5.32. Introducir el nuevo valor de la variable a modificar. . Figura 5.33. Tabla comparativa de resultados Al introducir el nuevo valor de la variable con su respectiva unidad, la herramienta redirige la pantalla a una tabla comparativa (figura 5.33.), donde se puede apreciar en el lado izquierdo, el ejercicio original denominado “Ejercicio 1” en donde se expresan los resultados originales, y en el lado derecho los resultados modificados gracias a la variable que se manipulo; denominado “Ejercicio 2”. Así mismo, en la parte de inferior, en un recuadro amarillo; se señala la variable que ha sido alterada. D H C E ER O SE E R S R S O D VA PROPIEDADES DE VAPOR DE AGUA Al iniciar sesión en la herramienta didáctica para evaporadores de un solo efecto, se tienen la página principal, en donde se pueden observar cuatro opciones que el usuario puede escoger para empezar a utilizar la herramienta, como son el tipo de solución, manual de usuario, propiedades de vapor de agua y convertidor de unidades. D R SE E R S O H C E ER S O D VA Figura 5.34. Propiedades de Vapor de Agua. Al seleccionar “Propiedades de vapor de agua”, (Ver figura 5.34) el usuario podrá escoger entre; Tablas de Capacidades Caloríficas, Tablas de Vapor de Agua o Calculadora de propiedades vapor. Al decidir por la primera de estas opciones se abrirá una ventana alterna, donde se pueden observar dos pequeñas tablas que contienen las capacidades caloríficas a diferentes temperaturas para el agua líquida y el vapor de agua, a presión atmosférica (figura 5.35). Así mismo, al seleccionar la opción “Tablas de Vapor de Agua”, la pantalla se redirige a una tabla de Excel que contiene las propiedades de vapor tabuladas, para que el usuario en caso de que lo requiera, pueda buscar alguna propiedad de ser necesario (figura 5.36). D R SE E R S O H C E ER S O D VA Figura 5.35. Tablas de capacidades caloríficas del agua. Figura 5.36. Tablas de propiedades de vapor de agua. Por último, al elegir la opción “Calculadora de propiedades de vapor”, se refiere a un mini-programa que permite calcular las propiedades del vapor de agua en condiciones de saturación y sobrecalentamiento (Ver figura 5.37). D R SE E R S O H C E ER S O D VA Figura 5.37. Calculadora de propiedades de vapor. Para condiciones saturadas, basta con especificar la temperatura o la presión de la corriente o sistema y presionar en conjunto la tecla Ctrl y la tecla “O” para obtener todas las demás propiedades. Así mismo, para condiciones de sobrecalentamiento o sobresaturación se deben especificar dos variables en conjunto, e igualmente se presiona la tecla Ctrl junto a la tecla “O” para verificar las propiedades a esas condiciones (Figura 5.38). Por otro lado para borrar el contenido de la calculadora, se deben presionar la tecla Ctrl y la tecla “M” de su teclado en conjunto y de esta forma se reinicia la calculadora para volver a hacer uso de ella nuevamente. Es importante señalar que la calculadora de propiedades de vapor trabaja con comas (,) a la hora de reportar los decimales. D R SE E R S O H C E ER S O D VA Figura 5.38. Determinación de propiedades a través de la calculadora de vapor. LIMITACIONES DE LA HERRAMIENTA La Herramienta Didáctica para Evaporadores de un Solo Efecto, es una propuesta de un simulador básico con finalidad académicos, el cual tiene la capacidad de reproducir el comportamiento de evaporadores bajo ciertos criterios, con la finalidad de facilitar o ayudar a la compresión del tema de evaporación en la cátedra de Operaciones Unitarias II, impartida en la Universidad Rafael Urdaneta. S O D VA Por tratarse de una herramienta con fines didácticos, se limitó su funcionamiento a ER S E R 1. Solo reproduce ejercicios de evaporación para efecto simple o un solo efecto. S O H C deben ser acuosas, es decir, que el solvente 2. Las soluciones a trabajar E R E presente D en la solución sea el agua. ciertas restricciones que a continuación se enumeran; 3. El sistema de unidades es el sistema internacional (SI), donde los flujos son requeridos y proporcionados exclusivamente en másicos. 4. Se restringieron los cálculos a cuatro tipos de casos; donde el caso 1 determina el área superficial del evaporador, el caso 2 busca hallar el coeficiente de transferencia de calor, el caso 3 pretende determinar la concentración del producto final y el caso 4 busca calcular el flujo o velocidad de la alimentación. 5. En la sección de comparación, solo se pueden manipular las variables bajo el mismo caso seleccionado anteriormente y el mismo tipo de solución. 6. En las ventanas alternas a las hojas de cálculo se deben especificar los valores decimales con punto (.). Así mismo, en las hojas de cálculo se deben especificar los valores decimales con coma (,). 7. El convertidor de unidades incluido en la herramienta solo convierte unidades dentro del sistema internacional, para ayudar al usuario a corregir valores. 8. El vapor de la corriente que entra al evaporador para llevar a cabo la evaporación, debe ser vapor de agua a condiciones de saturación. O H C E ER D SE E R S R APÉNDICE S O D VA 215 APÉNDICE A1 Método Tradicional (Soluciones Diluidas) La evaporación como proceso en las industrias químicas, se puede definir como una operación unitaria que se encarga de concentrar una solución mediante la S O D A V no volátiles y solventes volátiles; de forma que al llegar al punto de ebullición de la R E por la parte superior Ssaliendo E mezcla el solvente presente en la solución se evapore R S en estado líquido. De tal forma, O H del evaporador, mientras que el soluto se mantenga C E R E que se obtener la deseada. Dcomposición eliminación del disolvente por ebullición. Una de las principales características que debe presentar este tipo de soluciones, es que deben estar conformadas por solutos Cuando se habla de soluciones diluidas, se refiere a que el soluto presente en la solución a concentrar, se encuentra en un porcentaje relativamente bajo; por lo tanto las propiedades de la solución (desde una perspectiva académica) se pueden asumir iguales a las del solvente puro. Considerando que no existe un incremento en el punto de ebullición de la mezcla. De cierta forma, estas consideraciones facilitan el procedimiento matemático requerido para determinar las incógnitas. Ya que puede obviarse el uso de herramientas alternas a los cálculos como son los diagramas empleados para la determinación de entalpías y los diagramas de líneas de Duhring los cuales se encargan de determinar el incremento que se genera en la temperatura de evaporación de la solución con respecto a la concentración del soluto presente. A continuación, se desarrolla un ejercicio extraído del libro Procesos de Transporte y Operaciones Unitarias. C.J. Geankoplis (1998), del ejemplo 8.4-1 (pag. 554). Donde para especificar el diseño de un evaporador de simple efecto, desde una perspectiva didáctica es necesario para seguir el procedimiento matemático tradicional para soluciones diluidas. 216 Solución del ejemplo 4.6. Para soluciones diluidas Tomando de Geankoplis, (1998, p554). Área de transferencia de calor en un evaporador de un solo efecto Un evaporador continuo de efecto simple concentra 9072 kg/h de una solución de sal al 1% en peso que entra a 311 K, hasta una concentración final de 1,5% en peso. El vapor en el evaporador está a 101,325 kPa y el vapor de agua que se introduce está saturado a 143,3 kPa. El coeficiente total U = 1704 W/(m 2.K). Calcule las cantidades de vapor y de producto de líquido, así como el área de transferencia de calor que se requiere. Puesto que se trata de una solución diluida, suponga que su punto de ebullición es igual al del agua. R SE E R S O H C E ER S O D VA 1. Resumiendo los datos proporcionados por el ejercicio (Ejemplo 4.6). F = 9072 kg/h D Xf = 0,01 Tf = 311 K Cp = 4,14 kJ/kg.K Psist = 101,325 kPa Pvap = 143,3 kPa Xp = 0,015 U = 1704 W/m2.K (Condiciones de Saturación) 2. Se definieron las ecuaciones y la nomenclatura a utilizar. Balance de masa. F=P+V (Ec.4.5) Balance por componentes. F ∙ Xf = P ∙ Xp (Ec.4.6) Balance de energía. F ∙ hf + S ∙ (Hs - hs) = P ∙ hp + V ∙ Hv (Ec. 4.3) Ecuaciones para determinar el calor transferido en el evaporador. q=S∙λ q = A ∙ U ∙ (Ts - T1) (Ec. 4.2) (Ec. 2.14) 217 S O D VA R SE E R S Figura 4.1.4. Diagrama de un sistema de evaporación de un solo efecto. Señalando como incógnita principal el área superficial. Dónde: F: Xf: HO C E Flujo másico DERo velocidad de la alimentación del evaporador. Composición inicial del soluto en solución. Tf: Temperatura inicial a la entrada del evaporador. hf: Entalpía de la solución en la alimentación. P: Flujo másico o velocidad del producto final ya concentrado. Xp: Composición final del soluto en la solución. hp: Entalpía de la solución a la salida del evaporador. V: Flujo másico o velocidad del solvente evaporado. Hv: Entalpía del solvente a las condiciones del sistema. S: Flujo o velocidad del vapor de agua que se utiliza como calefacción. Ts: Temperatura de saturación del vapor de agua utilizado como calefacción. Pvap: Presión de vaporización del vapor de agua utilizado como calefacción. Hs; hs: Entalpías de vapor y líquido a las condiciones de saturación. λ: Calor latente del vapor de agua utilizado como calefacción. A: Área superficial del evaporador. U: Coeficiente global de transferencia de calor. Psist: Presión del evaporador. 218 T1: Temperatura del evaporador. q: Calor transferido desde la corriente de vapor de agua saturado hacia la solución. 3. Se realizaron los cambios de unidades respectivos en las variables que lo ameriten, de forma que se mantenga la consistencia y no genere errores en los resultados S O D VA Cambio de unidades en el coeficiente global de transferencia de calor (U): U = 1704 R kJ E S 6134,4 E h∙m ∙K SR J s 1kJ ∙3600 ∙ = 2 H 1000J S∙m ∙K O H C E ER D 2 4. Se realizaron el procedimiento matemático para determinar el área superficial de transferencia de calor en un evaporador de un solo efecto, considerando solución diluida. Utilizando la Ec.4.5, (Balance por componentes). Se determina el flujo másico de la solución concentrada a la salida del evaporador (P). F ∙ Xf = P ∙ Xp P= P= F ∙ Xf Xp (Ec. 4.7) (9072) ∙ 0,01 = 6048 kg/h 0,015 Luego de calcular el flujo de la solución de salida, se determina la velocidad de vapor evaporado de la solución (V), utilizando la Ec4.5, (Balance de masa). Se realiza un despeje de la variable que se desea obtener. F=P+V V=F- P ( Ec.4.8.) V = (9072) – (6048) = 3024 kg/h Definiendo la temperatura de ebullición de la solución (T1): 219 Al verificar el enunciado del ejercicio. En la última parte del mismo, hace referencia a la temperatura de ebullición de la mezcla; señalando que al tratarse de una solución diluida de origen acuoso, la temperatura del evaporador podría igualarse a la temperatura de ebullición del agua definida por la presión del evaporador. Es decir, que el incremento del punto de ebullición de la solución se puede igualar a 0. Se introducen a las tablas de saturación del agua con la presión del sistema. Psist = 101,325 kPa Condiciones de Saturación del Agua. D R SE E R S O H C E ER S O D VA Figura 6.1.1. Ampliación de las tablas de vapor para determinar la temperatura del evaporador en soluciones diluidas. T1 = 100 ⁰C 373,15 K 220 Así mismo, se procede a determinar las entalpías de la solución; a la entrada y a la salida del evaporador, por lo que se requiere especificar la temperatura que se utilizará como referencia en los cálculos respectivos. Por este motivo para facilitar los cálculos del método tradicional se iguala la temperatura de referencia con la temperatura del evaporador. Calculo de entalpías a partir de las capacidades caloríficas partiendo de Ec. 2.22: h = Cp ∙ (T - Tref) HO C E R Temperatura de la solución. DE h: Es la entalpía de la solución a determinar. Cp: Capacidad calorífica de la solución. T: R SE E R S Donde: S O D VA Tref: Temperatura que estimada para ubicar el punto de partida. Para la entalpía de solución en la alimentación se utilizó la Ec.4.4: hf = Cp ∙ (Tf - T1) hf = (4,14) ∙ (311 - 373,15) hf = -257,301 kJ/kg Para la entalpía de solución a la salida del evaporador se utilizó la Ec.4.5: hp = Cp ∙ (T1 - Tref) hp = (4,14) ∙ (373,15 - 373,15) hp = 0 kJ/kg La entalpía del agua evaporada; se consideró como la resta de las entalpías en las fases líquidas y vapor saturado, ya que se está trabajando con soluciones diluidas y la temperatura de referencia se igualó a la temperatura de ebullición de la solución. Volviendo a la figura 6.1.2, se toma a 101,325 kPa y 373,15 K (100 ⁰C) las entalpías en la parte de liq sat y vap sat. h (liquido) = 419,064 kJ/kg 221 H (vapor) = 2676 kJ/kg La entalpía para la corriente V sería la resta de estas, obteniendo el calor latente de la solución a 373,15 K y 101,325 kPa. Hv = (2676) – (419,064) Hv = 2257 kJ/kg S O D VA evaporador hasta el punto de ebullición de la mezcla.E ElR vapor de agua en la S corriente S se encuentra saturado a la presiónR de E 143,3 kPa. S O Htabla de vapor satura obtenemos: C E Ubicando la presión indicada, en la DER Así mismo, se debieron especificar las condiciones del vapor de agua que es utilizado como medio de calentamiento para elevar la temperatura dentro del Figura 6.1.2. Tabla de vapor de agua saturado, para determinar las condiciones de saturación en la corriente S 222 Al no existir un valor con la presión exacta que maneja la corriente (S) se debió realizar una interpolación entre los valores resaltados en la figura 6.1.3. Para obtener los siguientes resultados: Pvap = 143,3 kPa Ts = 109,928 ⁰C 383,12 K S O D VA Hs = 2691,202 kJ/kg ER S E R S A continuación, se procede a calcular O el flujo de la corriente de vapor de agua como H(Balance de Energía). C calefacción partiendo de la Ec.4.3 E DF ∙Ehf +RS ∙ (Hs - hs) = P ∙ hp + V ∙ Hv (Ec. 4.3.) hs = 461,023 kJ/kg . Despejando (S) de la ecuación 4.3. S= (P ∙ hp) + (V ∙ Hv) - (F ∙ hf) (Hs - hs) S= (6048 ∙ 0) + (3024 ∙ 2257) + (9072 ∙ 257,301) (2691, 20240 - 461,02364 ) (Ec. 4.9) S = 4108 kJ/kg Así mismo, se procede a determinar el calor transferido en el evaporador por la Ec.4.2 q = S ∙ (Hs - hs) (Ec. 4.2) q = (4108) ∙ (2691,2024 - 461,0236) q = 9153575 kJ/h 223 Finalmente, se procede a calcular el área partiendo de la Ec.2.14. . q = A ∙ U ∙ (Ts - T1) A= q (Ec.4.10) U ∙ (Ts - T1) 9153575 6134,4 ∙ (383,15 - 373,15) A = 149,3 m² A continuación, se reportan los resultados obtenidos del ejemplo 4.6 mediante los S O D VA cálculos anteriores, en la tabla 6.1.1. R SE E R S Tabla 6.1.1 Reporte de resultados obtenidos por el método tradicional, para el ejemplo HO C E R 4.6, CASO I, Solución diluida. Corriente DE Reporte de Resultados Manuales Alimentación Producto Vapor Sistema Corriente de Vapor como Calefacción Variable Flujo Temperatura Composición Capacidad Calorífica Entalpía Flujo Composición Temperatura Capacidad Calorífica Entalpía Flujo Temperatura Entalpía Estado Área Calor Temperatura Coeficiente de Transferencia de Calor Incremento del Punto de Ebullición Presión Sistema Economía Flujo Temperatura de Saturación Presión de vaporización Entalpía del Líquido Entalpía del Vapor Calor Latente Solución Tipo: CASO: Valor 9072 311 0,01 4,14 -257,301 6048 Diluida I Unidad kg/h K kJ/kg.K kJ/kg kg/h 0,015 373,15 K 4,14 kJ/kg.K 0 kJ/kg 3024 kg/h 373,15 K 2257 kJ/kg SATURADO 149,3 m² 9153575 kJ/h 373,15 K 6134,4 kJ/h.m².K 0 101,325 kPa 0,7361 4108 kg/h 383,12 K 143,3 kPa 461,023 kJ/kg 2691,202 kJ/kg 2230 kJ/kg 224 A través de la tabla anterior (tabla 6.1.1), se resumieron los resultados obtenidos en por el desarrollo del ejemplo 4.6, realizado mediante el método tradicional de cálculo. Dónde se resalta en color amarillo la principal incógnita determinada, especificando también; el caso respectivo. Igualmente se recrearon los procedimientos matemáticos descritos en el capítulo 4 de esta investigación, para cada uno de los ejemplos seleccionados de soluciones diluidas. Obteniendo los resultados correspondientes que posteriormente se destinaron a comparar con los S O D VA valores arrojados por la herramienta didáctica para evaporadores de un solo efecto. ER S E R cada ejemplo tomado de Geankoplis (1998). S HO C E R 4.7. Para soluciones diluidas DEEjemplo A continuación se reportan las tablas que resumen los resultados obtenidos para (Geankoplis 1998 p574). Coeficiente de transferencia de calor en un evaporador de efecto simple. Una alimentación de 4535 kg/h de solución de sal al 2% en peso a 311 K, entra continuamente a un evaporador para concentrarse a 3%. La evaporación se lleva a presión atmosférica y el área del evaporador es 69,7 m2. El calentamiento se logra con vapor de agua saturado a 383,2 K. Puesto que la solución es diluida, se puede suponer que tiene el mismo punto de ebullición del agua. Se estima que la capacidad calorífica de la alimentación es Cp = 4,10 kJ/kg.K. Calcule las cantidades de vapor y de líquido producido y el coeficiente total de transferencia de calor. 225 Tabla 6.1.2. Reporte de resultados obtenidos por el método tradicional, para el ejemplo 4.7, CASO II, Solución diluida. Solución Tipo: Reporte de Resultados Manuales Corriente Variable Alimentación Producto Vapor CASO: Flujo Temperatura Composición Capacidad Calorífica Entalpía Flujo Composición Temperatura Capacidad Calorífica Entalpía Flujo Temperatura Entalpía Estado Área Calor Temperatura Coeficiente de Transferencia de Calor Incremento del Punto de Ebullición Presión Sistema Economía D Sistema Corriente de Vapor como Calefacción Flujo Temperatura de Saturación Presión de vaporización Entalpía del Líquido Entalpía del Vapor Calor Latente 4535 311 0,02 4,10 -254,815 3023,33 Unidad kg/h K kJ/kg.K kJ/kg kg/h S O D VA R SE E R S O H C E ER Valor Diluida II 0,03 373,15 K 4,10 kJ/kg.K 0 kJ/kg 1511,667 kg/h 373,15 K 2256,936 kJ/kg SATURADO 69,7 m² 456321,564 kJ/h 373,15 K 6520,2275 kJ/h.m².K 0 101,325 kPa 0,73788 2048,6398 kg/h 383,2 K 144,56 kPa 462,1741 kJ/kg 2691,616 kJ/kg 2229,441 kJ/kg Ejemplo 4.8. Para soluciones diluidas (Geankoplis 1998 p574) Efectos de una alimentación más rápida en el evaporador. Con los mismos valores del área, U, presión del vapor de agua, presión del evaporador y temperatura de la alimentación del problema anterior. Calcule las cantidades de líquido y de vapor que salen y la concentración del líquido de salida cuando la velocidad de alimentación se aumenta a 6804 kg/h. 226 Tabla 6.1.3. Reporte de resultados obtenidos por el método tradicional, para el ejemplo 4.8, CASO III, Solución diluida. Solución Tipo: Reporte de Resultados Manuales Corriente Variable Alimentación Producto Vapor CASO: Flujo Temperatura Composición Capacidad Calorífica Entalpía Flujo Composición final Temperatura Capacidad Calorífica Entalpía Flujo Temperatura Entalpía Estado Área Calor Temperatura Coeficiente de Transferencia de Calor Incremento del Punto de Ebullición Presión Sistema Economía D Sistema Corriente de Vapor como Calefacción Flujo Temperatura de Saturación Presión de vaporización Entalpía del Líquido Entalpía del Vapor Calor Latente 6804 311 0,02 4,10 -254,815 5548,51 Unidad kg/h K kJ/kg.K kJ/kg kg/h S O D VA R SE E R S O H C E ER Valor Diluida III 0,0245 373,15 K 4,10 kJ/kg.K 0 kJ/kg 1255,49 kg/h 373,15 K 2256,936 kJ/kg SATURADO 69,7 m² 456321,56 kJ/h 373,15 K 6520,2275 kJ/h.m².K 0 101,325 kPa 0,612841 2048,6388 kg/h 383,2 K 144,5631 kPa 462,1741 kJ/kg 2691,6157 kJ/kg 2229,442 kJ/kg Ejemplo 4.9. Para soluciones diluidas (Geankoplis 1998 p574): Una alimentación de solución de sal al 2% en peso a 311 K, entra continuamente a un evaporador para concentrarse a 3%. La evaporación se lleva a una presión del evaporador de 41,4 kPa y el área del evaporador es 69,7 m2. El calentamiento se logra con vapor de agua saturado a 383,2 K. Puesto que la solución es diluida, se puede suponer que tiene el mismo punto de ebullición del agua. Se estima que la capacidad calorífica de la 227 alimentación es Cp = 4,10 kJ/kg.K. Determine la capacidad o velocidad de la alimentación en estas condiciones. Tabla 6.1.4. Reporte de resultados obtenidos por el método tradicional, para el ejemplo 4.9, CASO IV, Solución diluida. Solución Tipo: Reporte de Resultados Manuales Corriente Flujo Temperatura Composición Capacidad Calorífica Entalpía Flujo Composición Temperatura Capacidad Calorífica Entalpía Flujo Temperatura Entalpía Estado Área Calor Temperatura Coeficiente de Transferencia de Calor Incremento del Punto de Ebullición Presión Sistema Economía D Vapor Sistema Corriente de Vapor como Calefacción O H C E ER Valor R SE E R S Flujo Temperatura de Saturación Presión de vaporización Entalpía del Líquido Entalpía del Vapor Calor Latente IV S O D VA Variable Alimentación Producto CASO: Diluida 16283,1 311 0,02 4,10 -159,8 6808,44 Unidad kg/h K kJ/kg.K kJ/kg kg/h 0,03 373,15 K 4,10 kJ/kg.K 0 kJ/kg 5427,7 kg/h 373,15 K 2317,21 kJ/kg SATURADO 69,7 m² 15179000 kJ/h 373,15 K 6520,2275 kJ/h.m².K 0 101,325 kPa 0,797202 6808,44 kg/h 383,2 K 144,563 kPa 462,1741 kJ/kg 2691,6167 kJ/kg 2229,44 kJ/kg 228 APÉNDICE A2 Método Tradicional (Soluciones Concentradas) La evaporación como proceso en las industrias químicas, se puede definir como una operación unitaria que se encarga de concentrar una solución mediante la S O D A V no volátiles y solventes volátiles; de forma que al llegar al punto de ebullición de la R E por la parte superior Ssaliendo E mezcla el solvente presente en la solución se evapore R S en estado líquido. De tal forma, O H del evaporador, mientras que el soluto se mantenga C E R E que se obtener la deseada. Dcomposición eliminación del disolvente por ebullición. Una de las principales características que debe presentar este tipo de soluciones, es que deben estar conformadas por solutos Al hablar de soluciones concentradas, se dice que la composición del soluto presente en la mezcla es apreciable, de forma que al contrario de las soluciones diluidas; las propiedades de la solución no serán iguales a las del solvente puro. Dicha composición debió ser considerada al calcular la temperatura de ebullición del evaporador, e igualmente para determinar las entalpías de la solución. Por esta razón, es necesario hacer uso de diagramas específicos para diferentes mezclas a concentrar; los cuales complementan el procedimiento matemático de los sistemas de evaporación de efecto simple que trabajan con soluciones concertadas. Tomando en cuenta las referencias bibliográficas de las cuales se basó esta investigación; Se resolvió un ejercicio extraído del libro de Ocon y Tojo. Problemas de Ingeniería Química, del ejemplo 3-4 (pag. 172). Mediante el método tradicional. Desarrollando el procedimiento matemático planteado detalladamente en el capítulo 4 para soluciones concentradas. 229 Solución del ejemplo 4.10. Para soluciones diluidas (Ocon y Tojo, s.f. p172): En un evaporador simple se tratan 15000 kg/h de una disolución de NaOH al 10% que ha de concentrarse hasta el 50% en peso. El vapor empleado como medio de calefacción es vapor saturado a 3,5 atm, y una vez condensado sale a la temperatura de condensación. El vacío mantenido en la cámara de evaporación es de 620 mmHg, referido a la presión atmosférica normal. El coeficiente integral de transmisión de calor vale 1600 kcal/m².h.⁰C. Si la alimentación entra a 40⁰C y no se pierde calor con el exterior, determine; la superficie de calefacción. R SE E R S O H C E ER S O D VA 1. Resumiendo los datos proporcionados por el ejercicio (Ejemplo 4.10). F = 15000 kg/h D Psist = 620 mmHg (vacío) Xf = 0,1 Tf = 40 °C Pvap = 3,5 atm Xp= 0,5 U = 1600 kcal/m2.h.°C (Condiciones de Saturación) 2. Se definieron las ecuaciones y la nomenclatura a utilizar. Balance de masa. F=P+V (Ec.4.5) Balance por componentes. F ∙ Xf = P ∙ Xp (Ec.4.6) Balance de energía. F ∙ hf + S ∙ (Hs - hs) = P ∙ hp + V ∙ Hv (Ec. 4.3) Ecuaciones para determinar el calor transferido en el evaporador. q=S∙λ q = A ∙ U ∙ (Ts - T1) (Ec. 4.2) (Ec. 2.14) 230 S O D VA R SE E R S Figura 4.1.4. Diagrama de un sistema de evaporación de un solo efecto. Señalando como incógnita principal el área superficial. Dónde: F: HO C E ERo velocidad de la alimentación del evaporador. Flujo Dmásico Xf: Composición inicial del soluto en solución. Tf: Temperatura inicial a la entrada del evaporador. hf: Entalpía de la solución en la alimentación. P: Flujo másico o velocidad del producto final ya concentrado. Xp: Composición final del soluto en la solución. hp: Entalpía de la solución a la salida del evaporador. V: Flujo másico o velocidad del solvente evaporado. Hv: Entalpía del solvente a las condiciones del sistema. S: Flujo o velocidad del vapor de agua que se utiliza como calefacción. Ts: Temperatura de saturación del vapor de agua utilizado como calefacción. Pvap: Presión de vaporización del vapor de agua utilizado como calefacción. Hs; hs: Entalpías de vapor y líquido a las condiciones de saturación. λ: Calor latente del vapor de agua utilizado como calefacción. A: Área superficial del evaporador. U: Coeficiente global de transferencia de calor. 231 Psist: Presión del evaporador. T1: Temperatura del evaporador. q: Calor transferido desde la corriente de vapor de agua saturado hacia la solución. 3. Se realizaron los cambios de unidades respectivos en las variables que lo ameriten, de forma que se mantenga la consistencia y no genere errores S O D A(U): Cambio de unidades en el coeficiente global de transferencia deV calor R SE kJ E kcal R U = 1600 ∙4,1868 S = 6698,88 °C∙m ∙h HO h∙m ∙K C E DER en los resultados 2 2 Cambio de unidades para la presión del evaporador, llevándola igualmente a presión absoluta. P = (760 - 620) mmHg = 140 mmHg P = 140 mmHg ∙ 101,325 kPa = 760 mmHg 18,665 kPa Cambio de unidades para la presión de la corriente S. P = 3,5 atm ∙ 101,325 kPa = atm 354,637 kPa 4. Se realiza el procedimiento matemático para determinar el área superficial de transferencia de calor en el evaporador, considerando solución concentrada. Definiendo la Temperatura de ebullición de la solución (T1): Como se explicó anteriormente, al hablar de soluciones concentradas (como es el caso del ejemplo 4.10), es necesario hacer uso de diagramas especificados para esta etapa del proceso. 232 Los diagramas de Dühring, son gráficas que recrean el comportamiento de la temperatura de ebullición de una mezcla acuosa en comparación con las temperaturas de saturación del agua pura, para determinadas concentraciones del soluto. Para este caso, de utilizó el diagrama de Dühring para sistemas de NaOHH2O. Previamente, se debió identificar la temperatura del agua pura a la presión del S O D VA evaporador, haciendo uso de las tablas de vapor saturado. Presión del sistema: 18,665 kPa Condiciones de saturación del agua pura. O D H C E ER R SE E R S Figura 6.2.1. Ubicación de la temperatura de saturación para el solvente puro en las tablas de vapor saturado. Al no existir un valor con la presión exacta que maneja el evaporador se debió realizar una interpolación entre los valores resaltados en la figura 6.2.1. Para obtener de esta forma, la temperatura de saturación del agua a la presión del sistema: 233 Tagua° = 58,18629 ⁰C (136,73 °F) 331,336 K Partiendo de esta temperatura, y sabiendo que la composición del NaOH en la solución dentro del evaporador es igual a Xp = 0,5. Se procede a determinar la temperatura de ebullición de la solución ingresando al diagrama de Dühring, como se muestra en la figura 6.2.2, resaltado en color rojo. D R SE E R S O H C E ER S O D VA Figura 6.2.2. Identificación Temperatura de la solución concentrada, del ejemplo 4.12. Mediante el diagrama de Dühring. 234 Como se ilustra en la figura anterior, se entró con la temperatura de saturación del agua pura (136, 73°F), al diagrama para posteriormente ascender en forma vertical hasta cortar con la línea de composición respectiva para el ejemplo 4.10 (0,5 para NaOH), y ubicar en línea la temperatura de la solución en el lado izquierdo de la gráfica obteniendo: T1 = 210,51 °F (99,17 °C) 372,32 K S O D VA ER S E R concentrada. Para este paso, se requirióS hacer uso del diagrama de entalpía vs O H C concentración para el sistema NaOH-H O. E DER Ya defina la temperatura de ebullición de la mezcla, se procedió a determinar las entalpías; a las condiciones de la alimentación del evaporador y en la solución ya 2 Figura 6.2.3. Identificación de las entalpías de la solución para el ejemplo 4.10, en el diagrama entalpía vs concentración para el sistema NaOH-H2O. 235 Los diagramas de entalpía, permiten la identificación de estas variables para soluciones concentradas, entrando desde la parte inferior del mismo con la composición en que se encuentra el soluto dentro de la solución, para luego subir en una línea recta hasta cortar con la curva que represente la temperatura que define las condiciones del sistema en cuestión; leyendo posteriormente la entalpía respectiva en el extremo izquierdo de la gráfica. Estos diagramas se encuentran para diferentes sistemas en este caso en particular, se utilizó el diagrama de S O D VA entalpía vs concentración para el sistema NaOH-H2O. (Figura 6.2.3). ER S E R color verde a las condiciones especificadas por el ejercicio. Igualmente para la S O H y composición de la misma. Dando lugar a C entalpía de la solución a la E temperatura DER los siguientes resultados: En la figura 6.2.3, se identificó la entalpía para la alimentación, representada en hf = 68,79 Btu/lb hp = 226 Btu/lb 160 kJ/kg 525,68 kJ/kg Así mismo, en la corriente (V), la cual representa el vapor del solvente evaporado. De esta manera, por tratarse de una solución de base acuosa, el fluido se considera como vapor de agua sin presencia de solutos. Igualmente, debido a que la temperatura de la solución es mayor que la temperatura del agua pura a la presión de operación, el vapor generado sale en condiciones de sobresaturación. Por lo tanto, para especificar la entalpía del mismo se introdujo a las tablas de vapor del agua con la presión y temperaturas del evaporador. Como se ilustra en la figura a continuación, representando cada variable con los colores amarillo y rojo respectivamente. 236 R SE E R S O H C E ER D S O D VA Figura 6.2.4. Ubicación de la entalpía del vapor de agua sobrecalentado generado en el evaporador. Al igual que la figura 6.2.1. de no existir un valor de entalpía con las condiciones exactas que maneja el evaporador se realizó una interpolación entre los valores resaltados en la figura 6.2.4. Para obtener de esta forma, la entalpía de la corriente de vapor de agua originado por la evaporación del solvente en la solución: Hv = 2684,8716 kJ/kg Luego de identificar las entalpías de la solución, del vapor generado y la alimentación por medio del diagrama de entalpía vs concentración del sistema NaOH-H2O y las tablas de vapor de agua en sobrecalentamiento, se llevó a cabo el procedimiento descrito para el caso 1 en el capítulo 4. Obteniendo los siguientes resultados: Utilizando la Ec.4.5, (Balance por componentes). Se determina el flujo másico de la solución concentrada a la salida del evaporador (P). F ∙ Xf = P ∙ Xp P= P= F ∙ Xf Xp (15000) ∙ 0,1 = 3000 kg/h 0,5 (Ec. 4.7) 237 Luego de calcular el flujo de la solución de salida, se determina la velocidad de vapor evaporado de la solución (V), utilizando la Ec.4.5, (Balance de masa). Se realiza un despeje de la variable que se desea obtener. F=P+V V=F- P ( Ec.4.8.) V = (15000) – (3000) = 12000 kg/h S O D VA Así mismo, se debieron especificar las condiciones del vapor de agua que es utilizado como medio de calentamiento para elevar la temperatura dentro del evaporador hasta el punto de ebullición de la mezcla. El vapor de agua en la corriente S se encuentra saturado a la presión de 354,637 kPa. ER S E R S Ubicando la presión indicada, en la tabla de vapor satura obtenemos: O H C E R DE Figura 6.2.5. Tabla de vapor de agua saturado, para determinar las condiciones de saturación en la corriente S, para el ejemplo 4.10. De la misma manera que se ha venido explicando, de reflejarse el valor exacto de presión maneja la corriente se debió realizar una interpolación entre los valores resaltados en la figura 6.2.5. Para obtener los siguientes resultados: Pvap = 354,637 kPa 238 Ts = 139,322 ⁰C 412,472 K Hs = 2732,1749 kJ/kg hs = 586,21142 kJ/kg A continuación, se procede a calcular el flujo de la corriente de vapor de agua como calefacción partiendo de la Ec.4.3. (Balance de Energía). F ∙ hf + S ∙ (Hs - hs) = P ∙ hp + V ∙ Hv Despejando (S) de la ecuación 4.3. D S= R SE E R S O H C E (P ∙ hp) + (V ∙ Hv) - (F ∙ hf) S =R E (Hs - hs) S O D VA (Ec. 4.3) (Ec. 4.9) (3000 ∙ 525,68) + (12000 ∙ 2684,8716) + (15000 ∙ 160) (2732,1744 - 586,21142 ) S = 14630 kJ/kg Así mismo, se procede a determinar el calor transferido en el evaporador por la Ec.4.2 q = S ∙ (Hs - hs) Ec. 4.2 q = (14630) ∙ (2732,1744 - 586,21142) q = 31395500 kJ/h Finalmente, se procede a calcular el área partiendo de la Ec.2.14. . q = A ∙ U ∙ (Ts - T1) A= q (Ec.4.10) U ∙ (Ts - T1) 31395500 6698,88 ∙ (412,472 - 372,32) A = 116,753 m² 239 A continuación, se reportan los resultados obtenidos del ejemplo 4.10 mediante el procedimiento descrito anteriormente, en la tabla 6.2.1. Tabla 6.2.1. Reporte de resultados obtenidos por el método tradicional, para el ejemplo 4.10, CASO I, solución concentrada. Solución : Concentrada CASO: I Reporte de Resultados Manuales Corriente Variable Alimentación Producto Flujo Temperatura Composición Capacidad Calorífica Entalpía Flujo Composición Temperatura Capacidad Calorífica Entalpía Flujo Temperatura Entalpía Estado Área Calor Temperatura Coeficiente de Transferencia de Calor Incremento del Punto de Ebullición Presión Sistema Economía D Vapor Sistema Corriente de Vapor como Calefacción Flujo Temperatura de Saturación Presión de vaporización Entalpía del Líquido Entalpía del Vapor Calor Latente Unidad S O D VA R SE E R S O H C E ER Valor 15000 313,15 0,1 -160 3000 kg/h K kJ/kg kg/h 0,5 372,32 K -525,68 kJ/kg 12000 kg/h 372,32 K 2684,87 kJ/kg SOBRECALENTADO 116,753 m² 31395500 kJ/h 372,32 K 6698,88 kJ/h.m².K 40,984 18,665 kPa 0,82023 14630 kg/h 412,472 K 354,637 kPa 586,211 kJ/kg 2732,17 kJ/kg 2145,96 kJ/kg A través de la tabla anterior (tabla 6.2.1), se resumieron los resultados obtenidos en por el desarrollo del ejemplo 4.10, realizado mediante el método tradicional de cálculo. Dónde se resalta en color amarillo la principal incógnita determinada, especificando también; el caso respectivo. Igualmente se recrearon los procedimientos matemáticos descritos en el capítulo 4 de esta investigación, para 240 cada uno de los ejemplos seleccionados de soluciones concentradas. Obteniendo los resultados correspondientes, que posteriormente se destinaron a comparar con los valores arrojados por la herramienta didáctica para evaporadores de un solo efecto. A continuación se reportan las tablas que resumen los resultados obtenidos para cada ejemplo tomados de la bibliografía seleccionada para la investigación. S O D A V Ejemplo 4.11. Para soluciones concentradas R SE E R S O H C E R (Geankoplis 1998 p575): DE Coeficiente de transferencia de calor para evaporar NaOH. Para concentrar 4536 kg/h de una solución de NaOH al 10% en peso hasta 20% en peso, se usa un evaporador de efecto simple con área de 37,6 m 2. La alimentación entra a 21,1 ˚C. Se usa vapor de agua saturado a 110 ˚C como medio de calentamiento y la presión en el evaporador es 51,7 kPa. Calcule los kg/h de vapor de agua utilizado y el coeficiente total de transferencia de calor. 241 Tabla 6.2.2. Reporte de resultados obtenidos por el método tradicional, para el ejemplo 4.11, CASO II, solución concentrada. Solución : Reporte de Resultados Manuales Corriente Alimentación Producto Vapor Sistema Corriente de Vapor como Calefacción Variable CASO: Flujo Temperatura Composición Capacidad Calorífica Entalpía Flujo Composición Temperatura Capacidad Calorífica Entalpía Flujo Temperatura Entalpía Estado Área Calor Temperatura Coeficiente de Transferencia de Calor Incremento del Punto de Ebullición Presión Sistema Economía Valor C E R DE Flujo Temperatura de Saturación Presión de vaporización Entalpía del Líquido Entalpía del Vapor Calor Latente II Unidad kg/h K S O D VA SER E R S HO 4356 294,3 0,1 -98,47 2268 Concentrada kJ/kg kg/h 0,2 370,65 K -351,05 kJ/kg 2268 kg/h 370,65 K 2677,36 kJ/kg SOBRECALENTADO 37,6 m² 6421780 kJ/h 370,65 K 13663,4 kJ/h.m².K 15,47 51,7 kPa 0,787568 2879,75 kg/h 383,15 K 143,633 kPa 461,327 kJ/kg 2891,311 kJ/kg 2229,98 kJ/kg Ejemplo 4.12. Para soluciones concentradas El ejemplo 4.12. Es una modificación del ejemplo 4.10 de Ocon y Tojo, (s.f. p172): En un evaporador simple se tratan 15000 kg/h de una disolución de NaOH al 10% que ha de concentrarse. El vapor empleado como medio de calefacción es vapor saturado a 3,5 atm, y una vez condensado sale a la temperatura de condensación. El vacío mantenido en la cámara de evaporación es de 620 mmHg, referido a la presión atmosférica normal. El coeficiente integral de transmisión de calor vale 1600 kcal/m².h.⁰C y la superficie de transferencia de calor es igual a 120 m². Si la alimentación entra a 40⁰C y no se pierde calor con el exterior, determine; la 242 composición final del soluto a la salida del evaporador. Considere un IPE de 40,98 y un valor de entalpía para la corriente final de 790kJ/kg. Tabla 6.2.3. Reporte de resultados obtenidos por el método tradicional, para el ejemplo 4.12, CASO III, solución concentrada. Solución : Concentrada CASO: III Reporte de Resultados Manuales Corriente Alimentación Producto Vapor Sistema Corriente de Vapor como Calefacción Variable Flujo Temperatura Composición Capacidad Calorífica Entalpía Flujo Composición final Temperatura Capacidad Calorífica Entalpía Flujo Temperatura Entalpía Estado Área Calor Temperatura Coeficiente de Transferencia de Calor Incremento del Punto de Ebullición Presión Sistema Economía D Flujo Temperatura de Saturación Presión de vaporización Entalpía del Líquido Entalpía del Vapor Calor Latente Producción en un evaporador de efecto simple. kg/h K kJ/kg kg/h 0,5 372,32 K -790 kJ/kg 12000 kg/h 372,32 K 2684,87 kJ/kg SOBRECALENTADO 120 m² 32276800 kJ/h 372,32 K 6698,88 kJ/h.m².K 40,98 18,665 kPa 0,800933 15040,7 kg/h 412,472 K 354,637 kPa 586,211 kJ/kg 2732,17 kJ/kg 2145,96 kJ/kg Ejemplo 4.13. Para soluciones concentradas (Geankoplis 1998, p575): Unidad S O D VA 15000 313,15 0,1 -160 3000 R SE E R S O H C E ER Valor 243 Un evaporador concentra F kg/h a 311 K de una solución de NaOH al 20% en peso hasta 50% en peso. El vapor de agua saturado para el calentamiento está a 399,3 K. la presión en el evaporador es de 13,3 kPa abs. El coeficiente total es 1420 W/m2.K y el área es 86,4 m2. Calcule la velocidad de alimentación F del evaporador. Tabla 6.2.4. Reporte de resultados obtenidos por el método tradicional, para el ejemplo 4.13, CASO IV, solución concentrada. HO C E R Corriente Alimentación Producto Vapor Sistema Corriente de Vapor como Calefacción Variable Flujo Temperatura Composición Capacidad Calorífica Entalpía Flujo Composición Temperatura Capacidad Calorífica Entalpía Flujo Temperatura Entalpía Estado Área Calor Temperatura Coeficiente de Transferencia de Calor Incremento del Punto de Ebullición Presión Sistema Economía DE R SE E R S Reporte de Resultados Manuales Flujo Temperatura de Saturación Presión de vaporización Entalpía del Líquido Entalpía del Vapor Calor Latente S O D VA Solución : Concentrada CASO: IV Valor 8546,93 311 0,2 -140 3418,77 Unidad kg/h K kJ/kg kg/h 0,5 367,15 K -367,15 kJ/kg 2675,672 kg/h 367,15 K 2675,672 kJ/kg SOBRECALENTADO 86,4 m² 14199900 kJ/h 367,15 K 5112 kJ/h.m².K 43,37 13,3 kPa 0,788991 6499,64 kg/h 399,3 K 240,697 kPa 529,896 kJ/kg 2714,6139 kJ/kg 2184,72 kJ/kg 244 APÉNDICE B Error relativo Con la finalidad de validar los resultados obtenidos por la herramienta didáctica de evaporadores de un solo efecto, se procedió a calcular el error relativo que presentan en comparación al calculado por el método ordinario. Partiendo de la definición expresada en el capítulo 2 de esta investigación basada en Skoog (2001): S O D A y depende V al valor real de dicha magnitud. En general, el error relativo es ineludible R E para realizar la Sdisponible E básicamente del procedimiento elegido y la tecnología R S la siguiente expresión por donde se O H medición o calculo. Matemáticamente define C E R puede determinar DunEporcentaje de error relativo: El error relativo es una desviación del valor medido de una magnitud física respecto Valor medio-Valor real %Erelativo= | | *100 Valor real (Ec. 2.21) Donde Skoog (2001), explica que el valor medido es el valor que se obtuvo del resultado del experimento y el valor real es el dato con el que se va a comparar. Aplicando la ecuación anterior se pudo calcular el porcentaje de error de la siguiente manera. Tomando como modelo de cálculo de determinación del porcentaje de error experimental en los resultados obtenidos, se utilizará el ejemplo 4.6. Ejemplo 4.10. Para soluciones diluidas Tomando de Geankoplis, (1998, p554). Área de transferencia de calor en un evaporador de un solo efecto Un evaporador continuo de efecto simple concentra 9072 kg/h de una solución de sal al 1% en peso que entra a 311 K, hasta una concentración final de 1,5% en peso. El vapor en el evaporador está a 101,325 kPa y el vapor de agua que se introduce está saturado a 143,3 kPa. El coeficiente total U = 1704 W/(m 2.K). 245 Calcule las cantidades de vapor y de producto de líquido, así como el área de transferencia de calor que se requiere. Puesto que se trata de una solución diluida, suponga que su punto de ebullición es igual al del agua. Donde se obtuvieron los siguientes resultados por medio de la herramienta didáctica para evaporadores de un solo efecto: Incógnita principal para el ejemplo 4.6: A= 150,3917 m2 S O D VA R SE E R Skg/h P: O 6048 H C Flujo de la solución concentrada: Flujo del vapor generado mediante la evaporación del solvente: E R E D V: 3024 kg/h Flujo de vapor consumido por el evaporador: S: 4106,9393 kg/h Así mismo reportando los valores obtenidos de las mismas variables por el método manual se tiene: Incógnita principal para el ejemplo 4.6: A= 149,3 m2 Flujo de la solución concentrada: P: 6048 kg/h Flujo del vapor generado mediante la evaporación del solvente: V: 3024 kg/h Flujo de vapor consumido por el evaporador: 246 S: 4108 kg/h Calculando entonces el porcentaje de error relativo entre los valores reportados anteriormente, utilizando la ecuación 2.21, donde el valor medido representa el resultado obtenido por la herramienta y el valor real el determinado mediante el método ordinario se tiene: Valor medio-Valor real %Erelativo= | | *100 Valor real O H C E ER %Erelativo= | D 150,3917-149,3 | *100 149,3 0% Flujo del vapor generado mediante la evaporación del solvente: 3024-3024 %Erelativo= | | *100 3024 0,7307% Flujo de la solución concentrada: 6048-6048 %Erelativo= | | *100 6048 R SE E R S Para la incógnita principal del ejemplo 4.6 S O D VA (Ec. 2.21) 0% Flujo de vapor consumido por el evaporador: 4106,9393-4108 %Erelativo= | | *100 4108 0,0258% Finalmente se reportaron los porcentajes de errores experimentales por medio de las siguientes tablas especificadas por ejemplo: 247 Ejemplo 4.6. Para soluciones diluidas Tabla 4.6. Tabla comparativa entre los resultados obtenidos por medio de la herramienta didáctica y el método tradicional para el ejercicio 4.6. Variable Determinada Resultado Método Tradicional Resultado Herramienta Didáctica % Error Área superficial del evaporador 149,3 m² 150,391 m² 0,73074347 Flujo de producto concentrado (P) 6048 kg/h Flujo de vapor de agua para calefacción (S) O ECH DER Flujo de Solvente Evaporado (V) 4108 kg/h 3024 kg/h S O D VA R SE E R S 6048 kg/h 0 4106,9393 kg/h 0,02582035 3024 kg/h 0 Ejemplo 4.7. Para soluciones diluidas Tabla 4.12. Tabla comparativa entre los resultados obtenidos por medio de la herramienta didáctica y el método tradicional para el ejemplo 4.7. Variable Determinada Resultado Método Tradicional Resultado Herramienta Didáctica % Error Coeficiente de transferencia de calor 6520,225 kJ/m2.h.K 6424,34 kJ/m2.h.K 1,47057809 Flujo de producto concentrado (P) 3023,33 kg/h 3023,33 kg/h 0 Flujo de vapor de agua para calefacción (S) 2048,639 kg/h 2048,63796 kg/h 5,0765E-05 Flujo de Solvente Evaporado (V) 1511,667 kg/h 1511,666 kg/h 6,6152E-05 248 Ejemplo 4.8. Para soluciones diluidas Tabla 4.14. Tabla comparativa entre los resultados obtenidos por medio de la herramienta didáctica y el método tradicional para el ejemplo 4.8. Variable Determinada Resultado Método Tradicional Resultado Herramienta Didáctica Composición de el soluto a la salida 0,0245 0,02492 Flujo de producto concentrado (P) 5548,51 kg/h O H C E ER D S O D VA R SE E R S % Error 1,71428571 5232,445 kg/h 5,69639417 Flujo de vapor de agua para calefacción (S) 2048,638 kg/h 2048,63996 kg/h 9,5673E-05 Flujo de Solvente Evaporado (V) 1255,49 kg/h 1287,554 kg/h 2,55390326 Ejemplo 4.9. Para soluciones diluidas Tabla 4.16. Tabla comparativa entre los resultados obtenidos por medio de la herramienta didáctica y el método tradicional para el ejemplo 4.9. Variable Determinada Resultado Método Tradicional Resultado Herramienta Didáctica % Error Flujo de Alimentación 16283,1 kg/h 16368,5618 kg/h 0,52484969 Flujo de producto concentrado (P) 10855,4 kg/h 10912,3745 kg/h 0,52484938 Flujo de vapor de agua para calefacción (S) 6808,44 kg/h 6838,945 kg/h 0,44804684 Flujo de Solvente Evaporado (V) 5427,7 kg/h 5456,187 kg/h 0,52484478 249 Ejemplo 4.10. Para soluciones concentras Tabla 4.18. Tabla comparativa entre los resultados obtenidos por medio de la herramienta didáctica y el método tradicional para el ejemplo 4.10. Variable Determinada Resultado Método Tradicional Resultado Herramienta Didáctica Área Superficial del Evaporador 116,753 m2 116,7234 m2 Flujo de producto concentrado (P) 3000 kg/h O H C E ER D S O D VA R SE E R S 3000 kg/h % Error 0,0025335 0 Flujo de vapor de agua para calefacción (S) 14630 kg/h 14630,0249 kg/h 0,0001701 Flujo de Solvente Evaporado (V) 12000 kg/h 12000 kg/h 0 Ejemplo 4.11. Para soluciones concentras Tabla 4.20. Tabla comparativa entre los resultados obtenidos por medio de la herramienta didáctica y el método tradicional para el ejemplo 4.11 Variable Determinada Resultado Método Tradicional Resultado Herramienta Didáctica % Error Coeficiente de transferencia de calor 13663,4 kJ/m2.h.K 13663,3489 kJ/m2.h.K 0,00037399 Flujo de producto concentrado (P) 2268 kg/h 2268 kg/h 0 Flujo de vapor de agua para calefacción (S) 2879,75 kg/h 2879,7399 kg/h 0,00035072 Flujo de Solvente Evaporado (V) 2268 kg/h 2268 kg/h 0 250 Ejemplo 4.12. Para soluciones concentras Tabla 4.22. Tabla comparativa entre los resultados obtenidos por medio de la herramienta didáctica y el método tradicional para el ejemplo 4.12. Variable Determinada Resultado Método Tradicional Resultado Herramienta Didáctica Composición del soluto en la salida 0,5078 0,5078 Flujo de producto concentrado (P) 2953,41 kg/h O H C E ER S O D VA R SE E R S % Error 0 2953,3728 kg/h 0,00125956 Flujo de vapor de agua para calefacción (S) 15040,7 kg/h 15040,7086 kg/h 5,3189E-5 Flujo de Solvente Evaporado (V) 12046,6 kg/h 12046,6271 kg/h 0,00022496 D Ejemplo 4.13. Para soluciones concentras Tabla 4.24. Tabla comparativa entre los resultados obtenidos por medio de la herramienta didáctica y el método tradicional para el ejemplo 4.13. Variable Determinada Resultado Método Tradicional Resultado Herramienta Didáctica % Error Flujo de la Alimentación 8546,93 kg/h 8546,9373 kg/h 8,5411E-05 Flujo de producto concentrado (P) 3418,67 kg/h 3418,774 kg/h 0,00304212 Flujo de vapor de agua para calefacción (S) 6499,64 kg/h 6499,6533 kg/h 0,00020463 Flujo de Solvente Evaporado (V) 5128,16 kg/h 5128,1643 kg/h 8,3851E-05
© Copyright 2026