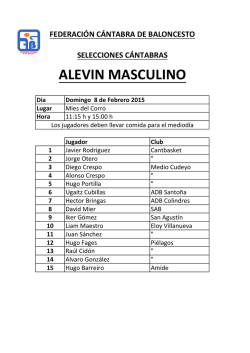
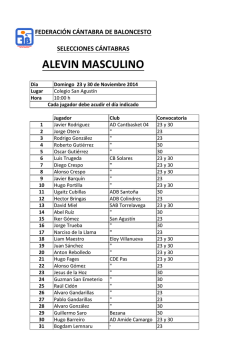
Haga clic aquí para ver el archivo
Diseño de experimentos
Hugo Alexer Pérez Vicente
Métodos complementarios al
análisis de varianza
Comparaciones múltiples
Comparación o pruebas de rangos
múltiples
• Después de que se rechazó la hipótesis nula en un
análisis de varianza, es necesario revisar a detalle y
ver cuáles tratamientos son diferentes.
• Por lo general, estas comparaciones consisten en
pruebas de hipótesis o en intervalos de confianza.
Diseño de experimentos - Hugo Alexer Pérez Vicente
Comparación o pruebas de rangos
múltiples
Algunas estrategias son:
Comparación de parejas de
medias de tratamientos:
• Método LSD (diferencia
significativa mínima de
Fisher)
• Método de Tukey
• Prueba del rango múltiple
de Duncan
Diseño de experimentos - Hugo Alexer Pérez Vicente
Comparación de tratamientos
con un control:
• Método
de
Dunnet
(exposición del grupo)
• Método de Hsu
Método LSD
Es posible probar la igualdad de todos los posibles
pares de medias con la hipótesis:
H 0 : i j
H A : i j
Para todo i distinto de j.
Por tanto, para k tratamientos se tiene k(k-1)/k pares
de medias.
Diseño de experimentos - Hugo Alexer Pérez Vicente
Método LSD
El estadístico de prueba t0 cada una de las hipótesis
planteadas anteriormente se calcula:
t0
yi y j
1
1
CM E
n
nj
i
Para una prueba de dos colas, el criterio de rechazo
sería:
1 1
yi y j LSD,
donde LSD t / 2 ,N a CM E
n
i
n j
A la expresión LSD se le llama diferencia mínima
significativa.
Diseño de experimentos - Hugo Alexer Pérez Vicente
Método LSD
Si el diseño es balanceado, n1=n2=…=na=n, entonces:
LSD t / 2 , N a
2CM E
n
Para usar este método, simplemente se compara la
diferencia observada entre cada par de promedios con la
LSD correspondiente. Si |ȳi. – ȳj.| > LSD, se concluye que
las medias poblacionales μi y μj difieren.
Note que un intervalo de confianza al 100(1−α)% para la
diferencia entre las medias de un solo par de
tratamientos cualesquiera µi – µj es igual a { ȳi. – ȳj. ± LSD}.
Diseño de experimentos - Hugo Alexer Pérez Vicente
Ejemplo: comparación de cuatro métodos
de ensamble
• Un equipo de mejora investiga el efecto de cuatro
métodos de ensamble A, B, C y D, sobre el tiempo de
ensamble en minutos.
• En primera instancia, la estrategia experimental es
aplicar cuatro veces los cuatro métodos de ensamble
en orden completamente aleatorio (las 16 pruebas
en orden aleatorio).
Diseño de experimentos - Hugo Alexer Pérez Vicente
Ejemplo: comparación de cuatro métodos
de ensamble
• Los tiempos de ensamble se muestran en la tabla
siguiente:
Métodos de ensamble
A
B
C
D
6
7
11
10
8
9
16
12
7
10
11
11
8
8
13
9
Diseño de experimentos - Hugo Alexer Pérez Vicente
Ejemplo: comparación de cuatro métodos
de ensamble
• Para investigar cuáles pares de medias son
estadísticamente diferentes, se prueban los seis
posibles pares de hipótesis:
H 0 : A B vs H A : A B
H 0 : A C vs H A : A C
H 0 : A D vs H A : A D
H 0 : B C vs H A : B C
H 0 : B D vs H A : B D
H 0 : C D vs H A : C D
Diseño de experimentos - Hugo Alexer Pérez Vicente
Ejemplo: comparación de cuatro métodos
de ensamble
• Después de realizar el ANOVA se obtiene:
CME = 2.46, G.L. Error = 16 - 4 =12
DISTR.T.INV(0.05,12)=2.18
LSD t / 2 ,N k
Diseño de experimentos - Hugo Alexer Pérez Vicente
2CM E
2 * 2.46
2.18
2.42
n
4
Ejemplo: comparación de cuatro métodos
de ensamble
• La decisión sobre cada una de las seis hipótesis
listadas antes se obtiene al comparar las
correspondientes diferencias muestrales en valor
absoluto con el número LSD. Por ejemplo:
A B 7.25 8.5 1.25 2.42
• Por tanto, la diferencia entre ambas medias no son
significativas.
Diseño de experimentos - Hugo Alexer Pérez Vicente
Resultados del procedimiento LSD del
ejemplo
𝑦𝐴. 𝑦𝐵.
7.25 8.5
Diseño de experimentos - Hugo Alexer Pérez Vicente
𝑦𝐷.
10.5
𝑦𝐶.
12.75
Prueba de Tukey
Tukey propuso una procedimiento para probar H0: μi = μj
contra H1: μi ≠ μj para todos los p pares posible de medias,
en el que el nivel de significación global es exactamente αg
para tamaños de muestras iguales y es, a lo sumo, αg para
tamaños de muestras diferentes. En este procedimiento se
utiliza el estadístico de rango estudentizado q.
ymax ymin
q
CM E / n
Donde ȳmax y ȳmin son las medias muestrales mayor y menor,
respectivamente, sacadas de un grupo de p medias
muestrales.
Diseño de experimentos - Hugo Alexer Pérez Vicente
Prueba de Tukey
La tabla de la siguiente diapositiva, contiene los valores
de qα, los puntos porcentuales αg superiores de q,
donde k es el número de tratamientos y df es el
número de grados de libertad asociados con el error
(CME).
Diseño de experimentos - Hugo Alexer Pérez Vicente
Tabla del estadístico de rango
estudentizado
Diseño de experimentos - Hugo Alexer Pérez Vicente
Prueba de Tukey
• Para una prueba de dos colas, el criterio de rechazo
para cada par de medias sería:
yi y j T g ,
donde T g
q g (k , df )
2
1 1
CM E
n n
j
i
• Si el diseño es balanceado, n1 = n2 =…= na = n,
entonces:
T g
Diseño de experimentos - Hugo Alexer Pérez Vicente
CM E
q g (k , df )
n
Prueba de Tukey
• De manera equivalente, podría construirse una serie
de intervalos de confianza de 100(1−αg)% para la
diferencia de todos los pares de medias de la
siguiente manera:
yi y j T g i j yi y j T g
Diseño de experimentos - Hugo Alexer Pérez Vicente
Ejemplo: comparación de cuatro métodos
de ensamble
• Usamos los datos de la comparación de métodos de
ensamble, con αg = 0.05 y df = 12 grados de libertad
para el error. Se obtiene que q0.05(4, 12) = 4.20 Así que:
T0.05
CM E
2.46
q0.05 (4,12)
4.20
3.294
n
4
• Por lo tanto, cualquier par de promedios de los
tratamientos que difiera en valor absoluto por más de
3.294 implicaría que el par correspondiente de medias
poblacionales es significativamente diferente.
Diseño de experimentos - Hugo Alexer Pérez Vicente
Ejemplo: comparación de cuatro métodos
de ensamble
• La decisión sobre cada una de las seis hipótesis
listadas antes se obtiene al comparar las
correspondientes diferencias muestrales en valor
absoluto con el número T g . Por ejemplo:
A B 7.25 8.5 1.25 3.294
• Por tanto, la diferencia entre ambas medias no son
significativas.
Diseño de experimentos - Hugo Alexer Pérez Vicente
Ejemplo: comparación de cuatro métodos
de ensamble
𝑦𝐴. 𝑦𝐵.
7.25 8.5
𝑦𝐷.
10.5
𝑦𝐶.
12.75
Resultados del Método de Tukey
Diseño de experimentos - Hugo Alexer Pérez Vicente
Prueba de rango múltiple de Duncan
Duncan propuso el siguiente procedimiento para
probar H0: μi = μj contra H1: μi ≠ μj para todos los pares
posibles de medias:
1. Los k promedio de los tratamientos se arreglan en orden
ascendente
2. El error estándar de cada promedio se determina como:
S yi
CM E
,
nh
donde
nh
k
k
i 1
(1 / ni )
Si el diseño es balanceado, n1 = n2 =…= nk = n, entonces nh
= n.
Diseño de experimentos - Hugo Alexer Pérez Vicente
Prueba de rango múltiple de Duncan
3. Los valores de rα(p, df), para p = 2, 3, …, a, donde α es el nivel
de significación, y df es el número de grados de libertad del
error
4. Luego obtenemos un conjunto de a – 1 rangos mínimos de
significación calculando:
R p r ( p, df ) S yi
Diseño de experimentos - Hugo Alexer Pérez Vicente
para p 2, 3, ..., k
Prueba de rango múltiple de Duncan
5. Se prueban todas las diferencias observadas entre las
medias, empezando con la más grande contra la menor, la
cual se compara con el rango mínimo de significación Rk.
Después, se calcula la diferencia de la mayor y la segunda
menor y se compara con Rk –1. Este proceso se continúa hasta
que todas las medias se han comparado con la media mayor.
Después se calcula la diferencia de la segunda media mayor y
la menor y se compara con Rk –1. Este proceso se continúa
hasta que todos los k(k – 1)/2 pares de medias posibles se
han comparado. Si alguna diferencia es mayor que su rango
de significación correspondiente, se concluye que ese par de
medias es significativamente diferente.
Diseño de experimentos - Hugo Alexer Pérez Vicente
Tabla de rangos para la prueba
Duncan
Diseño de experimentos - Hugo Alexer Pérez Vicente
Prueba de rango múltiple de Duncan
• En la prueba de Duncan, a medida que el número de
pares de medias aumenta, se requiere una diferencia
observada más grande para detectar pares de
medias significativamente diferentes. El nivel de
significación global de la prueba es 1 – (1 – α)a –1,
donde α es el nivel de significación para dos medias
adyacentes.
Diseño de experimentos - Hugo Alexer Pérez Vicente
Prueba de rango múltiple de Duncan
• El índice de error de reportar al menos una
diferencia significativa incorrecta entre medias que
están p pasos aparte es 1 – (1 – α)p – 1.
• Por ejemplo, si α = 0.05, entonces 1 – (1 – 0.05)¹ =
0.05 es el nivel de significación para comparar
cualquier par de medias adyacentes. 1 – (1 – 0.05)² =
0.0975 es el nivel de significación para medias que
están un paso aparte y así sucesivamente.
Diseño de experimentos - Hugo Alexer Pérez Vicente
Ejemplo: comparación de cuatro
métodos de ensamble
Continuando con el ejemplo anterior con α = 0.05 y
f = 12 grados de libertad para el cuadrado medio del
error.
1) Los promedios de los tratamientos en orden
ascendente son:
ȳA. = 7.25, ȳB. = 8.5, ȳD. = 10.5, ȳC. = 12.75
2) El error estándar de cada promedio es
Sȳ. = (2.46/4)½ = 0.784
Diseño de experimentos - Hugo Alexer Pérez Vicente
Ejemplo: comparación de cuatro
métodos de ensamble
3) De la tabla de rangos se obtienen los valores de
r0.05(p, 12), p = 2, 3, 4
r0.05 (2,12) =
r0.05 (3,12) =
r0.05 (4,12) =
3.081
3.225
3.312
4) Los rangos mínimos de significación quedan como:
R2 r0.05 ( 2, 12) S yi (3.081)(0.784) 2.416
R3 r0.05 (3, 12) S yi (3.225)(0.784) 2.529
R4 r0.05 ( 4, 12) S yi (3.312)(0.784) 2.597
Diseño de experimentos - Hugo Alexer Pérez Vicente
Ejemplo: comparación de cuatro
métodos de ensamble
5) Los resultados de las comparaciones serían:
Comparación
Diferencia
RSM
Resultado
C vs A
5.50
R4
2.59733451
Significativa
C vs B
4.25
R3
2.52910743
Significativa
C vs D
2.25
R2
2.41617984
No significativa
D vs A
3.25
R3
2.52910743
Significativa
D vs B
2.00
R2
2.41617984
No significativa
B vs A
1.25
R2
2.41617984
No significativa
Veamos una gráfica de resultados:
El nivel de significación global de la prueba es
1 – (1 – 0.05)4–1 = 0.142
Diseño de experimentos - Hugo Alexer Pérez Vicente
Método Hsu
• El método Hsu es usado después de realizar el
ANOVA y está diseñado para identificar cuál nivel de
que factor es el mejor, e identificar a aquellos que
están significativamente lejos de ése nivel.
Diseño de experimentos - Hugo Alexer Pérez Vicente
Método Hsu
• Puedes definir “el mejor” tanto como a la media más
alta y a las más pequeña, en dependencia del interés
para el experimento.
Diseño de experimentos - Hugo Alexer Pérez Vicente
Método Hsu
• El método HSU crea un intervalo de confianza para la
diferencia entre las medias de cada tratamiento y el
valor considerado como el mejor.
• Si el intervalo tiene cero como punto final hay una
diferencia estadísticamente significativa entre las
medias correspondientes. En caso contrario, no hay
diferencia estadísticamente significativa.
Diseño de experimentos - Hugo Alexer Pérez Vicente
Método Hsu
Específicamente:
Mayor es mejor
Menor es mejor
Intervalo de confianza contiene
el cero
No hay diferencia
No hay diferencia
Intervalo de confianza por
completo por encima de cero
Significativamente mejor
Significativamente peor
Intervalo de confianza en su
totalidad por debajo de cero
Significativamente peor
Significativamente mejor
Diseño de experimentos - Hugo Alexer Pérez Vicente
Ejemplo: comparación de cuatro
métodos de ensamble
Continuando con el ejemplo anterior y suponiendo que el menor tiempo
de ensamble será considerado como el mejor método, los resultados con
ayuda de Minitab 17, son:
Interpretando los intervalos de confianza y con ayuda de la tabla anterior
se puede decir que estadísticamente los peores métodos son D y A y, en
consecuencia, estadísticamente no existe un método mejor.
Diseño de experimentos - Hugo Alexer Pérez Vicente
Características y ventajas de algunos
métodos de comparaciones múltiples
Datos
Comparación Comparación
Fortaleza
normales
con un control por pares
La prueba más poderosa cuando se
Tukey
Sí
No
Sí
ejecutan comparaciones por pares
La prueba más poderosa cuando se
Dunnet
Sí
Sí
No
compara con un control
Procedimiento robusto, pero produce
Inecuación de
largos intervalos de confianza,
Sí
Bonferroni
Sí
usualmente conservador
Ligeramente mejor que el
Inecuación de
Sí
procedimiento de Bonferroni,
Sí
Sí
Sidák
usualmente conservador
La prueba más poderosa cuando no se
MCB de Hsu
Sí
tiene interés en las comparaciones por
No
Sí
pares.
Método
Diseño de experimentos - Hugo Alexer Pérez Vicente
Observaciones
• La elección del método de comparación depende de
la inferencia deseada. Es ineficiente usar el enfoque
de Tukey para todas las diferencias cuando se
dispone del método de Dunnett o de Hsu, ya que los
intervalos de confianza de Tukey son más anchos y
las pruebas de hipótesis menos potente para una
tasa de error de familia determinado.
• La elección entre Tukey y Fisher depende de si desea
especificar la familia o tasa de error individual.
Diseño de experimentos - Hugo Alexer Pérez Vicente
Observaciones
• El método Hsu sólo compara un subconjunto de
todas las posibles comparaciones por pares, a
diferencia del método de Tukey que hace todas las
comparaciones. Por lo tanto, el método Hsu va a
generar intervalos de confianza más estrictos y
pruebas más poderosas para cualquier tasa de error
especificado.
Diseño de experimentos - Hugo Alexer Pérez Vicente
Referencias
•
•
•
•
Gutiérrez, H. y de la Vara, R. (2012). Análisis y diseño de experimentos. Méxic: McGraw Hill.
Hsu, J. C. (1996). Multiple Comparisons: Theory and methods. EUA: Chapman and Hall/CRC.
Minitab 17 Statistical Software (2010). [Computer software]. State College, PA: Minitab, Inc.
(www.minitab.com)
Montgomery, D. (2007). Design and analysis of experiments. EUA: Limusa Wiley.
Diseño de experimentos - Hugo Alexer Pérez Vicente
© Copyright 2026