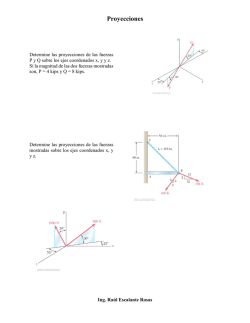
PROBLEMAS RESUELTOS
Prof. Egidio Verde PROBLEMAS RESUELTOS EQUILIBRIO DE CUERPOS RÍGIDOS 1. Una grúa móvil levanta una carga de madera que pesa W = 25 kN. El peso del mástil ABC y El peso combinado de la camioneta y el conductor son los indicados en la figura 1. Determine la reacción en las llantas a) delanteras, H, b) traseras, K. Figura 1 Se hace el diagrama de cuerpo libre. Se calcula el momento en K + ∑ Se calcula el momento en H + ∑ Prof. Egidio Verde 2. Cuando los automóviles C y D se detienen sobre un puente de dos carriles, las fuerzas que ejercen sus llantas sobre el puente son las indicadas en la figura. Determine las reacciones totales en A y B cuando a) a = 2.9 m, b) a = 8.1 m. Figura 2 Para a= 2,9 m + ∑ ; Ax=0 Se realiza la suma de fuerzas en X Se realiza el momento en B para hallar Ay. ∑ + ( ( ) ( ) ) Se realiza la suma de fuerzas en y para hallar By. +∑ Para a= 8,1 m + ∑ ( ( ) ) ( ) Prof. Egidio Verde + ∑ 3. Se aplican tres cargas, como indica la figura, sobre una viga ligera sostenida mediante cables unidos en B y D. Si se ignora el peso de la viga, determine el rango de valores de Q para los cuales ninguno de los cables pierde tensión cuando P = 0. Figura 3 7,5 kN Q P C A E B 0,5m D 0,75m 1,5m 0,75m Si P=0 y Q no es suficiente para mantener equilibrio la carga de 7,5 kN destensa el cable D. Para que Q tenga un valor mínimo TD =0. Se busca el momento en B. ∑ + Para Q máximo sin pérdida de tensión del cable B, TB=0 + ∑ El valor de Q debe estar en el intervalo de 27,5 kN a 1 250 kN Prof. Egidio Verde 4. Cuatro cajas están colocadas sobre una plancha de madera de 28 lb que descansa en dos caballetes. Si las masas de las cajas B y D son, respectivamente, de 9 y 90 lb, determine el rango de valores para la masa de la caja A si la plancha de madera permanece en equilibrio cuando se retira la caja C. Figura 4 4,5 ft 4,8 ft 1,5 ft 1,8 ft A F G E 3 ft D C B 3 ft Este ejercicio es parecido al anterior. Se busca una carga mínima de la caja A para que al retirar la caja D se conserve el equilibrio. Recuerde que G es el centro de gravedad de la tabla de 28 lb. Para peso de A mínimo, E=0 + ∑ Para peso de A máximo, F=0 + ∑ El peso de la caja A para mantener el equilibrio debe estar entre 4,64lb y 531,20lb. Prof. Egidio Verde 5. Determine la fuerza presente en cada elemento de la armadura Fink para techo que muestra la figura. Establezca si los elementos están en tensión o en compresión. Figura 5 2m 2m 2m 2m 4,2kN D 2,8kN 2,8kN 1m C 1,5m A 3m E B F 1,5m G Como primer paso se realiza el diagrama de cuerpo libre y se obtienen las reacciones del conjunto: 2m 2m 2m 2m 4,2kN D 2,8kN 2,8kN 1m C 1,5m A FAx FAy F 1,5m 3m E B G FGy ∑ + ∑ . Por simetría FGy=FAy Por la misma simetría se concluye que: FAB=FEG; FAC=FFG; FBC=FFE; FBD=FDE; FCD=FFD. Prof. Egidio Verde NODO A: FAB 4 3 FAC 2 5 A 4,9kN ∑ ∑ ; √ √ a tensión a Compresión NODO B: FBD 2,8kN 3 4 B 17,5kN 1 FBC 1 ( ∑ ) ( ∑ ) √ √ a compresión a compresión NODO C: FCD 2,26kN 1 4 1 15,8kN 3 2 5 C FCF Prof. Egidio Verde ∑ √ ( ) √ a tensión ∑ √ ( ) √ a tensión 6. Si WA = 25 Ib y ϴ = 30°, determine a) el valor mínimo de VB para que el sistema esté en equilibrio, b) el valor máximo de WB para que el sistema esté en equilibrio. µs=0,3 5 µk=0,2 Se realiza el diagrama de cuerpo libre de la caja B. ∑ ∑ Pero Sustituyendo F en la ecuación: ( ) Sería el valor mínimo si la caja B se desplaza hacia arriba. ∑ ( ) Sería el valor máximo si la caja se desplaza hacia abajo. Prof. Egidio Verde 7. La ménsula móvil que se muestra en la figura puede colocarse a cualquier altura a lo largo del tubo de 3 in. de diámetro. Si el coeficiente de fricción estática entre el tubo y la ménsula es de 0.25, determine la distancia mínima x a la cual se puede soportar la carga W, sin tomar en cuenta el peso de la ménsula ∑ ∑ Como NB es igual a NA ∑ ( ) + ( ) ( ) ( ) ( ( ) Si se divide todos los términos entre W y resolver la ecuación para x ) Prof. Egidio Verde PROBLEMAS PROPUESTOS 1. Determine la fuerza presente en cada elemento de la armadura que muestra la figura. Establezca si los elementos se encuentran en tensión o en compresión. Respuesta: FAC=8,20kips a tensión FBD=8 kips a compresión FCD= 1,34 kips a tensión FDG 9,43 kips a tensión FEG= 0,85 kips a tensión FFG= 6 kips a compresión FAB=8 kips a compresión FBC=0,6 kips a compresión FCE= 9,2 kips a compresión FDE= 0,3 kips a compresión FEF=10 kips a compresión FFH= 6 kips a compresión 2. Los elementos diagonales del panel central de la armadura mostrada en la figura son muy ligeros y solo pueden actuar en tensión; estos elementos se conocen como contravientos. Determine la fuerza presente en los elementos BD y CE y en el contraviento que actúa cuando P = 12 kN. Respuesta: Ay =10,7 kN FBD= 15,3 kN a compres. FCD= 2,42 kN a tensión FCE= 13,3 kN a tensión 3. Si el coeficiente de fricción estática entre el bloque de 30 Ib y el plano inclinado que se muestran en la figura es µS= 0.25, determine a) el valor mínimo de P necesario para mantener al bloque en equilibrio, b) el valor correspondiente de β. Prof. Egidio Verde Respuesta: Pmín= 21,6 lb β= 46° Un cajón de embalaje de 40 kg de masa debe ser recorrido sobre el piso hacia la izquierda sin ladearse. Si el coeficiente de fricción estática entre el cajón y el piso es de 0.35, determine a) el valor máximo permisible de α, b) la magnitud correspondiente de la fuerza P. Respuesta: α= 58° P= 166,4 N
© Copyright 2026