1. No category

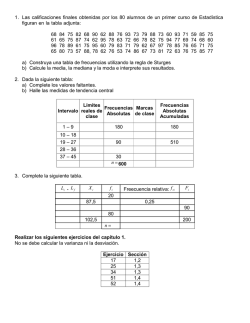
PROCESO: GESTIÓN DE FORMACIÓN
Procedimiento:
PLANIFICACIÓN Y PRESTACIÓN DEL SERVICIO
AREA: Matemáticas ASIGNATURA: Matemáticas - Estadística
GRADO: 10mo
PROFESOR: LEONARDO JAVIER RESTREPO VALENCIA
Código: PGF-03-R05
Fecha: Julio – Septiembre
Periodo: 3er
Guía No.1 Semana No.1 y 2 Es10300
Ámbitos conceptuales
Proyecto área Matemáticas: “Disfruta tu universo matemático”
Tercer periodo
¿Cómo utilizo la comunicación y comprensión de una situación para plantear soluciones frente a
problemáticas que afectan mi entorno de interacción?
Temas: Interpretación de gráficos estadísticos.
Eje derivado: ¿Cómo soluciono los problemas de interacción que se presentan en mi entorno para
favorecer mi crecimiento personal y social?
Competencia: Es1003
1. Observa, explica y presenta ejemplos de situaciones reales que conllevan a la solución de
problemas.
Indicadores de desempeño:
 Recorta gráficos estadísticos de prensa y revistas, trayéndolos para las clases.
 Interpreta y hace conclusiones de los gráficos estadísticos.
 Expone los gráficos estadísticos, compartiendo las conclusiones de cada uno.
I. CONTENIDOS BÁSICO:
TERCER PERIODO - Guía No.1 – Semana 1 y 2
Responda las siguientes preguntas en forma concreta. Las preguntas y respuestas deben quedar
consignadas en el cuaderno de matemáticas. Estas preguntas son complementarias. De cada tema
el estudiante es responsable en realizar ejercicios adicionales para comprender mejor la materia.
TEMA: ESTADISTICA
1. Historia de la estadística:
Su origen empieza posiblemente en la isla de Cerdeña, donde existen monumentos prehistóricos
pertenecientes a los Nuragas, las primeros habitantes de la isla; estos monumentos constan de
bloques de basalto superpuestos sin mortero y en cuyas paredes de encontraban grabados toscos
signos que han sido interpretados con mucha verosimilidad como muescas que servían para llevar
la cuenta del ganado y la caza.
Hacia el año 3.000 a.C. los babilonios usaban ya pequeñas tablillas de arcilla para recopilar datos
en tablas sobre la producción agrícola y los géneros vendidos o cambiados mediante trueque.
Los egipcios ya analizaban los datos de la población y la renta del país mucho antes de construir la
pirámides. En los antiguos monumentos egipcios se encontraron interesantes documentos en que
demuestran la sabia organización y administración de este pueblo; ellos llevaban cuenta de los
movimientos poblacionales y continuamente hacían censos. Tal era su dedicación por llevar
Pag.1/7
3P
Guía No.1
Semana 1 y 2
www.matematicaaplicada.co
leojavres.prenli.co
www.enmicoleaprendo.info
www.feyalegrialapaz.siacolegio.info
www.feyalegrialapaz.edu.co
[email protected]
[email protected]
siempre una relación de todo que hasta tenían a la diosa Safnkit, diosa de los libros y las cuentas.
Todo esto era hecho bajo la dirección del Faraón y fue a partir del año 3050 a.C.
En la Biblia observamos en uno de los libros del Pentateuco, bajo el nombre de Números, el censo
que realizó Moisés después de la salida de Egipto. Textualmente dice: "Censo de las tribus: El día
primero del segundo año después de la salida de Egipto, habló Yavpe a Moisés en el desierto de
Sinaí en el tabernáculo de la reunión, diciendo: "Haz un censo general de toda la asamblea de los
hijos de Israel, por familias y por linajes, describiendo por cabezas los nombres de todos los
varones aptos para el servicio de armas en Israel. En el llibro bíblico Crónicas describe el bienestar
material de las diversas tribus judías.
En China existían los censos chinos ordenados por el emperador Tao hacia el año 2.200 a.C.
Posteriormente, hacia el año 500 a.C., se realizaron censos en Roma para conocer la población
existente en aquel momento. Se erigió la figura del censor, cuya misión consistía en controlar el
número de habitantes y su distribución por los distintos territorios.
En la Edad Media, en el año 762, Carlomagno ordenó la creación de un registro de todas sus
propiedades, así como de los bienes de la iglesia.
Después de la conquista normanda de Inglaterra en 1.066, el rey Guillermo I, el Conquistador,
elaboró un catastro que puede considerarse el primero de Europa.
Los Reyes Católicos ordenaron a Alonso de Quintanilla en 1.482 el recuento de fuegos (hogares) de
las provincias de Castilla.
2. Estadística:
La estadística es la parte de las matemáticas que se ocupa de los métodos para recoger, organizar,
resumir y analizar datos, así como para sacar conclusiones válidas y tomar decisiones razonables
basadas en tal análisis.
En la antigüedad los egipcios hacían censos de las personas y de los bienes inmuebles que
permitían conocer la distribución de las propiedades para volver a restituirlos después de la
inundación anual que provoca el río Nilo. En la biblia hay referencias a censos del pueblo judío. Los
griegos y los romanos hacían censos de personas y de propiedades.
Sus orígenes se remontan a 1662, cuando John Graunt presento un estudio social de cifras sobre
nacimientos y defunciones ocurridos en Londres entre 1604 y 1661.
Un economista y profesor universitario llamado Gottfried Achenwall (prusiano, 1719-1772) fue
quien forjó la palabra "estadística" con el significado de "ciencia de las cosas que pertenecen al
Estado". Achenwall dijo que "la política enseña cómo deben ser los Estados, la Estadística explica
cómo son realmente".
Dentro del campo de la estadística pueden estudiarse características de la sociedad, de las
personas, de los animales, de las plantas, de determinados productos o de cualquier objeto de
interés humano en general, bien lejos del concepto de las "cosas que pertenecen al Estado".
Es la ciencia encargada d la recolección, organización, análisis, interpretación y representación de
datos para, a partir de esto, sacar conclusiones y establecer previsiones.
3. Datos:
Son cantidades o medidas obtenidas de observaciones, comparaciones u aplicaciones de
encuestas. Pueden ser presentados como enunciados o como conjuntos de números, en tablas y
en gráficos. Se llaman procesamiento de datos a la organización y transformación de los mismos
hasta convertirlos en información. La información es el resultado del procesamiento de datos.
Pag.2/7
3P
Guía No.1
Semana 1 y 2
www.matematicaaplicada.co
leojavres.prenli.co
www.enmicoleaprendo.info
www.feyalegrialapaz.siacolegio.info
www.feyalegrialapaz.edu.co
[email protected]
[email protected]
Se llama dato estadístico a cada uno de los datos numnericos que sirven pasra hacer un estudio
estadístico.
Variable: Característica que puede presentar distintas modalidades. Por ejemplo, la variable
"género" solo presenta dos modalidades (mujer y hombre), y la variable "depresión" presenta un
número infinito de modalidades, (las magnitudes de gravedad con que puede afectar a las
personas).
Constante: Característica que presenta una sola modalidad
Datos: Son números que representan las modalidades de las variables. Por ejemplo, el 1 puede
representar la modalidad "Mujer", el 6.3 representa una de las magnitudes que podemos registrar
en la variable "grado de conocimiento de las técnicas estadísticas". Los datos pueden ser
clasificados según diferentes criterios, uno de los cuales se basa en las modalidades que
presentan: Se dirá que son datos dicotómicos los que provienen de variables que solo admiten dos
modalidades (por ejemplo la variable "género"), son datos dicotomizados aquellos que presentan
dos categorías pero provienen de variables con más de dos modalidades (por ejemplo datos con
valores 1 y 0 que representan aprobado y suspenso).
4. Población:
Población: Conjunto completo de individuos, objetos o fenómenos.
Muestra: Subconjunto (parte o fragmento) de la población.
Muestreo: Procedimiento de selección de las muestras.
Representatividad de la muestra: Las muestras son partes de la población, pero no son la
población completa. Por ello, sus características no suelen coincidir con las de la población. La
medida en que la muestra aproxima a la población se denomina representatividad.
Sesgo: Es la discrepancia entre las características de las muestras y las de la población.
Análisis univariado: Analiza una sola variable. Es más sencillo, más fácil de entender y de
interpretar. En cambio, la sencillez puede comportar una simplificación excesiva de la realidad. Por
ejemplo, un investigador quiere hacer un estudio del rendimiento académico universitario, para lo
cual recoge las calificaciones de los estudiantes en los exámenes finales. Es claro que una
caracterización del rendimiento basada exclusivamente en las calificaciones académicas es
incompleta y que, si queremos conocer los condicionantes del rendimiento deberíamos incluir
otros variables (como actitud, preparación previa, etc.) y estudiar cómo interactúan para dar
cuenta de las variables de interés.
Análisis multivariado: Analiza los datos teniendo en cuenta las relaciones entre las variables. Es
más complejo y de comprensión más dificultosa, pero proporciona información más completa del
objeto estudiado.
Una variable estadística es cada una de las características o cualidades que poseen los individuos
de una población.
Tipos de variable estadísticas
Variable
cualitativa:
Las variables
cualitativas se
refieren
a características
o
cualidades que no pueden ser medidas con números. Podemos distinguir dos tipos:
Variable cualitativa nominal: Una variable cualitativa nominal presenta modalidades no
numéricas que no admiten un criterio de orden. (El estado civil, con las siguientes
modalidades: soltero, casado, separado, divorciado y viudo.)
Variable cualitativa ordinal o variable cuasicuantitativa:
Una variable cualitativa ordinal
presente modalidades no númericas, en las que existe un orden. (La nota en un
Pag.3/7
3P
Guía No.1
Semana 1 y 2
www.matematicaaplicada.co
leojavres.prenli.co
www.enmicoleaprendo.info
www.feyalegrialapaz.siacolegio.info
www.feyalegrialapaz.edu.co
[email protected]
[email protected]
examen: suspenso, aprobado, notable, sobresaliente. Puesto conseguido en una prueba
deportiva: 1º, 2º, 3º, ... Medallas de una prueba deportiva: oro, plata, bronce)
Variable cuantitativa: Una variable cuantitativa es la que se expresa mediante un número, por
tanto se pueden realizar operaciones aritméticas con ella. Podemos distinguir dos tipos:
Variable discreta
Una variable discreta es aquella que toma valores aislados, es decir no admite valores
intermedios entre dos valores específicos. (El número de hermanos de 5 amigos: 2, 1, 0, 1,
3.)
Variable continua: Una variable continua es aquella que puede tomar valores
comprendidos entre dos números. (La altura de los 5 amigos: 1.73, 1.82, 1.77, 1.69, 1.75.
En la práctica medimos la altura con dos decimales, pero también se podría dar con tres
decimales.)
Variable de intervalo: Este tipo de medición tiene las características de la medición ordinal,
y además separa las unidades de medición por intervalos equivalentes. Ejemplo: Los
tiempo de llegada a la carrera ciclista (expresados como minutos) están definidos de forma
que la diferencia entre 5 y 4 (60 segundos) es la misma que la que va del 2 al 3, o del 7 al 8
(60 segundos).
Variable de razón: Este tipo de medición tiene las características de la medición de
intervalo, y además tiene la propiedad de que el 0 es real. Ejemplo: Número de veces que
un individuo sonríe. (El 0 indica ninguna sonrisa).
5. Tablas de frecuencias – NO AGRUPADAS:
Distribución de frecuencias: La distribución de frecuencias o tabla de frecuencias es
una ordenación en forma de tabla de los datos estadísticos, asignando a cada dato su frecuencia
correspondiente.
Tipos de frecuencias (absoluta, relativa, acumulada)
Frecuencia absoluta: La frecuencia absoluta es el número de veces que aparece un
determinado valor en un estudio estadístico. Se representa por fi.
La suma de las frecuencias absolutas es igual al número total de datos, que se representa por N.
Para indicar resumidamente estas sumas se utiliza la letra griega Σ (sigma
mayúscula) que se lee suma o sumatoria.
Frecuencia relativa: La frecuencia relativa es el cociente entre la frecuencia
absoluta de un determinado valor y el número total de datos. Se puede expresar en
tantos por ciento y se representa por ni.
La suma de las frecuencias relativas es igual a 1.
Frecuencia absoluta acumulada: La frecuencia acumulada es la suma de las frecuencias
absolutas de todos los valores inferiores o iguales al valor considerado. Se representa por Fi.
Frecuencia relativa acumulada.
La frecuencia relativa acumulada es el cociente entre la frecuencia acumulada de un
determinado valor y el número total de datos. Se puede expresar en tantos por ciento.
Durante el mes de julio, en una ciudad se han registrado las siguientes temperaturas máximas:
32, 31, 28, 29, 33, 32, 31, 30, 31, 31, 27, 28, 29, 30, 32, 31, 31, 30, 30, 29, 29, 30, 30, 31, 30, 31, 34,
33, 33, 29, 29.
Pag.4/7
3P
Guía No.1
Semana 1 y 2
www.matematicaaplicada.co
leojavres.prenli.co
www.enmicoleaprendo.info
www.feyalegrialapaz.siacolegio.info
www.feyalegrialapaz.edu.co
[email protected]
[email protected]
En la primera columna de la tabla colocamos la variable ordenada de menor a mayor, en la
segunda hacemos el recuento y en la tercera anotamos la frecuencia absoluta.
6. Tablas de frecuencias – AGRUPADAS:
La distribución de frecuencias agrupadas o tabla con datos agrupados se emplea si las variables
toman un número grande de valores o la variable es continua.
Se agrupan los valores en intervalos que tengan la misma amplitud denominados clases. A cada
clase se le asigna su frecuencia correspondiente.
Límites de la clase: Cada clase está delimitada por el límite inferior de la clase y el límite superior
de la clase.
Amplitud de la clase: La amplitud de la clase es la diferencia entre el límite superior e inferior de
la clase.
Marca de clase: La marca de clase es el punto medio de cada intervalo y es el valor que representa
a todo el intervalo para el cálculo de algunos parámetros.
Construcción de una tabla de datos agrupados
3, 15, 24, 28, 33, 35, 38, 42, 43, 38, 36, 34, 29, 25, 17, 7, 34, 36, 39, 44, 31, 26, 20, 11, 13, 22, 27,
47, 39, 37, 34, 32, 35, 28, 38, 41, 48, 15, 32, 13.
1º Se localizan los valores menor y mayor de la distribución. En este caso son 3 y 48.
2º Se restan y se busca un número entero un poco mayor que la diferencia y que sea divisible por
el número de intervalos queramos establecer.
Es conveniente que el número de intervalos oscile entre 6 y 15.
En este caso, 48 - 3 = 45, incrementamos el número hasta 50 : 5 = 10 intervalos.
Se forman los intervalos teniendo presente que el límite inferior de una clase pertenece al
intervalo, pero el límite superior no pertenece intervalo, se cuenta en el siguiente intervalo.
Pag.5/7
3P
Guía No.1
Semana 1 y 2
www.matematicaaplicada.co
leojavres.prenli.co
www.enmicoleaprendo.info
www.feyalegrialapaz.siacolegio.info
www.feyalegrialapaz.edu.co
[email protected]
[email protected]
Taller de ejercicios No.1
1 Indica que variables son cualitativas y cuales cuantitativas :
1 Comida Favorita.
2 Profesión que te gusta.
3 Número de goles marcados por tu equipo favorito en la última
temporada.
4 Número de alumnos de tu Instituto.
5 El color de los ojos de tus compañer os de clase.
6 Coeficiente intelectu al de tus comp añeros de clase.
2 De las siguientes variables indica cu áles son discretas y cuales continuas.
1 Número de ac ciones vendidas cada día en la Bolsa.
2 Temperatur as registradas c ada hora en un observa torio.
3 Período de dur ación de un au tomóvil.
4 El diámetro de las ruedas de varios coches.
5 Número de hijos de 50 f amilias.
6 Censo anual de los españoles.
3 Clasificar las siguientes variables en cualitativas y cuantitativas discretas o
continuas.
1 La nacionalidad de una pe rsona.
2 Número de litros de agua contenido s en un depósito.
3 Número de libros en un est ante de librería.
Pag.6/7
3P
Guía No.1
Semana 1 y 2
www.matematicaaplicada.co
leojavres.prenli.co
www.enmicoleaprendo.info
www.feyalegrialapaz.siacolegio.info
www.feyalegrialapaz.edu.co
[email protected]
[email protected]
4 Suma de pun tos tenidos en el lanza miento de un par d e dados.
5 La profesión de una persona.
6 El área d e las distintas baldosas de un edificio.
4 Las puntuaciones obtenidas por un grupo en una prueba han sido:
15, 20, 15, 18, 22, 13, 13, 16, 15, 19, 18, 15, 16, 20, 16, 15, 18, 16, 14, 13.
Construir la tabla de distribución de frecuencias .
5 El número de estrellas de los hoteles de una ciudad viene dado por la
siguiente serie:
3, 3, 4, 3, 4, 3, 1, 3, 4, 3, 3, 3, 2, 1, 3, 3, 3, 2, 3, 2, 2, 3, 3, 3, 2, 2, 2, 2, 2, 3, 2, 1,
1, 1, 2, 2, 4, 1.
Construir la tabl a de distribución de frecuencia s .
6 Las calificaciones de 50 alumnos en Matemá ticas han sido las siguientes:
5, 2, 4, 9, 7, 4, 5, 6, 5, 7, 7, 5, 5, 2, 10, 5, 6, 5, 4, 5, 8, 8, 4, 0, 8, 4, 8, 6, 6, 3, 6,
7, 6, 6, 7, 6, 7 , 3, 5, 6, 9, 6, 1, 4, 6, 3, 5, 5, 6, 7.
Construir la tabla de distribución de frecuencias .
7 Los pesos de los 65 empleados de una fábrica vienen ag rupados y dados por la
siguiente tabla:
Peso
fi
[50, 60)
8
[60, 70)
10
[70, 80)
16
[80,90)
14
[90, 100)
10
[100, 110)
5
[110, 120)
2
1 Construir la tabla de frecuencias .
Bibliografía:
 Matemáticas 9 Incluye Proyecto Siglo XXI. Editorial Santillana, 1999. Ana Julia Mora
Torres, Claudia Galindo Urquijo.
 Baldor. Edime Organización Grafica, S. A., 1984. Dr. Aurelio Baldor
2015: “¡Atrévete a mirar! Busca tu estrella”
Lema I.E Fe y Alegría La Paz: “Construir vida con sentido”
“Enseñar es recordarles a los demás que saben tanto como tú.
Somos todos aprendices, ejecutores y maestros.“
Pag.7/7
3P
Guía No.1
Semana 1 y 2
www.matematicaaplicada.co
leojavres.prenli.co
www.enmicoleaprendo.info
www.feyalegrialapaz.siacolegio.info
www.feyalegrialapaz.edu.co
[email protected]
[email protected]