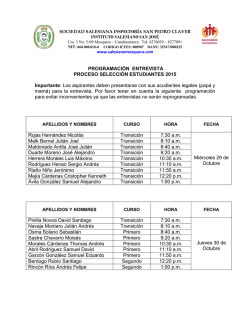
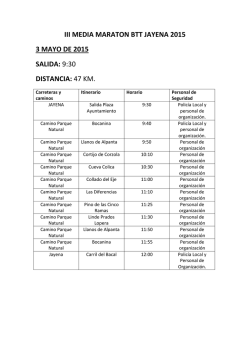
Título de la presentación que se envía a TIBETS
MÓDULO II. INGENIERÍA CRIPTOGRÁFICA Curso de Seguridad de la Información 2013 Ing. Felipe Andrés Corredor. Esp. M.Sc Tel: (8)6616800 Ext. 124 Fax: (8)6616800 Ext. 141 [email protected] - [email protected] Facultad de Ciencias Básicas e Ingeniería. Universidad de los Llanos. CRIPTOGRAFIA (Del gr. κρσπτός, oculto, y -grafía). Arte de escribir con clave secreta o de un modo enigmático. Real Academia Española © Todos los derechos reservados -> La seguridad de un sistema criptográfico reside en la robustez del algoritmo y en la adecuada custodia de la clave para que sólo sea conocida por las personas autorizadas para ello. Facultad de Ciencias Básicas e Ingeniería. Universidad de los Llanos. Felipe Andrés Corredor. Msc. [email protected] INGENIERÍA CRIPTOGRÁFICA Conceptos Criptografía (Cryptography) Criptoanálisis (cryptoanalysis) Criptología Mensaje (plaintext, cleartext) Cifrado, cifrar (encipherment, encipher) Algoritmo criptográfico Criptosistema Encriptado, encriptar (encryption, encrypt) Facultad de Ciencias Básicas e Ingeniería. Universidad de los Llanos. Felipe Andrés Corredor. Msc. [email protected] INGENIERIA CRIPTOGRÁFICA Conceptos . Esquema genérico de un sistema criptográfico Facultad de Ciencias Básicas e Ingeniería. Universidad de los Llanos. Felipe Andrés Corredor. Msc. [email protected] SECRETO PERFECTO Dado un criptograma, el sistema sería vulnerable si un criptoanalista es capaz de averiguar el mensaje en claro, o la clave. Shannon se apoyó en el hecho de que la recepción de un criptograma aporta al criptoanalista ciertas informaciones probabilísticas acerca del mensaje en claro del que procede. Un criptosistema es considerado de secreto perfecto si el conocimiento del mensaje cifrado c no aporta al criptoanalista información alguna acerca del mensaje en claro m. Ej. Dado un mi de 34 símbolos “El parcial de Telecom 3 esta fácil”, se cifra con un algoritmo y una clave que genera un Cj del mismo tamaño que mi . Si Cj fuese de secreto perfecto, el haberlo recibido sitúa al criptoanalista en tal situación que la probabilidad de que mi sea exactamente igual que la de cualquier otra combinación de 34 símbolos. Facultad de Ciencias Básicas e Ingeniería. Universidad de los Llanos. Felipe Andrés Corredor. Msc. [email protected] INGENIERÍA CRIPTOGRÁFICA La Criptografía ha estado ligada al mundo de la guerra y de la diplomacia. Criptografía clásica “las claves y el algoritmo son secretos. “ Criptografía moderna Asienta sus bases teóricas en siglo XIX, pero su verdadera aparición hay que situarla en la década de los setenta del pasado siglo, cuando aparecen algoritmos disponibles para usos civiles implementables mediante un programa de computador. “El algoritmo de cifrado debe ser de conocimiento público, y sólo la clave debe permanecer secreta. La seguridad del sistema reside en la robustez del algoritmo y en la adecuada custodia de la clave ” Facultad de Ciencias Básicas e Ingeniería. Universidad de los Llanos. Felipe Andrés Corredor. Msc. [email protected] TEORIA DE LA INFORMACIÓN A Mathematical Theory of Communication 1948 Claude Shannon Communication Theory of Secrecy Systems 1949 Claude Shannon Disquisitiones Arithmeticae. 1801 Carl Friedrich Gauss Logaritmo Discreto . Facultad de Ciencias Básicas e Ingeniería. Universidad de los Llanos. Felipe Andrés Corredor. Msc. [email protected] TEORIA DE LA INFORMACIÓN Cantidad de inf. de un Estado mi INFORMACIÓN E INCERTIDUMBRE Antes del suceso, la probabilidad de su ocurrencia, es una medida de la incertidumbre sobre la posibilidad de que este ocurra La entropía representa el número medio de bits necesarios para representar todos sus estados mediante dígitos binarios. Si los n estados posibles equiprobables, entonces la entropía: son bc → bc -l = Calculadora GNU. Shift+ctrl+u : 5e Facultad de Ciencias Básicas e Ingeniería. Universidad de los Llanos. Felipe Andrés Corredor. Msc. [email protected] CONJUNTOS FINITOS Operar sobre un conjunto finito de elementos con los que puedan realizarse las operaciones de suma y multiplicación, de tal modo que el resultado de cualquier operación fuese un elemento perteneciente a ese mismo conjunto finito de números. La relación de congruencia módulo n divide el conjunto infinito de números enteros en n clases de equivalencia, cada una de las cuales está «representada» por uno de los restos. La reducción módulo n supone un homomorfismo del anillo de los enteros al anillo de los enteros módulo n, constituido por un número finito de elementos. Facultad de Ciencias Básicas e Ingeniería. Universidad de los Llanos. Felipe Andrés Corredor. Msc. [email protected] ARITMÉTICA MODULAR El conjunto de números que forman los restos dentro de un cuerpo Zn será muy importante en criptografía. a y b se encuentran en la misma "clase de congruencia" módulo n, si ambos dejan el mismo resto al dividirlo por n, o, equivalentemente, si a − b es un múltiplo de n. Facultad de Ciencias Básicas e Ingeniería. Universidad de los Llanos. Felipe Andrés Corredor. Msc. [email protected] Ej. Aritmética Modular El conjunto de números que forman los restos dentro de un campo Z15. a y b se encuentran en la misma "clase de congruencia" módulo n, si ambos dejan el mismo resto al dividirlo por n, o, equivalentemente, si a − b es un múltiplo de n. Facultad de Ciencias Básicas e Ingeniería. Universidad de los Llanos. Felipe Andrés Corredor. Msc. [email protected] Calculo de Inversos (mod n) La función φ, indicadora de Euler. Si n es un número entero positivo, entonces φ(n) se define como el número de enteros positivos menores o iguales a n y primos relativos con n. Si p y q son primos y n=p*q, entonces Teorema de Euler Para todo par de enteros a, n tal que mcd(a, n) = 1, se cumple: Ej. Calcular Facultad de Ciencias Básicas e Ingeniería. Universidad de los Llanos. Felipe Andrés Corredor. Msc. [email protected] Tabla Teorema Eular Facultad de Ciencias Básicas e Ingeniería. Universidad de los Llanos. Felipe Andrés Corredor. Msc. [email protected] Logaritmos Discretos El problema de hallar y es irresoluble computacionalmente Diffie-Hellman / El Gamal Facultad de Ciencias Básicas e Ingeniería. Universidad de los Llanos. Felipe Andrés Corredor. Msc. [email protected] Criptografía Clásica Técnicas de sustitución: Los caracteres o letras del mensaje en claro se modifican o sustituyen por otros elementos o letras en la cifra. El criptograma tendrá entonces caracteres distintos a los que tenía el mensaje en claro. Técnicas de transposición: los caracteres o letras del mensaje en claro se redistribuyen sin modificarlos y según unas reglas, dentro del criptograma. El criptograma tendrá entonces los mismos caracteres del mensaje en claro pero con una distribución o localización diferente. Facultad de Ciencias Básicas e Ingeniería. Universidad de los Llanos. Felipe Andrés Corredor. Msc. [email protected] Criptografía Clásica Escítala Al desenrollar la cinta, las letras aparecerán desordenadas. La clave del sistema se encuentra en ... Facultad de Ciencias Básicas e Ingeniería. Universidad de los Llanos. Felipe Andrés Corredor. Msc. [email protected] Criptografía Clásica Polybios A B C D E A B C D E A F L Q V B G M R W C H N S X D IJ O T Y E K P U Z M1 = QUÉ BUENA IDEA C1 = DA DE AE AB DE AE CC AA BD AD AE EA 1 2 3 4 5 1 2 3 4 5 A F L Q V B G M R W C H N S X D IJ O T Y E K P U Z M2 = LA DEL GRIEGO C2 = 31 11 14 15 31 22 42 24 15 22 34 Facultad de Ciencias Básicas e Ingeniería. Universidad de los Llanos. Felipe Andrés Corredor. Msc. [email protected] Criptografía Clásica César SRYVCR Facultad de Ciencias Básicas e Ingeniería. Universidad de los Llanos. Felipe Andrés Corredor. Msc. [email protected] Criptografía Clásica Vigenère Sea K = CIFRA y el mensaje M = HOLA AMIGOS M = H O L A A M I G O S K = C I F R A C I F R A de un alfabeto: la C = J W P R A Ñ P L G Más S letra O se cifra de forma P != P Facultad de Ciencias Básicas e Ingeniería. Universidad de los Llanos. distinta. Felipe Andrés Corredor. Msc. [email protected] Criptografía Clásica Tabla de Vigenère A B C D E F G H I J K L M N Ñ O P Q R S T U V W X Y Z A B C D E F G H I J K L M N Ñ O P Q R S T U V W X Y Z A B C D E F G H I J K L M N Ñ O P Q R S T U V W X Y Z B C D E F G H I J K L M N Ñ O P Q R S T U V W X Y Z A C D E F G H I J K L M N Ñ O P Q R S T U V W X Y Z A B D E F G H I J K L M N Ñ O P Q R S T U V W X Y Z A B C E F G H I J K L M N Ñ O P Q R S T U V W X Y Z A B C D F G H I J K L M N Ñ O P Q R S T U V W X Y Z A B C D E G H I J K L M N Ñ O P Q R S T U V W X Y Z A B C D E F H I J K L M N Ñ O P Q R S T U V W X Y Z A B C D E F G I J K L M N Ñ O P Q R S T U V W X Y Z A B C D E F G H J K L M N Ñ O P Q R S T U V W X Y Z A B C D E F G H I K L M N Ñ O P Q R S T U V W X Y Z A B C D E F G H I J L M N Ñ O P Q R S T U V W X Y Z A B C D E F G H I J K M N Ñ O P Q R S T U V W X Y Z A B C D E F G H I J K L N Ñ O P Q R S T U V W X Y Z A B C D E F G H I J K L M Ñ O P Q R S T U V W X Y Z A B C D E F G H I J K L M N O P Q R S T U V W X Y Z A B C D E F G H I J K L M N Ñ P Q R S T U V W X Y Z A B C D E F G H I J K L M N Ñ O Q R S T U V W X Y Z A B C D E F G H I J K L M N Ñ O P R S T U V W X Y Z A B C D E F G H I J K L M N Ñ O P Q S T U V W X Y Z A B C D E F G H I J K L M N Ñ O P Q R T U V W X Y Z A B C D E F G H I J K L M N Ñ O P Q R S U V W X Y Z A B C D E F G H I J K L M N Ñ O P Q R S T V W X Y Z A B C D E F G H I J K L M N Ñ O P Q R S T U W X Y Z A B C D E F G H I J K L M N Ñ O P Q R S T U V X Y Z A B C D E F G H I J K L M N Ñ O P Q R S T U V W Y Z A B C D E F G H I J K L M N Ñ O P Q R S T U V W X Z A B C D E F G H I J K L M N Ñ O P Q R S T U V W X Y Facultad de Ciencias Básicas e Ingeniería. Universidad de los Llanos. Felipe Andrés Corredor. Msc. [email protected] Criptografía Clásica Vernam – Aprovecha la involución de XOR. Clave K Algoritmo Determinístico Clave K secuencia cifrante S MENSAJE M C Criptograma Facultad de Ciencias Básicas e Ingeniería. Universidad de los Llanos. S Algoritmo Determinístico M MENSAJE Felipe Andrés Corredor. Msc. [email protected] Criptografía Clásica Vernam – Código Baudot Código Binario 00000 00001 00010 00011 00100 00101 00110 00111 01000 01001 01010 01011 01100 01101 01110 01111 Carácter Código Binario Blanco E = A Espacio S I U < D R J N F C K 10000 10001 10010 10011 10100 10101 10110 10111 11000 11001 11010 11011 11100 11101 11110 11111 Facultad de Ciencias Básicas e Ingeniería. Universidad de los Llanos. Carácter T Z L W H Y P Q O B G M X V Felipe Andrés Corredor. Msc. [email protected] Criptografía Clásica Vernam – Código Baudot Usando el código Baudot se pide cifrar: M = BYTES K = VERNAM Solución: = = = = = C= Facultad de Ciencias Básicas e Ingeniería. Universidad de los Llanos. Felipe Andrés Corredor. Msc. [email protected] Criptografía Clásica Vernam – Código Baudot Usando el código Baudot se pide cifrar: M = BYTES K = VERNAM Solución: BV = 1100111110 = 00111 = U YE = 1010100001 = 10100 = H TR = 1000001010 = 11010 = G EN = 0000101100 = 01101 = F SA = 0010100011 = 00110 = I C = UHGFI Facultad de Ciencias Básicas e Ingeniería. Universidad de los Llanos. Felipe Andrés Corredor. Msc. [email protected] Clasificación de Frecuencias de Caracteres del Alfabeto Modulo 27 Facultad de Ciencias Básicas e Ingeniería. Universidad de los Llanos. Felipe Andrés Corredor. Msc. [email protected] Esteganografía Esteganografía “clásica”: * Se desconoce el canal * encubierto. Esteganografía moderna: El canal encubierto es Digital * Archivo de texto (inc. páginas web, código fuente, etc.) * Audio digital * Imágenes y vídeo digitales * Archivos ejecutables * Protocolos de comunicaciones Facultad de Ciencias Básicas e Ingeniería. Universidad de los Llanos. Felipe Andrés Corredor. Msc. [email protected] cat archivo.rar >> imagen.jpg “c://Archivos de programa/winrar/winrar.exe” x imagen.jpg /usr/local/bin/rar x /backup/datos.rar /misdatos Facultad de Ciencias Básicas e Ingeniería. Universidad de los Llanos. Felipe Andrés Corredor. Msc. [email protected] Facultad de Ciencias Básicas e Ingeniería. Universidad de los Llanos. Felipe Andrés Corredor. Msc. [email protected] Principios de Kerckhoffs JOURNAL DES SCIENCES MILITAIRES. Janvier 1883. 1. Si el sistema no es teóricamente irrompible, al menos debe serlo en la práctica. 2. La efectividad del sistema no debe depender de que su diseño permanezca en secreto. 3. La clave debe ser fácilmente memorizable de manera que no haya que recurrir a notas escritas. 4. Los criptogramas deberán dar resultados alfanuméricos. 5. El sistema debe ser operable por una única persona. 6. El sistema debe ser fácil de utilizar. Dr. Auguste Kerckhoffs http://www.petitcolas.net/fabien/kerckhoffs/ Facultad de Ciencias Básicas e Ingeniería. Universidad de los Llanos. Felipe Andrés Corredor. Msc. [email protected] Criptografía Simetrica La clave de cifrado y la usada para el descifrado son la misma Se apoyan en operaciones lógicas o algebraicas muy simples Imprescindibles para proporcionar servicios de confidencialidad en aplicaciones telematicas de alta velocidad. El número de claves necesarias para proporcionar confidencialidad en un entorno, donde participen un número considerable de entidades comunicantes, es elevado. La mayor vulnerabilidad de estos criptosistemas hace necesaria la renovacion periódica de las claves y hace impracticable una adecuada politica de distribución y renovación de claves. Facultad de Ciencias Básicas e Ingeniería. Universidad de los Llanos. Felipe Andrés Corredor. Msc. [email protected] Procesos de Cifrado Existen dos tipos básicos de cifradores, diferenciados en cuanto a como dividir el mensaje en claro para abordar la tarea de transformación. Procedimiento de cifrado en flujo. Procedimiento de cifrado en bloque. Facultad de Ciencias Básicas e Ingeniería. Universidad de los Llanos. Felipe Andrés Corredor. Msc. [email protected] Criptosistemas de Clave Secreta . . Esquema de la criptografía simétrica Facultad de Ciencias Básicas e Ingeniería. Universidad de los Llanos. Felipe Andrés Corredor. Msc. [email protected] Cifradores de Flujo Vernam -> . . Facultad de Ciencias Básicas e Ingeniería. Universidad de los Llanos. Felipe Andrés Corredor. Msc. [email protected] Implementación (pseudoaleatorios) en JAVA API colt -> http://acs.lbl.gov/~hoschek/colt/api/cern/jet/random/package-summary.html Beta Beta distribution; math definition and animated definition. Binomial Binomial distribution; See the math definition and animated definition. BreitWigner BreitWigner (aka Lorentz) distribution; See the math definition. Exponential Exponential Distribution (aka Negative Exponential Distribution); See the math definition animated definition. Gamma Gamma distribution; math definition, definition of gamma function and animated definition. Hyperbolic Hyperbolic distribution. HyperGeometric HyperGeometric distribution; See the math definition The hypergeometric distribution with parameters N, n and s is the probability distribution of the random variable X, whose value is the number of successes in a sample of n items from a population of size N that has s 'success' items and N - s 'failure' items. Logarithmic Logarithmic distribution. NegativeBinomial Negative Binomial distribution; See the math definition. Normal Normal (aka Gaussian) distribution; See the math definition and animated definition. Poisson Poisson distribution (quick); See the math definition and animated definition. StudentT StudentT distribution (aka T-distribution); See the math definition and animated definition. Uniform Uniform distribution; Math definition and animated definition. VonMises Von Mises distribution. Zeta Zeta distribution. Algoritmos de Cirfrado de Flujo •El emisor usa una semilla secreta y un algoritmo determinista (generador pseudoaleatorio) para generar una secuencia binaria. •Con la secuencia generada y el texto en claro expresado en binario se realiza bit a bit. •Realizando la misma operación con el texto cifrado y la misma secuencia pseudoaleatoria se recupera el texto en claro. PRINCIPALES ALGORITMOS VERNAM A5 -> “oscuro”: http://www.scard.org/gsm/a51.html (site outside North America) E0 -> 8 a 128 bits y Facultad de Ciencias Básicas e Ingeniería. Universidad de los Llanos. Felipe Andrés Corredor. Msc. [email protected] Algoritmos de Cirfrado de Bloque El mensaje en claro se divide en bloques y se aplica el algoritmo sobre cada uno de forma independiente con la misma clave de manera que: •El cifrado de cada símbolo depende de los demás símbolos del mismo bloque •Para descifrar una parte no es preciso descifrar el mensaje completo MODOS DE OPERACIÓN ECB CBC CFB OFB Facultad de Ciencias Básicas e Ingeniería. Universidad de los Llanos. Felipe Andrés Corredor. Msc. [email protected] ALGORITMOS DE CIFRADO DE BLOQUE MODOS DE OPERACIÓN ECB Electronic Code Book CBC Cipher Block Chaining. Ing. Felipe Andrés Corredor. Msc(c) Facultad de en Ciencias Básicas e Ingeniería. [email protected] Felipe Andrés Corredor. Msc. Especialización Ingeniería de Software. [email protected] 37 Universidad de Llanos. los Llanos. [email protected] Universidad de los Algoritmos de Cirfrado de Bloque MODOS DE OPERACIÓN CFB - Cipher Feedback. - Realimentación … Facultad de Ciencias Básicas e Ingeniería. Universidad de los Llanos. Felipe Andrés Corredor. Msc. [email protected] Algoritmos de Cirfrado de Bloque MODOS DE OPERACIÓN OFB - Output Feedback. Cifrado Tipo Feistel REDES DE FEISTEL “permite que el proceso de cifrado y descifrado sea el mismo.” Horst Feistel: trabajador de la IBM e inventor del cifrado en bloque LUCIFER a comienzos de los años 70, que fue utilizado por el Reino Unido. En 1974 se propone a la NSA como estándar y en ese año dará origen al escogido como estándar, DES. Facultad de Ciencias Básicas e Ingeniería. Universidad de los Llanos. Felipe Andrés Corredor. Msc. [email protected] Esquema DES Fuente: http://www.itl.nist.gov/fipspubs/fip46-2.htm Facultad de Ciencias Básicas e Ingeniería. Universidad de los Llanos. Felipe Andrés Corredor. Msc. [email protected] DES La primera etapa es una transposición, una permutación inicial (IP) del texto plano de 64 bits, independientemente de la clave. La última etapa es otra transposición (IP1), exactamente la inversa de la primera. La penúltima etapa intercambia los 32 bits de la izquierda y los 32 de la derecha. Las 16 etapas restantes son una Red de Feistel de 16 rondas. DES La función f de la red de Feistel se compone de una permutación de expansión (E), que convierte el bloque correspondiente de 32 bits en uno de 48. Después realiza una orexclusiva con el valor Ki, también de 48 bits, aplica ocho S-Cajas de 6*4 bits, y efectúa una nueva permutación (P). Facultad de Ciencias Básicas e Ingeniería. Universidad de los Llanos. Felipe Andrés Corredor. Msc. [email protected] DES En cada una de las 16 iteraciones se emplea un valor, Ki, obtenido a partir de la clave de 56 bits y distinto en cada iteración DES (I) Encriptación: 1.- Procesar la clave. 1.1.- Solicitar una clave de 64 bits al usuario. 1.2.- Calcular las subclaves. 1.2.1.- Realizar permutación en la clave de 64 bits reduciéndose a 56 bits Facultad de Ciencias Básicas e Ingeniería. Universidad de los Llanos. Felipe Andrés Corredor. Msc. [email protected] DES 1.2.2.- Dividir la clave permutada en dos mitades de 28 bits cada una. C(0) el bloque que contiene los 28 bits de mayor peso y D(0) los 28 bits restantes. 1.2.3.- Calcular las 16 subclaves 1.2.3.1.- Rotar a la izquierda C(i-1) y D(i-1) para obtener C(i) y D(i), respectivamente. 1.2.3.2.- Concatenar C(i) y D(i) y permutar como se indica a continuación. Así se obtiene K(i), que tiene una longitud de 48 bits. 1.2.3.3.- Ir a 1.2.3.1. hasta obtener K(16). Facultad de Ciencias Básicas e Ingeniería. Universidad de los Llanos. Felipe Andrés Corredor. Msc. [email protected] DES 2.- Procesar el bloque de datos de 64 bits. 2.1.- Obtener un bloque de datos de 64 bits. Si el bloque contiene menos de 64 bits debe ser completado para poder continuar con el siguiente paso. 2.2.- Realizar la siguiente permutación del bloque: 2.3.- Dividir el bloque resultante en dos mitades de 32 bits cada una. L(0) el bloque que contiene los 32 bits de mayor peso y R(0) el resto. 2.4.- Aplicar las 16 subclaves obtenidas en el paso 1 2.4.1.- E(R(i)). Expandir R(i) de 32 a 48 bits de acuerdo con la tabla: Facultad de Ciencias Básicas e Ingeniería. Universidad de los Llanos. Felipe Andrés Corredor. Msc. [email protected] DES 2.4.2.- E(R(i-1)) Xor K(i). Or-exclusiva del resultado del paso 2.4.1. con K(i) 2.4.3.- B(1), B(2),..., B(8). Partir E(R(i-1)) Xor K(i) en ocho bloques de seis bits. B(1) representa a los bits 1-6, B(2) representa a los bits 7-12,..., B(8) representa a los bits 43-48. 2.4.4.- S(1)(B(1)), S(2)(B(2)),..., S(8)(B(8)). Sustituir todos los B(j) por los valores correspondientes de las S-Cajas o tablas de sustitución (Substitution Boxes, SBoxes) de 6*4 bits. Todos los valores de las S-Cajas se consideran de 4 bits de longitud. 2.4.4.1.- Tomar los bits 1º y 6º de B(j) y formar un número de 2 bits que llamaremos m. Este valor nos indicará la fila en la tabla de sustitución correspondiente S(j). m=0 representa la 1ª fila y m=3 la última. 2.4.4.2.- Con los bits 2º a 5º de B(j) formar otro número, n, de cuatro bits que indicará la columna de S(j) en la que buscar el valor de sustitución. 2.4.4.3.- Reemplazar B(j) con S(j)(m,n), m fila y n columna 2.4.4.4.- Ejemplo. Sea B(3)=42 -> B(3)=101010. Buscaremos el nuevo valor de B(3) en S(3). Fila m y columna n, m=10, n=0101, y en decimal m=2 y n=5. Por tanto, B(3) será S(3)(2,5)=15 2.4.4.5.- Volver a 2.4.4.1. hasta que todos los bloques B(j) hayan sido reemplazados por el valor de S(j) adecuado. DES Facultad de Ciencias Básicas e Ingeniería. Universidad de los Llanos. Felipe Andrés Corredor. Msc. [email protected] DES 2.4.5.- P[S(1)(B(1))... S(2)(B(8))]. Concatenar los bloques B(1) a B(8) y permutar los 32 bits (cuatro bits cada B(j)) en función de esta tabla: 2.4.6.- R(i). Realizar una orexclusiva entre el valor resultante y L(i-1). Este valor será R(i). Por tanto, R(i)=L(i-1) Xor P[S(1)(B(1))... S(2)(B(8))] 2.4.7.- L(i). L(i)=R(i-1) Facultad de Ciencias Básicas e Ingeniería. Universidad de los Llanos. Felipe Andrés Corredor. Msc. [email protected] DES 2.4.8.- Repetir desde 2.4.1. hasta que se hayan aplicado las 16 subclaves. 2.5.- Hacer la siguiente permutación del bloque R(16)L(16). Obsérvese que esta vez R(16) precede a L(16) Facultad de Ciencias Básicas e Ingeniería. Universidad de los Llanos. Felipe Andrés Corredor. Msc. [email protected] Algoritmos de Cifrado de Bloque PRINCIPALES ALGORITMOS DES FEAL TEA KHUFU RC2 – RC4 – RC5 KHAFRE IDEA LOKI AES - RIJNDAEL GOST TWOFISH CAST SERPENT SKIPJACK BLOWFISH SHARK MARS Facultad de Ciencias Básicas e Ingeniería. Universidad de los Llanos. Felipe Andrés Corredor. Msc. [email protected] Actividad Independiente (entregar) Aspecto\Algoritmo AES TWOFIS H SERPENT … TEA Sigla Autor Fecha de creacion Tamaño de bloque Tamaño de llave (Mín. y Máx.) Usos/Aplicaciones/protocolos Técnica (Sustitucion – Permutacion - Feistel) Seleccionar 5 algoritmos (Diferentes a DES) y completar la tabla! Facultad de Ciencias Básicas e Ingeniería. Universidad de los Llanos. Felipe Andrés Corredor. Msc. [email protected] CIFRADO BLOQUE - SOPORTE PHP int mcrypt_cbc ( int $cipher , string $key , string $data , int $mode [, string $iv ] ) . METODOS mcrypt_cbc() mcrypt_cfb() mcrypt_ecb() mcrypt_ofb(). mcrypt_create_iv() MCRYPT_3DES MCRYPT_ARCFOUR_IV MCRYPT_ARCFOUR MCRYPT_BLOWFISH MCRYPT_CAST_128 MCRYPT_CAST_256 MCRYPT_CRYPT MCRYPT_DES MCRYPT_DES_COMPAT MCRYPT_ENIGMA MCRYPT_GOST MCRYPT_IDEA MCRYPT_LOKI97 MCRYPT_MARS MCRYPT_PANAMA MCRYPT_RIJNDAEL_128 MCRYPT_RIJNDAEL_192 MCRYPT_RIJNDAEL_256 MCRYPT_RC2 MCRYPT_RC4 MCRYPT_RC6 MCRYPT_RC6_128 MCRYPT_RC6_192 MCRYPT_RC6_256 MCRYPT_SAFER64 MCRYPT_SAFER128 MCRYPT_SAFERPLUS MCRYPT_SERPENT MCRYPT_SERPENT_128 MCRYPT_SERPENT_192 MCRYPT_SERPENT_256 MCRYPT_SKIPJACK MCRYPT_TEAN MCRYPT_THREEWAY MCRYPT_TRIPLEDES MCRYPT_TWOFISH MCRYPT_TWOFISH128 MCRYPT_TWOFISH192 MCRYPT_TWOFISH256 MCRYPT_WAKE MCRYPT_XTEA Ing. Felipe Andrés Corredor. Msc(c) Facultad de en Ciencias Básicas e Ingeniería. [email protected] Felipe Andrés Corredor. Msc. Especialización Ingeniería de Software. [email protected] 54 Universidad de Llanos. los Llanos. [email protected] Universidad de los CIFRADO BLOQUE - SOPORTE JAVA Cipher cifrador = Cipher.getInstance("AES/ECB/NoPadding","BC"); PAQUETES java.security.*; java.security.spec.*; javax.crypto.*; MÉTODOS cifrador.init(Cipher.ENCRYPT_MODE,keyspec,ivspec); cifrador.init(Cipher.DECRYPT_MODE,keyspec,ivspec); Security.addProvider SecretKeySpec IvParameterSpec Ing. Felipe Andrés Corredor. Msc(c) Facultad de en Ciencias Básicas e Ingeniería. [email protected] Felipe Andrés Corredor. Msc. Especialización Ingeniería de Software. [email protected] 55 Universidad de Llanos. los Llanos. [email protected] Universidad de los ALGORITMOS DE RESÚMEN CARACTERÍSTICAS Todos los números resumen generados con un mismo método tienen el mismo tamaño. APLICACIONES Integridad de mensaje Firmas digitales Es fácil y rápido calcular el resumen. Códigos de autenticación de mensaje Es imposible reconstruir el mensaje a partir del resumen. Verificación de contraseñas Es “imposible” que dos textos base Generación aleatorios de números seudo- diferentes tengan el mismo resumen. Ing. Felipe Andrés Corredor. Msc(c) Facultad de en Ciencias Básicas e Ingeniería. [email protected] Felipe Andrés Corredor. Msc. Especialización Ingeniería de Software. [email protected] 56 Universidad de Llanos. los Llanos. [email protected] Universidad de los ALGORITMOS DE RESUMEN PRINCIPALES ALGORITMOS MD2 MD5 (128 bits) SHA-1 (160) SHA-256 SHA-384 SHA-512 RIPEMD-160 Ing. Felipe Andrés Corredor. Msc(c) Facultad de en Ciencias Básicas e Ingeniería. [email protected] Felipe Andrés Corredor. Msc. Especialización Ingeniería de Software. [email protected] 57 Universidad de Llanos. los Llanos. [email protected] Universidad de los IMPLEMENTACION JAVA MD5 (128 bits) - http://www.ietf.org/rfc/rfc1321.txt import java.security.MessageDigest; String mensaje=“Felipe Andrés Corredor”; MessageDigest md = MessageDigest.getInstance("MD5"); md.reset(); byte[] b = md.digest(mensaje.getBytes()); Felipe Andres Corredor cifrado Seguridad Informatica Unillanos 123 : 23a15551f3d7c756c5fa60ad2b384b51 : 65faabd5a7c42829f7715f0dc2cc1885 : 202cb962ac59075b964b07152d234b70 : d41d8cd98f00b204e9800998ecf8427e Ing. Felipe Andrés Corredor. Msc(c) Facultad de en Ciencias Básicas e Ingeniería. [email protected] Felipe Andrés Corredor. Msc. Especialización Ingeniería de Software. [email protected] 58 Universidad de Llanos. los Llanos. [email protected] Universidad de los Criptosistemas de Clave Publica Se parte del supuesto de que es computacionalmente impracticable deducir el valor de la clave privada a partir del conocimiento de la clave pública. Facultad de Ciencias Básicas e Ingeniería. Universidad de los Llanos. Felipe Andrés Corredor. Msc. [email protected] Criptosistemas de Clave Publica Whitfield Diffie – Martin Hellman DIFFIE-HELLMAN (Key Exchange ) Negociación de Clave! Construcción de la clave entre dos usuarios A y B: • Sea p un primo grande. • A elige un entero (al azar) 0 < a < p, calcula ga y envía el resultado a B. • B elige un entero 0 < b <p, calcula gb y lo envía a A. • Ambos construyen la clave privada, gab Facultad de Ciencias Básicas e Ingeniería. Universidad de los Llanos. Felipe Andrés Corredor. Msc. [email protected] Negociación de Clave DH Facultad de Ciencias Básicas e Ingeniería. Universidad de los Llanos. Felipe Andrés Corredor. Msc. [email protected] Estructura de Clave Publica RSA Facultad de Ciencias Básicas e Ingeniería. Universidad de los Llanos. Felipe Andrés Corredor. Msc. [email protected] RSA- Estructura La primera propuesta de algoritmo que soporta el modelo de DH76 realizada por RSA78. Facultad de Ciencias Básicas e Ingeniería. Universidad de los Llanos. Felipe Andrés Corredor. Msc. [email protected] RSA- Ejemplo B -> m -> A m=“felipe” p = 5 y q = 11 -> n = 55 Φ(55)=40 y Φ(40)= Φ(23.5)=22(2-1).50(51)=16 e=3 d=3-1mod Φ(55) = 315mod 40=27 m1=f=5 m2=e=4 m3=l=11 … c1=m1e mod n = 53 mod 55 = 15 = o c2=m2e mod n = 43 mod 55 = 9 = j c3=m2e mod n = 113 mod 55 = 11 = l m1=c1d mod n = o = 1527 mod 55 = 5 = f m2=c2d mod n = j = 927 mod 55 = 4 = e m3=c3d mod n = l = 1127 mod 55 = 11 = l Algoritmo de Cifrado Asimétrico *UNIDIRECCIONAL: c->kPb[m] DE LA MOCHILA (MERKLE-HELLMAN) MASSEY-OMARA POHLIG-HELLMAN *BIDIRECCIONAL RABIN ELGAMAL DIFFIE-HELLMAN (Pat. < 1997) RSA (Pat. < 2000) DSA CURVAS ELIPTICAS - HIPERELIPTICAS Facultad de Ciencias Básicas e Ingeniería. Universidad de los Llanos. Felipe Andrés Corredor. Msc. [email protected] Envoltura Digital Proporciona los servicios de integridad y confidencialidad de los datos. A genera de forma aleatoria una clave de sesión k. A cifra el mensaje m mediante un criptosistema simetrico usando la clave k: c1 = Ek (m) A cifra k con la clave publica de B, usando un criptosistema asimetrico: c2 = Bp (k) A envia a B ambos criptogramas c1 y c2 B obtiene la clave de sesión descifrando c2 con su clave privada. B descifra el mensaje m usando el mismo criptosistema simétrico y la clave k obtenida. Facultad de Ciencias Básicas e Ingeniería. Universidad de los Llanos. Felipe Andrés Corredor. Msc. [email protected] Firma Digital, Certificados y PKIs FIRMA DIGITAL Cifrado con la clave privada - > “muestra reducida de m” CERTIFICADO DIGITAL una pieza de información, un documento digital, en el que se asocia el nombre de una entidad con su clave pública (pareja de la clave privada correspondiente) durante un determinado periodo de validez. emitido por una TTP denominada CA PKI’s Infraestructura de seguridad necesaria para la provisión y gestión de certificados. Facultad de Ciencias Básicas e Ingeniería. Universidad de los Llanos. Felipe Andrés Corredor. Msc. [email protected] Contexto de Uso de la Criptografía CASO 1 Escenario basado en sistemas simétricos, más rápidos y eficaces que los asimétricos, Pero … # entidades comunicantes = problema intercambio de claves. CASO 2 Escenario basado sistemas asimétricos, solamente sería necesario mantener un par de claves por cada usuario, con lo que la gestión de claves es mucho más sencilla y robusta. Pero … CASO 3 Escenario híbrido, usa un sistema de clave pública para intercambiar una clave secreta simétrica que será utilizada en una transacción concreta, de tal forma que esta clave sólo sirve para esa transacción y es desechada una vez termina. Reduce riesgo de interceptación. Facultad de Ciencias Básicas e Ingeniería. Universidad de los Llanos. Felipe Andrés Corredor. Msc. [email protected] Referencias MCRYPT - http://www.php.net/manual/en/book.mcrypt.php http://java.sun.com/developer/technicalArticles/Security/AES/AES_v1.html http://www.bouncycastle.org/latest_releases.html Federal Information Processing Standards Publication DES - http://www.itl.nist.gov/fipspubs/fip46-2.htm AES - http://csrc.nist.gov/publications/fips/fips197/fips-197.pdf Facultad de Ciencias Básicas e Ingeniería. Universidad de los Llanos. Felipe Andrés Corredor. Msc. [email protected] . ACLARACIÓN DE DUDAS! Facultad Ciencias Básicas e Ingeniería. Facultad dede Ciencias Básicas e Ingeniería. Universidad Llanos. Universidad dede loslos Llanos. Felipe Andrés Corredor. Msc. Msc. Felipe Andrés Corredor. [email protected] [email protected] Facultad Ciencias Básicas e Ingeniería. Facultad dede Ciencias Básicas e Ingeniería. Universidad Llanos. Universidad dede loslos Llanos. Felipe Andrés Corredor. Msc. Msc. Felipe Andrés Corredor. [email protected] [email protected]
© Copyright 2026