Download Report

Publicaciones AFAMaC
OMPR
Olimpiadas de Matemáticas
de Puerto Rico
2007-2008
Luis F. Cáceres
Jonathan Ho Fung
Arturo Portnoy
Departamento de Ciencias Matemáticas
Universidad de Puerto Rico
Recinto Universitario de Mayagüez
Primera Edición, 2008
c
Derechos AFAMaC
Director: Dr. Luis F. Cáceres
Ninguna parte de esta obra puede ser reproducida ni retransmitida por ningún
medio, electrónico, mecánico, fotocopiado, grabado u otro, excepto con el permiso
previo por escrito de AFAMaC.
Esta producción ha sido subvencionada por el proyecto AFAMaC mediante
proyectos del Departamento de Educación Puerto Rico. Contrato #2007-AF-0205
#O AF-081-07-0205
Realizado por
Luis F. Cáceres
Jonathan Ho Fung
Arturo Portnoy
Departamento de Ciencias Matemáticas
Universidad de Puerto Rico, Recinto Universitario de Mayagüez
Impreso y hecho en Puerto Rico
ii
Prólogo
Al igual que en los pasados años, miles de estudiantes provenientes
de las diversas escuelas públicas y privadas del paı́s participaron en los
procesos de selección de este nuevo ciclo olı́mpico. Luego de meses de
arduo trabajo para estos, el proceso culminó en el mes de mayo del
presente año con el anuncio de los miembros de los equipos que nos
representarán en la Olimpiada de Matemática de Centroamérica y El
Caribe, la Olimpiada Iberoamericana de Matemáticas y la Olimpiada
Internacional de Matemáticas.
Esperamos que esta publicación te sirva a ti, que participaste en este
proceso, de gran ayuda al momento de prepararte para los futuros ciclos;
o quizás, que la puedas conservar como un recuerdo de esos primeros
destellos de lo que ya es una carrera académica sumamente prometedora. También esperamos que el contenido de esta publicación, todos
los problemas y respectivas soluciones de los exámenes administrados,
sea lo suficientemente retador como para animar a participar a aquellos
estudiantes que aun no lo han hecho.
Puerto Rico, al igual que el resto del mundo, está atravesando por
momentos sumamente difı́ciles. Es por esto que se necesitan, tal vez
más que nunca, personas como tú que se distingan por su talento y la
capacidad de alcanzar logros en nombre del paı́s; en nombre de esos cuatro millones de personas que están amparadas bajo una misma bandera.
Eres parte de una generación que, dentro de pocos años, será responsable de los pasos que tomará nuestro pueblo; generación que formará
los pilares de nuestra sociedad y a la cual se le mirará en búsqueda de
inspiración en tiempos que prometen ser sumamente conflictivos. Demuestra la grandeza de la que eres capaz, ya que mucho, quizá todo;
depende de esto.
Jonathan Ho Fung
iii
AFAMaC
Alianza para el Fortalecimiento del Aprendizaje de las Ciencias y las
Matemáticas.
Estos proyectos están subvencionados por el Departamento
de Educación de Puerto Rico y son realizados en el
Departamento de Ciencias Matemáticas del Recinto
Universitario de Mayagüez de la Universidad de Puerto Rico.
iv
Tabla de Contenido
Página
Examen de Primera Fase: Nivel I
Examen de Primera Fase: Nivel II
Examen de Segunda Fase: Nivel I
Examen de Segunda Fase: Nivel II
Olimpiada de Matemáticas de Puerto Rico: Nivel I
Olimpiada de Matemáticas de Puerto Rico: Nivel II
Examen de Selección: Nivel II
Soluciones al Examen de Primera Fase: Nivel I
Soluciones al Examen de Primera Fase: Nivel II
Soluciones al Examen de Segunda Fase: Nivel I
Soluciones al Examen de Segunda Fase: Nivel II
Soluciones a la Olimpiada de Matemáticas: Nivel I
Soluciones a la Olimpiada de Matemáticas: Nivel II
Soluciones al Examen de Selección: Nivel II
5
6
12
21
25
29
31
33
34
41
51
55
60
64
70
COMPETENCIA PREOLÍMPICA DE
MATEMÁTICAS
Primera Fase 2007-2008
EXAMEN NIVEL I(4to, 5to y 6to grado)
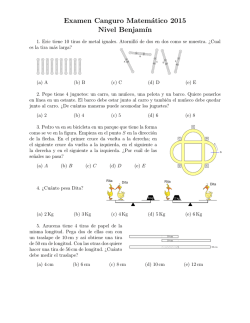
1. ¿Cuántos rectángulos puedes ver en la siguiente figura?
a. 4
d. 9
b. 5
e. 10
c. 7
2. ¿Cuáles dos números siguen en la sucesión 1, 4, 2, 8, 3, 12, 4, 16, 5, . . .?
a. 20,7
d. 20,6
b. 18,7
e. 18,7
c. 20,6
3. ¿Cuántos números de tres dı́gitos se pueden hacer usando solamente los dı́gitos 0 y 5?
a. 2
d. 8
b. 4
e. ninguna de las anteriores
c. 6
4. ¿Si 20 cajas de papayas pesan 1,600 libras y cada caja vacı́a pesa
media libra, cuánto pesan las papayas juntas?
a. 1,590 libras
d. 1,540 libras
b. 1,580 libras
e. 1,520 libras
c. 1,560 libras
6
5. Se dibujan en una misma hoja un cı́rculo y un cuadrado. ¿Cuál
es el máximo número de puntos comunes que pueden tener?
a. 2
d. 8
b. 4
e. 16
c. 6
6. Se sembraron 10 árboles en lı́nea recta con una separación entre
cada uno de ellos de 50 pies. ¿Qué distancia hay entre el primero
y el último árbol?
a. 300 pies
d. 450 pies
b. 350 pies
e. 500 pies
c. 400 pies
7. En una fiesta Marı́a, Ana y Rosa van a repartirse regalos de tal
manera que cada una da un regalo (no para ella misma) y recibe
un regalo. ¿De cuántas maneras se puede realizar la repartición?
a. 1
d. 4
b. 2
e. 5
c. 3
8. En una finca hay el mismo número de perros que de gallinas. ¿Si
contamos las patas de estos animales, cuántas podrı́a haber en
total?
a. 4
d. 24
b. 10
e. 32
c. 16
7
9. Cuando Mario tenı́a 27 años su hijo Pedro tenı́a 3 años. Ahora
Mario tiene tres veces la edad de Pedro. ¿Cuántos años tiene
Mario?
a. 36
d. 60
b. 48
e. 72
c. 54
10. En la suma
las letras diferentes representan dı́gitos diferentes, AH representa
un número de dos dı́gitos y HEE representa uno de tres dı́gitos.
Hallar H + E.
a. 1
d. 4
b. 2
e. 5
c. 3
11. ¿Cuál es el mı́nimo número de colores que se necesitan para pintar
un cubo de tal manera que dos caras adyacentes no tengan el
mismo color?
a. 2
d. 5
b. 3
e. 6
c. 4
8
12. ABCD es un rectángulo con área igual a 36 unidades cuadradas.
Los puntos E, F y G son los puntos medios de los lados en donde
ellos están localizados. ¿Cuál es el área del triángulo EF G?
a. 6
d. 36
b. 9
e. 48
c. 18
13. Si tienes un cubo de 5 centı́metros de lado formado por cubitos de
1 centı́metro de lado, ¿cuántos cubitos quedan totalmente ocultos
a la vista?
a. 4
d. 27
b. 8
e. 64
c. 9
14. Luis escribió todos los números desde el 1 hasta el 100. ¿Cuántos
dı́gitos en total tuvo que escribir Luis?
a. 152
d. 202
b. 182
e. 222
c. 192
15. ¿Si la base de un triángulo aumenta en un 10% y su altura disminuye en un 10%, cuánto cambia su área?
a. no cambia
d. aumenta 10
b. aumenta 1%
e. disminuye 10
c. disminuye 1
9
16. Una bombilla se enciende cada dos minutos y otra bombilla se
enciende cada tres minutos y medio. Las dos bombillas se encendieron simultáneamente a la media noche. ¿Cuándo será la
primera vez luego de la 1:00 am que las dos luces se volverán a
encender al mismo tiempo?
a. 1:10 am
d. 2:10 am
b. 1:20 am
e. 3:10 am
c. 2:10 am
17. Una hoja de papel cuadrada se dobla por la mitad como se muestra en la figura y se corta por el doblez en dos rectángulos. El
perı́metro de cada uno de los dos rectángulos es 18 centı́metros.
¿Cuál es el perı́metro del cuadrado original?
a. 12
d. 36
b. 18
e. 48
c. 24
18. El precio de la entrada de cine es $7. En el cine Balboa dan
cuatro funciones diarias. En la primera y en la segunda función,
las entrada están a mitad de precio. El jueves fueron a la cuarta
función el doble de espectadores que a la tercera función y a la
tercera función el doble de los que fueron a la primera y a la
segunda funciones juntas. El jueves se recaudaron $1183 en total.
¿Cuántos espectadores hubo ese dı́a en la cuarta función?
a. 26
d. 169
b. 52
e. 208
c. 104
10
19. En un triángulo equilátero de 75 cms de perı́metro se le sacan
3 triangulitos, también equiláteros, de 5 cms de lado; como se
muestra en la figura. ¿Cuál es el perı́metro de la figura rayada?
a. 25 centı́metros
d. 75 centı́metros
b. 40 centı́metros
e. 120 centı́metros
c. 60 centı́metros
20. Susana trabaja en un piso que tiene 5 oficinas. En el piso hay 3
plantas: un cactus, una azalea y un ficus. Todos los dı́as Susana
cambia las plantas de la oficina. ¿De cuántas maneras puede ubicarlas si nunca quiere poner las tres plantas en la misma oficina?
a. 15
d. 120
b. 30
e. 240
c. 60
11
COMPETENCIA PREOLÍMPICA DE
MATEMÁTICAS
Primera Fase 2007-2008
EXAMEN NIVEL II(7mo al 12mo grado)
1. Supongamos que un piano normal tiene 87 teclas de las cuales
son negras y el resto son blancas. ¿Cuántas teclas son blancas?
1
3
a. 29
d. 67
b. 32
e. ninguna de las anteriores
c. 58
2. Conchita logra duplicar sus ahorros. Con ese dinero paga $600
que debı́a y se queda con $200. ¿Cuánto dinero tenı́a Conchita al
principio?
a. $1600
d. $400
b. $1200
e. $200
c. $800
3. Antonio es tı́o de Rosa; Ana es abuela de Pedro; Fabiola es hermana de Antonio; Antonio es papá de Pedro. ¿Qué son Rosa y
Pedro?
a. hermanos
d. Pedro es padre de Rosa
b. primos
e. Pedro es nieto de Rosa
c. Rosa es hermana de Pedro
4. Considera 5 números enteros. ¿Cuántos deben ser impares para
que el producto de los cinco sea impar?
a. 1
d. 4
b. 2
e. 5
c. 3
12
5. En el siguiente arreglo, cada letra representa un número (no necesariamente distinto).
3 B
C
D E
8 G
H
I
¿Si la suma de cualesquiera tres números consecutivos es 18, cuánto
vale H?
a. 3
d. 11
b. 7
e. 15
c. 9
6. ¿Cuántos divisores positivos tiene 5 ∗ 4 ∗ 3 ∗ 2? (Los divisores
incluyen al número mismo y al 1)
a. 4
d. 12
b. 8
e. 16
c. 10
7. ¿Si las rectas horizontales son paralelas, cuánto mide el ángulo x?
a. 120◦
d. 65◦
b. 100◦
e. ninguna de las anteriores
c. 90◦
13
8. ¿Cuánto vale la suma de todos los dı́gitos del número 102007 −2007?
a. 18,055
d. 2007
b. 19,032
e. ninguna de las anteriores
c. 12,435
9. En la televisión de Marı́a se reciben los canales del 2 al 42. ¿Si
Marı́a enciende la televisión en el canal 15 y aprieta 518 veces
el botón para subir canales, en qué canal quedará la televisión
cuando se detenga?
a. 39
d. 42
b. 40
e. ninguna de las anteriores
c. 41
10. Pablo compró un artı́culo con el 15% de descuento por $106.25.
¿Cuál es el precio original?
a. Menos de $123
d. $127
b. $124
e. más de $127
c. $125
11. Simón escribe el número 3 en la pizarra, luego lo borra y lo reemplaza por su cuadrado, el 9, luego lo borra y lo reemplaza por su
cuadrado, el 81. El repite esto 2007 veces: cada vez reemplaza el
número escrito por su cuadrado. ¿Cuál es el dı́gito de la unidad
de su última respuesta?
a. 1
d. 7
b. 3
e. 9
c. 5
14
12. ¿De cuántas formas distinas se pueden reordenar las letras L, A,
P , I, Z de tal forma que la primera y última letras son vocales?
a. 6
d. 12
b. 8
e. 24
c. 10
13. Hay algunas canicas en una bolsa. Marı́a dice: “Hay sólo 3 canicas
en la bolsa y todas son negras”. Luis dice: “Sólo hay dos canicas
negras y dos canicas rojas en la bolsa”. Jorge dice: “Sólo hay
canicas negras en la bolsa”. ¿Sabiendo que sólo uno ha mentido,
cuántas canicas hay en la bolsa?
a. 1
d. 4
b. 2
e. no se puede saber
c. 3
14. En el siguiente dibujo, el segmento DE es paralelo al segmento
AB. Sabiendo que el área de DEC es 43 del área de ABC y que
AC es 1 metro, ¿cuál es la longitud de DC?
a.
√
2− 3
2
metros
√
b. (2 − 3) metros
d.
e.
√
c.
3
3
metros
15
3
4
√
3
2
metros
metros
15. Un vándalo pincha las gomas de todos los carros y motoras en
una calle. La policı́a lo arresta y cuenta que 44 vehı́culos (motoras
o carros) fueron dañados. ¿Considerando que 144 gomas fueron
pinchadas, cuántas motoras habı́a en esa calle?
a. menos de 10
d. mas de 19 y menos de 25
b. mas de 9 y menos de 15
e. mas de 24
c. mas de 14 y menos de 20
16. Las diagonales de un rombo estan en proporción 3:4 y su suma es
de 56 cm. ¿Cuál es el perı́metro del rombo?
a. 60 cm
d. 10 cm
b. 80 cm
e. 108 cm
c. 96 cm
17. Las columnas y las filas de un tablero 8x8 de ajedrez están numeradas del 1 al 8. Mauricio pone en cada cuadrado del tablero
tantas pesetas como la suma de su número de fila y su número de
columna. ¿Cuantás pesetas pone Mauricio en el tablero?
a. 482
d. 1024
b. 576
e. 1152
c. 768
16
18. Considera todos los números de 4 dı́gitos formados usando los
dı́gitos 3, 4, 6, 7, de tal forma que ningún dı́gito se repite. ¿Cuántos
de estos números son divisibles por 44?
a. 0
d. 3
b. 1
e. 4
c. 2
19. En el siguiente dibujo, el triángulo ABC es equilátero y DEF G es
un cuadrado. ¿Sabiendo que AB mide 1 metro, cuál es la longitud
de DE?
a.
1
3
c.
1
2
metros
√
b. (2 3 − 3) metros
d.
√
1+ 3
4
metros
√
e. ( 3 − 1) metros
metro
20. Si x es la solución de la ecuación
entonces
x+1
1
+
x+2
2
+ ... +
a. x = −2
d. x = 2
b. −1 ≤ x ≤ 1
e. x ≥ 3
c. x =
3
2
17
x+100
100
= 100,
21. En la figura tenemos un cuadrado pequeño inscrito en un cı́rculo
a su vez inscrito en un cuadrado grande. ¿Cuál es la razón entre
el área del cuadrado grande y el área del cuadrado chico?
√
d. 2 2
√
a.
b.
2
2
√
2
e. 4
c. 2
22. En una isla hay solo dos tipos de gente: los que siempre dicen
la verdad y los que siempre mienten. Tres habitantes de la isla
están hablando. Andrea dice: “Bárbara siempre dice la verdad”,
Bárbara dice: “Andrea y Carlos siempre dicen la verdad” y Carlos
dice: “Andrea miente”. Sabemos entonces que:
a. Los tres dicen la verdad
b. Andrea y Bárbara dicen la verdad, Carlos miente
c. Andrea dice la verdad, Bárbara y Carlos mienten
d. Andrea y Bárbara mienten, Carlos dice la verdad
e. Los tres mienten
23. ¿Considerando 50 números distintos, elegidos al azar del conjunto
{1,2,. . . ,100}, cuya suma total es 3000, cuál es la cantidad mı́nima
de números pares posibles entre los 50?
a. 2
d. 5
b. 3
e. 6
c. 4
18
24. Considere cualquier conjunto de 20 enteros consecutivos mayores
que 50. ¿Cuál es el mayor número de primos en el conjunto?
a. 4
d. 7
b. 5
e. 8
c. 6
25. Un estudiante pasó un cierto número de exámenes manteniendo un
promedio de 23. Después de pasar un examen más, su promedio
bajo a 22.25. ¿Cuál fue la última nota del estudiante, sabiendo
que todas sus notas están entre 18 y 30? (incluyendo 18 y 30)
a. 18
d. 21
b. 19
e. 22
c. 20
26. Un triángulo equilátero tiene el mismo perı́metro que un rectángulo
cuyos lados √
son b y h (b > h). ¿Considerando que el área del
triángulo es 3 veces el área del rectángulo, cuál es el valor de hb ?
a.
√
3
d.
b. 2
e.
√
c.
√
3+ 5
2
√
7+3 5
2
3+ 3
2
27. Sea Q un cubo y S una esfera centrada en uno de los vértices de
Q, con radio igual al lado de Q. El volumen de la intersección
entre Q y S es
a.
b.
c.
1
8
1
4
1
6
del volumen de la esfera
d.
del volumen de la esfera
e.
del volumen del cubo
19
1
4
1
2
del volumen del cubo
del volumen del cubo
28. Sea P (x) = x3 + ax2 + bx + c y suponga que la suma de dos raı́ces
del polinomio es cero. ¿Cuál de las siguientes relaciones entre los
coeficientes de P (x) siempre es cierta?
a. a ∗ b ∗ c = 0
d. b2 = a ∗ c
b. c = a ∗ b
e. ninguna de las anteriores
c. c = a + b
29. Sea ABC un triángulo isósceles con AB = BC 6= AC. Sea P
un punto en AB. ¿Cuántas posibles posiciones en el plano hay
para un punto Q tal que el triángulo AP Q sea similar al triángulo
ABC?
a. 0
d. 4
b. 2
e. 6
c. 3
30. Alberto, Bárbara, Clara y David mezclan una baraja con 40 cartas
y reparten 10 a cada uno de ellos. Alberto exclama sorprendido:
“¡Que raro, yo no tengo espadas!”. ¿Cuál es la probabilidad de
que Bárbara tampoco tenga espadas, si hay 10 cartas con espadas
en la baraja?
a.
b.
c.
30!
20!40!
20!
10!30!
30!30!
20!40!
d.
e.
20
20!20!
10!30!
30!
10!40!
COMPETENCIA PREOLÍMPICA DE
MATEMÁTICAS
Segunda Fase 2007-2008
EXAMEN NIVEL I(4to, 5to y 6to grado)
1. Rosita tiene una caja grande con 4 cajas medianas dentro; en cada
una de las cajas medianas hay 2 cajas chicas, que a su vez cada
una contiene 3 más pequeñas. ¿Cuántas cajas tiene Rosita?
a. 10
d. 36
b. 12
e. 37
c. 15
2. ¿Cuál número falta en la siguiente sucesión: 1, 3, 7, 15, ?, 63, 127?
a. 16
d. 31
b. 17
e. 62
c. 30
3. ¿Cuántos triángulos hay en la siguiente figura?
a. 5
d. 10
b. 6
e. 12
c. 8
21
4. Antonio, Beatriz, Carlos y Diana están sentados en una fila de 4
sillas numeradas del 1 al 4. Emilio los ve y dice:
• Beatriz está al lado de Carlos
• Antonio está entre Beatriz Carlos
¿Si las dos afirmaciones son falsas y Beatriz está en la silla 3, quién
ocupa la silla 2?
a. Beatriz
d. Antonio
b. Carlos
e. Emilio
c. Diana
5. Un domador de fieras tiene tres tigres y dos leones. Desea acomodarlos en una fila de modo que no queden dos tigres o dos leones
juntos. ¿Considerando que cada fiera es distinta a las otras, de
cuántas formas distintas puede acomodar sus fieras?
a. 3
d. 18
b. 6
e. 24
c. 12
6. ¿Qué número multiplicado por tres corresponde a las tres cuartas
partes de 120?
a. 20
d. 60
b. 30
e. 80
c. 40
7. Cada cuadrado tiene 6 cms de lado y el perı́metro de cada rectángulo
sombreado es el doble del perı́metro de cada cuadrado blanco.
¿Cuál es el perı́metro de la figura?
22
8. En cierto planeta hay tantos dı́as en una semana como semanas
en un mes como meses en un año. ¿Si un año tiene 1,000 dı́as,
cuantos dı́as tiene cada semana?
a. 10
d. 1000
b. 100
e. No se sabe
c. 333
9. Un pastel se corta quitando cada vez la tercera parte del pastel
que hay en el momento de hacer el corte. ¿Qué fracción del pastel
original queda después de cortar tres veces?
a.
b.
c.
2
3
4
3
4
9
d.
e.
8
9
8
27
10. A una cantidad le sumo el 10%, y a la cantidad ası́ obtenida le
resto su 10%. ¿Qué porcentaje de la cantidad original me queda?
a. 98
d. 101
b. 99
e. 102
c. 100
11. ¿Si efectuamos el producto de todos los impares entre el 1 y el
2008, cuál es el dı́gito de las unidades del resultado obtenido?
a. 1
d. 7
b. 3
e. 9
c. 5
23
12. Una sala de cine tiene 26 filas con 24 asientos cada una. El total
de asientos se numera de izquierda a derecha, comenzando por la
primera fila y hacia atrás. ¿En qué número de fila está el asiento
número 375?
a. 12
d. 15
b. 13
e. 16
c. 14
13. Marı́a tenı́a el número 4921508 y le pidió a Juan que borrara sus
dı́gitos de tal forma que obtuviera el número de tres dı́gitos mas
pequeño posible. ¿Qué número obtuvo Juan al final?
14. ¿Cuál es el dı́gito de las unidades de 22008 − 2?
15. ¿Si las rectas horizontales son paralelas, cuánto mide el ángulo x?
24
COMPETENCIA PREOLÍMPICA DE
MATEMÁTICAS
Segunda Fase 2007-2008
EXAMEN NIVEL II(7mo al 12mo grado)
1. En la televisión de Claudia se reciben los canales 2 al 42. ¿Si
Claudia enciende el televisor en el canal 15 y aprieta 518 veces el
botón para subir canales, en qué canal quedará el televisor cuando
se detenga?
a. 39
d. 42
b. 40
e. 2
c. 41
2. El domingo pasado Marta tuvo varios invitados. Cuando Pedro
llegó ya estaba Raúl. Jesús y Rita llegaron juntos. Luisa le abrió
la puerta a Arturo y Arturo a Jesús. Raúl llego después de Rita.
¿Quién fue el último en llegar?
a. Pedro
d. Rita
b. Raúl
e. Arturo
c. Jesus
3. En una jaula hay cerditos y palomas con un total de 14 ojos y 22
patas. ¿Cuántos cerditos y palomas hay en la jaula?
a. 2 cerdos y 2 palomas
d. 3 cerdos y 4 palomas
b. 2 cerdos y una paloma
e. 4 cerdos y 3 palomas
c. 3 cerdos y 3 palomas
25
4. En la pizarra está escrito un número de tres cifras que termina
en 2; si borramos ese 2 y lo escribimos al principio del número,
el número disminuye en 36. ¿Cuál es la suma de los dı́gitos del
número original?
a. 4
d. 9
b. 5
e. 10
c. 7
5. En la siguiente figura AD = DC, AB = AC, el ángulo ABC mide
75◦ y el ángulo ADC mide 50◦ . ¿Cuánto mide el ángulo BAD?
a. 30◦
d. 125◦
b. 85◦
e. 140◦
c. 95◦
6. A Julio le dieron el número secreto de su ATH y observó que la
suma de los cuatro dı́gitos del número es 9 y ninguno de ellos es
0; además el número es múltiplo de 5 y mayor que 1995. ¿Cuál es
el tercer dı́gito (de derecha a izquierda) de su número secreto?
a. 1
d. 4
b. 2
e. 5
c. 3
26
7. En el rectángulo de la figura, M y N son los puntos medios de AD
y BC, respectivamente, P y Q son las respectivas intersecciones
de AC con BM y con N D. ¿Suponiendo que AD mide 5 cm y que
AB mide 3 cm, cuántos centı́metros cuadrados tiene la superficie
del cuadrilátero M P QD?
a. 2.75
d. 3.75
b. 3
e. 4
c. 3.25
8. Un costal está lleno de canicas de 20 colores distintos. Al azar
se van sacando canicas del costal. ¿Cuál es el mı́nimo número
de canicas que deben sacarse para poder garantizar que en la
colección tomada habrá al menos 100 canicas del mismo color?
a. 1960
d. 1995
b. 1977
e. 2001
c. 1981
9. Juan eliminó un número de una lista de 10 números consecutivos.
La suma de los que quedaron es 2008. ¿Cuál es el número que
eliminó?
a. 225
d. 228
b. 226
e. Ninguna de las anteriores
c. 227
27
10. ¿Sı́ escribı́ todos los números del 1 al 1000, cuántas veces apareció
el dı́gito 5?
a. 110
d. 100
b. 1331
e. 300
c. 555
11. Se forma un cubo de 4 pulgadas de lado uniendo cubos de 1 pulgada de lado. Se dice que dos cubos están en contacto si tienen
una cara en común. ¿Cuántos de estos cubos de una pulgada están
en contacto con exactamente 4 otros cubos de 1 pulgada?
12. Un entero es tartamudo si todos sus dı́gitos son iguales a 1. ¿Cuántos enteros positivos menores que 100,000 cumplen que al multiplicarlos por 33 se obtiene un entero tartamudo?
13. ¿De cuántas maneras se pueden escoger en un tablero de ajedrez
una casilla blanca y una negra, de tal forma que no estén las dos
en una misma fila ni en una misma columna?
14. Dada la ecuación 1 + (n2 + n)(n2 + 5n + 6) = 1812 , donde n es un
número entero, el valor de n(n + 3) es:
cm2 ,
15. Si el área comprendida entre dos cı́rculos concéntricos es 25π
2
la longitud en cm de una cuerda de la circunferencia mayor, tangente a la menor, es:
28
OLIMPIADA DE MATEMÁTICAS DE PUERTO
RICO 2008
EXAMEN NIVEL I(4to, 5to y 6to grado)
1. Gabriel le está tomando unas fotos a sus amigas Carmen, Roxana
y Keyla. ¿De cuántas formas diferentes se pueden colocar ellas en
lı́nea para la foto?
2. La suma de tres números impares consecutivos es igual a 27. ¿Cuál
es el más peque no de estos tres números?
3. Con 8 ochos quiero formar varios números que sumados den 1000.
¿Cómo lo puedo hacer?
4. En la figura, ABC es un triángulo equilátero (es decir, todos sus
lados miden lo mismo) de 18 cms de perı́metro. Si CD = AC
y el cuadrilátero ACDE tiene 20 cms de perı́metro. ¿Cuál es el
perı́metro de ABCDE?
5. Julián tiene 8 lápices de colores distintos, entre ellos tiene uno rojo,
uno blanco y uno negro. Dibujó una banderita de tres franjas y
quiere pintar cada franja con un color diferente. Una de las franjas
la pintará de su color favorito: el rojo. En el centro no quiere
poner ni blanco ni negro. ¿De cuántas maneras puede pintar la
banderita que dibujó?
29
6. Un perro, sale desde su casa persiguiendo en lı́nea recta a un gato,
que está a 30 pies de la casa. Avanzan a los saltos. El perro da
saltos de 2 pies y el gato de 1 pie, pero el perro da dos saltos en
el tiempo que el gato da tres. ¿A qué distancia de la casa el perro
alcanzará al gato?
7. Se quieren colocar los números 1-2-3-4-5-6-7-8 en los vértices del
cubo de modo que la suma de los números que hay en los vértices
de cada una de las caras sea siempre la misma. Muestra como
hacerlo.
8. Me comı́ una rebanada de un pastel redondo que representaba el
15% del total del pastel, como indica la figura. ¿Cuál es el ángulo
que abarca la rebanada del pastel que me comı́?
9. Juan escribió todos los números impares desde el 1000 hasta el
2008. ¿Cuántas veces escribió el dı́gito 0?
10. Durante las vacaciones, Ana, Camilo y Marı́a se sacaron 35 fotos
en total. Ana está sola en 8 fotos. Camilo está solo en 10 fotos.
Ana está en 19 fotos. Marı́a siempre está sola. ¿En cuántas fotos
está Marı́a?
30
OLIMPIADA DE MATEMÁTICAS DE PUERTO
RICO 2008
EXAMEN NIVEL II(7mo al 12mo grado)
1. Marı́a, Ana y Luis leyeron un mismo libro de menos de 300 páginas.
Marı́a leyo 7 páginas el primer dı́a y el resto a 10 páginas por dı́a.
Ana leyó 2 páginas el primer dı́a y el resto a 11 páginas por dı́a.
Luis leyó 5 páginas el primer dı́a y el resto a 9 páginas por dı́a.
¿Cuántas páginas tiene el libro?
2. Javier tiene que armar una clave con 3 letras y 3 dı́gitos. La
clave debe empezar y terminar con una letra. Los dı́gitos deben
ponerse en forma creciente o decreciente. Elige las letras entre las
de su nombre, sin repetirlas. Elige los dı́gitos entre los impares,
sin repetirlos. ¿De cuántas maneras puede Javier armar esa clave?
3. Una hormiguita recorre cada hora una distancia igual a dos tercios
de lo recorrido la hora anterior. Si en tres horas recorrió 76 cms,
¿cuántos centı́metros recorrió durante la primera hora?
4. En la circunferencia de centro O y diámetro AB se marca el punto
C, como se muestra en la figura, de modo que ∠AOC = 36◦ .
¿Cuánto mide el ángulo ∠CBO?
5. En una fiesta de cumpleaños hay 40 niños y niñas en total, con
un promedio de edad de 7.4 años. El promedio de edad de las
niñas es de 7 años. El promedio de edad de los niños es de 8 años.
¿Cuántas niñas y cuántos niños hay en la fiesta?
6. Encuentra el número de enteros positivos de cuatro dı́gitos tales
que entre ellos hay al menos un 1 y al menos un 0.
31
7. Encuentre las soluciones enteras no negativas de
(x + y + z)2 + (x + y − z)2 + (x − y + z)2 = 40.
8. El centro del cı́rculo que pasa por todos los vértices de un pentágono
regular ABCDE es O, T es el punto medio de CD y AB = 2.
Encuentra el valor de (AO − T O) ∗ AT .
9. Encuentra todos los triángulos rectángulos
con catetos de longitud
√
entera e hipotenusa de longitud 2006.
√
10. Encuentra las soluciones reales de √x+6−8 √x−2 ≤ 6 − x + 1.
32
OLIMPIADAS DE MATEMÁTICAS
DE PUERTO RICO
EXAMEN DE SELECCIÓN
1. Se tiene un rectángulo de 1x25, dividido en 25 casillas de 1x1.
Decidir si es posible escribir los 25 números enteros del 1 al 25,
uno en cada casilla y sin repeticiones, de manera tal que la suma
de los dos números escritos en dos casillas adyacentes sea siempre
un cuadrado perfecto. Si la respuesta es afirmativa, mostrar una
distribución de los 25 números. Si es negativa, explicar porqué.
2. Usando los dı́gitos 1, 2, 3, 4, 5, 6, y sin repetirlos, se forman 3
números de 2 cifras cada uno. Se suman entre sı́ los 3 números de
2 cifras que se formaron. ¿Cuántos resultados diferentes se pueden
obtener mediante este procedimiento?
3. Un saco contiene piedras azules y rojas. Considera el siguiente
juego: se extraen sucesivamente (una por una) piedras hasta que,
por primera vez, el número de piedras azules y el número de
piedras rojas extraı́das son iguales. En un momento determinado
de un juego se observa que, al final, 10 piedras fueron extraı́das y
ningunas 3 sucesivas han sido del mismo color. Prueba que en ese
juego, la quinta y sexta piedras son de distinto color.
4. Si los lados de un triángulo tienen longitudes a, b, c y estas satisfacen las condiciones a + b − c = 2 y 2ab − c2 = 4, demuestra que
el triángulo es equilátero.
5. Considera un triángulo ABC con ángulo recto en A y AB < AC.
Sea D un punto en AC para el cual ∠ACB = ∠ABD. Tira la
altura DE en el triángulo BCD. ¿Si AC = BD + DE, cuánto
miden los ángulos ABC y ACB?
6. Sea n un número compuesto natural. Prueba que existen enteros
a1 , a2 , . . . , ak todos mayores que 1, tales que a1 + a2 + . . . + ak =
n( a11 + a12 + . . . + a1k ).
33
SOLUCIONES DE LOS PROBLEMAS
COMPETENCIA PREOLÍMPICA DE
MATEMÁTICAS
Primera Fase
EXAMEN NIVEL I(4to, 5to y 6to grado)
1. En la figura se pueden ver 10 rectángulos, los cuales aparecen
sombreados en la siguiete imagen:
2. Observe que si escribimos los números que se encuentran en las
posiciones impares (el número de la primera posición, tercera,
quinta, etc.) de la sucesión obtenemos la siguiente lista: 1, 2,
3, 4, 5. De aqui concluı́mos que el número que debe ir en la
undécima posición de la sucesión es el 6. Si hacemos la lista de
los números que quedan en las posiciones pares nos queda de la
siguiente forma: 4, 8, 12, 16. Ası́ que el número que debe ocupar la décima posición de la sucesión es el 20. De esta forma, la
sucesión es 1, 4, 2, 8, 3, 12, 4, 16, 5, 20, 6, . . ..
3. Se pueden formar cuatro: 500, 505, 550 y 555.
4. El peso de las cajas vacı́as es 20 ∗ ( 21 ) = 10 libras, lo que significa
que las papayas pesan 1600 − 10 = 1590 libras.
34
5. El número máximo de puntos comunes que pueden tener es 8. En
la siguiente figura se muestra una de las formas en que esto puede
suceder:
6. Observe que entre el primer y el último árbol existen 9 separaciones. Ası́ que la distancia entre estos es de 9 ∗ 50 = 450 pies.
7. Note que debido a las condiciones del problema se excluye la posibilidad de que dos de las amigas se regalen entre si (por ejemplo,
que Ana le regale a Rosa y que a su vez, Rosa le regale a Ana)
ya que la tercera se quedarı́a sin dar y sin recibir regalo. Con este
dato, es fácil ver que existen 2 posibilidades para la repartición:
• Ana le regala a Marı́a, Marı́a le regala a Rosa y Rosa le regala
a Ana
• Ana le regala a Rosa, Rosa le regala a Marı́a y Marı́a le regala
a Ana
8. Sea x el número de perros que hay en la finca. El número de
patas provenientes de los perros está dado por 4x y similarmente,
el número de patas provenientes de las gallinas está dado por 2x.
Esto significa que el número total de patas es 2x + 4x = 6x y
como x es un número entero, la única de las alternativas que no
se puede descartar es la correspondiente a 6 ∗ 4 = 24 patas.
9. Sea x la cantidad de años que han pasado desde que Mario tenı́a
27. La edad actual de Mario está dada por 27 + x, mientras
que la de Pedro está dada por 3 + x. Como en la actualidad
la edad de Mario es tres veces la edad de Pedro, tenemos que
3 ∗ (3 + x) = 27 + x. Resolviendo la ecuación, obtenemos que
x = 9 y que, por lo tanto, la edad actual de Mario es 36 años.
35
10. Tenemos que A 6= H 6= E, A 6= E y que H 6= 0 pues H ocupa el
lugar de las centenas del número de tres dı́gitos HEE. Observe
que otra manera de representar al número de dos dı́gitos AH es
a través de la suma 10A + H (un ejemplo concreto serı́a 86 =
10 ∗ 8 + 6). Similarmente, el número de tres dı́gitos HEE se puede
representar como 100 ∗ H + 10 ∗ E + E. De la suma original,
obtenemos la ecuación (10 ∗ A + H) + A = (100H + 10E + E), la
cual es equivalente a 11 ∗ (A − E) = 99 ∗ H. Dividiendo por 11
en ambos lados, tenemos que (A − E) = 9 ∗ H. Recordando que
A, E y H son dı́gitos distintos y que la diferencia mayor que se
puede obtener al restar dos dı́gitos es 9; se concluye que H = 1 y
que (A − E) = 9. Se sigue que A = 9, E = 0, la suma original del
problema era 91 + 9 = 100 y que H + E = 1 + 0 = 1.
11. Considere el siguiente diagrama en donde se le ha asignado un
número a cada una de las caras de un cubo (con excepción de la
frontal y de la posterior):
Suponga, sin pérdida de generalidad, que deseamos pintar la cara
1 de color azul. Queremos minimizar la cantidad de colores utilizados, ası́ que necesitamos tratar de repetir los colores. La única
otra cara que puede ser pintada de color azul es la cara 3, pues la
cara 2, la 4, la frontal y la posterior son cada una adyacente a la
cara 1. Suponga ahora que deseamos pintar la cara 2 de amarillo.
Por un análisis similar, concluı́mos que la única cara que también
puede ser pintada de este color es la cara 4. Ahora, nos queda
pintar la cara frontal y la posterior, pero ninguna de estas puede
ser ni azul, ni amarillo; por lo tanto, tienen que ser pintadas de
36
un tercer color. Ası́, el número mı́nimo de colores que se necesitan para pintar las caras de un cubo de tal forma que dos caras
adyacentes no sean del mismo color es 3.
12. Identifiquemos con O al punto medio del lado EG del diagrama
original:
Para simplificar la escritura escribiremos, por ejemplo, BC para
denotar el segmento BC o la medida del segmento BC según el
contexto. De acuerdo al problema, el área del rectángulo ABCD
es 36 unidades cuadradas; por lo tanto, (BC)∗(AB) = 36. Ahora,
el área del triángulo EF G está dado por 21 EG ∗ F O. Observe
que EG = BC y F O = 12 AB, ası́ que el área del triángulo =
( 21 )(BC)∗(( 12 )AB) = ( 12 ∗ 12 )(área del rectángulo ABCD)= 14 ∗36 =
9 unidades cuadradas.
13. Construyamos el cubo de 5 centı́metros de lado de la siguiente
forma: utilizando 25 cubitos de lado 1, formamos un panel. Formamos 5 de estos paneles y los colocamos uno detrás del otro
obteniendo un cubo como el del siguiente diagrama:
Observe que 9 de los cubitos de los 3 paneles que forman el “interior” del cubo de lado de 5 centı́metros quedan ocultos. Es por
37
esto, que el número de cubitos ocultos es 9 ∗ 3 = 27.
14. Para escribir los enteros del 1 al 9, Luis necesita 9 dı́gitos. Para
escribir los enteros del 10 al 99, necesita 2 ∗ 90 = 180 dı́gitos,
mientras que para escribir el número 100 necesita 3. Por lo tanto,
Luis necesita 9 + 180 + 3 = 192 dı́gitos para escribir los enteros
del 1 al 100.
15. Sean b y h las medidas de la base y la altura del triángulo original,
respectivamente. Sean Aoriginal el área del triángulo original y
Amodif icado el área del nuevo triángulo. Tenemos que Aoriginal =
1
∗ b ∗ h y que Amodif icado = ( 12 ) ∗ (1.1b) ∗ (.9h). Trabajando con
2
la segunda ecuación obtenemos Amodif icado = .99 ∗ ( 12 ) ∗ b ∗ h =
.99 ∗ Aoriginal . El área disminuye 1%.
16. Necesitamos saber cada cuanto tiempo las luces se encienden al
mismo tiempo. Esta cantidad está dada por el mı́nimo común
múltiplo de 120 = 23 ∗3∗5 segundos (2 minutos) y 210 = 2∗3∗5∗7
segundos (3 minutos y medio) que es 23 ∗ 3 ∗ 5 ∗ 7 = 840 segundos
(14 minutos). Tenemos que por cada 14 minutos que pasan desde
la media noche, las luces se encienden al mismo tiempo. Esto
significa que esto ocurre a las 12:14 am, 12:28 am, 12:42 am, 12:56
am y 1:10 am, siendo esta última la hora que nos pide el problema.
17. Sea x la medida de un lado del cuadrado original. Considere uno
de los rectángulos que se obtiene al cortar este:
Dicho rectángulo tiene dos lados que miden x y dos lados que
miden x2 y su perı́metro está dado por x + x + x2 + x2 = 18. Resolviendo para x, tenemos x = 6 y el perı́metro del cuadrado
original es x + x + x + x = 6 + 6 + 6 + 6 = 24 centı́metros.
38
18. Sea z el número de espectadores que fueron a la primera y a la
segunda función juntas. Entonces 2z representa la cantidad de
espectadores que fueron a la tercera función y 2 ∗ (2z) representa
la cantidad de espectadores que fueron a la cuarta función. Se
sabe que, en total, se recaudaron $1183; ası́ que 3.5z + 7 ∗ (2z) +
7 ∗ (2 ∗ 2z) = 1183. Simplificando, nos queda que 45.5z = 1183
y que z = 26. Sustituyendo en la expresión para la cantidad de
personas que fueron a la cuarta función, tenemos que esta cantidad
es 2 ∗ (2z) = 4z = 4 ∗ 26 = 104 personas.
19. Como el triángulo original es equilátero y su perı́metro es de 75
centı́metros, cada uno de sus lados mide 25 centı́metros. Si se le
quitan 3 triángulitos equiláteros de 5 centı́metros de lado, la nueva
figura tiene las siguientes dimensiones:
Su perı́metro es 5 + 15 + 5 + 15 + 5 + 15 = 60 centı́metros.
20. Tenemos que analizar dos situaciones: las maneras en que se
pueden acomodar las tres plantas en tres oficinas distinas y las
maneras en que se pueden acomodar las plantas de tal forma que
dos (y solo dos) de estas se encuentren en una misma oficina.
Para el primer caso, note que tenemos 5 posibilidades para acomodar la primera planta, 4 posibilidades (recuerde que estamos
considerando el caso en que ninguna de las 3 plantas se pueden
encontrar en la misma oficina) para acomodar la segunda y 3 posibilidades para acomodar la tercera. En total, tenemos 5∗4∗3 = 60
maneras en las que se pueden acomodar las plantas de tal forma
que cada una se encuentre en una oficina distinta. Ahora, para
el segundo caso (2 plantas se encuentran en una misma oficina, la
39
tercera en otra), suponga que tomamos dos de las plantas; digamos
el cactus y la azalea. Existen 5 posibilidades para acomodarlas,
mientras que para la planta restante (ficus) solamente tenemos
4 posibilidades. Esto significa que existen 5 ∗ 4 = 20 posibles
maneras en las que se pueden acomodar. Ahora, si en vez de considerar la pareja cactus-azalea, consideramos la pareja cactus-ficus
y la pareja ficus-azalea; tenemos 20 + 20 = 40 posibles arreglos
adicionales. Finalmente, el número de formas en que se pueden
acomodar las tres plantas en las cinco oficinas sin que las tres se
encuentren en una misma oficina es 60 + 20 + 40 = 120.
40
COMPETENCIA PREOLÍMPICA DE
MATEMÁTICAS
Primera Fase
EXAMEN NIVEL II(7mo al 12mo grado)
1. Como
2
3
de las teclas son blancas, tenemos 87 ∗ ( 23 ) = 58 de estas.
2. Conchita tenı́a 600 + 200 = $800 al final, ası́ que sus ahorros
originales eran 800 ∗ ( 12 ) = $400.
3. Como Antonio es tı́o de Rosa y papá de Pedro, Rosa y Pedro son
primos.
4. Si el producto es impar, significa que en su factorización prima no
aparece ningún 2. Esto a su vez implica, que en las respectivas
factorizaciones primas de los 5 enteros, no aparece ningún 2. En
otras palabras, los 5 enteros tienen que ser impares.
5. Tenemos que las siguientes ecuaciones se cumplen simultaneamente: 3 + B + C = 18, B + C + D = 18, C + D + E = 18,
D + E + 8 = 18, E + 8 + G = 18, 8 + G + H = 18 y G + H + I = 18.
Despejando para B + C en la primera ecuación, obtenemos que
B + C = 15 y si sustituimos esta cantidad en la segunda; obtenemos que D = 3. Sustituyendo el valor de D en la cuarta ecuación
y resolviendo, obtenemos que E = 7 y si esta cantidad es sustituida en la quinta ecuación y resolvemos, obtenemos que G = 3.
Finalmente, sustituyendo el valor de G en la sexta ecuación, obtenemos que H = 7.
6. Para hallar la cantidad total de divisores positivos de cualquier
entero positivo n, podemos usar su factorización prima. Suponga
ti−1
que la factorización prima de n es n = pt11 ∗ pt22 ∗ . . . ∗ pi−1
∗ ptii .
Entonces, el número de divisores positivos de n está dado por
(t1 + 1) ∗ (t2 + 1) ∗ . . . ∗ (ti−1 + 1) ∗ (ti + 1). En el caso particular
de n = 120, n = 5 ∗ 3 ∗ 23 , ası́ que el número de divisores positivos
es (1 + 1) ∗ (1 + 1) ∗ (3 + 1) = 2 ∗ 2 ∗ 4 = 16.
41
7. Podemos hallar la medida de 3 ángulos del diagrama ya que la
medida de un ángulo llano es 180◦ , ángulos alternos internos tienen
la misma medida y la suma de los tres ángulos internos de un
triángulo es 180◦ :
Ahora, x + 60◦ = 180◦ y resolviendo para x, tenemos x = 120◦ .
8. Note que 102007 es un número que se escribe utilizando un dı́gito
1, seguido de 2007 dı́gitos 0. Si a 102007 , le restamos 2007, obtendremos un número con un 3 en las unidades, un 9 en las decenas,
un 9 en las centenas, un 7 en las milésimas; seguido de 2003 dı́gitos
9. Es por esto, que la suma de los dı́gitos de la resta original es
(2003 ∗ 9) + 7 + 9 + 9 + 3 = 18055.
9. Observe que si el televisor se encuentra en el canal 15 y se aprieta
41 veces el botón para subir el canal, regresaremos a este mismo
canal. Si dividimos 518 entre 41, obtendremos un cociente igual a
12 y un residuo igual a 26. Esto significa que el televisor de Marı́a
pasó 12 veces adicionales por el canal 15 y se detuvo en el canal
15 + 26 = 41.
10. Si Pablo compró el artı́culo con un 15% de descuento, $106.25
es el 85% de la cantidad original. Si x representa la cantidad
original, tenemos la ecuación .85x = 106.25 y si resolvemos para
x, obtenemos x = $125.
11. Note que el cuadrado de un entero cuyo dı́gito de la unidad es 1 es,
nuevamente, un número cuyo dı́gito de la unidad es 1. Es por esto,
que el cuadrado de 81 terminará en 1 y que, a su vez; el cuadrado
del resultado también terminará en 1. No importa cuantas veces
se realice la operación “cuadrar”, el resultado siempre terminará
en 1.
42
12. El número de formas distintas en que se pueden ordenar las letras
de tal manera que la primera y última letra sean vocales es 2 ∗ 3 ∗
2 ∗ 1 ∗ 1 = 12.
13. Suponga que Marı́a miente. Entonces existe por lo menos una
canica que no es negra o no hay 3 canicas. Si hay por lo menos una
que no es negra, Jorge también estarı́a mintiendo, ası́ que todas
son negras; pero entonces Luis estarı́a mintiendo. Suponga ahora
que Jorge está mintiendo. Por un análisis similar, llegarı́amos
a la conclusión de que Marı́a también estarı́a mintiendo ası́ que
descartamos esta segunda posibilidad. Finalmente, si analizamos
lo que sucede al suponer que Luis es el que miente, nos damos
cuenta que la conclusión es consistente con las condiciones del
problema: Marı́a y Jorge dicen la verdad. Por lo tanto, hay 3
canicas en la bolsa.
14. Como el segmento DE y el segmento AB son paralelos, el triángulo
ABC y el triángulo DEC son similares:
Sean x la medida del segmento DC, (ABC) el área del triángulo
ABC, (DEC) el área del triángulo DEC y lAC la medida del
segmento AC. Recordando que la razón entre las áreas de dos
triángulos similares es igual a la razón de los cuadrados de los la(ABC)
AC 2
dos correspondientes tenemos que: (DEC)
= ( llDC
) . Sustituyendo
las expresiones corrspondientes,
(ABC)
3
(ABC)
4
= ( x1 )2 . Expandiendo,
simplificando y resolviendo para x concluı́mos que x =
√
3
2
metros.
15. Sea x la cantidad de carros y z la cantidad de motoras. Tenemos
que x + z = 44 y 4x + 2z = 144. Despejando para x en la primera
ecuación obtenemos que x = 44 − z y sustituyendo en la segunda
nos que da que 4(44 − z) + 2z = 144. Resolviendo para z tenemos
43
que z = 16, ası́ que el número de motoras es mayor que 14 y menor
que 20.
16. Recuerde que las diagonales de un rombo se intersecan formando
un ángulo recto y considere el siguiente diagrama:
Sea r la medida de una de las diagonales, s la medida de la otra
diagonal (con r < s) y z la medida de uno de los lados del rombo.
Note que podemos utilizar el Teorema de Pitágoras para uno de
los triángulos rectángulos, obteniendo ( 2r )2 + ( 2s )2 = z 2 . Como el
problema nos dice que 3s = 4r y r + s = 56, despejando para s
en la primera y sustituyendo en la segunda y resolviendo, tenemos
que s = 32 y r = 24. Sustituyendo estos valores en la ecuación
obtenida del Teorema de Pitágoras y resolviendo, llegamos a z =
20 y como el perı́metro del rombo está dado por 4z, el perı́metro
es 4z = 4(20) = 80 cm.
17. Consideremos la suma del número de pesetas que Mauricio colocó
en cada cuadrado de la primera columna. Este número está dado
por (1+1)+(1+2)+(1+3)+. . .+(1+7)+(1+8) = 1(8)+(1+2+3+
4 + 5 + 6 + 7 + 8) = 8 + 36 = 44. Similarmente, la suma del número
de pesetas que colocó en cada cuadrado de la segunda columna
asciende a (2+1)+(2+2)+(2+3)+. . .+(2+7)+(2+8) = 2(8)+
(1 + 2 + 3 + 4 + 5 + 6 + 7 + 8) = 16 + 36 = 52. De hecho, la suma del
número de pesetas que Mauricio coloca en la i-ésima fila es igual
a i ∗ 8 + 36 (en donde i es algún entero entre 1 y 8). Finalmente,
el número total de pesetas que Mauricio colocó en el tablero es
(1∗8+36)+(2∗8+36)+(3∗8+36)+. . .+(7∗8+36)+(8∗8+36) =
8∗(1+2+3+. . .+7+8)+8∗(36) = 8∗(36)+8∗(36) = 16∗(36) = 576.
18. Para que un número sea divisible por 44, tiene que ser divisible
por 4 y por 11. En particular, para que un número sea divisible
por 4, el número formado al tomar los últimos dos dı́gitos de este
44
tiene que ser divisible por 4. Los únicos números que se pueden
formar bajo las condiciones del problema y que son divisibles por
4 son: 4736, 7436, 3764, 7364, 3476 y 4376. De estos, los únicos
que son divisibles por 11 son el 7436 y el 3476. En otras palabras,
sólo se pueden formar 2 números que son divisibles entre 44.
19. Primero, observe que el triángulo GCF es equilátero. Sea x la
medida de un lado del cuadrado DEF G, r la medida del segmento
AD y el segmento EB respectivamente y considere el siguiente
diagrama:
Tratemos de hallar una expresión para r en términos de x. Para
hacer esto, aplicamos el Teorema de Pitágoras
en el triángulo
√
rectángulo ADG y encontramos que r = 1 − 2x (esto nos sirve
también para concluir que 0 < x < 12 ). Como la medida del segmento AB es 1 metro, tenemos la ecuación 2r + x = 1.
Sustituyendo
la expresión para r en términos de x obtenemos
√
2 1 − 2x + x = 1 y si pasamos x al lado derecho de la ecuación y
luego cuadramos ambos lados, tenemos 4(1 − 2x) = 1 − 2x + x2 .
Esta última ecuación es equivalente a x2 + 6x −√3 = 0 y utilizando
la fórmula cuadrática llegamos a x = −3 ± 2 3. Como x es la
medida de uno de los lados del cuadrado DEF G, esta cantidad
tiene que ser positiva, ası́
√ que descartamos una de las soluciones
y concluı́mos que x = 2 3 − 3 metros.
20. Considere el lado izquierdo de la ecuación original:
x+1
+ x+2
+ . . . + x+100
1
2
100
Esta expresión es equivalente a
x
( x1 + 1) + ( x2 + 1) + . . . + ( 100
+ 1)
Note que tenemos 100 paréntesis y en cada uno de estos el dı́gito 1
aparece como un término. Esto nos permite reescribir la expresión
45
x
como ( x1 + x2 + . . . + 100
) + 100, la cual a su vez, es equivalente
1
a x( 11 + 12 + . . . + 100
) + 100. Sustituyendo esta expresión en el
lado izquierdo de la ecuación original, tenemos x( 11 + 12 + . . . +
1
1
) + 100 = 100. Finalmente, x( 11 + 12 + . . . + 100
) = 0 y como el
100
producto de dos números solo puede ser igual a 0 si y solo si uno
de estos es 0, x = 0. Por lo tanto, −1 ≤ x ≤ 1.
21. Sean d y x la medida de la diagonal y la medida de un lado del
cuadrado pequeño, respectivamente:
Observe que d corresponde a la medida del diámetro del cı́rculo
como también a la medida de un lado del cuadrado grande. Ası́
que el área del cuadrado pequeño Apeq es Apeq = x2 , mientras
que el área del cuadrado grande Agrande es Agrande = d2 . Ahora,
utilizando el Teorema de Pitágoras tenemos que x2 + x2 = d2
2
2
Agrande
y resolviendo obtenemos x2 = d2 . Finalmente, A
= xd2 =
peq
d2
d2
2
= 2. La razón entre el área del cuadrado grande y el área del
cuadrado pequeño es 2.
22. Andrea dice:“Bárbara siempre dice la verdad”, Bárbara dice: Andrea y Carlos siempre dicen la verdad” y Carlos dice: “Andrea
miente”. Estudiemos cada una de las alternativas y descartemos
una por una hasta llegar a la respuesta.
Suponga que los tres dicen la verdad. En particular, Carlos dice
la verdad y afirma que “Andrea miente”, pero esto contradice la
suposición inicial ası́ que descartamos esta posibilidad.
Suponga que los tres mienten. En particular, como Carlos miente
y dice “Andrea miente” significa que Andrea dice la verdad. Esto,
nuevamente, contradice la suposición y descartamos esta posibilidad.
46
Suponga ahora, que Andrea y Bárbara dicen la verdad y que Carlos miente. Como Carlos miente, tenemos que Andrea dice la verdad. Andrea dice “Bárbara siempre dice la verdad” ası́ que lo que
dice Bárbara es cierto. Sin embargo, Bárbara dice que “Andrea y
Carlos siempre dicen la verdad”, lo cual contradice la suposición
de que Carlos miente.
Considere la posibilidad de que Andrea dice la verdad y que Bárbara y Carlos mienten. Como Carlos miente, su enunciado de que
“Andrea miente” es falso, ası́ que Andrea dice la verdad. Pero
Andrea dice “Bárbara siempre dice la verdad” y esto contradice
la suposición de que Bárbara miente.
Finalmente, si realizamos un análisis similar a la única alternativa
que nos queda, concluiremos que es la única en donde no se llega
a una contradicción. Por lo tanto, Andrea y Bárbara mienten,
mientras que Carlos dice la verdad.
23. Note que la suma de los 50 impares que se encuentran en el conjunto es 100 ∗ 25 = 2500 (se pueden formar 25 parejas de números
impares, de tal forma que la suma de los miembros de cada una
de las parejas sea 100 y ninguno de los impares se repita: 1 + 99,
3 + 97, . . . , 47 + 53, 49 + 51).
Considere la posibilidad de que la cantidad mı́nima de números
pares es 2. El conjunto de 50 números distintos cuya suma total
es 3000 estarı́a formado por 48 números impares y 2 pares. Sin
embargo, como la suma de los 50 impares del conjunto original es
2500, la suma de los 48 impares que se escogieron es menor que
esta cantidad. Esto significa que la suma de los 2 pares tendrı́a
que ser mayor que 500 para poder llegar a 3000, pero la suma
mayor de 2 pares distintos es 100 + 98 = 198; ası́ que tenemos que
descartar esta posibilidad.
Por argumentos similares, se pueden descartar las posibilidades
de que la cantidad mı́nima de números pares sean 3, 4 ó 5. Ası́
que la cantidad mı́nima de números pares que puede haber entre
los 50 números que se escogieron al azar es 6. Uno de los conjuntos que cumple con las propiedades descritas por el problema es
{56, 92, 94, 96, 98, 100} ∪ {13, 15, 17, 19, . . . , 91, 95, 97, 99}.
24. Considere el siguiente conjunto: {97, 98, . . . , 115, 116}. En este,
47
hay 6 primos: 97, 101, 103, 107, 109 y 113. Seis primos es el
máximo número que puede haber en un conjunto que cumpla las
condiciones del problema, ya que entre los 20 números hay 10
pares. De los 10 impares restantes hay, al menos, tres múltiplos
de 3; quedando ası́, un máximo de siete candidatos que aún no
pueden ser eliminados. Ahora, en los 20 números hay, al menos;
cuatro múltiplos de 5. De estos, dos son impares y, a lo sumo;
uno de estos impares es múltiplo de 3. Nos quedan entonces, un
máximo de seis candidatos.
25. Sea x el número de exámenes que el estudiante tomó antes de
que su promedio bajó a 22.25 y sea z la última nota. Tenemos
dos expresiones que nos dan el total de puntos acumulados por el
estudiante hasta el momento: 23x + z y 22.25(x + 1). Considere la
ecuación 23x + z = 22.25(x + 1), la cual al despejar para z toma
la forma z = 22.25 − .75x. Si trabajamos con la representación
en fracciones y simplificamos, la ecuación nos queda como z =
1
(89 − 3x). Recordando que 18 ≤ z ≤ 30, 18 ≤ 41 (89 − 3x) ≤ 30.
4
Resolviendo la doble desigualdad para x, obtenemos 1 ≤ x ≤ 5.
Como x y z son números enteros, tenemos que averiguar para
cuál de los posibles valores para x (1,2,3,4 ó 5) obtenemos un
correspondiente valor de z entero. Resulta que solamente para
x = 3, obtenemos un valor de z entero: z = 41 (89 − (3 ∗ 3)) = 20.
El estudiante obtuvo una puntuación de 20 en el último exámen.
26. Sea x la medida de un lado del triángulo equilátero. Como los
perı́metros del triángulo y del rectángulo son iguales, 3x = 2(b+h)
y despejando para x tenemos x = 23 (b + h). Recordando √que
la altura a de un triángulo equilátero de lado x es a = 23 x,
podemos obtener
una√ expresión para el área A4 del triángulo:
√
3
1
A4 = 2 (x)( 2 x) = 43 x2 . Sustituyendo la expresión√para x en
términos de b y de h y simplificando, tenemos A4 = 93 (b + h)2 .
Como el área
√ del rectángulo√3A es A2 =√bh y según el problema A4 = 3A , tenemos 9 (b + h) = 3bh. Expandiendo y
simplificando podemos llegar a la siguiente ecuación equivalente:
b2 − 7bh + h2 = 0. Ahora, dividiendo por h2 en ambos lados de la
ecuación: ( hb )2 − 7( hb ) + 1 = 0. Utilizando la Fórmula Cuadrática
48
√
b
para hb obtenemos hb = 7±32 5 , pero como b > h, la razón
>1y
√ h
7+3 5
b
descartamos una de las soluciones. Finalmente h = 2 .
27. Sea x la medida del radio de S y un lado de Q. La intersección
entre S y Q consiste de una región cuyo volumen es 18 del volumen
de la esfera S y cuya forma es bosquejada en el siguiente diagrama:
Como S es una esfera centrada en uno de los vértices del cubo Q,
con radio igual al lado de Q, la intersección entre S y Q consiste de
una región cuyo volumen es 81 del volumen de la esfera S. Note,
además, que el volumen de esta región es ( 81 )( 34 )πx3 = ( π6 )x3 y
como el volumen del cubo es x3 ; las alternativas que están en
términos del volumen del cubo pueden ser descartadas.
28. Sean r1 , r2 y r3 , con r1 + r2 = 0, las tres raı́ces del polinomio
P (x) = x3 + ax2 + bx + c.
Podemos escribir a P (x) de la siguiente manera:
P (x) = (x − r1 )(x − r2 )(x − r3 ) =
x3 − ((r1 + r2 ) + r3 )x2 + (r1 r2 + r3 (r1 + r2 ))x − r1 r2 r3
En otras palabras:
a = −((r1 + r2 ) + r3 ) = −(0 + r3 ) = −r3
b = r1 r2 + r3 (r1 + r2 ) = r1 r2 + r3 (0) = r1 r2
c = −r1 r2 r3
De las alternativas, la única que siempre es cierta es c = ab.
29. Considere el triángulo isósceles ABC que hemos dibujado en el
siguiente diagrama:
49
Observe que existen 6 posibilidades para la posición del punto Q si
no se tiene en cuenta el orden de las letras en la semejante, esto es,
2 casos en donde AQP ∼ ABC, 2 casos en donde P AQ ∼ ABC y
2 casos en donde AP Q ∼ ABC. Sin embargo, tomando en cuenta
el orden de las letras en la semejante, descartamos los primeros 4
casos y tenemos 2 posibles posiciones para el punto Q:
30. Como quedan 30 cartas (20 de estas no son espadas), el número
de formas en que se le pueden repartir 10 cartas a Bárbara
20!de
20
tal manera que ninguna sea espada está dado por 10 = 10!10! .
Similarmente, el número total de formas (sin importar orden) en
que se pueden escoger 10 cartas de un total de 30 está dado por
30
30!
= 10!20!
. Finalmente, la probabilidad deseada está dada por
10
20!
10!10!
30!
10!20!
=
20!20!
.
10!30!
50
COMPETENCIA PREOLÍMPICA DE
MATEMÁTICAS
Segunda Fase 2007-2008
EXAMEN NIVEL I(4to, 5to y 6to grado)
1. Tenemos 1 caja grande, 4 cajas medianas, 4 ∗ 2 = 8 cajas chicas
y 8 ∗ 3 = 24 cajas de las más pequeñas. En total, Rosita tiene
1 + 4 + 8 + 24 = 37 cajas.
2. Observe que la diferencia entre el segundo y primer término de
la sucesión es 3 − 1 = 2, la diferencia entre el tercer y segundo
término es 7−3 = 4 y la diferencia entre el cuarto y tercer término
es 15 − 7 = 8. Estas diferencias corresponden a las primeras 3
potencias (positivas) de 2 y si seguimos el patrón, la diferencia
entre el quinto y el cuato término deberı́a ser 16. Esto significa
que el quinto término de la sucesión es 31 y, si analizamos las
diferencias entre el sexto y quinto término y entre el séptimo y el
sexto término, el patrón se sigue cumpliendo.
3. En la figura se pueden identificar 10 triángulos:
4. Como la afirmación “Beatriz está al lado de Carlos” es falsa y
Beatriz se encuentra en la silla 3, Carlos está en la silla 1. Ahora,
como Antonio no está entre Beatriz y Carlos; tenemos que Antonio
está en la silla 4. Finalmente, Diana está en la silla 2.
5. Como no pueden quedar dos leones ni dos tigres juntos, el domador
tiene que colocar a los animales en la siguiente forma: tigre-leóntigre-león-tigre. Ahora, cualquiera de los 3 tigres puede ocupar
el primer espacio (de izquierda a derecha), para el segundo espacio tenemos 2 posibilidades, para el tercer espacio 2 posibilidades,
51
mientras que para el cuarto y quinto espacio tenemos una posibilidad; respectivamente. Esto significa que el número de formas
distintas en que puede acomodar las fieras es 3 ∗ 2 ∗ 2 ∗ 1 ∗ 1 = 12.
6. 90 es tres cuartas partes de 120. 3 ∗ 30 = 90, ası́ que el número
que buscamos es 30.
7. Sea y la medida que desconocemos del lado de uno de los rectángulos
sombreados:
Note que la medida de cada uno de los 8 lados de la figura a
considerar que no están rotulados mide 6 centı́metros.
El perı́metro de uno de los cuadrados blancos es 6 + 6 + 6 + 6 =
24 centı́metros y como el perı́metro de uno de los rectángulos
sombreados es el doble de esta cantidad: 6+y +6+y = 2∗24 = 48.
Resolviendo para y, obtenemos y = 18. El perı́metro deseado está
dado por: 6 + 6 + 6 + y + 6 + 6 + 6 + y + 6 + 6 = 6 + 6 + 6 + 18 +
6 + 6 + 6 + 18 + 6 + 6 = 84 centı́metros.
8. Sea x el número de dı́as en una semana de este planeta. Según
las condiciones del problema, hay x semanas en un mes y x meses
en un año. El número de dı́as en un año de este planeta entonces
está dado por x ∗ x ∗ x = x3 . Como hay 1000 dı́as en un año,
tenemos x3 = 1000 y resolviendo para x encontramos que x = 10.
Cada semana tiene 10 dı́as.
9. Luego del primer corte queda 1 − 1 ∗ ( 31 ) = 23 del pastel original.
Luego del segundo corte queda 23 −( 23 )∗( 31 ) = 49 del pastel original.
8
Finalmente, luego del tercer corte queda 49 −( 49 )∗( 13 ) = 27
del pastel
original.
52
10. Sea x la cantidad original. Si le sumo su 10%, obtengo x + .1x =
1.1x. Ahora, si a esta cantidad obtenida le resto su 10% tengo
1.1x − .1 ∗ (1.1x) = .99x, en otras palabras el 99% de la cantidad
original.
11. Si realizamos el producto de todos los impares entre el 1 y el 10
obtenemos 1 ∗ 3 ∗ 5 ∗ 7 ∗ 9 = 945. Considere el producto de todos
los impares entre 11 y 20: 11 ∗ 13 ∗ 15 ∗ 17 ∗ 19. El dı́gito de
las unidades del resultado depende exclusivamente del producto
de los dı́gitos de las unidades de cada uno de los números de la
multiplicación, por lo que 11∗13∗15∗17∗19 termina en 5. Ahora,
el producto de dos números (no importa el número de dı́gitos del
que se componga cada uno) cuyo dı́gito de las unidades es 5 es un
número que también termina en 5. Esto significa que el producto
de todos los números impares entre el 1 y el 20 termina en 5.
Extendiendo este resultado, es fácil ver que el producto de todos
los números impares entre 1 y el 2008 tiene como dı́gito de las
unidades al 5.
12. Si dividimos 375 entre 24, obtenemos que 375 = 24 ∗ 15 + 15. Esto
significa que para enumerar 375 asientos en la forma que describe
el problema, se necesitan 15 filas de 24 asientos cada una y 15
asientos adicionales. En otras palabras, la silla 375 se encuentra
en la fila 16.
13. El número más pequeño de tres dı́gitos que se puede obtener al
borrar dı́gitos del número original es 108.
14. Note que el producto de dos números cuyo dı́gito de las unidades
es 6, es otro número cuyo dı́gito de las unidades es 6. Ahora, si
consideramos el número 16 y extendemos el resultado mencionado;
llegamos a la conclusión de que cualquier potencia positiva de 16
(por ejemplo, 162 , 1610 , etc.) también termina en 6. Observe que
22008 − 2 = (24 )502 − 2 = 16502 − 2. 16502 termina en 6 y si le
restamos 2, el resultado es un número cuyo dı́gito de la unidades
es 4.
53
15. Considere la figura original:
Podemos identificar la medida de uno de los ángulos ya que es
suplementario al de 100◦ :
También, por un resultado en ángulos alternos internos tenemos:
Ahora, como la suma de los ángulos de un triángulo es 180◦ , el
ángulo que forma un ángulo llano con el ángulo de medida x mide
60◦ . Esto implica, que x = 120◦ .
54
COMPETENCIA PREOLÍMPICA DE
MATEMÁTICAS
Segunda Fase 2007-2008
EXAMEN NIVEL II(7mo al 12mo grado)
1. Observe que si el televisor se encuentra en el canal 15 y se aprieta
41 veces el botón para subir el canal, regresaremos a este mismo
canal. Si dividimos 518 entre 41, obtendremos un cociente igual
a 12 y un residuo igual a 26. Esto significa que el televisor de
Claudia pasó 12 veces adicionales por el canal 15 y se detuvo en
el canal 15 + 26 = 41.
2. Con la información dada, se puede terminar que el orden de llegada
fue el siguiente: Luisa llegó primero, luego Arturo, seguido por
Jesús y Rita, luego Raúl y finalmente Pedro.
3. Sea x el número de cerdos y z el número de palomas. Tenemos
que 2x + 2z = 14 y 4x + 2z = 22. Despejando para x en la primera
ecuación, obtenemos x = 7 − z y sustituyendo en la segunda tenemos 4(7 − z) + 2z = 22. Resolviendo, z = 3 y sustituyendo este
valor en la primera ecuación; tenemos x = 4. Hay 4 cerdos y 3
palomas.
4. Denote por AB2 (en donde A y B son enteros, 1 ≤ A ≤ 9 y
0 ≤ B ≤ 9) el número descrito por el problema (por ejemplo,
si el número fuese 532, A = 5 y B = 3). Observe que AB2 =
100A + 10B + 2 y que según el problema (100A + 10B + 2) −
(100(2)+10A+B) = 36. Expandiendo y reagrupando, la ecuación
nos queda como 10(10A − A) + (10 − 1)B − 198 = 36. Si seguimos
trabajando con esta, llegamos a (10A + B) = 26. Esta última
ecuación tiene solución única A = 2, B = 6. El número original
era 262 y la suma de sus dı́gitos es 10.
5. Como AD = DC tenemos ∠DAC = ∠ACD y como AB = AC
tenemos que ∠ABC = ∠BCA. Con esta información y dado al
hecho de que la suma de las medidas de los ángulos internos de un
triángulo es 180◦ , podemos hallar las cantidades necesarias para
resolver el problema.
55
Considere el siguiente diagrama:
La medida del ángulo BAD es 30◦ + 65◦ = 95◦ .
6. Denote por ABCD el número de su ATH (en donde A, B, C y
D representan cada uno de los cuatro dı́gitos). Como ninguno
de los dı́gitos es 0 y el número es múltiplo de 5, D = 5. Además
A+B +C +D = A+B +C +5 = 9 y, por consiguiente, A+B +C =
4. Si unimos esto con el hecho de que el número de su ATH es
mayor que 1995 y que B y C son enteros tales que 1 ≤ B ≤ 9 y
1 ≤ C ≤ 9, llegamos a la conclusión de que A = 2. Por lo tanto,
B + C = 2 y debido a las restricciones del problema y a lo que
hemos deducido, B = C = 1. El número de su ATH es 2115 y el
tercer dı́gito, de izquierda a derecha, es 1.
7. El rectángulo ABCD (cuyo área es 15 cm2 ) está compuesto por
los triángulos congruentes ABM y CDN y por los cuadriláteros
con igual área M P QD y BP QN :
56
El área de cada uno de los triángulos es ( 12 )(3)( 52 ) = 15
cm2 ,
4
15
mientras que el área (total) de los dos cuadriláteros es 15−2( 4 ) =
15
cm2 . Por lo tanto, la superficie del cuadrilátero M P QD tiene
2
15
2
2
=
15
4
= 3.75 cm2 .
8. Observe que en el peor de los casos puede suceder lo siguiente: se
sacan 99 canicas del primer color, luego 99 canicas del segundo
color, luego 99 canicas del tercer color, etc. Esto puede continuar
hasta tener 99 canicas para cada uno de los 20 colores. Es por esto
que para garantizar que en la colección tomada haya por lo menos
100 canicas de un mismo color se deben sacar 99 ∗ 20 + 1 = 1981
canicas.
9. Sean x, (x + 1), (x + 2), . . . , (x + 8) y (x + 9) los 10 enteros
consecutivos y sea (x + k) (k entero y 0 ≤ k ≤ 9) el número que
eliminó. Según el problema, x + (x + 1) + (x + 2) + . . . + (x + 8) +
(x + 9) − (x + k) = 2008. Manipulando la ecuación tenemos que
9x = 1963 + k. Como x es un entero, (1963 + k) es divisible por 9.
El único valor para k que hace esto posible es k = 8, significando
que el número que eliminó de la lista fue (x + 8). Para hallar el
valor de x, considere x + (x + 1) + (x + 2) + . . . + (x + 8) +
(x + 9) − (x + 8) = (10x + 45) − (x + 8) = 2008. Resolviendo,
x = 219 y el número que Juan eliminó fue el x+8 = 219+8 = 227.
10. Note que en los números del 1 al 100, el dı́gito 5 aparece en 5,
15, 25, 35, 45, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 65, 75, 85
y 95, en otras palabras; aparece 20 veces. Realizando un análisis
similar, encontraremos que en los números del 101 al 200, 201
al 300, 301 al 400, 601 al 700, 801 al 900 y 901 al 1000 también
aparece 20 veces (por cada “bloque” de números). En los números
del 401 al 500 aparece 21 veces, mientras que en los números del
501 al 600 aparece 119 veces. Por lo tanto, el dı́gito 5 aparece
8(20) + 21 + 119 = 300 veces en los números del 1 al 1000.
57
11. Los cubos en los que estamos interesados son aquellos que tienen
exactamente dos caras expuestas. Considere el siguiente diagrama:
18 de los cubos que buscamos están identificados por un punto
negro y si le sumamos los 6 cubos que cumplen con las propiedades
y que no se ven en el diagrama, tenemos un total de 24 cubos que
están en contacto con exactamente 4 otros cubos.
12. Observe que 100, 000 ∗ 33 = 3, 300, 000. El problema se reduce
a conseguir aquellos números tartamudos menores que 3,300,000
que son divisibles por 33. Los números tartamudos menores que
3,300,000 son 1,111,111; 111,111; 11,111; 1,111; 111; 11 y 1. Los
únicos de la lista que son divisibles por 3 son 111,111 y 111 y,
entre estos dos, el único que es divisible por 11 es 111,111. Por lo
tanto, el único entero positivo que es menor que 100,000 y que al
multiplicarlo por 33 se obtiene un número tartamudo es el 3367
(3367 ∗ 33 = 111, 111).
13. Si escogemos una casilla negra en particular, tenemos que rechazar
las casillas blancas que se encuentren en la misma fila y en la
misma columna, quedando ası́, 24 casillas blancas que se pueden
escoger. En el siguiente diagrama, se muestran dos casillas negras
y las respectivas casillas blancas que se pueden escoger:
58
Como hay 32 casillas negras, el número de formas en que se pueden
escoger una casilla blanca y una negra de tal forma que las dos no
esten en la misma fila ni en la misma columna es 32 ∗ 24 = 768.
14. Manipulando la ecuación original esta toma la forma
(n2 + n)(n2 + 5n + 6) = (1812 − 1) y si factorizamos; tenemos
n(n + 1)(n + 2)(n + 3) = (181 − 1)(181 + 1). Factorizando una
vez mas, n(n + 1)(n + 2)(n + 3) = 23 ∗ 32 ∗ 5 ∗ 7 ∗ 13. El problema
se reduce a encontrar cuatro enteros consecutivos cuyo producto
concuerde con el lado derecho de la ecuación. Podemos empezar
con el caso en que 13 es el entero menor. Los enteros serı́an 13,
14 = 2 ∗ 7, 15 = 3 ∗ 5 y 16. Observamos que nos sobra 22 ∗ 3 que no
alcanza para formar el 16, ası́ que descartamos esta posibilidad.
Si consideramos los enteros 12 = 22 ∗ 3, 13, 14 = 2 ∗ 7 y 15 = 3 ∗ 5
y realizamos el producto, notamos que los factores coinciden exactamentemente con el lado derecho de la ecuación. Inspeccionando
los otros casos posibles se concluye que esta lista es la única posible. Como n = 12 y (n + 3) = 15, n(n + 3) = 12 ∗ 15 = 180.
15. Sea r el radio del cı́rculo menor, R el radio del cı́rculo mayor y c la
medida de una cuerda de la circunferencia mayor que es tangente
a la circunferencia menor. Considere el siguiente diagrama en
donde se han dibujado las dos circunferencias, una cuerda de la
circunferencia mayor tangente a la circunferencia menor y un radio
de cada cı́rculo que interseca dicha cuerda:
La mitad de la cuerda y los dos radios forman un triángulo rectángulo y si aplicamos el Teorema de Pitágoras: r2 + ( 2c )2 = R2 .
√
Resolviendo para c tenemos c = 2 R2 − r2 . Note que según el
problema, πR2 − πr2 = 25π
ası́ que (R2 − r2 ) = 25
cm2 . Susti2
2
q
√
tuyendo en la expresión para c, c = 2 25
= 5 2 cm.
2
59
OLIMPIADA DE MATEMÁTICAS DE PUERTO
RICO 2008
EXAMEN NIVEL I(4to, 5to y 6to grado)
1. Hay tres lugares que ocupar en la fila. Hay 3 posibilidades para
llenar el primer espacio y luego de hacerlo, quedan dos posibilidades para llenar el segundo. Luego de llenar el segundo, solamente quedarı́a una posibilidad para llenar el tercer espacio. El
número de formas en que se pueden colocar para tomarse la foto
es 3 ∗ 2 ∗ 1 = 6.
2. Sea x en primer número impar. El segundo y tercer número impar
están dados por x + 2 y x + 4, respectivamente. Tenemos que
x + (x + 2) + (x + 4) = 3x + 6 = 27. Resolviendo, tenemos que
x = 7.
3. Observe que la cantidad de números que se necesitan formar debe
ser un factor de 5, ya que esta es la única forma en que la suma
de los miembros de una colección de números cuyo dı́gito de las
unidades es 8 termine en 0. Como tenemos solamente 8 ochos, la
cantidad de números que se necesitan formar es 5. Ası́ que tenemos
5 de los 8 ochos comprometidos para formar 5 números, tenemos
que analizar en donde van los 3 ochos que nos sobran. Existen 3
listas de 5 números a considerar: (88,88,88,8,8), (888,88,8,8,8) y
(8888,8,8,8,8). De estas, la única que satisface las condiciones del
problema es la segunda, pues 888 + 88 + 8 + 8 + 8 = 1000.
4. Como el triángulo ABC es equilátero y su perı́metro es 18 cms,
AC = CB = AB = 6 cm y como CD = AC, CD = 6 cms. Ahora,
note que como el perı́metro del cuadrilátero ACDE es 20 cms y
CD = AC = 6 cms, DE + EA = 20 − 6 − 6 = 8 cms. Por lo tanto,
el perı́metro de ABCDE es 6 + 6 + 6 + 8 = 26 cms.
5. Suponga que Julián pinta de rojo la franja superior. Como no
quiere pintar la del centro ni de blanco ni de negro, puede escoger
entre 5 colores para pintar esta franja; mientras que para la franja
inferior le quedarı́an 6 colores para pintarla. Por lo tanto, Julián
puede obtener 1 ∗ 5 ∗ 6 = 30 banderas distintas con la franja
60
superior roja. Suponga ahora que Julián pinta la franja del medio
roja. Tiene 7 colores entre los cuales puede escoger para la franja
superior y 6 colores entre los cuales puede escoger para la franja
inferior, ası́ que el número de banderas distintas con la franja del
medio roja es 7 ∗ 1 ∗ 6 = 42. Finalmente, el análisis para el caso
en que pinte la franja inferior de color rojo es similar al primer
caso, de donde se obtienen 30 banderas distintas adicionales. El
número total de banderas distintas es 30 + 42 + 30 = 102.
6. Observe que en el tiempo en que el perro da dos saltos, este ha
recorrido 2∗2 = 4 pies. En este mismo periodo, el gato ha recorrido
1 ∗ 3 = 3 pies. De esta forma, la distancia de la casa a la que se
encuentra el perro luego de x de estos periodos está dada por
4x. Similarmente, la distancia de la casa a la que se encuentra
el gato luego de x de dichos periodos es 30 + 3x. Queremos que
4x = 30 + 3x y si resolvemos, x = 30, lo que significa que el perro
alcanzará al gato a 4(30) = 30 + 3(30) = 120 pies de la casa.
7. Considere el siguiente diagrama en donde se ha rotulado cada
vértice con una variable:
Sea z la suma de los números que hay en cada uno de los vértices
de una cara. Tenemos el siguiente sistema de ecuaciones:
a+b+c+d=z
a+c+g+e=z
e+f +g+h=z
b+d+f +h=z
a+b+e+f =z
c+d+g+h=z
61
Sumando las 6 ecuaciones y simplificando, tenemos
3(a + b + c + d + e + f + g + h) = 6z
Como a + b + c + d + e + f + g + h = 36, z = 18, en otras palabras;
la suma de los números que aparecen en los vértices de cada cara
tiene que ser 18. Observe ahora, que podemos formar 4 parejas
de números cuya suma es 9: 1 + 8 = 2 + 7 = 3 + 6 = 4 + 5 = 9.
Si desarrollamos una estrategia adecuada de tal forma que dada
una cara en particular, tengamos dos de estas parejas ocupando
los vértices (2 ∗ 9 = 18), habremos terminado. Coloquemos al 1 y
al 8 en los vértices que se muestran:
Note que, en particular, la suma de los números que vamos a
colocar en la cara superior debe ser 18. Como ya colocamos al 1,
debemos escoger 3 números cuya suma sea 17. Con los números
que nos quedan, la única alternativa es utilizar al 4, 6 y 7. Una
forma de colocarlos es la siguiente:
Finalmente, rotulamos los vértices de la cara inferior que no han
sido ocupados de la siguiente manera: dado un vértice en particular, miramos el número del vértice que se encuentra justamente
arriba y escribimos el número que al sumarle a este, nos da como
resultado 9.
62
Realizando esto, nos queda:
Con esta estrategia, tenemos varias formas de colocar los números,
en otras palabras; la solución no es única.
8. Si 360◦ equivalen a 100% del pastel, 15% equivale a
360◦ ∗15
100
= 54◦ .
9. Para escribir los números impares entre 1000 y 1099 se necesitan
55 dı́gitos 0. Por otro lado, para escribir los números impares del
1100 al 1199, 1200 al 1299, 1300 al 1399, 1400 al 1499, 1500 al
1599, 1600 al 1699, 1700 al 1799, 1800 al 1899 y 1900 al 1999, se
necesitan 5 dı́gitos 0 respectivamente. Finalmente, para escribir
los números impares del 2000 al 2008 se necesitan 8 dı́gitos 0. Es
por esto que Juan escribió 55 + 9(5) + 8 = 108 veces el dı́gito 0.
10. Aná está sola en 8 fotos, Camilo está solo en 10 fotos y Marı́a
siempre está sola en las fotos. Como Ana sale en 19 fotos en total,
significa que sale en 19 − 8 = 11 fotos con Camilo. Por lo tanto,
Marı́a sale en 35 − 8 − 10 − 11 = 6 fotos.
63
OLIMPIADA DE MATEMÁTICAS DE PUERTO
RICO 2008
EXAMEN NIVEL II(7mo al 12mo grado)
1. Sea x el número de páginas que tiene el libro. Además, sean
m, a y l el número de dı́as adicionales al primero que le tomó a
Marı́a, Ana y a Luis terminar de leerlo, respectivamente. Según el
problema, x = 7 + 10m = 2 + 11a = 5 + 9l. Como x es un entero
tal que 0 < x < 300, tenemos que los enteros m y l son tales que
1 ≤ m ≤ 29 y 1 ≤ l ≤ 27. Sustituyendo cada uno de los posibles
valores para m y l en las expresiones para x correspondientes, nos
damos cuenta que los únicos posibles valores para x que aparecen
repetidos son 167 (m = 16 y l = 15) y 277 (m = 27 y l = 25).
Observando la expresión x = 5+9l nos damos cuenta que al dividir
el valor de x por 9, el residuo es 5. Como esto sólo se cumple para
167, descartamos la otra posibilidad.
2. Javier tiene a escoger entre 6 letras y 5 dı́gitos para formar la
letra (en
clave que posee la siguiente estructura: letra
donde los espacios del medio deben ser ocupados por una letra y
tres dı́gitos). Observe que tenemos 10 formas de escoger los tres
dı́gitos que utilizaremos para la parte del medio de la clave. Los
10 conjuntos son: {1, 3, 5}, {1, 3, 7}, {1, 3, 9}, {1, 5, 7}, {1, 5, 9},
{1, 7, 9}, {3, 5, 7}, {3, 5, 9}, {3, 7, 9} y {5, 7, 9}. Note que como
los dı́gitos deben ponerse en forma creciente o decreciente, existen
2 “órdenes” asociados a cada uno de los conjuntos (por ejemplo,
considere el conjunto {1, 3, 5}, podemos escribirlos como 1-3-5 o
como 5-3-1), elevándose a 2 ∗ 10 = 20 las formas en escribir los
dı́gitos en la parte del medio de la clave. Considere el caso en
que Javier pone una letra en el segundo espacio (de izquierda a
derecha): tiene 6 posibilidades para llenar el primer espacio, 5
posibilidades para llenar el segundo, 4 posibilidades para llenar el
último y 20 posibilidades (los dı́gitos) para llenar los tres espacios
restantes. El número de posibles claves de este estilo es 6 ∗ 5 ∗
4 ∗ 20 = 2400. Estudiando el caso en donde Javier pone una
letra en el tercer espacio, el caso en donde pone una letra en el
cuarto espacio y el caso en donde pone una letra en el quinto; nos
damos cuenta que existen también 2400 claves adicionales para
64
cada uno de estos. Por lo tanto, Javier puede armar la clave en
4 ∗ 2400 = 9600 formas distintas.
3. Sea x la distancia recorrida en la primera hora. Según el problema,
la hormiga recorre una distancia de ( 23 )x en el segundo periodo
de una hora y ( 23 )( 32 )x = ( 49 )x en el tercer periodo de una hora.
Además, x + ( 23 x) + ( 49 )x = 76 y resolviendo, x = 36 cms.
4. Considere el siguiente diagrama:
Observe que como el ángulo BOC y el ángulo COA forman un
ángulo llano, ∠BOC = 144◦ . Además, como el segmento OB y
el segmento OC corresponden cada uno a un radio del cı́rculo; los
respectivos ángulos que los sostienen miden lo mismo. Sea x la
medida del ángulo CBO y considere la ecuación x + x + 144◦ =
180◦ . Resolviendo, obtenemos x = 18◦ , ası́ que la medida del
ángulo CBO es 18◦ .
5. Sea x el número de niños, n el número de niñas, z la suma de las
edades de todos los niños y niñas, r la suma de las edades de los
niños y s la suma de las edades de las niñas. Según el problema:
z
= 7.4 (z = 296), xr = 8 (r = 8x) y ns = 7 (s = 7n).
x + n = 40, 40
Además, tenemos que z = r + s y si sustitumos las expresiones
correspondientes: 296 = 8x+7n. Si multiplicamos por 7 en ambos
lados de la ecuación x + n = 40 y restamos la ecuación resultante
de la ecuación anterior, obtenemos x = 16. Sustituyendo ahora
este valor en la ecuacion x + n = 40 y resolviendo, obtenemos
n = 24. Por lo tanto, habı́a 16 niños y 24 niñas.
6. Contemos aquellos números de cuatro dı́gitos que tienen exactamente un dı́gito 1 y un dı́gito 0. Todo número que tenga esta
propiedad, tiene que ser de uno de los siguientes 9 estilos: 10 ,
65
1 0 , 1 0, 10 , 1 0, 01 , 10, 0 1 ó 01. Cada uno de los espacios en blanco puede ser llenado de 8 formas distintas, ası́ que la
cantidad de números de cuatro dı́gitos con exactamente un dı́gito
1 y un dı́gito 0 es 9 ∗ 8 ∗ 8 = 576. Similarmente, podemos realizar
conteos para los demás casos.
En la siguiente tabla resumimos los resultados:
Cantidad dı́gitos 1 Cantidad dı́gitos 0 Números
1
1
576
1
2
48
1
3
1
2
1
72
2
2
3
3
1
3
Por lo tanto, existen 576 + 48 + 1 + 72 + 3 + 3 = 703 números de
4 dı́gitos que tienen por lo menos un dı́gito 1 y un dı́gito 0.
7. Observe que 40 solamente puede ser expresado como la suma de
tres cuadrados perfectos de la siguiente forma: 40 = 0 + 4 + 36.
Esto nos produce un conjunto de sistemas de ecuaciones:
x+y+z =a
x+y−z =b
x−y+z =c
Note que a 6= b 6= c y a 6= c, a = 0, 2 o 6, b = 0, ±2 o ±6 y c = 0, ±2
o ±6. Si a = 0, no tenemos solución no negativa ya que x+y +z =
0 implica que por lo menos una de las variables es negativa (las
tres variables no pueden ser igual a 0 simultáneamente). Si a 6= 0,
tenemos que b = 0 o c = 0 y note que en ambos casos al sumar
las últimas dos ecuaciones del sistema; obtenemos 2x = (b + c).
Resolviendo, x = b+c
. Si b = 0, c no puede ser negativa pues x
2
lo serı́a también, ası́ que descartamos este caso. Similarmente, se
66
descarta la posibilidad de que b sea negativa. Resumiendo estos
resultados, hemos disminuido significativamente la cantidad de
sistemas de ecuaciones a inspeccionar a 4, pues ahora a = 2 o
6, b = 0, 2 o 6 y c = 0, 2 o 6. El caso en que a = 2, los dos
sistemas de ecuaciones asociados no producen soluciones no negativas, mientras que los dos sistemas de ecuaciones asociados al
caso en que a = 6 producen (1, 2, 3) y (1, 3, 2) (el primer número
de cada terna es el valor de x, el segundo el valor de y y el tercero
el valor de z).
8. Considere el siguiente diagrama en donde, además de utilizar la
información dada por el problema, hemos trazado el segmento
OD:
Aplicando el Teorema de Pitágoras en el triángulo OT D: OD2 =
OT 2 + 12 . Manipulando la ecuación obtenemos 1 = OD2 − OT 2
y factorizando: 1 = (OD + P T )(OD − OT ). Observe que OD =
AO y al sustituir en la última ecuación tenemos que 1 = (AO +
OT )(AO −OT ). Finalmente, como (AO +OT ) = AT , AT ∗(AO −
OT ) = 1.
9. Sean a y b las medidas de los catetos. Por el Teorema de Pitágoras,
tenemos a2 + b2 = 2006. Observe que la operación “cuadrar” conserva paridad, es decir, el cuadrado de un número par es par y
el cuadrado de un número impar es impar. Además, la única
forma de que la suma de dos números sea par, es que ambos sean
pares o que ambos sean impares. Considere el caso en que a y
b sean pares. Esto significa que para algún k y algún l (enteros)
se pueden escribir de la siguiente forma: a = 2k, b = 2l. Sustituyendo, (2k)2 + (2l)2 = 4(k 2 + l2 ) = 2006. Como la expresión
67
que está dentro del paréntesis es un entero, la ecuación nos está
diciendo que 2006 es divisible por 4; pero como esto es falso significa que este caso no produce solución. Suponga ahora que a
y b son impares. Recuerde que todo número impar deja residuo
1 o residuo 3 al ser dividido entre 4. Debido a esto, tenemos 3
casos a considerar: a y b dejan residuo 1 al ser divididos entre 4,
a y b dejan residuo 3 al ser divididos entre 4 o uno deja residuo
1 y el otro deja residuo 3 al ser divididos entre 4. Suponga que
ambos dejan residuo 1. Podemos escribir a = 4k + 1 y b = 4l + 1
y sustituyendo en la ecuación asociada al Teorema de Pitágoras:
(4k + 1)2 + (4l + 1)2 = 2006. Expandiendo y factorizando, tenemos
8(2(k 2 + l2 ) + k + l) = 2004, lo cual es una contradicción ya que 8
no divide a 2004; significando que este caso no produce soluciones.
Suponga ahora que a y b dejan residuo 3 al ser divididos entre 4.
Tenemos a = 4k + 3 y b = 4l + 3. Luego de sustituir como en el
caso anterior y manipular adecuadamente la ecuación resultante,
obtenemos: 8(2(k 2 + l2 ) + 3(k + l)) = 1988. Nuevamente llegamos
a una contradicción. Finalmente, suponga que uno deja residuo
1 y el otro deja residuo 3 al ser divididos entre 4. Considere, sin
pérdida de generalidad, que a = 4k + 1 y b = 4l + 3. Realizando
lo mismo que para los casos anteriores, llegaremos a la ecuación
8(2(k 2 + l2 ) + k + 3l) = 1996, obteniendo nuevamente una contradicción. Por lo tanto, no existe ningún triángulo
con catetos
√
de longitud entera e hipotenusa de longitud 2006.
√
10. Considere la desigualdad original √x+6−8 √x−2 ≤ 6 − x + 1. Note
que el dominio de la expresión, es decir los valores posibles para
x, son todas las x reales tales que x ≥ 2. Si racionalizamos el lado
izquierdo, tenemos:
√
√
√
8( x + 6 + x − 2)
≤6− x+1
(x + 6) − (x − 2)
Luego
de combinar términos semejantes, cancelar factores y sumar
√
x + 1 en ambos lados:
√
x+6+
√
x−2+
√
x+1≤6
El dominio de esta expresión es nuevamente todas las x reales tales
68
que x ≥ 2. Observe que la expresión de la izquierda es creciente
en todo el dominio y si la evaluamos en x = 3:
√
x+6+
√
x−2+
√
x+1=
√
9+
√
1+
√
4=6
Es por esto que las soluciones de la desigualdad original son todas
las x reales tales que 2 ≤ x ≤ 3.
69
OLIMPIADAS DE MATEMÁTICAS
DE PUERTO RICO
EXAMEN DE SELECCIÓN
1. Por inspección, nos damos cuenta que para el número 18 sólo existe
un número que sumado a este, el resultado nos da un cuadrado
perfecto: el 7. Esto significa que el 18 tiene que escribirse en
uno de los extremos del rectángulo 1x25. Además, para cada
uno de los siguientes números, existen exactamente dos números
que satisfacen la condición necesaria (esto es, que la suma sea un
cuadrado perfecto, por ejemplo; para el 8 tenemos al 1 y al 17):
8, 9, 10, 16, 17, 19, 20, 21, 22, 23 y 25. Aprovechando estos datos,
podemos formar las siguientes sucesiones:
1-8-17-19-6-10-15-21-4
3-22-14
2-23-13
11-25-24
5-20-16-9-7-18
En estas, hemos utilizado todos los enteros de la lista, con excepción del 12. Para terminar, tenemos que escribir las 5 sucesiones (añadiendo el número 12) una detrás de la otra, respetando
la condición del problema. En la siguiente tabla, mostramos los
números que sumados a cada uno de los números que se encuentran en los extremos de las sucesiones (añadiendo el 12), producen
un cuadrado perfecto:
70
Número escrito en extremo Números que sumados al original
producen cuadrado perfecto
1
3,24
4
5,12
3
1,13
14
2,11
2
14
13
3,12
11
5,14
24
1,12
5
4,11
12
4,13,24
Observe que el 2 solo puede ir al lado del 14. Esto nos obliga a
escribir el 11 al lado del 5, mientras que el 4 tiene que se escrito
al lado del 12. Las sucesiones quedan de la siguiente forma:
1-8-17-19-6-10-15-21-4-12
24-25-11-5-20-16-9-7-18
3-22-14-2-23-13
Finalmente, si escribimos el 1 al lado del 24 y el 13 al lado del 12,
tendrı́amos una de las distribuciones posibles:
3-22-14-2-23-13-12-4-21-15-10-6-19-17-8-1-24-25-11-5-20-16-9-7-18
2. Denote por ab, cd y ef los tres números que se forman (si ab = 23,
por ejemplo, a = 2 y b = 3). Considere la suma de estos: ab + cd +
ef = (10a+b)+(10c+d)+(10e+f ) = 10(a+c+e)+(b+d+f ). El
problema se reduce a determinar los posibles valores para (a+c+e)
y los correspondientes valores para (b + d + f ) y estudiar las sumas
obtenidas. Note que (a + b + c + d + e + f ) siempre es 21 y que
la suma de tres números distintos escogidos al azar entre 1, 2, 3,
4, 5 y 6 es mayor o igual que 6; pero menor o igual que 15 (en
donde cualquier entero que se encuentre en este intervalo puede ser
obtenido). Teniendo en cuenta estos datos, podemos concluir que
para cada posible valor de (a + c + e) existe exactamente un valor
correspondiente para (b + d + f ). Existen 10 casos a considerar,
los resultados están resumidos en la siguiente tabla:
71
(a + c + e) (b + d + f ) 10(a + c + e) + (b + d + f )
6
15
75
7
14
84
8
13
93
9
12
102
10
11
111
11
10
120
12
9
129
13
8
138
14
7
147
15
6
156
Por lo tanto, se pueden obtener 10 resultados distintos siguiendo
las instrucciones del problema.
3. Demostraremos el resultado por contradicción. Suponga que al
final, 10 piedras fueron extraı́das, ningunas 3 sucesivas fueron del
mismo color y que la quinta y sexta piedra son del mismo color.
Tenemos que considerar dos casos: cuando la quinta y sexta piedra
son azules y cuando la quinta y sexta piedra son rojas. Consideremos el primer caso. Denotemos por a una piedra de color azul,
por r una de color rojo y por x una piedra cuyo color será determinado. Como la quinta y sexta piedra (de izquierda a derecha)
son azules, tenemos xxxxaaxxxx. Ahora, como no hay 3 piedras
sucesivas del mismo color, la cuarta y séptima piedra tienen que
ser rojas: xxxraarxxx. Tomando, nuevamente, en cuenta el hecho de que no hay 3 piedras sucesivas del mismo color; llegamos
a la conclusión de que las únicas posibilidades para los colores
de las primeras 3 piedras son: aar, rar, raa y rra. Similarmente, las únicas posibilidades para los colores de las últimas 3
piedras son: raa, rar, aar y arr. Como 5 piedras tienen que ser
rojas y 5 tienen que ser azules, existen 8 posibles arreglos que
satisfacen esta condición: aarraarrar, aarraararr, rarraarraa,
rarraaraar, raaraarrar, raarraaraar, rraraarraa y rraraararr.
Sin embargo, tenemos que descartar todos estos arreglos, pues el
primero, segundo, quinto y sexto tenı́an que detenerse al sacar la
cuarta piedra (en cada uno de estos casos tendrı́amos 2 piedras ro72
jas y dos azules); mientras que el tercero, cuarto, séptimo y octavo
tenı́an que detenerse al sacar la sexta piedra. Por lo tanto, si la
quinta y sexta piedra son azules; no se pueden cumplir las condiciones del problema. Similarmente, para el caso en que suponemos
que la quinta y sexta piedra fueron rojas, llegamos a una contradicción del mismo tipo. Por lo tanto, si al final del juego se
extraen 10 piedras y ninguna 3 consecutivas son del mismo color,
entonces la quinta y sexta son de distintos colores. Por ejemplo,
aaraarrarr es un arreglo en donde las condiciones del problema
se cumplen y la quinta y sexta piedra son de distinto color.
4. Sean a, b y c la medida de los lados del triángulo, las cuales satisfacen a + b − c = 2 y 2ab − c2 = 4. Tenemos que (a + b − c)2 =
22 = 4 = 2ab − c2 , o sea, (a + b − c)2 = 2ab − c2 . Expandiendo
el lado izquierdo, (a2 + 2ab − 2ac − 2bc + b2 + c2 ) = (2ab − c2 ).
Restando 2ab a ambos lados y manipulando los términos de la
ecuación resultante tenemos que (b2 − 2bc + c2 ) = (−a2 + 2ac − c2 ).
Factorizando, (b − c)2 = −((a − c)2 ) y como cualquier número
elevado al cuadrado es 0 o positivo; la única forma de que la
ecuación se cumpla es que (b − c) = (a − c) = 0. Por lo tanto,
a = b = c, lo que significa que el triángulo es equilátero.
5. Demostraremos primero un resultado que será utilizado para obtener las medidas de los ángulos que nos pide el problema. Sean
w, x, y y z enteros positivos tales que x < z y y > w. Si xy = zw
y x + y = z + w, entonces y = z y x = w. Demostración:
Suponga que las hipótesis se cumplen y considere x + y = z + w.
Multiplicando por yz a ambos lados de la ecuación y expandiendo,
tenemos (xy)z + y 2 z = yz 2 + y(zw). Como xy = zw, podemos
reemplazar en esta ecuación para obtener z 2 w + y 2 z = yz 2 + xy 2 .
Factorizando, tenemos que y 2 (z − x) = z 2 (y − w). Ahora, de la
segunda ecuación de la hipótesis tenemos que z − x = y − w.
Reemplazando, y 2 (z − x) = z 2 (z − x) y como (z − x) 6= 0 (x < z)
podemos dividir en ambos lados para obetener y 2 = z 2 . De esta
ecuación, tenemos que y = z y, finalmente; x = w.
Regresando al problema original, sea α la medida del ángulo ACB
y del ángulo ABD. Considere el siguiente diagrama:
73
Note que como los triángulos ABD y ECD son similares, tenemos
AD
que ED
= BD
, de donde se obtiene que AD ∗ CD = BD ∗ ED.
CD
También, AD + CD = AC y como según el problema, AC =
BD + DE; tenemos que AD + CD = BD + DE. Observe que
AD < BD (AD es cateto del triángulo rectángulo ABD y BD
es la hipotenusa) y que DE < CD (argumento similar, usando
triángulo rectángulo DEC). Analizando todos estos datos, nos
damos cuenta que se cumplen las condiciones del resultado demostrado al principio, por lo tanto; AD = DE y BD = CD.
Esto implica que los triángulos rectángulos ABD y EBD son congruentes y que, en particular, ∠ABD = ∠EBD = α. Finalmente,
tenemos 2α + α = 90◦ y resolviendo; α = 30◦ . Esto implica que
∠ACB = 30◦ y ∠ABC = 60◦ .
6. Sea n un número compuesto natural. Observe que este puede ser
escrito de la forma n = a ∗ b, en donde a y b son enteros y a, b > 1.
Considere a ∗ b( a1 + 1b ). Simplificando esta expresión, nos damos
cuenta que es igual a (a + b), lo cual satisface las condiciones del
problema.
74

Examen Canguro Matemático 2015 Nivel Benjam´ın

Enunciados de los problemas

Segunda Fase,, Nivel 1 - Olimpiada Nacional Escolar de Matemática

Enigmas lógicos - Olimpiadas Regionales de Matemática

¿Cuántos números reversibles?

Publicaciones AFAMaC OMPR Olimpiadas de Matemáticas de

Examen Canguro Matemático 2015 Nivel Benjam´ın

Enunciados de los problemas

Segunda Fase,, Nivel 1 - Olimpiada Nacional Escolar de Matemática

Enigmas lógicos - Olimpiadas Regionales de Matemática

¿Cuántos números reversibles?

EsDocs.com