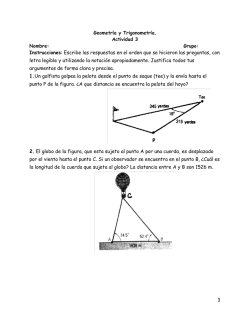
Ondas estacionarias en una cuerda tensa
FS-200 Fı́sica General II UNAH Universidad Nacional Autónoma de Honduras Facultad de Ciencias Escuela de Fı́sica Ondas estacionarias en una cuerda tensa Objetivos 1. Producir los modos normales de vibración de una cuerda fija en los extremos. 2. Calcular la frecuencia de un oscilador mecánico que produce las ondas estacionarias en la cuerda fija en los extremos. 3. Establecer y demostrar la relación entre la tensión en una cuerda y su longitud, con la cantidad de nodos y antinodos de una onda estacionaria que se forma en la cuerda Materiales y equipo 1. Montaje especial con cuerda (hilo de ‘nylon’), vibrador, prensas y polea 3. Vaso de plástico 2. Balanza granataria 5. Cinta métrica 6. Soporte de mesa, nuez y varilla roscada 4. Recipiente con agua 7. Transportadores Figura 1: Modos diferentes de ondas estacionarias en una cuerda a frecuencia de oscilación constante y tensión en la cuerda variable. 1 FS-200 Fı́sica General II UNAH Marco teórico Se llaman ondas estacionarias, por contraposición de ondas viajeras, a aquellas mediante las cuales no se puede transmitir energı́a. Es sencillo producirlas generando ondas mecánicas en una cuerda fija en ambos extremos o utilizando ondas sonoras en un tubo cerrado o abierto en un extremo, en el primer caso las ondas estacionarias son transversales y en el segundo caso son longitudinales. La manera habitual de crear este tipo de ondas consiste en permitir la interferencia entre ondas incidentes y reflejadas. Si una onda incidente, inicialmente viajera, es de la forma yinc = Asen(kx− ωt) y una reflejada necesariamente habrá de representarse como yref = Asen(kx + ωt) de forma que la onda resultante de la interferencia de estas dos: 1. Tiene dirección opuesta a la incidente, de ahı́ el cambio de signo en el argumento del coseno 2. Debido a que el extremo en donde la onda incidente choca está fijo, la onda reflejada cambia de fase en π . Entonces, cuando interfiere una incidente con una reflejada la onda resultante presenta la forma: y(x, t) = yinc (x, t) + yref (x, t) = 2Asen(kx)cos(ωt) (1) De este tipo de onda resultante vale la pena hacer notar las siguientes cosas: 1. Ya no es una onda viajera, pues no tiene el argumento caracterı́stico:kx ± ωt 2. Para un determinado punto de la cuerda en x = x0 , la ecuación para y(x0 , t) representa la ecuación del movimiento armónico simple de ese elemento del medio en x = x0 , para cualquier tiempo t. Es decir: y(x0 , t) = 2Asen(kx)cos(ωt) Donde la amplitud de oscilación de ese punto es evidentemente A(x0 ) = 2Asen(kx) 3. Este valor de amplitud muestra que un punto o elemento de la cuerda en x = x0 oscila con amplitud igual a 2Asen(kx0 ), mientras que hay elementos del medio que oscilan con amplitud 2A (cuando sen(kx0 ) = 1), en esa posición se dice que se genera un antinodo de la onda estacionaria, y que hay puntos o elementos del medio que no oscilan nunca o que tienen amplitud de oscilación igual a cero (cuando sen(kx0 ) = 0), en esa posición se dice que se genera un nodo de la onda estacionaria. 4. Si tomamos un cierto valor fijo para el tiempo,t = t0 , y(x, t0 ) representa la forma senoidal que adopta la cuerda en ese momento: y(x, t0 ) = α(t0 )sen(kx), donde ahora α(t0 ) = 2Acos(ωt0 ). 5. En este caso el valor para la amplitud nos permite entender que habrá momentos en que la cuerda esté completamente horizontal, cuando cos(ωt) = 0, y otros momentos en que la sinusoide tendrá amplitud máxima, 2A, cuando cos(ωt) = 1. 2 FS-200 Fı́sica General II UNAH Modos normales de vibración en una cuerda tensa Debido a que la cuerda está inicialmente sujeta fijamente en sus extremos, en ellos no puede haber oscilación; entonces si llamamos L a la longitud de la cuerda, obligatoriamente ha de cumplirse que: en el primer extremo en x = 0; y(0, t) = 0 0 y en el segundo extremo en x = L; y(L, t) = 0. La primera condición impuesta se cumple inmediatamente en la ecuación 1; el imponer la segunda lleva a que:sen(kL) = 0. De ahı́ que los distintos valores que puede presentar k para que sea posible la anulación en el extremo x = L nos dan las distintas longitudes de onda que puede presentar la cuerda de modo que sean acordes con el hecho obligado de no oscilación en los extremos fijos. Estos valores corresponden a kL = π, 2π, 3π, ..., nπo de forma equivalente: λn = 2L, 2L 2L 2L , , ..., 2 3 n (2) Este resultado nos dice que la cuerda fija en esos extremos solo puede vibrar con esas longitudes de onda, y por lo tanto baj o unas frecuencias igualmente bien definidas. A cada uno de esos modos de vibración se les denomina MODOS NORMALES DE VIBRACIÓN, o también ARMÓNICOS, y cada uno de ellos aparece visualmente con la forma caracterı́stica de un cierto número de bucles: Cada bucle mide una media longitud de onda. Si la cuerda forma un bucle, ello indica que la cuerda está en el primer armónico; si hay presentes dos bucles, la cuerda vibra en el segundo armónico, y si hay tres bucles, vibre en el tercer armónico, y ası́ sucesivamente. La relación frecuencia-longitud de onda-velocidad nos permite decir también: s v n T v = (3) =n fn = λn 2L 2L µ Donde: f , frecuencia en Hz; v, velocidad de la onda en m/s; λ, longitud de onda en m; L, longitud de la cuerda en m T , tensión a que la cuerda esté sometida en N; µ, densidad lineal de masa de la cuerda en kg/m n, número natural que indica en qué armónico o modo normal está vibrando la cuerda. 3 FS-200 Fı́sica General II UNAH Montaje experimental para la formación de ondas estacionarias en una cuerda tensa Para observar en el laboratorio los antes llamados bucles, la técnica habitual es hacer que uno de los extremos de la cuerda quede unido a un vibrador de frecuencia constante y que el otro permita regular la tensión a la que se somete la cuerda. (a) (b) (c) Figura 2: Fotografı́as del montaje a utilizar en el laboratorio. (a) Vibrador, (b) Polea y soporte, (c) Vaso con agua para aumentar o reducir la tensión en la cuerda. Figura 3: Esquema básico del montaje a utilizar en el laboratorio. 4 FS-200 Fı́sica General II UNAH Cuando una onda incidente y otra reflejada con las mismas caracterı́sticas se interfieren en la cuerda, se forma un patrón de onda estacionaria que se caracteriza por la formación de bucles vibrantes, la formación de estas ondas estacionarias en la cuerda se da bajo ciertas condiciones especı́ficas, para nuestro caso en el laboratorio tenemos la facilidad de cambiar: 1. La velocidad de propagación de la onda. 2. La longitud de la cuerda en donde se forman las ondas estacionarias. Para entender mejor cómo desarrollar esta experiencia, y teniendo en cuenta que T = mg, reescribimos la ecuación (3) de modo que podamos examinarla desde el punto de vista de nuestro laboratorio: 4f 2 µ n2 = (4) g m Donde se ha sustituido la tensión en la cuerda T por mg donde m corresponde a la masa del vaso con agua, analizando un poco esta ecuación podemos apreciar que al aumentar la masa colgante aumenta la tensión en la cuerda y esto tiene como resultado una reducción en el valor entero n 2 , es decir que se observarán menos bucles de onda estacionaria a medida que la tensión en la cuerda aumenta, y se observarán mas bucles a medida que la tensión en la cuerda disminuye. Obs: Note que en esta experiencia el extremo en que está el vibrador no está fijo. Pero ello no altera esencialmente los resultados ya que solo se toman en cuenta las mediciones desde el primer nodo. Procedimiento experimental 1. Antes de conectar el vibrador: Asegúrese de que en el montaje, la polea y el vibrador está bien firmes sobre la mesa. 2. Proceda a medir la masa (Figura 4), y la longitud de una sección de cuerda que servirá para determinar la densidad lineal de masa de la cuerda a utilizar, anote su valor. µ= kg/m (5) También anote estos valores en el Cuadro 1. Figura 4: Sección de cuerda en 3. Encienda el vibrador y coloque lentamente cierta cantidad la balanza. de agua en el vaso hasta que se forme una onda estacionaria. Tenga muy en cuenta que una onda estacionaria válida será aquella que no forma un óvalo tridimensional como bucle, sino aquella que forma bucles “planos”. 4. Una vez que haya obtenido su primera forma de onda estacionaria no coloque más agua en el vaso y procesa a medir la longitud desde el primer nodo hasta la polea (es decir de nodo a nodo en los extremos de la onda estacionaria), anote esta cantidad, ası́ como el número de nodos y antinodos en el Cuadro 1. 5. Obtenido el modo normal, mida las longitudes de cada uno de los bucles, cuente el número de nodos y el número de antinodos. Del mejor modo que le sea posible, mida también la distancia nodo-antinodo. 5 FS-200 Fı́sica General II UNAH 6. Después de haber obtenido ese armónico, vaya aumentando la tensión en la cuerda colocando lentamente más agua en el vaso, deténgase hasta observar el siguiente modo de onda estacionaria. Cada vez que obtenga uno repita el paso anterior. 7. Trate en la medida de lo posible realizar como mı́nimo tres mediciones de la misma cantidad, esto permitirá obtener un error estadı́stico agregando a los resultados una incertidumbre por observación, haga una vez todas las mediciones en secuencia y luego vuelva a empezar todas las mediciones de nuevo. Registro de datos 1. Registre los datos correspondientes a: a) Longitud de la parte horizontal de la cuerda en donde se forma una onda estacionaria completa con nodos en los extremos. b) Masa y longitud de cuerda usada para obtener la densidad lineal. 2. Registre igualmente los datos obtenidos para cada armónico: a) Longitud de un bucle formado por cada armónico en la cuerda. b) Masa colgante (agua mas vaso). c) Ubique en cada caso la posición de los nodos y de los antinodos (hubo de medir lo mejor posible la longitud entre un nodo y el antinodo inmediatamente posterior). Tratamiento de datos experimentales 1. Densidad lineal de masa de la cuerda a utilizar, con su incertidumbre. 2. Tensión de la cuerda en cada armónico con su incertidumbre. 3. Velocidad de la cuerda en cada armónico con su incertidumbre. 4. Valor que se obtiene para la frecuencia en cada armónico con su incertidumbre. Resultados 1. Tabla completa con la información de cada armónico (Cuadro 1) 2. Gráfica de cuadrado de n(n2 ) vrs. el inverso de masa colgante ( m1 ) (utilice regresión lineal) 3. Frecuencia de vibración del vibrador: a) Como resultado de la pendiente en la gráfica anterior. b) Utilizando el promedio de las frecuencias calculadas con la ecuación (3), en la última fila del Cuadro 1. 6 FS-200 Mediciones para las Ondas Estacionarias Formadas en la Cuerda Tensa Longitud horizontal de la cuerda (de nodo a nodo extremo) (L ± ∆L) Cantidad de bucles observados Cantidad de nodos observados Cantidad de antinodos observados Orden del modo normal correspondiente (n) Longitud de nodo a antinodo (medido) Cuarto de longitud de onda (Calculada a partir de L) Longitud de nodo a nodo (medido) Media longitud de onda (Calculada a partir de L) Masa del vaso con agua (Kg) Tensión (N ) Densidad lineal de masa (kg/m) Velocidad de propagación (m/s) Frecuencia del vibrador (Hz) Fı́sica General II Columna Correspondiente al armónico Columna Correspondiente al armónico UNAH Columna Correspondiente al armónico Columna Correspondiente al armónico Cuadro 1: Información sobre las ondas estacionarias formadas en la cuerda tensa Obs: Utilice las unidades e incertidumbres correspondientes, para el cálculo de la tensión T , la densidad lineal de masa µ, la velocidad de propagación v, y la frecuencia de oscilación del vibrador f ; será necesario utilizar la propagación de errores, Vea anexo. 7 FS-200 Fı́sica General II UNAH Cuestionario 1. Explique por qué se dice que las ondas que viajan por esta cuerda son transversales. 2. ¿Por qué los nodos no vibran? Ilustre qué podrı́a hacerse en esta experiencia para mostrar claramente que efectivamente los nodos no vibran. Explique entonces por qué este tipo de ondas no permiten transmitir energı́a. 3. Explique por qué el extremo en donde está el vibrador nunca puede llegar a ser ni un nodo ni un antinodo. ¿Qué representarı́a entonces ese extremo? 4. Actuando con su mano en el extremo vertical de la cuerda, ¿cómo podrı́a cambiar el modo normal; es decir aumentar o disminuir el número de bucles? 8
© Copyright 2026