1. No category

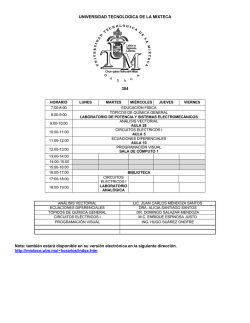
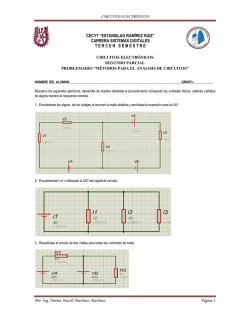
ELT – 2410 ‘CIRCUITOS ELÉCTRICOS I’
GESTIÓN 2010
LABORATORIO No 8
TEOREMA DE THEVENIN y TEOREMA DE NORTON
7.1. OBJETIVO GENERAL.
Finalizada la presente práctica, estaremos en condiciones de encarar circuitos lineales de un par de
terminales con ayuda de los teoremas de Thevenin y Norton.
7.1.1. OBJETIVOS ESPECÍFICOS.
Para alcanzar el objetivo general, debemos usar y aplicar correctamente los siguientes parámetros eléctricos
involucrados:






Circuito Abierto
Resistencia equivalente
Cortocircuito
Resistencia en vacío
Divisor de Tensión
Divisor de Corriente
7.2. PUNTUALIZACIONES TEÓRICAS.
Cualquier dipolo activo A-B compuesto de combinaciones de elementos activos y pasivos, puede
representarse con respecto a sus terminales, como un circuito serie formado por una fuente ideal de tensión
Vo(t) y un elemento operativo, impedancia equivalente, Zs(p) entre los terminales A-B.
La fuente de tensión Vo(t) es el voltaje entre los terminales A-B, del dipolo activo debido a las fuentes en su
interior cuando está conectado a sus terminales. (voltaje en circuito abierto). Ver figura:
Zs(p) es la impedancia de excitación de las terminales a-b, del dipolo si todas las fuentes del interior de la
red A se hacen cero (Fuentes de tension se cortocircuitan y fuentes de corrientes se ponen en circuito
abierto).
Si la red A tiene fuentes controladas, estas no pueden hacerse cero, y la impedancia equivalente se puede
determinar mediante la ecuación siguiente:
Donde:
FACULTAD NACIONAL DE INGENIERÍA
CARRERA DE ING. ELÉCTRICA E ING. ELECTRÓNICA
ELT – 2410 ‘CIRCUITOS ELÉCTRICOS I’
GESTIÓN 2010

Es la corriente que circula entre los terminales a-b cuando estos se cortocircuitan (Corriente de
corto circuito).

Es la tensión existente entre los terminales a-b, cuando estos se abren ( Tensión en circuito
abierto)
Como toda combinación serie de una fuente de tensión y una impedancia puede representarse como una
combinación paralela de una fuente de corriente y una impedancia, toda red activa puede representarse con
respecto a los terminales a-b por dicha fuente de corriente.
El valor de la fuente de corriente Io es la corriente entre terminales a-b de la red A, cuando estos sé
cortorcicuitan. Por la relación entre el teorema de THEVENIN y el teorema de NORTON esta dado por:
V = Io * Zs(p)
De forma tal que el circuito equivalente de THEVENIN o el de NORTON pueden obtenerse por el
conocimiento de la tensión de circuito abierto o la corriente de corto circuito
7.3. MATERIAL Y EQUIPO A UTILIZAR.
•
•
•
•
•
•
•
•
•
Resistencias de Carbón:
20, 30, 50, 45, 10 KΩ
Fuente de alimentación:
0-30 V, 1A
Multímetro Electrónico:
Escala de tensión 50 V.
Escala de Corriente 300 mA
Escala de Resistencia 200 Ω
Alambres de conexión.
7.4. CIRCUITO DE ANÁLISIS.
THÉVENIN:
 Circuito Propuesto:
FACULTAD NACIONAL DE INGENIERÍA
CARRERA DE ING. ELÉCTRICA E ING. ELECTRÓNICA
ELT – 2410 ‘CIRCUITOS ELÉCTRICOS I’
GESTIÓN 2010
 Circuito de Medición de Corriente:
 Circuito de Medición de Voltaje:
 Circuitode aplicación del Teorema de Thévenin para la determinación de la corriente en R2 en
forma práctica experimental:
Circuito de Medición de la Tensión de Thévenin,
FACULTAD NACIONAL DE INGENIERÍA
CARRERA DE ING. ELÉCTRICA E ING. ELECTRÓNICA
ELT – 2410 ‘CIRCUITOS ELÉCTRICOS I’
GESTIÓN 2010
La lectura del voltímetro es igual a
Circuito de Medición de la Resistencia Equivalente de Thévenin,
Circuito Equivalente de Thévenin:
La corriente en R2:
(A)
Circuito para el cálculo analítico de la Tensión de Thévenin:
FACULTAD NACIONAL DE INGENIERÍA
CARRERA DE ING. ELÉCTRICA E ING. ELECTRÓNICA
ELT – 2410 ‘CIRCUITOS ELÉCTRICOS I’
GESTIÓN 2010
Según el circuito podemos expresar a la tensión A-Y (Tensión en Vacío ó Tensión de thévenin):
Por lo que es necesario encontrar las corrientes
:
Para
........... (2)
Para
( R4 y R5 en serie y ellos en paralelo con R3 y su equivalente en serie con R1)
Reemplazando ecuación (2) en (1):
Para
La Tensión de Thévenin será: De ecuaciones (5), (4) en (1):
La resistencia equivalente de Thévenin:
FACULTAD NACIONAL DE INGENIERÍA
CARRERA DE ING. ELÉCTRICA E ING. ELECTRÓNICA
ELT – 2410 ‘CIRCUITOS ELÉCTRICOS I’
GESTIÓN 2010
(
)
NORTON:
 Circuitode aplicación del Teorema de Norton, para la determinación de la corriente en R2 en
forma práctica experimental:
Circuito de Medición de la Corriente de Norton,
La lectura del amperímetro es igual a
:
Circuito de Medición de la Resistencia Equivalente de Norton,
FACULTAD NACIONAL DE INGENIERÍA
CARRERA DE ING. ELÉCTRICA E ING. ELECTRÓNICA
ELT – 2410 ‘CIRCUITOS ELÉCTRICOS I’
GESTIÓN 2010
Circuito Equivalente de Norton:
La corriente en R2:
(A)
7.5. LECTURA DE DATOS.
Determinación de Resistencias en línea:
TENSIÓN DE ALIMENTACIÓN
CORRIENTE DE ALIMENTACIÓN
RESISTENCIA
TENSIÓN V
CORRIENTE mA
V
A
RESISTENCIA VACÍO Ω
RESISTENCIA LÍNEA Ω
R1
R2
R3
R4
R5
FACULTAD NACIONAL DE INGENIERÍA
CARRERA DE ING. ELÉCTRICA E ING. ELECTRÓNICA
ELT – 2410 ‘CIRCUITOS ELÉCTRICOS I’
GESTIÓN 2010
Aplicación del Teorema de Thévenin para la determinación experimental de la corriente en R2:
LECTURA DEL VOLTÍMETRO
LECTURA DEL ÓHMETRO
V
Ω
Lectura de Datos para la verificación de las resistencias en línea de la rama abierta en terminales A-Y:
TENSIÓN DE ALIMENTACIÓN
CORRIENTE DE ALIMENTACIÓN
RESISTENCIA
TENSIÓN V
CORRIENTE mA
V
A
RESISTENCIA VACÍO Ω
RESISTENCIA LÍNEA Ω
R1
R3
R4
R5
Aplicación del Teorema de Norton para la determinación experimental de la corriente en R2:
LECTURA DEL VOLTÍMETRO
LECTURA DEL ÓHMETRO
V
Ω
Lectura de Datos para la verificación de las resistencias en línea de la rama cortocircuitada en terminales AY:
TENSIÓN DE ALIMENTACIÓN
CORRIENTE DE ALIMENTACIÓN
RESISTENCIA
TENSIÓN V
CORRIENTE mA
V
A
RESISTENCIA VACÍO Ω
RESISTENCIA LÍNEA Ω
R1
R3
R4
R5
7.6. CUESTIONARIO.
1. Demuestre el teorema de Thevenin y el Teorema de Norton
2. Determine el circuito equivalente de Thevenin en forma analítica y en forma experimental luego compare
los errores existentes.
3. Compare la corriente en la resistencia R2 encontrada por lectura con la calculada en forma analítica y
experimental, el error no debe sobrepasar el
4. Determine el circuito equivalente de Norton en forma analítica y en forma experimental luego compare
los errores existentes.
5. Compare la corriente en la resistencia R2 encontrada por lectura y por cálculo, en forma analítica y
experimental, el error no debe sobrepasar el
FACULTAD NACIONAL DE INGENIERÍA
CARRERA DE ING. ELÉCTRICA E ING. ELECTRÓNICA
ELT – 2410 ‘CIRCUITOS ELÉCTRICOS I’
GESTIÓN 2010
7.7. CONCLUSIONES.
7.8. BIBLIOGRAFÍA.
Circuitos Magnéticos y transformadores
Matemática para Ingeniería y Ciencias
Análisis básico de circuitos eléctricos
Análisis de Circuitos en Ingeniería
Fundamentos de Circuitos Electricos
Circuitos Eléctricos
Redes Eléctricas
Circuitos eléctricos I
Circuitos Eléctricos Laboratorio
Electrotecnia Curso Básico
E. E. Staff – M. I. T.
Bajpay - Calus - Fairley
David E. Jonson
Kemmerly
Sadiku-Alexander
Dorf-svoboda
Balabanian
Ing. Gustavo Nava
Oscar Anave León
GTZ
ANTERIOR
SIGUIENTE
INDICE
FACULTAD NACIONAL DE INGENIERÍA
CARRERA DE ING. ELÉCTRICA E ING. ELECTRÓNICA