1. No category

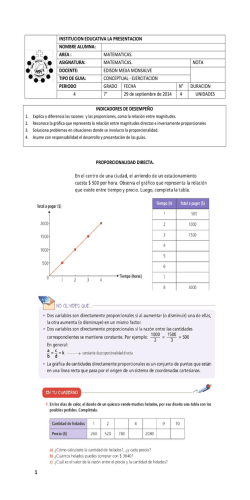
COLEGIO COLOMBO BRITÁNICO
“Formación en la Libertad y para la Libertad”
MATEMÁTICAS
GRADO:7O
DOCENTE: Nubia E. Niño C. FECHA: 22 / 09 / 15
Guía Didáctica
4-3
Desempeños:* Reconoce y aplica las propiedades de las proporciones y determina magnitudes directas e
inversamente proporcionales. * Plantea una regla de tres simple o compuesta, a partir de una situación problemática
planteada.
APRENDE:
Proporcionalidad inversa:
Magnitudes inversamente correlacionadas: Dos magnitudes son inversamente correlacionadas, cuando al
aumentar una de ellas, la otra disminuye o, cuando disminuye una de ellas, la otra aumenta; no hay constante de
proporcionalidad; la gráfica es una recta y no pasa por el origen.
Ejemplo:
Magnitud A
1
2
3
4
Magnitud B
80
70
60
50
Dos magnitudes son inversamente proporcionales si: 1) Al aumentar una de las magnitudes, la otra disminuye; o al
disminuir una de las magnitudes la otra aumenta, es decir son (inversamente correlacionadas). 2) El producto de
las dos magnitudes es siempre el mismo (constante = K) y su gráfica es una línea recta o curva como la que se
muestra en la gráfica.
Ejemplo:
# Vacas
2
4
8
16
35
64
Días Alimento
64
32
16
8
4
2
Aplicaciones de Proporcionalidad:
Regla de tres simple: La regla de tr es es un procedim iento para c alcular el valor de una cantidad ,
com parándola c on otras tres o m ás cantidades conocidas.
Regla de tres simple y direct a:
Se aplic a cuando dadas dos cantidades correspondientes a m agnitudes directamente
proporcionales, hay que calcular la c antidad de una de estas m agnitudes correspondiente a una
cantidad dada de la otr a m agnitud.
Ejemplo:
Un autom óvil recorre 240 km en 3 hor as. ¿Cuántos k ilóm etros habrá recorrido en 2 horas ,
em pleando la m ism a veloc idad ?
240 km
3 h
x
2 h
km
Regla de tres simple inversa :
Un problema se denomina de regla de tres simple inversa, cuando las magnitudes que intervienen en el problem son
inversamente proporcionales.
Ejemplo:
3 obreros constru yen un m uro en 12 horas, ¿cuánto tardarán en cons truirlo 6 obreros , si trabajan
en las m ism as condiciones ?
3 obreros
12 h
6 obreros
x h
APOYO - VÍDEOS RECOMENDADOS:
Observa estos vídeos que te ayudarán a aprender y diferenciar los temas propuestos:
Proporcionalidad inversa: https://youtu.be/8PDMiGp0jJA
Proporcionalidad inversa: https://youtu.be/MD4n9qyFk9Q
Regla de 3 Simple directa: http://youtu.be/hP6F-0oDvGk
Regla de 3 Simple Inversa: http://youtu.be/ljCKQG3Pfkc
APLICACIÓN:
NOTA  Todo el taller se desarrolla en el cuaderno; mostrar proceso y dar claramente la(s) respuesta(s).
Trabajar ordenadamente.
ACTIVIDADES:
1) Completar las siguientes tablas, decir cómo se relacionan; si hay una constante hallarla y hacer las gráficas
correspondientes:
a)
# obreros
2
3
Días de trabajo
15
10
Magnitud A
1
2
Magnitud B
80
70
# peajes
1
2
Distancia Km
72
36
5
6
3
b)
3
50
c)
3
4
2) Establecer si las magnitudes representadas en la gráfica son inversamente correlacionadas o inversamente
proporcionales. Si hay constante hallarla. Sustentar la respuesta.
a)
3) Analizar las tablas dadas a continuación y determinar si entre las magnitudes hay proporcionalidad inversa o
correlación inversa. Si las magnitudes son inversamente proporcionales, hallar la constante de proprcionalidad; en
cada caso hacer la gráfica.
a)
Magnitud X
Magnitud Y
1
30
2
15
5
6
15
2
2
15
4
8
5
6
10
3
b)
Magnitud A
Magnitud B
4) Determinar cuáles de los siguientes pares de magnitudes son inversamente proporcionales. Explicar la respuesta:
a) Velocidad y tiempo
b) radio de una circunferencia y longitud de la circunferencia
c) El mercado mensaual y el día del mes en que estamos.
d) Tiempo y cantidad de alimento para un grupo de ovejas.
e) La longitud del lado de un cuadrado y su área
f) La velocidad de un coche y el tiempo que tarda en recorrer una distancia.
g) El número de limpiadores de un edificio y el tiempo que tardan.
h) El número de ladrillos de una pared y su altura.
i) El peso de la fruta y el dinero que cuesta.
j) La velocidad de un corredor y la distancia que recorre.
k) El número de llaves o canillas de un tanque y el tiempo que tarda en llenarse.
5) En una clase de electricidad se midió la corriente que pasa por diferentes resistencias cuando se conectan a una
pila de 9 voltios. Los resultados fueron:
Resistencia
1
1,5
3
4,5
6
Corriente
9
6
3
2
1,5
a) Representar los datos gráficamente
b) Determinar si las magnitudes son inversamente proporcionales; si lo son hallar la constante de proporcionalidad.
c) Hallar el valor de la corriente para una resistencia de 2,5 y 9 respectivamente.
6) La siguiente tabla representa magnitudes inversamente proporcionales. Hallar los valores de a, b, c, y d:
a
2
50
4
25
b
5
40
c
200
200
d
7) Identificar cuáles de las siguientes situaciones se pueden solucionar aplicando regla de tres simple y determinar si
es directa o inversa:
a) Pepito compra 6 libras de arroz con $8000 ¿Cuántas libras compra con $12000?
b) Una familia consume en tres días 1,5 bolsas de leche. ¿Cuántas necesitan para toda la familia?
c) Luis gasta $15000 en transporte para cinco días de la semana. ¿Cuánto dinero necesita para su transporte en estos
5 días?
d) En una finca hay pasto para alimentar 600 reses durante 5 meses. Si se venden 100 reses, ¿para cuánto tiempo
alcanzará el pasto que se tiene?
8) Leer, analizar y resolver los siguientes problemas aplicando la regla de tres simple; en cada uno indicar cuál es
la regla de tres que se aplica:
a) Dos ruedas están unidas por una correa transm isora. La prim era tiene un radio de 25 cm y la
segunda de 75 cm. Cuando la prim era ha dado 300 vueltas, ¿cuántas vueltas habrá dado la
segunda?
b) En 50 litros de agua de m ar hay 1300g de sal. ¿Cuántos litros hacen falta para 5200g de sal?
c) Un automóvil gasta 5 litros de gasolina cada 100Km . ¿Cuantos Km recorrerá con 28 litros?
d) 5 obreros hacen una pared en 15 días. ¿Cuánto tardaran 3 obreros en hacer la misma pared y
trabajando en las mismas condiciones?
e) Un campesino tiene pasto para alim entar a sus 12 vacas durante 45 días. Si compra 3 vacas más,
¿Cuánto le dur ará el pasto?
f) Un grupo de cinco cocineros iban a preparar un banquete en 6 horas. ¿Qué tiempo demoran 3 cocineros en
preparar dicho banquete?
g) Un avión recorre cierta distancia en 5 horas empleando una velocidad de 600 km/h. ¿Qué velocidad debe tener otro
avión similar para recorrer el mismo trayecto en 3 horas?
h) En un restaurante peruano, para preparar una rica ensalada se necesitan 6 latas de atún que cuestan S/. 20 soles,
¿Cuánto costarán 2 docenas de latas de atún?
i) Para la preparación de una ensalada peruana que rinde 10 porciones se necesitan 5 kilos de zanahoria. ¿Cuántos
kilos se necesitarán para 4 porciones de la misma ensalada?
j) Un crucero de verano tiene víveres para 25 días si lleva 36 tripulantes. ¿Cuánto pueden durar los víveres si viajan
45 tripulantes?
k) En un conocido restaurante de Medellín, 9 cocineros pueden preparar un menú para 120 personas en 4 horas.
¿Cuántos cocineros serán necesarios para prepararlo en sólo 3 horas?
l) En una cafetería de Bogotá se han comprado 12 frascos de nescafé tradicional por $ 42000. ¿Cuál será el costo de
25 frascos de nescafé?
m) Si 6 revistas científicas valen $ 51000, ¿Cuánto es el costo de 9 revistas?
n) Un crucero de verano tiene víveres para 14 días si lleva 40 tripulantes. ¿Cuánto pueden durar los víveres si viajan
sólo 28 tripulantes?
ñ) Ocho obreros pueden remodelar un restaurante en 35 días. ¿Cuántos hombres se necesitarán para hacerlo en 28
días?
o) Una cuadrilla de 42 obreros cavan 140m de zanja en cierto tiempo. ¿Cuántos metros de zanja harán 60 en el
mismo tiempo?
p) Si 25 carpinteros se comprometieron en hacer un tablado en 35 días. ¿Cuántos carpinteros de la misma capacidad
deberán ser contratados si se quiere terminar el tablado en 7 días?
q) Si 6 obreros terminan una obra en 10 días, ¿En cuántos días terminaran la misma obra 12 obreros?
r) Una familia compuesta por 6 adultos, hace un mercado que alcanza para 15 días. Para las vacaciones llegan de
visita 3 personas. ¿Para cuántos días alcanza el mismo mercado?
s) Un deportista recorre 4.500 m. en 10 minutos. ¿Cuántos km. recorrerá en media hora?
t) Con un depósito de agua pueden beber 30 caballos durante 8 días. Si se venden 6 caballos, ¿cuántos días durará
el agua?
APOYO – ACTIVIDADES INTERACTIVAS (LÚDICAS):
En estas páginas encontraras actividades interesantes (Interactivas) para el estudio de la materia.
Magnitudes inversamente proporcionales: http://www.vitutor.com/di/p/a_8e.html
Regla de 3 simple y directa: http://www.vitutor.com/di/p/a_5e.html
Regla de 3 simple inversa: http://www.vitutor.com/di/p/a_9e.html
Regla de 3 compuesta: http://www.vitutor.com/di/p/a_11e.html
Fuentes Bibliográficas:
Rubiano Cifuentes, Julián. Hipertexto 7, Editorial Santillana, 2010
Joya Vega, Anneris del Rocío. Nuevas Matemáticas 7, Editorial Santillana, 2007
Morales Piñeros, Miriam del Carmen y Otros. Aritmética y Geometría II, Grado 7, Editorial Santillana, 2004
http://www.vitutor.com/di/p/a_8.html
http://www.profesorenlinea.cl/matematica/Proporcionalidad.htm
http://recursostic.educacion.es/descartes/web/materiales_didacticos/Proporcionalidad_lbc/maginversprop.htm
http://www.vitutor.com/di/p/a_5.html
http://www.ditutor.com/proporcionalidad/regla_tres.html
http://www.vitutor.com/di/p/p_e.html
http://matesdeangeles.blogspot.com/2013/05/proporcionalidad-directa-e-inversa.html
http://www.curriculumenlineamineduc.cl/605/articles-27662_recurso_pdf.pdf
http://video-educativo.blogspot.com/2013/02/regla-de-tres-inversa-ejercicios.html
http://www.matesymas.es/rai/1eso/Ejercicios%20de%20proporcionalidad%20num%C3%A9rica%20con%20soluci%C3
%B3n.pdf
http://www.amolasmates.es/almacen/1eso/fichas_%201eso_sant/pdf_8-ProporNumerica.pdf
Imágenes de: http://alfredoscandon.blogspot.com/p/ejercicios-de-proporcionalidad.html
http://es.slideshare.net/miguelpuerto/proporcionalidad-inversa-11820926
http://www.ditutor.com/proporcionalidad/regla_tres.html
http://alfredoscandon.blogspot.com/p/ejercicios-de-proporcionalidad.html
http://es.slideshare.net/miguelpuerto/proporcionalidad-inversa-11820926
http://www.ditutor.com/proporcionalidad/regla_tres.html
http://matesdeangeles.blogspot.com/2013/05/proporcionalidad-directa-e-inversa.html
http://www.winmates.net/ayuda/arbol/129rp_r3.php
“En las matEmáticas Es dondE El Espíritu EncuEntra los ElEmEntos quE más ansía: la
continuidad y la pErsEvErancia”
Jacques Anatole