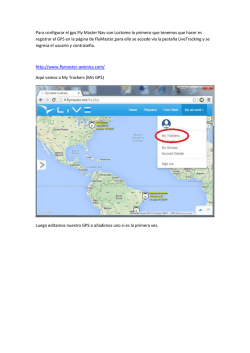
Instructora Prof. Linda L. Vélez Rodríguez Catedrá ca Departamento
Centro de Transferencia de Tecnología en Transportación Departamento de Ingeniería Civil y Agrimensura UPR-‐Recinto Universitario de Mayagüez Call Box 9000 * Mayagüez, PR 00681 Tel. 787-‐834-‐6385 * Fax: 787-‐265-‐5695 * www.uprm.edu/prt2 29 Años de Excelencia en el Adiestramiento de Oficiales de Transportación a Nivel Municipal, Estatal, y Federal en Puerto Rico e Islas Vírgenes Instructora Prof. Linda L. Vélez Rodríguez Catedrá/ca Departamento de Ingeniería Civil y Agrimensura UPR – Recinto Universitario de Mayagüez 8 de mayo de 2015 Índice Módulo 1 – Notas de la Instructora Módulo 2 – Definiciones de Datums Módulo 3 – Base de Datos Geográficos Módulo 4 – Geo-‐Based Informa/on Matrix Módulo 5 – Ley Núm. 264 del año 2002: Ley para adoptar el Sistema de Coordenadas Planas Estatales de Puerto Rico Módulo 6 – Sección 5.2.3 -‐ Sistema de Coordenadas Planas Estatales Módulo 7 – Modern Terrestrial Reference Systems – Part 1 Módulo 8 – Modern Terrestrial Reference Systems – Part 2: The Evolu/on of NAD 83 Módulo 9 – Modern Terrestrial Reference Systems – PART 3: WGS 84 and ITRS Módulo 10 – Modern Terrestrial Reference Systems – Part 4: Prac/cal Considera/ons for Accurate Posi/oning Módulo 11 – Notas sobre Agrimensura Módulo 1 Notas de la Instructora CONCEPTOS BÁSICOS DE SISTEMAS DE COORDENADAS EN LA RELOCALIZACIÓN DE UTILIDADES EN PROYECTOS DE CARRETERAS por Prof. Linda L. Vélez-Rodríguez, MS, PE, PLS Catedrática Univ. de PR-Recinto Universitario de Mayaguez e-mail: [email protected] Tel. 787-265-5405 (Ofic) 787-313-4740 (Cel) Temas - AM • Introducción • Requerimientos por Ley y Reglamento • Conceptos Básicos de: – Gedésia y sus superficies – Marcos de Referencia y la Ley 264 del 2002 – Agrimensura y como se obtienen las Coordenadas Planas X,Y • Referencia “NOTAS SOBRE AGRIMENSURA” – Cartografía y sus proyecciones cartográficas • Referencia “SISTEMA LAMBERT” en www.revistatp.com Temas - PM • National Geodetic Survey (NGS): sus Datasheets y sistemas de coordenadas – Referencia: www.ngs.noaa.gov/ • Coordenadas Geo-Referenciadas N,E • Utilidades y sus Atributos • Caso de carretera PR-106 Km 1.6 Mayaguez • Carretera PR-3108 conecta la PR-2 y PR108 Realidad vs. transformación Realidad vs. transformación Estructura VS. Datos Geo-Espaciales Que nos requieren • Ley 264 del 16 de noviembre del 2002 - Para adoptar el Sistema de Coordenadas Planas Estatales utilizando el método de la Proyección Conforme Cónica Lambert y el North American Datum of 1983, o su versión más reciente Que nos requieren • Reglamento Conjunto para Obras de Construcción y Usos de Terrenos vigende desde el 29 de noviembre del 2010 en su Sección 5.2.3 – Sistema de Coordenadas Planas Estatales Geodesia • Se define como la rama de la matemática aplicada que tiene que ver con el estudio de la forma y tamaño de la Tierra al igual que su campo gravitacional. Es una de las Geo-Ciencias o Ciencias Terrestres, junto con: Geografia, Geologia, Geofisica y Geomorfologia Eratostenes: Padre de la Geodesia Tres Superficies Una Realidad • Topografía - superficie de nuestro planeta donde nosotros hacemos las observaciones • Elipsoide - superficie matemática que usamos para describir la tierra • Geoide- superficie física que denota el potencial de gravedad de nuestro planeta Geoide • nosotros habitamos un planeta cuya forma es única y puede ser descrita por el término geoide. Esta palabra procede del griego “geoeides” que quiere decir “perteneciente a la tierra” (GE de tierra y EIDOS de forma). • El geoide es la forma que tiene la superficie de la tierra allí donde el nivel del mar es uniforme y siempre es perpendicular a la dirección de la gravedad. EL GEOIDE ¿Que es ? TEORICAMENTE: G UNA SUPERFICIE A NIVEL EN ESPECIFICO DEL CAMPO GRAVITACIONAL EN LA PRACTICA: • REFERENCIA CERO PARA ELEVACIONES Y PROFUNDIDAD • “MEAN SEA LEVEL” CONTINUO EN LOS CONTINENTES • LA SURPERFICIE PERPENDICULAR A LA DIRECCION DE LA GRAVEDAD 5000 ft 3000 ft G G G G En busca del Geoide… ONDULACION GEOIDE PERPENDICULAR al GEOIDE (linea de la plomada) PERPENDICULAR al ELIPSOIDE DEFLECCION DE LA VERTICAL RELACION GEOIDE-ELIPSOIDE Relación de alturas (height) y las Tres superficies Gravity Recovery And Climate Experiment (GRACE) DATUMS • Un DATUM es un conjunto de parámetros que definen un sistema de coordenadas y un conjunto de puntos de control cuya relación geométrica es conocida ya sea por medidas o cálculos. Dewhurst, 1990 • Todos los DATUMS se fundamentan en un elipsoide, el cual aproxima la forma de la Tierra. EL ELIPSOIDE MODELO MATEMATICO DE APROXIMACION DE LA TIERRA a = Semi Eje Mayor b = Semi Eje Menor f = a-b = Achatamiento a N b a S Datum Horizontales y sus Elipsoides • • • • PR Datum NAD27 NAD83 WGS84 Clarke 1866 Clarke 1866 GRS80 WGS84 NORTH AMERICAN DATUMS NAD 27 & NAD 83 EL GEOIDE Y DOS ELIPSOIDES GEOIDE CLARK 1866 ELLIPSOID CENTRO DE MASA GRS 80 ELLIPSOID Mezcla de Datums Mapa en PR Datum y Datos en WGS84 NSRS Coordinate Systems Latitud & Longitud Coordenadas Planas Estatales Coordenadas UTM “Earth-Centered Earth-Fixed” NAD 83 NAD 27 NGVD 29 NAVD 88 PRVD 02 ITRF00 AGRIMENSURA: localización = coordenadas • Se define como el arte, ciencia y tecnologia de determinar la posicion de un punto en, sobre o bajo la superficie de la tierra, o establecer la posicion de dichos puntos. Envuelve todo lo que tenga que ver con nuestro ambiente pues TODO tiene una definicion en el espacio que habitamos, y de eso es de lo que se trata el NEGOCIO de la AGRIMENSURA, de la localizacion. La superficie se considera plana, asi que se geometria plana. Al agrimensor se le conoce como geometra. Medidas Básicas en Agrimensura • • • • • Distancias Horizontales Distancias Verticales Distancias en Pendiente Angulos Horizontales Angulos Verticales Total Station, Prisma y Baston con Bipode Distancias Ángulos Poligono de Control que se usa en agrimensura; existen poligonos cerrados, o poligonos abiertos, o lineas bases o un punto. Los mas optimos son los poligonos cerrados por la redundancia que ofrecen. Se denominan de control pues es un control o referencia para obtener los datos necesarios para hacer el levantamiento de los datos necesarios para hacer nuestro diseño En los vertices del Poligono de Control debe existir una marca Permanente que se denomina PUNTO DE CONTROL, muchos Agrimensores usan varillas de acero. Se procede a medir los angulos interiores del poligono cerrado y Las distancias entre dichos vertices, y con estos datos se procede a ajustar esos datos (angulos interiores y distancias) Datos sin ajustar nos dan una diferencia en la ubicación de A A’ Las coordenadas se calculan usando los "Balanced Latitude" y "Balance Departure". Estos son los componentes en Y y X ajustados por eso “Balanced” La coordenada X de un punto es igual a la coordenada X del punto anterior más el "Balanced Departure" entre esos puntos. La coordenada Y de un punto es igual a la coordenada Y del punto anterior más el "Balanced Latitude" entre esos puntos. Esto es: Xn = Xn-1 + "Balanced Departure”(n @ n-1) Yn = Yn-1 + "Balanced Latitude”(n @ n-1) Si usamos la analogia del vector y sus componentes en X & Y; el vector es uno del lados de la poligonal y su componente en X es del Departure y el componente en el eje de Y es el Latitude, refierase al poligono ABCD ilustrado a continuacion: El Ajuste de los datos se puede hacer con uno de varios metodos disponibles, que cada uno de ellos pondera una u otras de los observaciones que se hagan. Sistemas de Coordenadas Planas Sistemas de Coordenadas Esfericas COORDENADAS Por definición son cantidades lineales o ángulares, o ambas, que designa la posición de un punto relativo a un marco de referencia. Se dividen en agrimensura generalmente en dos: (1) polares y (2) rectangulares. Se subdividen en tres clases: coordenadas; (1) planas, (2) esfericas y (3) Espaciales. Distancia Lineal DISTANCIA LINEAL • Entre dos puntos con coordenadas conocidas tenemos que la distancia D1-2 es igual a la raiz cuadrada del cuadrado de las diferencias de las Y mas el cuadrado de las diferencias de las X. • Es decir: D1-2 = ((Y2 - Y1)2 + (X2 - X1) 2)1/2 Rosa de los vientos ANGULOS/DIRECCIONES • Para rumbos y acimuts tenemos que la tangente del rumbo o acimut es igual a las diferencias de las X dividido por la diferencia de la Y. • Es decir: tan B1-2 = X2 - X1/ Y2 - Y1 AREA CON COORDENADAS • Dos veces el área de un polígono cerrado usando coordenadas se calcula de la siguiente forma: • 2A = X1(Y2 - Yn) + X2(Y3 - Y1)+. . .+ Xn-1(Yn - Yn-2) + Xn(Y1 - Yn-1) ó • 2A = Y1(X2 - Xn) + Y2(X3 - X1)+. . .+ Yn-1(Xn - Xn-2) + Yn(X1 - Xn-1) Se usa el valor absoluto, pues una sera el negativo de la otra, y no tenemos áreas negativas. Que nos requieren: •Ley 264 del 16 de noviembre del 2002 •Sección 5.2.3 – Sistema de Coordenadas Planas Estatales del Reglamento Conjunto para Obras de Construcción y Usos de Terrenos vigende desde 29 de noviembre del 2010 TRANSFORMACION Se define como una función que relaciona coordenadas en un sistema de coordenadas con otro sistema de coordenadas. Usualmente envuelve cambios en traslación, rotación y/o escala. - “affine transformation” - “conformal transformation” LAS PROYECCIONES CARTOGRAFICAS SON UNA ABSTRACCION MATEMATICA DE LA REALIDAD Matriz del GIS de Puerto Rico Sistema Nacional de Referencia Espacial “National Spatial Reference System” (NSRS) De esto consiste el Sistema Nacional de Coordenadas • Latitud • Longitud • Altura • Escala • Gravedad • Orientacioón Y como estos valores cambian con el tiempo Variedad de fuentes de datos geo-espaciales – OJO con GI-GO Datos de Infraestructura – – – – – – – – – – Localización Geográfica Carreteras Aceras Servicios de Agua Servicios de Alcantarillado Sanitarios Luminarias en Calles Servicios Electricos Tuberías (pipelines) Facilidades de Comunicación Servicios de Control de Trafico – Facilidades de Parques/Recreación – Carriles (lanes) – Escuelas – Inventario de Arboles/Arbustos – Estacionamiento – Puentes – Utilidades extranjeras – Red/Facilidades de Carreteras (Viales) Infraestructura y Atributos – Carreteras • • • • • • • • Tipo Superficie Fecha de Construcción Propietario Fecha del Ultimo Mantenimiento Número de Carriles Ancho Profundidad – Aceras • • • • • • Tipo Superficie Fecha de Construcción Propietario Fecha del Ultimo Mantenimiento Ancho/Profundidad Infraestructura y Atributos – Luminarias en Calles • • • • • Postes Transformadores Alambrado Edad Profundidad – Servicios de Control de Trafico • • • • Tipo Activo/Pasivo Fecha de Instalación Fecha del Ultimo Mantenimiento Infraestructura y Atributos – Puentes • • • • • – Tipo Superficie Fecha de Construcción Número de Carriles Fecha del Ultimo Mantenimiento Utilidades extranjeras • • • • • • • • • Cablevision Propietario Localizacion de Planta Tuberías Propietario Capacidad Localizacion de Planta Caracteristicas Especiales Profundidad – Redes Viales • • • • Tipo Ruta Rasgos Especiales Facilidades – Carriles (lanes) • • • • • Localización Tipo Superficie Propietario Dimensiones Fisicas Infraestructura y Atributos – Servicios de Agua • • • • • • • • • Hidrantes Capacidad Válvulas Líneas Presión/Edad Profundidad Fecha de Instalación Fecha de Ultimo Mantenimiento Estaciones de Bombeo – Servicios de Alcantarillado Sanitarios • • • • • Líneas Válvulas Profundidad Estaciones de Bombeo Tipos Utilidades Soterradas ¿Como las ubicamos? Cartografía • Definición: – Ciencia, Arte y Tecnología de hacer mapas junto con su estudio como documento científico y trabajo de arte. Los mapas son una representación de la tierra o parte de ella a escala. – La escala es la relación entre el tamaño real del área y la porción reducida que aparece en el mapa. Son productos cartográficos, los planos, secciones transversales, modelos en tercera dimensión, entre otros. Escala Escala como fracción representativa: Una razón, tal como 1:1,000,000. Si se asume que el mapa esta en centímetros, significa que un centímetro en el mapa es igual a un millón de centímetros en la Tierra. Esta escala se podría también escribir como fracción proporcional (1/1,000,000). Superficies Desarrollables • son superficies que se desarrollan en un plano, fundamentales para las Proyecciones Cartograficas. Ellas son: – el cono – el cilindro y – el plano Sistema de Coordenadas Planas Estatales • El gobierno federal desarrollo el Sistema de Coordenadas Planas Estatales (SPCS)para cada estado y sus territorios. • En el caso en particular de Puerto Rico e Islas Virgenes se usa la proyección conforme cónica Lambert con dos paralelos standard, teniendo los siguientes parametros para el NAD 83: φN = 18°-26’ N; φS = 18°-02’ N; φ0 = 17°-50’ N; λ0 = 66°- 26’ W; Nb = 200,000.m; E0 = 200,000.m Sistema de Coordenadas Planas Estatales Limites de las zonas son 158 millas Sistema de Coordenadas Planas Estatales Sistema de Coordenadas Planas Estatales = f (, ) = f (, ) DESIGNATION - VÉLEZ PID - DE5545 COUNTRY - PUERTO RICO NAD 83(2002)- 18 26 41.28060(N) SPC PRVI UTM 19 - 067 08 48.93357(W) ADJUSTED North East Units Scale Converg. 267,825.241 124,618.857 MT 1.00000071 -0 13 23.8 2,040,399.173 695,701.034 MT 1.00007349 +0 35 11.3 Universal Transversa Mercator • Para el sistema Universal Transversa Mercator, mejor conocido por sus siglas en ingles UTM, el globo esta dividido en 60 zonas. – Se asume que el esferoide del DATUM es una esfera • Cada zona se extiende seis grados de longitud, con un solape de 30 minutos con las zonas adyacentes. • Cada zona tiene su propio meridiano central del cual se extiende 3 grados al este y 3 grados al oeste Universal Transversa Mercator • Las coordenadas de este sistemas están en metros. • El origen de cada zona es en el ecuador y en su meridiano central. • El valor dado al meridiano central es un "falso este" igual a 500,000 metros. Universal Transversa Mercator • La cuadrícula del sistema UTM se extiende alrededor del globo desde la latitud 80° N a la 80° S. • Cada zona en el Ecuador tiene dos falsos nortes 0 metros para la mitad norte y 10,000,000 metros en la mitad sur. – Lo cual significa que cada Iocalización en el Ecuador tiene dos conjuntos de coordenadas UTM 60 Zonas del Sistema UTM Estas zonas dependen de la Longitud # de Zona = (180° - λW)/6 para Longitudes al Oeste (λW ) del Meridiano de Greenwich # de Zona = (180° + λE)/6 para Longitudes al Este (λE) del Meridiano de Greenwich Si el resultado de la ecuación no es un entero se designa el entero proximo como el número de zona Puerto Rico esta en las zonas 19 y 20 del sistema UTM Red de Triangulación Red del CRIM del 1995 (Centro de Recaudación de Ingresos Municipales) Red de Control establecida en 1995 por el CRIM Las Marias 2 Control Geodésico establecido en 1995 por el CRIM Posiciones • Horizontal • Vertical • Temporal , o , , ,h o ,, t Datum Verticales • Los Datums Verticales son locales – Puerto Rico Vertical Datum 2002 (PRVD02) – Se usa en PR en el epoch del 1982-2001 de datos del mareógrafo de La Puntilla – El cero esta en las Oficinas de la Guardia Costanera en La Puntilla en el Viejo San Juan – Se corrió una nivelación en Mayo del 2002 desde La Puntilla hasta Aguadilla bajo el auspicio del National Geodetic Survey (NGS) – Este proyecto del PRVD02 lo están realizando dos firmas de agrimensores de Puerto Rico, siguiendo los “standards” del NGS pues es una nivelación de primer orden. Rutas propuestas en el proyecto de control vertical de Puerto Rico-PRVD02 para un total de 925 kilómetros incluyendo Vieques y Culebra PRVD02 –Importancia • Como parte de este proyecto se realizaron observaciones gravimétricas en Mayagüez y Aguadilla, y se efectuó un vuelo en enero del 2009 con un gravímetro en el avión como parte del proyecto denominado GRAV-D (Gravity for the Re-definition of the American Vertical Datum). • Se integrara esta tecnología para tener un solo datum uniendo el Horizontal y el Vertical, obteniendo asi alturas ortometricas derivadas. Daniel Winester, Geodesta del NGS monumentando estación en CI-019-RUM MAYAGUEZ A A 2008 MAYAGUEZ A A 2008 Observaciones Gravimetricas por 48 horas PRVD02 –Importancia • El gobierno del Estado Libre Asociado de Puerto Rico aporto $3,000,000 por conducto de tres de sus agencias ellas son la Oficina de Presupuesto y Gerencia; el Departamento de Transportación y Obras Públicas y la Autoridad de Energía Eléctrica. • El Colegio de Ingenieros y Agrimensores de Puerto Rico ha tenido un rol muy importante en este proyecto, pues se esta muy conciente de la importancia del mismo y lo que significa para el desarrollo de la infraestructura del país, junto con los cambios que ocasionara en el desempeño de la profesión de la agrimensura en lo referente a obtener elevaciones. Controles Verticales del USGS Vélez 2002 Vélez 2002 PID - DE5545 • HORZ ORDER - B • NAD 83(2002)– φ=18° 26’ 41.28060” N λ=67° 08’ 48.93357” W – SPC PRVI – N=267,825.241m E=124,618.857m – UTM 19 – N=2,040,399.173m E=695,701.034m • VERT ORDER - FIRST CLASS II • PRVD02 - 134.320meters 440.68feet National Geodetic Survey, Retrieval Date = APRIL 26, 2007 *********************************************************************** DESIGNATION - VELEZ PID - DE5545 STATE/COUNTY- PR/AGUADILLA H=h-N USGS QUAD - DE5545 DE5545 DE5545 DE5545 DE5545 DE5545 134.32 = 90.42 - (- 44.20) DE5545 *CURRENT SURVEY CONTROL 134.32 134.62 DE5545 ___________________________________________________________________ DE5545* NAD 83(2002)- 18 26 41.28060(N) 067 08 48.93357(W) ADJUSTED DE5545* PRVD02 134.320 (meters) 440.68 (feet) ADJUSTED DE5545 ___________________________________________________________________ DE5545 X 2,350,644.082 (meters) COMP DE5545 Y - -5,577,493.184 (meters) COMP DE5545 Z 2,005,175.775 (meters) COMP DE5545 LAPLACE CORR3.52 (seconds) DEFLEC99 DE5545 ELLIP HEIGHT90.42 (meters) (08/30/05) GPS OBS DE5545 GEOID HEIGHT-44.20 (meters) GEOID03 DE5545 DE5545 HORZ ORDER - B DE5545 VERT ORDER - FIRST CLASS II DE5545 ELLP ORDER - THIRD CLASS I NAD 83 (NSRS 2007) = 90.388 DE5545 DE5545.The horizontal coordinates were established by GPS observations DE5545.and adjusted by the National Geodetic Survey in August 2005.. DE5545.This is a SPECIAL STATUS position. See SPECIAL STATUS under the DE5545.DATUM ITEM on the data sheet items page. DE5545 DE5545.The orthometric height was determined by differential leveling DE5545.and adjusted by the National Geodetic Survey in April 2003 Los GPS (Sistemas de Posicionamiento Global) Segmentos que componen el sistema GPS Civil GPS Use Satellite Ops -Ephemeris, Timing Power Grid Interfaces Personal Navigation Surveying & Mapping Trucking & Shipping Aviation Recreation Communications -Network Synchronization and Timing Railroads Fishing & Boating Off shore Drilling Un Satelite Dos Satelites Tres Satelites Cuatro Satelites X23 y23 z23 d23 x14 y14 z14 x19 y19 z19 d19 x21 y21 z21 d14 d21 Measured: x y z Non-Differential GPS (Autonomous or Stand-alone) X23 y23 z23 x19 y19 z19 Measured: x y z Delta: x y z _________ Corrections applied after survey True: x y z Differential GPS x14 y14 z14 x21 y21 z21 True: x y z Measured: x y z ______________ Delta: x y z X23 y23 z23 x19 y19 z19 x14 y14 z14 x21 y21 z21 Measured: x y z Delta: x y z _________ True: x y z Corrections applied during the survey True: x y z Measured: x y z _____________ Delta: x y z Real-Time Differential GPS GPS • • Los datos obtenidos con los receptores de GPS se pueden incorporar a los mapas topográficos en formato digital, si estos estan en el mismo datum y sistemas de coordenadas. Como aplicacion, si obtenemos las coordenadas de los límites municipales de los cuadrángulos estos límites se pueden establecer sobre el terreno usando GPS Transformación de Coordenadas • El procedimiento para transformar unas coordenadas consiste de tres partes: – Escala – Rotación – Traslación • Se tiene un listado de coordenadas planas y se conocen las coordenadas planas del sistema al que se transformará en dos o más puntos. Transformación de Coordenadas • Frecuentemente se trasforman coordenadas de sistemas arbitrarios a sistemas estales o globales, por lo general con la observación de GPS/RTK en dos de los puntos de controles (Linea Base). • Al completar las observaciones de GPS/RTK se obtienen coordenadas en el sistema de coordenadas planas estatales (SPCS) o coordenadas geodésicas. • De obtener coordenadas geodésicas existen herramientas (Geodetic Tools) del National Geodetic Survey (NGS) para la transformación de estas al SPCS. Transformación de Coordenadas • El procedimiento discutido a continuación considera que se conocen las coordenadas en dos de los puntos de control en el sistema al que se transformará. • De conocer las coordenadas en más de dos controles puedes completar el procedimiento con dos de los puntos y utilizar los demás para cotejar y comparar los resultados obtenidos de la transformación. Transformación de Coordenadas • De desear utilizar más de dos puntos para establecer la solución de la transformación, deberá completar un procedimiento de mínimos cuadrados. • Esto pudiera ser recomendable en proyectos de grandes extensiones, donde el cambio en escala en distintas localizaciones del proyecto y los efectos de curvatura deben ser considerados. Transformación de Coordenadas • Procedimiento: Para diferenciar ambos sistemas de coordenadas, se identificaran: X, Y sistema de original E, N sistema al que se transformará. de tener algún subscrito éste identificará el punto. Transformación de Coordenadas • Aplicación de escala E = SX N = SY • Aplicación de traslación E = X + ΔE N = Y + ΔN • Aplicación de escala, traslación y rotación E = (S cos Θ) X – (S sin Θ) Y + ΔE N = (S sin Θ) X + (S cos Θ) Y + ΔN Transformación de Coordenadas • Luego de considerado los efectos de escala, rotación y traslación, obtenemos las siguientes ecuaciones para la obtención de E y N: (S cos Θ) X – (S sin Θ) Y + ΔE = E (S cos Θ) Y + (S sin Θ) X + ΔN = N Transformación de Coordenadas • Con el objetivo de simplificar las pasadas ecuaciones, se reescribirán considerando: a = S cos Θ c = ΔE b = S sin Θ d = ΔN aX–bY+c=E aY+bX+d=N Transformación de Coordenadas • Para continuar se utilizará un listado de coordenadas que contiene los controles 1 y 2, de los cuales se obtuvieron coordenadas planas estales mediante el uso de GPS. • Al tener datos de dos de los puntos, obtendríamos cuatros ecuaciones con cuatros desconocidas (a, b, c, d): a X1 – b Y1 + c = E1 a Y1 + b X1 + d = N1 a X2 – b Y2 + c = E2 a Y2 + b X2 + d = N2 Transformación de Coordenadas • Reescribiremos el sistema de ecuaciones de forma matricial para su solución. a X1 – b Y1 + c = E1 a Y1 + b X1 + d = N1 a X2 – b Y2 + c = E2 a Y2 + b X2 + d = N2 X1 Y 1 X2 Y2 Y1 X1 Y2 X2 1 0 0 1 1 0 0 1 E1 a N b 1 E2 c d N2 Transformación de Coordenadas • Recordando que: X1 a Y b 1 X2 c d Y2 Y1 X1 Y2 X2 1 0 0 1 1 0 0 1 1 E1 N 1 E2 N2 podemos así obtener los valores de las variables a, b, c y d. Transformación de Coordenadas • Considerando los siguientes, obtenemos como resultado de las variables a, b, c y d: • • • • Punto X Y E N 1 1000.000 1000.00 133880.807 241647.576 2 1032.454 1018.109 133910.982 241625.858 a = 0.424274607 b = -0.905934788 c = 132550.5976 d = 242129.2362 Transformación de Coordenadas • Translación ΔE = c = 132550.5976 ΔN = d = 242129.2362 • Rotación b a - 0.905934788 tan 1 1.132805821rad 64.90499255 0.424274607 Escala S a cos 0.424274607 S 1.000363325 cos(1.132805821) tan 1 • Transformación de Coordenadas • Una vez obtenidos todos los valores de a, b, c y d, se puede computar las coordenadas de cualquier punto utilizando las ecuaciones antes mencionadas: aX–bY+c=E E=aX–bY+c aY+bX+d=N N =aY+bX+d • Ejemplo: (Punto 12) E12 = a X12 – b Y12 + c E12 = a 1001.019 – b 1026.355 + c = 133905.115 N12 = a Y12 + b X12 + d N12 = a 1026.355 + b 1001.019 + d = 241657.835 Transformación de Coordenadas • Unidades – Al momento de efectuar la transformación, las coordenadas originales pueden encontrarse en cualquier sistema de unidades. – En caso que el sistema de coordenadas al cual se transformará sea distinto, éste se armonizará incluyendo la conversión en la escala. – Las coordenadas resultantes contendrán las unidades utilizadas por el sistema de coordenadas al cual se transformó. Transformación de Coordenadas • Escala – La escala incluirá el factor para el cambio de unidades entre sistemas en caso de ser unidades distintas. – Incluirá el factor de escala combinado perteneciente a la proyección cartografica utilizada de las coordenadas transformadas. • En caso de que las coordenada originales y las que se transformarán tengan las misma unidades, el factor escala debe ser similar al que obtendría del reporte de las observaciones de GPS en la localización. Transformación de Coordenadas • Escala – Al computar la escala en la transformación se está utilizando la distancia entre los puntos observados con GPS. Por tal razón al utilizar resultados de la observación de GPS erróneos o de pobre calidad, no solo se está localizando (trasladando y rotando) incorrectamente, sino que también se están modificando todas las dimensiones (escala) erróneamente. Transformación de Coordenadas • Escala – Recordemos que al trasformar las coordenadas a un sistema que proviene de una proyección cartografica, estas coordenadas son propias de la proyección y las dimensiones y áreas entre estas son en la proyección. Carretera PR-106 cerrada en el Km 1.6 por Puente Roto desde comienzos de marzo de 2012, luego de estar en ese lugar cerrado un carril, por mas de 12 meses, al comenzar los trabajos colapsa el carril que servia. Desvio Oficial por PR-351 a la PR-108 PR-106 Km 1.6 CERRADA Puente Colapsado en PR-106 Km.1.6 desde Marzo del 2012-Desvio Oficial PR-351 www.ngs.noaa.gov www.revistatp.com –un “Dominio” al servicio de la comunidad geo-espacial www.gitpr.org Módulo 2 Definiciones de Datums GEODETIC DATUMS Classical HORIZONTAL – 2 D (Latitude and Longitude) (e.g. NAD 27, NAD 83 (1986)) VERTICAL – 1 D (Orthometric Height) (e.g. NGVD 29, NAVD 88, IGLD 85) Contemporary PRACTICAL – 3 D (Latitude, Longitude and Ellipsoid Height) Fixed and Stable – Coordinates seldom change (e.g. NAD 83 (1992)) SCIENTIFIC – 4 D (Latitude, Longitude, Ellipsoid Height, Velocity) – Coordinates change with time (e.g. ITRF00, ITRF05) VERTICAL DATUMS A set of fundamental elevations to which other elevations are referred. Datum Types Tidal – Defined by observation of tidal variations over a specified epoch of time Geodetic – Typically based on Mean Sea Level at one or more tidal stations for a specified epoch of time U.S. VERTICAL DATUMS NAVD 88 Conterminous US Tied to primary CHS BM (60-78) at Father’s Point – Quebec, CD NAVD 88 Alaska GPS Ellipsoid Height + Geoid06 Puerto Rico Vertical Datum 2002 (PRVD 02) Defined by MSL (83-01) at 975 5371 A American Samoa Vertical Datum of 2002 Defined by MSL (83-01) at 177 0000 S Guam Vertical Datum of 2003 Defined by MSL (83-01) at 163 0000 TIDAL 4 Marianas Vertical Datum of 2003 Defined by MSL (83-01) at 163 3227 UH-2C Hawaii Vertical Datums ???? Módulo 3 Base de Datos Geográficos BASE DE DATOS GEOGRAFICOS FUENTE: Robert Liley & Associates Management Consultants Exhibit 33 1- Records de Propiedad a. Información Maestra • Localización Geografica • Dirección Civil • Nombre del dueño • Dirección/teléfono del dueño (si es diferente al anterior) • Numero de residentes • Descripción Legal (including stata title units) • Valor de la ultima transacción de la venta • Fecha de la ultima venta • “Covenants” b. Tasación • Clasificación • Exención contributiva/razones • Avalúo (assessment) • Impuestos actuales • Taza de tasación (TaxRate) • Balance Actual de impuestos • Status • Mejoras Locales • Historia c. Propiedades Gubernamentales • Fecha de adquisición/método de adquisición • Código de localización • Costo original • Valor actual del mercado • Seguros 1. Cobertura 2. Carrier Policy Cross Referente • Hipotecas 1. Cantidad original 2. Balance Pendiente 3. Datos de Interés 4. Términos 5. Tenedor de la Hipoteca • Datos de Alquiler (Rental Data) 1. Renter 2. Covenants 3. Terms 4. Fecha de Pago 5. Renovaciones 6. Pago 7. Balance Corriente 8. Insurance Cross Referente (Third Party) • Datos de Renta 1. Renter 2. Covenants 3. Terms 4. Fecha de Pago 5. Renovaciones 6. Pago 7. Deposito de seguridad 8. Balance Corriente 9. Insurance Cross Referente (Third Party) • Disposición 1. Precio de Venta 2. Costos 3. Dólares que no se venden 4. “Grants” d. Características Físicas • Indicadores de agua en lote • Dimensiones del lote • Huella del edificio • Fecha de la Primera construcción • Fecha de la ultima modificación • Referencias de permisos “cross” • Zonificación actual • Uso de Terreno actual • Indicador de no-conformidad legalmente • Conexión de utilidades • Servidumbres • Conexión de Utilidades extranjeras e. Información de Incendios (FIRE) • Características funcionales del Edificio • Peligros (Hazards) • Necesidades Especiales/Limitaciones • Incidentes con Incendios • Inspección 1. Itinerario 2. Hallazgos 3. Asuntos por hacer (Action Ítems) 4. Fecha de la Ultima Inspección • Perfil del Edificio • Tipo de equipo en expediente/localización f. Información Policiaca • Perfil del Edificio (Planificación Táctica) • querellas/Incidentes • Cursos de Acción • Resoluciones g. Asistencia Social • Educación • PAN • Desempleo • Otras Formas de Asistencia Social 2- Datos Ambientales • Tipo de Suelo • Drenaje • Cuenca Hidrográfica • Hidrológia • Vertedero de sustancias Toxicas • Incidentes Ambientales • Topografía • Recursos Naturales 1. Tipo 2. Localización de Referencia • Identificación de Áreas Inundables • Huracanes • Áreas de Deslizamientos • Estudios de Impacto Ambiental 3- Datos Estadísticos a. Crímenes • Fecha del Evento(s) • Tipo • Localización/Dirección • Historia b. Incendios • Fecha del Evento(s) • Tipo • Localización/Dirección • Historia c. Salud/Ambiente • Fecha del Evento(s) • Tipo • Localización/Dirección • Historia d. Datos Censales/Demográficos • Tracto Censal • Nacionalidad • Numero de Personas • Distribución por Edad • Niveles de Ingresos • Idioma • Nivel de Educación • Status Civil • Sexo • Afiliación Política e. Datos Económicos • Importar/Exportar • Turismo • Tipos de Industrias • Producción de Cemento • Gastos/Ingresos • Gastos Capitales • Salario Bruto Pagado • Indicadores del Componentes de Actividad Económica f. Cuentas Nacionales • Balance de Pagos • GNP • Componentes de la Tasación • Datos de Deposito del Banco • Ingresos Gubernamentales • Gastos Gubernamentales • Actividad del Sector Privado • Datos de Importación/Exportación g. Accidentes • Tipos • Fecha del ultimo evento • Localización/Dirección • Historia Previa 4- Datos de Infraestructura a. Localización Geográfica b. Carreteras • Tipo • Superficie • Fecha de Construcción • Propietario • Fecha del Ultimo Mantenimiento • Número de Carriles • Ancho • Profundidad c. Aceras • Tipo • Superficie d. e. f. g. h. • Fecha de Construcción • Propietario • Fecha del Ultimo Mantenimiento • Ancho/Profundidad Servicios de Agua • Hidrantes • Capacidad • Válvulas • Líneas • Presión/Edad • Profundidad • Fecha de Instalación • Fecha de Ultimo Mantenimiento • Estaciones de Bombeo Servicios de Alcantarillado Sanitarios • Líneas • Válvulas • Profundidad • Estaciones de Bombeo • Tipos Luminarias en Calles • Postes • Transformadores • Alambrado • Edad • Profundidad Servicios Eléctricos • Edad • Estaciones de Potencia • Sub-Estaciones • Transformadores • Embobinado (Wiring) • Postes • Cuadricula (Área de Cobertura) • voltaje • “Wattage” • Profundidad Tuberías (pipelines) • Tipo • Construcción • Edad • Profundidad • Tamaño • Capacidad i. Facilidades de Comunicación • Red/Planta de Teléfonos • Postes • Repetidores • Tamaño del Cable/Capacidad • Tipo de Cable • Fecha de Instalación • Fecha de la Ultima Modificación • Propietario • Facilidades de microondas/satélite • Área de Servicio/mantenimiento j. Servicios de Control de Trafico • Tipo • Activo/Pasivo • Fecha de Instalación • Fecha del Ultimo Mantenimiento k. Facilidades de Parques/Recreación • Tipo • Tamaño/Dimensiones • Fecha de Construcción • Rasgos • Código de Mantenimiento • Capacidad • Características Únicas l. Carriles (lanes) • Localización • Tipo • Superficie • Propietario • Dimensiones Físicas m. Escuelas • Tipo • Número de Salones de Clases • Capacidad • Fecha de Edificación • Características Físicas • Rasgos Especiales • Itinerario de usos n. Inventario de Árboles/Arbustos • Tipo • Numero • Fecha de Sembrado • Fecha de Remoción • Fecha de Transferencia o. Estacionamiento • Capacidad • Medido/Sin Medidor • “Signed” p. Puentes • Tipo • Superficie • Fecha de Construcción • Número de Carriles • Fecha del Ultimo Mantenimiento q. Utilidades extranjeras • Cablevisión • Propietario • Localización de Planta • Tuberías • Propietario • Capacidad • Localización de Planta • Características Especiales • Profundidad r. Red/Facilidades de Carreteras (Viales) • Tipo • Ruta • Rasgos Especiales • Facilidades Módulo 4 Geo-‐Based Informa2on Matrix Geo-Based Information Matrix Mapa Base “Assessments” Facilidades de Comunicaciones Estadísticas criminales Demografía Estadísticas Económicas Plantas Eléctricas Datos Ambientales Datos Financieros Edificios Gubernamentales Peligros (Hazards) Vertederos de Sustancias Peligrosas Hidrológica Datos de Inmigración Datos de Importación/Exportación Parcelas de Terrenos Datos de Usos de Terrenos Licencias Recursos Naturales Datos de Tenencia/Ocupación Permisos Utilidades Privadas Facilidades de Recreación Residencial, Comercial, Industrial Carreteras/Aceras Facilidades Agua/Alcantarillados Datos de Servicios Sociales Suelos Luminarias de Calles Impuestos Topografía Facilidades de Transportación o Viales Drenajes Pluviales y Cuencas Zonificación Lista de Agencias Junta de Planificación Autoridad de Edificios Públicos ARPE Defensa Civil Departamento de Agricultura Administración de Desarrollo Económico Departamento de Comercio Federal Administración de Servicios Generales Banco Gubernamental de Fomento Municipios Guardia Nacional Autoridad de Acueductos y Alcantarillados Autoridad de Comunicaciones Departamento de Comercio Departamento de Recursos Naturales y Ambientales Departamento de Transportación y Obras Públicas Autoridad de Energía Eléctrica Compañía de Fomento Industrial (PRIDCO) Departamento de Salud Compañía de Teléfonos (PRTC) Junta de Calidad Ambiental Departamento de Servicios Sociales o Familia Policía de Puerto Rico Compañía de Turismo Departamento de Haciendas Universidad de Puerto Rico Módulo 5 Ley Núm. 264 del año 2002: Ley para adoptar el Sistema de Coordenadas Planas Estatales de Puerto Rico Ley Núm. 264 del año 2002 (P. del S. 990), 2002, ley 264 Ley para adoptar el Sistema de Coordenadas Planas Estatales de Puerto Rico Ley Núm. 264 aprobada en 16 de noviembre de 2002 Para adoptar el Sistema de Coordenadas Planas Estatales utilizando el método de la Proyección Conforme Cónica Lambert y el North American Datum of 1983, o su versión más reciente, como el sistema de mapa oficial de las agencias, instrumentalidades y municipios del Estado Libre Asociado de Puerto Rico, a los fines de uniformar el uso de proyecciones cartográficas por los organismos gubernamentales, disponer lo relativo a la certificación de ubicaciones o posiciones geográficas, y para otros fines. EXPOSICION DE MOTIVOS La Junta de Planificación del Estado Libre Asociado de Puerto Rico es el organismo gubernamental responsable de guiar el desarrollo integral de Puerto Rico de modo coordinado, adecuado y económico, para atender necesidades actuales y futuras. La Junta también sirve como centro de información para el Gobierno y para la ciudadanía en general. Una de las herramientas de mayor importancia, para la evaluación y estudio de casos que se someten ante la Junta de Planificación, es el Archivo Gráfico. En este Archivo se recopila información gráfica en mapas, relacionada con las consultas que se someten ante la Junta, asi como la información relacionada con mapas de zonificación, zonas inundables y planes de usos de terrenos y expansión urbana. Este recurso de la Junta ofrece un marco de referencia abarcador y preciso, el desarrollo físico y estructural de Puerto Rico. Las agencias gubernamentales, los municipios y las empresas privadas utilizan este banco de datos continuamente para planificar sus proyectos Más eficientemente. Por ello, la Junta de Planificación mecanizó sus sistemas de información a fin de poder curnplir con la continua demanda de información del sector público y privado y para atender la cantidad de casos radicados. Para mantener actualizada esta información, se ha requerido, que toda consulta radicada ante la Junta presente la ubicación exacta del centro del proyecto propuesto, utilizando para ello la proyección de coordenadas geográficas conocida como Coordenadas Lambert. El Servicio Geodésico Nacional ha diseñado para los estados y territorios de los Estados Unidos de América, una red de sistemas de coordenadas conocido como Sistemas de Coordenadas Planas Estatales. El propósito de dichos sistemas es lograr la mejor representación cartográfica de las características geográficas de cada uno de los estados o territorios. Las proyecciones que utilizan dichos Sistemas toman en consideración diferentes criterios. Así por ejemplo, se utiliza la extensión del área cuando se trata de un hemisferio, un estado o un continente; la localización del área, esto es, si está en los polos, latitudes medias o en el Ecuador; o la forma de la extensión predominante, si el área discurre de norte a sur o de este a oeste. La Proyección Conforme Cónica Lambert, con dos paralelos estindares, es la base para el Sistema de Coordenadas Planas Estatales diseñado para zonas de dimensiones limitadas de norte a sur y para extensiones de terrenos indefinidas que corren de este a oeste. Varias agencias e instrumentalidades gubernamentales, como el Departamento de Recursos Naturales y Ambientales, la Autoridad de Carreteras, el Departamento de la Vivienda, la Autoridad de Tierras, la Administración de Terrenos y la propia Junta de Planificación, utilizan como referencia los mapas oficiales del Servicio Geológico de los Estados Unidos. Estos mapas de Puerto Rico están representados y utilizan la Proyección Conforme Cónica Lambert. La adopción en la jurisdicción del Estado Libre Asociado de Puerto Rico de una proyección cartográfica uniforme como el Sistema de Coordenadas Lambert y el North American Datum of 1983, o su versión más reciente, contribuirá a que el intercambio de información geográfica se realice de forma rápida, clara y eficiente. Por ello, conviene al interés público que se establezca por Ley que el Sistema de Coordenadas Planas Estatales con el método de Proyección Cónica Lambert serd el sistema de mapa oficial para toda la Isla, de forma tal que se utilice una sola proyeeción cartográfica para determinar la ubicación de un lugar específico en la jurisdicción de Puerto Rico. También se dispone que el gobierno central adoptará un modelo matemático que represente el esferoide terrestre, conocido como datum, de modo que sea estindar o uniforme para todas las agencias e instrumentalidades públicas. DECRETASE POR LA ASAMBLEA LEGISLATIVA DE PUERTO RICO: Artículo 1.- Adopción del Sistema de Coordenadas Planas Estatales.Se adopta el Sistema de Coordenadas Planas Estatales con el método de Proyección Conforme Cónica Lambert como el sisterna de mapa oficial para todas las agencias, instrumentalidades y municipios del Estado Libre Asociado de Puerto Rico, a los fines de uniformar el uso de proyecciones cartográficas por los organismos gubernamentales. Se dispone, además, que el gobierno central adoptará dentro de un (1) año de la aprobación de esta Ley, el North American Datum of 1983, o su versión más reciente, como el modelo matemático para representar el elipsoide terrestre de modo que sea estándar o uniforme para todas las agencias e instrumentalidades públicas. Artículo 2.- Certificación de Ubicaciones o Posiciones Geográficas.Toda ubicación o posición geográfica, que se presente ante las agencias, instrumentalidades y municipios del Estado Libre Asociado de Puerto Rico deberá cumplir con una de las siguientes alternativas: (a) En el caso de la ubicación de estructuras, edificaciones o construcciones deberá estar certificada por un profesional autorizado, de acuerdo con lo establecido en la Ley Núm. 185 de 26 de diciernbre de 1997, según enmendada, conocida como "Ley de la Junta Examinadora de Ingenieros, Arquitectos, Agrimensores y Arquitectos Paisajistas de Puerto Rico." (b) En el caso de estudios, investigaciones, o evaluaciones de naturaleza técnica o científica, deberá estar acompañada de un documento debidamente juramentado por la persona que lo presenta, en el cual se incluya por lo menos la siguiente información: (i) Equipo de mensura utilizado, o sea si es, un equipo del sistema de posicionamiento global o un equipo convencional, asi como la marca, modelo y precisión máxima del equipo. (ii) Modelo matemático o datum utilizado al momento de hacer la medición. (iii) Tiempo requerido en tomar la medición, expresado en horas:minutos:segundos o en la forma establecida por reglamentación. Todas las agencias, instrumentalidades y municipios del Estado Libre Asociado de Puerto Rico ante las cuales haya que presentarse una certificación sobre la ubicación o posición geográfica de una estructura, propiedad, proyecto, desarrollo, estudio científico o técnico, adoptarán un documento o formulario uniforme para tales propósitos. Mediante dicho documento o formulario uniforme para todas las entidades públicas se dispondrá referente a los métodos de certificación de ubicación o posición establecidos en los incisos (a) y (b) de este Artículo. Este documento o formulario uniforme se adoptará por reglamento dentro de los noventa (90) días contados a partir de la aprobación de esta Ley, luego de consultar y contar con las recomendaciones de la Oficina de Gerencia y Presupuesto, del Departamento de Recursos Naturales y Ambientales, de la Junta de Planificación y de la Administración de Reglamentos de Permisos, del Instituto de Cultura Puertorriqueña, así como de la Junta de Calidad Ambiental. Artículo 3.- Esta Ley comenzará regir inmediatamente después de su aprobación. ___________________ Presidente del Senado ____________________ Presidnete de la Cámara Nota Importante: Esta ley es copia de la ley original cuando fue aprobada, no incluye enmiendas posteriores. Módulo 6 Sección 5.2.3 -‐ Sistema de Coordenadas Planas Estatales Sección 5.2.3 Sistema de Coordenadas Planas Estatales a. A tenor con las disposiciones de la Ley 264 de 16 de noviembre de 2002, se adopta un Sistema de Coordenadas Planas Estatales homogéneo que permita el establecimiento de un sistema cartográfico preciso y confiable. b. Toda solicitud ante la OGPe que implique la creación de nuevas parcelas, que contenga medidas agrarias, que requiera la delimitación para su ubicación precisa, que conlleve cambios en la topografía existente, nuevas construcciones o funciones similares, deberá estar geo-referenciado al Sistema de Coordenadas Oficial del Gobierno de Puerto Rico y contar con la Certificación de un Agrimensor Profesional o autorizado a ejercer la profesión de la agrimensura, la cual debe cumplir con lo siguiente: 1. El Agrimensor certificará el Datum Horizontal y su revisión en o posterior al 1997. Esta debe contener un tracto que demuestre que la determinación procede de un punto de control oficial del National Geodetic Survey (NGS) y evidenciar el método de Global Positioning System (GPS) utilizado para la determinación. 2. Evidenciar el equipo y los monumentos de control establecidos en el proyecto. Los monumentos deben estar representados en el plano con las coordenadas tanto planas como geodésicas. 3. En aquellos proyectos que contengan elevaciones, se especificará el Datum vertical y se evidenciará mediante un tracto que su determinación proviene de un Bench Mark (BM) oficial de las entidades relacionadas de gobierno, como pueden ser: NGS y FEMA. 4. Se requerirá que los planos contengan la información de los Datums horizontal y/o vertical, junto a la certificación del Agrimensor responsable de esa determinación. 5. La posición del polígono debe garantizar un error estándar que no exceda el cero punto cero cinco (±0.05) metros equivalentes a dos (2) pulgadas dentro del Datum utilizado. 6. El Archivo deberá estar en formato DXF y georeferenciado en coordenadas State Plane Nad 83 que incluya parcela, huella de los edificios y/o estructura, aceras y calles. Cada uno de estos deben estar hechos en capas (layers) individuales y en polígonos cerrados. 7. Para aquellos proyectos que no impacten toda la parcela deben entregar Archivo en formato DXF y georeferenciado en coordenadas State Plane NAD83 que incluya parcela, límite del proyecto, huella de los edificios y/o estructura, aceras y calles. Cada uno de estos deben estar hechos en capas (layers) individuales y en polígonos cerrados. Módulo 7 Modern Terrestrial Reference Systems – Part 1 REFERENCE SYSTEMS Modern Terrestrial Reference Systems (Part 1) Dr. Richard A. Snay and Dr. Tomás Soler S urveyors, GIS/LIS professionals, engineers, cartographers, and others who work in North America face the challenge of dealing with at least three different 3D terrestrial reference systems. For many legal activities, these people express positional coordinates in the reference system known as the North American Datum of 1983 (NAD 83). Alternatively, they often favor using the World Geodetic System of 1984 (WGS 84) for various practical positioning activities involving the Global Positioning System (GPS), or they find the International Terrestrial Reference System (ITRS) more suitable for achieving superior positional accuracy. While these three reference systems differ from one another only slightly in concept, they differ significantly in how they have been realized, where the realization of a particular reference system is called a “reference frame”. A particular reference frame is usually established by designating positions and velocities for several identifiable points. To date there have been several realizations of each of these three reference systems, as institutions have systematically revised positions and velocities from time to time to keep pace with how evolving technology has improved positioning accuracy. Here, we review the evolution of these reference frames, and we discuss transforming positions between different reference frames. Finally, we address some practical considerations for accurate positioning and discuss plans for a new NAD 83 realization. Defining a Reference System The modern approach to defining a 3D terrestrial reference system may be divided into four steps. The first step links the axes of a 3D cartesian coordinate system to a configuration of physically measurable locations on or within the earth. As a result, the location and orientation of the three coordinate axes are defined. The second step relates the concept of distance to physically measurable quantities whereby a unit of length is introduced. The third step introduces an auxiliary geometric surface that approximates the size and shape of the earth. Finally, Figure 1 the fourth step addresses the question of how Earth’s gravity field contributes to the notion of position, and especially that of height. We shall be concerned here with only the first three steps, thus focusing on the geometric aspects involved in defining a reference system. For the first step, most scientists involved in defining modern reference systems agree that the origin of the 3D cartesian system should be located at Earth’s center of mass (geocenter); also that the cartesian system’s z-axis should pass through the conventional definition of the North Pole, or more precisely, the International Reference Pole (IRP) as defined by the International Earth Rotation Service (IERS), an international organization established in 1988 and headquartered in Paris, France. The x-axis should go through the point of zero longitude located on the plane of the conventional equator, which is also defined by the IERS. The meridian going through this point is located very close to the meridian of Greenwich although the two are not coincident. The y-axis forms a righthanded coordinate frame with the x- and z-axes. Indeed, each of the three refer- ence systems—NAD 83, WGS 84, and ITRS—has been accordingly defined in concept. They differ, however, as we shall soon discuss, in their realizations; that is, in how the location and orientation of their respective cartesian axes have been physically materialized as well as their respective concepts of distance. Unfortunately, what initially appears to be a simple geometric procedure is complicated by Earth’s dynamic behavior. For example, Earth’s center of mass is moving relative to Earth’s surface. Also, there are variations of Earth’s rotation rate as well as motions of Earth’s rotation axis both with respect to space (precession and nutation) and to Earth’s surface (polar motion). Moreover, points on the earth’s crust are moving relative to one another as a result of plate tectonics, earthquakes, volcanic/magmatic activity, postglacial rebound, people’s extraction of underground fluids, solid Earth tides, ocean loading, and several other geophysical phenomena. Modern terrestrial reference systems, hence, need to account for these motions. One option is to relate the cartesian axes to the locations of selected points measured at a particu- COPYRIGHT PROFESSIONAL SURVEYOR • December 1999 • All Rights Reserved 1 REFERENCE SYSTEMS lar instant of time (epoch). This alternative is generally used when dealing with the motion of the earth’s rotational axis and with the motions associated with plate tectonics. Other types of motion (for example, subsidence) are accounted for by fixing the cartesian axes to some temporal average of the locations for selected points. As we shall see, a fundamental difference among the various reference frames involves how they address the motion associated with plate tectonics. For the second step, scientists concerned with defining up-to-date terrestrial reference systems agree that the unit of length, the meter or “metre”, corresponds to the length of path traveled by light in a vacuum during a time interval of exactly 1/299,792,458 seconds. This solves the problem of relating the concept of distance to a physically measurable quantity in theory, but not in realization. Each of the various reference frames associated with NAD 83, WGS 84, and ITRS relies on a distinct set of measurements that were performed using one or more of several widely different types of instruments and techniques, among the most representative: GPS, electrooptical distance measuring instrumentation, Doppler satellite positioning, very long baseline interferometry (VLBI), and satellite laser ranging (SLR). While each measurement type had been calibrated to fit the definition of a meter as best as possible, the observations, nevertheless, contain uncertainties. Consequently, the “scale” of any particular reference frame is somewhat less than perfect. In particular, when old classical terrestrial frames are compared with modern “space-age” frames, scale errors at the part-per-million (ppm) level may often be detected. Because of recent technological advances in the measurement of time and, consequently, distance, scale differences between modern frames are now approaching the part-per-billion (ppb) level. For the third step, the earth’s surface is approximated in size and shape by the geometric surface that is formed by rotating an ellipse about its smaller axis (Figure 1). The generated surface is termed an “ellipsoid of revolution” or simply ellipsoid. The ellipsoid’s geometric center should be located at the origin of the 3D cartesian system, and its axis of radial symmetry (semi-minor axis) should coincide with the cartesian z-axis of the selected terrestrial reference frame. The size and shape of the rotated ellipse may be completely specified using two parameters: the length of its semi-major axis, usually denoted a, which approximates the distance from the geocenter to a point on the equator (approximately 6,378 km); and the length of the semi-minor axis, de2 noted b, which approximates the distance from the geocenter to the North Pole. The value of b is about 0.3% shorter than a. The fact that a is longer than b is a consequence of the force imparted by Earth’s rotation causing our home planet to bulge outward around its equator. Often, instead of b, the ellipsoid’s flattening, f = (a - b)/a, is used. D i ff e rent ellipsoids have been adopted for the different reference systems. NAD 83 uses the same ellipsoid as the Geodetic Reference System of 1980 which was adopted by the International Association of Geodesy. WGS 84 uses an ellipsoid adopted by the National Imagery and Mapping Agency (NIMA, formerly the Defense Mapping Agency), and ITRS uses an ellip- soid adopted by the IERS. Corresponding values of a and f are presented in the table below. Given values for a and b (or f), people can convert 3D cartesian coordinates—x, y, z— into the curvilinear coordinates—latitude, longitude, and ellipsoidal height—and vice versa. These curvilinear coordinates embody a certain intuitive appeal in specifying locations on and near the earth’s surface, as they relate to our innate sense of the horizontal and vertical dimensions. DR. RICHARD A. SNAY is Manager of the National Continuously Operating Reference Station (CORS) program and a geodesist with the National Geodetic Survey. DR. TOMÁS SOLER, is Chief, Global Positioning System Branch, Spatial Reference Systems Division, National Geodetic Survey. Reference System Semi-major axis, m Flattening, unitless NAD 83 6,378,137.0 1/298.257222101 WGS 84 6,378,137.0 1/298.257223563 ITRS 6,378,136.49 1/298.25645 COPYRIGHT PROFESSIONAL SURVEYOR • December 1999 • All Rights Reserved Módulo 8 Modern Terrestrial Reference Systems – Part 2: The Evolu2on of NAD 83 Modern Terrestrial Reference Systems PART 2: The Evolution of NAD 83 Dr. Richard A. Snay and Dr. Tomás Soler he first realization of NAD 83 was introduced in 1986 by a group of institutions representing the various North American countries to upgrade the previous reference system; that is, the North American Datum of 1927 or NAD 27. In particular, the National Geodetic Survey (NGS) represented the United States, and this federal institution officially refers to the first NAD 83 realization as NAD 83 (1986). For this realization, the group of institutions relied heavily on Doppler satellite observations collected at a few hundred sites to estimate the lo cation of the Earth’s center of mass and the orientation of the 3D cartesian axes. They also relied on these same Doppler observations to provide scale for NAD 83 (1986). More precisely, the group of institutions relied on 3D Doppler-derived positions that had been transformed by: • a translation of 4.5 m along the z-axis • a clockwise rotation of 0.814 arc sec onds about the z-axis • a scale change of -0.6 ppm The Doppler-derived positions were so transformed to make them more consistent with the very long baseline interferometry (VLBI), satellite laser ranging (SLR), and terrestrial azimuth measurements that were available in the early 1980s. While NAD 83 (1986) is 3D in scope, NGS adopted only horizontal coordinates (latitude and longitude) for over 99% of the approximately 250,000 U.S. control points that were involved in defining this reference frame. Unfortunately, this first realization of NAD 83 occurred a few years before GPS technology made the vertical dimension economically accessible. spirit leveling, and not geometric heights relative to an abstract mathematical surface (the ellipsoid), as obtained with GPS. The attitude towards using GPS to measure heights gradually evolved, however, as NGS and other institutions developed improved geoidal models for determining the spatial separation between mean sea level and the ellipsoid. These improvements enabled people to convert ellipsoidal heights into orthometric heights with greater and greater accuracy. Moreover, practitioners can measure heights much more economically with GPS than with spirit leveling. As GPS matured, so did other spaceage geodetic technologies; in particular, SLR and VLBI. Within a few years after 1986, both GPS and SLR measurements had allowed geodesists to locate Earth’s center of mass with a precision of a few centimeters. In doing so, these technologies revealed that the center of mass that was adopted for NAD 83 (1986) is displaced by about 2 m from the true geocenter. Similarly, GPS, SLR, and VLBI revealed that the orientation of the NAD 83 (1986) cartesian axes is misaligned by over 0.03 arc seconds relative to their true orientation, and that the NAD 83 (1986) scale differs by about 0.0871 ppm from the true definition of a meter. These discrepancies caused significant concern as the use of highly accurate GPS measurements proliferated. In particular, starting with Tennessee in 1989, each state–in collaboration with NGS and various other institutions–used GPS technology to establish regional reference frames that were to be consistent with NAD 83. The corresponding networks of GPS control points were originally called High Precision Geodetic Networks (HPGN). Currently, they are referred to as High Accuracy Reference Networks (HARN). This latter name reflects the fact that relative accuracies among HARN control points are better than 1 ppm, whereas relative accuracies among pre-existing control points were nominally only 10 ppm. For defining these regional reference frames, NGS retained the location of the geocenter and the orientation of the 3D cartesian axes which had been derived in 1986 from the transformed Doppler observations. This agency, however, opted to introduce a new scale that would be consistent with the scale of the then cur- GPS Changed Everything Around the same time that NGS adopted NAD 83 (1986), the agency had begun using GPS technology, instead of triangulation and/or trilateration, for horizontal positioning. The fact that GPS technology also provided accurate ellipsoidal heights was somewhat overlooked in the 1980s because surveyors, hydrologists, and other users of vertical positions required orthometric heights relative to mean sea level, as obtained with tide gauges and COPYRIGHT PROFESSIONAL SURVEYOR • February 2000 • All Rights Reserved 1 A P P L I C AT I O N rent ITRS realization which is known as the International Terrestrial Reference Frame of 1989 (ITRF89). As we shall discuss later, the ITRF89 scale was based on a combination of GPS, SLR, VLBI, and lunar-laser-ranging (LLR) measurements. The resulting scale change, equal to -0.0871 ppm, altered existing NAD 83 latitudes and longitudes insignificantly, but it systematically decreased all ellipsoidal heights by about 0.6 m ( = 0.0871•10-6 • R where R is the radius of the Earth). Nevertheless, this change to a more accurate scale facilitated the migration toward using GPS technology for deriving accurate heights. Let us call this second realization NAD 83 (HPGN) or NAD 83 (HARN); but keep in mind that this second realization is actually a collection of regional realizations that were formulated over a period of several years (1989-1997) with each new regional realization being “adjusted” to fit with those that preceded it. Third Realization of NAD 83 Incorporated CORS In late 1994, NGS introduced a third realization of NAD 83 when the agency organized a network of continuously operating reference stations (CORS). Each CORS includes a GPS receiver whose data NGS collects, processes, and disseminates for public use. Surveyors and other professionals can apply CORS data to position points at which other GPS data have been collected with accuracies that approach a few centimeters, both horizontally and vertically. The CORS system started with about a dozen sites in December 1994, and it has grown at a rate of about three sites per month. Figure 2 depicts the recent status of the National CORS network. Positional coordinates of the early CORS sites were first computed in the ITRS realization known as ITRF93. Equivalent NAD 83 coordinates were then computed by applying a Helmert transformation; that is, a transformation of the form xNAD83 = Tx + (1+s) • xITRF + Rz • yITRF - Ry • zITRF (1a) yNAD83 = Ty - Rz • xITRF + (1+s) • yITRF + Rx • zITRF (1b) zNAD83 = Tz + Ry • xITRF - Rx • yITRF + (1+s) • zITRF (1c) where Tx, Ty, and Tz represent three translation along the xaxis, y-axis, and z-axis, respectively, which will bring the origin of the two frames into coincidence. Rx, Ry, and Rz represent three rotations about the x-axis, y-axis, and z-axis, respectively, which, in combination, will bring the three axes of one frame into parallel alignment with their corresponding axes in the other frame. Finally, s represents the difference in scale between the two frames. The values of Tx, Ty, Tz, Rx, Ry, and Rz had been estimated so that the ITRF93 positional coordinates of nine VLBI sites in the United States would transform as best as possible (in a least squares sense) to their adopted NAD 83 (HARN) positional coordinates. The scale difference, s, was set to equal zero. These VLBI sites were used because they had highly accurate positions (cm-level) in both ITRF93 and NAD 83 (HARN). Let us use the label NAD 83 (CORS93) to identify the reference frame obtained by applying this transformation to convert CORS positions from ITFR93 to NAD 83. In the spring of 1996, NGS computed positional coordinates for all the then existing CORS in yet another ITRS realization, known as ITRF94. Similarly, the agency developed a Helmert 2 transformation from ITRF94 to NAD 83 using eight of the same VLBI sites (a VLBI site in California was not used here because of crustal motion concerns). Again, the scale difference was set to equal zero. NGS applied this new transformation to convert ITRF94 coordinates for the CORS sites to a fourth NAD 83 realization which we call NAD 83 (CORS94). Most recently in the fall of 1998, NGS computed positional coordinates for all the then existing CORS in the ITRS realization known as ITRF96. This time, however, NGS collaborated with representatives from Canada’s Geodetic Survey Division to derive a Helmert transformation based on eight VLBI sites in the United States and four VLBI sites in Canada. Again, a scale difference equal to zero was enforced. Other adopted parameters for this transformation are presented in the sidebar box. NGS applied the resulting transformation to convert ITRF96 positional coordinates for the CORS sites to a fifth NAD 83 realization which we call NAD 83 (CORS96). NGS, however, continues to use NAD 83 (CORS94) positions for all CORS sites, except those that have come online since the fall of 1998 and those whose NAD 83 (CORS96) position differs from their corresponding NAD 83 (CORS94) position by more than 2 cm horizontally or 4 cm vertically. In summary, surveyors and others have witnessed five realizations of NAD 83 in the United States. A similar evolution occurred in Canada, but the two countries at least agree on their first and last realizations. The five U.S. realizations are consistent in their choice of origin and orientation; they differ, however, in their choice of scale. While the scale difference between NAD 83 (1986) and NAD 83 (HARN) equals -0.0871 ppm, the scale difference between NAD 83 (HARN) and any NAD 83 (CORSxx) is smaller than 0.005 ppm in magnitude. It should be noted that the NAD 83 (HARN) latitude and/or longitude of a given control point may differ by up to a meter from its corresponding NAD 83 (1986) coordinate. Fortunately, the horizontal discrepancy between the NAD 83 (CORS93) and NAD 83 (HARN) positions for a control point is almost always less than 10 cm, and the horizontal discrepancy between any two NAD 83 (CORSxx) positions for a control point is almost always less than 2 cm. In addition, as NAD 83 has evolved from mostly a horizontal reference system to a full 3D reference system, the number of control points with measured ellipsoidal heights has grown dramatically. Finally, for the present discussion, we intentionally omitted the role of crustal motion on the evolution of NAD 83. We will address this topic in some detail, however, after discussing the evolution of ITRS, as this international reference system provides the global perspective that will help us understand certain concepts associated with crustal motion. DR. RICHARD A. SNAY is Manger of the National Continuously Operating Reference Station (CORS) program and a geodesist with the National Geodetic Survey. DR. TOMÁS SOLER is Chief, Global Positioning System Branch, Spatial Reference Systems Division, National Geodetic Survey. COPYRIGHT PROFESSIONAL SURVEYOR • February 2000 • All Rights Reserved Módulo 9 Modern Terrestrial Reference Systems – Part 3: WGS 84 and ITRS Modern Terrestrial Reference Systems PART 3: WGS 84 and ITRS Dr. Richard A. Snay and Dr. Tomás Soler he Department of Defense (DoD) realization of the International Terrestrial (starting at 0h UTC, 2 January 1994) when developed the WGS 84 reference Reference System (ITRS). NIMA started expressing their derived GPS system to support global activities involvThe original WGS 84 realization essenorbits in this frame. The latest WGS 84 reing mapping, charting, positioning, and tially agrees with NAD 83 (1986). Subsealization, called WGS 84 (G873), is also navigation. More specifically, DoD introquent WGS 84 realizations, however, apbased completely on GPS observations. duced WGS 84 to express satellite orbits; proximate certain ITRS realizations. BeAgain, the letter G reflects this fact, and that is, satellite positions as a function of cause GPS satellites broadcast the predict“873” refers to the GPS week number starttime. Accordingly, WGS 84 is widely used ed WGS 84 orbits, people who use this ing at 0h UTC, 29 September 1996. Alfor “absolute” positioning activities wherebroadcast information for positioning though NIMA started computing GPS orby people assume that satellite orbits are points automatically obtain coordinates bits in this frame on this date, the GPS Opsufficiently accurate to serve as the sole that are consistent with WGS 84. Hence, erational Control Segment did not adopt source of control for positioning points of the popularity of using GPS for real-time WGS 84 (G873) until 29 January 1997. interest. In particular, absolute positioning positioning has promoted greater use of The origin, orientation, and scale of does not rely on using positional coordiWGS 84. Despite its popularity, people WGS 84 (G873) are determined relative to nates for pre-existing terrestrial points for generally do not use WGS 84 for high-preadopted positional coordinates for 15 GPS control, except indirectly in that orbits are cision positioning activities, because such tracking stations: five of them are mainderived from adopted positions for a small activities require the use of highly accurate tained by the Air Force and ten by NIMA set of tracking stations (Fig. 3). The generpositions on pre-existing terrestrial points (see Fig. 3). NIMA chose their sites to comal user, however, never needs to know the for control. For example, various differenplement the somewhat equatorial distribupositions of these tracking stations. tial GPS techniques use known positions tion of the Air Force sites and to optimize DoD provides both “predicted” and for one or more pre-existing terrestrial multiple station visibility from each GPS “postfit” orbits in the WGS 84 reference points to remove certain systematic errors satellite. People may anticipate further imsystem. As implied by the name, predicted in computing highly precise positions for provements of WGS 84 in the future, as orbits are calculated ahead of time by apnew points. Consequently, before WGS 84 new GPS tracking sites may be added or plying physical principles to extrapolate can support high-precision positioning acexisting antennas may be relocated or recurrently observed satellite positions. On tivities, a rather extensive network of acplaced. NIMA is dedicated to take approthe other hand, postfit orbits are calculated curately positioned WGS 84 terrestrial conpriate measures to guarantee the highest from previously observed satellite positrol points would have to be established. possible degree of quality and to perpetutions. Postfit orbits are more precise than DoD established the original WGS 84 ate the accuracy of WGS 84. As mentioned predicted orbits both because they do not reference frame in 1987 using Doppler obearlier, however, most regions lack a netinvolve predicting the future and because servations from the Navy Navigation Satelwork of accessible reference points that they are usually derived using a larger lite System (NNSS) or TRANSIT. The WGS might serve as control points from which number of tracking stations. GPS predicted 84 frames have evolved significantly since highly accurate WGS 84 coordinates may orbits and satellite clock parameters are the mid-1980s. In 1994, DoD introduced a be propagated using an appropriate static generated by the Air Force at the GPS Oprealization of WGS 84 that is based comdifferential GPS technique involving carrierational Control Segment, located at pletely on GPS observations, instead of er phase observables. Another minor Schriever AFB, Colorado. The Air Force Doppler observations. This new realization drawback affecting accurate GPS work is then uploads these predicted quantities to is officially known as WGS 84 (G730) the unavailability to the general GPS user the GPS satellites so that this information where the letter G stands for “GPS” and of the crustal velocities at the WGS 84 may be included in the radio signal trans“730” denotes the GPS week number tracking stations. More information about mitted by these satellites. These predicted WGS 84 may be obtained via the Internet orbits support all real-time positionby accessing: http:// ing and navigation activities in164.214.2.59/GandG/tr8350_2.html volving GPS. Postfit GPS orbits and satellite clock parameters The Evolution of ITRS are generated by the National In the late 1980s, the InternaImagery and Mapping tional Earth Rotation Service Agency (NIMA), who current(IERS) introduced ITRS to suply makes this information port those scientific activities that available on its Geodesy and require highly accurate positionGeophysics World Wide Web al coordinates; for example, pages. A number of other ormonitoring crustal motion and ganizations also generate the motion of Earth’s rotational postfit GPS orbits which they axis. The initial ITRS realization Figure 3. Combined DoD tracking network that defines WGS 84. usually express in a particular was called the International Ter- T COPYRIGHT PROFESSIONAL SURVEYOR • March 2000 • All Rights Reserved 1 A P P L I C AT I O N restrial Reference Frame of 1988 (ITRF88). Accordingly, IERS published positions and velocities for a worldwide network of several hundred stations. The IERS, with the help of several cooperating institutions, derived these positions and velocities using various highly precise geodetic techniques including GPS, VLBI, SLR, LLR, and DORIS (Doppler orbitography and radiopositioning integrated by satellite). Every year or so since introducing ITRF88, the IERS has developed a new ITRS realization –ITRF89, ITRF90, ..., ITRF97– whereby they have published revised positions and velocities for previously existing sites, as well as new positions and velocities for those sites that had been established since after earlier realizations had been developed. Each new realization not only incorporated at least an additional year of data, but also the most current understanding of Earth’s dynamic behavior. The ITRF96 frame is defined by the positions and velocities of 508 stations dispersed among 290 globally distributed sites (Fig. 4). Recall that a particular site may involve one or more co-located instruments employing various space-related techniques (e.g., GPS, VLBI, SLR, LLR, and DORIS). The accuracy and rigor of ITRS has proven contagious, and its popularity is steadily growing among those who engage in positioning activities. Furthermore, ITRS is the first major international reference system to directly address plate tectonics and other forms of crustal motion by publishing velocities as well as positions for its control points. To appreciate the need for velocities, consider the theory of plate tectonics. According to this theory, Earth’s outer shell consists of about 20 plates that are essentially rigid, and these plates move mostly laterally relative to one another like several large sheets of ice on a body of water. The relative motion between points on different plates are, in some cases, as large as 150 mm/yr, which is easily detectable using GPS and other modern day positioning techniques. Given the fact that each tectonic plate is moving relative to the others, one may ask how crustal velocities may be expressed in “absolute” terms. The people responsible for ITRS currently address this 2 Figure 4. Sites defining ITRF96. dilemma by assuming that the Earth’s surface, as a whole, does not move “on average” relative to Earth’s interior. Said differently, the ITRS developers assume that the total angular momentum of Earth’s outer shell is zero. Hence, the angular momentum associated with the motion of any one plate is compensated by the combined angular momentum associated with the motions of the remaining plates. Consequently, points on the North American plate generally move horizontally at measurable rates according to the ITRS definition of absolute motion. In particular, horizontal ITRF96 velocities have magnitudes between 10 and 20 mm/yr in the coterminous 48 states. Moreover, horizontal ITRF96 velocities have even greater magnitudes in Alaska and Hawaii. In contrast, the NAD 83 reference system addresses plate motion under the assumption that the North American plate, as a whole, does not move “on average” relative to Earth’s interior. Hence, points on the North American plate generally have no horizontal velocity relative to NAD 83 unless they are located near the plate’s margin (California, Oregon, Washington, and Alaska) and/or they are affected by some other deformational process (volcanic/magmatic activity, postglacial rebound, etc.). The NAD 83 reference system, however, does make special accommodations for certain U.S. regions that are located completely on another plate. In Hawaii, for example, NAD 83 positional coordinates are defined as if the Pacific plate is not moving. This approach is convenient for people who are involved with positioning activities solely in Hawaii. This approach, however, introduces a layer of complexity for people who are involved in positioning points in Hawaii relative to points in North America. In the realm of crustal motion, it is inappropriate to specify positional coordinates without specifying the “epoch date” for these coordinates; that is, the date to which these coordinates correspond. Accordingly, ITRF96 positions are usually specified for the epoch date of 1 January 1997 (often denoted in units of years as 1997.0). To obtain positions for another time, t, people need to apply the formula x(t) = x(1997.0) + vx • ( t - 1997.0 ) (2) and similar formulas for y(t) and z(t). Here, x(t) denotes the point’s x-coordinate at time t, x(1997.0) denotes the point’s xcoordinate on 1 January 1997, and vx denotes the x-component of the point’s velocity. NGS furnishes easy access to the ITRF96 reference frame through a set of over 170 stations belonging to the National CORS network (recall Fig. 2). Positions, velocities, and other pertinent information for these stations are available via the Internet by accessing: ftp://www.ngs.noaa. gov/cors/coord/coord_96. Transforming Between Reference Frames In 1998, U.S. and Canadian officials jointly adopted a Helmert transformation to convert positional coordinates between ITRF96 and NAD 83 (CORS96). The IERS has also adopted appropriate Helmert transformations for converting between ITRF96 and other ITRS realizations. NGS has encoded all these transformations into a software package, called HTDP (Horizontal Time-Dependent Positioning), which is freely available via the Internet: http://www.ngs.noaa.gov/TOOLS/ Htdp/Htdp.html This software enables people to transform individual positions entered interactively or a collection of positions entered as a formatted file. Also, if people expect to transform only a few positions, then they may run HTDP interactively from this web page. While Helmert transformations, as encoded into HTDP, are appropriate for transforming positions between any two ITRS realizations or between any ITRS realization and NAD 83 (CORS96), more complicated transformations are required COPYRIGHT PROFESSIONAL SURVEYOR • March 2000 • All Rights Reserved A P P L I C AT I O N for conversions that involve NAD 27, NAD 83 (1986), or NAD 83 (HARN). These complications arise because these frames contain large local and regional distortions that can not be quantified by a simple Helmert transformation. For instance, NAD 27 contains distortions at the 10 m level. That is, if one applied the best possible Helmert transformation from NAD 27 to NAD 83 (CORS96), then the converted NAD 27 positions may still be in error by as much as 10 m. In a similar manner, NAD 83 (1986) contains distortions at the 1 m level, and NAD 83 (HARN) contains distortions at the 0.1 m level. NGS has developed a software package, called NADCON (), that embodies rather intricate transformations to convert positional coordinates between any pair of the following reference frames: NAD 27, NAD 83 (1986), and NAD 83 (HARN). Referring to a pair of 2D grids that span the United States, NADCON contains appropriate values for each grid node to transform its positional coordinates from one reference frame to another. Furthermore, NADCON interpolates these gridded values to transform points located within the grid’s span. It should be noted that NADCON may be used only to transform horizontal coordinates (latitude and longitude), because ellipsoidal heights— relative to NAD 27 or NAD 83 (1986)— have never been adopted for most control points. While HTDP may be used with pairs of certain reference frames (NAD 83 (CORS96), ITRF88, ITRF89,. . . , and ITRF97) and NADCON with pairs of other reference frames (NAD 27, NAD 83 (1986), and NAD 83 (HARN)), no NGSsanctioned software exists for transforming coordinates from any member of one set to any member of the other. Also, no NGS-sanctioned software exists for transforming NAD 83 (CORS93) and/or NAD 83 (CORS94) positions to other reference frames. Regarding the WGS 84 reference system, it is generally assumed that WGS 84 (original) is identical to NAD 83 (1986), that WGS 84 (G730) is identical to ITRF92, and that WGS 84 (G873) is identical to ITRF96. Other transformations between pairs of the WGS 84 realizations, however, have also appeared in the literature. DR. RICHARD A. SNAY is Manager of the National Continuously Operating Reference Station (CORS) program and a geodesist with the National Geodetic Survey. DR. TOMÁS SOLER is Chief, Global Positioning System Branch, Spatial Reference Systems Division, National Geodetic Survey. COPYRIGHT PROFESSIONAL SURVEYOR • March 2000 • All Rights Reserved 3 Módulo 10 Modern Terrestrial Reference Systems – Part 4: Prac2cal Considera2ons for Accurate Posi2oning Modern Terrestrial Reference Systems—Part 4: Practical Considerations for Accurate Positioning Dr. Richard A. Snay and Dr. Tomás Soler P rior to the space-age, people primarily used terrestrial techniques like triangulation and/or trilateration to position points. In those days, they had essentially only one choice for a nationwide reference frame; namely, NAD 27. To position new points, a person would measure distances and angles that related the unknown positional coordinates of the new points to the known coordinates of some pre-existing terrestrial control points. More often than not, these known coordinates were referred to NAD 27. Hence, calculated positions for the new points were automatically referred to NAD 27. In the 1970s, people started using Earth-orbiting satellites for positioning points. In particular, before GPS became operational, a number of people used the Doppler satellite system, known as TRANSIT, to position points with an accuracy of several meters relative to the geocenter. Now people use GPS to posi- tion points even more accurately. Hence, satellites have become flying control points whose time-dependent positions are well known thanks to diligent work by several institutions. Currently, GPS satellite orbits are available in appropriate realizations of both WGS 84 and ITRS, but not in any NAD 83 realization. Confusion Can Be Introduced Techniques that position new points by using only satellites as control automatically yield positional coordinates that are referred to the same reference frame as that used for the orbits, either some realization of WGS 84 or some realization of ITRS. Satellite-only positioning techniques, however, do not currently enable the centimeter-level positioning accuracy that is possible with techniques, like the static differential carrier phase GPS technique, that involve using both satellite and pre-existing terrestrial points as control. The use of an integrat- Figure 5: GPS stations defining the National Spatial Reference System: NAD 83 (NSRS) ed approach, however, introduces confusion when the satellite orbits are referred to one reference frame and the terrestrial control points are referred to another, as the newly computed positions will be referred to some ambiguous hybrid reference frame. Although this hybrid reference frame will approximate the reference frame of the terrestrial control points, the error of this approximation at a given point depends on many factors including the distances and directions from this point to the various terrestrial control points being used as well as the magnitude and orientation of the vector connecting the origins of the two reference frames. For the case of a single terrestrial control point referred to NAD 83 with the GPS orbits referred to ITRF96, the error of this approximation at a point will grow less than 1 cm for every 100 km of distance to the terrestrial control point. Hence, for accurate positioning, people should use the same reference frame for both the orbits and the terrestrial control points, especially if the distance to the nearest terrestrial control point is large. If for some reason the available orbits are expressed in one reference frame while the terrestrial control is expressed in another, then the positions of the terrestrial control points should ideally be transformed into the given reference frame of the orbits, as may be accomplished, for example, by using the HTDP software. Alternatively, one could transform the orbits to the reference frame of the terrestrial control points, but this option is likely to involve more computations. Moreover, the software being used to process GPS data may require the orbits to be expressed in a realization of a specific reference system. Thus, it is usually better to transform the terrestrial control points rather than to transform the orbits. Now, once the orbits and the terrestrial control are expressed in a common reference frame, the computed coordi- COPYRIGHT PROFESSIONAL SURVEYOR • April 2000 • All Rights Reserved 1 REFERENCE SYSTEMS nates of the newly positioned points will also be referred to this reference frame. Hence, if people need these positional coordinates to be expressed relative to some other reference frame, then they will need to transform these coordinates. Again, the HTDP software will serve this purpose. For rigorous computations, the epoch date of the positional coordinates of the terrestrial control should agree with the date that the GPS observations were performed. This agreement is especially important when computations are performed in an ITRS realization because terrestrial points are moving relative to this reference system. As previously mentioned, ITRF96 velocities have magnitudes ranging between 10 and 20 mm/yr in the coterminous United States, and these magnitudes are even higher in Alaska and Hawaii. If velocities at the control points are known, then equation (2) may be applied to convert the positional coordinates of these points from their given epoch date to the date that the GPS observations were performed. If velocities of these control points are unknown, then these velocities may be predicted using the HTDP software. sites have been positioned with great accuracy, as they form the foundation of the National Spatial Reference System. Each site contains a geodetic-quality GPS receiver whose carrier phase and code range measurements are transmitted to NGS headquarters in Maryland. NGS then makes these data freely available via the Internet. In particular, people may download CORS data either via Use of Precise Orbits Recommended As previously implied, we are recommending the use of highly precise postfit GPS orbits expressed in ITRS coordinates for accurate GPS positioning. The International GPS Service (IGS) freely distributes such orbits through their website http://igscb.jpl.nasa.gov/. The IGS orbits are the result of computational efforts involving seven different institutions located in four different countries: Canada, Germany, Switzerland, and the United States. Three of these seven institutions are U.S. based: the Jet Propulsion Laboratory, Scripps Institute of Oceanography, and NGS. Each of the seven institutions computes GPS orbits essentially independently, and then IGS rigorously combines the seven solutions to produce the orbits that they distribute. Also, the NGS-derived postfit orbits are available at www.ngs.noaa.gov/GPS/GPS.html Finally for accurate positioning, sites from the National CORS system provide good terrestrial control. These CORS 2 COPYRIGHT PROFESSIONAL SURVEYOR • April 2000 • All Rights Reserved REFERENCE SYSTEMS anonymous FTP (file transfer protocol) using the address ftp://www.ngs. noaa.gov/cors/ or through the World Wide Web using the address http://www.ngs.noaa.gov/CORS/. Furthermore, people may pose CORS-related questions to NGS via the email address [email protected]. Whether using CORS or other sites as terrestrial control, it is usually best to include several points for the sake of redundancy and to suppress those systematic errors that grow as a function of distance. The Species of "Origins" In 1859, Charles Darwin published his revolutionary book, The Origin of Species, in which he documented evidence for the theory of how various forms of life evolve to better adapt to their environment. Inasmuch as this theory of evolution applies to humans, it may also apply to the products that humans develop. In particular, the theory of evolution may apply in large measure to terrestrial reference systems, as these human artifacts evolve to adapt to our knowledge of our environment and to become commensurate with our ability to position points with ever increasing accuracy. In this series of articles, we have discussed how three particular species of reference systems—NAD 83, WGS 84, and ITRS—have evolved over the past couple of decades. Surely, they will continue to evolve into the future. Indeed, U.S. and Canadian representatives are already planning to introduce a new realization of NAD 83. The U.S. geospatial community will come to know this new realization as NAD 83 (NSRS) where NSRS is an acronym for National Spatial Reference System. NAD 83 (NSRS) will serve to supercede the conglomeration of regional reference frames that comprise NAD 83 (HARN). In particular, NAD 83 (NSRS) will incorporate newly computed positional coordinates for all HARN control points, as well as other control points, so that these new positions will be consistent with adopted CORS positions (Figure 5). Currently, horizontal discrepancies as large as 7 cm exist between NAD 83 (HARN) positions of control points and their idealized NAD 83 (CORS96) positions. Significantly greater discrepancies exist in the ver- tical dimension, because the accuracy of ellipsoidal heights measured during the earlier HARN surveys compares poorly relative to today’s height-measuring capability. Consequently to obtain more accurate heights, NGS is cooperating with several organizations to resurvey the HARN in each State. These HARN resurveys reflect NGS’s Height Modernization Initiative to support the public’s growing use of GPS to measure accurate heights. NGS expects to complete the HARN resurveys around 2002. Moreover, NGS will wait until these resurveys have been completed before releasing NAD 83 (NSRS), as this agency plans to combine these new observations rigorously with existing observations to compute accurate ellipsoidal heights that are con- sistent across the country. NGS is also developing more and more accurate geoid models to convert such ellipsoidal heights to appropriate orthometric heights. Additional details about this forthcoming NAD 83 realization may be found at the Internet address: http://www.ngs.noaa.gov/initiatives/new _reference.shtml. DR. RICHARD A. SNAY is Manager of the National Continuously Operating Reference Station (CORS) program and a geodesist with the National Geodetic Survey. DR. TOMÁS SOLER is Chief, Global Positioning System Branch, Spatial Reference Systems Division, National Geodetic Survey. Transformation Parameters from ITRF96 to NAD83 (CORS96) In the summer of 1998, NGS and Canada’s Geodetic Survey Division adopted the following parameters for transforming positions in North America from ITRF96 to NAD 83 (CORS96) via equation (1) : For the three shifts: Tx = 0.9910 m Ty = -1.9072 m Tz = -0.5129 m. For the scale factor: s = 0.0 (unitless). For the three rotations (counterclockwise sense positive): Rx = [25.79 + 0.0532 • (t - 1997.0)]• mr radians Ry = [ 9.65 - 0.7423 • (t -1997.0)]• mr radians Rz = [11.66 - 0.0316 • (t - 1997.0)]• mr radians. In the above equations, mr = 4848.13681• (10**-12) is the conversion factor from milli-arcseconds to radians; t is the “epoch date” in years (e.g., 1999.3096 0h UTC, 23 April 1999). Recall that the epoch date is the date to which the given positions correspond. Note that the rotations, Rx, Ry, and Rz, are time dependent because the North American tectonic plate moves relative to ITRF96 while this plate is essentially stable relative to NAD 83 (CORS96). Because ITRF94 and ITRF97 have the same origin, orientation, and scale as ITRF96, these same parameters are applicable for transforming these other two ITRS realizations to NAD83 (CORS96). On the other hand, these parameters are not applicable for transforming ITRF93 and earlier ITRS realizations to NAD 83 (CORS96). COPYRIGHT PROFESSIONAL SURVEYOR • April 2000 • All Rights Reserved 3 Módulo 11 Notas sobre Agrimensura
© Copyright 2026