1. No category

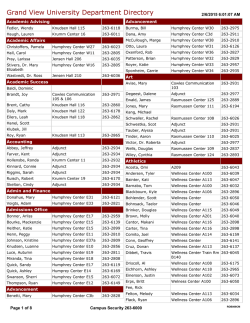
สูตร ตรี โกณ (Trigonometry)
sin2 A + cos 2 A = 1
มุมสองเท่า
sec 2 A − tan2 A = 1
2𝑡𝑎𝑛
sin2A = 2sinAcosA = 1+𝑡𝑎𝑛
2𝐴
cos2A = cos2 A − sin2 A
cosec 2 A − cot 2 A = 1
cos2A = 2cos 2 A − 1
sinA. cosecA = 1
cos2A = 1 − 2sin2 A
1 − tan2 A
cos2A =
1 + tan2 A
cosA. secA = 1
tanA. cotA = 1
tanA. =
ให้ A + B = 90° ,
1 − cos2A
sinA = ±√
2
sinA
cosA
sinA = cosB
1 + cos2A
cosA = ±√
2
secA = cosecB
tanA. = cotB
มุมติดลบ
มุมสามเท่า
cos3A = 4cos3 A − 3cosA
sin(−A) = −sinA
3tanA − tan3 A
tan3A =
1 − 3tan2 A
cos(−A) = cosA
tan(−A) = −tanA
cot 3 A − 3cotA
cot3A =
3cot 2 A − 1
ผลบวก – ผลต่างของมุม
sin (A+B) = sin A cos B + cos A sin B
sin3A = 3sin A − 4sin3 A
มุมครึ่ งเท่า
sin (A-B) = sin A cos B - cos A sin B
sin
tanA+tanB
tan (A+B) = 1−tanA
tanB
tanA−tanB
tan (A-B) = 1+tanA
tanB
cot (A+B) = cotAcotB−1
cotB+ cotA
cotAcotB+1
cot (A-B) = cotB− cotA
2
= ±√
2
A
1 + cosA
= ±√
2
2
tan
A
1 − cosA
= ±√
2
1 + cosA
A
sinA
2
1+cosA
tan =
ผลคูณ
1−cosA
cos
cos (A+B) = cos A cos B - sin A sin B
cos (A-B) = cos A cos B + sin A sin B
A
=
1−cosA
sinA
2sinAcosB = sin(A + B) + sin(A − B)
2cosAsin B = sin(A + B) − sin(A − B)
2cosAcosB = cos(A + B) + cos(A − B)
2sinAsinB = cos(A − B) − cos(A + B)
สูตรตรีโกณ(ต่อ)
ให้ มมุ A + B + C = 180 °
ผลบวก→ผลคูณ
A
sinA + sinB = 2sin
(A + B)
(A − B)
cos
2
2
sinA − sinB = 2cos
(A + B)
(A − B)
sin
2
2
(A + B)
(A − B)
cosA + cosB = 2cos
cos
2
2
(A + B)
(A − B)
cosA − cosB = −2sin
sin
2
2
ผลต่างกาลังสอง
C
A
เอกลักษณ์ ของอินเวอร์ ส (Arc)
arcsin x + arccos x =
π
arctan x + arccot x =
π
2
2
2
x+y
arcsin x = arccos √1 − x 2
arccos x = arcsin √1 − x 2
2x
y = a sinθ + b cosθ คือ ± √a2 + b 2
sinA
π
arctax x + arctan y = arctan(1−xy)
ค่าต่าสุดหรื อสูงสุดของฟั งก์ชนั
=
C
tanA + tanB + tanC = tanA tanB tanC
cos(A + B)cos(A − B) = cos 2 A − sin2 B
a
B
cosA + cosB + cosC = 1 + 4sin 2 sin 2 sin 2
arccosec x + arcsec x =
sin(A + B)sin(A − B) = sin2 A − sin2 B
กฎของไซน์
B
sinA + sinB + sinC = 4cos 2 cos 2 cos 2
b
sinB
=
c
2arctan x = arctan(1−x2)
arcsin (sinx) = x
sinC
sin(arcsin x) = x
กฎของโคไซน์
arccos (cosx) = x
a2 = b2 + c 2 − 2bc cosA
cos(arccos x) = x
b2 = a2 + c 2 − 2ac cosB
arctan (tanx) = x
c 2 = b2 + a2 − 2ab cosC
tan(arctan x) = x
กฎของโปรเจกชัน
Function
Y =arcsin x
a = b cosC + c cosB
Y =arccos x
b = a cosC + c cosA
Y =arctan x
c = a cosB + b cosA
Y=arccsc x
พื ้นที่สามเหลี่ยม
Y =arcsec x
1
1
1
∆ABC = 2 absinC = 2 bcsinA = 2 acsinB
Y =arccot x
โดเมน
[-1,1]
[-1,1]
R
(-,1][1,)
(-,1][1,)
R
เรนจ์
π π
[− , ]
2 2
[0,π]
π π
(− , )
2 2
π
[− , 0)(0 , ]
π
2
,π
2
[0, − 2 ) ( 2 , ]
π
(0,)
ชื่อ..........................................ชัน้ ...........เลขที่....................
สูตร ตรี โกณ (…………………………….)
1.sin (A+B) = ………………………………...........
16. sinA − sinB =…………………………………..
2.sin (A-B) = ………………………………………..
17. sin2A = ………………………………………..
3.cos (A+B) =…………………………..…………...
หรื อ18. sin2A = ……………………………………..
4.cos (A-B) = ……………………………..…………
19.cos2A =……………………………………………
5.tan (A+B) =………………………..……….……..
หรื อ20.cos2A =….……………………………………
6. tan (A-B) =.…………………………..………….
หรื อ 21.cos2A =…………………………………..…..
7.cot (A+B) =……………………………………….
หรื อ 22.cos2A =………………………………………
8. cot (A-B) =………………………………………..
23. tan2A =………..…………………………………
9. 2sinAcosB =.……………………………………..
24. cot2A=………….………………………………...
10. 2cosAsin B = .…………………………………
25. sin
11. 2cosAcosB = ..…………………………………
26. cos
12. 2sinAsinB = ……………………………………
27. tan
A
13. cosA + cosB =………………………………...
28. cot
A
14. cosA − cosB =………………………………..
29. sin3A =……………..…………………………….
15. sinA + sinB =………………………………...
30. cos3A = ………………………………………….
A
2
A
2
2
2
=…………..…………….………………….
=………….……………………………….
=…………….……………………………..
=………..…………………………………..
ยังมีอกี นะครับ++++