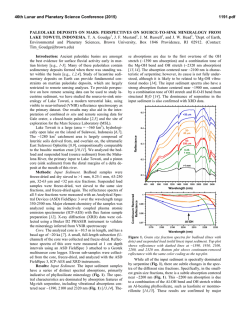
46th Lunar and Planetary Science Conference (2015) 1325.pdf CUMULATIVE VOLUME OF WATER REQUIRED TO CARVE THE NOACHIAN VALLEY NETWORKS. E. N. Rosenberg1 and J. W. Head1, 1Department of Earth, Environmental, and Planetary Sciences, Brown University, Providence, RI 02912. Introduction: The Martian valley networks, a majority of which ceased activity by the Noachian-Hesperian boundary [1], represent an excellent source of information about the climate of ancient Mars. Their formation required sustained flow of noncatastrophic fluxes of liquid water, which would not be possible on present-day Mars [2]. However, there are several competing hypotheses as to the mechanism that supplied the water [2-4]. Here, we first perform an order of magnitude estimate of the volume of water required to carve the valleys, which puts a constraint on plausible hypotheses for the source of the water that eroded the valley networks. Then we develop a method for estimating the cumulative water volume required to erode a particular valley network, which, when implemented, will place further constraints on plausible formation hypotheses. Methods: The required cumulative volume of water depends on the strength of the flow through each valley network. A very weak flow is highly inefficient at transporting sediment, so large quantities of water would be required to produce the observed erosion. A strong flow is more efficient, so less water would be required [5]. We define flow strength 𝛼 as 𝜏/𝜏𝑐 , where 𝜏 is the shear stress between the bottom of the flow and the bed and 𝜏𝑐 is the critical value of this parameter required to initiate transport of 50% of the sediment particles (those with diameters smaller than the median diameter 𝐷50 ). 𝛼 is equivalent to 𝜏 ∗ ⁄𝜏𝑐∗ , where 𝜏 ∗ is a dimensionless ℎ𝑆 parameter called the Shields stress, which is equal to , 𝐷𝑅 where ℎ is the hydraulic radius (or approximately the flow depth when the channel width ≫ depth), 𝑆 is the slope, 𝐷 is a representative grain size (here 𝐷50 ), and 𝑅 is the submerged specific gravity of the sediment (equal to 𝜌𝑠 /𝜌 − 1, where 𝜌𝑠 and 𝜌 are, respectively, the densities of sediment and water). To estimate 𝜏𝑐∗ , we use Equation 2-59a from [5]: −0.6 −0.6 𝜏𝑐∗ = 0.22 𝑅𝑒𝑝 + 0.06 exp(−17.77 𝑅𝑒𝑝 ), where 𝑅𝑒𝑝 ≔ √𝑔𝑅𝐷𝐷/𝜈, in which 𝑔 is the acceleration due to gravity and 𝜈 is the kinematic viscosity of water. We take this equation to account for all of the effects of gravity. To see this, note that the fluid flux is given by 𝑄𝑓 = 𝑈𝑊ℎ = √8⁄𝑓 √𝑔ℎ𝑆𝑊ℎ, where 𝑈 is the mean flow speed, 𝑊 is the flow width, ℎ is the mean flow depth, and 𝑓 is the Darcy-Weisbach friction factor, which is a function of 𝐷 and ℎ (see, for example, Equations 2-29 and 2-30 of [5]). Similarly, the bedload sediment flux is given by 𝑄𝑏 = 𝜙𝑏 𝑊√𝑅𝑔𝐷3 , where 𝜙𝑏 , called the Einstein parameter, is a function of 𝜏 ∗ and 𝜏𝑐∗ (see Equation 2-89 of [5] and the subsequent examples). Thus, when 𝑄𝑓 and 𝑄𝑏 are divided, the √𝑔 cancels, and the only dependence on 𝑔 is through 𝜏𝑐∗ . This dependence is very weak. For reasonable values of R, D, and 𝜈, 𝜏𝑐∗ only decreases by at most about 10% in going from Earth gravity to Mars gravity. In our analysis here, we include the suspended sediment, in addition to the bedload sediment, but we assume that the dependence on 𝑔 is still primarily through 𝜏𝑐∗ . Note also that, using many of the equations for 𝜙𝑏 given in [5], the ratio 𝑄𝑓 /𝑄𝑏 is primarily a function of 𝛼. Thus, we use this as our measure of flow strength. From measurements of terrestrial rivers reported in the literature [6], we find an empirical relationship between the ratio (volumetric fluid flux)/(volumetric sediment flux) = 𝑄𝑓 /𝑄𝑠 and the flow strength 𝛼. We then multiply this ratio by an estimate of the total eroded volume of the valley networks in order to estimate the volume of water that would be required for different flow strengths. Fluid/Sediment Flux Ratio: By plotting the data compiled by [6] (after converting the sediment fluxes to volumetric fluxes rather than mass fluxes and eliminating data points which infinite values for the ratio), we obtain the following empirical relationship between 𝛼 and 𝑄𝑓 /𝑄𝑠 : 𝑄𝑓 −0.1778 = 𝑒 11.95𝛼 . 𝑄𝑠 As seen in Figure 1, the predicted ratios are accurate to about an order of magnitude in either direction. Figure 1: Empirical relationship between 𝑞𝑓 /𝑞𝑠 and 𝛼 (top) and histogram showing error of regression curve (bottom). 46th Lunar and Planetary Science Conference (2015) Thus, for 𝛼 = 3, we predict a fluid/sediment flux ratio on the order of 10,000 (or the range 1,000 –100,000 within error). Similarly, for 𝛼 = 10, we predict a ratio on the order of 1000, and for 𝛼 = 100, we predict a ratio on the order of 100. For comparison, in the Mississippi River, 𝛼 varies between ~2 at the shallowest point (1 m deep at headwaters) and ~120 at the deepest point (60 m deep at New Orleans) (calculated using data from [78]). Similarly, for the Colorado River, 𝛼 varies between ~130 at the shallowest point (2 m) and ~1000 at the deepest point (30 m) (calculated using data from [910]). Water Volume: Based on data provided by Williams and Phillips [11-12] and Hoke, et al. [13], we estimate the total volume of sediment eroded out of the valley networks to be at least, and on the order of, 104 km3 . To calculate the cumulative volume of water required to produce this erosion requires knowledge of time-varying fluid fluxes and flow strengths in each of the valleys. However, to make an order of magnitude estimate, we assume a representative value of 𝛼 to be between 3 and 100. Hence, we favor cumulative water volumes on the order of 106 − 108 km3 , corresponding to global equivalent layers on the order of 10 m – 1 km. With the error on the empirical fit, this interval becomes 1 m – 10 km. Note that this volume of water need not have existed on Mars at any one time; it represents the cumulative volume, including recycled water. For comparison, using the sediment volumes and estimated fluid and sediment fluxes from [13] leads to a required water volume of ~10 km GEL. However, the methods used in [13] to estimate the flow depth rely on terrestrial analogies and assumptions about stability rather than estimates of the instantaneous fluid flux into the river, which is what physically determines the flow depth. We suggest that using the latter would be a more reliable method. We note that if the erosion was into bedrock, more water would have been required, as the flow must also do work to break the sediment particles loose [14]. Next Steps: The globally representative flow strength 𝛼 is poorly constrained. Thus, a better approach would be to estimate the volume of water required to erode particular valley networks. This is a function of (1) the geometry of the valley, (2) the sediment grain size and density, and (3) the hypothetical volumetric fluid flux into the valley, which together determine the flow depth h and flow strength 𝛼. Thus, they determine, to an order of magnitude, the water volume required to erode the valley. (1) can be measured from stereo-image DEMs and MOLA data [11-13]. (2) can be estimated from what is known of the minerology and geologic history of Mars and from lander/rover data. (3) is dependent on the hypothetical source of the water that carved 1325.pdf the valleys. Thus, this method can be used to check the consistency of the hypotheses in question, such as rainfall in a warm and wet climate [2], meltwater in a lateNoachian icy highlands model [3], or rainfall induced by giant impacts [15]. For example, if a hypothesis predicts a low instantaneous fluid flux, then large cumulative fluid volumes would be required. But if these volumes are too large to have been provided by the hypothetical mechanism in a reasonable amount of time, then this is reason to reject the hypothesis. References: [1] C. Fassett and J. W. Head, Icarus, 195, 61 (2008). [2] R. Craddock and A. Howard, J. Geophys. Res., 107, no. E11, 5111 (2002). [3] I. Halevy and J. W. Head, Nature Geoscience, 7, 865 (2014). [4] T. Segura, et al., J. Geophys. Res, 113, E1107 (2008). [5] M. Garcia, "Sediment Transport and Morphodynamics," in Sedimentation Engineering: Processes, Measurements, Modeling, and Practice, Reston, Virginia, American Society of Civil Engineers (ASCE) (2008), 21-163. [6] T. Cleveland, et al., "Technical Memorandum 0-6549: Hydraulic Performance of Staggered-Barrel Culverts for Stream Crossings: Literature Review," Texas Tech University (2010). [7] L. Moya and G. Haglund, "Mississippi River Resource Page," Caleuche (2014). [Online]. [Accessed 2014]. [8] C. F. Nordin and B. S. Queen, "Particle Size Distributions of Bed Sediments Along the Thalweg of the Mississippi River, Cairo, Illinois, to Head of Passes, September 1989," US Army Corps of Engineers: Lower Mississippi Valley Division, Vicksburg, MS, 1992. [9] B. Ribokas, "Grand Canyon Explorer: The Colorado River" (2000). [Online]. [Accessed 2014]. [10] D. M. Rubin and e. al., "20,000 Grain Size Observations from the Bed of the Colorado River, and Implications for Sediment Transport Through the Grand Canyon," in 2nd Joint Federal Interagency Conference on Sedimentation and Hydrologic Modeling, Las Vegas, Nevada (2010). [11] R. Williams and R. Phillips, J. Geophys. Res, 106, 23737 (2001). [12] R. Williams, personal communication (2014). [13] M. Hoke and et al., Earth and Planetary Science Letters, 312, 1 (2011). [14] M. Lamb, et al., J. Geophys. Res, 113, F03025 (2008). [15] T. Segura, B. Toon and A. Colaprete, J. Geophys. Res, 113, E1107, (2008). Acknowledgements: ENR received support from a Brown University Undergraduate Teaching and Research Award (UTRA). ENR and JWH are currently supported by a Mars Express/NASA Project Extended Mission grant. This abstract benefited from the helpful comments of Tim Goudge.