1. Educación

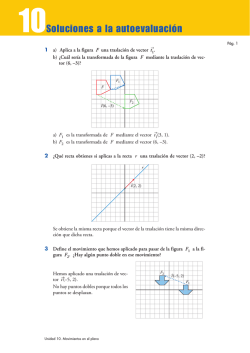
unidad 11 Transformaciones geométricas
Cómo dibujar ángulos de 60° con regla y compás
La cuerda de un arco de 60° (apertura del compás) es igual al radio
con que se ha trazado.
Veamos el proceso:
Así se traza un ángulo de 60° de vértice V y lado l.
l
V
l
V
l
V
60°
actividades
1 Dibuja en tu cuaderno, ayudándote del compás, algunos ángulos de 60°.
Página 1
unidad 11 Transformaciones geométricas
Cómo trazar ángulos rectos sobre papel cuadriculado
(con los lados no paralelos a las líneas de la cuadrícula)
Observa cómo se traza, en cada caso, un ángulo recto de vértice V y lado l :
a
c
b
l
l
l
90°
90°
V
90°
V
V
El caso a) es muy fácil. Para los casos b) y c), conviene tener en cuenta la igualdad de los
triángulos señalados que, como es natural, en la práctica no hace falta señalar expresamente.
actividades
2 Dibuja en tu cuaderno, apoyándote en la cuadrícula, varios ángulos de 90°.
Página 2
unidad 11 Transformaciones geométricas
Cómo representar puntos y rectas en un sistema
de ejes cartesianos
Las expresiones analíticas de las rectas son ecuaciones de primer grado en x e y. Por ejemplo:
y = 2x – 3, y = x, y = 5, x = 0, y = 0
•Para representar una recta, basta con obtener dos de sus puntos.
y = 2x + 3
x = 0 8 y = 3
x = 2 8 y = 7. La recta pasa por (0, 3) y (2, 7)
•Hay algunas rectas muy sencillas que deberías ser capaz de reconocer de un solo golpe de
vista.
y=2
y=x
x = 0 es el eje Y
y = 0 es el eje X
actividades
3 Representa:
a) y = x – 4
b) y = 5x – 10
c) y = 4
d) x = –3
e) y = –x
Página 3
unidad 11 Transformaciones geométricas
Figuras simétricas. Ejes de simetría
En la naturaleza, en la técnica, en el arte, en nuestro mundo cotidiano estamos rodeados de
figuras simétricas. Su estudio es interesante.
E J E DE SIMETRÍA DE UNA FIGURA
Una figura plana es simétrica respecto a una recta si al doblarla por dicha recta las dos
mitades coinciden.
e
A
A'
B
B'
En una simetría respecto a un eje o simetría axial:
• La recta e se llama eje de simetría.
• A y A' son simétricos respecto a e, porque e es la mediatriz del segmento AA'. Lo mismo ocurre con B y B'.
•C
ada punto del eje es simétrico de sí mismo: C = C'.
C = C'
La simetría de las figuras planas se aprecia a simple vista y suele ser sencillo identificar su
eje de simetría. No obstante, puede ser de gran ayuda valerse de un espejo para comprobar si una cierta recta es o no eje de simetría de una figura.
Las siguientes figuras tienen dos, tres y cinco ejes de simetría, respectivamente:
90
36
60
Si una figura tiene n ejes de simetría, estos se cortan en un punto, y cada dos ejes conti180°
.
guos forman un ángulo de
n
actividades
1 Señala todos los ejes de simetría de cada una de las siguientes figuras.
a)
b)
c)
d)
e)
Página 4
UNIDAD 11 Transformaciones geométricas
2. Iniciación: traslaciones
8
1 Aplica a la figura F y a la recta r una traslación de vector t (8, 4). ¿Qué le sucede a r ?
8
2 Aplica a la circunferencia C una traslación de vector t (5, –1).
3 Escribe las coordenadas del vector que corresponde a la traslación que transforma F en F´.
8
t
(
,
)
Pág. 1 de 1
UNIDAD 11 Transformaciones geométricas
3. Iniciación: giros
Pág. 1 de 1
1 Aplica un giro de centro O y ángulo a = 90° al triángulo ABC.
2 Aplica un giro de centro O y ángulo a = 90° a la circunferencia de centro (3, 0) y radio 2 y a la circunferencia de centro O y radio 5. ¿Qué le ocurre a esta última?
3 Hemos aplicado al triángulo ABC un giro de centro O y ángulo a y hemos obtenido la figura A'B'C'.
¿Cuál es el ángulo de giro?
a=
UNIDAD 11 Transformaciones geométricas
4. Ampliación: ejes de simetría y centro
de giro en las figuras planas
Pág. 1 de 3
En la naturaleza, en la técnica, en el arte, en nuestro mundo cotidiano,
estamos rodeados de figuras simétricas. Su estudio es interesante.
Simetría respecto a un eje (simetría axial)
Si se pliega una hoja de papel, se recorta cualquier motivo y se despliega, aparece una figura simétrica respecto
a un eje.
Cada mitad es como la imagen en un espejo de la otra mitad.
En una simetría respecto a un eje o simetría axial:
• La recta e se llama eje de simetría.
• A y A' son simétricos respecto a e, porque e es la mediatriz del segmento AA'.
Lo mismo ocurre con B y B'.
• Cada punto del eje es simétrico de sí mismo: C = C'.
La simetría de las figuras planas se aprecia a simple vista y suele ser sencillo identificar su eje de simetría. No
obstante, puede ser de gran ayuda valerse de un espejo para comprobar si una cierta recta es o no eje de simetría de una figura.
UNIDAD 11 Transformaciones geométricas
4. Ampliación: ejes de simetría y centro
de giro en las figuras planas
Pág. 2 de 3
Simetría respecto a un punto (simetría central)
La figura de la derecha es simétrica. Sin embargo, no tiene ningún
eje de simetría (se puede comprobar viendo que no es posible
reproducir una mitad mirando con un espejo la otra mitad).
Se trata de una simetría respecto a un punto o simetría central.
En una simetría respecto a un punto o simetría central:
• O se llama centro de simetría.
• A y A' son simétricos respecto de O, porque O es el punto medio del
segmento AA'. Lo mismo ocurre con B y B'.
Una simetría central es un giro de 180°.
Figuras con varios ejes de simetría
Las figuras de la derecha tienen más de un
eje de simetría.
La primera figura tiene dos ejes de simetría.
La segunda tiene tres. La tercera, cuatro.
Figuras con centro de giro
Si se calca la figura de la derecha (sin colorearla) en papel transparente, se re c o rta, se
superpone a esta misma, se pincha con un alfiler en O y se hace girar, se podrían
o b s e rvar tres posiciones distintas en las que las dos figuras (la original y la copia)
coinciden. Por eso se dice que esta figura tiene un c e n t ro de giro, O, de orden 3.
Se comprueba, siguiendo el mismo procedimiento de arriba, que esta otra figura
tiene un centro de giro de orden 4.
Esta figura se puede construir copiando cuatro veces el módulo de la derecha,
girándolo cada vez 90° respecto de la posición anterior.
Una figura plana se dice que tiene un centro de giro, O, de orden n cuando, al girarla alrededor de O, coincide consigo misma n veces, contando la posición inicial.
En tal caso, la figura puede descomponerse en n trozos idénticos (módulos), cada uno correspondiente a un
ángulo de 360°: n.
UNIDAD 11 Transformaciones geométricas
4. Ampliación: ejes de simetría y centro
de giro en las figuras planas
Pág. 3 de 3
Relación de los giros con las simetrías centrales
Estas figuras tienen, todas ellas, centro de giro. Sus órdenes son, respectivamente, 2, 3, 4 y 6.
La segunda no tiene centro de simetría, las restantes, sí. Se comprueba, reflexionando sobre estas figuras y sobre
otras con centro de giro, que las figuras con centro de giro tienen centro de simetría si el orden del giro es par.
Relación de los giros con las simetrías axiales
Observando estas figuras se razona la siguiente afirmación:
1 eje de
simetría
2 ejes de
simetría
3 ejes de
simetría
4 ejes de
simetría
5 ejes de
simetría
6 ejes de
simetría
Las figuras con un único eje de simetría no tienen centro de giro.
Si una figura tiene n ejes de simetría, estos se cortan en un punto que es centro de giro de orden n.
UNIDAD 11 Transformaciones geométricas
5. Iniciación: simetrías
Pág. 1 de 1
1 Aplica al triángulo ABC y a la recta r una simetría cuyo eje sea el eje Y. ¿Qué para con r ?
2 Aplica a la figura F una simetría de eje e.
3 Escribe SÍ o NO para indicar si las siguientes figuras permanecen o no invariantes al aplicarles una simetría
cuyo eje sea el eje Y.
• Circunferencia de centro (0, 2) y radio 1. 8
• Triángulo de vértices (0, 0), (2, 0) y (1, 2). 8
• Triángulo de vértices (–1, 0), (0, 2) y (1, 0). 8
UNIDAD 11 Transformación de movimientos
6. Iniciación: composición de movimientos
Pág. 1 de 1
8
1 Llamamos T a la traslación de vector t (5, 2) y S a la simetría de eje e. Obtén la transformada de la figura F mediante T seguido de S.
8
2 Llamamos T a la traslación de vector t (2, 3) y G al giro de centro O(0, 0) y ángulo a = 90°. Obtén la
transformada de la figura F mediante T seguido de G.
3 Llamamos S1 a la simetría de eje e1 y S2 a la simetría de eje e2. Obtén la transformada de la figura F
mediante S1 seguido de S2.
UNIDAD 11 Transformación de movimientos
7. Ampliación: composición de movimientos
Pág. 1 de 3
Se llama composición de dos transformaciones, T1 y T2, a una nueva transformación, que se designa
T2°T1, que transforma cada punto del siguiente modo:
T1
T2
P Ä
Ä8 P' Ä
Ä8 P''
T2°T1
(T2°T1) (P) = T2(P' ) = P''
Es decir, para transformar un punto P o una figura F
mediante T2°T1, lo transformamos mediante T1, y el resultado, mediante T2.
Para componer T1 con T2 ponemos T2° T1. Es decir, T2° T1 se lee de derecha a izquierda.
Veamos sobre un ejemplo cómo se componen movimientos.
8
Definimos un giro G de centro O(0, 0) y ángulo a = 90° y una traslación T de vector t (4, 2). Veamos
qué resulta al transformar un triángulo F de vértices A(0, 2), B(4, 1) y C(2, –5) mediante la transformación G °T.
Primeramente se aplica T y, sobre la figura obtenida, se aplica G.
Veamos ahora qué resulta al transformar la misma figura F mediante T° G. Primeramente se aplica G y,
sobre la figura obtenida, se aplica T.
Se puede observar que en ambos procesos el triángulo F se transforma en otro triángulo con la misma forma.
Sin embargo, los triángulos F'' y F2 están situados en lugares distintos, es decir, no es lo mismo G °T que
T° G.
UNIDAD 11 Transformación de movimientos
7. Ampliación: composición de movimientos
Resultados interesantes al componer movimientos
COMPOSICIÓN
DE TRASLACIONES
Al componer dos traslaciones de vec8
8
tores t1 y t2, el resultado es otra tras8
8
lación cuyo vector es la suma t1 + t2.
COMPOSICIÓN
DE GIROS DEL
MISMO CENTRO
El resultado de componer dos giros
con el mismo centro, O, y ángulos
a y b, es un nuevo giro de centro O
y ángulo a + b.
Si a y b son de sentidos opuestos, la
amplitud de a + b es la diferencia de
sus amplitudes.
COMPOSICIÓN
DE SIMETRÍAS
AXIALES CON EJES
PARALELOS
El resultado de componer dos simetrías, S1 y S2, de ejes e1 y e2 paralelos, es una traslación T, cuyo vec8
tor t es perpendicular a los ejes y
cuya longitud es el doble de la distancia que los separa, 2d.
8
(El sentido de t es el que va de e1 a e2.)
COMPOSICIÓN
DE SIMETRÍAS
AXIALES CON EJES
QUE SE CORTAN
El resultado de componer dos simetrías, S1 y S2, de ejes e1 y e2 que
se cortan bajo un ángulo a, es un giro de ángulo 2a y centro el punto de
corte de los dos ejes.
El ángulo a que forman los ejes es
un ángulo orientado.
`
e1(a
e2 =es el menor de los ángulos que forman
los ejes al cortarse y tiene el sentido de e1
a e2.)
En general, el resultado de componer dos movimientos es otro movimiento:
• Si ambos son deslizamientos, el resultado es un deslizamiento.
• Si ambos son movimientos inversos, el resultado es un deslizamiento.
• Si uno es directo y el otro inverso, el resultado es un movimiento inve r s o.
Pág. 2 de 3
UNIDAD 11 Transformación de movimientos
7. Ampliación: composición de movimientos
Pág. 3 de 3
Veamos dos ejemplos de composición de movimientos.
Ejemplo 1
8
8
T1 y T2 son traslaciones de vectores respectivos t1(6, 4) y t2(–5, 5).
F es un triángulo de vértices A(7, 0), B(9, 4) y C(12, –2).
Hemos pasado del triángulo ABC al A'B'C' por la traslación T1. Y
del A'B'C' al A''B''C'' mediante la traslación T2.
Pero podríamos haber pasado directamente de ABC a A''B''C'' me8
8
diante la traslación T2°T1, cuyo vector es t1 + t2 (1, 9).
Ejemplo 2
Se consideran las simetrías S1 y S2 cuyos ejes e1 y e2 son las rectas e1 : y = 4 y e2 : y = x.
F es un triángulo de vértices A(8, 0), B(12, 0) y C(11, 2).
En la siguiente gráfica se puede observar cómo se transforma F mediante S2°S1 .
El resultado final (paso del triángulo negro al rojo) es un giro de centro O'(4, 4) y ángulo 90° (positivo, pues es contrario al sentido de las
agujas del reloj).
Y en esta otra cómo se transforma F mediante S1°S2 .
El resultado final, en este otro caso, es un giro de centro O' y ángulo
–90°.
UNIDAD 11 Transformaciones geométricas
8. Ampliación: mosaicos
Pág. 1 de 4
1 Este mosaico, formado por hexágonos, cuadrados y triángulos equiláteros, se puede construir uniendo balsodas iguales a la que tienes a la derecha. Complétalo.
2 También puedes construirlo uniendo piezas más pequeñas, como las que aquí tienes. Inténtalo.
UNIDAD 11 Transformaciones geométricas
8. Ampliación: mosaicos
Pág. 2 de 4
3 Este mismo mosaico puede construirse utilizando piezas rectangulares. Inténtalo con esta.
4 Hay muchas traslaciones que hacen coincidir el mosaico consigo mismo. Aquí te hemos propuesto algunas
de ellas. Colorea algunas piezas del mosaico siguiendo las traslaciones indicadas.
UNIDAD 11 Transformaciones geométricas
8. Ampliación: mosaicos
5 También hay muchos giros que hacen coincidir el mosaioco consigo mismo. Por ejemplo:
• Giros de centro A y ángulos de: 60° ó 120° ó 180° ó 240° ó 300°.
• Giro de centro B y ángulo de 180°.
• Giros de centro C y ángulos de 120° ó 240°.
Colorea algunas piezas del mosaico siguiendo los giros de centro y ángulos indicados.
Pág. 3 de 4
UNIDAD 11 Transformaciones geométricas
8. Ampliación: mosaicos
Pág. 4 de 4
6 Hay muchas simetrías que hacen que el mosaico coincida consigo mismo. Aquí te señalamos tres de ellas y,
en el siguiente gráfico, otras tres. Colorea algunas piezas del mosaico según los ejes de simetría marcados.